Types de base de transformations d'expressions contenant des racines carrées. Utiliser les propriétés des racines lors de la transformation d'expressions irrationnelles, d'exemples, de solutions

Pour utiliser les aperçus de présentation, créez un compte Google et connectez-vous : https://accounts.google.com

Légendes des diapositives :

Aperçu:

Cours d'algèbre en 8e année

sur le thème « Conversion d'expressions contenant des racines carrées »

Professeur de mathématiques: Kiryukhina Yu.A.

Établissement d'enseignement municipal école secondaire du nom. I.A. Pankova s. Golovinchtchino

Année académique 2010-2011

Objectifs:

1. répéter la définition de la racine carrée arithmétique, les propriétés de la racine carrée arithmétique ;
2. consolider les compétences et les capacités de résolution d'exemples sur des transformations identiques d'expressions contenant des racines carrées arithmétiques ;
3. résumer et systématiser les connaissances des étudiants sur ce sujet ;
4. développer des compétences de maîtrise de soi et de contrôle mutuel, un intérêt pour le sujet.

Équipement : projecteur multimédia, tableau blanc interactif, fiches d'évaluation, fiches de test, fiches de devoirs.

Pendant les cours.

I. Moment organisationnel

Aujourd'hui, dans la leçon, nous répéterons les règles pour transformer des expressions contenant des racines carrées, convertir des racines à partir d'un produit, d'une fraction et d'un degré, multiplier et diviser des racines, retirer un facteur du signe racine, mettre un facteur sous le signe racine, amener des valeurs similaires termes et se débarrasser de l'irrationalité dans le dénominateur d'une fraction.La fiche d'évaluation vous aidera à résumer la leçon d'aujourd'hui. Signez vos feuilles et répondez à la première question « Humeur au début du cours » en choisissant l'une des émoticônes.

II. Message du sujet de la leçon

Le sujet de notre leçon est « Conversion d'expressions contenant des racines carrées arithmétiques ». (Diapositive n°1)

Il y a quelque chose dans les mathématiques

Provoquer le plaisir humain.
F. Hausdorff(Diapositive n°2)

III. Travail oral

1) Enquête frontale.(Diapositive n°3)

1. Donnez la définition d’une racine carrée arithmétique. (La racine carrée arithmétique d'un nombre est un nombre non négatif dont le carré est égal à).
2. Énumérez les propriétés de la racine carrée arithmétique. (La racine carrée arithmétique du produit de facteurs non négatifs est égale au produit des racines de ces facteurs. La racine carrée arithmétique d'une fraction dont le numérateur est non négatif et dont le dénominateur est positif est égale à la racine du numérateur divisée par la racine du dénominateur).
3. 2 ? (|x| ).
4. Quelle est la racine carrée arithmétique de x ? 2 , si x≥0 ? xx. -X ).

2) Comptage oral (Diapositive n°4)

Allez, mets les crayons de côté !

Pas de dominos. Pas de stylos. Pas de craie.

« Comptage verbal ! » Nous faisons cette chose

Uniquement par le pouvoir de l'esprit et de l'âme.

Les nombres convergent quelque part dans l'obscurité,

Et les yeux commencent à briller,

Et il n’y a que des visages intelligents.

Parce qu'on compte dans notre tête !

(Diapositive n° 5-9)

1. Supprimez le multiplicateur sous le signe racine :

2. Entrez le multiplicateur sous le signe racine :

3. Carré :

4. Donnez des termes similaires :

IV. Travailler sur le sujet de la leçon

1 ) Travail individuel(Diapositive n°10)

La coccinelle a des taches rouges, jaunes et vertes. Le vert correspond aux tâches de niveau basique, le jaune aux tâches de niveau avancé, le rouge aux tâches de haut niveau. Les étudiants choisissent la tâche à leur propre discrétion. Trois étudiants, ayant reçu une tâche, la résolvent dans leurs cahiers. (Diapositive n° 11-13)

2) Travailler avec un tableau blanc interactif.

Le reste des étudiants résolvent les tâches suivantes :

1. Simplifiez l'expression : a) 4b+4b-4b ; b) 9a+49a-64a ;

B) 63-175+97 ; d) 28a+0,345c-418a+0,01500c.

2. Suivez les étapes et trouvez la bonne réponse : 15-1215-23 , 4+22-2 , 2-32+3 , 3-422 .

Réponses : -1 ; 6-22 ; 27-125;41-242.

3. Libérez-vous de l'irrationalité du dénominateur de la fraction.

une) b5 ; b) 23 ; c) 737 ; d) hache+a.

4. Réduisez la fraction.

a) 5-x2 5+x ; b) un -2a2-2 ; c) 3-33 ; d) a+ba-b.

VI. Référence historique(Diapositive 14-16)

Radix a deux significations : côté et racine. Les mathématiciens grecs, au lieu d’« extraire la racine », disaient « trouver le côté du carré à partir de sa valeur (aire) donnée ».

À partir du XIIIe siècle, les mathématiciens italiens et européens ont désigné la racine avec le mot latin Radix, ou R en abrégé (d'où le terme « radical »).

Mathématiciens allemands du XVe siècle. pour désigner la racine carrée nous avons utilisé le point ·5

Plus tard, au lieu d'un point, ils ont commencé à mettre un diamant 5

Puis Ú 5. Puis le signe Ú et la ligne a commencé à être tracée.

VII. Test (Diapositive n°17, 18)

Le philosophe anglais Herbert Spencer a dit : « Les trésors ne sont pas les connaissances qui se déposent dans le cerveau comme la graisse, les trésors sont ceux qui se transforment en muscles mentaux. »

A ce stade de la leçon, vous devez appliquer vos connaissances pour résoudre des exercices pendant le test.

VI. Examen par les pairs(Diapositive n°19)

Code de réponse correct : Option 1 – 12312, version II - 32132.

VIII. Exercice pour les yeux(Diapositive n° 20, 21)

VII. Devoirs.(Diapositive n°22)

VIII. Résumé de la leçon

Remplissez complètement la fiche d’évaluation. (Diapositive n°23). Notes de cours.

Je veux finir la leçonun poème de la grande mathématicienne Sofia Kovalevskaya. (Diapositive n° 24, 25)

Si dans la vie tu es ne serait-ce qu'un instant

J'ai ressenti la vérité dans mon cœur,

S'il y a un rayon de lumière à travers l'obscurité et le doute

Votre chemin était illuminé d'un éclat lumineux :

Quelle que soit votre décision immuable

Le destin ne vous a pas prévu d'avance,

Le souvenir de ce moment sacré

Gardez-le pour toujours comme un sanctuaire dans votre poitrine.

Les nuages ​​se rassembleront en une masse discordante,

Le ciel sera couvert d'une brume noire,

Avec une détermination claire, avec une foi calme

Vous rencontrez la tempête et faites face à l'orage.

Ce poème exprime le désir de connaissance, la capacité de surmonter tous les obstacles qui se présentent sur le chemin. La leçon est terminée. Merci pour la leçon! (Diapositive n°26)

Application

FICHE QUESTIONNAIRE

FI. étudiant___________________________

1. Ambiance au début de la leçon : a) b) c)

2. Ma perception du sujet de la leçon :

a) tout appris ; b) a presque tout appris ; c) partiellement compris, j'ai besoin d'aide.

3. Nombre de réponses incorrectes au test : _________

4. J'ai travaillé en classe :

a) excellent ; b) bon ; c) satisfaisant ; d) insatisfaisant.

5. J'évalue mon travail comme ______ (donnez une note)

6. J'évalue la leçon _____ (donnez-lui une note)

7. Ambiance à la fin du cours : a) b c)

Type de cours : cours sur l'apprentissage de nouvelles matières.

Le but de la leçon : systématiser, élargir et approfondir les connaissances et les compétences des étudiants en apportant des termes similaires d'expressions contenant des racines carrées. Favoriser le développement de l’observation, la capacité d’analyser et de tirer des conclusions. Encouragez les élèves à exercer un contrôle mutuel.

Équipement : fiches chiffrées, projecteur, présentation.

Étapes du cours :

1. Organisation du début du cours. Fixation d'objectifs. Répétition du matériel couvert.
2. Exercices oraux. Obtenez la photo.
3. Référence historique.
4. Apprendre du nouveau matériel.
5. Travail indépendant avec supervision mutuelle.
6. Résumer.
7. Devoirs.
8. Réflexion.

Pendant les cours

JE. Organisation du début du cours. Communiquer le sujet et fixer l’objectif.

Professeur. Si nous ouvrons le Grand Dictionnaire Encyclopédique, nous pouvons lire ce que signifie le mot « transformation ». Ainsi, « la transformation est le remplacement d’un objet mathématique par un objet similaire obtenu à partir du premier selon certaines règles ».

Dans le Dictionnaire explicatif de S.I. Ozhegov, nous lisons : "Transformer - ... refaire complètement, transformer d'un type à un autre, changer pour le mieux."

Le but des transformations mathématiques est d'amener l'expression à une forme plus pratique pour les calculs numériques ou d'autres transformations.

Jusqu'à présent, nous avons effectué des transformations uniquement d'expressions rationnelles, en utilisant pour cela les règles d'opérations sur les polynômes. Il y a quelques leçons, nous avons introduit une nouvelle opération : l’opération racine carrée.

Passons en revue les informations de base sur la racine carrée arithmétique.

Préparez des cartes avec les chiffres 1, 2, 3 pour les exercices oraux. Pour répondre, levez la carte avec le numéro de la bonne affirmation.

Racine carrée arithmétique d'un nombre un appelé:

1) Un nombre dont le carré est égal à un.
2) Un nombre égal à un.
3) Un nombre non négatif dont le carré est égal à un.

„ Pour saisir un facteur sous le signe de la racine, il faut :

1) Multiplier les expressions radicales ;
2) Mettez le facteur au carré ;
3) Écrivez le carré du multiplicateur sous la racine.

... Pour déplacer le multiplicateur au-delà du signe racine, vous devez :

1) Présenter l’expression radicale comme le produit de plusieurs
multiplicateurs;
2) Appliquer la règle de la racine carrée du produit de non négatif
multiplicateurs.

II. Obtenez la photo.

Résolvez les exemples et coloriez la case avec la bonne réponse. Si tout est fait correctement, vous obtiendrez une photo. Annexe 1.

Réponse : signe racine carrée. Annexe 2.

III. Référence historique.

Le signe racine carrée a été introduit par nécessité pratique. Connaissant la superficie, nos ancêtres ont tenté au XVIe siècle de calculer le côté de la place. C'est ainsi qu'est apparue l'opération d'extraction de la racine carrée. Mais la forme moderne du signe n’a pas été déterminée immédiatement.
À partir du XIIIe siècle, de nombreux mathématiciens italiens et européens ont désigné la racine avec le mot latin Radix (racine) ou R x en abrégé. Au XVe siècle, on écrivait R 2 12 au lieu de . Au 16ème siècle, au lieu de Ö, on écrivait V‚. Le mathématicien néerlandais A. Girard a introduit une notation de la racine proche de la notation moderne.
Ce n'est qu'en 1637 que le mathématicien français René Descartes utilisa le signe racine moderne dans sa Géométrie. Ce signe n'est devenu d'usage général qu'au début du XVIIIe siècle.

IV. Apprendre du nouveau matériel.

Simplifiez l'expression :

V. Travail indépendant.

Option 1.	Option 2.

VI. Résumer.

Cours d'algèbre en 8e année

Sujet: Leçon générale.

Conversion d'expressions contenant des racines carrées

Professeur de mathématiques: Baitourova A.R. école kola-gymnase n°31, Astana

Année académique 2012-2013

Cible: répétition du concept de racine carrée et de ses propriétés ; développer la capacité de simplifier des expressions et de calculer des racines carrées.

Tâches:

consolider les connaissances, compétences et aptitudes précédemment acquises des étudiants sur le sujet étudié ;

consolider les compétences dans la conversion d'expressions contenant des racines carrées ;

promouvoir la formation d'un choix indépendant de la méthode de solution.

Type de cours : Améliorer les connaissances des élèves en matière d'apprentissage

Les méthodes de travail:

Actif (le processus de cognition vient des étudiants),

Visuellement - démonstratif,

Partiellement - recherche (nous apprenons aux enfants à observer, analyser, comparer, tirer des conclusions et des généralisations sous la direction de l'enseignant),

Pratique

Formes de travail: classe entière, individuel..

Équipement: tableau blanc interactif, diapositives PowerPoint, fiches d'évaluation, fiches de test, fiches de devoirs.

Technologies innovantes :

Formation en informatique,

Approche activité de l'enseignement (les connaissances viennent de l'étudiant),

Verbalement productif (au stade de la réflexion),

Apprentissage personnalisé (chaque enfant pourra répondre).

Pendant les cours.

JE. Organisation du temps

- Bonjour, asseyez-vous (Bonjour, asseyez-vous). Regardez le sujet de notre leçon et dites ce que cela signifierait ( Regardez notre leçon et dites-moi ce que cela signifie).

C'est vrai, aujourd'hui, dans la leçon, nous répéterons les règles de transformation des expressions contenant des racines carrées, de transformation des racines d'un produit, d'une fraction et d'un degré, de multiplication et de division de racines, de placement d'un multiplicateur derrière le signe racine, d'introduction d'un multiplicateur sous le signe racine, apporter des termes similaires et se débarrasser de l'irrationalité au dénominateur de la fraction. La page estimée aidera à résumer une leçon d'aujourd'hui ( Une fiche d'évaluation vous aidera à résumer la leçon d'aujourd'hui.)

Signez les feuilles de papier et répondez à la première question « Humeur au début d'un cours », en choisissant un des smileys.( Signez vos mots et répondez à la première question « Humeur au début du cours » en choisissant l'une des émoticônes).

II. Message du sujet de la leçon

Sujet de notre leçon : « Conversion d'expressions contenant des racines carrées arithmétiques. » (Diapositive n°1)

Il y a quelque chose dans les mathématiques

provoquant le plaisir humain. F. Hausdorff(Diapositive n°2)

III. Travail oral

1) Sondage frontal. (Diapositive n°3)

1.Donnez la définition d’une racine carrée arithmétique. (La racine carrée arithmétique de a est un nombre non négatif dont le carré est égal à a).

2.Énumérez les propriétés de la racine carrée arithmétique. (La racine carrée arithmétique d'un produit de facteurs non négatifs est égale au produit des racines de ces facteurs. La racine carrée arithmétique d'une fraction dont le numérateur est non négatif et dont le dénominateur est positif est égale à la racine du numérateur divisé par la racine du dénominateur).

3.Quelle est la valeur de la racine carrée arithmétique de x 2 ? (|x|).

4.Quelle est la valeur de la racine carrée arithmétique de x 2 si x≥0 ? X<0? (х. –х).

2) Récit oral ( Oral vérifier) (Diapositive n°4)

Allez, mets les crayons de côté !

Pas de dominos. Pas de stylos. Pas de craie.

« Comptage verbal ! » Nous faisons cette chose

Uniquement par le pouvoir de l'esprit et de l'âme.

Les nombres convergent quelque part dans l'obscurité,

Et les yeux commencent à briller,

Et il n’y a que des visages intelligents.

Parce qu'on compte dans notre tête !

(Diapositive n° 5-8)

1. Supprimez le facteur sous le signe racine : ; 2) ; 3) ; 4) ; 5) ; 6) ; 7) ; 8)

2. Saisissez un multiplicateur sous le signe racine : 1) ; 2) ; 3) ; 4) ; 5) ; 6) ; 7) ; 8)

3. Carré (Carré) : 2, 6, 7, 9, 11, 13,15, 18, 22, 25

4. Donnez des termes similaires :

IV. Travailler sur le sujet de la leçon

1) Travail individuel (Travail individuel) (Diapositive n°9)

Le vert correspond aux tâches d'un niveau de base, le jaune – aux tâches du niveau élevé, le rouge – aux tâches de haut niveau.(Le vert correspond aux tâches de niveau basique, le jaune aux tâches de niveau avancé, le rouge aux tâches de haut niveau). Les étudiants choisissent la tâche à leur propre discrétion. Trois étudiants, ayant reçu une tâche, la résolvent dans leurs cahiers

niveau

Supprimez le multiplicateur sous le signe racine :
1)
2)
3)

Entrez le multiplicateur sous le signe racine :
1)
; 2)
; 3)
;

Comparez les chiffres :
1) Et; 2) Et;

niveau

Simplifiez l'expression :
1) ; 2) ; 3)

Trouvez le montant :
1)
2)

1) ; 2)

3ème niveau

Simplifiez l'expression :
1) ; 2) .
Transformez l'expression :
1) ; 2) ;

Ouvrez les parenthèses et simplifiez l'expression :
1) ;

2) ; 3) ;

2) Travaillez avec un tableau interactif. (Diapositive n° 10-13)

Le reste des étudiants résolvent les tâches suivantes :

1. Trouvez le sens de l'expression :
1)
2)

3)

2. Transformez l'expression :
1)
; 2)
; 3)
.

3. Simplifiez l'expression :
1)
; 2)
; 3)
.

4. Débarrassez-vous de l'irrationalité dans le dénominateur :
1) ; 2)
; 3)
; 4)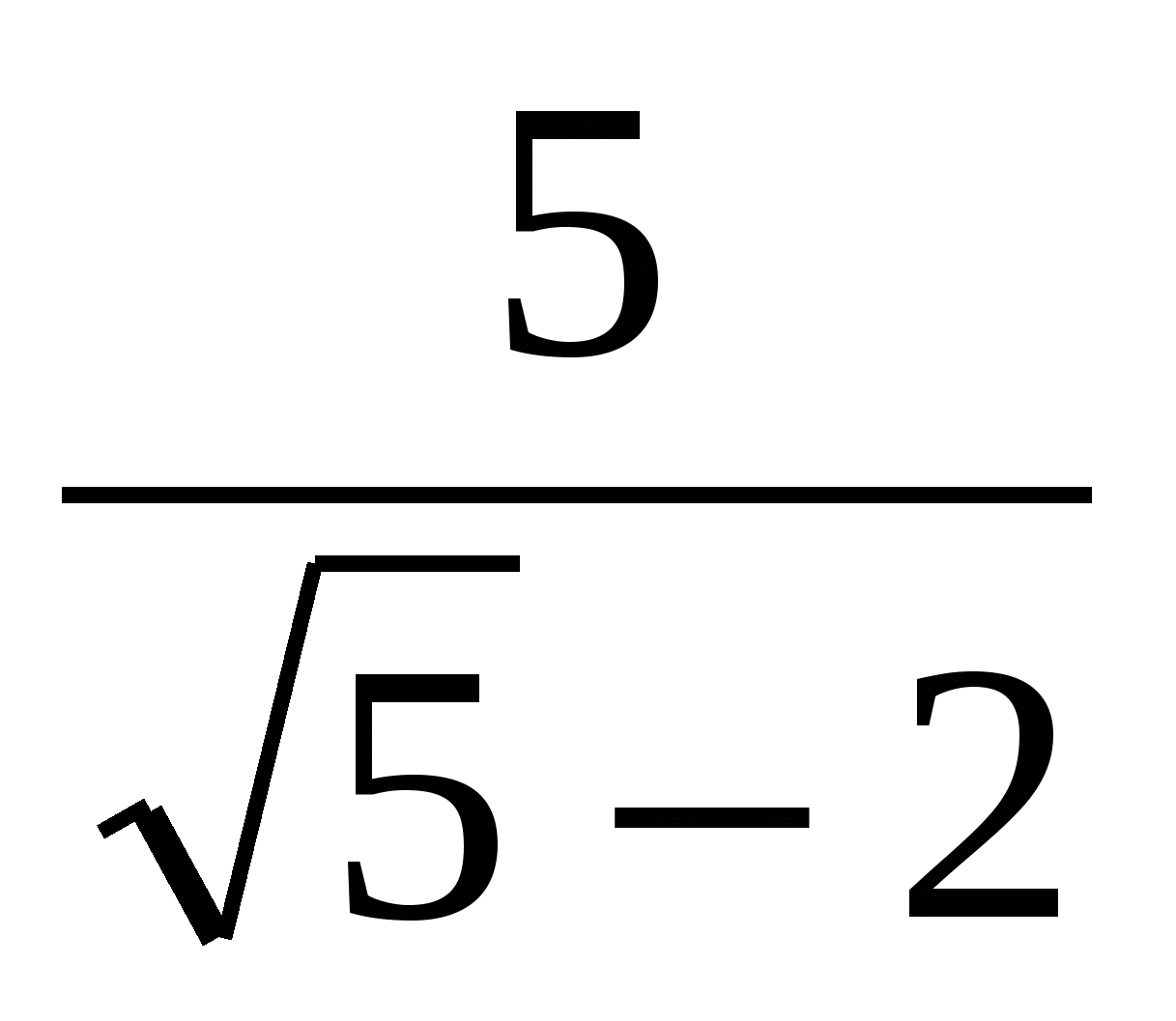
.

VI. Information historique( Référence historique) (Diapositive 14-26)

Radix a deux significations : côté et racine. Les mathématiciens grecs, au lieu d’« extraire la racine », disaient « trouver le côté du carré à partir de sa valeur (aire) donnée ».

À partir du XIIIe siècle, les mathématiciens italiens et européens ont désigné la racine avec le mot latin Radix, ou R en abrégé (d'où le terme « radical »).

Mathématiciens allemands du XVe siècle. pour désigner la racine carrée nous avons utilisé le point ·5

Plus tard, au lieu d'un point, ils ont commencé à mettre un diamant 5

Puis Ú 5. Ensuite, le signe Ú et la ligne ont commencé à être connectés.

VI. Test ( Test)

Le philosophe anglais Herbert Spencer a dit : "Les routes ne sont pas la connaissance qui se dépose dans le cerveau comme la graisse, les routes sont celles qui se transforment en muscles mentaux."(Diapositive n°27)

A ce stade de la leçon, il est nécessaire d'appliquer les connaissances acquises à la résolution des exercices lors de la mise en œuvre du test.(À ce stade de la leçon, vous devez appliquer vos connaissances à la résolution d'exercices pendant le test).

VII. Tests mutuels ( Examen par les pairs) (Diapositive n°28)

Code de bonnes réponses : Option I – 3124111, variante II - 2131222

VIII. Devoirs.(Diapositive n°29)

Quel nombre est le plus petit
ou
?

B 2. Simplifiez l'expression :
,

à
.

B 3. Suivez ces étapes :
.

Écrivez soigneusement et lisiblement sur une feuille de papier les solutions détaillées et fondées aux tâches de cette partie.

C 1. Réduisez la fraction :
.

C 2. Prenez la racine carrée de l'expression :
.

VIII. Résumé de la leçon

Remplissez complètement la fiche d’évaluation. Notes pour une leçon.

Je veux terminer la leçon avec un poème de la grande mathématicienne Sofia Kovalevskaya. (Diapositive n°30)

Si dans la vie tu es ne serait-ce qu'un instant

J'ai ressenti la vérité dans mon cœur,

S'il y a un rayon de lumière à travers l'obscurité et le doute

Votre chemin était illuminé d'un éclat lumineux :

Quelle que soit votre décision immuable

Le destin ne vous a pas prévu d'avance,

Le souvenir de ce moment sacré

Gardez-le pour toujours comme un sanctuaire dans votre poitrine.

Les nuages ​​se rassembleront en une masse discordante,

Le ciel sera couvert d'une brume noire,

Avec une détermination claire, avec une foi calme

Vous rencontrez la tempête et faites face à l'orage.

Ce poème exprime le désir de connaissance, la capacité de surmonter tous les obstacles qui se présentent sur le chemin.

La leçon est terminée. Merci pour une leçon! ( La leçon est terminée. Merci pour la leçon !) (Diapositive n°31)

Application

FICHE QUESTIONNAIRE

FI. étudiant___________________________

1. Ambiance au début de la leçon : a) c)

2. Ma perception du sujet de la leçon :

a) tout appris ; b) a presque tout appris ; c) partiellement compris, j'ai besoin d'aide.

3. Nombre de réponses incorrectes au test : _________

4. J'ai travaillé en classe :

a) excellent ; b) bon ; c) satisfaisant ; d) insatisfaisant.

5. J'évalue mon travail comme ______ (donnez une note)

6. J'évalue la leçon _____ (donnez-lui une note)

7. Ambiance à la fin du cours :

UN)b) V)

Test 1 possibilité

A 1. Calculer
.

1) 7; 2)
; 3) 5; 4)
.

A 2. Calculer
.

1) 7; 2)
; 3)
; 4) 4.

La leçon vidéo « Transformation d'expressions contenant l'opération d'extraction d'une racine carrée » est une aide visuelle qui permet à un enseignant de développer plus facilement des compétences dans la résolution de problèmes contenant des expressions avec une racine carrée. Au cours de la leçon, nous rappelons les fondements théoriques qui servent de base à la réalisation d'opérations sur les nombres et les variables présentes dans les expressions radicales, décrivons la solution de nombreux types de problèmes pouvant nécessiter la capacité d'utiliser des formules de conversion d'expressions contenant une racine carrée , et fournissent des méthodes pour se débarrasser de l'irrationalité du dénominateur d'une fraction.

La leçon vidéo commence par la démonstration du titre du sujet. Il est à noter que plus tôt dans les leçons, des transformations d'expressions rationnelles ont été réalisées. Dans ce cas, des informations théoriques sur les monômes et les polynômes, les méthodes de travail avec les polynômes, les fractions algébriques, ainsi que les formules de multiplication abrégées ont été utilisées. Ce didacticiel vidéo traite de l'introduction de l'opération racine carrée pour transformer des expressions. On rappelle aux élèves les propriétés de l’opération racine carrée. Parmi ces propriétés, il est indiqué qu'après avoir pris la racine carrée du carré d'un nombre, le nombre lui-même est obtenu, la racine du produit de deux nombres est égale au produit de deux racines de ces nombres, la racine du quotient de deux nombres est égal au quotient des racines des termes du quotient. La dernière propriété discutée consiste à prendre la racine carrée d’un nombre élevé à une puissance paire √a 2 n, ce qui donne un nombre élevé à la puissance a n. Les propriétés considérées sont valables pour tout nombre non négatif.

Des exemples sont considérés qui nécessitent des transformations d'expressions contenant une racine carrée. Il est indiqué que ces exemples supposent que a et b sont des nombres non négatifs. Dans le premier exemple, il faut simplifier les expressions √16a 4 /9b 4 et √a 2 b 4 . Dans le premier cas, une propriété est appliquée qui détermine que la racine carrée du produit de deux nombres est égale au produit de leurs racines. À la suite de la transformation, l'expression ab 2 est obtenue. La deuxième expression utilise la formule permettant de convertir la racine carrée d'un quotient en quotient de racines. Le résultat de la transformation est l'expression 4a 2 /3b 3.

Dans le deuxième exemple, il faut supprimer le facteur sous le signe racine carrée. La solution des expressions √81а, √32а 2, √9а 7 b 5 est considérée. À l'aide de l'exemple de la transformation de quatre expressions, nous montrons comment la formule de transformation de la racine d'un produit de plusieurs nombres est utilisée pour résoudre des problèmes similaires. Dans ce cas, les cas sont notés séparément lorsque les expressions contiennent des coefficients et des paramètres numériques à un degré pair ou impair. À la suite de la transformation, les expressions √81а=9√а, √32а 2 =4а√2, √9а 7 b 5 =3а 3 b 2 √ab sont obtenues.

Dans le troisième exemple, il faut effectuer une opération inverse à celle du problème précédent. Pour saisir un facteur sous le signe racine carrée, vous devez également être capable d'utiliser les formules que vous avez apprises. Il est proposé d'introduire un facteur devant les parenthèses sous le signe de la racine dans les expressions 2√2 et 3a√b/√3a. En utilisant des formules connues, le facteur devant le signe racine est mis au carré et placé comme facteur dans le produit sous le signe racine. Dans la première expression, la transformation donne l’expression √8. La deuxième expression utilise d'abord la formule du produit cheval pour transformer le numérateur, puis la formule de la racine du quotient pour transformer l'expression entière. Après avoir réduit le numérateur et le dénominateur dans l’expression radicale, on obtient √3ab.

Dans l'exemple 4, vous devez effectuer des actions dans les expressions (√a+√b)(√a-√b). Pour résoudre cette expression, de nouvelles variables sont introduites qui remplacent les monômes contenant le signe de la racine √a=x et √b=y. après substitution de nouvelles variables, la possibilité d'utiliser la formule de multiplication abrégée est évidente, après quoi l'expression prend la forme x 2 -y 2. En revenant aux variables d'origine, nous obtenons a-b. La deuxième expression (√a+√b) 2 peut également être convertie à l'aide de la formule de multiplication abrégée. Après avoir ouvert les parenthèses, on obtient le résultat a+2√ab+b.

Dans l'exemple 5, les expressions 4a-4√ab+b et x√x+1 sont factorisées. Pour résoudre ce problème, il est nécessaire d’effectuer des transformations et d’isoler les facteurs communs. Après avoir appliqué les propriétés de la racine carrée pour résoudre la première expression, la somme est convertie au carré de la différence (2√a-√b) 2. Pour résoudre la deuxième expression, vous devez saisir le facteur avant le signe racine sous la racine, puis appliquer la formule de la somme des cubes. Le résultat de la transformation est l'expression (√x+1)(x 2 -√x+1).

L'exemple 6 montre la solution à un problème où vous devez simplifier l'expression (a√a+3√3)(√a-√3)/((√a-√3) 2 +√3a). La tâche est résolue en quatre étapes. Dans un premier temps, le numérateur est converti en produit à l'aide de la formule de multiplication abrégée - la somme des cubes de deux nombres. Dans la deuxième action, le dénominateur de l’expression est transformé, qui prend la forme a-√3a+3. Après la conversion, il devient possible de réduire la fraction. La dernière étape applique également la formule de multiplication abrégée, qui permet d'obtenir le résultat final a-3.

Dans le septième exemple, il faut se débarrasser de la racine carrée dans les dénominateurs des fractions 1/√2 et 1/(√3-√2). Lors de la résolution du problème, la propriété de base d'une fraction est utilisée. Pour se débarrasser de la racine du dénominateur, le numérateur et le dénominateur sont multipliés par le même nombre, à l'aide duquel l'expression radicale est mise au carré. À la suite des calculs, nous obtenons 1/√2=√2/2 et 1/(√3-√2)=√3+√2.

Les caractéristiques du langage mathématique lorsque l'on travaille avec des expressions contenant une racine sont indiquées. Il est à noter que le contenu de la racine carrée dans le dénominateur d'une fraction signifie le contenu de l'irrationalité. Et se débarrasser du signe racine dans un tel dénominateur est considéré comme se débarrasser de l'irrationalité dans le dénominateur. Des méthodes sont décrites pour se débarrasser de l'irrationalité - pour transformer un dénominateur de la forme √a, il est nécessaire de multiplier le numérateur simultanément avec le dénominateur par le nombre √a, et d'éliminer l'irrationalité pour un dénominateur de la forme √a -√b, le numérateur et le dénominateur sont multipliés par l'expression conjuguée √a+√ b. Il est à noter que se débarrasser de l'irrationalité dans un tel dénominateur simplifie grandement la solution du problème.

A la fin de la leçon vidéo, une simplification de l'expression 7/√7-2/(√7-√5)+4/(√5+√3) est discutée. Pour simplifier l'expression, les méthodes décrites ci-dessus pour éliminer l'irrationalité du dénominateur des fractions sont utilisées. Les expressions résultantes sont ajoutées, après quoi la forme simplifiée de l'expression ressemble à √5-2√3.

La leçon vidéo « Transformation d'expressions contenant l'opération d'extraction d'une racine carrée » est recommandée pour être utilisée dans une leçon scolaire traditionnelle pour développer les compétences nécessaires pour résoudre des problèmes contenant une racine carrée. Dans le même but, la vidéo peut être utilisée par l'enseignant lors de l'enseignement à distance. Le matériel peut également être recommandé aux étudiants pour un travail indépendant à la maison.

1. Résumé de la leçon sur le thème : « Transformation d'expressions contenant des racines carrées » Sujet : algèbre, année : 8e, auteurs des manuels : Yu.N. Makarychev, N.G. Mindyuk, K.I. Neshkov, S.B. Souvorov, éd. S.A. Téliakovsky. Sujet de cours : Transformation d'expressions contenant des racines carrées (§ 7, paragraphe 19). Nombre total d'heures sur le sujet : 16 Numéro de cours sur le sujet : 14 Type de cours : généralisation et systématisation des connaissances. Objectif de la leçon : organiser les conditions permettant aux élèves d'obtenir des résultats pédagogiques sur le thème : « Transformation d'expressions contenant des racines carrées »  généraliser et systématiser les connaissances des élèves sur les transformations d'expressions, incl. contenant des racines carrées;  développer l'activité, l'initiative, l'indépendance, l'entraide dans l'accomplissement des tâches tout en résolvant des problèmes sur le sujet ;  lancer des activités de création, de recherche et de projet des étudiants ;  formation de méta-sujet UUD (réglementaire, cognitif, communicatif) ;  établir la relation entre les composantes et les résultats des actions ;  suivi des connaissances et compétences acquises ;  utilisation de technologies préservant la santé pendant le cours. Objectifs de la leçon : généralisation par les étudiants du contenu de la matière (théorique et pratique) sur le thème « Transformation d'expressions contenant des racines carrées » :  capacité à appliquer les connaissances et compétences sur le sujet pour résoudre des problèmes pratiques,  contrôle du niveau de maîtrise du matériel,  développement d'activités éducatives universelles méta-matières. Le sujet sait : prescriptions pour les résultats éducatifs prévus Méta-sujet (UD) Réglementaire Cognitif Communicatif  définition éducative  acceptation et  construit des objectifs de monologue dans le processus de maîtrise de la préservation des déclarations à l'oral Personnel  établissement du sens de la transformation des expressions contenant des racines carrées ; Peut : saisir un multiplicateur sous le signe racine, supprimer le multiplicateur sous le signe racine ; se débarrasser de l'irrationalité dans le dénominateur d'une fraction ; simplifier les expressions contenant des racines carrées ; Pour simplifier les expressions contenant des racines carrées, utilisez la factorisation, notamment en utilisant des formules de multiplication abrégées. informations pédagogiques;  corrélation des informations pédagogiques identifiées avec ses propres connaissances et compétences ; décider du recours à l'assistance ;  suivi de l'assimilation des informations pédagogiques ;  évaluation des résultats des activités réalisées ;  autodiagnostic et correction de ses propres actions éducatives. objectif cognitif ;  structurer l'information et les connaissances et les comprendre ;  effectuer des actions signe-symboliques  choisir des moyens efficaces pour résoudre les problèmes en fonction de conditions spécifiques ;  maîtrise de soi et auto-évaluation du processus et des résultats des activités  construction d'une chaîne logique de raisonnement. formulaire;  travaille en groupe, s'entraide, révise les réponses des camarades ;  organise le contrôle mutuel, la vérification mutuelle, etc. à toutes les étapes des activités éducatives et cognitives ;  donne des présentations sur l'histoire des mathématiques, le lien entre les mathématiques et l'art, la pratique, etc. ;  participe à la discussion des discours. les résultats de leurs activités pour satisfaire leurs besoins, motivations, intérêts ;  attitude positive envers l'apprentissage, envers l'activité cognitive, le désir d'acquérir de nouvelles connaissances, compétences et d'améliorer celles existantes ;  soyez conscient de vos difficultés et efforcez-vous de les surmonter. Devoirs de cours Tâche 1 Transformation d'expressions rationnelles a c ac Addition de fractions avec des dénominateurs similaires   b b b 1. Additionnez les numérateurs (lors de l'ajout de numérateurs, ouvrez les parenthèses et apportez des termes similaires). 2. Laissez le dénominateur inchangé. 3. Si possible, réduisez le résultat obtenu (fraction) en présentant le numérateur et le dénominateur sous forme de produit. Addition de fractions ayant des dénominateurs différents a c ad  cb   b d bd 1. Factoriser les dénominateurs. 2. Trouvez le plus petit dénominateur commun (le produit de tous les facteurs des dénominateurs, pris un à la fois, à la plus grande puissance). 3. Trouvez des facteurs supplémentaires pour chaque fraction. 4. Multipliez le numérateur et le dénominateur de chaque fraction par un facteur supplémentaire. 5. Additionnez des fractions avec les mêmes dénominateurs (algorithme 1). Multiplier des fractions a c ac   b d bd 1. Factoriser le numérateur et le dénominateur de chaque fraction. 2. Multipliez les numérateurs sans ouvrir les parenthèses et écrivez-les au numérateur. Multipliez les dénominateurs sans ouvrir les parenthèses et écrivez le dénominateur. 3. Réduisez le résultat autant que possible. a c a d ad Division de fractions :    b d b c bc 1. Multipliez la première fraction par l'inverse de la seconde. 2. Regardez l'algorithme de multiplication des fractions. Méthodes de factorisation 1. Sortez le facteur commun entre parenthèses (s'il y en a un) ab±ac = a(b±c) 2. Essayez de factoriser le polynôme à l'aide de formules de multiplication abrégées 3. Essayez d'appliquer la méthode de regroupement (si le les méthodes précédentes n'ont pas conduit à des objectifs) ab+dc+ac+db=a(b+c)+d(b+c)=(b+c)(a+d) Transformation d'expressions contenant des racines Algorithme de suppression du multiplicateur sous le signe de la racine 1. Imaginez une expression radicale sous la forme d'un produit de tels facteurs afin que la racine carrée puisse être extraite d'un. 2. Appliquons le théorème sur la racine d'un produit. 3. Extraire la racine Algorithme pour introduire un multiplicateur sous le signe racine 1. Imaginons le produit sous la forme d'une racine carrée arithmétique. 2. Transformez le produit de racines carrées en racine carrée du produit d’expressions radicales. 3. Effectuez la multiplication sous le signe racine. Algorithme pour se débarrasser de l'irrationalité du dénominateur d'une fraction 1. Factoriser le dénominateur de la fraction en facteurs. 2. Si le dénominateur a la forme ou contient un numérateur facteur et que le dénominateur doit être multiplié par, alors. Si le dénominateur est de la forme ou ou contient un facteur de ce type, alors le numérateur et le dénominateur de la fraction doivent être multipliés par ou par, respectivement. 3. 3) Convertissez le numérateur et le dénominateur de la fraction, si possible, puis réduisez la fraction résultante. Tâche 2 1 niveau 2 niveau 1. Simplifiez les expressions : a)4 2  50  18 1. Simplifiez les expressions : 1 a) 12  2 27  75 2 b)3 2 (5 2  32) b) 3 ( 2 3  12) c)(5  2) 2 d)(3  2)(3  2) 2. Réduire les fractions : 3 3 b2 3. Résoudre l'équation, a) ; b) 2 3 (b  2) (b  2) ayant préalablement simplifié son côté droit : x 2  36  100  c) 4  5 2 2. Réduire les fractions : 1. Simplifier l'expression : a) 4√ + 4√ − 4√ ; b) √9 + √49 − √64 ; c) √63 − √175 + 9√7 ; d) 2√8a + 0,3√45s − 4√18a + 0,01√500s. 2. Complétez les étapes et faites correspondre la bonne réponse : -1 (√15 − √12)(√15 − 2√3) 6 -2√2 (4 + √2)(2 − √2) (√2 − √3 )(√2 + √3) 27 − 12√5 2 41 − 24√2 (3 − 4√2) 3. Libérez-vous de l'irrationalité du dénominateur de la fraction. 2 7 a) ; b) ; c)3√7 ; d) + . √5 √3 √ √ 4. Réduisez la fraction. √5+x ; b) une −√2 a2 −2 ; c) 3−√3 √3 ; d) √à+√ . − a) 5 5 ; b) 4b  2 10  5 2 2 b 2 3. Montrer que cette équation a des racines entières et trouver : Tâche 3 5− 2 2 g)(7  2 3)(7  2 3) x2  a)  10  3  10  3 Tâche 4 2 niveau 1 niveau Simplifier l'expression 1. √2 si > 0, 2. √ 2 si c< 0, 3. 3√с + 8√с − 9√с. Выполните действия 4. (2 + √3) ∙ (1 − √3) 5. (√2 + с) ∙ (с − √2) Освободитесь от иррациональности в знаменателе 6. . Вычислить 1. √852 − 842 Упростить выражение 2. -2√0.81а2 , если а<0 3. √10, если a> 0 4. (5√7 - √63 + √14) √7 5. (5√3- √11) ∙ (√11 + 5√3) Réduire la fraction 6. √3 a2 −3 (a+ √3) Libre vous-même de l'irrationalité au dénominateur Tâche n° 1 2 3 A K D E -m c 3√ −√3 −2 -2m √ 2√ √3 +2 m 2c -2√ −2 + √3 √ -c2 2c −√3 + 2 5 c2+2 c-2 2 − √2 c2-2 6 3 3√ 3 2 3 √3 3 4 P 2 7. T 2 m -c 20c -m -√ -2c 2√3 −2√3 − √ 2 3 2 2 − 2√2 √3 3 4 √10+√6 Nombre U de la tâche 1 10 2 1.8a 3 2 4 14 - 7√2 5 6 75 a + √3 7 √10+√6 L L RFO 12 -à 5 14√27 11 √à - 3 13 0,8à −5 2√14 -7 86 √à + 3 10 + √6 8 à −2 72√7 -64 à√3 4√10 - 6 15 2à 10 12 + √7 64 à 2 - 3 14 -2 à −10 7+ √14 -86 à 2 +3 √10 √6 -12 0,9 à 14+7 √2 -75 3√ à 2 √16 6+ √ 10 Tâche 5 Niveau 1 Niveau 2 64√10 1. Simplifiez les expressions : 1 a) 12  2 27  75 2 b)3 2 (5 2  32)  c) 4  5 2 1. Simplifiez les expressions : 1 3 a ) 300  4  75 5 16   8  2 c) 5  2   3  5  d)1  3 7  83 7  8 b) 3 2  1  2 2 g)(7  2 3)(7  2 3) 2. Réduire les fractions : a) 5 5 10  5 2 ; b) 4b  2 2. Réduire les fractions : a) 2 b 2 3. Résoudre l'équation : x2  100  6  2 2 6 6 3 ; b) 4a 2  4a b  b 4a 2  b 3. Résoudre l'équation : 100  6 x 2   6  2 5  6  2 5    2 Structure organisationnelle de la leçon Étapes de la leçon Moment d'organisation Devise de la leçon : « Il y a quelque chose dans les mathématiques qui évoque le plaisir humain » F. Hausdorff Objectifs de l'étape Vérifier l'état de préparation pour la leçon. Attitude positive envers la classe. Motivation Déterminer le sujet, les buts et les objectifs de la leçon. Autodétermination dans l'activité. Motivation pour les activités d'apprentissage. Activités de l'enseignant Accueille les élèves, vérifie l'état de préparation des élèves au cours, note les absents, organise le remplissage des fiches d'évaluation. Activités des élèves Les enseignants saluent, vérifient leur état de préparation pour la leçon, remplissent les fiches d'évaluation Annexe 4. Aide les élèves à formuler le sujet, les objectifs, les buts et le contenu de la leçon (travail frontal avec la classe). Devoir : De quoi parlent ces déclarations ? « L’arbre, la fleur l’ont, les équations l’ont. Formulez les tâches et les objectifs de la leçon, répondez aux questions de l'enseignant et notez le sujet de la leçon dans un cahier. Ils travaillent en binôme avec une carte posée sur leur bureau « Prenons note » Annexe 1 ; Temps 1 4 Excursion dans l'histoire Actualisation des connaissances Atelier 1. Travail individuel Développement de l'activité cognitive, du regard, de l'intérêt pour le sujet. Les connaissances sont mises à jour, les activités des étudiants sont organisées pour systématiser l'information pédagogique au niveau « connaissances ». Les activités des étudiants sont organisées pour maîtriser l'information pédagogique au niveau « compétence ». Et il y a un signe spécial - radical, qui y est sans aucun doute associé. C'est le résultat de nombreuses tâches, et nous ne contestons pas cela. Nous espérons que tout le monde a pu répondre : c'est... (la racine). Aide à résumer le travail de groupe. Organise le processus pédagogique 1. Vérifier les connaissances des étudiants sur la théorie sur le sujet (instructions pour transformer les expressions, y compris celles contenant des racines carrées). Tâche 1 2. Vérifiez vos devoirs. (travail frontal avec la classe). Suivi des performances professionnelles des étudiants. Explique le principe du travail individuel. L'agaric mouche a des taches blanches et jaunes. Les blancs correspondent aux tâches de niveau de base, les jaunes – aux tâches de niveau avancé. Les élèves choisissent une tâche à leur discrétion. Tâche 2. Organise le travail avec tout ; réalise la tâche « Faire un dessin » Annexe 2. Résumer le travail, comparer le résultat avec le tableau. (les résultats sont inscrits sur la fiche d'évaluation). L’élève raconte à la classe des informations historiques sur l’histoire de l’origine du signe radical Annexe 3. Il répond aux questions de l’enseignant, dessine des schémas et des consignes dans un cahier et les compare avec le tableau. 2 Autotest et auto-évaluation d.z. 5 (inscrire les résultats sur la feuille de match). Quatre étudiants, ayant choisi les tâches à leur discrétion, les résolvent individuellement dans leurs cahiers. Ensuite, ils participent à l’ensemble du travail. 15 Un élève à la fois travaille en classe Tâche 3. 2. Travailler avec le tableau Cours d'éducation physique Travail indépendant Soulager les tensions, déchargement Organise le processus de relaxation à l'aide de l'EER (cours d'éducation physique du site videouroki.net). Effectuer le contrôle et Organise et contrôle les évaluations de leurs actions, le processus de résolution des problèmes, en apportant les ajustements appropriés à leur mise en œuvre. Auto-test Résumé de la leçon Organise un test de travail indépendant. Identifie la qualité et le niveau d'acquisition des connaissances, et établit également les causes des erreurs identifiées. Résumer. Mener une auto-analyse et une auto-évaluation de ses propres activités en classe. Dirige les activités des élèves dans l'auto-évaluation du travail de la leçon. Résume les résultats globaux et annonce ses notes aux étudiants qui travaillent activement. Identifie la qualité et le niveau d'acquisition des connaissances, et établit également les causes des erreurs identifiées. au tableau, le reste dans des cahiers. Fais les excerises. 2 Travaillez de manière autonome sur les tâches (fiches par niveau). En conséquence, ils obtiennent les noms de mathématiciens célèbres mentionnés dans la référence historique de la leçon. Les élèves analysent leur travail, expriment à voix haute leurs difficultés et discutent de l'exactitude de la résolution des problèmes. L'auto-évaluation pour le travail indépendant est incluse dans la fiche d'évaluation. Les étudiants évaluent indépendamment leur travail en classe et notent sur la feuille d'évaluation. 10 2 2 Devoirs. S'assurer que les élèves comprennent le but, le contenu et les méthodes de réalisation des devoirs. Fin du cours. Donne des instructions sur la façon d’effectuer la tâche. Tâche 5. Les élèves reçoivent un rapport de devoirs, l'écrivent dans un journal et posent des questions à l'enseignant. Merci aux étudiants pour la leçon. Les élèves rangent leur espace de travail et remettent leurs fiches d’évaluation au bureau du professeur. Dites au revoir au professeur. 2 Annexe 1 Prenons note 1. Environ 75 % des maladies de l'adulte sont acquises pendant l'enfance. Les enfants qui fument raccourcissent leur vie de √225 %. Déterminer l'espérance de vie des enfants qui fument actuellement, si l'espérance de vie moyenne en Russie est de 56 ans ? 2. Nous regardons la télévision pendant des heures, restons assis devant l'ordinateur toute la journée sans pause, parlons sans arrêt sur notre téléphone portable, et nous ne comprenons pas pourquoi nos maux de tête sont si intenses et pourquoi nous sommes si fatigués que nous pouvons le faire. je ne vois rien. Souviens-toi! Il est recommandé de travailler sur l'ordinateur pendant √400 minutes maximum, puis d'exercer vos yeux. Vous ne devriez pas parler au téléphone portable plus de √1 600 secondes. Ne regardez pas la télévision plus de √4 heures. 3. Un étudiant soucieux de sa santé doit manger correctement. 1 1 1 Vous ne pouvez pas manger plus de √100 kg de sucreries par jour, la consommation quotidienne de pain est de √25 kg, de beurre √64 kg. Combien de grammes de friandises, de pain, de beurre un élève peut-il manger par jour ? Annexe 2 -16 100 441 17 -10 -3 11 625 12 -2.1 36 -9 18 -2.4 -2 -6 0 8 55 5 25 49 13 54 3 169 1 14 94 6 7 75 81 45 9 0 ,7 -5 121 16 34 -2.7 -3.7 Annexe 3 À partir du XIIIe siècle, les mathématiciens italiens et européens désignaient la racine avec le mot latin radix (en abrégé r) ou en abrégé R (d'où le terme « radical »). Mathématiciens allemands du XVe siècle. Le point ·5 a été utilisé pour désigner la racine carrée. Plus tard, au lieu d'un point, ils ont commencé à mettre un losange 5. En 1525, dans le livre de H. Rudolf « Calcul rapide et beau à l'aide de règles d'algèbre habiles, communément appelées « Coss » », apparaît la notation V pour la racine carrée. En 1626, le mathématicien hollandais A. Girard introduisit la notation V, qui remplaça bientôt le signe r, tandis qu'une ligne horizontale était placée au-dessus de l'expression radicale. La notation moderne de la racine est apparue pour la première fois dans le livre Géométrie de René Descartes, publié en 1637. Annexe 4 Nom Nom de l'élève Date du cours Auto-évaluation pour les devoirs Auto-évaluation pour l'oral Évaluation de l'enseignant pour le travail individuel Auto-évaluation pour le travail autonome Évaluation globale du cours