Cette leçon couvrira des informations de base sur les expressions rationnelles et leurs transformations, ainsi que des exemples de transformations d'expressions rationnelles. Ce sujet résume les sujets que nous avons étudiés jusqu'à présent. Les transformations d'expressions rationnelles impliquent l'addition, la soustraction, la multiplication, la division, l'exponentiation de fractions algébriques, la réduction, la factorisation, etc. Dans le cadre de la leçon, nous examinerons ce qu'est une expression rationnelle et analyserons également des exemples de leur transformation.
Sujet:Fractions algébriques. Opérations arithmétiques sur les fractions algébriques
Leçon:Informations de base sur les expressions rationnelles et leurs transformations
Définition
Expression rationnelle est une expression composée de nombres, de variables, d'opérations arithmétiques et d'opérations d'exponentiation.
Regardons un exemple d'expression rationnelle :
Cas particuliers d'expressions rationnelles :
1er degré : ![]() ;
;
2. monôme : ;
3. fraction : .
Conversion d'une expression rationnelle est une simplification d’une expression rationnelle. L'ordre des actions lors de la transformation d'expressions rationnelles : il y a d'abord les opérations entre parenthèses, puis les opérations de multiplication (division), puis les opérations d'addition (soustraction).
Examinons plusieurs exemples de transformation d'expressions rationnelles.
Exemple 1
Solution:
Résolvons cet exemple étape par étape. L'action entre parenthèses est exécutée en premier.
![]()
![]()
Répondre:
Exemple 2
![]()
Solution:
Répondre:
Exemple 3
Solution:
Répondre: .
Note: Peut-être qu’en voyant cet exemple, une idée vous est venue : réduire la fraction avant de la réduire à un dénominateur commun. En effet, c'est tout à fait correct : il convient d'abord de simplifier au maximum l'expression, puis de la transformer. Essayons de résoudre le même exemple de la deuxième manière.
Comme vous pouvez le constater, la réponse s'est avérée absolument similaire, mais la solution s'est avérée un peu plus simple.
Dans cette leçon, nous avons examiné expressions rationnelles et leurs transformations, ainsi que plusieurs exemples précis de ces transformations.
Références
1. Bashmakov M.I. Algèbre 8e année. - M. : Éducation, 2004.
2. Dorofeev G.V., Suvorova S.B., Bunimovich E.A. et autres. Algèbre 8. - 5e éd. - M. : Éducation, 2010.
Du cours d'algèbre scolaire, nous passons aux détails. Dans cet article, nous étudierons en détail un type particulier d'expressions rationnelles - fractions rationnelles, et considérons également quelle caractéristique est identique conversions de fractions rationnelles avoir lieu.
Notons tout de suite que les fractions rationnelles au sens où nous les définissons ci-dessous sont appelées fractions algébriques dans certains manuels d'algèbre. Autrement dit, dans cet article, nous comprendrons les fractions rationnelles et algébriques comme une seule et même chose.
Comme d'habitude, commençons par une définition et des exemples. Nous parlerons ensuite de la façon d’amener une fraction rationnelle à un nouveau dénominateur et de changer les signes des membres de la fraction. Après cela, nous verrons comment réduire les fractions. Enfin, regardons la représentation d'une fraction rationnelle comme une somme de plusieurs fractions. Nous fournirons toutes les informations avec des exemples et des descriptions détaillées des solutions.
Navigation dans les pages.
Définition et exemples de fractions rationnelles
Les fractions rationnelles sont étudiées dans les cours d'algèbre de 8e année. Nous utiliserons la définition d'une fraction rationnelle, qui est donnée dans le manuel d'algèbre pour la 8e année de Yu N. Makarychev et al.
Cette définition ne précise pas si les polynômes du numérateur et du dénominateur d'une fraction rationnelle doivent être des polynômes de la forme standard ou non. Par conséquent, nous supposerons que les notations des fractions rationnelles peuvent contenir à la fois des polynômes standards et non standard.
En voici quelques-uns exemples de fractions rationnelles. Donc x/8 et  - les fractions rationnelles. Et les fractions
- les fractions rationnelles. Et les fractions  et ne correspondent pas à la définition déclarée d'une fraction rationnelle, puisque dans le premier d'entre eux le numérateur ne contient pas de polynôme, et dans le second, le numérateur et le dénominateur contiennent des expressions qui ne sont pas des polynômes.
et ne correspondent pas à la définition déclarée d'une fraction rationnelle, puisque dans le premier d'entre eux le numérateur ne contient pas de polynôme, et dans le second, le numérateur et le dénominateur contiennent des expressions qui ne sont pas des polynômes.
Conversion du numérateur et du dénominateur d'une fraction rationnelle
Le numérateur et le dénominateur de toute fraction sont des expressions mathématiques autosuffisantes ; dans le cas de fractions rationnelles, ce sont des polynômes dans un cas particulier, des monômes et des nombres ; Ainsi, des transformations identiques peuvent être effectuées avec le numérateur et le dénominateur d'une fraction rationnelle, comme pour toute expression. Autrement dit, l’expression au numérateur d’une fraction rationnelle peut être remplacée par une expression identiquement égale, tout comme le dénominateur.
Vous pouvez effectuer des transformations identiques au numérateur et au dénominateur d'une fraction rationnelle. Par exemple, au numérateur, vous pouvez regrouper et réduire des termes similaires, et au dénominateur, vous pouvez remplacer le produit de plusieurs nombres par sa valeur. Et comme le numérateur et le dénominateur d'une fraction rationnelle sont des polynômes, il est possible d'effectuer avec eux des transformations caractéristiques des polynômes, par exemple une réduction à une forme standard ou une représentation sous forme de produit.
Pour plus de clarté, considérons des solutions à plusieurs exemples.
Exemple.
Convertir une fraction rationnelle  de sorte que le numérateur contient un polynôme de forme standard et que le dénominateur contient le produit de polynômes.
de sorte que le numérateur contient un polynôme de forme standard et que le dénominateur contient le produit de polynômes.
Solution.
La réduction de fractions rationnelles à un nouveau dénominateur est principalement utilisée pour additionner et soustraire des fractions rationnelles.
Changer les signes devant une fraction, ainsi que dans son numérateur et son dénominateur
La propriété principale d'une fraction peut être utilisée pour changer les signes des membres d'une fraction. En effet, multiplier le numérateur et le dénominateur d'une fraction rationnelle par -1 équivaut à changer leurs signes, et le résultat est une fraction identiquement égale à celle donnée. Cette transformation doit être utilisée assez souvent lorsqu'on travaille avec des fractions rationnelles.
Ainsi, si vous changez simultanément les signes du numérateur et du dénominateur d'une fraction, vous obtiendrez une fraction égale à celle d'origine. Cette affirmation trouve une réponse par l’égalité.
Donnons un exemple. Une fraction rationnelle peut être remplacée par une fraction identiquement égale avec des signes modifiés du numérateur et du dénominateur de la forme.
Avec les fractions, vous pouvez effectuer une autre transformation identique, dans laquelle le signe du numérateur ou du dénominateur change. Énonçons la règle correspondante. Si vous remplacez le signe d'une fraction par le signe du numérateur ou du dénominateur, vous obtenez une fraction identique à celle d'origine. L'énoncé écrit correspond aux égalités et .
Prouver ces égalités n’est pas difficile. La preuve est basée sur les propriétés de multiplication des nombres. Démontrons le premier d'entre eux : . En utilisant des transformations similaires, l’égalité est prouvée.
Par exemple, une fraction peut être remplacée par l'expression ou.
Pour conclure ce point, nous présentons deux autres égalités utiles et . Autrement dit, si vous changez uniquement le signe du numérateur ou uniquement du dénominateur, la fraction changera de signe. Par exemple, ![]() Et
Et ![]() .
.
Les transformations considérées, qui permettent de changer le signe des termes d'une fraction, sont souvent utilisées lors de la transformation d'expressions rationnelles fractionnaires.
Réduire les fractions rationnelles
La transformation suivante de fractions rationnelles, appelée réduction de fractions rationnelles, est basée sur la même propriété fondamentale d'une fraction. Cette transformation correspond à l'égalité , où a, b et c sont des polynômes, et b et c sont non nuls.
De l'égalité ci-dessus, il devient clair que réduire une fraction rationnelle implique de se débarrasser du facteur commun dans son numérateur et son dénominateur.
Exemple.
Annulez une fraction rationnelle.
Solution.
Le facteur commun 2 est immédiatement visible, effectuons une réduction par celui-ci (lors de l'écriture, il est pratique de rayer les facteurs communs par lesquels on réduit). Nous avons  . Puisque x 2 =x·x et y 7 =y 3 ·y 4 (voir si nécessaire), il est clair que x est un facteur commun au numérateur et au dénominateur de la fraction résultante, tout comme y 3. Réduisons par ces facteurs :
. Puisque x 2 =x·x et y 7 =y 3 ·y 4 (voir si nécessaire), il est clair que x est un facteur commun au numérateur et au dénominateur de la fraction résultante, tout comme y 3. Réduisons par ces facteurs :  . Ceci termine la réduction.
. Ceci termine la réduction.
Ci-dessus, nous avons effectué la réduction des fractions rationnelles de manière séquentielle. Ou il était possible d'effectuer la réduction en une seule étape, réduisant immédiatement la fraction de 2 x y 3. Dans ce cas, la solution ressemblerait à ceci :  .
.
Répondre:
 .
.
Lors de la réduction de fractions rationnelles, le principal problème est que le facteur commun du numérateur et du dénominateur n'est pas toujours visible. De plus, cela n’existe pas toujours. Afin de trouver un facteur commun ou de vérifier son absence, il faut factoriser le numérateur et le dénominateur d'une fraction rationnelle. S’il n’y a pas de facteur commun, alors la fraction rationnelle originale n’a pas besoin d’être réduite, sinon une réduction est effectuée.
Diverses nuances peuvent survenir lors du processus de réduction de fractions rationnelles. Les principales subtilités sont abordées dans l'article réduction des fractions algébriques à l'aide d'exemples et en détail.
En concluant la conversation sur la réduction des fractions rationnelles, on constate que cette transformation est identique, et la principale difficulté de sa mise en œuvre réside dans la factorisation des polynômes au numérateur et au dénominateur.
Représentation d'une fraction rationnelle comme somme de fractions
Assez spécifique, mais dans certains cas très utile, est la transformation d'une fraction rationnelle, qui consiste en sa représentation comme la somme de plusieurs fractions, ou la somme d'une expression entière et d'une fraction.
Une fraction rationnelle, dont le numérateur contient un polynôme représentant la somme de plusieurs monômes, peut toujours s'écrire comme une somme de fractions de mêmes dénominateurs, dont les numérateurs contiennent les monômes correspondants. Par exemple,  . Cette représentation s'explique par la règle d'addition et de soustraction de fractions algébriques de mêmes dénominateurs.
. Cette représentation s'explique par la règle d'addition et de soustraction de fractions algébriques de mêmes dénominateurs.
En général, toute fraction rationnelle peut être exprimée comme une somme de fractions de différentes manières. Par exemple, la fraction a/b peut être représentée comme la somme de deux fractions : une fraction arbitraire c/d et une fraction égale à la différence entre les fractions a/b et c/d. Cette affirmation est vraie, puisque l’égalité est vraie  . Par exemple, une fraction rationnelle peut être représentée comme une somme de fractions de différentes manières : Imaginons la fraction originale comme la somme d'une expression entière et d'une fraction. En divisant le numérateur par le dénominateur avec une colonne, on obtient l'égalité
. Par exemple, une fraction rationnelle peut être représentée comme une somme de fractions de différentes manières : Imaginons la fraction originale comme la somme d'une expression entière et d'une fraction. En divisant le numérateur par le dénominateur avec une colonne, on obtient l'égalité  . La valeur de l'expression n 3 +4 pour tout entier n est un entier. Et la valeur d’une fraction est un entier si et seulement si son dénominateur est 1, −1, 3 ou −3. Ces valeurs correspondent respectivement aux valeurs n=3, n=1, n=5 et n=−1.
. La valeur de l'expression n 3 +4 pour tout entier n est un entier. Et la valeur d’une fraction est un entier si et seulement si son dénominateur est 1, −1, 3 ou −3. Ces valeurs correspondent respectivement aux valeurs n=3, n=1, n=5 et n=−1.
Répondre:
−1 , 1 , 3 , 5 .
Références.
- Algèbre: manuel pour la 8ème année. enseignement général institutions / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova] ; édité par S.A. Telyakovsky. - 16e éd. - M. : Éducation, 2008. - 271 p. : je vais. - ISBN978-5-09-019243-9.
- Mordkovitch A.G. Algèbre. 7e année. En 2 heures Partie 1. Manuel pour les étudiants des établissements d'enseignement général / A. G. Mordkovich. - 13e éd., rév. - M. : Mnémosyne, 2009. - 160 pp. : ill. ISBN978-5-346-01198-9.
- Mordkovitch A.G. Algèbre. 8e année. En 2 heures Partie 1. Manuel pour les étudiants des établissements d'enseignement général / A. G. Mordkovich. - 11e éd., effacée. - M. : Mnémosyne, 2009. - 215 p. : ill. ISBN978-5-346-01155-2.
- Gusev V.A., Mordkovitch A.G. Mathématiques (un manuel pour ceux qui entrent dans les écoles techniques) : Proc. allocation.- M.; Plus haut école, 1984.-351 p., ill.
Complexe éducatif Torez
« École polyvalente des niveaux І-ІІ n°1 – Lycée « Spectre »
Sujet. Transformations identiques d'expressions rationnelles
Développement de cours pour la 8e année
Kirilyuk Natalya Anatolevna,
professeur de mathématiques de la catégorie la plus élevée,
professeur principal
Torez – 2014
Objectifs:
Continuer à développer les compétences des élèves dans la transformation des expressions rationnelles ; consolider la capacité d'appliquer des formules de multiplication abrégées, d'ajouter, de soustraire, de multiplier et de diviser des expressions rationnelles ;
Promouvoir le développement de la pensée logique ;
Favoriser le développement chez les enfants de la capacité de se fixer des objectifs et de planifier leurs activités ; procéder à l'auto-évaluation et à l'autocorrection des activités éducatives ; capacité à travailler à temps;
Promouvoir l’attention, l’activité et une culture de la communication.
Type de cours: cours pédagogique et de développement avec des éléments d'activité commerciale.
Équipement: des cartes pour le jeu "Champ des Miracles", "actions d'entreprises", un tableau d'évaluation des élèves en cours, du matériel avec des tâches différenciées pour le jeu "Échange de connaissances"
Formes et méthodes de travail
I Motivation pour les activités d'apprentissage. Buts et objectifs auto-fixés pour la leçon.
II Actualisation des connaissances de base :
1) Enquête frontale ;
2) Exercices oraux ;
3) Dominos mathématiques.
1) Jeu « Champ des Miracles » (travail en binôme) ;
2) Tâche logique.
V Tâche intéressante.
VI Devoirs.
I Motivation du processus éducatif. Objet du message. Buts et objectifs auto-fixés pour la leçon.
On sait beaucoup de choses depuis longtemps, mais on ne sait pas grand-chose. Tout comme dans une goutte d’eau on peut voir toutes les innombrables richesses de l’océan, de même dans un manuel scolaire il y a mille ans d’expérience. Le passé vous attend pour comprendre les connaissances acquises avec beaucoup de difficulté, et l'avenir espère que vous apporterez quelque chose de nouveau et le transmettrez à vos enfants et petits-enfants.
« La théorie sans la pratique est morte ou stérile, et la pratique sans la théorie est impossible ou désastreuse. »
La théorie nécessite des connaissances, la pratique nécessite des compétences.
Alexeï Nikolaïevitch Krylov
Aujourd'hui, dans la leçon, nous acquerrons les compétences nécessaires pour additionner, soustraire, multiplier et diviser des expressions rationnelles en utilisant la théorie : méthodes de factorisation des polynômes.
En fonction du sujet et des objectifs de la leçon, formulez vos objectifs pour la leçon.
Résultat attendu :
1.améliorer la capacité d'effectuer l'addition, la soustraction, la multiplication et la division de fractions rationnelles ;
2. effectuer des transformations identiques d'expressions rationnelles.
Enseignant : Devant tout le monde il y a un tableau de notation. Dans ce tableau, vous saisirez les points gagnés pendant le cours.
II Actualisation des connaissances de référence.
1. Enquête frontale(contrôle mutuel « Enseignant-élève », 1b.)
Quelle expression est dite rationnelle ?
Comment additionner deux fractions rationnelles de dénominateurs différents ?
Quelles méthodes de factorisation d’un polynôme connaissez-vous ?
Comment trouver le produit d’expressions rationnelles ?
Quelle est la procédure à suivre pour effectuer des transformations d’identité ?
2. Exercices oraux(auto-évaluation, 1b.)
3. Domino mathématique(contrôle mutuel, 1b.)
Factoriser (choisissez la bonne réponse)

III Activation de l'activité mentale :
1) Jeu « Champ des Miracles »(travailler en binôme, 2 points chacun) ;
Il faut s'amuser en apprenant pour absorber les connaissances,
il faut les digérer avec brio.
Anatole France
1)  15)
15) 
2)  16)
16) 
3)  17)
17) 
4)  18)
18) 
5)  19)
19) 
6)  20)
20) 
7)  21)
21) 
8)  22)
22) 
9)  23)
23) 
10)  24)
24) 
11)  25)
25) 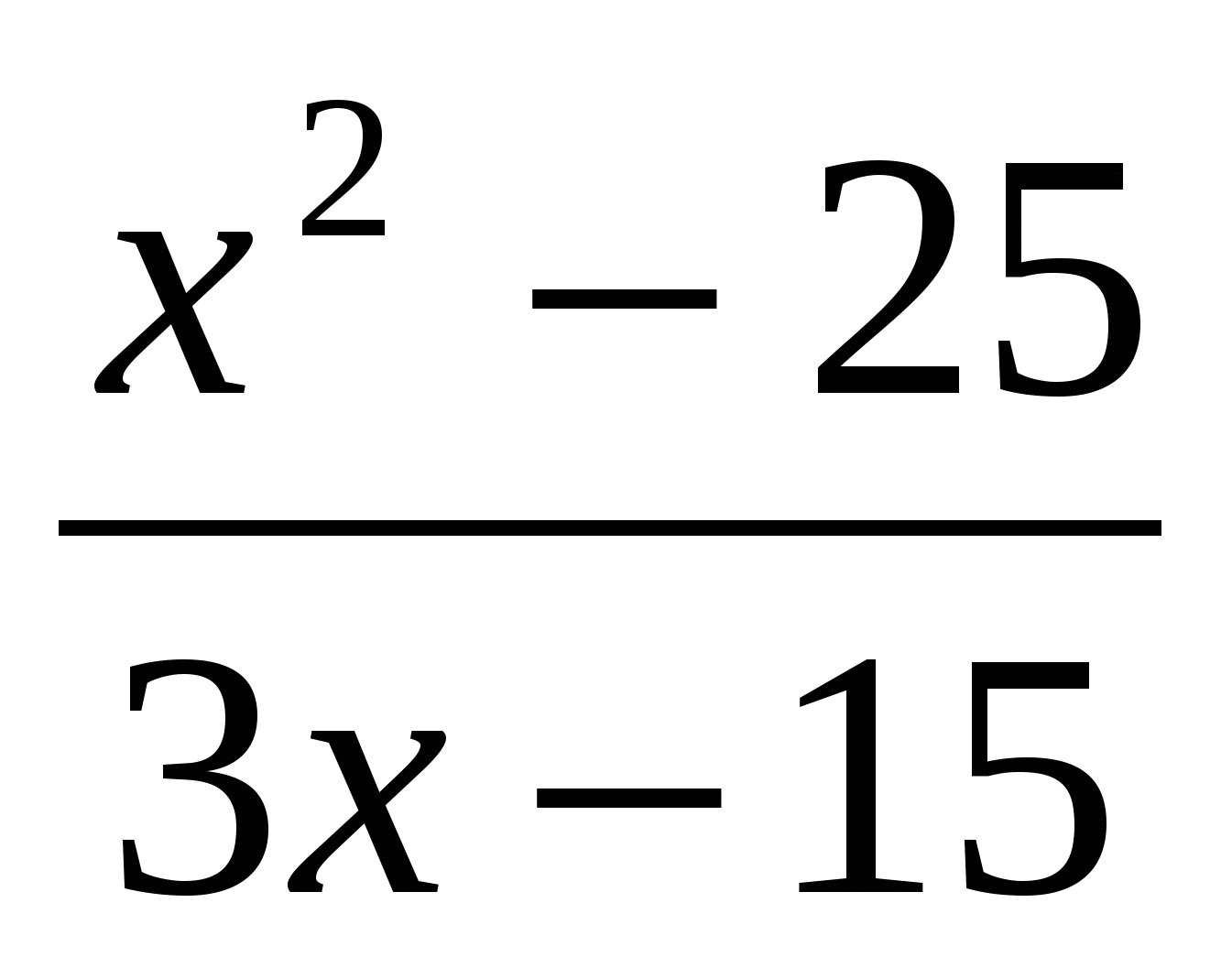
12)  26)
26) 
13)  27)
27) 
14)  28)
28) 
UN
DANS
D
E
ET
L
M
N
X-Y
b-4

a+b
5xy
AVEC
T
U
H
Ch
Oui
je
9ab
X-6
5
Enseignant : Le résultat est l'expression : « La réflexion commence par la surprise. » Aristote l’a dit il y a 2 500 ans.
Notre compatriote V. Sukhomlinsky estimait que « le sentiment de surprise est une source puissante du désir de savoir. De la surprise à la connaissance, il n’y a qu’un pas », et les mathématiques sont une merveilleuse source de surprise.

2) Tâche logique(2b.)
Professeur : Je vais essayer de vous surprendre maintenant en prouvant que 2 nombres sont égaux entre eux, en utilisant des lois algébriques et en effectuant des transformations identiques
5=6
Preuve
35+10-45=42+12-54
5(7+2-9)=6(7+2-9)
5=6
Ai-je raison ? Quelle loi a été enfreinte ? Trouvez l'erreur.
IV Jeu économique « Échange de connaissances » (travail en groupe).
Nous allons maintenant participer aux travaux de la « bourse ».
Informations générales "échange de connaissances".
Échange– une entreprise commerciale de production de services intermédiaires, où sont effectuées des opérations d'achat et de vente.
Bourse– une bourse sur laquelle sont négociés les principaux types de titres et d’actions.
Commerçant– un membre de la bourse qui effectue des transactions à ses frais.
Courtier– un membre de la bourse qui reçoit une rémunération pour l'exécution des ordres des clients.
Greffier– un membre de la bourse qui possède des informations commerciales, c'est-à-dire vendre des actions.
Comité d'arbitrage– un organisme qui règle les litiges concernant une transaction et les relations entre les participants aux échanges commerciaux.
Investissements- investissement de fonds.
Promotion– le type de sécurité, c'est-à-dire copie papier du capital.
Imaginez que vous soyez membres de la « bourse » - des « commerçants », dont la tâche est de préserver le capital initial, de l'augmenter en faisant le bon choix en « investissement ».
Après avoir accompli la tâche correctement, vous recevrez des « revenus » et achèterez des actions de l’entreprise correspondante.
Lors de l'exécution des tâches, vous pouvez recourir aux services d'un consultant intermédiaire.
Nous avons 5 groupes de courtiers. Chaque entreprise achète une tâche après avoir déterminé « l’investissement » le plus rentable (Annexe 1).
“Sieste"
2 talents
"Zinger"
3 talents
"Chocolat d'Ukraine"
4 talents
№32(1)
Page 13
№32(3)
Page 13
№32(4)
Page 13
№39(1)
Page 14
№39(2)
Page 14
№39(3)
Page 14
Les résultats sont résumés et la meilleure société de courtage est mise en avant. En récompense, une licence est délivrée qui vous permet de fournir des services de courtage aux clients.
(Annexe 2)
V Tâche intéressante.

VI Devoirs. (répéter le §8. effectuer le test)

VII Résumé de la leçon(évaluation de la notation des étudiants)
grade
Nombre de points
9-10
11-12
13-14
15-16
17-18
19-20
21-22
23-24
Plus de 25 ans
L'enseignant résume la leçon, lit les résultats de l'évaluation
"Micro ouvert"
1.Qu'est-ce qui était intéressant dans la leçon ?
2. Qu'est-ce qui a été difficile ?
Annexe 1. Actions d'entreprise

Annexe 2. Licence

ALGÈBRE
Tous les cours pour la 8e année
Leçon n°19
Sujet. Transformations identiques d'expressions rationnelles
Objectif : consolider les connaissances des étudiants sur les algorithmes de transformations identiques d'expressions rationnelles, les méthodes de transformation du rapport de deux expressions fractionnaires et les schémas d'application des propriétés des opérations arithmétiques lors de la transformation d'expressions rationnelles.
Type de cours : correction des connaissances, développement des compétences.
Visualisation et équipement : résumé de base « Transformations identiques d'expressions algébriques ».
Progression de la leçon
I. Étape organisationnelle
II.
Vérification des devoirs
Les exercices sur l'utilisation de techniques de transformation d'expressions qui ont la forme d'un rapport de deux expressions rationnelles (« fractions de quatre étages ») font l'objet d'une analyse minutieuse. Pour rendre ce travail plus conscient, vous pouvez demander aux élèves de remplir le tableau :
Il est clair que ce travail ne peut être efficace qu’en cas de corrections ultérieures.
Pour les élèves maîtrisant bien les techniques de travail avec des expressions soumises à contrôle à ce stade de la leçon, l'enseignant peut proposer des tâches supplémentaires de ce type et évaluer leur mise en œuvre.
III.
Formulation de vengeance et d'objectifs de cours
Un contrôle de l'achèvement des devoirs et une analyse des erreurs possibles en eux-mêmes créent une motivation pour les étudiants à travailler pour éliminer la cause des erreurs (correction des connaissances), ainsi qu'à améliorer les compétences (formation de compétences). Atteindre les meilleurs résultats de cette activité - corriger les connaissances et développer les compétences des élèves pour transformer des expressions rationnelles à l'aide des algorithmes étudiés pour effectuer des opérations arithmétiques avec des fractions rationnelles - constitue l'objectif didactique principal de la leçon.
Compte tenu de l'objectif didactique (accent mis sur le travail correctionnel) et afin de diversifier les formes de travail dans le cours, vous pouvez inviter les élèves à ce stade du cours à réaliser une enquête rapide (ou à réaliser un exercice interactif « Microphone ») ; la condition principale est une réponse claire et concise à la question.
1. Comment est formulée la propriété principale d'une fraction ?
2. Qu'arrive-t-il au signe d'une fraction si vous remplacez le signe de son numérateur ; dénominateur; numérateur et dénominateur ?
3. Comment additionner des fractions ayant les mêmes dénominateurs ?
4. Comment soustraire des fractions de dénominateurs identiques ?
5. Comment additionner des fractions avec des dénominateurs différents ? Donnez un exemple des fractions : a) et ; groupe .
6. Comment multiplier deux fractions ?
7. Quelle règle connaissez-vous pour élever une fraction à une puissance ?
8. Formulez la règle de division des fractions.
9. Parlez-nous de la procédure de conversion des expressions : a)  ; b)
; b)  ; V) .
; V) .
V. Formation de compétences
Réaliser des exercices oraux
1. Écrivez l’expression suivante sous forme de fraction irréductible :
UN) ; b)  ; V)
; V)  ; G) ; d) ; e) ; et) ; h) ; Et) ; À) ; j)
; G) ; d) ; e) ; et) ; h) ; Et) ; À) ; j)  .
.
2. Nommez le plus petit dénominateur commun des fractions (expressions) :
a) et ; b) une ; Et ; c) et ; Et ; d) et .
3. A quelles valeurs de la variable la valeur de la fraction est-elle égale à zéro ?
Faire des exercices d'écriture
Lors d'un cours de correction des connaissances et de mise en pratique des compétences, il serait logique de demander aux élèves de résoudre des exercices ayant approximativement le contenu suivant :
1. Conversion d'une expression rationnelle en fraction rationnelle (selon le schéma général établi dans la leçon 17).
1) Simplifiez l'expression : a) ; b)  ; V)
; V)  .
.
2) Simplifiez l'expression : a) ; b)  ; V) .
; V) .
3) Simplifiez l'expression :
UN)  ; b)
; b)  ; V)
; V)  ; G)
; G)  .
.
4) Suivez ces étapes :
UN)  ; b)
; b)  ; V)
; V)  ; G)
; G)  .
.
5) Simplifiez l'expression :
UN)  ; b)
; b)  ; V)
; V)  ;
;
G)  ; d)
; d)  ; e)
; e)  .
.
2. Représentation du rapport des expressions rationnelles fractionnaires sous la forme d'un rapport de polynômes (en utilisant la propriété fondamentale d'une fraction).
1) Présenté sous forme de fraction rationnelle :  .
.
2) Trouvez le sens de l'expression :
a) avec a = , b = ; b) à a = -8, b = 0,6.
3) Présenter sous forme de fraction rationnelle :
UN) ; b)  ; V) ; G) .
; V) ; G) .
3. Preuve que la valeur de l'expression ne dépend pas de la valeur de la variable.
1) Montrer que pour toutes les valeurs possibles des lettres, la valeur de l'expression  est égal à 0.
est égal à 0.
2) Montrer que pour tout n naturel la valeur de l'expression  est un nombre naturel.
est un nombre naturel.
4. Preuves d'identité.
Prouvez l’identité :
UN) ;
b) .
5. Exercices de répétition (notamment sur la recherche du CV d'une expression rationnelle et la recherche des valeurs des variables pour lesquelles la valeur de l'expression est égale à zéro).
6. Exercices logiques et tâches d'un niveau de complexité accru pour les étudiants ayant des niveaux de connaissances suffisants et élevés.
1) Présenter l'expression sous forme de fraction rationnelle : a) ; b) .
2) Montrer que pour toutes les valeurs admissibles des variables, la valeur de l'expression  ne dépend pas de a et b.
ne dépend pas de a et b.
3) l'expression manque-t-elle ?
|
|
@ Comme mentionné ci-dessus, la tâche de conversion d'expressions rationnelles en fractions rationnelles dans le cas général est une tâche assez complexe, car elle nécessite une maîtrise fluide des algorithmes permettant d'effectuer diverses opérations arithmétiques avec des fractions rationnelles, ainsi qu'un niveau de compétences assez élevé pour appliquer ces algorithmes dans la pratique et passer d'un algorithme à un autre. Ainsi, l'enseignant choisit le niveau de difficulté des tâches en fonction du niveau de connaissances et de compétences des élèves, sans sous-estimer les exigences des élèves, mais en créant en même temps une situation de réussite. Afin de préparer les étudiants à la perception de la section suivante (« Équations rationnelles »), ils doivent continuer à résoudre des exercices sur la recherche de l'ODZ d'une expression rationnelle et la recherche des valeurs des variables auxquelles la valeur de l'expression est égale. à zéro.
3. Répéter : définition d'un tout rationnel, expressions rationnelles rationnelles et fractionnaires, ODZ d'une expression rationnelle ; définition d'une équation, propriétés d'équivalence des équations, concept d'équation linéaire à une variable et algorithme de résolution d'une équation linéaire ; résoudre des équations linéaires (y compris des équations avec paramètres) ; répéter le contenu du concept de « proportion » et la propriété principale de proportion, résoudre plusieurs équations pour l'application de cette propriété (voir niveau 6).
Leçon et présentation sur le thème : "Transformation d'expressions rationnelles. Exemples de résolution de problèmes"
Matériel supplémentaire
Chers utilisateurs, n'oubliez pas de laisser vos commentaires, avis, souhaits. Tous les documents ont été vérifiés par un programme antivirus.
Supports pédagogiques et simulateurs dans la boutique en ligne Integral pour la 8e année
Manuel pour le manuel Muravin G.K. Un manuel pour le manuel de Makarychev Yu.N.
Le concept d'expression rationnelle
Le concept d'« expression rationnelle » est similaire au concept de « fraction rationnelle ». L'expression est également représentée sous forme de fraction. Seuls nos numérateurs ne sont pas des nombres, mais diverses sortes d'expressions. Il s'agit le plus souvent de polynômes. Une fraction algébrique est une expression fractionnaire composée de nombres et de variables.En résolvant de nombreux problèmes dans les classes élémentaires, après avoir effectué des opérations arithmétiques, nous avons reçu des valeurs numériques spécifiques, le plus souvent des fractions. Maintenant, après avoir effectué les opérations, nous obtiendrons des fractions algébriques. Les gars, n'oubliez pas : pour obtenir la bonne réponse, vous devez simplifier autant que possible l'expression avec laquelle vous travaillez. Il faut obtenir le plus petit degré possible ; les expressions identiques aux numérateurs et aux dénominateurs doivent être réduites ; avec des expressions qui peuvent être réduites, il faut le faire. Autrement dit, après avoir effectué une série d’actions, nous devrions obtenir la fraction algébrique la plus simple possible.
Procédure avec expressions rationnelles
La procédure pour effectuer des opérations avec des expressions rationnelles est la même que pour les opérations arithmétiques. On effectue d’abord les opérations entre parenthèses, puis la multiplication et la division, l’exponentiation et enfin l’addition et la soustraction.Prouver une identité signifie montrer que pour toutes les valeurs des variables, les côtés droit et gauche sont égaux. Il existe de nombreux exemples de preuves d’identité.
Les principaux moyens de résoudre les identités comprennent.
- Transformez le côté gauche pour qu'il soit égal au côté droit.
- Transformez le côté droit pour qu'il soit égal au côté gauche.
- Transformez les côtés gauche et droit séparément jusqu'à obtenir la même expression.
- Le côté droit est soustrait du côté gauche et le résultat devrait être zéro.
Conversion d'expressions rationnelles. Exemples de résolution de problèmes
Exemple 1.Prouvez l’identité :
$(\frac(a+5)(5a-1)+\frac(a+5)(a+1)):(\frac(a^2+5a)(1-5a))+\frac(a ^2+5)(a+1)=a-1$.
Solution.
Il faut évidemment transformer le côté gauche.
Commençons par suivre les étapes entre parenthèses :
1) $\frac(a+5)(5a-1)+\frac(a+5)(a+1)=\frac((a+5)(a+1)+(a+5)(5a -1))((a+1)(5a-1))=$
$=\frac((a+5)(a+1+5a-1))((a+1)(5a-1))=\frac((a+5)(6a))((a+1 )(5a-1))$
Vous devriez essayer d’appliquer au maximum les facteurs communs.
2) Transformez l'expression par laquelle on divise :
$\frac(a^2+5a)(1-5a)=\frac(a(a+5))((1-5a)=\frac(a(a+5))(-(5a-1) )$
.3) Effectuer l'opération de division :
$\frac((a+5)(6a))((a+1)(5a-1)):\frac(a(a+5))(-(5a-1))=\frac((a +5)(6a))((a+1)(5a-1))*\frac(-(5a-1))(a(a+5))=\frac(-6)(a+1) $.
4) Effectuez l'opération d'addition :
$\frac(-6)(a+1)+\frac(a^2+5)(a+1)=\frac(a^2-1)(a+1)=\frac((a-1 )(a+1))(a+))=a-1$.
Les parties droite et gauche coïncidaient. Cela signifie que l'identité est prouvée.
Les gars, pour résoudre cet exemple, nous avions besoin de connaître de nombreuses formules et opérations. Nous voyons qu’après la transformation, la grande expression s’est transformée en une très petite. Lors de la résolution de presque tous les problèmes, les transformations conduisent généralement à des expressions simples.
Exemple 2.
Simplifiez l'expression :
$(\frac(a^2)(a+b)-\frac(a^3)(a^2+2ab+b^2)):(\frac(a)(a+b)-\frac( un^2)(a^2-b^2))$.
Solution.
Commençons par les premières parenthèses.
1. $\frac(a^2)(a+b)-\frac(a^3)(a^2+2ab+b^2)=\frac(a^2)(a+b)-\frac (a^3)((a+b)^2)=\frac(a^2(a+b)-a^3)((a+b)^2)=$
$=\frac(a^3+a^2 b-a^3)((a+b)^2)=\frac(a^2b)((a+b)^2)$.
2. Transformez les deuxièmes parenthèses.
$\frac(a)(a+b)-\frac(a^2)(a^2-b^2)=\frac(a)(a+b)-\frac(a^2)((a-b )(a+b))=\frac(a(a-b)-a^2)((a-b)(a+b))=$
$=\frac(a^2-ab-a^2)((a-b)(a+b))=\frac(-ab)((a-b)(a+b))$.
3. Faisons la division.
$\frac(a^2b)((a+b)^2) :\frac(-ab)((a-b)(a+b))=\frac(a^2b)((a+b)^2 )*\frac((a-b)(a+b))((-ab))=$
$=-\frac(a(a-b))(a+b)$
Réponse : $-\frac(a(a-b))(a+b)$.
Exemple 3.
Suivez ces étapes :
$\frac(k-4)(k-2):(\frac(80k)((k^3-8)+\frac(2k)(k^2+2k+4)-\frac(k-16 )(2-k))-\frac(6k+4)((4-k)^2)$.
Solution.
Comme toujours, vous devez commencer par les parenthèses.
1. $\frac(80k)(k^3-8)+\frac(2k)(k^2+2k+4)-\frac(k-16)(2-k)=\frac(80k)( (k-2)(k^2+2k+4)) +\frac(2k)(k^2+2k+4)+\frac(k-16)(k-2)=$
$=\frac(80k+2k(k-2)+(k-16)(k^2+2k+4))((k-2)(k^2+2k+4))=\frac(80k +2k^2-4k+k^3+2k^2+4k-16k^2-32k-64)((k-2)(k^2+2k+4))=$
$=\frac(k^3-12k^2+48k-64)((k-2)(k^2+2k+4))=\frac((k-4)^3)((k-2 )(k^2+2k+4))$.
2. Faisons maintenant la division.
$\frac(k-4)(k-2):\frac((k-4)^3)((k-2)(k^2+2k+4))=\frac(k-4)( k-2)*\frac((k-2)(k^2+2k+4))((k-4)^3)=\frac((k^2+2k+4))((k- 4)^2)$.
3. Utilisons la propriété : $(4-k)^2=(k-4)^2$.
4. Effectuons l'opération de soustraction.
$\frac((k^2+2k+4))((k-4)^2)-\frac(6k+4)((k-4)^2)=\frac(k^2-4k) ((k-4)^2)=\frac(k(k-4))((k-4)^2)=\frac(k)(k-4)$.
Comme nous l'avons dit plus tôt, vous devez simplifier la fraction autant que possible.
Réponse : $\frac(k)(k-4)$.
Problèmes à résoudre de manière autonome
1. Prouvez l’identité :$\frac(b^2-14)(b-4)-(\frac(3-b)(7b-4)+\frac(b-3)(b-4))*\frac(4-7b )(9b-3b^2)=b+4$.
2. Simplifiez l'expression :
$\frac(4(z+4)^2)(z-2)*(\frac(z)(2z-4)-\frac(z^2+4)(2z^2-8)-\frac (2)(z^2+2z))$.
3. Suivez ces étapes :
$(\frac(a-b)(a^2+2ab+b^2)-\frac(2a)((a-b)(a+b))+\frac(a-b)((a-b)^2))*\ frac(a^4-b^4)(8ab^2)+\frac(2b^2)(a^2-b^2)$.










