Équation d'une tangente au graphique d'une fonction. Équations fonctionnelles

Une tangente est une ligne droite , qui touche le graphique de la fonction en un point et dont tous les points sont à la distance la plus courte du graphique de la fonction. Par conséquent, la tangente passe tangentiellement au graphique de la fonction sous un certain angle, et plusieurs tangentes sous des angles différents ne peuvent pas passer par le point de tangence. Les équations tangentes et les équations normales au graphique d'une fonction sont construites à l'aide de la dérivée.

L'équation de la tangente est dérivée de l'équation de la droite .

Dérivons l'équation de la tangente, puis l'équation de la normale au graphique de la fonction.

oui = kx + b .

En lui k- coefficient angulaire.

De là, nous obtenons l'entrée suivante :

oui - oui 0 = k(X - X 0 ) .

Valeur dérivée F "(X 0 ) les fonctions oui = F(X) à ce point X0 égale à la pente k= tg φ tangente au graphique d'une fonction tracée par un point M0 (X 0 , oui 0 ) , Où oui0 = F(X 0 ) . C'est signification géométrique de la dérivée .

Ainsi, nous pouvons remplacer k sur F "(X 0 ) et obtenez ce qui suit équation de la tangente au graphique d'une fonction :

oui - oui 0 = F "(X 0 )(X - X 0 ) .

Dans les problèmes impliquant la composition de l'équation d'une tangente au graphique d'une fonction (et nous y reviendrons bientôt), il est nécessaire de réduire l'équation obtenue à partir de la formule ci-dessus à équation d'une droite sous forme générale. Pour ce faire, vous devez déplacer toutes les lettres et tous les chiffres vers la gauche de l'équation et laisser zéro sur le côté droit.

Parlons maintenant de l’équation normale. Normale - il s'agit d'une droite passant par le point de tangence au graphique de la fonction perpendiculaire à la tangente. Équation normale :

(X - X 0 ) + F "(X 0 )(oui - oui 0 ) = 0

Pour vous échauffer, il vous est demandé de résoudre vous-même le premier exemple, puis d’examiner la solution. Il y a tout lieu d’espérer que cette tâche ne sera pas une « douche froide » pour nos lecteurs.

Exemple 0. Créer une équation tangente et une équation normale pour le graphique d'une fonction en un point M (1, 1) .

Exemple 1.Écrire une équation tangente et une équation normale au graphique d'une fonction , si l'abscisse est tangente .

Trouvons la dérivée de la fonction :

Nous avons maintenant tout ce qui doit être substitué dans l’entrée donnée dans l’aide théorique pour obtenir l’équation tangente. On a

Dans cet exemple, nous avons eu de la chance : la pente s'est avérée être nulle, il n'était donc pas nécessaire de réduire séparément l'équation à sa forme générale. Nous pouvons maintenant créer l'équation normale :

Dans la figure ci-dessous : le graphique de la fonction est bordeaux, la tangente est verte, la normale est orange.

L'exemple suivant n'est pas non plus compliqué : la fonction, comme dans le précédent, est également un polynôme, mais la pente ne sera pas égale à zéro, donc une étape supplémentaire sera ajoutée - amenant l'équation à une forme générale.

Exemple 2.

Solution. Trouvons l'ordonnée du point tangent :

Trouvons la dérivée de la fonction :

.

Trouvons la valeur de la dérivée au point de tangence, c'est-à-dire la pente de la tangente :

Nous remplaçons toutes les données obtenues dans la « formule vierge » et obtenons l'équation tangente :

On ramène l'équation à sa forme générale (on rassemble toutes les lettres et chiffres autres que zéro sur le côté gauche, et on laisse zéro à droite) :

On compose l'équation normale :

Exemple 3.Écrivez l'équation de la tangente et l'équation de la normale au graphique de la fonction si l'abscisse est le point de tangence.

Solution. Trouvons l'ordonnée du point tangent :

Trouvons la dérivée de la fonction :

.

Trouvons la valeur de la dérivée au point de tangence, c'est-à-dire la pente de la tangente :

.

On retrouve l'équation tangente :

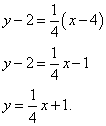
Avant de ramener l'équation à sa forme générale, il faut la « peigner » un peu : multiplier terme par terme par 4. On fait cela et amener l'équation à sa forme générale :

On compose l'équation normale :

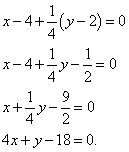
Exemple 4.Écrivez l'équation de la tangente et l'équation de la normale au graphique de la fonction si l'abscisse est le point de tangence.

Solution. Trouvons l'ordonnée du point tangent :

.

Trouvons la dérivée de la fonction :

Trouvons la valeur de la dérivée au point de tangence, c'est-à-dire la pente de la tangente :

.

On obtient l'équation tangente :

On ramène l'équation à sa forme générale :

On compose l'équation normale :

Une erreur courante lors de l'écriture d'équations tangentes et normales est de ne pas remarquer que la fonction donnée dans l'exemple est complexe et de calculer sa dérivée comme la dérivée d'une fonction simple. Les exemples suivants proviennent déjà de fonctions complexes(la leçon correspondante s'ouvrira dans une nouvelle fenêtre).

Exemple 5.Écrivez l'équation de la tangente et l'équation de la normale au graphique de la fonction si l'abscisse est le point de tangence.

Solution. Trouvons l'ordonnée du point tangent :

Attention! Cette fonction est complexe, puisque l'argument tangent (2 X) est elle-même une fonction. On trouve donc la dérivée d’une fonction comme la dérivée d’une fonction complexe.

Il existe donc une volonté naturelle de réduire une équation d’ordre supérieur à la première à une équation d’ordre inférieur. Dans certains cas, cela peut être fait. Regardons-les.

1. Les équations de la forme y (n) =f(x) sont résolues par intégration séquentielle n fois
, ,… .
Exemple. Résolvez l'équation xy""=1. On peut donc écrire y"=ln|x| + C 1 et, en intégrant à nouveau, on obtient finalement y=∫ln|x| + C 1 x + C 2

2. Dans les équations de la forme F(x,y (k) ,y (k +1) ,..,y (n))=0 (c'est-à-dire ne contenant pas explicitement une fonction inconnue et certaines de ses dérivées), l'ordre est réduit en changeant la variable y (k) = z(x). Alors y (k +1) =z"(x),...,y (n) = z (n - k) (x) et on obtient l'équation F(x,z,z",..,z (n - k)) d'ordre n-k. Sa solution est la fonction z = φ(x,C 1 ,C 2 ,…,C n) ou, en nous rappelant ce qu'est z, nous obtenons l'équation y (n- k) = φ(x,C 1 ,C 2 , …, C n - k) considéré dans le cas du type 1.
Exemple 1. Résolvez l'équation x 2 y"" = (y") 2. Effectuez le remplacement y"=z(x) . Alors y""=z"(x). En remplaçant dans l'équation d'origine, nous obtenons x 2 z"=z 2. En séparant les variables, nous obtenons . En intégrant, nous avons , ou, ce qui revient au même, . La dernière relation s'écrit sous la forme , d'où . En intégrant, on obtient finalement
Exemple 2. Résolvez l'équation x 3 y"" +x 2 y"=1. Nous effectuons un changement de variables : y"=z; y""=z"
x 3 z"+x 2 z=1. On fait un changement de variables : z=u/x; z"=(u"x-u)/x 2
x 3 (u"x-u)/x 2 +x 2 u/x=1 ou u"x 2 -xu+xu=1 ou u"x^2=1. De : u"=1/x 2 ou du/ dx=1/x 2 ou u = int(dx/x 2) = -1/x+c 1
Puisque z=u/x, alors z = -1/x 2 +c 1 /x. Puisque y"=z, alors dy/dx=-1/x 2 +c 1 /x
y = int(c 1 dx/x-dx/x 2) =c 1 ln(x) + 1/x + c 2. Réponse : y = c 1 ln(x) + 1/x + c 2

3. L'équation suivante qui peut être réduite dans l'ordre est une équation de la forme F(y,y",y"",…,y (n))=0, qui ne contient pas explicitement de variable indépendante. L'ordre de l'équation est réduite en remplaçant la variable y" =p(y) , où p est la nouvelle fonction souhaitée en fonction de y. Alors
= et ainsi de suite. Par induction, nous avons y (n) =φ(p,p",..,p (n-1)). En substituant dans l'équation d'origine, nous réduisons son ordre de un.

Exemple. Résolvez l'équation (y") 2 +2yy""=0. Nous effectuons le remplacement standard y"=p(y), puis y″=p′·p. En substituant dans l'équation, on obtient En séparant les variables, pour p≠0, on a en intégrant, on obtient. ou, ce qui est la même chose, . Alors ou. En intégrant la dernière égalité, on obtient finalement En séparant les variables, on pourrait perdre la solution y=C, qui est obtenue pour p=0, ou, ce qui revient au même, pour y"=0, mais elle est contenue dans celle obtenue ci-dessus.

4. Parfois, il est possible de remarquer une fonctionnalité qui vous permet d'abaisser l'ordre de l'équation d'une manière différente de celles évoquées ci-dessus. Montrons cela avec des exemples.

Exemples.
1. Si les deux côtés de l'équation yy"""=y′y″ sont divisés par yy″, nous obtenons une équation qui peut être réécrite comme (lny″)′=(lny)′. De la dernière relation, il s'ensuit que lny″=lny + lnC, ou, ce qui revient au même, y″=Cy Le résultat est une équation d'un ordre de grandeur inférieur et du type discuté précédemment.
2. De même, pour l'équation yy″=y′(y′+1) nous avons, ou (ln(y"+1))" = (lny)". De la dernière relation il résulte que ln(y"+ 1) = lny + lnC 1, ou y"=C 1 y-1. En séparant les variables et en intégrant, on obtient ln(C 1 y-1) = C 1 x+C 2
Décider équations qui peuvent être réduites dans l'ordre possible en utilisant un service spécial

Soit une fonction f, qui à un moment donné x 0 a une dérivée finie f (x 0). Alors la droite passant par le point (x 0 ; f (x 0)), ayant un coefficient angulaire f '(x 0), est appelée tangente.

Que se passe-t-il si la dérivée n'existe pas au point x 0 ? Il existe deux options :

1. Il n’y a pas non plus de tangente au graphique. Un exemple classique est la fonction y = |x | au point (0 ; 0).
2. La tangente devient verticale. C'est vrai par exemple pour la fonction y = arcsin x au point (1 ; π /2).

Équation tangente

Toute droite non verticale est donnée par une équation de la forme y = kx + b, où k est la pente. La tangente ne fait pas exception, et pour créer son équation en un point x 0, il suffit de connaître la valeur de la fonction et la dérivée en ce point.

Soit donc une fonction y = f (x) qui a une dérivée y = f '(x) sur le segment. Alors en tout point x 0 ∈ (a ; b) une tangente peut être tracée au graphique de cette fonction, qui est donnée par l'équation :

y = f '(x 0) (x − x 0) + f (x 0)

Ici f '(x 0) est la valeur de la dérivée au point x 0, et f (x 0) est la valeur de la fonction elle-même.

Tâche. Étant donné la fonction y = x 3 . Écrivez une équation pour la tangente au graphique de cette fonction au point x 0 = 2.

Équation tangente : y = f '(x 0) · (x − x 0) + f (x 0). Le point x 0 = 2 nous est donné, mais il faudra calculer les valeurs f (x 0) et f '(x 0).

Tout d’abord, trouvons la valeur de la fonction. Tout est simple ici : f (x 0) = f (2) = 2 3 = 8 ;
Trouvons maintenant la dérivée : f '(x) = (x 3)' = 3x 2 ;
Nous substituons x 0 = 2 dans la dérivée : f '(x 0) = f '(2) = 3 2 2 = 12 ;
Au total, nous obtenons : y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
C'est l'équation tangente.

Tâche. Écrivez une équation pour la tangente au graphique de la fonction f (x) = 2sin x + 5 au point x 0 = π /2.

Cette fois, nous ne décrirons pas chaque action en détail, nous indiquerons seulement les étapes clés. Nous avons:

f (x 0) = f (π /2) = 2sin (π /2) + 5 = 2 + 5 = 7 ;
f '(x) = (2sin x + 5)' = 2cos x ;
f '(x 0) = f '(π /2) = 2cos (π /2) = 0 ;

Équation tangente :

y = 0 · (x − π /2) + 7 ⇒ y = 7

Dans ce dernier cas, la ligne droite s'est avérée horizontale, car son coefficient angulaire k = 0. Il n'y a rien de mal à cela - nous sommes juste tombés sur un point extrême.

Soit l'équation f(x) = 0 . Nombre X est appelé racine d'une équation donnée si, lorsqu'elle est substituée dans l'équation, elle la transforme en une égalité, c'est-à-dire f(x) = 0 . Nombre X appelé le zéro d'une fonction f(x) .Trouver les racines d’une équation avec une certaine précision peut être divisé en deux étapes :

1) séparation des racines, c'est-à-dire l'établissement d'intervalles contenant une racine de l'équation ;

2) calcul de la racine appartenant à l'intervalle sélectionné avec une précision donnée.

On sait que si la fonction f(x) est continu et prend les extrémités du segment [un B] significations de différents signes, c'est-à-dire f(une)× f(b)< 0 , alors à l'intérieur de ce segment il y a un zéro de la fonction.

Pour séparer (ou localiser) la racine de l'équation f(x) = 0 pour une fonction continue dans le domaine de définition f(x) vous pouvez créer un tableau de valeurs de fonctions y = f(x) à un certain intervalle de changement d'argument X . Si pour certaines valeurs adjacentes de l'argument les valeurs de la fonction ont des signes différents, alors le zéro de la fonction est situé entre elles.

Soit l'équation f(x) = 0 , où la fonction f(x) continu sur le segment [un B] Et f(une)× f(b)< 0 .Pour calculer la racine de cette équation
x О[un B] est le milieu de ce segment x1 = 0,5(a+b) . Si f(x 1) ¹ 0 , puis pour continuer les calculs, sélectionnez une des parties de ce segment
[une, x 1] ou [x1,b] , aux extrémités duquel la fonction f(x) a des signes opposés. Les extrémités du nouveau segment sont indiquées un 1 Et b1 . Nouveau segment [une 1 , b 1] à nouveau divisé en deux et les calculs sont effectués selon le schéma décrit, et ainsi de suite. Le résultat est soit la racine exacte d'une équation donnée à un moment donné, soit une séquence de segments imbriqués [un B] ,
[une 1 , b 1] , … , [a n, b n] , ..., tel que:

f(une n)× f(b n)< 0 , n =1, 2, …

Nombre X - limite générale des séquences (un) Et (milliards) – est la racine de l’équation f(x) = 0 .

Estimation de l'erreur de solution par n La -ème étape des calculs a la forme.

2.2 Méthodologie de résolution d'équations et d'inégalités

Les équations et les inégalités sont un sujet traditionnel dans le cours de mathématiques scolaire, occupant une place importante, depuis les classes inférieures, où les équations et inégalités les plus simples sont introduites jusqu'à l'introduction d'une théorie basée sur les propriétés des opérations arithmétiques, et se terminant par le niveau supérieur. niveaux, où les équations transcendantales sont résolues.

Les équations et les inégalités représentent l'appareil algébrique, le langage dans lequel divers types de problèmes sont traduits, y compris les problèmes appliqués, et leurs modèles mathématiques sont construits.

Utiliser la monotonie des fonctions pour résoudre des équations et des inégalités. L’une des idées les plus fréquemment rencontrées est bien illustrée par la résolution de l’inégalité simple suivante :

1. Résoudre les inégalités :.

Solution. Il existe deux solutions standards : la quadrature (fournie
; si
, l'inégalité est satisfaite) et remplacement de l'inconnue
.

Considérons une autre méthode - non standard. La fonction située sur le côté gauche augmente de façon monotone, tandis que la fonction de la première partie diminue. D'après des considérations graphiques évidentes, il s'ensuit que l'équation
X 0 est la solution de cette équation, alors quand
sera, et la solution à cette inégalité sera
. Signification X 0 est facile à sélectionner : X 0 = 1.

Répondre.
.

2. Résous l'équation:
.

Solution. Cette équation a une solution évidente X= 1. Montrons qu'il n'y a pas d'autres solutions. Divisons les deux parties par , on a
. Le côté gauche est une fonction décroissante de façon monotone. Par conséquent, il prend chacune de ses valeurs une fois, c'est-à-dire cette équation a une solution unique.

Répondre. X = 1.

Ainsi, l’idée de base sur laquelle reposaient les solutions de ces deux exemples est assez simple : si F(X) augmente de façon monotone, et φ (X) diminue de façon monotone, alors l'équation F(X) = φ (X) a au plus une solution, et si X = X 0 est la solution de cette équation, alors quand X > X 0 (X est dans le cadre des deux fonctions F(X) Et φ (X) ) volonté F(X) > φ (X) , et quand X X 0 sera

F(X) φ (X) .

Il convient de prêter attention à une modification de cette idée, à savoir : si F(X) est une fonction monotone, alors de l'égalité F(X) = F(oui) il s'ensuit que X = oui .

3.Résous l'équation:.

Solution . Transformons l'équation :

.

Considérez la fonction
.

Prouvons que lorsque t > 1 cette fonction diminue de façon monotone. Cela peut être fait, par exemple, de manière standard : trouver la dérivée

et prouver que lorsque t > 1
. Montrons une autre manière :

.

La fonction résultante est évidemment décroissante (la base augmente, sous le signe du logarithme la fonction diminue).

Notre équation a la forme : , ce qui signifie . A gauche se trouve une fonction croissante, donc la solution est unique, elle se trouve facilement par sélection : X = 4.

Répondre. X = 4 .

Équations de la formeF ( F ( X )) = X . Lors de la résolution d’équations de ce type, le théorème suivant est utile :

Si y = f(x) est une fonction croissante de façon monotone, alors les équations

F(X) = X(UN)

F (F (X)) = X (B)

équivalent.

Preuve. Le fait que l’équation (B) soit une conséquence de l’équation (A) est évident : toute racine (A) satisfait (B). (Si

F (X 0 ) = X 0 , Que F (F (X 0 )) = F (X 0 ) = X 0.). Montrons que toute racine de l'équation (B) satisfait l'équation (A). Laisser X 0 tel que F (F (X 0 )) = X 0 .Supposons que F (X 0 ) ≠ X 0 et pour plus de précision F (X 0 ) > X 0 . Alors F (F (X 0 )) > F (X 0 ) > X 0, ce qui contredit l'hypothèse ( F (F (X 0 )) = X 0). Le théorème a été prouvé.

Le théorème est-il vrai pour une fonction décroissante monotone ?

Commentaire. Si oui = F (X) augmente de façon monotone, alors pour tout kéquations
Et F (X) = X sont équivalents.

Donnons quelques exemples d'utilisation de ce théorème.

1. Résous l'équation:
.

Solution. Réécrivons l'équation.
. Considérez la fonction
. Cette fonction augmente de façon monotone. Nous avons l'équation

F (F (X)) = X. Conformément au théorème, nous le remplaçons par l'équation équivalente F (X) = X ou .

Répondre.

2. Résous l'équation:

.

Solution. Transformons l'équation :
.

Cette équation ressemble à : F (F (X)) = X, Où
.

D'après le théorème, nous avons une équation équivalente :
,

Répondre.
.

3. Résoudre un système d'équations:
.

Solution. Considérons la fonction. Parce que le

Devant tout le monde t, Que F (t) augmente.

Le système a la forme oui = F (X), z = F (oui), X = F (z), ceux. X = F (F (F (X))).

D'après le théorème X satisfait l'équation F (X) = X ou

Répondre.(0, 0, 0), (-1, -1, -1).

Utilisation des propriétés extrêmes des fonctions considérées. Notes. Les idées principales de ce point sont assez clairement visibles à partir des exemples :

1. Résous l'équation:
.

Solution. Le côté gauche de cette équation ne dépasse pas 2 et le côté droit ne dépasse pas 2. Par conséquent, l'égalité ne peut se produire que si les côtés gauche et droit sont égaux à 2, c'est-à-dire X = 0.

Commentaire. Cette situation, où la plus petite valeur d'une fonction située dans une partie de l'équation est égale à la plus grande valeur d'une fonction située dans l'autre partie, peut être généralisée. Un cas plus général est celui des équations de la forme F (X) = φ (X) , Pour qui
acceptable pour tous X(formellement, nous pouvons réécrire cette équation comme

F (X) = φ (X) = 0, nous arrivons donc à la situation déjà considérée, puisque la plus grande valeur du membre de droite est zéro).

2. Résous l'équation:.

Montrons que cette équation n'a pas de solutions. Passons à la conséquence (potentialiser) :
.

Estimons le membre de gauche en fonction de l'inégalité entre la moyenne géométrique et la moyenne arithmétique

:

ceux. le côté gauche est plus petit que le droit. L'équation n'a pas de solutions.

Répondre. Il n'y a pas de décision.

3. Résolvez le système d'équations :

Solution. Prouvons-le.

Laissez pour certitude X 5 > X 4, puis à partir des deux premières équations on obtient, à partir desquelles
et particulièrement . Ensuite, à partir du troisième et du quatrième, nous obtenons
et particulièrement
. De la dernière paire, nous trouvons . Le résultat est une contradiction (et
, c'est à dire. , mais on a supposé que
).

Moyens,
, d'ici
etc., toutes les inconnues sont égales les unes aux autres.

Répondre.(0, 0, 0, 0,0);
.

Problèmes dont la formulation est non standard et qui impliquent des équations ou des inégalités. Cette catégorie comprend notamment des problèmes dans lesquels il faut déterminer le nombre de racines d'une équation donnée, prouver l'existence d'une racine sur un certain intervalle et résoudre une équation ou une inégalité sur un intervalle donné. Regardons quelques exemples.

1. Montrer que l'équation
a un positif décision et une décision négative. méthodes d'enseignement des mathématiques en moyenne école: Cahier de texte. manuel de l'élève....