ફંક્શનની સીમા શોધો. કાર્યમાં વધારો, ઘટાડો અને ચરમસીમા

કાર્યની સીમા શું છે અને એક્સ્ટ્રીમમ માટે જરૂરી સ્થિતિ શું છે?

ફંક્શનની સીમા એ ફંક્શનની મહત્તમ અને ન્યૂનતમ છે.

પૂર્વશરતફંક્શનની મહત્તમ અને ન્યૂનતમ (એક્સ્ટ્રીમમ) નીચે મુજબ છે: જો ફંક્શન f(x) ની સીમા x = a બિંદુ પર છે, તો આ બિંદુએ ડેરિવેટિવ કાં તો શૂન્ય છે, અથવા અનંત છે, અથવા અસ્તિત્વમાં નથી.

આ સ્થિતિ જરૂરી છે, પરંતુ પૂરતી નથી. બિંદુ x = a પરનું વ્યુત્પન્ન શૂન્ય, અનંત સુધી જઈ શકે છે અથવા આ બિંદુએ એક્સ્ટ્રીમમ ધરાવતા ફંક્શન વિના અસ્તિત્વમાં નથી.

તે કેવું છે પૂરતી સ્થિતિકાર્યની સીમા (મહત્તમ અથવા લઘુત્તમ)?

પ્રથમ શરત:

જો, બિંદુ x = a ની પર્યાપ્ત નિકટતામાં, વ્યુત્પન્ન f?(x) a ની ડાબી બાજુએ સકારાત્મક અને a ની જમણી બાજુ નકારાત્મક હોય, તો બિંદુ x = a પર f(x) ફંક્શન ધરાવે છે મહત્તમ

જો, બિંદુ x = a ની પૂરતી નિકટતામાં, વ્યુત્પન્ન f?(x) a ની ડાબી બાજુએ ઋણ અને a ની જમણી બાજુ ધન હોય, તો બિંદુ x = a પર f(x) ફંક્શન ધરાવે છે ન્યૂનતમપૂરી પાડવામાં આવેલ છે કે ફંકશન f(x) અહીં સતત છે.

તેના બદલે, તમે ફંક્શનના અંતિમ ભાગ માટે બીજી પર્યાપ્ત સ્થિતિનો ઉપયોગ કરી શકો છો:

બિંદુ x = a પ્રથમ વ્યુત્પન્ન f?(x) અદ્રશ્ય થવા દો; જો બીજું વ્યુત્પન્ન f??(a) ઋણ છે, તો ફંકશન f(x) બિંદુ x = a પર મહત્તમ છે, જો તે હકારાત્મક છે, તો તેની પાસે ન્યૂનતમ છે.

ફંક્શનનું નિર્ણાયક બિંદુ શું છે અને તેને કેવી રીતે શોધવું?

આ ફંક્શન આર્ગ્યુમેન્ટનું મૂલ્ય છે કે જેના પર ફંક્શનની એક્સ્ટ્રીમમ (એટલે ​​​​કે મહત્તમ અથવા ન્યૂનતમ) છે. તેને શોધવા માટે તમારે જરૂર છે વ્યુત્પન્ન શોધોફંક્શન f?(x) અને, તેને શૂન્ય સાથે સરખાવીને, સમીકરણ ઉકેલો f?(x) = 0. આ સમીકરણના મૂળ, તેમજ તે બિંદુઓ કે જેના પર આ ફંક્શનનું વ્યુત્પન્ન અસ્તિત્વમાં નથી, તે નિર્ણાયક બિંદુઓ છે, એટલે કે, દલીલના મૂલ્યો કે જેના પર એક્સ્ટ્રીમમ હોઈ શકે છે. તેમને જોઈને સરળતાથી ઓળખી શકાય છે વ્યુત્પન્ન ગ્રાફ: અમે દલીલના તે મૂલ્યોમાં રસ ધરાવીએ છીએ કે જેના પર ફંક્શનનો ગ્રાફ એબ્સીસા અક્ષ (ઑક્સ અક્ષ) ને છેદે છે અને તે મૂલ્યો કે જેના પર આલેખ વિરામનો ભોગ બને છે.

ઉદાહરણ તરીકે, ચાલો શોધીએ પેરાબોલાના અંતિમ ભાગ.

કાર્ય y(x) = 3x2 + 2x - 50.

ફંક્શનનું વ્યુત્પન્ન: y?(x) = 6x + 2

સમીકરણ ઉકેલો: y?(x) = 0

6x + 2 = 0, 6x = -2, x = -2/6 = -1/3

IN આ કિસ્સામાંનિર્ણાયક બિંદુ x0=-1/3 છે. તે આ દલીલ મૂલ્ય સાથે છે જે ફંક્શન ધરાવે છે આત્યંતિક. તેને શોધો, "x" ને બદલે ફંક્શન માટે અભિવ્યક્તિમાં મળેલ સંખ્યાને બદલો:

y0 = 3*(-1/3)2 + 2*(-1/3) - 50 = 3*1/9 - 2/3 - 50 = 1/3 - 2/3 - 50 = -1/3 - 50 = -50.333.

કાર્યની મહત્તમ અને લઘુત્તમ કેવી રીતે નક્કી કરવી, એટલે કે. તેના સૌથી મોટા અને નાના મૂલ્યો?

જો વ્યુત્પત્તિની નિશાની જ્યારે પસાર થાય છે નિર્ણાયક બિંદુ x0 “પ્લસ” થી “માઈનસ” માં બદલાય છે, પછી x0 છે મહત્તમ બિંદુ; જો વ્યુત્પન્નનું ચિહ્ન માઈનસથી વત્તામાં બદલાય છે, તો x0 છે ન્યૂનતમ બિંદુ; જો ચિહ્ન બદલાતું નથી, તો પછી બિંદુ x0 પર મહત્તમ અથવા લઘુત્તમ નથી.

ધ્યાનમાં લેવાયેલા ઉદાહરણ માટે:

અમે નિર્ણાયક બિંદુની ડાબી બાજુએ દલીલનું મનસ્વી મૂલ્ય લઈએ છીએ: x = -1

x = -1 પર, વ્યુત્પન્નનું મૂલ્ય y હશે?(-1) = 6*(-1) + 2 = -6 + 2 = -4 (એટલે ​​​​કે ચિહ્ન "માઈનસ" છે).

હવે આપણે નિર્ણાયક બિંદુની જમણી તરફ દલીલનું મનસ્વી મૂલ્ય લઈએ છીએ: x = 1

x = 1 પર, વ્યુત્પન્નનું મૂલ્ય y(1) = 6*1 + 2 = 6 + 2 = 8 હશે (એટલે ​​​​કે ચિહ્ન "વત્તા" છે).

જેમ તમે જોઈ શકો છો, નિર્ણાયક બિંદુમાંથી પસાર થતી વખતે વ્યુત્પન્ન ચિહ્ન માઈનસથી વત્તામાં બદલાયું છે. આનો અર્થ એ છે કે નિર્ણાયક મૂલ્ય x0 પર આપણી પાસે ન્યૂનતમ બિંદુ છે.

સૌથી મહાન અને સૌથી નાનું મૂલ્યકાર્યો અંતરાલ પર(એક સેગમેન્ટ પર) એ જ પ્રક્રિયાનો ઉપયોગ કરીને જોવા મળે છે, ફક્ત એ હકીકતને ધ્યાનમાં લેતા કે, કદાચ, બધા નિર્ણાયક મુદ્દાઓ નિર્દિષ્ટ અંતરાલમાં આવેલા નથી. તે નિર્ણાયક મુદ્દાઓ કે જે અંતરાલની બહાર છે તે વિચારણામાંથી બાકાત રાખવા જોઈએ. જો અંતરાલની અંદર માત્ર એક જ નિર્ણાયક બિંદુ હોય, તો તેની પાસે મહત્તમ અથવા લઘુત્તમ હશે. આ કિસ્સામાં, ફંક્શનના સૌથી મોટા અને નાના મૂલ્યો નક્કી કરવા માટે, અમે અંતરાલના અંતે ફંક્શનના મૂલ્યોને પણ ધ્યાનમાં લઈએ છીએ.

ઉદાહરણ તરીકે, ચાલો ફંક્શનના સૌથી મોટા અને નાના મૂલ્યો શોધીએ

y(x) = 3sin(x) - 0.5x

અંતરાલો પર:

તેથી, કાર્યનું વ્યુત્પન્ન છે

y?(x) = 3cos(x) - 0.5

આપણે સમીકરણ 3cos(x) - 0.5 = 0 હલ કરીએ છીએ

cos(x) = 0.5/3 = 0.16667

x = ±arccos(0.16667) + 2πk.

અમને અંતરાલ [-9; 9]:

x = arccos(0.16667) - 2π*2 = -11.163 (અંતરાલમાં સમાવેલ નથી)

x = -arccos(0.16667) – 2π*1 = -7.687

x = arccos(0.16667) - 2π*1 = -4.88

x = -arccos(0.16667) + 2π*0 = -1.403

x = આર્કોસ(0.16667) + 2π*0 = 1.403

x = -arccos(0.16667) + 2π*1 = 4.88

x = આર્કોસ(0.16667) + 2π*1 = 7.687

x = -arccos(0.16667) + 2π*2 = 11.163 (અંતરાલમાં સમાવેલ નથી)

અમને ફંક્શનની કિંમતો અહીં મળે છે નિર્ણાયક મૂલ્યોદલીલ

y(-7.687) = 3cos(-7.687) - 0.5 = 0.885

y(-4.88) = 3cos(-4.88) - 0.5 = 5.398

y(-1.403) = 3cos(-1.403) - 0.5 = -2.256

y(1.403) = 3cos(1.403) - 0.5 = 2.256

y(4.88) = 3cos(4.88) - 0.5 = -5.398

y(7.687) = 3cos(7.687) - 0.5 = -0.885

તે જોઈ શકાય છે કે અંતરાલ પર [-9; 9] ઉચ્ચતમ મૂલ્યફંક્શનમાં x = -4.88 છે:

x = -4.88, y = 5.398,

અને સૌથી નાનું - x = 4.88 પર:

x = 4.88, y = -5.398.

અંતરાલ પર [-6; -3] આપણી પાસે માત્ર એક જટિલ બિંદુ છે: x = -4.88. x = -4.88 પર ફંક્શનનું મૂલ્ય y = 5.398 બરાબર છે.

અંતરાલના અંતે ફંક્શનની કિંમત શોધો:

y(-6) = 3cos(-6) - 0.5 = 3.838

y(-3) = 3cos(-3) - 0.5 = 1.077

અંતરાલ પર [-6; -3] આપણી પાસે ફંક્શનની સૌથી મોટી કિંમત છે

y = 5.398 x = -4.88 પર

સૌથી નાનું મૂલ્ય -

y = 1.077 x = -3 પર

ફંક્શન ગ્રાફના ઇન્ફ્લેક્શન બિંદુઓને કેવી રીતે શોધી શકાય અને બહિર્મુખ અને અંતર્મુખ બાજુઓ કેવી રીતે નક્કી કરવી?

રેખા y = f(x) ના તમામ વિક્ષેપ બિંદુઓ શોધવા માટે, તમારે બીજું વ્યુત્પન્ન શોધવાની જરૂર છે, તેને શૂન્ય સાથે સરખાવવી (સમીકરણ ઉકેલો) અને x ના તે બધા મૂલ્યોને ચકાસવાની જરૂર છે જેના માટે બીજું વ્યુત્પન્ન શૂન્ય છે, અનંત અથવા અસ્તિત્વમાં નથી. જો, આ મૂલ્યોમાંથી કોઈ એકમાંથી પસાર થતી વખતે, બીજા વ્યુત્પન્ન ફેરફારોનું ચિહ્ન હોય, તો ફંક્શનના આલેખમાં આ બિંદુએ એક વળાંક હોય છે. જો તે બદલાતું નથી, તો ત્યાં કોઈ વળાંક નથી.

સમીકરણ એફ ના મૂળ? (x) = 0, તેમજ ફંક્શનની અસંતુલિતતાના સંભવિત બિંદુઓ અને બીજા ડેરિવેટિવ, ફંક્શનની વ્યાખ્યાના ડોમેનને સંખ્યાબંધ અંતરાલોમાં વિભાજીત કરો. તેમના દરેક અંતરાલો પરની બહિર્મુખતા બીજા ડેરિવેટિવની નિશાની દ્વારા નક્કી કરવામાં આવે છે. જો અભ્યાસ હેઠળના અંતરાલ પરના બિંદુ પરનું બીજું વ્યુત્પન્ન ધન છે, તો રેખા y = f(x) અંતર્મુખ ઉપરની તરફ છે, અને જો નકારાત્મક છે, તો નીચેની તરફ.

બે ચલોના ફંક્શનની સીમા કેવી રીતે શોધવી?

ફંક્શન f(x,y) ની સીમા શોધવા માટે, તેના સ્પષ્ટીકરણના ડોમેનમાં અલગ પડે છે, તમારે આની જરૂર છે:

1) નિર્ણાયક મુદ્દાઓ શોધો, અને આ માટે - સમીકરણોની સિસ્ટમ હલ કરો

fх? (x,y) = 0, fу? (x,y) = 0

2) દરેક નિર્ણાયક બિંદુ P0(a;b) માટે તપાસ કરો કે શું તફાવતનું ચિહ્ન યથાવત છે

P0 ની નજીકના તમામ બિંદુઓ (x;y) માટે. જો તફાવત રહે છે સકારાત્મક સંકેત, પછી બિંદુ P0 પર આપણી પાસે ન્યૂનતમ છે, જો નકારાત્મક હોય, તો આપણી પાસે મહત્તમ છે. જો તફાવત તેના ચિહ્નને જાળવી રાખતો નથી, તો બિંદુ P0 પર કોઈ અંતિમ નથી.

ફંક્શનની સીમાઓ માટે સમાન રીતે નક્કી કરવામાં આવે છે વધુદલીલો

ઇન્ટરનેટ પર બ્રાયન્સ્ક ક્ષેત્રમાં રાજ્ય શ્રમ નિરીક્ષકની સત્તાવાર વેબસાઇટ ક્યાંથી મેળવવી
www.rostrud.ru - રોસ્ટ્રુડની સત્તાવાર વેબસાઇટ - ફેડરલ સેવાશ્રમ અને રોજગાર પર રોસ્ટ્રડ સંદર્ભ - 8-800-707-88-41 રોસ્ટ્રુડને ઇલેક્ટ્રોનિક અપીલ મોકલો (ઇમેઇલ સરનામું: [ઇમેઇલ સુરક્ષિત]) git77.rostrud.ru &mda

તમે સ્પેનિશ ફૂટબોલ વિશે માહિતી ક્યાંથી મેળવી શકો છો?
પ્રાઇમરા ડિવિઝન (સ્પેનિશ: Primera División) એ સ્પેનમાં એક વ્યાવસાયિક ફૂટબોલ લીગ છે (સ્પેનિશ: Liga de Fútbol Profesional, LFP), જેને ફક્ત પ્રાઇમરા અથવા લા લિગા (સ્પેનિશ: La Liga) તરીકે પણ ઓળખવામાં આવે છે, તે એક વ્યાવસાયિક ફૂટબોલ ટુર્નામેન્ટ છે.

રશિયાનું સત્તાવાર ચલણ શું છે
દેશનું નામ - પૈસા/સિક્કો બદલો ઑસ્ટ્રેલિયા ઑસ્ટ્રેલિયન ડૉલર/સેન્ટ ઑસ્ટ્રિયા ઑસ્ટ્રિયન શિલિંગ/ગ્રોઝ - યુરો અઝરબૈજાન મનત અલ્બેનિયા લેક/કિંડારકા અલ્જેરિયા અલ્જેરિયા દીનાર/સેન્ટીમો આર્જેન્ટિના આર્જેન્ટિના ઑસ્ટ્રેલ/સેન્ટાવો અફઘાનિસ્તાન અફઘાનિસ્તાન/પુલ બાંગ્લાદેશ ટાકા/પૈસ બેલ્જિયમ બેલ્જિયન ફ્રેન્ક/સેન્ટીમો - યુરો બલ્ગેરિયા લેવ/સ્ટોટિન્કા

જે પ્રખ્યાત લોકોનું 2 નવેમ્બરના રોજ અવસાન થયું હતું
2 નવેમ્બર એ વર્ષનો 306મો દિવસ છે (307મો લીપ વર્ષ) વી ગ્રેગોરિયન કેલેન્ડર. વર્ષના અંત સુધી 59 દિવસ બાકી છે 2 નવેમ્બર રાષ્ટ્રીય: વર્જિન આઇલેન્ડ્સ (યુએસએ) - સ્વતંત્રતા દિવસ; બેલારુસ - દાદા (મેમરી ડે); લાઇબેરિયા - થેંક્સગિવીંગ ડે; મેક્સિકો, પોલેન્ડ, પો

શૂન્ય રચનાત્મક પ્રત્યય શું છે?
શૂન્ય પ્રત્યય એટલે શું? શૂન્ય પ્રત્યયનો ઉપયોગ કરીને શબ્દો બનાવવાની પદ્ધતિને કેટલાક માર્ગદર્શિકાઓમાં પ્રત્યય-મુક્ત અને અન્યમાં શૂન્ય પ્રત્યય કહેવામાં આવે છે. શૂન્ય પ્રત્યય ગ્રાફિકલી &ઓસ્લા દ્વારા દર્શાવેલ છે

એન્કર ભાડૂત કોણ છે?
એન્કર ભાડૂત - માં મુખ્ય ભાડૂત શોપિંગ સેન્ટર, તે ખરીદદારોને આકર્ષે છે. એક સૌથી મહત્વપૂર્ણ સંકેતો"એન્કરો" ગ્રાહકોમાં તેની ઓળખને ધ્યાનમાં લે છે, જે એક અલગ સ્ટોરના ફોર્મેટમાં બ્રાન્ડના પ્રમોશન અને અસ્તિત્વને સૂચિત કરે છે - શેરી છૂટક, ઉદાહરણ તરીકે, ઝારા, એમ-વિડિયો જેવા

રશિયન ઇકોનોમિક એકેડમીની સત્તાવાર વેબસાઇટનું નામ શું છે. જી.વી. પ્લેખાનોવ (REA)
નીચે મુખ્યની સત્તાવાર વેબસાઇટ્સ છે રાજ્ય યુનિવર્સિટીઓમોસ્કો: મોસ્કોવ્સ્કી રાજ્ય યુનિવર્સિટીએમ.વી. લોમોનોસોવ એકેડેમી ઓફ પ્રોસીક્યુટર જનરલ ઓફિસ રશિયન ફેડરેશનરાજ્ય એકેડેમી ફાયર સર્વિસરશિયા એકેડેમીના EMERCOM રાષ્ટ્રીય અર્થતંત્રરશિયન ફેડરેશન (ANH) એકેડેમી ઓફ લેબરની સરકાર હેઠળ અને સામાજિક સંબંધો(ATiSO) શિક્ષણવિદ

16 મેના રોજ કઈ રજાઓ ઉજવવામાં આવે છે
16 મે એ ગ્રેગોરીયન કેલેન્ડરમાં વર્ષનો 136મો (લીપ વર્ષમાં 137મો) દિવસ છે. વર્ષ પૂરું થવામાં 229 દિવસ બાકી છે. 16 મેના રોજ ઉજવવામાં આવતી ઘટનાઓ અને રજાઓ: એઇડ્સથી મૃત્યુ પામેલા લોકો માટે વિશ્વ સ્મૃતિ દિવસ; જીવનચરિત્રકારો દિવસ; ભારતમાં અપરા એકાદશી. ધાર્મિક ઘટનાઓ રૂઢિચુસ્તતા: પેચેર્સ્કના સેન્ટ થિયોડોસિયસનો દિવસ; થી

નીંદણ રાગવીડના વિતરણની ભૂગોળ શું છે?
એમ્બ્રોસિયા વોર્મવુડ વાર્ષિક, અંતમાં વસંત. બાયોલોજી અને મોર્ફોલોજી 20-200 સે.મી. ઊંચું, સીધું, ગભરાટભર્યું ડાળીઓવાળું, ટોચ પર કોણીય, નબળા અથવા તેના બદલે મજબૂત બ્રસ્ટલી પ્યુબસેન્સ સાથે. મૂળ ટેપરુટ છે, જમીનમાં 4 મીટરની ઊંડાઈ સુધી પ્રવેશ કરે છે. પાંદડા 4-15 સેમી લાંબા, ઉપર ઘેરા લીલા, લગભગ ચમકદાર, નીચે રાખોડી-લીલા, ગીચ બરછટ-પ્યુબસેન્ટ હોય છે; ઉપલા

પોઇકિલોથર્મિક પ્રાણીઓ શું છે?
પોઇકિલોથર્મિક પ્રાણીઓ ઠંડા લોહીવાળા પ્રાણીઓ છે, અસ્થિર આંતરિક શરીરનું તાપમાન ધરાવતા પ્રાણીઓ જે તાપમાનના આધારે બદલાય છે બાહ્ય વાતાવરણ. પોઇકિલોથર્મિક પ્રાણીઓમાં તમામ અપૃષ્ઠવંશી પ્રાણીઓનો સમાવેશ થાય છે, અને કરોડઅસ્થિધારી પ્રાણીઓમાં માછલી, ઉભયજીવી અને સરિસૃપનો સમાવેશ થાય છે. પોઇકિલોથર્મિક પ્રાણીઓના શરીરનું તાપમાન સામાન્ય રીતે આસપાસના તાપમાન કરતાં માત્ર 1-20C વધારે હોય છે.

પુલ-અપ્સ યોગ્ય રીતે કેવી રીતે કરવું
પુલ-અપ્સ - મૂળભૂત કસરતહાથ, પીઠ અને છાતીના સ્નાયુઓ માટે. ઉપર ખેંચો છે કી કસરત, વિકાસશીલ શક્તિ. પુલ-અપ્સ ગમે ત્યારે અને લગભગ ગમે ત્યાં કરી શકાય છે; તેમને કોઈ ખાસ સાધનોની જરૂર નથી પડતી અથવા જિમમાં જવાની જરૂર નથી, જે ખૂબ જ મહત્વપૂર્ણ છે. બાર પર પુલ-અપ્સ સૌથી વધુ છે અસરકારક કસરતચાલુ

જેમ તમે જોઈ શકો છો, ફંક્શનના એક્સ્ટ્રીમમના આ ચિહ્ન માટે બિંદુ પર ઓછામાં ઓછા બીજા ક્રમમાં વ્યુત્પન્નનું અસ્તિત્વ જરૂરી છે.

ઉદાહરણ.

ફંક્શનની સીમા શોધો.

ઉકેલ.

ચાલો વ્યાખ્યાના ડોમેન સાથે પ્રારંભ કરીએ:

ચાલો મૂળ કાર્યને અલગ કરીએ:

x=1, એટલે કે, આ સંભવિત ચરમસીમાનો એક બિંદુ છે. આપણે ફંક્શનનું બીજું ડેરિવેટિવ શોધીએ છીએ અને તેના મૂલ્યની ગણતરી કરીએ છીએ:

x = 1 x=1તેથી, એક્સ્ટ્રીમ માટે બીજી પર્યાપ્ત સ્થિતિ દ્વારા, - મહત્તમ બિંદુ. પછી

- મહત્તમ કાર્ય.

ગ્રાફિક ચિત્ર.

જવાબ:

કાર્યના અંતિમ ભાગ માટે ત્રીજી પર્યાપ્ત સ્થિતિ. કાર્ય કરવા દો y=f(x) સુધીના ડેરિવેટિવ્ઝ ધરાવે છે n -બિંદુના પડોશમાં -મો ક્રમ અને સુધીના ડેરિવેટિવ્ઝ n+1

ઉદાહરણ.

-પોઈન્ટ પર જ ક્રમ. રહેવા દો. .

ઉકેલ.

કાર્યના અંતિમ બિંદુઓ શોધો

મૂળ કાર્ય એક તર્કસંગત સમગ્ર કાર્ય છે; તેની વ્યાખ્યાનું ક્ષેત્ર વાસ્તવિક સંખ્યાઓનો સંપૂર્ણ સમૂહ છે.

ચાલો ફંક્શનને અલગ કરીએ: ડેરિવેટિવ શૂન્ય પર જાય છે

, તેથી, આ સંભવિત અંતિમ બિંદુઓ છે. ચાલો એક્સ્ટ્રીમમ માટે ત્રીજી પર્યાપ્ત સ્થિતિનો ઉપયોગ કરીએ.

અમે બીજું વ્યુત્પન્ન શોધીએ છીએ અને શક્ય છેડાના બિંદુઓ પર તેની કિંમતની ગણતરી કરીએ છીએ (અમે મધ્યવર્તી ગણતરીઓને છોડી દઈશું): પરિણામે, મહત્તમ બિંદુ છે (આપણી પાસેના ત્રીજા પર્યાપ્ત ચિહ્ન માટે n=1

અને). બિંદુઓની પ્રકૃતિ શોધવા માટે

આપણે ત્રીજું વ્યુત્પન્ન શોધીએ છીએ અને આ બિંદુઓ પર તેની કિંમતની ગણતરી કરીએ છીએ: તેથી, ફંક્શનનો ઇન્ફ્લેક્શન બિંદુ છે ( n=1

તે બિંદુ સાથે વ્યવહાર કરવા માટે રહે છે. અમે ચોથું વ્યુત્પન્ન શોધીએ છીએ અને આ બિંદુએ તેના મૂલ્યની ગણતરી કરીએ છીએ:

તેથી, કાર્યનો લઘુત્તમ બિંદુ છે.

- મહત્તમ કાર્ય.

ગ્રાફિક ચિત્ર.

મહત્તમ બિંદુ એ કાર્યનો લઘુત્તમ બિંદુ છે.

10. ફંક્શનની એક્સ્ટ્રીમા એક્સ્ટ્રીમમની વ્યાખ્યા

ફંક્શન y = f(x) કહેવાય છે વધારો (ઘટતું) ચોક્કસ અંતરાલમાં, જો x 1 માટે< x 2 выполняется неравенство (f(x 1) < f (x 2) (f(x 1) >f(x 2)).

જો ડિફરન્સિબલ ફંક્શન y = f(x) અંતરાલ પર વધે (ઘટે), તો આ અંતરાલ પર તેનું વ્યુત્પન્ન f " (x)  0

(f " (x)  0).

ડોટ x ઓકહેવાય છે સ્થાનિક મહત્તમ બિંદુ (ન્યૂનતમ) ફંક્શન f(x), જો બિંદુની પડોશી હોય x ઓ, જે તમામ બિંદુઓ માટે અસમાનતા f(x) ≤ f(x о) (f(x) ≥ f(x о)) સાચી છે.

મહત્તમ અને લઘુત્તમ પોઈન્ટ કહેવામાં આવે છે આત્યંતિક બિંદુઓ, અને આ બિંદુઓ પરના કાર્યના મૂલ્યો તેના છે ચરમસીમા

એક્સ્ટ્રીમ પોઈન્ટ

એક્સ્ટ્રીમ માટે જરૂરી શરતો. જો બિંદુ x ઓફંક્શન f(x) નું આત્યંતિક બિંદુ છે, પછી કાં તો f " (x o) = 0, અથવા f (x o) અસ્તિત્વમાં નથી. આવા બિંદુઓ કહેવામાં આવે છે જટિલ,અને કાર્ય પોતે નિર્ણાયક બિંદુ પર વ્યાખ્યાયિત થયેલ છે. ફંક્શનનો અંતિમ ભાગ તેના નિર્ણાયક મુદ્દાઓ વચ્ચે શોધવો જોઈએ.

પ્રથમ પૂરતી સ્થિતિ.દો x ઓ- નિર્ણાયક બિંદુ. જો કોઈ બિંદુમાંથી પસાર થતી વખતે f "(x) x ઓવત્તા ચિહ્નને માઈનસમાં બદલે છે, પછી બિંદુ પર x ઓફંક્શનમાં મહત્તમ છે, અન્યથા તેની પાસે ન્યૂનતમ છે. જો, નિર્ણાયક બિંદુમાંથી પસાર થતી વખતે, વ્યુત્પન્ન ચિહ્ન બદલાતું નથી, તો બિંદુ પર x ઓત્યાં કોઈ આત્યંતિક નથી.

બીજી પર્યાપ્ત સ્થિતિ.બિંદુની નજીકમાં ફંક્શન f(x) ને ડેરિવેટિવ f " (x) રાખવા દો x ઓઅને પોઈન્ટ પર જ બીજું ડેરિવેટિવ x ઓ. જો f "(x o) = 0, >0 (<0), то точка x ઓફંક્શન f(x) નો સ્થાનિક લઘુત્તમ (મહત્તમ) બિંદુ છે. જો =0, તો તમારે કાં તો પ્રથમ પર્યાપ્ત શરતનો ઉપયોગ કરવો અથવા ઉચ્ચ ડેરિવેટિવ્ઝનો ઉપયોગ કરવાની જરૂર છે.

સેગમેન્ટ પર, ફંક્શન y = f(x) તેના ન્યૂનતમ અથવા મહત્તમ મૂલ્ય સુધી નિર્ણાયક બિંદુઓ પર અથવા સેગમેન્ટના છેડે પહોંચી શકે છે.

ઉદાહરણ 3.22.ફંક્શન f(x) = 2x 3 - 15x 2 + 36x - 14 ની સીમા શોધો.

ઉકેલ. f "(x) = 6x 2 - 30x +36 = 6(x ​​-2)(x - 3), ત્યારથી x 1 = 2 અને x 2 = 3 ફંક્શનના નિર્ણાયક બિંદુઓ. એક્સ્ટ્રીમા ફક્ત આ બિંદુઓ જ્યારે x 1 = 2માંથી પસાર થાય છે ત્યારે વ્યુત્પત્તિ તેના ચિહ્નને વત્તાથી માઇનસમાં બદલે છે, તો આ બિંદુએ જ્યારે x 2 = 3 બિંદુમાંથી પસાર થાય છે ત્યારે વ્યુત્પન્ન તેના ચિહ્નને માઇનસથી બદલે છે વત્તા માટે, તેથી પોઈન્ટ x 2 = 3 પર ફંક્શનમાં ન્યૂનતમ હોય છે પોઈન્ટ x 1 = 2 અને x 2 = 3 પર ફંક્શનના મૂલ્યોની ગણતરી કર્યા પછી, આપણે ફંક્શનની સીમા શોધીએ છીએ: મહત્તમ f( 2) = 14 અને ન્યૂનતમ f(3) = 13.

સતત કાર્યના ગ્રાફને ધ્યાનમાં લો કાર્ય કરવા દોઆકૃતિમાં બતાવેલ છે.

એક બિંદુ પર કાર્ય મૂલ્ય x 1 ડાબી અને જમણી બાજુના તમામ પડોશી બિંદુઓ પર ફંક્શન મૂલ્યો કરતા વધારે હશે x 1. આ કિસ્સામાં અમે કહીએ છીએ કે કાર્ય બિંદુ પર છે x 1 મહત્તમ. બિંદુએ xકાર્ય 3 દેખીતી રીતે પણ મહત્તમ છે. જો આપણે મુદ્દાને ધ્યાનમાં લઈએ x 2, તો તેમાં ફંક્શન મૂલ્ય તમામ પડોશી મૂલ્યો કરતાં ઓછું છે. આ કિસ્સામાં અમે કહીએ છીએ કે કાર્ય બિંદુ પર છે x 2 ન્યૂનતમ. એ જ રીતે બિંદુ માટે x 4 .

કાર્ય કાર્ય કરવા દોબિંદુ પર x 0 ધરાવે છે મહત્તમ, જો આ બિંદુએ ફંક્શનનું મૂલ્ય બિંદુ ધરાવતા કેટલાક અંતરાલના તમામ બિંદુઓ પર તેના મૂલ્યો કરતા વધારે હોય x 0, એટલે કે. જો કોઈ બિંદુનો આવો પડોશી હોય x 0, જે દરેક માટે છે x≠x 0 , આ પડોશી સાથે જોડાયેલા, અસમાનતા ધરાવે છે f(x)<f(x 0 ) .

કાર્ય કાર્ય કરવા દોધરાવે છે ન્યૂનતમબિંદુ પર x 0 , જો કોઈ બિંદુનો આવો પડોશી હોય x 0 , તે દરેક માટે છે x≠x 0 આ પડોશી સાથે જોડાયેલા છે, અસમાનતા ધરાવે છે f(x)>f(x 0.

જે બિંદુઓ પર ફંક્શન તેની મહત્તમ અને લઘુત્તમ સુધી પહોંચે છે તેને એક્સ્ટ્રીમ પોઈન્ટ કહેવામાં આવે છે, અને આ બિંદુઓ પરના ફંક્શનના મૂલ્યોને ફંક્શનના એક્સ્ટ્રીમા કહેવામાં આવે છે.

ચાલો એ હકીકત પર ધ્યાન આપીએ કે સેગમેન્ટ પર વ્યાખ્યાયિત ફંક્શન માત્ર વિચારણા હેઠળના સેગમેન્ટમાં સમાવિષ્ટ બિંદુઓ પર મહત્તમ અને ન્યૂનતમ સુધી પહોંચી શકે છે.

નોંધ કરો કે જો કોઈ ફંક્શન એક બિંદુ પર મહત્તમ હોય, તો તેનો અર્થ એ નથી કે તે બિંદુએ ફંક્શનની વ્યાખ્યાના સમગ્ર ડોમેનમાં સૌથી વધુ મૂલ્ય છે. ઉપર ચર્ચા કરેલ આકૃતિમાં, બિંદુ પરનું કાર્ય x 1 માં મહત્તમ છે, જો કે એવા બિંદુઓ છે કે જેના પર કાર્ય મૂલ્યો બિંદુ કરતા વધારે છે x 1 . ખાસ કરીને, f(x 1) < f(x 4) એટલે કે કાર્યનું લઘુત્તમ મહત્તમ કરતા વધારે છે. મહત્તમની વ્યાખ્યાથી તે ફક્ત એટલું જ અનુસરે છે કે આ મહત્તમ બિંદુની નજીકના બિંદુઓ પર કાર્યનું સૌથી મોટું મૂલ્ય છે.

પ્રમેય 1. (એક્સ્ટ્રીમમના અસ્તિત્વ માટે જરૂરી શરત.)જો વિભેદક કાર્ય કાર્ય કરવા દોબિંદુ પર છે x= x 0 એક્સ્ટ્રીમમ, પછી આ બિંદુએ તેનું વ્યુત્પન્ન શૂન્ય બને છે.

પુરાવો. ચાલો, નિશ્ચિતતા માટે, બિંદુએ x 0 ફંક્શન મહત્તમ છે. પછી, પૂરતી નાની વૃદ્ધિ માટે Δ xઅમારી પાસે છે f(x 0 + Δ x) 0 ) , એટલે કે પણ પછી

આ અસમાનતાઓને Δ પરની મર્યાદામાં પસાર કરવી x→ 0 અને ધ્યાનમાં લેતા કે વ્યુત્પન્ન f "(x 0) અસ્તિત્વમાં છે, અને તેથી ડાબી બાજુની મર્યાદા કેવી રીતે Δ પર આધારિત નથી x→ 0, આપણને મળે છે: Δ પર x → 0 – 0 f"(x 0) ≥ 0 a at Δ x → 0 + 0 f"(x 0) ≤ 0. ત્યારથી f"(x 0) સંખ્યાને વ્યાખ્યાયિત કરે છે, તો પછી આ બે અસમાનતાઓ સુસંગત હોય તો જ f"(x 0) = 0.

સાબિત પ્રમેય જણાવે છે કે મહત્તમ અને લઘુત્તમ બિંદુઓ દલીલના તે મૂલ્યોમાં જ હોઈ શકે છે કે જેના પર વ્યુત્પન્ન શૂન્ય બને છે.

જ્યારે ફંક્શન ચોક્કસ સેગમેન્ટના તમામ બિંદુઓ પર વ્યુત્પન્ન હોય ત્યારે અમે તે કેસને ધ્યાનમાં લીધો. વ્યુત્પન્ન અસ્તિત્વમાં ન હોય તેવા કિસ્સામાં પરિસ્થિતિ શું છે? ચાલો ઉદાહરણો જોઈએ.

ઉદાહરણો.

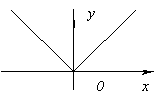
1. y=|x|.

   કાર્યમાં બિંદુ પર કોઈ વ્યુત્પન્ન નથી x=0 (આ બિંદુએ ફંક્શનના ગ્રાફમાં નિર્ધારિત સ્પર્શક નથી), પરંતુ આ બિંદુએ ફંક્શન ન્યૂનતમ છે, કારણ કે y(0)=0, અને બધા માટે x≠ 0y > 0.



ફંક્શનમાં કોઈ વ્યુત્પન્ન નથી x=0, કારણ કે તે અનંત પર જાય છે x=0. પરંતુ આ બિંદુએ કાર્ય મહત્તમ છે.



ફંક્શનમાં કોઈ વ્યુત્પન્ન નથી x=0, ત્યારથી ખાતે x→0. આ બિંદુએ ફંક્શનમાં મહત્તમ કે લઘુત્તમ નથી. ખરેખર, f(x)=0 અને ખાતે x<0f(x)<0, а при x>0f(x)>0.



આમ, આપેલા ઉદાહરણો અને પ્રમેય ઘડવામાંથી, તે સ્પષ્ટ છે કે ફંક્શન માત્ર બે કિસ્સાઓમાં જ એક્સ્ટ્રીમમ હોઈ શકે છે: 1) એવા બિંદુઓ પર જ્યાં વ્યુત્પન્ન અસ્તિત્વ ધરાવે છે અને શૂન્યની બરાબર છે; 2) તે બિંદુ પર જ્યાં વ્યુત્પન્ન અસ્તિત્વમાં નથી.

જો કે, જો કોઈ સમયે x 0 તે આપણે જાણીએ છીએ f "(x 0 ) =0, તો પછી કોઈ આના પરથી નિષ્કર્ષ લઈ શકતું નથી કે બિંદુ પર x 0 ફંક્શનમાં એક્સ્ટ્રીમમ છે.

ઉદાહરણ તરીકે. .



પરંતુ સમયગાળો x=0 એ અંતિમ બિંદુ નથી, કારણ કે આ બિંદુની ડાબી બાજુએ કાર્ય મૂલ્યો ધરીની નીચે સ્થિત છે બળદ, અને ઉપર જમણી બાજુએ.

ફંક્શનના ડોમેનમાંથી દલીલના મૂલ્યો કે જેના પર ફંક્શનનું વ્યુત્પન્ન અદૃશ્ય થઈ જાય છે અથવા અસ્તિત્વમાં નથી તેને કહેવામાં આવે છે નિર્ણાયક મુદ્દાઓ.




ઉપરોક્ત તમામમાંથી તે અનુસરે છે કે કાર્યના અંતિમ બિંદુઓ નિર્ણાયક બિંદુઓમાંના છે, અને, જો કે, દરેક નિર્ણાયક બિંદુ એ એક્સ્ટ્રીમ પોઈન્ટ નથી. તેથી, ફંક્શનની સીમા શોધવા માટે, તમારે ફંક્શનના તમામ નિર્ણાયક બિંદુઓ શોધવાની જરૂર છે, અને પછી આ દરેક બિંદુઓને મહત્તમ અને લઘુત્તમ માટે અલગથી તપાસો. નીચેનો પ્રમેય આ હેતુને સેવા આપે છે.

પ્રમેય 2. (એક ચરમસીમાના અસ્તિત્વ માટે પૂરતી સ્થિતિ.)નિર્ણાયક બિંદુ ધરાવતા કેટલાક અંતરાલ પર કાર્યને સતત રહેવા દો x 0, અને આ અંતરાલના તમામ બિંદુઓ પર અલગ છે (સિવાય કે, કદાચ, બિંદુ પોતે x 0). જો, જ્યારે આ બિંદુ દ્વારા ડાબેથી જમણે ખસેડવામાં આવે છે, ત્યારે વ્યુત્પન્ન ફેરફારો ચિહ્ન વત્તાથી માઈનસ સુધી, પછી બિંદુ પર x = x 0 ફંક્શન મહત્તમ છે. જો, જ્યારે પસાર થાય છે x 0 ડાબેથી જમણે, વ્યુત્પન્ન ફેરફારો બાદબાકીથી વત્તામાં સાઇન કરે છે, પછી ફંક્શન આ બિંદુએ ન્યૂનતમ હોય છે.

આમ, જો

પુરાવો. ચાલો પહેલા માની લઈએ કે જ્યારે પસાર થઈ રહ્યા છીએ x 0 વ્યુત્પન્ન ફેરફારોનું ચિહ્ન વત્તાથી ઓછા સુધી, એટલે કે. દરેકની સામે x, બિંદુની નજીક x 0 f "(x)>માટે 0 x< x 0 , f "(x)< માટે 0 x>x 0 ચાલો લેગ્રેન્જના પ્રમેયને તફાવત પર લાગુ કરીએ f(x) - f(x 0 ) = f "(c)(x- x 0), ક્યાં cવચ્ચે આવેલું છે xઅને x 0 .

1. દો x< x 0 પછી c< x 0 અને f "(c)> 0. તેથી જ f "(c)(x- x 0)< 0 અને તેથી

   f(x) - f(x 0 )< 0, એટલે કે. f(x)< f(x 0 ).

2. દો x > x 0 પછી c>x 0 અને f "(c)< 0. અર્થ f "(c)(x- x 0)< 0. તેથી જ f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .

આમ, બધા મૂલ્યો માટે xપૂરતી નજીક x 0 f(x)< f(x 0 ) . અને આનો અર્થ એ છે કે બિંદુ પર x 0 ફંક્શન મહત્તમ છે.

લઘુત્તમ પ્રમેયનો બીજો ભાગ એ જ રીતે સાબિત થાય છે.



ચાલો આકૃતિમાં આ પ્રમેયનો અર્થ સમજાવીએ. દો f "(x 1 ) =0 અને કોઈપણ માટે x,પૂરતી નજીક x 1, અસમાનતાઓ સંતુષ્ટ છે

f "(x)< 0 પર x< x 1 , f "(x)> 0 પર x>x 1 .

પછી બિંદુની ડાબી બાજુએ x 1 કાર્ય વધે છે અને જમણી બાજુએ ઘટે છે, તેથી, જ્યારે x = x 1 ફંક્શન વધવાથી ઘટતા જાય છે, એટલે કે, તેની પાસે મહત્તમ છે.

એ જ રીતે, આપણે મુદ્દાઓ પર વિચાર કરી શકીએ x 2 અને x 3 .


ઉપરોક્ત તમામને ચિત્રમાં યોજનાકીય રીતે દર્શાવી શકાય છે:

એક્સ્ટ્રીમમ માટે ફંક્શન y=f(x) નો અભ્યાસ કરવાનો નિયમ

1. ફંક્શનનું ડોમેન શોધો f(x).
2. ફંક્શનનું પ્રથમ વ્યુત્પન્ન શોધો f "(x).
3. આ માટે નિર્ણાયક મુદ્દાઓ નક્કી કરો:
   1. સમીકરણના વાસ્તવિક મૂળ શોધો f "(x)=0;
   2. બધા મૂલ્યો શોધો xજેના માટે વ્યુત્પન્ન f "(x)અસ્તિત્વમાં નથી.
4. નિર્ણાયક બિંદુની ડાબી અને જમણી તરફ વ્યુત્પન્નની નિશાની નક્કી કરો. વ્યુત્પન્નની નિશાની બે નિર્ણાયક બિંદુઓ વચ્ચે સ્થિર રહેતી હોવાથી, નિર્ણાયક બિંદુની ડાબી બાજુએ એક બિંદુ અને જમણી બાજુએ એક બિંદુએ વ્યુત્પન્નની નિશાની નક્કી કરવા માટે તે પૂરતું છે.
5. અંતિમ બિંદુઓ પર કાર્યના મૂલ્યની ગણતરી કરો.

ઉદાહરણો. ન્યૂનતમ અને મહત્તમ માટે કાર્યોનું અન્વેષણ કરો.




સેગમેન્ટ પરના કાર્યના મહત્તમ અને નાનામાં નાના મૂલ્યો

સૌથી મોટુંઅંતરાલ પરના કાર્યનું મૂલ્ય આ અંતરાલ પરના તેના તમામ મૂલ્યોમાં સૌથી મોટું છે, અને સૌથી નાનું- તેના તમામ મૂલ્યોમાં સૌથી નાનું.

કાર્યને ધ્યાનમાં લો કાર્ય કરવા દોસેગમેન્ટ પર સતત [ a, b]. જેમ જાણીતું છે, આવા કાર્ય તેના મહત્તમ અને લઘુત્તમ મૂલ્યો સુધી પહોંચે છે, કાં તો સેગમેન્ટની સીમા પર અથવા તેની અંદર. જો ફંક્શનનું સૌથી મોટું અથવા સૌથી નાનું મૂલ્ય સેગમેન્ટના આંતરિક બિંદુ પર પ્રાપ્ત થાય છે, તો આ મૂલ્ય ફંક્શનની મહત્તમ અથવા લઘુત્તમ છે, એટલે કે, તે નિર્ણાયક બિંદુઓ પર પ્રાપ્ત થાય છે.

આમ, અમને નીચેના મળે છે સેગમેન્ટ પર ફંક્શનની સૌથી મોટી અને સૌથી નાની કિંમતો શોધવાનો નિયમ[ a, b] :

1. અંતરાલમાં કાર્યના તમામ નિર્ણાયક બિંદુઓ શોધો ( a, b) અને આ બિંદુઓ પર કાર્ય મૂલ્યોની ગણતરી કરો.
2. જ્યારે સેગમેન્ટના છેડે ફંક્શનના મૂલ્યોની ગણતરી કરો x = a, x = b.
3. બધા પ્રાપ્ત મૂલ્યોમાંથી, સૌથી મોટું અને સૌથી નાનું પસંદ કરો.

પરિચય

વિજ્ઞાનના ઘણા ક્ષેત્રોમાં અને વ્યવહારિક પ્રવૃત્તિઓમાં, વ્યક્તિએ ઘણીવાર કાર્યના અંતિમ ભાગને શોધવાની સમસ્યાનો સામનો કરવો પડે છે. હકીકત એ છે કે ઘણા તકનીકી, આર્થિક, વગેરે. પ્રક્રિયાઓ એક ફંક્શન અથવા ઘણા ફંક્શન્સ દ્વારા મોડલ કરવામાં આવે છે જે ચલ પર આધારિત હોય છે - મોડેલિંગ કરવામાં આવી રહેલી ઘટનાની સ્થિતિને પ્રભાવિત કરતા પરિબળો. શ્રેષ્ઠ (તર્કસંગત) સ્થિતિ અને પ્રક્રિયાના નિયંત્રણને નિર્ધારિત કરવા માટે આવા કાર્યોની સીમા શોધવાની જરૂર છે. તેથી અર્થશાસ્ત્રમાં, ખર્ચ ઘટાડવા અથવા નફો વધારવાની સમસ્યાઓ ઘણીવાર હલ થાય છે - કંપનીની માઇક્રોઇકોનોમિક સમસ્યા. આ કાર્યમાં, અમે મોડેલિંગ મુદ્દાઓને ધ્યાનમાં લેતા નથી, પરંતુ સરળ સંસ્કરણમાં ફંક્શનના એક્સ્ટ્રીમા શોધવા માટે માત્ર અલ્ગોરિધમ્સને ધ્યાનમાં લઈએ છીએ, જ્યારે ચલો (બિનશરતી ઑપ્ટિમાઇઝેશન) પર કોઈ નિયંત્રણો લાદવામાં આવ્યા નથી, અને એક્સ્ટ્રીમમ માત્ર એક ઉદ્દેશ્ય કાર્ય માટે માંગવામાં આવે છે.

કાર્યની એક્સ્ટ્રીમા

સતત કાર્યના ગ્રાફને ધ્યાનમાં લો કાર્ય કરવા દોઆકૃતિમાં બતાવેલ છે. એક બિંદુ પર કાર્ય મૂલ્ય x 1 ડાબી અને જમણી બાજુના તમામ પડોશી બિંદુઓ પર ફંક્શન મૂલ્યો કરતા વધારે હશે x 1. આ કિસ્સામાં અમે કહીએ છીએ કે કાર્ય બિંદુ પર છે x 1 મહત્તમ. બિંદુએ xકાર્ય 3 દેખીતી રીતે પણ મહત્તમ છે. જો આપણે મુદ્દાને ધ્યાનમાં લઈએ x 2, તો તેમાં ફંક્શન મૂલ્ય તમામ પડોશી મૂલ્યો કરતાં ઓછું છે. આ કિસ્સામાં અમે કહીએ છીએ કે કાર્ય બિંદુ પર છે x 2 ન્યૂનતમ. એ જ રીતે બિંદુ માટે x 4 .

કાર્ય કાર્ય કરવા દોબિંદુ પર x 0 ધરાવે છે મહત્તમ, જો આ બિંદુએ ફંક્શનનું મૂલ્ય બિંદુ ધરાવતા કેટલાક અંતરાલના તમામ બિંદુઓ પર તેના મૂલ્યો કરતા વધારે હોય x 0, એટલે કે. જો કોઈ બિંદુનો આવો પડોશી હોય x 0, જે દરેક માટે છે x ≠x 0 , આ પડોશી સાથે જોડાયેલા, અસમાનતા ધરાવે છે f(x) <f(x 0 ) .

કાર્ય કાર્ય કરવા દોધરાવે છે ન્યૂનતમબિંદુ પર x 0 , જો કોઈ બિંદુનો આવો પડોશી હોય x 0 , તે દરેક માટે છે x ≠x 0 આ પડોશી સાથે જોડાયેલા છે, અસમાનતા ધરાવે છે f(x) >f(x 0 .

જે બિંદુઓ પર ફંક્શન તેની મહત્તમ અને લઘુત્તમ સુધી પહોંચે છે તેને એક્સ્ટ્રીમ પોઈન્ટ કહેવામાં આવે છે, અને આ બિંદુઓ પરના ફંક્શનના મૂલ્યોને ફંક્શનના એક્સ્ટ્રીમા કહેવામાં આવે છે.

ચાલો એ હકીકત પર ધ્યાન આપીએ કે સેગમેન્ટ પર વ્યાખ્યાયિત ફંક્શન માત્ર વિચારણા હેઠળના સેગમેન્ટમાં સમાવિષ્ટ બિંદુઓ પર મહત્તમ અને ન્યૂનતમ સુધી પહોંચી શકે છે.

નોંધ કરો કે જો કોઈ ફંક્શનમાં એક બિંદુ પર મહત્તમ હોય, તો તેનો અર્થ એ નથી કે તે બિંદુએ ફંક્શનની વ્યાખ્યાના સમગ્ર ડોમેનમાં સૌથી વધુ મૂલ્ય છે. ઉપર ચર્ચા કરેલ આકૃતિમાં, બિંદુ પરનું કાર્ય x 1 માં મહત્તમ છે, જો કે એવા બિંદુઓ છે કે જેના પર કાર્ય મૂલ્યો બિંદુ કરતા વધારે છે x 1 . ખાસ કરીને, f (x 1) < f (x 4) એટલે કે કાર્યનું લઘુત્તમ મહત્તમ કરતા વધારે છે. મહત્તમની વ્યાખ્યાથી તે ફક્ત એટલું જ અનુસરે છે કે આ મહત્તમ બિંદુની નજીકના બિંદુઓ પર કાર્યનું સૌથી મોટું મૂલ્ય છે.

પ્રમેય 1. (એક્સ્ટ્રીમમના અસ્તિત્વ માટે જરૂરી શરત.) જો વિભેદક કાર્ય કાર્ય કરવા દોબિંદુ પર છે x= x 0 એક્સ્ટ્રીમમ, પછી આ બિંદુએ તેનું વ્યુત્પન્ન શૂન્ય બને છે.

પુરાવો. ચાલો, નિશ્ચિતતા માટે, બિંદુએ x 0 ફંક્શન મહત્તમ છે. પછી, પૂરતી નાની વૃદ્ધિ માટે Δ xઅમારી પાસે છે f(x 0 + Δ x) 0 ) , એટલે કે

પણ પછી

આ અસમાનતાઓને Δ પરની મર્યાદામાં પસાર કરવી x→ 0 અને ધ્યાનમાં લેતા કે વ્યુત્પન્ન f "(x 0) અસ્તિત્વમાં છે, અને તેથી ડાબી બાજુની મર્યાદા કેવી રીતે Δ પર આધારિત નથી x→ 0, આપણને મળે છે: Δ પર x → 0 – 0 f" (x 0) ≥ 0 a at Δ x → 0 + 0 f" (x 0) ≤ 0. ત્યારથી f" (x 0) સંખ્યાને વ્યાખ્યાયિત કરે છે, તો પછી આ બે અસમાનતાઓ સુસંગત હોય તો જ f" (x 0) = 0.

સાબિત પ્રમેય જણાવે છે કે મહત્તમ અને લઘુત્તમ બિંદુઓ દલીલના તે મૂલ્યોમાં જ હોઈ શકે છે કે જેના પર વ્યુત્પન્ન શૂન્ય બને છે.

જ્યારે ફંક્શન ચોક્કસ સેગમેન્ટના તમામ બિંદુઓ પર વ્યુત્પન્ન હોય ત્યારે અમે તે કેસને ધ્યાનમાં લીધો. વ્યુત્પન્ન અસ્તિત્વમાં ન હોય તેવા કિસ્સામાં પરિસ્થિતિ શું છે? ચાલો ઉદાહરણો જોઈએ.

y =|x |.

કાર્યમાં બિંદુ પર કોઈ વ્યુત્પન્ન નથી x=0 (આ બિંદુએ ફંક્શનના ગ્રાફમાં નિર્ધારિત સ્પર્શક નથી), પરંતુ આ બિંદુએ ફંક્શન ન્યૂનતમ છે, કારણ કે y(0)=0, અને બધા માટે x ≠ 0y > 0.

પર કોઈ વ્યુત્પન્ન નથી x=0, કારણ કે તે અનંત પર જાય છે x=0. પરંતુ આ બિંદુએ કાર્ય મહત્તમ છે. પર કોઈ વ્યુત્પન્ન નથી x=0, ત્યારથી ખાતે x→0. આ બિંદુએ ફંક્શનમાં મહત્તમ કે લઘુત્તમ નથી. ખરેખર, f(x)=0 અને ખાતે x <0f(x) <0, а при x >0f(x) >0.

આમ, આપેલા ઉદાહરણો અને પ્રમેય ઘડવામાંથી, તે સ્પષ્ટ છે કે ફંક્શન માત્ર બે કિસ્સાઓમાં જ એક્સ્ટ્રીમમ હોઈ શકે છે: 1) એવા બિંદુઓ પર જ્યાં વ્યુત્પન્ન અસ્તિત્વ ધરાવે છે અને શૂન્યની બરાબર છે; 2) તે બિંદુ પર જ્યાં વ્યુત્પન્ન અસ્તિત્વમાં નથી.

જો કે, જો કોઈ સમયે x 0 તે આપણે જાણીએ છીએ f "(x 0 ) =0, તો પછી કોઈ આના પરથી નિષ્કર્ષ લઈ શકતું નથી કે બિંદુ પર x 0 ફંક્શનમાં એક્સ્ટ્રીમમ છે.

ઉદાહરણ તરીકે.

.

પરંતુ સમયગાળો x=0 એ અંતિમ બિંદુ નથી, કારણ કે આ બિંદુની ડાબી બાજુએ કાર્ય મૂલ્યો ધરીની નીચે સ્થિત છે બળદ, અને ઉપર જમણી બાજુએ.

ફંક્શનના ડોમેનમાંથી દલીલના મૂલ્યો કે જેના પર ફંક્શનનું વ્યુત્પન્ન અદૃશ્ય થઈ જાય છે અથવા અસ્તિત્વમાં નથી તેને કહેવામાં આવે છે નિર્ણાયક મુદ્દાઓ .

ઉપરોક્ત તમામમાંથી તે અનુસરે છે કે કાર્યના અંતિમ બિંદુઓ નિર્ણાયક બિંદુઓમાંના છે, અને, જો કે, દરેક નિર્ણાયક બિંદુ એ એક્સ્ટ્રીમ પોઈન્ટ નથી. તેથી, ફંક્શનની સીમા શોધવા માટે, તમારે ફંક્શનના તમામ નિર્ણાયક બિંદુઓ શોધવાની જરૂર છે, અને પછી આ દરેક બિંદુઓને મહત્તમ અને લઘુત્તમ માટે અલગથી તપાસો. નીચેનો પ્રમેય આ હેતુને સેવા આપે છે.

પ્રમેય 2. (એક્સ્ટ્રીમમના અસ્તિત્વ માટે પૂરતી શરત.) નિર્ણાયક બિંદુ ધરાવતા કેટલાક અંતરાલ પર કાર્યને સતત રહેવા દો x 0, અને આ અંતરાલના તમામ બિંદુઓ પર અલગ છે (સિવાય કે, કદાચ, બિંદુ પોતે x 0). જો, જ્યારે આ બિંદુ દ્વારા ડાબેથી જમણે ખસેડવામાં આવે છે, ત્યારે વ્યુત્પન્ન ફેરફારો ચિહ્ન વત્તાથી માઈનસ સુધી, પછી બિંદુ પર x = x 0 ફંક્શન મહત્તમ છે. જો, જ્યારે પસાર થાય છે x 0 ડાબેથી જમણે, વ્યુત્પન્ન ફેરફારો બાદબાકીથી વત્તામાં સાઇન કરે છે, પછી ફંક્શન આ બિંદુએ ન્યૂનતમ હોય છે.

આમ, જો

f "(x)>0 વાગ્યે x <x 0 અને f "(x)< 0 પર x>x 0, પછી x 0 - મહત્તમ બિંદુ;

ખાતે x <x 0 અને f "(x)> 0 પર x>x 0, પછી x 0 - ન્યૂનતમ બિંદુ.

પુરાવો. ચાલો પહેલા માની લઈએ કે જ્યારે પસાર થઈ રહ્યા છીએ x 0 વ્યુત્પન્ન ફેરફારોનું ચિહ્ન વત્તાથી ઓછા સુધી, એટલે કે. દરેકની સામે x, બિંદુની નજીક x 0 f "(x)>માટે 0 x< x 0 , f "(x)< માટે 0 x>x 0 ચાલો લેગ્રેન્જના પ્રમેયને તફાવત પર લાગુ કરીએ f(x) - f(x 0 ) = f "(c)(x- x 0), ક્યાં cવચ્ચે આવેલું છે xઅને x 0 .

દો x< x 0 પછી c< x 0 અને f "(c)> 0. તેથી જ f "(c)(x- x 0)< 0 અને તેથી

f(x) - f(x 0 )< 0, એટલે કે. f(x)< f(x 0 ).

દો x > x 0 પછી c>x 0 અને f "(c)< 0. અર્થ f "(c)(x- x 0)< 0. તેથી જ f(x) - f(x 0 ) <0,т.е.f(x) < f(x 0 ) .

આમ, બધા મૂલ્યો માટે xપૂરતી નજીક x 0 f(x) < f(x 0 ) . અને આનો અર્થ એ છે કે બિંદુ પર x 0 ફંક્શન મહત્તમ છે.

લઘુત્તમ પ્રમેયનો બીજો ભાગ એ જ રીતે સાબિત થાય છે.

ચાલો આકૃતિમાં આ પ્રમેયનો અર્થ સમજાવીએ. દો f "(x 1 ) =0 અને કોઈપણ માટે x,પૂરતી નજીક x 1, અસમાનતાઓ સંતુષ્ટ છે

f "(x)< 0 પર x< x 1 , f "(x)> 0 પર x>x 1 .

પછી બિંદુની ડાબી બાજુએ x 1 કાર્ય વધે છે અને જમણી બાજુએ ઘટે છે, તેથી, જ્યારે x = x 1 ફંક્શન વધવાથી ઘટતા જાય છે, એટલે કે, તેની પાસે મહત્તમ છે.

એ જ રીતે, આપણે મુદ્દાઓ પર વિચાર કરી શકીએ x 2 અને x 3 .

ઉપરોક્ત તમામને ચિત્રમાં યોજનાકીય રીતે દર્શાવી શકાય છે:

એક્સ્ટ્રીમમ માટે ફંક્શન y=f(x) નો અભ્યાસ કરવાનો નિયમ

ફંક્શનનું ડોમેન શોધો f(x).

ફંક્શનનું પ્રથમ વ્યુત્પન્ન શોધો f "(x) .

આ માટે નિર્ણાયક મુદ્દાઓ નક્કી કરો:

સમીકરણના વાસ્તવિક મૂળ શોધો f "(x) =0;

બધા મૂલ્યો શોધો xજેના માટે વ્યુત્પન્ન f "(x)અસ્તિત્વમાં નથી.

નિર્ણાયક બિંદુની ડાબી અને જમણી તરફ વ્યુત્પન્નની નિશાની નક્કી કરો. વ્યુત્પન્નની નિશાની બે નિર્ણાયક બિંદુઓ વચ્ચે સ્થિર રહેતી હોવાથી, નિર્ણાયક બિંદુની ડાબી બાજુએ એક બિંદુ અને જમણી બાજુએ એક બિંદુએ વ્યુત્પન્નની નિશાની નક્કી કરવા માટે તે પૂરતું છે.

અંતિમ બિંદુઓ પર કાર્યના મૂલ્યની ગણતરી કરો.

આ ગણિતનો એક રસપ્રદ વિભાગ છે, જે સંપૂર્ણપણે બધા સ્નાતકો અને વિદ્યાર્થીઓનો સામનો કરે છે. જો કે, દરેકને મટન ગમતું નથી. કેટલાક મોટે ભાગે પ્રમાણભૂત કાર્ય અભ્યાસ જેવી મૂળભૂત બાબતો પણ સમજી શકતા નથી. આ લેખ આવી અવગણનાને સુધારવાનો છે. કાર્ય વિશ્લેષણ વિશે વધુ જાણવા માંગો છો? શું તમે જાણવા માગો છો કે એક્સ્ટ્રીમ પોઈન્ટ્સ શું છે અને તેમને કેવી રીતે શોધી શકાય? તો પછી આ લેખ તમારા માટે છે.

કાર્યના ગ્રાફનો અભ્યાસ કરવો

પ્રથમ, તમારે ગ્રાફનું વિશ્લેષણ કરવાની જરૂર કેમ છે તે સમજવું યોગ્ય છે. ત્યાં સરળ કાર્યો છે જે દોરવા મુશ્કેલ નથી. આવા કાર્યનું આકર્ષક ઉદાહરણ પેરાબોલા છે. ગ્રાફ દોરવો મુશ્કેલ નહીં હોય. ફંક્શન 0 ની કિંમત લે છે તે સંખ્યાઓ શોધવા માટે, સરળ પરિવર્તનનો ઉપયોગ કરીને, ફક્ત એટલું જ જરૂરી છે. અને સૈદ્ધાંતિક રીતે, પેરાબોલાનો ગ્રાફ દોરવા માટે તમારે આ બધું જાણવાની જરૂર છે.

પરંતુ જો આપણે ગ્રાફ માટે જે કાર્યની જરૂર છે તે વધુ જટિલ હોય તો શું? જટિલ કાર્યોના ગુણધર્મો તદ્દન સ્પષ્ટ ન હોવાથી, સંપૂર્ણ વિશ્લેષણ હાથ ધરવા જરૂરી છે. આ પછી જ કાર્યને ગ્રાફિકલી ચિત્રિત કરી શકાય છે. આ કેવી રીતે કરવું? તમે આ લેખમાં આ પ્રશ્નનો જવાબ શોધી શકો છો.

કાર્ય વિશ્લેષણ યોજના

પ્રથમ વસ્તુ જે આપણે કરવાની જરૂર છે તે ફંક્શનનો સુપરફિસિયલ અભ્યાસ કરવાની છે, જે દરમિયાન આપણે વ્યાખ્યાનું ડોમેન શોધીએ છીએ. તેથી, ચાલો ક્રમમાં શરૂ કરીએ. વ્યાખ્યાનું ડોમેન એ મૂલ્યોનો સમૂહ છે જેના દ્વારા કાર્ય વ્યાખ્યાયિત કરવામાં આવે છે. સરળ શબ્દોમાં કહીએ તો, આ એવા નંબરો છે જેનો x ને બદલે ફંક્શનમાં ઉપયોગ કરી શકાય છે. અવકાશ નક્કી કરવા માટે, તમારે ફક્ત રેકોર્ડ જોવાની જરૂર છે. ઉદાહરણ તરીકે, તે સ્પષ્ટ છે કે ફંક્શન y (x) = x 3 + x 2 - x + 43 પાસે વ્યાખ્યાનું ડોમેન છે જે વાસ્તવિક સંખ્યાઓનો સમૂહ છે. સારું, (x 2 - 2x)/x જેવા ફંક્શન સાથે બધું થોડું અલગ છે. કારણ કે છેદમાં સંખ્યા 0 ની બરાબર હોવી જોઈએ નહીં, આ કાર્યની વ્યાખ્યાનું ડોમેન શૂન્ય સિવાયની બધી વાસ્તવિક સંખ્યાઓ હશે.

આગળ, તમારે ફંક્શનના કહેવાતા શૂન્ય શોધવાની જરૂર છે. આ દલીલ મૂલ્યો છે જેના પર સમગ્ર કાર્ય શૂન્ય મૂલ્ય લે છે. આ કરવા માટે, કાર્યને શૂન્ય સાથે સમાન કરવું જરૂરી છે, તેને વિગતવાર ધ્યાનમાં લો અને કેટલાક પરિવર્તનો કરો. ચાલો પહેલાથી જ પરિચિત ફંક્શન y(x) = (x 2 - 2x)/x લઈએ. શાળાના અભ્યાસક્રમમાંથી આપણે જાણીએ છીએ કે જ્યારે અંશ શૂન્ય બરાબર હોય ત્યારે અપૂર્ણાંક 0 ની બરાબર હોય છે. તેથી, અમે છેદ કાઢી નાખીએ છીએ અને અંશ સાથે કામ કરવાનું શરૂ કરીએ છીએ, તેને શૂન્ય સાથે સરખાવીએ છીએ. આપણને x 2 - 2x = 0 મળે છે અને x ને કૌંસની બહાર મુકીએ છીએ. તેથી x (x - 2) = 0. પરિણામે, આપણે શોધીએ છીએ કે જ્યારે x 0 અથવા 2 ની બરાબર હોય ત્યારે આપણું કાર્ય શૂન્યની બરાબર છે.

ફંક્શનના ગ્રાફનો અભ્યાસ કરતી વખતે, ઘણા લોકો એક્સ્ટ્રીમ પોઈન્ટના સ્વરૂપમાં સમસ્યાઓનો સામનો કરે છે. અને તે વિચિત્ર છે. છેવટે, ચરમસીમા એ એકદમ સરળ વિષય છે. મારા પર વિશ્વાસ નથી થતો? લેખનો આ ભાગ વાંચીને તમારા માટે જુઓ, જેમાં અમે ન્યૂનતમ અને મહત્તમ પોઈન્ટ વિશે વાત કરીશું.

પ્રથમ, એ સમજવું યોગ્ય છે કે એક્સ્ટ્રીમ શું છે. એક્સ્ટ્રીમમ એ મર્યાદા મૂલ્ય છે જે ફંક્શન ગ્રાફ પર પહોંચે છે. તે તારણ આપે છે કે ત્યાં બે આત્યંતિક મૂલ્યો છે - મહત્તમ અને લઘુત્તમ. સ્પષ્ટતા માટે, તમે ઉપરનું ચિત્ર જોઈ શકો છો. અભ્યાસ કરેલ ક્ષેત્રમાં, બિંદુ -1 એ કાર્ય y (x) = x 5 - 5x નું મહત્તમ છે, અને બિંદુ 1, તે મુજબ, લઘુત્તમ છે.

ઉપરાંત, ખ્યાલોને ગૂંચવશો નહીં. ફંક્શનના એક્સ્ટ્રીમમ પોઈન્ટ એ એવી દલીલો છે કે જેના પર આપેલ ફંક્શન આત્યંતિક મૂલ્યો મેળવે છે. બદલામાં, એક્સ્ટ્રીમમ એ ફંક્શનના ન્યૂનતમ અને મહત્તમનું મૂલ્ય છે. ઉદાહરણ તરીકે, ઉપરની આકૃતિને ફરીથી ધ્યાનમાં લો. -1 અને 1 એ ફંક્શનના એક્સ્ટ્રીમા પોઈન્ટ છે, અને 4 અને -4 એ એક્સ્ટ્રીમા પોઈન્ટ છે.

એક્સ્ટ્રીમ પોઈન્ટ શોધવી

પરંતુ તમે હજુ પણ ફંક્શનના એક્સ્ટ્રીમ પોઈન્ટ કેવી રીતે શોધી શકશો? બધું એકદમ સરળ છે. પ્રથમ વસ્તુ એ સમીકરણનું વ્યુત્પન્ન શોધવાનું છે. ચાલો કહીએ કે અમને કાર્ય પ્રાપ્ત થયું છે: "ફંક્શન y (x) ના અંતિમ બિંદુઓ શોધો, x એ દલીલ છે, ચાલો ફંક્શન y (x) = x 3 + 2x 2 + x + 54 લઈએ. ચાલો તફાવત કરીએ અને નીચે આપેલ સમીકરણ મેળવો: 3x 2 + 4x + 1. પરિણામે, અમારી પાસે એક પ્રમાણભૂત ચતુર્ભુજ સમીકરણ છે જે આગળ કરવાનું છે તે શૂન્ય સાથે સરખું કરવું અને મૂળ શોધવાનું છે કારણ કે ભેદભાવ શૂન્ય (D = 16 - 12 = 4), આ સમીકરણ બે મૂળ દ્વારા નક્કી કરવામાં આવે છે અને તેમને બે મૂલ્યો મળે છે: 1/3 અને -1 આ કાર્યના અંતિમ બિંદુઓ હશે કોણ છે ? 1. આ મૂલ્યને આપણા સમીકરણમાં બદલીએ છીએ. બદલામાં, આનો અર્થ એ છે કે માઇનસ અનંતથી 1/3 અને -1 થી વત્તા અનંત સુધીના અંતરાલ પર કાર્ય ઘટે છે. આમ, આપણે નિષ્કર્ષ પર આવી શકીએ છીએ કે સંખ્યા 1/3 એ અભ્યાસ કરેલ અંતરાલ પર કાર્યનો લઘુત્તમ બિંદુ છે, અને -1 એ મહત્તમ બિંદુ છે.

એ નોંધવું પણ યોગ્ય છે કે યુનિફાઇડ સ્ટેટ પરીક્ષા માટે માત્ર એક્સ્ટ્રીમ પોઈન્ટ્સ શોધવાની જરૂર નથી, પરંતુ તેમની સાથે અમુક પ્રકારની કામગીરી (ઉમેરવું, ગુણાકાર, વગેરે) પણ કરવું જરૂરી છે. તે આ કારણોસર છે કે સમસ્યાની પરિસ્થિતિઓ પર વિશેષ ધ્યાન આપવું યોગ્ય છે. છેવટે, બેદરકારીને લીધે, તમે પોઈન્ટ ગુમાવી શકો છો.