Med funkcionalnimi vrstami zavzemajo najpomembnejše mesto potenčne vrste.

Potenčna vrsta je vrsta

katerih členi so potenčne funkcije, urejene v naraščajočih nenegativnih celih potencah x, A c0 , c 1 , c 2 , c n - konstantne vrednosti. Številke c1 , c 2 , c n - koeficienti členov serije, c0 - brezplačen član. Členi potenčne vrste so definirani na celotni številski premici.

Spoznajmo se s konceptom območja konvergence potenčnih vrst. To je niz vrednosti spremenljivk x, za katerega serija konvergira. Potenčne vrste imajo dokaj preprosto konvergenčno območje. Za realne spremenljive vrednosti x konvergenčno območje je sestavljeno iz ene točke ali je določen interval (konvergenčni interval) ali sovpada s celotno osjo Ox .

Pri zamenjavi vrednosti v vrsto moči x= 0 bo povzročil niz številk

c0 +0+0+...+0+... ,

ki konvergira.

Zato, ko x= 0 vsaka potenčna vrsta konvergira in zato njegovo območje konvergence ne more biti prazen niz. Struktura območja konvergence vseh potenčnih vrst je enaka. Lahko se ugotovi z uporabo naslednjega izreka.

Izrek 1 (Abelov izrek). Če potenčna vrsta konvergira pri neki vrednosti x = x 0 , drugačen od nič, potem konvergira in poleg tega absolutno za vse vrednosti |x| < |x 0 | . Upoštevajte: tako začetna vrednost "X je nič" kot katera koli vrednost "X", ki se primerja z začetno vrednostjo, se vzameta po modulu - brez upoštevanja predznaka.

Posledica. če potenčne vrste se razhajajo po neki vrednosti x = x 1 , potem se razhaja za vse vrednosti |x| > |x 1 | .

Kot smo že prej ugotovili, vsaka potenčna vrsta konvergira pri vrednosti x= 0. Obstajajo potenčne vrste, ki konvergirajo le, če x= 0 in se razlikujejo za druge vrednosti X. Če ta primer izključimo iz obravnave, predpostavimo, da potenčna vrsta konvergira pri neki vrednosti x = x 0 , drugačen od nič. Potem po Abelovem izreku konvergira v vseh točkah intervala ]-| x0 |, |x 0 |[ (interval, katerega leva in desna meja sta vrednosti x, pri katerih konvergira potenčna serija, vzeta z znakom minus oziroma znakom plus), simetričen glede na izvor.

Če se potenčne vrste razhajajo pri določeni vrednosti x = x 1 , potem na podlagi posledice Abelovega izreka divergira na vseh točkah zunaj segmenta [-| x1 |, |x 1 |] . Iz tega sledi, da za vsako potenčno vrsto obstaja interval, simetričen glede na izvor, imenovan konvergenčni interval , v vsaki točki katere serija konvergira, na mejah lahko konvergira ali pa se razhaja in ne nujno istočasno, zunaj segmenta pa serija divergira. številka R se imenuje polmer konvergence potenčne vrste.

V posebnih primerih konvergenčni interval potenčnih vrst lahko degenerira do točke (tedaj vrsta konvergira le, če x= 0 in velja, da je R= 0) ali predstavljajo celotno številsko premico (tedaj serija konvergira v vseh točkah številske premice in predpostavimo, da ).

Tako je določitev območja konvergence potenčne vrste sestavljena iz določitve njenega konvergenčni polmer R in preučevanje konvergence vrste na mejah konvergenčnega intervala (pri ).

2. izrek.Če so vsi koeficienti potenčne serije, začenši z določeno, različni od nič, potem je njen polmer konvergence enak meji pri razmerju absolutnih vrednosti koeficientov skupnih naslednjih članov serije , tj.

Primer 1. Poiščite območje konvergence potenčne vrste

rešitev. Tukaj

S formulo (28) najdemo polmer konvergence te serije:

Preučimo konvergenco vrste na koncih konvergenčnega intervala. Primer 13 kaže, da ta vrsta konvergira pri x= 1 in se razhaja pri x= -1. Posledično je območje konvergence polovični interval.

Primer 2. Poiščite območje konvergence potenčne vrste

rešitev. Koeficienti serije so pozitivni in

Poiščimo mejo tega razmerja, tj. polmer konvergence potenčne vrste:

Preučimo konvergenco vrste na koncih intervala. Zamenjava vrednosti x= -1/5 in x= 1/5 v tej vrstici daje:

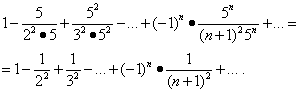
Prvi od teh nizov konvergira (glej primer 5). Toda potem na podlagi izreka v razdelku »Absolutna konvergenca« konvergira tudi druga vrsta, območje njene konvergence pa je segment

Primer 3. Poiščite območje konvergence potenčne vrste

rešitev. Tukaj

S formulo (28) najdemo polmer konvergence niza:

Preučimo konvergenco vrste za vrednosti . Če jih zamenjamo v tej seriji, dobimo oz

Obe vrsti se razhajata, ker nujni pogoj za konvergenco ni izpolnjen (njuni skupni členi ne težijo k ničli pri ). Torej, na obeh koncih konvergenčnega intervala se ta niz razhaja in območje njegove konvergence je interval.

Primer 5. Poiščite območje konvergence potenčne vrste

rešitev. Najdemo razmerje, kjer je , in :

Po formuli (28) je polmer konvergence te serije

to pomeni, da vrsta konvergira le, ko x= 0 in se razlikuje za druge vrednosti X.

Primeri kažejo, da se vrste na koncu konvergenčnega intervala obnašajo drugače. V primeru 1 na enem koncu konvergenčnega intervala vrsta konvergira, v primeru 2 pa na obeh koncih; v primeru 3 se razhaja na obeh koncih.

Formulo za polmer konvergence potenčne vrste dobimo ob predpostavki, da so vsi koeficienti členov vrste, začenši z določene točke, različni od nič. Zato je uporaba formule (28) dopustna samo v teh primerih. Če je ta pogoj kršen, je treba polmer konvergence potenčne vrste iskati z uporabo d'Alembertov znak, ali z zamenjavo spremenljivke preoblikovanje serije v obliko, v kateri je podani pogoj izpolnjen.

Primer 6. Poiščite interval konvergence potenčne vrste

rešitev. Ta serija ne vsebuje izrazov z neparnimi stopnjami X. Zato preoblikujemo serijo, nastavitev . Potem dobimo serijo

da bi našli polmer konvergence, lahko uporabimo formulo (28). Ker , a , potem polmer konvergence te vrste

Iz enakosti, ki jo dobimo, torej ta vrsta konvergira na intervalu.

Vsota potenčnih vrst. Diferenciranje in integracija potenčnih vrst

Let za potenčne vrste

polmer konvergence R> 0, tj. ta niz konvergira na intervalu .

Nato vsaka vrednost X iz konvergenčnega intervala ustreza določeni vsoti vrste. Zato je vsota potenčnih vrst funkcija X na konvergenčnem intervalu. Označujemo ga z f(x), lahko zapišemo enakost

razumeti v smislu, da je vsota serije v vsaki točki X iz konvergenčnega intervala je enaka vrednosti funkcije f(x) na tej točki. V istem smislu bomo rekli, da potenčna vrsta (29) konvergira k funkciji f(x) na konvergenčnem intervalu.

Izven konvergenčnega intervala enakost (30) nima smisla.

Primer 7. Poiščite vsoto potenčne vrste

rešitev. To je geometrijska vrsta, za katero a= 1, a q= x. Zato je njegova vsota funkcija . Niz konvergira, če je in je njegov konvergenčni interval. Torej enakost

velja samo za vrednosti, čeprav funkcija določeno za vse vrednosti X, razen X= 1.

Lahko se dokaže, da je vsota potenčne vrste f(x) je zvezna in diferencibilna na katerem koli intervalu znotraj konvergenčnega intervala, zlasti na kateri koli točki v konvergenčnem intervalu vrste.

Predstavimo izreke o člen za členom diferenciacije in integracije potenčnih vrst.

1. izrek. Potenčne vrste (30) v intervalu svoje konvergence lahko člen za členom diferenciramo neomejeno številokrat, nastale potenčne vrste pa imajo enak polmer konvergence kot izvirne vrste, njihove vsote pa so enake .

2. izrek. Potenčne vrste (30) lahko integriramo člen za členom neomejeno število krat v območju od 0 do X, če , in posledična potenčna vrsta imata enak polmer konvergence kot izvirna vrsta, njuni vsoti pa sta ustrezno enaki

Razširitev funkcij v potenčne vrste

Naj bo funkcija podana f(x), ki ga je treba razširiti v potenčni niz, tj. predstavi v obliki (30):

Naloga je določiti koeficiente vrstica (30). Da bi to naredili, z razlikovanjem enakosti (30) po izrazih dosledno ugotovimo:

……………………………………………….. (31)

Ob predpostavki v enačbah (30) in (31) X= 0, ugotovimo

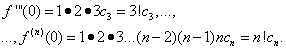
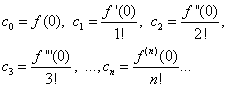
Če nadomestimo najdene izraze v enakost (30), dobimo

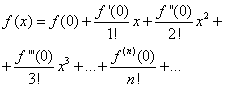(32)

Poiščimo Maclaurinovo vrstno razširitev nekaterih elementarnih funkcij.

Primer 8. Razširite funkcijo v seriji Maclaurin

rešitev. Izpeljanke te funkcije sovpadajo s samo funkcijo:

Zato, ko X= 0 imamo

Če nadomestimo te vrednosti v formulo (32), dobimo želeno razširitev:

(33)

Ta niz konvergira na celotni številski premici (njen polmer konvergence).

Primer 1. Poiščite območje konvergence potenčne vrste:

A) ; b) ;

V) ; G)
;

d)
.

A) Poiščimo polmer konvergence R. Ker
,
, To

x
, to je interval konvergence vrste
.

pri
dobimo številsko serijo . Ta vrsta konvergira, ker je posplošena harmonična vrsta pri
.

pri
dobimo številsko serijo
. Ta serija je absolutno konvergentna, saj je serija sestavljena iz absolutnih vrednosti njenih členov , konvergentno.

b) Poiščimo polmer konvergence R. Ker
, To
.

Torej, konvergenčni interval vrste
.

Preučujemo konvergenco tega niza na koncih konvergenčnega intervala.

pri
imamo niz številk

.

pri
imamo niz številk
. Ta serija je različna, ker
ne obstaja.

Torej, območje konvergence te serije
.

V) Poiščimo polmer konvergence R. Ker
,
to
.

Torej, konvergenčni interval
. Konvergenčno območje te serije sovpada s konvergenčnim intervalom, to pomeni, da serija konvergira za katero koli vrednost spremenljivke x.

G) Poiščimo polmer konvergence R. Ker
,
to
.

Ker
, potem vrsta konvergira le v točki
. To pomeni, da je območje konvergence te vrste ena točka
.

d) Poiščimo polmer konvergence R.

Ker
,
, To

Torej, serija konvergira za absolutno vse x, ki izpolnjuje neenakost
, to je
.

Od tod
− konvergenčni interval,
− polmer konvergence.

Preglejmo to vrsto glede konvergence na koncih konvergenčnega intervala.

pri
dobimo številsko serijo

ki divergira (harmonični niz).

pri
dobimo številsko serijo
, ki pogojno konvergira (vrsta konvergira po Leibnizovem kriteriju, serija, sestavljena iz absolutnih vrednosti njenih članov, pa se razhaja, ker je harmonična).

Torej območje konvergence vrste
.

2.3. Serija Taylor in Maclaurin.

Razširitev funkcij v potenčne vrste.

Uporaba potenčnih vrst za približne izračune

Primeri reševanja problemov

Primer 1. Razširite funkcijo v potenčni niz:

A)
; b)
;

V)
; G)
.

A) Zamenjava v formuli
x na
, dobimo želeno razširitev:

Kje

b) Nadomeščanje v enakosti

Kje
x na
, dobimo želeno razširitev:

V) To funkcijo lahko zapišemo takole:
. Če želite najti želeno serijo, je dovolj, da razširite

Kje
nadomestek
. Potem dobimo:

G) To funkcijo lahko prepišemo takole: .

funkcija
lahko razširimo v potenčno vrsto tako, da dodamo binomsko vrsto
, bomo prejeli.

Kje
.

Da bi dobili želeno razširitev, je dovolj, da pomnožimo nastale serije (zaradi absolutne konvergence teh serij).

torej

, Kje
.

Primer 2. Poiščite približne vrednosti teh funkcij:

A)
z natančnostjo 0,0001;

b)
z natančnostjo 0,00001.

A) Ker
, nato v širitev funkcije, kjer
zamenjajmo
:

Ker
, potem bo zahtevana natančnost zagotovljena, če se omejimo le na prva dva člena nastale razširitve.

Uporabljamo binomsko vrsto

Kje
.

Verjeti
in
, dobimo naslednjo razširitev:

Če se v zadnjem izmeničnem nizu upoštevata le prva dva člena, ostali pa se zavržejo, potem je napaka v izračunu
absolutna vrednost ne bo presegla 0,000006. Potem napaka v izračunu
ne bo presegla številke. torej

Primer 3. Izračunaj na 0,001 natančno:

A)
; b)
.

A)
.

Razširimo integrand v potenčno vrsto. Da bi to naredili, zamenjajmo v binomskem nizu
in zamenjajte x na :

Od segmenta integracije
pripada območju konvergence nastale serije
, potem bomo integrirali člen za izrazom znotraj navedenih omejitev:

V dobljenem nizu izmeničnih predznakov je četrti člen manjši od 0,001 v absolutni vrednosti. Posledično bo zahtevana natančnost zagotovljena, če se upoštevajo le prvi trije členi vrste.

Ker ima prvi izmed zavrženih členov predznak minus, bo dobljena približna vrednost v presežku. Zato je odgovor na 0,001 natančno 0,487.

b) Najprej predstavimo integrand kot potenčno vrsto. Zamenjajmo v razširitvi funkcije

Kje

x na
, dobimo:

Potem
.

Nastali izmenični nizi izpolnjujejo pogoje Leibnizovega kriterija. Četrti člen niza je manjši od 0,001 v absolutni vrednosti. Za zagotovitev zahtevane natančnosti je dovolj, da poiščemo vsoto prvih treh izrazov.

torej
.

Funkcionalna serija. Potenčne vrste.
Območje konvergence vrste

Smeh brez razloga je znak d'Alemberta

Odbila je ura funkcionalnih činov. Če želite uspešno obvladati temo in še posebej to lekcijo, morate dobro razumeti navadne številske serije. Morali bi dobro razumeti, kaj serija je in biti sposobni uporabiti primerjalna merila za preučevanje konvergence serije. Torej, če ste šele začeli študirati temo ali ste začetnik v višji matematiki, potrebno delajte tri lekcije v zaporedju: Vrstice za lutke,D'Alembertov znak. Cauchyjevi znaki in Izmenične vrste. Leibnizov test. Vsekakor vse tri! Če imate osnovno znanje in veščine reševanja nalog s številskimi vrstami, bo obvladovanje funkcionalnih serij povsem preprosto, saj novega gradiva ni veliko.

V tej lekciji si bomo ogledali koncept funkcionalne vrste (kaj sploh je), se seznanili s potenčnimi vrstami, ki jih najdemo v 90 % praktičnih nalog, in se naučili rešiti pogost tipičen problem iskanja polmera konvergence, konvergenčnega intervala in konvergenčnega območja potenčne vrste. Nato priporočam, da razmislite o gradivu o razširitev funkcij v potenčne vrste, začetniku pa bo zagotovljena prva pomoč. Ko malo zajamemo sapo, preidemo na naslednjo stopnjo:

Tudi v delu funkcijskih serij jih je veliko aplikacije za približno računalništvo, in na nek način izstopajo Fourierjevi nizi, ki jim je v izobraževalni literaturi praviloma namenjeno posebno poglavje. Imam samo en članek, vendar je dolg in je veliko, veliko dodatnih primerov!

Torej, mejniki so postavljeni, gremo:

Pojem funkcionalne vrste in potenčne vrste

Če se izkaže, da je meja neskončna, potem konča svoje delo tudi algoritem reševanja in podamo končni odgovor na nalogo: “Ver konvergira pri ” (ali pri ”). Glej primer št. 3 prejšnjega odstavka.

Če se izkaže, da meja ni ne nič ne neskončna, potem imamo najpogostejši primer v praksi št. 1 - vrsta konvergira na določenem intervalu.

V tem primeru je meja. Kako najti interval konvergence vrste? Sestavimo neenakost:

IN VSAKA tovrstna naloga na levi strani neenakosti mora biti rezultat izračuna omejitve, in na desni strani neenakosti – strogo enota. Ne bom natančno razlagal, zakaj je taka neenakost in zakaj je na desni strani. Pouk je praktično naravnan in že je zelo dobro, da moje zgodbe niso obesile učiteljskega zbora in so nekateri izreki postali jasnejši.

Tehnika dela z modulom in reševanja dvojnih neenačb je bila podrobneje obravnavana v prvem letniku v članku Domena funkcije, vendar bom zaradi udobja poskušal komentirati vsa dejanja čim bolj podrobno. Neenačbo razkrijemo z modulom po šolskem pravilu . V tem primeru:

Pol poti je mimo.

Na drugi stopnji je potrebno raziskati konvergenco serije na koncih najdenega intervala.

Najprej vzamemo levi del intervala in ga nadomestimo v našo vrsto moči:

pri

Dobili smo številsko vrsto in jo moramo pregledati na konvergenco (naloga, ki jo poznamo že iz prejšnjih lekcij).

1) Serija je izmenična.
2) – členi serije se zmanjšajo po modulu. Poleg tega je vsak naslednji član niza manjši od prejšnjega v absolutni vrednosti: , kar pomeni, da je zmanjšanje monotono.
Zaključek: serija konvergira.

Z uporabo serije, sestavljene iz modulov, bomo natančno ugotovili, kako:
– konvergira (»standardni« niz iz družine generaliziranih harmoničnih nizov).

Tako dobljeni številski niz absolutno konvergira.

pri – konvergira.

! spomnim te da je vsaka konvergentna pozitivna vrsta tudi absolutno konvergentna.

Tako potenčna vrsta konvergira in absolutno na obeh koncih najdenega intervala.

odgovor: območje konvergence preučevane vrste moči:

Druga oblika odgovora ima pravico do življenja: Niz konvergira, če

Včasih izjava o problemu zahteva, da navedete polmer konvergence. Očitno je, da v obravnavanem primeru.

Primer 2

Poiščite območje konvergence potenčne vrste

rešitev: najdemo interval konvergence vrste z uporabo d'Alembertov znak (vendar ne atribut BY! – tak atribut ne obstaja za funkcionalne serije):

Serija konvergira pri

levo moramo oditi samo, zato obe strani neenakosti pomnožimo s 3:

– Serije se izmenjujejo.
– – členi serije se zmanjšajo po modulu. Vsak naslednji član niza je po absolutni vrednosti manjši od prejšnjega: , kar pomeni, da je zmanjšanje monotono.

Zaključek: serija konvergira.

Preučimo naravo konvergence:

Primerjajmo to serijo z divergentno serijo.
Uporabljamo omejevalni primerjalni kriterij:

Dobimo končno število, ki je različno od nič, kar pomeni, da serija odstopa od serije.

Tako serija pogojno konvergira.

2) Kdaj – divergira (glede na dokazano).

odgovor: Območje konvergence preučevane vrste moči: . Ko niz pogojno konvergira.

V obravnavanem primeru je območje konvergence potenčne vrste polovični interval, v vseh točkah intervala pa potenčna vrsta absolutno konvergira, in na točki , kot se je izkazalo – pogojno.

Primer 3

Poiščite interval konvergence potenčne vrste in raziščite njegovo konvergenco na koncih najdenega intervala.

To je primer, ki ga morate rešiti sami.

Poglejmo si nekaj primerov, ki so redki, a se pojavljajo.

Primer 4

Poiščite območje konvergence serije:

rešitev: Z d'Alembertovim testom najdemo interval konvergence tega niza:

(1) Sestavimo razmerje med naslednjim članom niza in prejšnjim.

(2) Znebimo se štirinadstropne frakcije.

(3) Po pravilu operacij s potencami spravimo kocke pod eno potenco. V števniku premeteno razširimo stopnjo, tj. Uredimo ga tako, da lahko v naslednjem koraku ulomek zmanjšamo za . Faktorijele podrobno opišemo.

(4) Pod kocko delimo števec z imenovalcem člen za členom, kar pomeni, da . Z delčkom zmanjšamo vse, kar se da zmanjšati. Faktor vzamemo preko mejnega znaka; lahko ga izvzamemo, saj v njem ni ničesar, kar bi bilo odvisno od "dinamične" spremenljivke "en". Upoštevajte, da znak modula ni narisan - iz razloga, ker ima nenegativne vrednosti za kateri koli "x".

V limitu dobimo ničlo, kar pomeni, da lahko podamo končni odgovor:

odgovor: Serija konvergira pri

Toda sprva se je zdelo, da bo to vrstico s "strašnim polnilom" težko rešiti. Nič ali neskončnost v meji je skoraj darilo, saj je rešitev opazno zmanjšana!

Primer 5

Poiščite območje konvergence serije

To je primer, ki ga morate rešiti sami. Bodite previdni;-) Celotna rešitev je na koncu lekcije.

Poglejmo si še nekaj primerov, ki vsebujejo element novosti v smislu uporabe tehničnih prijemov.

Primer 6

Poiščite konvergenčni interval niza in raziščite njegovo konvergenco na koncih najdenega intervala

rešitev: Skupni člen potenčne vrste vključuje faktor, ki zagotavlja menjavo predznaka. Algoritem rešitve je v celoti ohranjen, vendar pri sestavljanju meje ta dejavnik ignoriramo (ne pišemo), saj modul uniči vse "minuse".

Interval konvergence vrste najdemo z d'Alembertovim testom:

Ustvarimo standardno neenakost:
Serija konvergira pri
levo moramo oditi samo modul, zato obe strani neenakosti pomnožimo s 5:

Zdaj odpremo modul na znan način:

Na sredini dvojne neenakosti morate za ta namen pustiti samo "X", od vsakega dela neenakosti odštejemo 2:

– interval konvergence preučevanega potenčnega niza.

Raziskujemo konvergenco vrste na koncih najdenega intervala:

1) Nadomestite vrednost v našo vrsto moči :

Bodite zelo previdni, množitelj ne zagotavlja menjave predznaka za noben naravni "en". Nastali minus vzamemo izven niza in pozabimo nanj, saj (kot vsaka faktorska konstanta) nikakor ne vpliva na konvergenco ali divergenco številskega niza.

Ponovno upoštevajte da se je med substitucijo vrednosti v splošnem členu potenčne vrste naš faktor zmanjšal. Če se to ne bi zgodilo, bi to pomenilo, da smo limit narobe izračunali ali pa modul narobe razširili.

Torej moramo preučiti številsko vrsto za konvergenco. Tukaj je najlažji način, da uporabimo omejevalni primerjalni kriterij in to vrsto primerjamo z divergentno harmonično vrsto. Ampak, če sem iskren, sem zelo utrujen od omejujočega znaka primerjave, zato bom v rešitev dodal nekaj raznolikosti.

Torej, serija konvergira pri

Obe strani neenakosti pomnožimo z 9:

Iz obeh delov izluščimo koren, pri tem pa se spomnimo stare šolske šale:

Razširitev modula:

in dodajte enega vsem delom:

– interval konvergence preučevanega potenčnega niza.

Raziščimo konvergenco potenčne vrste na koncih najdenega intervala:

1) Če , dobimo naslednjo številsko serijo: