Enačba tangente na graf funkcije. Funkcionalne enačbe

Tangenta je ravna črta , ki se dotika grafa funkcije v eni točki in katere vse točke so od grafa funkcije najmanj oddaljene. Zato tangenta prehaja tangentno na graf funkcije pod določenim kotom in več tangent pod različnimi koti ne more potekati skozi točko dotika. Tangentne enačbe in normalne enačbe na graf funkcije so sestavljene z uporabo odvoda.

Tangentna enačba izhaja iz enačbe premice .

Izpeljimo enačbo tangente, nato pa še enačbo normale na graf funkcije.

l = kx + b .

V njem k- kotni koeficient.

Od tu dobimo naslednji vnos:

l - l 0 = k(x - x 0 ) .

Izpeljana vrednost f "(x 0 ) funkcije l = f(x) na točki x0 enaka naklonu k= tg φ tangenta na graf funkcije, narisan skozi točko M0 (x 0 , l 0 ) , Kje l0 = f(x 0 ) . To je geometrijski pomen izpeljanke .

Tako lahko zamenjamo k na f "(x 0 ) in dobite naslednje enačba tangente na graf funkcije :

l - l 0 = f "(x 0 )(x - x 0 ) .

Pri težavah, ki vključujejo sestavljanje enačbe tangente na graf funkcije (kmalu bomo prešli nanje), je treba enačbo, dobljeno iz zgornje formule, zmanjšati na enačba premice v splošni obliki. Če želite to narediti, morate premakniti vse črke in številke na levo stran enačbe in pustiti nič na desni strani.

Zdaj o normalni enačbi. normalno - to je ravna črta, ki poteka skozi točko tangente na graf funkcije, pravokotno na tangento. Normalna enačba :

(x - x 0 ) + f "(x 0 )(l - l 0 ) = 0

Za ogrevanje vas prosimo, da sami rešite prvi primer in nato pogledate rešitev. Z vsemi razlogi lahko upamo, da ta naloga za naše bralce ne bo "hladen tuš".

Primer 0. Sestavite tangentno enačbo in normalno enačbo za graf funkcije v točki M (1, 1) .

Primer 1. Napišite enačbo tangente in enačbo normale za graf funkcije , če je abscisa tangenta .

Poiščimo odvod funkcije:

Zdaj imamo vse, kar je treba nadomestiti z vnosom v teoretični pomoči, da dobimo enačbo tangente. Dobimo

V tem primeru smo imeli srečo: izkazalo se je, da je naklon enak nič, zato enačbe ni bilo treba posebej reducirati na njeno splošno obliko. Zdaj lahko ustvarimo normalno enačbo:

Na spodnji sliki: graf funkcije je bordo, tangenta zelena, normala oranžna.

Naslednji primer prav tako ni zapleten: funkcija je, tako kot v prejšnjem, tudi polinom, vendar naklon ne bo enak nič, zato bo dodan še en korak - enačba se spravi v splošno obliko.

Primer 2.

rešitev. Poiščimo ordinato tangentne točke:

Poiščimo odvod funkcije:

.

Poiščimo vrednost odvoda v točki tangente, to je naklon tangente:

Vse dobljene podatke nadomestimo v "prazno formulo" in dobimo tangentno enačbo:

Enačbo spravimo v splošno obliko (na levi strani zberemo vse črke in številke, razen nič, na desni pa pustimo nič):

Sestavimo normalno enačbo:

Primer 3. Zapišite enačbo tangente in enačbo normale na graf funkcije, če je abscisa točka dotika.

rešitev. Poiščimo ordinato tangentne točke:

Poiščimo odvod funkcije:

.

Poiščimo vrednost odvoda v točki tangente, to je naklon tangente:

.

Najdemo tangentno enačbo:

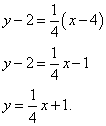
Preden enačbo spravite v splošno obliko, jo morate malo "prečesati": člen za členom pomnožite s 4. To naredimo in enačbo spravimo v splošno obliko:

Sestavimo normalno enačbo:

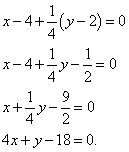
Primer 4. Zapišite enačbo tangente in enačbo normale na graf funkcije, če je abscisa točka dotika.

rešitev. Poiščimo ordinato tangentne točke:

.

Poiščimo odvod funkcije:

Poiščimo vrednost odvoda v točki tangente, to je naklon tangente:

.

Dobimo tangentno enačbo:

Enačbo pripeljemo do splošne oblike:

Sestavimo normalno enačbo:

Pogosta napaka pri pisanju tangentnih in normalnih enačb je, da ne opazimo, da je funkcija, podana v primeru, kompleksna, in izračunamo njen odvod kot odvod preproste funkcije. Naslednji primeri so že iz kompleksne funkcije(ustrezna lekcija se odpre v novem oknu).

Primer 5. Zapišite enačbo tangente in enačbo normale na graf funkcije, če je abscisa točka dotika.

rešitev. Poiščimo ordinato tangentne točke:

Pozor! Ta funkcija je kompleksna, saj argument tangente (2 x) je sama funkcija. Zato najdemo odvod funkcije kot odvod kompleksne funkcije.

Zato obstaja naravna želja po redukciji enačbe višjega reda od prvega na enačbo nižjega reda. V nekaterih primerih je to mogoče storiti. Poglejmo jih.

1. Enačbe oblike y (n) =f(x) so rešene s sekvenčno integracijo n-krat
, ,… .
Primer. Rešite enačbo xy""=1. Zato lahko zapišemo y"=ln|x| + C 1 in s ponovnim integriranjem končno dobimo y=∫ln|x| + C 1 x + C 2

2. V enačbah oblike F(x,y (k) ,y (k +1) ,..,y (n))=0 (to je, ki ne vsebuje eksplicitno neznane funkcije in nekaterih njenih odvodov), vrstni red se zmanjša s spremembo spremenljivke y (k) = z(x). Potem je y (k +1) =z"(x),...,y (n) = z (n - k) (x) in dobimo enačbo F(x,z,z",..,z (n - k)) reda n-k. Njena rešitev je funkcija z = φ(x,C 1 ,C 2 ,…,C n) ali če se spomnimo, kaj je z, dobimo enačbo y (n- k) = φ(x,C 1 ,C 2 , …, C n - k), upoštevano v primeru tipa 1.
Primer 1. Rešite enačbo x 2 y"" = (y") 2. Izvedite zamenjavo y"=z(x) . Potem je y""=z"(x). Če nadomestimo v prvotno enačbo, dobimo x 2 z"=z 2. Če ločimo spremenljivke, dobimo. Integracija, imamo , ali, kar je isto, . Zadnja relacija je zapisana v obliki , od koder je . Integracijo, končno dobimo
Primer 2. Rešimo enačbo x 3 y"" +x 2 y"=1. Izvedemo menjavo spremenljivk: y"=z; y""=z"
x 3 z"+x 2 z=1. Izvedemo spremembo spremenljivk: z=u/x; z"=(u"x-u)/x 2
x 3 (u"x-u)/x 2 +x 2 u/x=1 ali u"x 2 -xu+xu=1 ali u"x^2=1. Iz: u"=1/x 2 ali du/ dx=1/x 2 ali u = int(dx/x 2) = -1/x+c 1
Ker je z=u/x, potem je z = -1/x 2 +c 1 /x. Ker je y"=z, potem je dy/dx=-1/x 2 +c 1 /x
y = int(c 1 dx/x-dx/x 2) =c 1 ln(x) + 1/x + c 2. Odgovor: y = c 1 ln(x) + 1/x + c 2

3. Naslednja enačba, ki jo je mogoče reducirati po vrsti, je enačba oblike F(y,y",y"",…,y (n))=0, ki eksplicitno ne vsebuje neodvisne spremenljivke. Vrstni red enačba se zmanjša z zamenjavo spremenljivke y" =p(y) , kjer je p nova želena funkcija, odvisna od y. Potem
= in tako naprej. Z indukcijo imamo y (n) =φ(p,p",..,p (n-1)). S substitucijo v prvotni enačbi znižamo njen vrstni red za ena.

Primer. Rešite enačbo (y") 2 +2yy""=0. Naredimo standardno zamenjavo y"=p(y), nato pa y″=p′·p. Če nadomestimo v enačbo, dobimo Če ločimo spremenljivke za p≠0, dobimo ali, kar je isto, . Potem oz. Z integracijo zadnje enakosti končno dobimo Pri ločevanju spremenljivk bi lahko izgubili rešitev y=C, ki jo dobimo za p=0 ali, kar je isto, za y"=0, vendar je vsebovana v zgoraj dobljeni.

4. Včasih je mogoče opaziti lastnost, ki vam omogoča znižanje vrstnega reda enačbe na načine, ki se razlikujejo od tistih, ki so obravnavani zgoraj. Pokažimo to s primeri.

Primeri.
1. Če obe strani enačbe yy"""=y′y″ delimo z yy″, dobimo enačbo, ki jo lahko prepišemo kot (lny″)′=(lny)′. Iz zadnje relacije sledi, da lny″=lny +lnC ali, kar je enako, y″=Cy. Rezultat je enačba za red velikosti nižja in vrste, o kateri smo govorili prej.
2. Podobno velja za enačbo yy″=y′(y′+1) ali (ln(y"+1))" = (lny)". Iz zadnje relacije sledi, da je ln(y"+ 1) = lny + lnC 1 ali y"=C 1 y-1. Z ločevanjem spremenljivk in integracijo dobimo ln(C 1 y-1) = C 1 x+C 2
Odločite se enačbe, ki jih je mogoče reducirati po vrstnem redu možno z uporabo posebne storitve

Naj bo podana funkcija f, ki ima v neki točki x 0 končni odvod f (x 0). Potem se ravna črta, ki poteka skozi točko (x 0 ; f (x 0)) in ima kotni koeficient f ’(x 0), imenuje tangenta.

Kaj se zgodi, če odvod v točki x 0 ne obstaja? Obstajata dve možnosti:

1. Tudi tangente na graf ni. Klasičen primer je funkcija y = |x | v točki (0; 0).
2. Tangenta postane navpična. To velja na primer za funkcijo y = arcsin x v točki (1; π /2).

Tangentna enačba

Vsaka nenavpična ravna črta je podana z enačbo v obliki y = kx + b, kjer je k naklon. Tangenta ni nobena izjema in da bi ustvarili njeno enačbo v neki točki x 0, je dovolj poznati vrednost funkcije in odvod na tej točki.

Torej, naj bo dana funkcija y = f (x), ki ima odvod y = f ’(x) na segmentu. Potem lahko v kateri koli točki x 0 ∈ (a ; b) na graf te funkcije potegnemo tangento, ki je podana z enačbo:

y = f ’(x 0) (x − x 0) + f (x 0)

Tu je f ’(x 0) vrednost odvoda v točki x 0, f (x 0) pa vrednost same funkcije.

Naloga. Dana je funkcija y = x 3 . Zapišite enačbo za tangento na graf te funkcije v točki x 0 = 2.

Tangentna enačba: y = f ’(x 0) · (x − x 0) + f (x 0). Točka x 0 = 2 nam je dana, vendar bo treba izračunati vrednosti f (x 0) in f ’(x 0).

Najprej poiščimo vrednost funkcije. Tukaj je vse enostavno: f (x 0) = f (2) = 2 3 = 8;
Zdaj pa poiščimo odvod: f ’(x) = (x 3)’ = 3x 2;
V odvod zamenjamo x 0 = 2: f ’(x 0) = f ’(2) = 3 2 2 = 12;
Skupaj dobimo: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
To je tangentna enačba.

Naloga. Zapišite enačbo za tangento na graf funkcije f (x) = 2sin x + 5 v točki x 0 = π /2.

Tokrat ne bomo podrobno opisovali vsakega dejanja - navedli bomo le ključne korake. Imamo:

f (x 0) = f (π /2) = 2sin (π /2) + 5 = 2 + 5 = 7;
f ’(x) = (2sin x + 5)’ = 2cos x;
f '(x 0) = f '(π /2) = 2cos (π /2) = 0;

Tangentna enačba:

y = 0 · (x − π /2) + 7 ⇒ y = 7

V slednjem primeru se je ravna črta izkazala za vodoravno, ker njegov kotni koeficient k = 0. S tem ni nič narobe - le naleteli smo na ekstremno točko.

Naj bo podana enačba f(x) = 0 . številka x se imenuje koren dane enačbe, če jo, ko jo zamenjamo v enačbo, spremeni v enačbo, tj. f(x) = 0 . številka x imenujemo ničla funkcije f(x) .Iskanje korenin enačbe z določeno natančnostjo lahko razdelimo na dve stopnji:

1) ločevanje korenin, to je vzpostavitev intervalov, ki vsebujejo en koren enačbe;

2) izračun korena, ki pripada izbranemu intervalu z dano natančnostjo.

Znano je, da če funkcija f(x) je neprekinjen in zavzame konce segmenta [a, b] pomene različnih znakov, tj f(a)× f(b)< 0 , potem je znotraj tega segmenta ničla funkcije.

Ločiti (ali lokalizirati) koren enačbe f(x) = 0 za zvezno funkcijo v domeni definicije f(x) lahko ustvarite tabelo funkcijskih vrednosti y = f(x) v določenem intervalu spremembe argumenta X . Če imajo za nekatere sosednje vrednosti argumenta vrednosti funkcije različne znake, potem je med njimi ničla funkcije.

Naj bo podana enačba f(x) = 0 , kjer je funkcija f(x) neprekinjeno na segmentu [a, b] in f(a)× f(b)< 0 .Za izračun korena te enačbe
x O[a, b] je sredina tega segmenta x 1 = 0,5(a+b) . če f(x 1) ¹ 0 , nato pa za nadaljevanje izračunov izberite enega od delov tega segmenta
[a, x 1] oz [x 1, b] , na koncih katerih funkcija f(x) ima nasprotna predznaka. Označeni so konci novega segmenta a 1 in b 1 . Nov segment [a 1, b 1] ponovno razdelimo na polovico in izračuni se opravijo v skladu z začrtano shemo itd. Rezultat je natančen koren dane enačbe na neki stopnji ali zaporedje ugnezdenih segmentov [a, b] ,
[a 1, b 1] , … , [a n, b n] , ..., tako da:

f(a n)× f(b n)< 0 , n =1, 2, …

številka x - splošna omejitev zaporedij (a n) in (bn) – je koren enačbe f(x) = 0 .

Ocena napake rešitve na n -th korak izračunov ima obliko.

2.2 Metodologija reševanja enačb in neenačb

Enačbe in neenačbe so tradicionalna tema v šolskem tečaju matematike, ki zavzemajo veliko mesto, od nižjih razredov, kjer se uvedejo najpreprostejše enačbe in neenačbe do uvedbe teorije, ki temelji na lastnostih aritmetičnih operacij, in konča z višjim razredom. stopnje, kjer se rešujejo transcendentne enačbe.

Enačbe in neenačbe predstavljajo algebraični aparat, jezik, v katerega se prevajajo različni problemi, tudi uporabni, in gradijo njihovi matematični modeli.

Uporaba monotonosti funkcij za reševanje enačb in neenačb. Ena najpogostejših idej je dobro ponazorjena z reševanjem naslednje preproste neenakosti:

1. Reši neenačbo:.

rešitev. Obstajata dve standardni rešitvi: kvadriranje (priloženo
; če
, je neenakost izpolnjena) in zamenjava neznanke
.

Razmislimo o drugi metodi - nestandardni. Funkcija, ki se nahaja na levi strani, monotono narašča, medtem ko funkcija v prvem delu pada. Iz očitnih grafičnih premislekov sledi, da enačba
x 0 je rešitev te enačbe, potem ko
bo in rešitev te neenakosti bo
. Pomen x 0 je enostavno izbrati: x 0 = 1.

Odgovori.
.

2. Reši enačbo:
.

rešitev. Ta enačba ima očitno rešitev x= 1. Dokažimo, da drugih rešitev ni. Oba dela razdelimo na , dobimo
. Leva stran je monotono padajoča funkcija. Posledično vzame vsako svojo vrednost enkrat, tj. ta enačba ima edinstveno rešitev.

Odgovori. x = 1.

Torej je osnovna ideja, na kateri sta temeljili rešitvi teh dveh primerov, precej preprosta: če f(x) monotono narašča in φ (x) monotono pada, potem enačba f(x) = φ (x) ima največ eno rešitev in če x = x 0 je rešitev te enačbe, potem ko x > x 0 (x je v okviru obeh funkcij f(x) in φ (x) ) volja f(x) > φ (x) , in kdaj x x 0 bo

f(x) φ (x) .

Vredno je biti pozoren na eno spremembo te ideje, in sicer: če f(x) je monotona funkcija, potem iz enakosti f(x) = f(l) temu sledi x = l .

3.Reši enačbo:.

rešitev . Transformirajmo enačbo:

.

Upoštevajte funkcijo
.

Dokažimo, da ko t > 1 ta funkcija monotono pada. To lahko storite na primer na standarden način: poiščite izpeljanko

in dokazati, da ko t > 1
. Pokažimo še en način:

.

Dobljena funkcija je očitno padajoča (osnova narašča, pod znakom logaritma funkcija pada).

Naša enačba ima obliko: , kar pomeni . Na levi je naraščajoča funkcija, zato je rešitev edinstvena, zlahka jo najdete z izbiro: x = 4.

Odgovori. x = 4 .

Enačbe oblikef ( f ( x )) = x . Pri reševanju tovrstnih enačb je uporaben naslednji izrek:

Če je y = f(x) monotono naraščajoča funkcija, potem enačbe

f(x) = x(A)

f (f (x)) = x (B)

enakovreden.

Dokaz. Dejstvo, da je enačba (B) posledica enačbe (A), je očitno: vsak koren (A) ustreza (B). (Če

f (x 0 ) = x 0 , to f (f (x 0 )) = f (x 0 ) = x 0 .). Dokažimo, da vsak koren enačbe (B) ustreza enačbi (A). Pustiti x 0 tako, da f (f (x 0 )) = x 0 .Predpostavimo, da f (x 0 ) ≠ x 0 in za določnost f (x 0 ) > x 0 . Potem f (f (x 0 )) > f (x 0 ) > x 0, kar je v nasprotju s predpostavko ( f (f (x 0 )) = x 0). Izrek je dokazan.

Ali izrek velja za monotono padajočo funkcijo?

Komentiraj.če l = f (x) monotono narašča, potem za katero koli k enačbe
in f (x) = x so enakovredne.

Naj navedemo nekaj primerov uporabe tega izreka.

1. Reši enačbo:
.

Rešitev. Prepišimo enačbo
. Upoštevajte funkcijo
. Ta funkcija monotono narašča. Imamo enačbo

f (f (x)) = x. V skladu z izrekom jo nadomestimo z ekvivalentno enačbo f (x) = x ali .

Odgovori.

2. Reši enačbo:

.

rešitev. Transformirajmo enačbo:
.

Ta enačba izgleda takole: f (f (x)) = x, Kje
.

Po izreku imamo ekvivalentno enačbo:
,

Odgovori.
.

3. Reši sistem enačb:
.

rešitev. Razmislimo o funkciji. Zaradi

Pred vsemi t, To f (t) poveča.

Sistem ima obliko l = f (x), z = f (l), x = f (z), tiste. x = f (f (f (x))).

Po izreku x izpolnjuje enačbo f (x) = x oz

Odgovori.(0, 0, 0), (-1, -1, -1).

Uporaba ekstremnih lastnosti obravnavanih funkcij. Ocene. Glavne ideje te točke so precej jasno vidne iz primerov:

1. Reši enačbo:
.

rešitev. Leva stran te enačbe ne presega 2, desna stran pa ne presega 2. Torej do enakosti lahko pride le, če sta leva in desna stran enaki 2, tj. x = 0.

Komentiraj. To situacijo, ko je najmanjša vrednost funkcije, ki se nahaja v enem delu enačbe, enaka največji vrednosti funkcije, ki se nahaja v drugem delu, je mogoče posplošiti. Splošnejši primer so enačbe oblike f (x) = φ (x) , za katerega
za vse sprejemljivo x(formalno lahko to enačbo prepišemo kot

f (x) = φ (x) = 0, posledično pridemo do že obravnavane situacije, saj je največja vrednost desne strani nič).

2. Reši enačbo:.

Dokažimo, da ta enačba nima rešitev. Preidimo na posledico (potenciramo):
.

Ocenimo levo stran na podlagi neenakosti med geometrično sredino in aritmetično sredino

:

tiste. leva stran je manjša od desne. Enačba nima rešitev.

Odgovori. Odločitve ni.

3. Rešite sistem enačb:

rešitev. Dokažimo to.

Naj za gotovost x 5 > x 4, potem iz prvih dveh enačb dobimo, iz katerega
in še posebej. Naprej, od tretjega in četrtega dobimo
in predvsem
. Od zadnjega para, ki ga najdemo. Rezultat je protislovje (in
, tj. , vendar se je domnevalo, da
).

pomeni,
, od tod
itd., so vse neznanke med seboj enake.

Odgovori.(0, 0, 0, 0,0);
.

Problemi, ki so v svoji formulaciji nestandardni in vključujejo enačbe ali neenakosti. V to kategorijo spadajo predvsem naloge, pri katerih je treba določiti število korenin dane enačbe, dokazati obstoj korena na določenem intervalu, rešiti enačbo ali neenačbo na danem intervalu. Poglejmo si nekaj primerov.

1. Dokaži, da je enačba
ima eno pozitivno odločbo in eno negativno odločbo. metodika poučevanja matematike v povprečje šola: Učbenik. študentski priročnik...