Formula za drugo izjemno mejo je lim x → ∞ 1 + 1 x x = e. Druga oblika zapisa je videti takole: lim x → 0 (1 + x) 1 x = e.

Ko govorimo o drugi izjemni meji, imamo opravka z negotovostjo oblike 1 ∞, tj. enotnost do neskončne stopnje.

Yandex.RTB R-A-339285-1

Razmislimo o težavah, pri katerih bo koristna sposobnost izračuna druge izjemne meje.

Primer 1

Poiščite mejo lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 .

rešitev

Nadomestimo zahtevano formulo in opravimo izračune.

lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = 1 - 2 ∞ 2 + 1 ∞ 2 + 1 4 = 1 - 0 ∞ = 1 ∞

Izkazalo se je, da je naš odgovor ena do neskončnosti. Za določitev metode reševanja uporabimo tabelo negotovosti. Izberimo drugo izjemno mejo in spremenimo spremenljivke.

t = - x 2 + 1 2 ⇔ x 2 + 1 4 = - t 2

Če x → ∞, potem t → - ∞.

Poglejmo, kaj smo dobili po zamenjavi:

lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = 1 ∞ = lim x → ∞ 1 + 1 t - 1 2 t = lim t → ∞ 1 + 1 t t - 1 2 = e - 1 2

odgovor: lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = e - 1 2 .

Primer 2

Izračunajte mejo lim x → ∞ x - 1 x + 1 x .

rešitev

Zamenjajmo neskončnost in dobimo naslednje.

lim x → ∞ x - 1 x + 1 x = lim x → ∞ 1 - 1 x 1 + 1 x x = 1 - 0 1 + 0 ∞ = 1 ∞

V odgovoru smo ponovno dobili isto kot v prejšnjem problemu, zato lahko ponovno uporabimo drugo izjemno mejo. Nato moramo izbrati celoten del na dnu funkcije moči:

x - 1 x + 1 = x + 1 - 2 x + 1 = x + 1 x + 1 - 2 x + 1 = 1 - 2 x + 1

Po tem ima omejitev naslednjo obliko:

lim x → ∞ x - 1 x + 1 x = 1 ∞ = lim x → ∞ 1 - 2 x + 1 x

Zamenjaj spremenljivke. Predpostavimo, da je t = - x + 1 2 ⇒ 2 t = - x - 1 ⇒ x = - 2 t - 1 ; če x → ∞, potem t → ∞.

Po tem zapišemo, kaj smo dobili v prvotni omejitvi:

lim x → ∞ x - 1 x + 1 x = 1 ∞ = lim x → ∞ 1 - 2 x + 1 x = lim x → ∞ 1 + 1 t - 2 t - 1 = = lim x → ∞ 1 + 1 t - 2 t 1 + 1 t - 1 = lim x → ∞ 1 + 1 t - 2 t lim x → ∞ 1 + 1 t - 1 = = lim x → ∞ 1 + 1 t t - 2 1 + 1 ∞ = e - 2 · (1 + 0) - 1 = e - 2

Za izvedbo te transformacije smo uporabili osnovne lastnosti limitov in potenc.

odgovor: lim x → ∞ x - 1 x + 1 x = e - 2 .

Primer 3

Izračunajte mejo lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 .

rešitev

lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = lim x → ∞ 1 + 1 x 3 1 + 2 x - 1 x 3 3 2 x - 5 x 4 = = 1 + 0 1 + 0 - 0 3 0 - 0 = 1 ∞

Po tem moramo preoblikovati funkcijo, da uporabimo drugo veliko mejo. Dobili smo naslednje:

lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = 1 ∞ = lim x → ∞ x 3 - 2 x 2 - 1 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5

lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5

Ker imamo zdaj enaka eksponenta v števcu in imenovalcu ulomka (enaka šest), bo meja ulomka v neskončnosti enaka razmerju teh koeficientov pri višjih potencah.

lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 6 2 = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 3

Z zamenjavo t = x 2 + 2 x 2 - 1 - 2 x 2 + 2 dobimo drugo izjemno mejo. Pomeni kaj:

lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 3 = lim x → ∞ 1 + 1 t t - 3 = e - 3

odgovor: lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = e - 3 .

zaključki

Negotovost 1 ∞, tj. enotnost na neskončno potenco je stopenjska negotovost, zato jo je mogoče razkriti z uporabo pravil za iskanje meja eksponentnih potenčnih funkcij.

Če v besedilu opazite napako, jo označite in pritisnite Ctrl+Enter

Iz zgornjega članka lahko izveste, kakšna je meja in s čim se uživa - to je ZELO pomembno. Zakaj? Morda ne razumete, kaj so determinante in jih uspešno rešite; Če pa ne razumete, kaj je meja, bo reševanje praktičnih nalog težko. Dobro bi bilo tudi, da se seznanite z vzorčnimi rešitvami in mojimi oblikovalskimi priporočili. Vse informacije so predstavljene v preprosti in dostopni obliki.

In za namene te lekcije bomo potrebovali naslednja učna gradiva: Čudovite meje in Trigonometrične formule. Najdete jih na strani. Najbolje je, da priročnike natisnete - to je veliko bolj priročno, poleg tega pa se jih boste morali pogosto sklicevati brez povezave.

Kaj je tako posebnega na izjemnih mejah? Zanimivo pri teh mejah je to, da so jih dokazali največji umi slavnih matematikov in hvaležnim zanamcem ni treba trpeti zaradi strašnih mej s kopico trigonometričnih funkcij, logaritmov, potence. To pomeni, da bomo pri iskanju meja uporabili že pripravljene rezultate, ki so teoretično dokazani.

Obstaja več čudovitih omejitev, toda v praksi imajo izredni študenti v 95 % primerov dve čudoviti omejitvi: Prva čudovita meja, Druga čudovita meja. Treba je opozoriti, da gre za zgodovinsko uveljavljena imena in ko na primer govorijo o "prvi izjemni meji", s tem mislijo na zelo specifično stvar in ne na neko naključno mejo, vzeto s stropa.

Prva čudovita meja

Upoštevajte naslednjo omejitev: (namesto domače črke "he" bom uporabil grško črko "alfa", to je bolj priročno z vidika predstavitve gradiva).

V skladu z našim pravilom za iskanje omejitev (glej članek Omejitve. Primeri rešitev) v funkcijo poskušamo nadomestiti nič: v števcu dobimo nič (sinus nič je nič), v imenovalcu je očitno tudi nič. Tako se soočamo z negotovostjo oblike, ki je na srečo ni treba razkrivati. Med matematično analizo je dokazano, da:

To matematično dejstvo se imenuje Prva čudovita meja. Ne bom dal analitičnega dokaza meje, vendar si bomo ogledali njen geometrijski pomen v lekciji o infinitezimalne funkcije.

Pogosto so v praktičnih nalogah funkcije lahko razporejene drugače, to pa ne spremeni ničesar:

- ista prva čudovita meja.

Ne morete pa sami preurediti števca in imenovalca! Če je limita podana v obliki , jo je treba rešiti v isti obliki, ne da bi karkoli preurejali.

V praksi lahko kot parameter ne deluje samo spremenljivka, ampak tudi elementarna funkcija ali kompleksna funkcija. Pomembno je le, da teži k ničli.

Primeri:
, , ,

Tukaj, , , , in vse je v redu - velja prva čudovita omejitev.

Toda naslednji vnos je herezija:

Zakaj? Ker polinom ne teži k nič, teži k pet.

Mimogrede, hitro vprašanje: kakšna je meja? ? Odgovor najdete na koncu lekcije.

V praksi ni vse tako gladko; študentu skoraj nikoli ni ponujeno, da bi rešil brezplačni limit in dobil enostavno prepustnico. Hmmm ... pišem te vrstice in mi je prišla na misel zelo pomembna misel - navsezadnje si je bolje zapomniti "proste" matematične definicije in formule na pamet, to je lahko v neprecenljivo pomoč pri testu, ko bo vprašanje odločati med »dvojko« in »trojko«, učitelj pa se odloči, da bo učencu postavil kakšno preprosto vprašanje ali ponudil rešitev preprostega primera (»mogoče še ve kaj?«).

Preidimo na praktične primere:

Primer 1

Poiščite mejo

Če v meji opazimo sinus, bi nas to moralo takoj napeljati k razmišljanju o možnosti uporabe prve izjemne meje.

Najprej poskusimo zamenjati 0 v izraz pod mejnim znakom (to naredimo miselno ali v osnutku):

Imamo torej negotovost glede oblike obvezno navedite pri odločanju. Izraz pod mejno oznako je podoben prvi čudoviti meji, vendar to ni ravno to, je pod sinusom, ampak v imenovalcu.

V takih primerih moramo prvo opazno mejo organizirati sami z umetno tehniko. Razmišljanje bi lahko bilo naslednje: "pod sinusom imamo , kar pomeni, da moramo priti tudi v imenovalec."
In to se naredi zelo preprosto:

To pomeni, da je imenovalec v tem primeru umetno pomnožen s 7 in deljen z istimi sedmimi. Zdaj je naše snemanje dobilo znano podobo.
Ko je naloga sestavljena ročno, je priporočljivo označiti prvo opazno mejo s preprostim svinčnikom:

Kaj se je zgodilo? Pravzaprav se je naš obkroženi izraz spremenil v enoto in izginil v delu:

Zdaj ostane le še, da se znebimo trinadstropne frakcije:

Kdo je pozabil na poenostavitev večnivojskih ulomkov, osvežite gradivo v priročniku Vroče formule za šolski tečaj matematike .

pripravljena Končni odgovor:

Če ne želite uporabljati oznak s svinčnikom, lahko rešitev zapišete takole:

“

Uporabimo prvo čudovito mejo

“

Primer 2

Poiščite mejo

Spet vidimo ulomek in sinus v meji. Poskusimo zamenjati nič v števec in imenovalec:

Dejansko imamo negotovost in zato moramo poskušati organizirati prvo čudovito mejo. Pri lekciji Omejitve. Primeri rešitev upoštevali smo pravilo, da moramo, ko imamo negotovost, faktorizirati števec in imenovalec. Tu gre za isto stvar, stopnje bomo predstavili kot produkt (množitelje):

Podobno kot v prejšnjem primeru, s svinčnikom narišemo izjemne meje (tukaj sta dve) in označimo, da težijo k enotnosti:

Pravzaprav je odgovor pripravljen:

V naslednjih primerih ne bom delal umetnosti v Paintu, mislim, kako pravilno pripraviti rešitev v zvezku - že razumete.

Primer 3

Poiščite mejo

V izraz pod mejnim znakom zamenjamo ničlo:

Pridobljena je bila negotovost, ki jo je treba razkriti. Če je v meji tangens, se skoraj vedno pretvori v sinus in kosinus z dobro znano trigonometrično formulo (mimogrede, približno enako naredijo s kotangensom, glejte metodološko gradivo Vroče trigonometrične formule Na strani Matematične formule, tabele in referenčni materiali).

V tem primeru:

Kosinus nič je enak ena in se ga je enostavno znebiti (ne pozabite označiti, da se nagiba k ena):

Torej, če je v meji kosinus MNOŽITELJ, potem ga je treba, grobo rečeno, spremeniti v enoto, ki izgine v produktu.

Tu se je vse izkazalo bolj preprosto, brez množenja in deljenja. Tudi prva izjemna meja se spremeni v eno in izgine v izdelku:

Posledično dobimo neskončnost in to se zgodi.

Primer 4

Poiščite mejo

Poskusimo zamenjati nič v števec in imenovalec:

Dobljena je negotovost (kosinus nič, kot se spomnimo, je enak ena)

Uporabljamo trigonometrično formulo. Upoštevajte! Iz nekega razloga so omejitve, ki uporabljajo to formulo, zelo pogoste.

Premaknimo konstantne faktorje čez ikono meje:

Organizirajmo prvo čudovito mejo:

Tukaj imamo samo eno izjemno omejitev, ki se v izdelku spremeni v eno in izgine:

Znebimo se trinadstropne strukture:

Meja je dejansko rešena, pokažemo, da preostali sinus teži k ničli:

Primer 5

Poiščite mejo

Ta primer je bolj zapleten, poskusite ga ugotoviti sami:

Nekatere omejitve je mogoče zmanjšati na 1. izjemno mejo s spremembo spremenljivke, o tem si lahko preberete malo kasneje v članku Metode za reševanje limitov.

Druga čudovita meja

V teoriji matematične analize je bilo dokazano, da:

To dejstvo se imenuje druga čudovita meja.

Referenca: je iracionalno število.

Parameter je lahko ne samo spremenljivka, ampak tudi kompleksna funkcija. Pomembno je le, da stremi v neskončnost.

Primer 6

Poiščite mejo

Ko je izraz pod mejnim znakom v stopinjah, je to prvi znak, da morate poskusiti uporabiti drugo čudovito mejo.

Toda najprej, kot vedno, poskušamo v izraz nadomestiti neskončno veliko število, princip, po katerem se to naredi, je obravnavan v lekciji Omejitve. Primeri rešitev.

Zlahka opazimo, da ko osnova stopnje je , eksponent pa je , to pomeni, da obstaja negotovost oblike:

Ta negotovost je natančno razkrita s pomočjo druge izjemne meje. Toda, kot se pogosto zgodi, druga čudovita meja ne leži na pladnju in jo je treba umetno organizirati. Lahko razmišljate takole: v tem primeru je parameter , kar pomeni, da moramo organizirati tudi indikator. Da bi to naredili, dvignemo osnovo na moč in da se izraz ne spremeni, jo dvignemo na moč:

Ko je naloga ročno opravljena, označimo s svinčnikom:

Skoraj vse je pripravljeno, strašna stopnja se je spremenila v lepo pismo:

V tem primeru samo ikono omejitve premaknemo na indikator:

Primer 7

Poiščite mejo

Pozor! Ta vrsta omejitve se pojavlja zelo pogosto, zato zelo natančno preučite ta primer.

Poskusimo v izraz pod mejnim znakom nadomestiti neskončno veliko število:

Rezultat je negotovost. Toda druga izjemna meja se nanaša na negotovost oblike. Kaj storiti? Pretvoriti moramo osnovo stopnje. Razmišljamo takole: v imenovalcu imamo , kar pomeni, da moramo tudi v števcu urediti .

Ta spletni matematični kalkulator vam bo pomagal, če ga boste potrebovali izračunati limit funkcije. Program meje raztopine ne le daje odgovor na problem, ampak vodi podrobna rešitev z obrazložitvijo, tj. prikaže postopek izračuna meje.

Ta program je lahko koristen za srednješolce v splošnih šolah, ko se pripravljajo na teste in izpite, pri preverjanju znanja pred enotnim državnim izpitom in za starše, da nadzorujejo rešitev številnih problemov iz matematike in algebre. Ali pa vam je morda predrago najeti mentorja ali kupiti nove učbenike? Ali pa želite kar se da hitro narediti domačo nalogo iz matematike ali algebre? V tem primeru lahko uporabite tudi naše programe s podrobnimi rešitvami.

Na ta način lahko izvajate lastno usposabljanje in/ali usposabljanje svojih mlajših bratov ali sester, hkrati pa se dvigne raven izobrazbe na področju reševanja problemov.

Ugotovljeno je bilo, da nekateri skripti, potrebni za rešitev te težave, niso bili naloženi in program morda ne bo deloval.
Morda imate omogočen AdBlock.
V tem primeru ga onemogočite in osvežite stran.

Ker Veliko ljudi je pripravljenih rešiti problem, vaša zahteva je v čakalni vrsti.
Čez nekaj sekund se spodaj prikaže rešitev.
Prosim počakaj sek...

Če ti opazil napako v rešitvi, potem lahko o tem pišete v obrazcu za povratne informacije.
Ne pozabi navedite, katero nalogo ti se odloči kaj vnesite v polja.

Naše igre, uganke, emulatorji:

Malo teorije.

Meja funkcije pri x->x 0

Naj bo funkcija f(x) definirana na neki množici X in naj bo točka \(x_0 \in X\) ali \(x_0 \notin X\)

Vzemimo iz X zaporedje točk, ki se razlikuje od x 0:
x 1 , x 2 , x 3 , ..., x n , ... (1)
konvergira k x*. Vrednosti funkcij na točkah tega zaporedja prav tako tvorijo številsko zaporedje
f(x 1), f(x 2), f(x 3), ..., f(x n), ... (2)
in lahko se postavi vprašanje o obstoju njegove meje.

Opredelitev. Število A se imenuje meja funkcije f(x) v točki x = x 0 (ali pri x -> x 0), če je za katero koli zaporedje (1) vrednosti argumenta x drugačno od x 0 konvergira k x 0, ustrezno zaporedje (2) funkcij vrednosti konvergira k številu A.

$$ \lim_(x\to x_0)( f(x)) = A $$

Funkcija f(x) ima lahko samo eno limito v točki x 0. To izhaja iz dejstva, da zaporedje
(f(x n)) ima samo eno omejitev.

Obstaja še ena definicija limita funkcije.

OpredelitevŠtevilo A se imenuje limita funkcije f(x) v točki x = x 0, če za katero koli število \(\varepsilon > 0\) obstaja število \(\delta > 0\), tako da za vse \ (x \in X, \; x \neq x_0 \), ki izpolnjuje neenakost \(|x-x_0| Z uporabo logičnih simbolov lahko to definicijo zapišemo kot
\((\forall \varepsilon > 0) (\obstaja \delta > 0) (\forall x \in X, \; x \neq x_0, \; |x-x_0| Upoštevajte, da neenakosti \(x \neq x_0 , \; |x-x_0|. Prva definicija temelji na konceptu meje številskega zaporedja, zato se pogosto imenuje definicija "v jeziku zaporedij". \(\varepsilon - \delta \)«.
Ti dve definiciji limita funkcije sta enakovredni in lahko uporabite eno od njiju, odvisno od tega, katera je primernejša za reševanje določenega problema.

Upoštevajte, da se definicija limita funkcije “v jeziku zaporedij” imenuje tudi definicija limita funkcije po Heineju in definicija limita funkcije “v jeziku \(\varepsilon - \delta \)« imenujemo tudi definicija limita funkcije po Cauchyju.

Limit funkcije pri x->x 0 - in pri x->x 0 +

V nadaljevanju bomo uporabljali koncepte enostranskih limitov funkcije, ki so definirani na naslednji način.

OpredelitevŠtevilo A imenujemo desna (leva) meja funkcije f(x) v točki x 0, če za katero koli zaporedje (1), ki konvergira k x 0, katerega elementi x n so večji (manjši od) x 0, velja ustrezno zaporedje (2) konvergira k A.

Simbolično je zapisano takole:
$$ \lim_(x \to x_0+) f(x) = A \; \left(\lim_(x \to x_0-) f(x) = A \desno) $$

Enakovredno definicijo enostranskih limitov funkcije lahko podamo "v jeziku \(\varepsilon - \delta \)":

Opredelitevštevilo A imenujemo desna (leva) meja funkcije f(x) v točki x 0, če za katerikoli \(\varepsilon > 0\) obstaja \(\delta > 0\), tako da za vse x velja neenakosti \(x_0 Simbolični vnosi:

V tej temi bomo analizirali formule, ki jih je mogoče dobiti z uporabo druge izjemne meje (nahaja se tema, ki je neposredno posvečena drugi izjemni meji). Naj vas spomnim na dve formulaciji druge izjemne meje, ki bosta potrebni v tem razdelku: $\lim_(x\to\infty)\left(1+\frac(1)(x)\right)^x=e $ in $\lim_(x \to\ 0)\levo(1+x\desno)^\frac(1)(x)=e$.

Običajno predstavljam formule brez dokazov, vendar mislim, da bom za to stran naredil izjemo. Bistvo je, da dokaz o posledicah druge izjemne meje vsebuje nekaj tehnik, ki so uporabne pri neposrednem reševanju problemov. No, na splošno je priporočljivo vedeti, kako je ta ali ona formula dokazana. To vam omogoča, da bolje razumete njegovo notranjo strukturo in tudi meje uporabnosti. Ker pa dokazi morda ne bodo zanimivi za vse bralce, jih bom skril pod opombe, ki se nahajajo za vsako posledico.

Posledica #1

Dokaz posledice št. 1: pokaži\skrij

Ker imamo pri $x\to 0$ $\ln(1+x)\to 0$, potem je v obravnavani meji negotovost v obliki $\frac(0)(0)$. Da razkrijemo to negotovost, predstavimo izraz $\frac(\ln(1+x))(x)$ v naslednji obliki: $\frac(1)(x)\cdot\ln(1+x)$ . Sedaj pa faktorizirajmo $\frac(1)(x)$ v moč izraza $(1+x)$ in uporabimo drugo izjemno omejitev:

$$ \lim_(x\to\ 0) \frac(\ln(1+x))(x)=\levo| \frac(0)(0) \desno|= \lim_(x\do\ 0) \levo(\frac(1)(x)\cdot\ln(1+x)\desno)=\lim_(x\ na\ 0)\ln(1+x)^(\frac(1)(x))=\ln e=1. $$

Spet imamo negotovost v obliki $\frac(0)(0)$. Zanesli se bomo na formulo, ki smo jo že dokazali. Ker je $\log_a t=\frac(\ln t)(\ln a)$, potem $\log_a (1+x)=\frac(\ln(1+x))(\ln a)$.

$$ \lim_(x\to\ 0) \frac(\log_a (1+x))(x)=\levo| \frac(0)(0) \right|=\lim_(x\to\ 0)\frac(\ln(1+x))( x \ln a)=\frac(1)(\ln a)\ lim_(x\do\ 0)\frac(\ln(1+x))( x)=\frac(1)(\ln a)\cdot 1=\frac(1)(\ln a). $$

Posledica št. 2

Dokaz posledice št. 2: pokaži\skrij

Ker imamo pri $x\to 0$ $e^x-1\to 0$, potem je v obravnavani meji negotovost v obliki $\frac(0)(0)$. Da razkrijemo to negotovost, spremenimo spremenljivko in označimo $t=e^x-1$. Ker je $x\na 0$, potem $t\na 0$. Nato iz formule $t=e^x-1$ dobimo: $e^x=1+t$, $x=\ln(1+t)$.

$$ \lim_(x\to\ 0) \frac(e^x-1)(x)=\levo| \frac(0)(0) \desno|=\levo | \začetek(poravnano) & t=e^x-1;\; t\na 0.\\ & x=\ln(1+t).\end (poravnano) \desno|= \lim_(t\na 0)\frac(t)(\ln(1+t))= \lim_(t\to 0)\frac(1)(\frac(\ln(1+t))(t))=\frac(1)(1)=1. $$

Spet imamo negotovost v obliki $\frac(0)(0)$. Zanašali se bomo na formulo, ki smo jo že dokazali. Ker $a^x=e^(x\ln a)$, potem:

$$ \lim_(x\to\ 0) \frac(a^(x)-1)(x)=\levo| \frac(0)(0) \right|=\lim_(x\to 0)\frac(e^(x\ln a)-1)(x)=\ln a\cdot \lim_(x\to 0) )\frac(e^(x\ln a)-1)(x \ln a)=\ln a \cdot 1=\ln a. $$

Posledica št. 3

Dokaz posledice št. 3: pokaži\skrij

Spet imamo opravka z negotovostjo oblike $\frac(0)(0)$. Ker $(1+x)^\alpha=e^(\alpha\ln(1+x))$, dobimo:

$$ \lim_(x\to\ 0) \frac((1+x)^\alpha-1)(x)= \levo| \frac(0)(0) \desno|= \lim_(x\to\ 0)\frac(e^(\alpha\ln(1+x))-1)(x)= \lim_(x\to\ \ 0)\levo(\frac(e^(\alpha\ln(1+x))-1)(\alpha\ln(1+x))\cdot \frac(\alpha\ln(1+x) )(x) \desno)=\\ =\alpha\lim_(x\to\ 0) \frac(e^(\alpha\ln(1+x))-1)(\alpha\ln(1+x) ))\cdot \lim_(x\to\ 0)\frac(\ln(1+x))(x)=\alpha\cdot 1\cdot 1=\alpha. $$

Primer št. 1

Izračunajte mejo $\lim_(x\to\ 0) \frac(e^(9x)-1)(\sin 5x)$.

Imamo negotovost v obliki $\frac(0)(0)$. Da bi razkrili to negotovost, bomo uporabili formulo. Za prilagoditev naše omejitve tej formuli ne smemo pozabiti, da morata izraza v potenci $e$ in v imenovalcu sovpadati. Z drugimi besedami, v imenovalcu ni mesta za sinus. Imenovalec mora biti $9x$. Poleg tega bo rešitev tega primera uporabila prvo izjemno omejitev.

$$ \lim_(x\to\ 0) \frac(e^(9x)-1)(\sin 5x)=\levo|\frac(0)(0) \desno|=\lim_(x\to\ 0) \levo(\frac(e^(9x)-1)(9x)\cdot\frac(9x)(\sin 5x) \desno) =\frac(9)(5)\cdot\lim_(x\ do\ 0) \levo(\frac(e^(9x)-1)(9x)\cdot\frac(1)(\frac(\sin 5x)(5x)) \desno)=\frac(9)( 5)\cdot 1 \cdot 1=\frac(9)(5). $$

Odgovori: $\lim_(x\to\ 0) \frac(e^(9x)-1)(\sin 5x)=\frac(9)(5)$.

Primer št. 2

Izračunajte mejo $\lim_(x\to\ 0) \frac(\ln\cos x)(x^2)$.

Imamo negotovost oblike $\frac(0)(0)$ (naj vas spomnim, da je $\ln\cos 0=\ln 1=0$). Da bi razkrili to negotovost, bomo uporabili formulo. Najprej upoštevajmo, da je $\cos x=1-2\sin^2 \frac(x)(2)$ (glej izpis o trigonometričnih funkcijah). Zdaj $\ln\cos x=\ln\left(1-2\sin^2 \frac(x)(2)\right)$, tako da bi morali v imenovalcu dobiti izraz $-2\sin^2 \ frac(x )(2)$ (za prilagoditev našega primera formuli). V nadaljnji rešitvi bo uporabljena prva opazna meja.

$$ \lim_(x\to\ 0) \frac(\ln\cos x)(x^2)=\levo| \frac(0)(0) \desno|=\lim_(x\to\ 0) \frac(\ln\levo(1-2\sin^2 \frac(x)(2)\desno))(x ^2)= \lim_(x\to\ 0) \levo(\frac(\ln\levo(1-2\sin^2 \frac(x)(2)\desno))(-2\sin^2 \frac(x)(2))\cdot\frac(-2\sin^2 \frac(x)(2))(x^2) \right)=\\ =-\frac(1)(2) \lim_(x\to\ 0) \levo(\frac(\ln\levo(1-2\sin^2 \frac(x)(2)\desno))(-2\sin^2 \frac(x )(2))\cdot\levo(\frac(\sin\frac(x)(2))(\frac(x)(2))\desno)^2 \desno)=-\frac(1)( 2)\cdot 1\cdot 1^2=-\frac(1)(2). $$

Odgovori: $\lim_(x\to\ 0) \frac(\ln\cos x)(x^2)=-\frac(1)(2)$.

Obstaja več izjemnih limitov, vendar sta najbolj znani prvi in ​​drugi izjemni limit. Izjemna stvar pri teh omejitvah je, da se pogosto uporabljajo in da je z njihovo pomočjo mogoče najti druge omejitve, na katere naletimo pri številnih težavah. To bomo storili v praktičnem delu te lekcije. Za reševanje problemov tako, da jih zmanjšamo na prvo ali drugo izjemno mejo, ni treba razkriti negotovosti, ki jih vsebujejo, saj so vrednosti teh meja že dolgo izpeljali veliki matematiki.

Prva izjemna meja se imenuje meja razmerja med sinusom infinitezimalnega loka in istim lokom, izražena v radianski meri:

Pojdimo k reševanju problemov na prvi opazni meji. Opomba: če je pod mejnim znakom trigonometrična funkcija, je to skoraj zanesljiv znak, da je ta izraz mogoče zmanjšati na prvo opazno mejo.

Primer 1. Poiščite mejo.

rešitev. Namesto tega zamenjava x ničla vodi v negotovost:

.

Imenovalec je sinus, zato lahko izraz pripeljemo do prve opazne meje. Začnimo preobrazbo:

.

Imenovalec je sinus treh X, števec pa ima samo en X, kar pomeni, da morate v števcu dobiti tri X. Za kaj? Za predstavitev 3 x = a in dobite izraz.

In pridemo do različice prve izjemne meje:

ker ni pomembno, katera črka (spremenljivka) v tej formuli stoji namesto X.

X pomnožimo s tri in takoj delimo:

.

V skladu s prvo opaženo opazno omejitvijo nadomestimo frakcijski izraz:

Zdaj lahko končno rešimo to mejo:

.

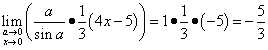Primer 2. Poiščite mejo.

rešitev. Neposredna zamenjava spet vodi do negotovosti "nič deljeno z nič":

.

Da bi dobili prvo opazno mejo, je potrebno, da imata x pod sinusom v števcu in samo x v imenovalcu enak koeficient. Naj bo ta koeficient enak 2. Če želite to narediti, si predstavljajte trenutni koeficient za x, kot je prikazano spodaj, z izvajanjem operacij z ulomki dobimo:

.

Primer 3. Poiščite mejo.

rešitev. Pri zamenjavi spet dobimo negotovost "nič deljeno z ničlo":

.

Verjetno že razumete, da lahko iz izvirnega izraza dobite prvo čudovito mejo, pomnoženo s prvo čudovito mejo. To naredimo tako, da kvadrata x v števcu in sinusa v imenovalcu razčlenimo na enake faktorje, in da dobimo enaka koeficienta za x in sinus, x v števcu delimo s 3 in takoj pomnožimo. do 3. Dobimo:

.

Primer 4. Poiščite mejo.

rešitev. Ponovno dobimo negotovost "nič deljeno z nič":

.

Dobimo lahko razmerje med prvima dvema izjemnima mejama. Tako števec kot imenovalec delimo z x. Nato, tako da koeficienti za sinuse in xes sovpadata, pomnožimo zgornji x z 2 in takoj delimo z 2, spodnji x pa pomnožimo s 3 in takoj delimo s 3. Dobimo:

Primer 5. Poiščite mejo.

rešitev. In spet negotovost "nič deljeno z nič":

Iz trigonometrije se spomnimo, da je tangens razmerje med sinusom in kosinusom, kosinus nič pa je enak ena. Izvedemo transformacije in dobimo:

.

Primer 6. Poiščite mejo.

rešitev. Trigonometrična funkcija pod znakom limite ponovno nakazuje uporabo prve izjemne limite. Predstavimo ga kot razmerje med sinusom in kosinusom.