Koncepti i zonës
Koncepti i zonës së çdo figure gjeometrike, në veçanti një trekëndësh, do të shoqërohet me një figurë të tillë si një katror. Për sipërfaqen e njësisë së çdo figure gjeometrike do të marrim sipërfaqen e një katrori, ana e të cilit është e barabartë me një. Për plotësi, le të kujtojmë dy veti themelore për konceptin e zonave të figurave gjeometrike.
Prona 1: Nëse figurat gjeometrike janë të barabarta, atëherë edhe sipërfaqet e tyre janë të barabarta.
Prona 2:Çdo figurë mund të ndahet në disa figura. Për më tepër, sipërfaqja e figurës origjinale është e barabartë me shumën e sipërfaqeve të të gjitha figurave përbërëse të saj.
Le të shohim një shembull.
Shembulli 1
Natyrisht, njëra nga anët e trekëndëshit është një diagonale e një drejtkëndëshi, njëra anë e të cilit ka një gjatësi prej $5$ (pasi ka qeliza $5$) dhe tjetra është $6$ (pasi ka qeliza $6$). Prandaj, zona e këtij trekëndëshi do të jetë e barabartë me gjysmën e një drejtkëndëshi të tillë. Sipërfaqja e drejtkëndëshit është
Atëherë sipërfaqja e trekëndëshit është e barabartë me
Përgjigje: 15 dollarë.
Më pas, ne do të shqyrtojmë disa metoda për gjetjen e zonave të trekëndëshave, përkatësisht duke përdorur lartësinë dhe bazën, duke përdorur formulën dhe sipërfaqen e Heronit trekëndësh barabrinjës.
Si të gjeni sipërfaqen e një trekëndëshi duke përdorur lartësinë dhe bazën e tij
Teorema 1
Sipërfaqja e një trekëndëshi mund të gjendet sa gjysma e produktit të gjatësisë së një brinjë dhe lartësisë në atë anë.
Matematikisht duket kështu
$S=\frac(1)(2)αh$
ku $a$ është gjatësia e anës, $h$ është lartësia e tërhequr drejt saj.
Dëshmi.
Konsideroni një trekëndësh $ABC$ në të cilin $AC=α$. Lartësia $BH$ është tërhequr në këtë anë, e cila është e barabartë me $h$. Le ta ndërtojmë atë deri në katrorin $AXYC$ si në Figurën 2.
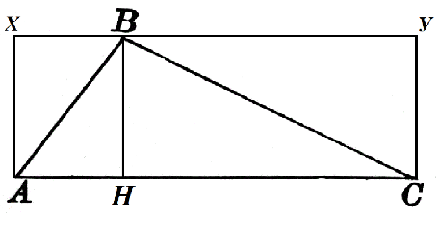
Sipërfaqja e drejtkëndëshit $AXBH$ është $h\cdot AH$ dhe sipërfaqja e drejtkëndëshit $HBYC$ është $h\cdot HC$. Pastaj
$S_ABH=\frac(1)(2)h\cdot AH$, $S_CBH=\frac(1)(2)h\cdot HC$
Prandaj, sipërfaqja e kërkuar e trekëndëshit, nga vetia 2, është e barabartë me
$S=S_ABH+S_CBH=\frac(1)(2)h\cdot AH+\frac(1)(2)h\cdot HC=\frac(1)(2)h\cdot (AH+HC)=\ frac(1)(2)αh$
Teorema është vërtetuar.
Shembulli 2
Gjeni sipërfaqen e trekëndëshit në figurën më poshtë nëse qeliza ka një sipërfaqe të barabartë me një
Baza e këtij trekëndëshi është e barabartë me 9$ (pasi 9$ janë katrorë $9$). Lartësia është gjithashtu 9 $. Pastaj, nga teorema 1, marrim
$S=\frac(1)(2)\cdot 9\cdot 9=40,5$
Përgjigje: 40,5 dollarë.
Formula e Heronit
Teorema 2
Nëse na jepen tre brinjë të trekëndëshit $α$, $β$ dhe $γ$, atëherë zona e tij mund të gjendet si më poshtë
$S=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
këtu $ρ$ nënkupton gjysmëperimetrin e këtij trekëndëshi.
Dëshmi.
Merrni parasysh figurën e mëposhtme:
Nga teorema e Pitagorës, nga trekëndëshi $ABH$ marrim
Nga trekëndëshi $CBH$, sipas teoremës së Pitagorës, kemi
$h^2=α^2-(β-x)^2$
$h^2=α^2-β^2+2βx-x^2$
Nga këto dy marrëdhënie marrim barazinë
$γ^2-x^2=α^2-β^2+2βx-x^2$
$x=\frac(γ^2-α^2+β^2)(2β)$
$h^2=γ^2-(\frac(γ^2-α^2+β^2)(2β))^2$
$h^2=\frac((α^2-(γ-β)^2)((γ+β)^2-α^2))(4β^2)$
$h^2=\frac((α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α))(4β^2)$
Meqenëse $ρ=\frac(α+β+γ)(2)$, atëherë $α+β+γ=2ρ$, që do të thotë
$h^2=\frac(2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α))(4β^2)$
$h^2=\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2)$
$h=\sqrt(\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2))$
$h=\frac(2)(β)\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
Nga teorema 1, marrim
$S=\frac(1)(2) βh=\frac(β)(2)\cdot \frac(2)(β) \sqrt(ρ(ρ-α)(ρ-β)(ρ-γ) )=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
Për të përcaktuar zonën e një trekëndëshi, mund të përdorni formula të ndryshme. Nga të gjitha metodat, më e lehta dhe më e përdorura është të shumëzoni lartësinë me gjatësinë e bazës dhe më pas të ndani rezultatin me dy. Megjithatë këtë metodë larg nga i vetmi. Më poshtë mund të lexoni se si të gjeni sipërfaqen e një trekëndëshi duke përdorur formula të ndryshme.
Më vete, ne do të shikojmë mënyrat për të llogaritur sipërfaqen lloje specifike trekëndësh - drejtkëndëshe, dykëndëshe dhe barabrinjës. Ne e shoqërojmë secilën formulë me një shpjegim të shkurtër që do t'ju ndihmojë të kuptoni thelbin e saj.
Metodat universale për gjetjen e sipërfaqes së një trekëndëshi
Formulat e mëposhtme përdorin shënime të veçanta. Ne do të deshifrojmë secilën prej tyre:
- a, b, c – gjatësitë e tri brinjëve të figurës që po shqyrtojmë;
- r është rrezja e rrethit që mund të futet në trekëndëshin tonë;
- R është rrezja e rrethit që mund të përshkruhet rreth tij;
- α është madhësia e këndit të formuar nga brinjët b dhe c;
- β është madhësia e këndit ndërmjet a dhe c;
- γ është madhësia e këndit të formuar nga brinjët a dhe b;
- h është lartësia e trekëndëshit tonë, e ulur nga këndi α në brinjën a;
- p – gjysma e shumës së brinjëve a, b dhe c.
Është logjikisht e qartë pse ju mund të gjeni sipërfaqen e një trekëndëshi në këtë mënyrë. Trekëndëshi mund të plotësohet lehtësisht në një paralelogram, në të cilin njëra anë e trekëndëshit do të veprojë si një diagonale. Sipërfaqja e një paralelogrami gjendet duke shumëzuar gjatësinë e njërës anë të tij me vlerën e lartësisë së tërhequr në të. Diagonalja e ndan këtë paralelogram të kushtëzuar në 2 trekëndësha identikë. Prandaj, është mjaft e qartë se zona e trekëndëshit tonë origjinal duhet të jetë e barabartë me gjysmën e sipërfaqes së këtij paralelogrami ndihmës.
S=½ a b sin γ
Sipas kësaj formule, sipërfaqja e një trekëndëshi gjendet duke shumëzuar gjatësitë e dy brinjëve të tij, domethënë a dhe b, me sinusin e këndit të formuar prej tyre. Kjo formulë rrjedh logjikisht nga ajo e mëparshme. Nëse e ulim lartësinë nga këndi β në brinjën b, atëherë, sipas vetive të trekëndëshit kënddrejtë, kur shumëzojmë gjatësinë e brinjës a me sinusin e këndit γ, fitojmë lartësinë e trekëndëshit, domethënë h. .
Zona e figurës në fjalë gjendet duke shumëzuar gjysmën e rrezes së rrethit që mund të futet në të me perimetrin e saj. Me fjalë të tjera, gjejmë prodhimin e gjysmëperimetrit dhe rrezes së rrethit të përmendur.
S= a b c/4R
Sipas kësaj formule, vlera që na nevojitet mund të gjendet duke e ndarë prodhimin e anëve të figurës me 4 rreze të rrethit të përshkruar rreth saj.
Këto formula janë universale, pasi ato bëjnë të mundur përcaktimin e sipërfaqes së çdo trekëndëshi (shkallë, izosceles, barabrinjës, drejtkëndësh). Kjo gjithashtu mund të bëhet duke përdorur më shumë llogaritjet komplekse, për të cilën nuk do të ndalemi në detaje.
Zonat e trekëndëshave me veti specifike

Si të gjeni sipërfaqen e një trekëndëshi kënddrejtë? E veçanta e kësaj figure është se dy anët e saj janë njëkohësisht lartësitë e saj. Nëse a dhe b janë këmbë, dhe c bëhet hipotenuzë, atëherë e gjejmë zonën si kjo:
Si të gjeni zonën trekëndëshi dykëndësh? Ka dy brinjë me gjatësi a dhe një anë me gjatësi b. Rrjedhimisht, sipërfaqja e saj mund të përcaktohet duke pjesëtuar me 2 produktin e katrorit të brinjës a me sinusin e këndit γ.
Si të gjeni sipërfaqen e një trekëndëshi barabrinjës? Në të, gjatësia e të gjitha anëve është e barabartë me a, dhe madhësia e të gjitha këndeve është α. Lartësia e saj është e barabartë me gjysmën e prodhimit të gjatësisë së brinjës a dhe rrënjës katrore prej 3. Për të gjetur sipërfaqen trekëndëshi i rregullt, duhet të shumëzoni katrorin e anës a me rrënjën katrore të 3 dhe të pjesëtoni me 4.
Koncepti i zonës
Koncepti i zonës së çdo figure gjeometrike, në veçanti një trekëndësh, do të shoqërohet me një figurë të tillë si një katror. Për sipërfaqen e njësisë së çdo figure gjeometrike do të marrim sipërfaqen e një katrori, ana e të cilit është e barabartë me një. Për plotësi, le të kujtojmë dy veti themelore për konceptin e zonave të figurave gjeometrike.
Prona 1: Nëse figurat gjeometrike janë të barabarta, atëherë edhe sipërfaqet e tyre janë të barabarta.
Prona 2:Çdo figurë mund të ndahet në disa figura. Për më tepër, sipërfaqja e figurës origjinale është e barabartë me shumën e sipërfaqeve të të gjitha figurave përbërëse të saj.
Le të shohim një shembull.
Shembulli 1
Natyrisht, njëra nga anët e trekëndëshit është një diagonale e një drejtkëndëshi, njëra anë e të cilit ka një gjatësi prej $5$ (pasi ka qeliza $5$) dhe tjetra është $6$ (pasi ka qeliza $6$). Prandaj, zona e këtij trekëndëshi do të jetë e barabartë me gjysmën e një drejtkëndëshi të tillë. Sipërfaqja e drejtkëndëshit është
Atëherë sipërfaqja e trekëndëshit është e barabartë me
Përgjigje: 15 dollarë.
Më pas, ne do të shqyrtojmë disa metoda për gjetjen e zonave të trekëndëshave, përkatësisht duke përdorur lartësinë dhe bazën, duke përdorur formulën e Heronit dhe sipërfaqen e një trekëndëshi barabrinjës.
Si të gjeni sipërfaqen e një trekëndëshi duke përdorur lartësinë dhe bazën e tij
Teorema 1
Sipërfaqja e një trekëndëshi mund të gjendet sa gjysma e produktit të gjatësisë së një brinjë dhe lartësisë në atë anë.
Matematikisht duket kështu
$S=\frac(1)(2)αh$
ku $a$ është gjatësia e anës, $h$ është lartësia e tërhequr drejt saj.
Dëshmi.
Konsideroni një trekëndësh $ABC$ në të cilin $AC=α$. Lartësia $BH$ është tërhequr në këtë anë, e cila është e barabartë me $h$. Le ta ndërtojmë atë deri në katrorin $AXYC$ si në Figurën 2.

Sipërfaqja e drejtkëndëshit $AXBH$ është $h\cdot AH$ dhe sipërfaqja e drejtkëndëshit $HBYC$ është $h\cdot HC$. Pastaj
$S_ABH=\frac(1)(2)h\cdot AH$, $S_CBH=\frac(1)(2)h\cdot HC$
Prandaj, sipërfaqja e kërkuar e trekëndëshit, nga vetia 2, është e barabartë me
$S=S_ABH+S_CBH=\frac(1)(2)h\cdot AH+\frac(1)(2)h\cdot HC=\frac(1)(2)h\cdot (AH+HC)=\ frac(1)(2)αh$
Teorema është vërtetuar.
Shembulli 2
Gjeni sipërfaqen e trekëndëshit në figurën më poshtë nëse qeliza ka një sipërfaqe të barabartë me një
Baza e këtij trekëndëshi është e barabartë me 9$ (pasi 9$ janë katrorë $9$). Lartësia është gjithashtu 9 $. Pastaj, nga teorema 1, marrim
$S=\frac(1)(2)\cdot 9\cdot 9=40,5$
Përgjigje: 40,5 dollarë.
Formula e Heronit
Teorema 2
Nëse na jepen tre brinjë të trekëndëshit $α$, $β$ dhe $γ$, atëherë zona e tij mund të gjendet si më poshtë
$S=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
këtu $ρ$ nënkupton gjysmëperimetrin e këtij trekëndëshi.
Dëshmi.
Merrni parasysh figurën e mëposhtme:
Nga teorema e Pitagorës, nga trekëndëshi $ABH$ marrim
Nga trekëndëshi $CBH$, sipas teoremës së Pitagorës, kemi
$h^2=α^2-(β-x)^2$
$h^2=α^2-β^2+2βx-x^2$
Nga këto dy marrëdhënie marrim barazinë
$γ^2-x^2=α^2-β^2+2βx-x^2$
$x=\frac(γ^2-α^2+β^2)(2β)$
$h^2=γ^2-(\frac(γ^2-α^2+β^2)(2β))^2$
$h^2=\frac((α^2-(γ-β)^2)((γ+β)^2-α^2))(4β^2)$
$h^2=\frac((α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α))(4β^2)$
Meqenëse $ρ=\frac(α+β+γ)(2)$, atëherë $α+β+γ=2ρ$, që do të thotë
$h^2=\frac(2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α))(4β^2)$
$h^2=\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2)$
$h=\sqrt(\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2))$
$h=\frac(2)(β)\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
Nga teorema 1, marrim
$S=\frac(1)(2) βh=\frac(β)(2)\cdot \frac(2)(β) \sqrt(ρ(ρ-α)(ρ-β)(ρ-γ) )=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
Një trekëndësh është si ky figura gjeometrike, i cili përbëhet nga tre vija që lidhen në pika që nuk shtrihen në të njëjtën linjë. Pikat e lidhjes së vijave janë kulmet e trekëndëshit, të cilat janë të përcaktuara me shkronja latine(p.sh. A, B, C). Vijat e drejta lidhëse të një trekëndëshi quhen segmente, të cilat zakonisht shënohen gjithashtu me shkronja latine. Dalloni llojet e mëposhtme trekëndëshat:
- Drejtkëndëshe.
- I mpirë.
- Këndore akute.
- I gjithanshëm.
- Barabrinjës.
- Isosceles.
Formula të përgjithshme për llogaritjen e sipërfaqes së një trekëndëshi
Formula për sipërfaqen e një trekëndëshi bazuar në gjatësinë dhe lartësinë
S= a*h/2,
ku a është gjatësia e brinjës së trekëndëshit sipërfaqja e të cilit duhet gjetur, h është gjatësia e lartësisë së tërhequr në bazë.
Formula e Heronit
S=√р*(р-а)*(р-b)*(p-c),
ku është √ rrënjë katrore, p është gjysmëperimetri i trekëndëshit, a,b,c është gjatësia e secilës anë të trekëndëshit. Gjysmëperimetri i një trekëndëshi mund të llogaritet duke përdorur formulën p=(a+b+c)/2.


Formula për sipërfaqen e një trekëndëshi bazuar në këndin dhe gjatësinë e segmentit
S = (a*b*sin(α))/2,
Ku b,c është gjatësia e brinjëve të trekëndëshit, sin(α) është sinusi i këndit ndërmjet dy brinjëve.


Formula për sipërfaqen e një trekëndëshi duke pasur parasysh rrezen e rrethit të brendashkruar dhe tre brinjët
S=p*r,
ku p është gjysmëperimetri i trekëndëshit sipërfaqja e të cilit duhet gjetur, r është rrezja e rrethit të brendashkruar në këtë trekëndësh.


Formula për sipërfaqen e një trekëndëshi të bazuar në tre anët dhe rrezen e rrethit të rrethuar rreth tij
S= (a*b*c)/4*R,
ku a,b,c është gjatësia e secilës anë të trekëndëshit, R është rrezja e rrethit të rrethuar rreth trekëndëshit.


Formula për sipërfaqen e një trekëndëshi duke përdorur koordinatat karteziane të pikave
Koordinatat karteziane të pikave janë koordinata në sistemin xOy, ku x është abshisa, y është ordinata. Sistemi kartezian koordinatat xOy në rrafsh quhen reciprokisht pingule boshtet numerike Ooh dhe Oy me fillimi i përbashkët referencë në pikën O. Nëse koordinatat e pikave në këtë plan janë dhënë në formën A(x1, y1), B(x2, y2) dhe C(x3, y3), atëherë mund të llogarisni sipërfaqen e trekëndëshit duke përdorur formulën e mëposhtme, e cila është marrë nga produkt vektorial dy vektorë.
S = |(x1 – x3) (y2 – y3) – (x2 – x3) (y1 – y3)|/2,
ku || qëndron për modul.


Si të gjeni sipërfaqen e një trekëndëshi kënddrejtë
Një trekëndësh kënddrejtë është një trekëndësh me një kënd që mat 90 gradë. Një trekëndësh mund të ketë vetëm një kënd të tillë.
Formula për sipërfaqen e një trekëndëshi kënddrejtë në dy anët
S= a*b/2,
ku a,b është gjatësia e këmbëve. Këmbët janë anët ngjitur me një kënd të drejtë.


Formula për sipërfaqen e një trekëndëshi kënddrejtë bazuar në hipotenuzën dhe këndin akut
S = a*b*sin(α)/ 2,
ku a, b janë këmbët e trekëndëshit, dhe sin(α) është sinusi i këndit në të cilin drejtëzat a, b priten.


Formula për sipërfaqen e një trekëndëshi kënddrejtë bazuar në anën dhe këndin e kundërt
S = a*b/2*tg(β),
ku a, b janë këmbët e trekëndëshit, tan(β) është tangjentja e këndit në të cilin lidhen këmbët a, b.


Si të llogarisni sipërfaqen e një trekëndëshi dykëndësh
Një trekëndësh izosceles është një trekëndësh që ka dy anët e barabarta. Këto anë quhen anët, dhe ana tjetër është baza. Për të llogaritur sipërfaqen e një trekëndëshi dykëndësh, mund të përdorni një nga formulat e mëposhtme.
Formula bazë për llogaritjen e sipërfaqes së një trekëndëshi dykëndësh
S=h*c/2,
ku c është baza e trekëndëshit, h është lartësia e trekëndëshit të ulur në bazë.


Formula e një trekëndëshi izoscelular bazuar në anën dhe bazën
S=(c/2)* √(a*a – c*c/4),
ku c është baza e trekëndëshit, a është madhësia e njërës nga brinjët anësore të trekëndëshit dykëndësh.


Si të gjeni sipërfaqen e një trekëndëshi barabrinjës
Një trekëndësh barabrinjës është një trekëndësh në të cilin të gjitha anët janë të barabarta. Për të llogaritur sipërfaqen e një trekëndëshi barabrinjës, mund të përdorni formulën e mëposhtme:
S = (√3*a*a)/4,
ku a është gjatësia e brinjës së trekëndëshit barabrinjës.


Formulat e mësipërme do t'ju lejojnë të llogarisni zonën e kërkuar të trekëndëshit. Është e rëndësishme të mbani mend se për të llogaritur sipërfaqen e trekëndëshave, duhet të merrni parasysh llojin e trekëndëshit dhe të dhënat e disponueshme që mund të përdoren për llogaritjen.
Ndonjëherë në jetë ka situata kur duhet të thellohesh në kujtesën tënde në kërkim të të harruarit prej kohësh njohuritë shkollore. Për shembull, duhet të përcaktoni sipërfaqen e një trualli trekëndësh, ose ka ardhur koha për një rinovim tjetër në një apartament ose shtëpi private, dhe duhet të llogaritni se sa material do të nevojitet për sipërfaqen me formë trekëndore. Kishte një kohë kur mund ta zgjidhnit një problem të tillë në disa minuta, por tani po përpiqeni dëshpërimisht të mbani mend se si të përcaktoni sipërfaqen e një trekëndëshi?
Mos u shqetësoni për këtë! Në fund të fundit, është mjaft normale kur truri i një personi vendos të transferojë njohuritë e papërdorura prej kohësh diku në një cep të largët, nga i cili ndonjëherë nuk është aq e lehtë ta nxjerrësh atë. Në mënyrë që të mos keni nevojë të luftoni me kërkimin e njohurive të harruara të shkollës për të zgjidhur një problem të tillë, ky artikull përmban metoda të ndryshme, të cilat e bëjnë të lehtë gjetjen e zonës së kërkuar të trekëndëshit.
Dihet mirë se një trekëndësh është një lloj shumëkëndëshi që është minimalisht i kufizuar numri i mundshëm anët Në parim, çdo shumëkëndësh mund të ndahet në disa trekëndësha duke i lidhur kulmet e tij me segmente që nuk i kryqëzojnë brinjët e tij. Prandaj, duke ditur trekëndëshin, mund të llogaritni sipërfaqen e pothuajse çdo figure.
Ndër të gjithë trekëndëshat e mundshëm që ndodhin në jetë, mund të dallohen llojet e mëposhtme të veçanta: dhe drejtkëndëshe.
Mënyra më e lehtë për të llogaritur sipërfaqen e një trekëndëshi është kur një nga këndet e tij është i drejtë, domethënë në rastin e një trekëndëshi kënddrejtë. Është e lehtë të shihet se është gjysmë drejtkëndësh. Prandaj, sipërfaqja e saj është e barabartë me gjysmën e produktit të anëve që formojnë një kënd të drejtë me njëra-tjetrën.
Nëse e dimë lartësinë e një trekëndëshi, të rënë nga një nga kulmet e tij në anën e kundërt, dhe gjatësia e kësaj faqeje, e cila quhet bazë, atëherë sipërfaqja llogaritet sa gjysma e prodhimit të lartësisë dhe bazës. Kjo është shkruar duke përdorur formulën e mëposhtme:
S = 1/2*b*h, në të cilën
S është zona e kërkuar e trekëndëshit;
b, h - përkatësisht lartësia dhe baza e trekëndëshit.
Është kaq e lehtë për të llogaritur sipërfaqen e një trekëndëshi izoscelular, sepse lartësia do të përgjysmojë anën e kundërt dhe mund të matet lehtësisht. Nëse zona përcaktohet, atëherë është e përshtatshme të merret gjatësia e njërës prej anëve që formojnë një kënd të drejtë si lartësi.
E gjithë kjo është sigurisht e mirë, por si të përcaktohet nëse një nga këndet e një trekëndëshi është i drejtë apo jo? Nëse madhësia e figurës sonë është e vogël, atëherë mund të përdorim një kënd ndërtimi, një trekëndësh vizatimi, një kartolinë ose një objekt tjetër me formë drejtkëndëshe.
Por çka nëse kemi një trekëndësh truall? Në këtë rast, veproni si më poshtë: numëroni nga maja e të pritshmeve kënd i drejtë në njërën anë distanca është shumëfish i 3-shit (30 cm, 90 cm, 3 m), dhe nga ana tjetër distanca është shumëfish i 4-it (40 cm, 160 cm, 4 m) i matur në të njëjtin proporcion. Tani ju duhet të matni distancën midis pikat fundore këto dy segmente. Nëse rezultati është një shumëfish i 5 (50 cm, 250 cm, 5 m), atëherë mund të themi se këndi është i drejtë.
Nëse dihet gjatësia e secilës prej tre anëve të figurës sonë, atëherë sipërfaqja e trekëndëshit mund të përcaktohet duke përdorur formulën e Heronit. Për të pasur një formë më të thjeshtë, përdoret një vlerë e re, e cila quhet gjysmëperimetri. Kjo është shuma e të gjitha brinjëve të trekëndëshit tonë, të ndarë në gjysmë. Pasi të jetë llogaritur gjysmëperimetri, mund të filloni të përcaktoni zonën duke përdorur formulën:
S = sqrt(p(p-a)(p-b)(p-c)), ku
sqrt - rrënjë katrore;
p - vlera gjysmë-perimetrike (p = (a+b+c)/2);
a, b, c - skajet (anët) e trekëndëshit.
Por çka nëse trekëndëshi ka formë të çrregullt? Këtu ka dy mënyra të mundshme. E para është të përpiqemi ta ndajmë një figurë të tillë në dysh trekëndësh kënddrejtë, shuma e sipërfaqeve të të cilave llogaritet veçmas dhe më pas shtohet. Ose, nëse dihet këndi midis dy anëve dhe madhësia e këtyre anëve, atëherë zbatoni formulën:
S = 0,5 * ab * sinC, ku
a,b - anët e trekëndëshit;
c është madhësia e këndit ndërmjet këtyre anëve.
Rasti i fundit në praktikë është e rrallë, por megjithatë, në jetë gjithçka është e mundur, kështu që formula e mësipërme nuk do të jetë e tepërt. Fat i mirë me llogaritjet tuaja!








