Artan ve azalan fonksiyonlar

işlev sen = F(X) [ aralığında artan olarak adlandırılır A, B], eğer herhangi bir nokta çifti içinse X Ve X", a ≤ x eşitsizliği geçerlidir F(X) ≤ F (X") ve kesinlikle artıyor - eğer eşitsizlik F (X) F(X"). Azalan ve tam olarak azalan fonksiyonlar benzer şekilde tanımlanır. Örneğin, fonksiyon en = X 2 (pirinç. , a) segmentte kesinlikle artar ve

(pirinç. , b) bu ​​segmentte kesinlikle azalır. Artan fonksiyonlar belirlendi F (X) ve azalan F (X)↓. F (X Türevlenebilir bir fonksiyon için ) segmentte artıyordu [, B A F"(X], türevinin olması gerekli ve yeterlidir ) segmentte artıyordu [, B].

) [ üzerinde negatif değildi en = F (X Bir fonksiyondaki artış ve azalışın yanı sıra, bir fonksiyonun bir noktadaki artış ve azalışını da dikkate alıyoruz. İşlev X) noktasında artan denir X Noktayı içeren bir aralık (α, β) varsa 0 X 0, herhangi bir nokta için (α, β), X x> F (X 0) ≤ F (X 0 , eşitsizlik geçerli X 0, herhangi bir nokta için ) ve herhangi bir nokta için F (X) x 0, eşitsizlik geçerli (X≤ f X 0). Bir fonksiyonun noktadaki kesin artışı benzer şekilde tanımlanır. F"(X 0) > 0. Eğer F(X 0, ardından işlev X 0). Bir fonksiyonun noktadaki kesin artışı benzer şekilde tanımlanır. F (X) noktada kesinlikle artar A, B) aralığın her noktasında artar (

), sonra bu aralıkta artar.

S. B. Stechkin.. 1969-1978 .

Büyük Sovyet Ansiklopedisi. - M .: Sovyet Ansiklopedisi

Diğer sözlüklerde “Artan ve azalan fonksiyonlar”ın neler olduğuna bakın: Matematiksel analiz kavramları. f(x) fonksiyonuna, NÜFUSUN YAŞ YAPISI segmentinde artan nüfusun farklı yaş grubu sayılarının oranı denir. Doğum ve ölüm oranlarına, insanların yaşam beklentisine bağlı...

Büyük Ansiklopedik Sözlük Matematiksel analiz kavramları. Herhangi bir x1 ve x2 nokta çifti için a≤x1 ... ise, f(x) fonksiyonunun parça üzerinde artan olduğu söylenir.

Ansiklopedik Sözlük<или=х1 <х<или=b, выполняется неравенство f(x1)Matematik kavramları. analiz. f(x) fonksiyonu çağrılır. herhangi bir x1 ve x2 noktası çifti için [a, b] segmentinde artan ve

Doğa bilimi. Ansiklopedik Sözlük Fonksiyonların türevlerini ve diferansiyellerini ve bunların fonksiyon çalışmalarına uygulamalarını inceleyen bir matematik dalı. D. ve. Bağımsız bir matematik disiplinine dönüşmesi I. Newton ve G. Leibniz'in (17. yüzyılın ikinci yarısı) isimleriyle ilişkilidir.

Türev ve diferansiyel kavramlarının ve bunların fonksiyon çalışmalarına nasıl uygulandığının incelendiği bir matematik dalı. D.'nin gelişimi ve. İntegral hesabının gelişimiyle yakından ilgilidir. İçerikleri de ayrılamaz. Birlikte temeli oluştururlar... ... Matematik Ansiklopedisi

Bu terimin başka anlamları da vardır, bkz. işlevi. "Görüntüleme" isteği buraya yönlendirilir; diğer anlamlara da bakın... Vikipedi

Aristoteles ve Peripatetikler- Aristoteles Sorusu Aristoteles'in Hayatı Aristoteles 384/383 yılında doğmuştur. M.Ö. e. Makedonya sınırındaki Stagira'da. Nikomakhos adındaki babası, Philip'in babası Makedon kralı Amyntas'ın hizmetinde bir doktordu. Ailesi ile birlikte genç Aristoteles... ... Kökeninden günümüze Batı felsefesi

- (QCD), kuantum görüntüsünde yerleşik kuarklar ve gluonların güçlü etkileşiminin kuantum alan teorisi. "renk" gösterge simetrisine dayalı elektrodinamik (QED). QED'den farklı olarak QCD'deki fermiyonlar tamamlayıcı özelliklere sahiptir. serbestlik derecesi kuantumu. sayı,… … Fiziksel ansiklopedi

I Heart Kalp (Latince cor, Yunanca kardia), pompa görevi görerek dolaşım sistemindeki kanın hareketini sağlayan içi boş bir fibromüsküler organdır. Anatomi Kalp, Perikardın ön mediasteninde (Mediastinum) bulunur. Tıp ansiklopedisi

Bir bitkinin yaşamı, diğer canlı organizmalar gibi, birbiriyle ilişkili karmaşık süreçlerden oluşur; Bunlardan en önemlisi bilindiği gibi çevreyle madde alışverişidir. Çevre, kaynağı olan... ... Biyolojik ansiklopedi

Türev. Bir fonksiyonun türevi aralığın herhangi bir noktasında pozitifse fonksiyon artar, negatifse azalır.

Bir fonksiyonun artış ve azalış aralıklarını bulmak için tanım kümesini, türevini bulmanız, F'(x) > 0 ve F'(x) formundaki eşitsizlikleri çözmeniz gerekir.

Çözüm.

3. y' > 0 ve y' 0 eşitsizliklerini çözün;
(4 - x)/x³

Çözüm.
1. Fonksiyonun tanım tanım kümesini bulalım. Açıkçası, paydadaki ifadenin her zaman sıfırdan farklı olması gerekir. Bu nedenle 0, tanım alanının dışında bırakılır: fonksiyon x ∈ (-∞; 0)∪(0; +∞) için tanımlanır.

2. Fonksiyonun türevini hesaplayın:
y'(x) = ((3 x² + 2 x - 4)' x² – (3 x² + 2 x - 4) (x²)')/x^4 = ((6 x + 2) x² – (3 x² + 2 x - 4) 2 x)/x^4 = (6 x³ + 2 x² – 6 x³ – 4 x² + 8 x)/x^ 4 = (8 x – 2 x²)/x^4 = 2 (4 -x)/x³.

3. y' > 0 ve y' 0 eşitsizliklerini çözün;
(4 - x)/x³

4. Eşitsizliğin sol tarafında bir reel x = 4 vardır ve x = 0'da döner. Dolayısıyla x = 4 değeri hem aralığa hem de azalan aralığa dahil edilir ve 0 noktası dahil edilmez.
Yani gerekli fonksiyon x ∈ (-∞; 0) ∪ aralığında artar.

4. Eşitsizliğin sol tarafında bir reel x = 4 vardır ve x = 0'da döner. Dolayısıyla x = 4 değeri hem aralığa hem de azalan aralığa dahil edilir ve 0 noktası dahil edilmez.
Yani gerekli fonksiyon x ∈ (-∞; 0) ∪ aralığında artar.

Kaynaklar:

• bir fonksiyonda azalan aralıklar nasıl bulunur

Bir fonksiyon, bir sayının diğerine kesin bağımlılığını veya bir fonksiyonun (y) bir argüman (x) üzerindeki değerini temsil eder. Her süreç (sadece matematikte değil), karakteristik özelliklere sahip olan kendi fonksiyonuyla tanımlanabilir: azalma ve artış aralıkları, minimum ve maksimum noktaları vb.

İhtiyacın olacak

• - kağıt;
• - dolma kalem.

Talimatlar

Örnek 2.
Azalan f(x)=sinx +x aralıklarını bulun.
Bu fonksiyonun türevi şuna eşit olacaktır: f'(x)=cosx+1.
Cosx+1 eşitsizliğinin çözümü

Aralık monotonluk bir fonksiyona, fonksiyonun yalnızca arttığı veya yalnızca azaldığı bir aralık adı verilebilir. Bir dizi özel eylem, bu tür cebirsel problemlerde sıklıkla gerekli olan, fonksiyon için bu tür aralıkların bulunmasına yardımcı olacaktır.

Talimatlar

Bir fonksiyonun monoton olarak arttığı veya azaldığı aralıkları belirleme problemini çözmenin ilk adımı bu fonksiyonu hesaplamaktır. Bunu yapmak için, fonksiyonun değerini bulabileceğiniz tüm argüman değerlerini (x ekseni boyunca değerler) bulun. Süreksizliklerin gözlendiği noktaları işaretleyin. Fonksiyonun türevini bulun. Türevi temsil eden ifadeyi belirledikten sonra onu sıfıra eşitleyin. Bundan sonra ortaya çıkan köklerini bulmalısınız. İzin verilen alanla ilgili değil.

Fonksiyonun veya türevinin sıfıra eşit olduğu noktalar aralıkların sınırlarını temsil eder monotonluk. Bu aralıklar ve onları ayıran noktalar tabloya sırayla girilmelidir. Ortaya çıkan aralıklarda fonksiyonun türevinin işaretini bulun. Bunu yapmak için aralıktaki herhangi bir bağımsız değişkeni türevine karşılık gelen ifadeyle değiştirin. Sonuç pozitifse bu aralıktaki fonksiyon artar, aksi takdirde azalır. Sonuçlar tabloya girilir.

F'(x) fonksiyonunun türevini belirten satırda, argümanların karşılık gelen değerleri yazılır: "+" - türev pozitifse, "-" - negatif veya "0" - sıfıra eşitse. Bir sonraki satırda orijinal ifadenin monotonluğuna dikkat edin. Yukarı ok artışa, aşağı ok ise düşüşe karşılık gelir. İşlevleri kontrol edin. Bunlar türevin sıfır olduğu noktalardır. Bir ekstremum maksimum nokta veya minimum nokta olabilir. Fonksiyonun bir önceki bölümü artmış ve mevcut bölümü azalmışsa bu maksimum noktadır. Fonksiyonun belirli bir noktadan önce azaldığı ve şimdi arttığı durumda bu minimum noktadır. Fonksiyonun ekstremum noktalarındaki değerlerini tabloya girin.

Kaynaklar:

• monotonluğun tanımı nedir

Bir argümana karmaşık bağımlılığı olan bir fonksiyonun davranışı, türev kullanılarak incelenir. Türevdeki değişimin doğası gereği, fonksiyonun kritik noktalarını ve büyüme veya azalış alanlarını bulabilirsiniz.

Bir fonksiyonun artan, azalan ve ekstremum değerleri

Bir fonksiyonun artış, azalma ve ekstremum aralıklarını bulmak hem bağımsız bir görevdir hem de diğer görevlerin önemli bir parçasıdır. tam fonksiyon çalışması. Fonksiyonun artış, azalış ve ekstremum değerlerine ilişkin ilk bilgiler aşağıda verilmiştir. türev üzerine teorik bölümÖn çalışma için şiddetle tavsiye ettiğim (veya tekrarlama)– ayrıca aşağıdaki materyalin aynı temele dayanması nedeniyle esas olarak türev, bu makalenin uyumlu bir devamı niteliğindedir. Ancak zaman kısaysa, bugünkü dersten alınan örneklerin tamamen resmi bir şekilde uygulanması da mümkündür.

Ve bugün havada nadir görülen bir birlik ruhu var ve orada bulunan herkesin arzuyla yandığını doğrudan hissedebiliyorum. Türevini kullanarak bir fonksiyonu keşfetmeyi öğrenin. Bu nedenle makul, iyi, ebedi terminoloji hemen monitör ekranlarınızda belirir.

Ne için? Sebeplerden biri en pratik olanıdır: böylece belirli bir görevde genel olarak sizden ne istendiğinin netleşmesi için!

Fonksiyonun monotonluğu. Bir fonksiyonun ekstremum noktaları ve ekstremumları

Biraz fonksiyon düşünelim. Basitçe söylemek gerekirse, onun olduğunu varsayıyoruz. sürekli tüm sayı doğrusunda:

Her ihtimale karşı, özellikle yeni tanışan okuyucular için olası yanılsamalardan bir an önce kurtulalım. fonksiyonun sabit işaretli aralıkları. Şimdi biz İLGİLİ DEĞİL, fonksiyonun grafiğinin eksene göre nasıl yerleştirildiği (eksenin kesiştiği yerde yukarıda, aşağıda). İkna edici olmak için eksenleri zihinsel olarak silin ve bir grafik bırakın. Çünkü ilginin yattığı yer burası.

İşlev artar Bir aralıkta, bu aralığın ilişkiyle birbirine bağlanan herhangi iki noktası için eşitsizlik doğrudur. Yani, argümanın daha büyük bir değeri, fonksiyonun daha büyük bir değerine karşılık gelir ve grafiği "aşağıdan yukarıya" doğru gider. Gösterim işlevi aralık boyunca büyür.

Aynı şekilde, fonksiyon azalır Belirli bir aralığın herhangi iki noktası için eşitsizlik doğru olacak şekilde bir aralıkta. Yani, argümanın daha büyük bir değeri, fonksiyonun daha küçük bir değerine karşılık gelir ve grafiği "yukarıdan aşağıya" doğru gider. Fonksiyonumuz aralıklarla azalır .

Bir fonksiyon belirli bir aralıkta artıyor veya azalıyorsa buna denir. kesinlikle monoton bu aralıkta. Monotonluk nedir? Kelimenin tam anlamıyla alın – monotonluk.

Ayrıca tanımlayabilirsiniz azalmayan fonksiyon (ilk tanımda rahat durum) ve artmayan fonksiyon (2. tanımda yumuşatılmış durum). Bir aralıkta azalmayan veya artmayan bir fonksiyona, belirli bir aralıkta monotonik fonksiyon denir (katı monotonluk, “basitçe” monotonluğun özel bir durumudur).

Teori aynı zamanda yarım aralıklar, bölümler de dahil olmak üzere bir fonksiyonun artışını/azalışını belirlemeye yönelik diğer yaklaşımları da dikkate alır, ancak başınıza yağ-yağ-yağ dökmemek için kategorik tanımlarla açık aralıklarla çalışmayı kabul edeceğiz. - bu daha açık ve birçok pratik sorunu çözmek için oldukça yeterli.

Böylece, Makalelerimde "bir fonksiyonun monotonluğu" ifadesi neredeyse her zaman gizlenecek aralıklar katı monotonluk(kesinlikle artan veya kesinlikle azalan fonksiyon).

Bir noktanın mahallesi. Ardından öğrencilerin bulabildikleri her yere kaçtıkları ve köşelerde dehşet içinde saklandıkları sözler. ...her ne kadar gönderiden sonra Cauchy sınırları Muhtemelen artık saklanmıyorlar, sadece hafifçe titriyorlar =) Endişelenmeyin, artık matematiksel analiz teoremlerinin kanıtı olmayacak - tanımları daha kesin bir şekilde formüle etmek için çevreye ihtiyacım vardı ekstrem noktalar. Hatırlayalım:

Bir noktanın mahallesi Belirli bir noktayı içeren bir aralık denir ve kolaylık sağlamak için aralığın genellikle simetrik olduğu varsayılır. Örneğin bir nokta ve onun standart komşuluğu:

Aslında tanımlar:

Nokta denir kesin maksimum nokta, Eğer var onun mahallesi, herkes için değerleri, noktanın kendisi dışında eşitsizliktir. Özel örneğimizde bu bir noktadır.

Nokta denir kesin minimum nokta, Eğer var onun mahallesi, herkes için değerleri, noktanın kendisi dışında eşitsizliktir. Çizimde “a” noktası var.

Not : Komşuluk simetrisi gerekliliği hiç de gerekli değildir. Ayrıca önemli varoluşun gerçeği belirtilen koşulları karşılayan mahalle (küçük veya mikroskobik)

Noktalara denir kesinlikle ekstremum noktalar ya da sadece ekstrem noktalar işlevler. Yani maksimum puanlar ve minimum puanlar için genelleştirilmiş bir terimdir.

“Aşırı” kelimesini nasıl anlıyoruz? Evet, monotonluk kadar doğrudan. Hız trenlerinin uç noktaları.

Monotonluk durumunda olduğu gibi, gevşek varsayımlar mevcuttur ve teoride daha da yaygındır. (tabii ki, dikkate alınan katı davalar da bu kapsamdadır!):

Nokta denir maksimum nokta, Eğer varçevresi öyle herkes için
Nokta denir minimum puan, Eğer varçevresi öyle herkes için Bu mahallenin değerleri, eşitsizliği barındırıyor.

Son iki tanıma göre, sabit bir fonksiyonun (veya bir fonksiyonun "düz bölümünün") herhangi bir noktasının hem maksimum hem de minimum nokta olarak kabul edildiğini unutmayın! Bu arada fonksiyon hem artmayan hem de azalmayan, yani monotondur. Bununla birlikte, bu düşünceleri teorisyenlere bırakacağız, çünkü pratikte neredeyse her zaman geleneksel "tepeleri" ve "çukurları" (çizime bakınız) benzersiz bir "tepenin kralı" veya "bataklığın prensesi" ile düşünürüz. Bir çeşitlilik olarak ortaya çıkar uç, yukarı veya aşağı yönlendirilmiş, örneğin noktadaki fonksiyonun minimumu.

Ah, kraliyetten bahsetmişken:
– anlamı denir maksimum işlevler;
– anlamı denir minimum işlevler.

Ortak ad – aşırılıklar işlevler.

Lütfen sözlerinize dikkat edin!

Ekstrem noktalar– bunlar “X” değerleridir.
Aşırılıklar– “oyun” anlamları.

! Not : Bazen listelenen terimler doğrudan fonksiyonun KENDİSİNİN GRAFİĞİ üzerinde yer alan “X-Y” noktalarına atıfta bulunur.

Bir fonksiyonun kaç ekstremum değeri olabilir?

Yok, 1, 2, 3,... vb. sonsuza dek. Örneğin sinüsün sonsuz sayıda minimum ve maksimum değeri vardır.

ÖNEMLİ!"Maksimum fonksiyon" terimi aynı değil"bir fonksiyonun maksimum değeri" terimi. Değerin yalnızca yerel bir mahallede maksimum olduğunu ve sol üstte "daha havalı yoldaşların" bulunduğunu fark etmek kolaydır. Aynı şekilde “bir fonksiyonun minimumu” ile “bir fonksiyonun minimum değeri” aynı değildir ve çizimde değerin sadece belirli bir alanda minimum olduğunu görüyoruz. Bu bakımdan ekstremum noktalara da denir. yerel ekstremum noktaları ve ekstremum – yerel aşırılıklar. Yakınlarda yürürler ve dolaşırlar ve küresel kardeşler. Yani herhangi bir parabolün tepe noktasında küresel minimum veya küresel maksimum. Ayrıca, aşırı uç türleri arasında ayrım yapmayacağım ve açıklama daha çok genel eğitim amaçlı olarak dile getirildi - "yerel"/"küresel" ek sıfatları sizi şaşırtmamalı.

Teoriye yaptığımız kısa geziyi bir deneme çekimiyle özetleyelim: "Fonksiyonun monotonluk aralıklarını ve ekstremum noktalarını bulma" görevi ne anlama geliyor?

İfade sizi şunu bulmaya teşvik ediyor:

– artan/azalan fonksiyon aralıkları (azalmayan, artmayan çok daha az sıklıkla görülür);

– maksimum ve/veya minimum puanlar (varsa). Başarısızlığı önlemek için minimumları/maksimumları kendiniz bulmak daha iyidir ;-)

Bütün bunlar nasıl belirlenir? Türev fonksiyonunu kullanma!

Artan, azalan aralıklar nasıl bulunur?
Fonksiyonun ekstrem noktaları ve ekstremumları?

Aslında pek çok kural zaten biliniyor ve anlaşılıyor. türevin anlamı hakkında ders.

Teğet türev boyunca fonksiyonun arttığına dair sevindirici bir haber getiriyor tanım alanı.

Kotanjant ve türevi ile durum tam tersidir.

Ark sinüs aralık boyunca artar - buradaki türev pozitiftir: .
Fonksiyon tanımlı ancak türevlenebilir olmadığında. Ancak kritik noktada sağdan türev ve sağdan teğet vardır, diğer kenarda ise bunların solak karşılıkları vardır.

Ark kosinüs ve türevi için de benzer akıl yürütmenin sizin için çok zor olmayacağını düşünüyorum.

Yukarıdaki durumların tümü, bunların çoğu tablosal türevler, hatırlatırım, doğrudan şuradan takip edin türev tanımları.

Neden bir fonksiyonu türevini kullanarak araştıralım?

Bu fonksiyonun grafiğinin neye benzediğini daha iyi anlamak için: "aşağıdan yukarıya" gittiği yer, "yukarıdan aşağıya" gittiği yer, minimum ve maksimumlara ulaştığı yer (eğer ulaşıyorsa). Tüm fonksiyonlar o kadar basit değildir; çoğu durumda belirli bir fonksiyonun grafiği hakkında hiçbir fikrimiz yoktur.

Daha anlamlı örneklere geçmenin ve düşünmenin zamanı geldi Bir fonksiyonun monotonluk ve ekstremum aralıklarını bulmak için algoritma:

Örnek 1

Fonksiyonun artış/azalış aralıklarını ve ekstremumlarını bulun

Çözüm:

1) İlk adım bulmaktır bir fonksiyonun alanı ve ayrıca kesme noktalarını (varsa) not edin. Bu durumda fonksiyon tüm sayı doğrusunda süreklidir ve bu eylem bir dereceye kadar resmidir. Ancak bazı durumlarda burada ciddi tutkular alevlenir, bu yüzden paragrafı küçümsemeden ele alalım.

2) Algoritmanın ikinci noktası şundan kaynaklanmaktadır:

bir ekstremum için gerekli koşul:

Bir noktada bir ekstremum varsa o zaman değer de mevcut değildir.

Sonu kafanız mı karıştı? “Modül x” fonksiyonunun ekstremumu .

Şart gerekli ama yeterli değil ve bunun tersi her zaman doğru değildir. Dolayısıyla eşitlikten fonksiyonun noktasında maksimum veya minimuma ulaştığı sonucu çıkmaz. Yukarıda klasik bir örnek zaten vurgulanmıştı - bu kübik bir parabol ve onun kritik noktasıdır.

Ancak öyle de olsa, bir ekstremum için gerekli koşul, şüpheli noktaların bulunması ihtiyacını zorunlu kılmaktadır. Bunu yapmak için türevi bulun ve denklemi çözün:

İlk makalenin başında fonksiyon grafikleri hakkında Bir örnek kullanarak hızlı bir şekilde parabolün nasıl oluşturulacağını anlattım. : “...birinci türevi alıp sıfıra eşitliyoruz: ...Yani denklemimizin çözümü: - parabolün tepe noktası tam da bu noktada...”. Sanırım artık herkes parabolün tepe noktasının neden tam olarak bu noktada bulunduğunu anladı =) Genel olarak burada da benzer bir örnekle başlamalıyız ama bu çok basit (bir çaydanlık için bile). Ayrıca dersin en sonunda bir analog var. bir fonksiyonun türevi. Bu nedenle dereceyi artıralım:

Örnek 2

Fonksiyonun monotonluk ve ekstremum aralıklarını bulun

Bu kendi başınıza çözebileceğiniz bir örnektir. Dersin sonunda tam bir çözüm ve problemin yaklaşık nihai örneği.

Kesirli-rasyonel fonksiyonlarla uzun zamandır beklenen buluşma anı geldi:

Örnek 3

Birinci türevi kullanarak bir fonksiyonu keşfedin

Bir ve aynı görevin ne kadar değişken biçimde yeniden formüle edilebileceğine dikkat edin.

Çözüm:

1) Fonksiyon noktalarda sonsuz süreksizliklere maruz kalır.

2) Kritik noktaları tespit ediyoruz. Birinci türevi bulup sıfıra eşitleyelim:

Denklemi çözelim. Payı sıfır olduğunda bir kesir sıfırdır:

Böylece üç kritik nokta elde ediyoruz:

3) Tespit edilen TÜM noktaları sayı doğrusu üzerinde çizeriz ve aralık yöntemi TÜREVİN işaretlerini tanımlarız:

Aralıkta bir nokta alıp türevin değerini hesaplamanız gerektiğini size hatırlatırım. ve işaretini belirleyin. Saymak bile değil, sözlü olarak "tahmin etmek" daha karlı. Örneğin aralığa ait bir noktayı alalım ve yerine koyma işlemini gerçekleştirelim: .

Dolayısıyla iki "artı" ve bir "eksi" bir "eksi" verir, bu da türevin tüm aralık boyunca negatif olduğu anlamına gelir.

Anladığınız gibi eylemin altı aralığın her biri için gerçekleştirilmesi gerekiyor. Bu arada, pay faktörünün ve paydanın herhangi bir aralıktaki herhangi bir nokta için kesinlikle pozitif olduğunu ve bunun görevi büyük ölçüde basitleştirdiğini unutmayın.

Yani türev bize FONKSİYONUN KENDİSİNİN şu kadar arttığını söyledi: ve kadar azalır. Birleştir simgesiyle aynı türdeki aralıkları birleştirmek uygundur.

Fonksiyonun maksimuma ulaştığı noktada:
Fonksiyonun minimuma ulaştığı noktada:

İkinci değeri neden yeniden hesaplamak zorunda olmadığınızı düşünün ;-)

Bir noktadan geçerken türev işaret değiştirmez, dolayısıyla fonksiyonun orada EKSTREMİ YOKTUR - hem azaldı hem de azalan kaldı.

! Önemli bir noktayı tekrarlayalım: noktalar kritik olarak kabul edilmez - bir işlev içerirler tanımlanmamış. Buna göre burada Prensipte hiçbir aşırılık olamaz(türev işaret değiştirse bile).

Cevap: fonksiyon şu kadar artar: ve azalır Fonksiyonun maksimum değerine ulaşıldığı noktada: , ve bu noktada – minimum: .

Monotonluk aralıkları ve ekstremum bilgisi, yerleşik bilgilerle birlikte asimptotlar zaten fonksiyon grafiğinin görünümü hakkında çok iyi bir fikir veriyor. Ortalama eğitime sahip bir kişi, bir fonksiyonun grafiğinin iki dikey asimptotu ve bir eğik asimptotu olduğunu sözlü olarak belirleyebilir. İşte kahramanımız:

Çalışmanın sonuçlarını bu fonksiyonun grafiğiyle ilişkilendirmeyi bir kez daha deneyin.
Kritik noktada ekstremum yoktur ancak dönüm noktası(kural olarak benzer durumlarda olur).

Örnek 4

Fonksiyonun ekstremumunu bulun

Örnek 5

Fonksiyonun monotonluk aralıklarını, maksimumlarını ve minimumlarını bulun

…bugün neredeyse bir nevi “küpün içindeki X” tatiline benziyor....
Soooo, galeride kim bunun için içki içmeyi teklif etti? =)

Her görevin kendine özgü nüansları ve teknik incelikleri vardır ve bunlar dersin sonunda yorumlanır.

Fonksiyonun ekstremum değerleri

Tanım 2

Bir $x_0$ noktasına, eğer bu noktanın bir komşuluğu varsa, bu komşuluktaki tüm $x$ için $f(x)\le f(x_0) eşitsizliği varsa, $f(x)$ fonksiyonunun maksimum noktası denir. $ tutar.

Tanım 3

Bir $x_0$ noktasına, eğer bu noktanın bir komşuluğu varsa, bu komşuluktaki tüm $x$ için $f(x)\ge f(x_0) eşitsizliği varsa, $f(x)$ fonksiyonunun maksimum noktası denir. $ tutar.

Bir fonksiyonun ekstremum kavramı, bir fonksiyonun kritik noktası kavramıyla yakından ilişkilidir. Tanımını tanıtalım.

Tanım 4

Aşağıdaki durumlarda $x_0$, $f(x)$ fonksiyonunun kritik noktası olarak adlandırılır:

1) $x_0$ - tanım alanının iç noktası;

2) $f"\left(x_0\right)=0$ veya mevcut değil.

Ekstremum kavramı için onun varlığı için yeterli ve gerekli koşullar üzerine teoremler formüle edebiliriz.

Teorem 2

Bir ekstremum için yeterli koşul

$x_0$ noktası $y=f(x)$ fonksiyonu için kritik olsun ve $(a,b)$ aralığında olsun. Her $\left(a,x_0\right)\ ve\ (x_0,b)$ aralığında $f"(x)$ türevinin mevcut olduğunu ve sabit bir işareti koruduğunu varsayalım. Sonra:

1) $(a,x_0)$ aralığında türev $f"\left(x\right)>0$ ise ve $(x_0,b)$ aralığında türev $f"\left( ise x\sağ)

2) $(a,x_0)$ aralığında $f"\left(x\right)0$ türevi varsa, o zaman $x_0$ noktası bu fonksiyon için minimum noktadır.

3) Hem $(a,x_0)$ aralığında hem de $(x_0,b)$ aralığındaysa $f"\left(x\right) >0$ türevi veya $f"\left(x türevi \Sağ)

Bu teorem Şekil 1'de gösterilmektedir.

Şekil 1. Ekstremin varlığı için yeterli koşul

Aşırılık örnekleri (Şekil 2).

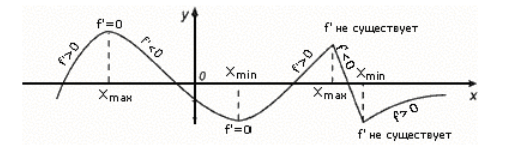
Şekil 2. Ekstrem noktalara örnekler

Bir fonksiyonu ekstremum için inceleme kuralı

2) $f"(x)$ türevini bulun;

7) Teorem 2'yi kullanarak her aralıkta maksimum ve minimumların varlığı hakkında sonuçlar çıkarın.

Artan ve azalan fonksiyonlar

Önce artan ve azalan fonksiyonların tanımlarını verelim.

Tanım 5

$X$ aralığında tanımlanan bir $y=f(x)$ fonksiyonunun, $x_1 noktasındaki herhangi bir $x_1,x_2\in X$ noktası için artan olduğu söylenir.

Tanım 6

$X$ aralığında tanımlanan bir $y=f(x)$ fonksiyonunun, $x_1f(x_2)$ için herhangi bir $x_1,x_2\in X$ noktası için azalan olduğu söylenir.

Artan ve azalan bir fonksiyonun incelenmesi

Türevi kullanarak artan ve azalan fonksiyonları inceleyebilirsiniz.

Bir fonksiyonu artan ve azalan aralıklara göre incelemek için aşağıdakileri yapmanız gerekir:

1) $f(x)$ fonksiyonunun tanım tanım kümesini bulun;

2) $f"(x)$ türevini bulun;

3) $f"\left(x\right)=0$; eşitliğinin sağlandığı noktaları bulun.

4) $f"(x)$'ın bulunmadığı noktaları bulun;

5) Bulunan tüm noktaları ve bu fonksiyonun tanım alanını koordinat çizgisi üzerinde işaretleyin;

6) Ortaya çıkan her aralıkta $f"(x)$ türevinin işaretini belirleyin;

7) Bir sonuca varın: $f"\left(x\right)0$ aralığında fonksiyon artar.

Artan, azalan fonksiyonları ve ekstremum noktaların varlığını incelemek için problem örnekleri

Örnek 1

Arttırma ve azaltma fonksiyonunu ve maksimum ve minimum noktaların varlığını inceleyin: $f(x)=(2x)^3-15x^2+36x+1$

İlk 6 nokta aynı olduğundan önce onları geçelim.

1) Tanım alanı - tüm gerçek sayılar;

2) $f"\left(x\right)=6x^2-30x+36$;

3) $f"\left(x\right)=0$;

\ \ \

4) $f"(x)$ tanım alanının tüm noktalarında mevcuttur;

5) Koordinat çizgisi:

Şekil 3.

6) Her aralıkta $f"(x)$ türevinin işaretini belirleyin:

\ \}