Karmaşık integraller
Bu makale belirsiz integraller konusunu sonlandırıyor ve oldukça karmaşık bulduğum integralleri içeriyor. Ders, sitede daha zor örneklerin incelenmesini istediklerini ifade eden ziyaretçilerin tekrarlanan talepleri üzerine oluşturuldu.
Bu metnin okuyucusunun iyi hazırlanmış olduğu ve temel entegrasyon tekniklerini nasıl uygulayacağını bildiği varsayılmaktadır. İntegrallere pek güvenmeyenler ve aptallar ilk derse bakmalıdır - Belirsiz integral. Çözüm örnekleri, konuya neredeyse sıfırdan hakim olabileceğiniz yer. Daha deneyimli öğrenciler, makalelerimde henüz karşılaşılmayan entegrasyon teknik ve yöntemlerine aşina olabilirler.
Hangi integraller dikkate alınacak?
Öncelikle çözümü için art arda kullandığımız köklü integralleri ele alacağız. değişken değiştirme Ve parçalara göre entegrasyon. Yani bir örnekte iki teknik aynı anda birleştirilmiştir. Ve daha da fazlası.
O zaman ilginç ve orijinal ile tanışacağız İntegrali kendine indirgeme yöntemi. Pek çok integral bu şekilde çözülür.
Programın üçüncü sayısı, önceki makalelerde kasanın önünden geçen karmaşık kesirlerden integraller olacak.
Dördüncü olarak trigonometrik fonksiyonlardan ek integraller analiz edilecektir. Özellikle zaman alıcı evrensel trigonometrik ikameyi önleyen yöntemler vardır.
(2) İntegral fonksiyonunda payı paydaya terime böleriz.
(3) Belirsiz integralin doğrusallık özelliğini kullanıyoruz. Hemen son integralde fonksiyonu diferansiyel işaretinin altına koyun.
(4) Kalan integralleri alıyoruz. Logaritmada modül yerine parantez kullanabileceğinizi unutmayın, çünkü .
(5) Doğrudan değiştirmeden “te”yi ifade ederek ters değiştirme işlemi yaparız:
Mazoşist öğrenciler, az önce yaptığım gibi, cevabı ayırt edebilir ve orijinal integrand'ı elde edebilirler. Hayır, hayır, kontrolü doğru anlamda yaptım =)
Gördüğünüz gibi, çözüm sırasında ikiden fazla çözüm yöntemi kullanmak zorunda kaldık, bu tür integrallerle başa çıkmak için kendinize güvenen entegrasyon becerilerine ve oldukça fazla deneyime ihtiyacınız var.
Pratikte elbette karekök daha yaygındır; işte bunu kendiniz çözmeniz için üç örnek:
Örnek 2
Belirsiz integrali bulun
Örnek 3
Belirsiz integrali bulun
Örnek 4
Belirsiz integrali bulun
Bu örnekler aynı türde olduğundan makalenin sonundaki tam çözüm yalnızca Örnek 2 için olacaktır; Örnek 3-4 aynı cevaplara sahiptir. Kararların başında hangi ikamenin kullanılacağının açık olduğunu düşünüyorum. Neden aynı türden örnekleri seçtim? Genellikle rollerinde bulunurlar. Daha sık, belki de şöyle bir şey ![]() .
.
Ancak her zaman değil, arktanjant, sinüs, kosinüs, üstel ve diğer fonksiyonlar altında doğrusal bir fonksiyonun kökü olduğunda, aynı anda birkaç yöntem kullanmanız gerekir. Bazı durumlarda "kolayca kurtulmak" mümkündür, yani değiştirmeden hemen sonra kolayca alınabilecek basit bir integral elde edilir. Yukarıda önerilen görevlerin en kolayı, değiştirme sonrasında nispeten basit bir integralin elde edildiği Örnek 4'tür.
İntegrali kendine indirgeyerek
Esprili ve güzel bir yöntem. Türün klasiklerine bir göz atalım:
Örnek 5
Belirsiz integrali bulun
Kökün altında ikinci dereceden bir binom vardır ve bu örneği entegre etmeye çalışmak çaydanlığa saatlerce baş ağrısı verebilir. Böyle bir integral parçalara ayrılarak kendisine indirgenir. Prensip olarak zor değil. Nasıl olduğunu biliyorsan.
Söz konusu integrali Latin harfiyle gösterelim ve çözüme başlayalım: ![]()
Parçalara göre integral alalım: 

(1) Dönem dönem bölünme için integrand fonksiyonunu hazırlayın.
(2) İntegral fonksiyon terimini terime bölüyoruz. Herkes için net olmayabilir, ancak daha ayrıntılı olarak anlatacağım:
(3) Belirsiz integralin doğrusallık özelliğini kullanıyoruz.
(4) Son integrali alın ("uzun" logaritma).
Şimdi çözümün başlangıcına bakalım: 
Ve sonunda: 
Ne oldu? Yaptığımız manipülasyonlar sonucunda integral kendine indirgendi!
Başlangıç ve bitişi eşitleyelim: ![]()
Burç değişikliği ile sol tarafa geçin: ![]()
Ve ikisini sağ tarafa kaydırıyoruz. Sonuç olarak: ![]()
Kesin olarak konuşursak, sabitin daha önce eklenmesi gerekirdi, ancak sonunda ekledim. Buradaki titizliğin ne olduğunu okumanızı şiddetle tavsiye ederim:
Not:
Daha doğrusu çözümün son aşaması şöyle görünür:
Böylece:
Sabit ile yeniden tasarlanabilir. Neden yeniden tasarlanabilir? Çünkü hala kabul ediyor herhangi değerler ve bu anlamda sabitler arasında bir fark yoktur.
Sonuç olarak:
Sürekli yeniden açıklama içeren benzer bir numara yaygın olarak kullanılmaktadır. diferansiyel denklemler. Ve orada katı olacağım. Ve burada böyle bir özgürlüğe yalnızca gereksiz şeylerle kafanızı karıştırmamak ve dikkati tam olarak entegrasyon yönteminin kendisine odaklamak için izin veriyorum.
Örnek 6
Belirsiz integrali bulun
Bağımsız çözüm için başka bir tipik integral. Dersin sonunda tam çözüm ve cevap. Önceki örnekteki cevapta bir fark olacak!
Karekökün altında bir kare trinomial varsa, o zaman çözüm her durumda analiz edilen iki örneğe iner.
Örneğin integrali düşünün ![]() . İlk önce yapmanız gereken tek şey tam bir kare seç:
. İlk önce yapmanız gereken tek şey tam bir kare seç:
.
Daha sonra, "herhangi bir sonuç olmadan" yapılan doğrusal bir değiştirme gerçekleştirilir:
, integralle sonuçlanır . Tanıdık bir şey, değil mi?
Veya ikinci dereceden binomlu bu örnek:
Tam bir kare seçin:
Ve doğrusal değiştirmeden sonra, daha önce tartışılan algoritma kullanılarak çözülen integrali elde ederiz.
Bir integralin kendisine nasıl indirgeneceğine ilişkin iki tipik örneğe daha bakalım:
– üstel çarpımın sinüs ile integrali;
– üstel sayının kosinüs ile çarpımının integrali.
Parçalara göre listelenen integrallerde iki kez integral almanız gerekecektir:
Örnek 7
Belirsiz integrali bulun
İntegral üstel sayının sinüsle çarpımıdır.
Parçalara göre iki kere integral alırız ve integrali kendisine indirgeriz: ![]()



Parçalara göre çift integrasyon sonucunda integral kendine indirgenmiştir. Çözümün başlangıcını ve sonunu eşitliyoruz:
İşaret değişikliği ile sola kaydırıp integralimizi ifade ediyoruz: 
Hazır. Aynı zamanda sağ tarafı da taramanız tavsiye edilir, yani. üssü parantezlerden çıkarın ve parantez içine sinüs ve kosinüsü "güzel" bir sıraya yerleştirin.
Şimdi örneğin başlangıcına, daha doğrusu parçalara göre entegrasyona geri dönelim:
Üssü olarak belirledik. Şu soru ortaya çıkıyor: Her zaman ile gösterilmesi gereken üs mü? Mutlaka değil. Aslında, ele alınan integralde temelde önemli değil, ne demek istiyoruz, diğer tarafa da gidebilirdik: 
Bu neden mümkün? Üstel kendisine dönüştüğü için (hem türev alma hem de integral alma sırasında), sinüs ve kosinüs karşılıklı olarak birbirine dönüşür (yine hem türev alma hem de integral alma sırasında).
Yani trigonometrik bir fonksiyonu da gösterebiliriz. Ancak ele alınan örnekte kesirler ortaya çıkacağından bu daha az rasyoneldir. Dilerseniz bu örneği ikinci yöntemle çözmeyi deneyebilirsiniz; cevapların eşleşmesi gerekir.
Örnek 8
Belirsiz integrali bulun
Bu kendi başınıza çözebileceğiniz bir örnektir. Karar vermeden önce, bu durumda üstel fonksiyon olarak mı yoksa trigonometrik fonksiyon olarak mı belirtilmenin daha avantajlı olduğunu düşünün. Dersin sonunda tam çözüm ve cevap.
Ve elbette, bu dersteki cevapların çoğunun farklılaştırma yoluyla kontrol edilmesinin oldukça kolay olduğunu unutmayın!
Ele alınan örnekler en karmaşık örnekler değildi. Pratikte, sabitin hem üste hem de trigonometrik fonksiyonun argümanında olduğu durumlarda integraller daha yaygındır, örneğin: . Birçok insanın böyle bir integral konusunda kafası karışacaktır ve benim de çoğu zaman kafam karışır. Gerçek şu ki, çözümde kesirlerin ortaya çıkma olasılığı yüksektir ve dikkatsizlik nedeniyle bir şeyi kaybetmek çok kolaydır. Ayrıca işaretlerde hata olasılığı yüksektir; üssün eksi işaretine sahip olduğunu ve bunun da ek zorluk yarattığını unutmayın.
Son aşamada sonuç genellikle şöyle olur:
Çözümün sonunda bile son derece dikkatli olmalı ve kesirleri doğru anlamalısınız: 
Karmaşık Kesirlerin İntegrallenmesi
Dersin ekvatoruna yavaş yavaş yaklaşıyoruz ve kesirlerin integrallerini düşünmeye başlıyoruz. Tekrar ediyorum, hepsi çok karmaşık değil; sadece şu ya da bu nedenle diğer makalelerdeki örnekler biraz "konu dışı"ydı.
Kökler temasına devam ediliyor
Örnek 9
Belirsiz integrali bulun
Kökün altındaki paydada ikinci dereceden bir üç terimli artı kökün dışında "X" şeklinde bir "ek" vardır. Bu türden bir integral, standart bir ikame kullanılarak çözülebilir.
Biz karar veriyoruz: ![]()
Buradaki değişim basittir: ![]()
Değişimden sonraki hayata bakalım: 
(1) Yer değiştirme işleminden sonra kök altındaki terimleri ortak bir paydaya indiririz.
(2) Onu kökün altından çıkarıyoruz.
(3) Pay ve payda azaltılır. Aynı zamanda kök altında terimleri uygun bir sıraya göre yeniden düzenledim. Biraz tecrübeyle, yorumlanan eylemleri sözlü olarak gerçekleştirerek (1), (2) adımları atlanabilir.
(4) Sonuçta ortaya çıkan integral, dersten hatırladığınız gibi Bazı Kesirlerin İntegrali, karar veriliyor tam kare çıkarma yöntemi. Tam bir kare seçin.
(5) İntegral yoluyla sıradan bir "uzun" logaritma elde ederiz.
(6) Ters değiştirme işlemini gerçekleştiriyoruz. Başlangıçta ise, sonra geri: .
(7) Son eylem, sonucu düzeltmeyi amaçlamaktadır: kök altında terimleri tekrar ortak bir paydaya getiriyoruz ve kökün altından çıkarıyoruz.
Örnek 10
Belirsiz integrali bulun ![]()
Bu kendi başınıza çözebileceğiniz bir örnektir. Burada tek "X"e bir sabit eklenir ve değiştirme neredeyse aynıdır: ![]()
Ek olarak yapmanız gereken tek şey, gerçekleştirilen değiştirme işlemindeki "x" i ifade etmektir: ![]()
Dersin sonunda tam çözüm ve cevap.
Bazen böyle bir integralin kökü altında ikinci dereceden bir binom bulunabilir, bu çözüm yöntemini değiştirmez, hatta daha basit olacaktır. Farkı hissedin:
Örnek 11
Belirsiz integrali bulun
Örnek 12
Belirsiz integrali bulun
Dersin sonunda kısa çözümler ve cevaplar. Örnek 11'in tam olarak aynı olduğuna dikkat edilmelidir. binom integraliÇözüm yöntemi sınıfta tartışılan İrrasyonel fonksiyonların integralleri.
2. dereceden ayrıştırılamaz bir polinomun üssüne integrali
(paydadaki polinom)
Daha nadir görülen bir integral türü, ancak yine de pratik örneklerde karşımıza çıkıyor.
Örnek 13
Belirsiz integrali bulun
Ama şanslı sayı 13 ile olan örneğe dönelim (dürüst olmak gerekirse doğru tahmin etmedim). Bu integral aynı zamanda nasıl çözeceğinizi bilmiyorsanız oldukça sinir bozucu olabilecek integrallerden biridir.
Çözüm yapay bir dönüşümle başlar: 
Sanırım herkes payın payda terimine göre nasıl bölüneceğini zaten anlıyor.
Ortaya çıkan integral parçalar halinde alınır: 

( – doğal sayı) formunun bir integrali için türetiyoruz tekrarlayan azaltma formülü:
, Nerede ![]() – daha düşük bir derecenin integrali.
– daha düşük bir derecenin integrali.
Çözülmüş integral için bu formülün geçerliliğini doğrulayalım.
Bu durumda: , , formülü kullanırız: 
Gördüğünüz gibi cevaplar aynı.
Örnek 14
Belirsiz integrali bulun
Bu kendi başınıza çözebileceğiniz bir örnektir. Örnek çözüm yukarıdaki formülü arka arkaya iki kez kullanır.
Derecenin altında ise bölünmez kare trinomial, daha sonra çözüm, mükemmel kareyi izole ederek bir binoma indirgenir, örneğin:
Payda ek bir polinom varsa ne olur? Bu durumda belirsiz katsayılar yöntemi kullanılır ve integral fonksiyonu kesirlerin toplamına genişletilir. Ama benim uygulamamda böyle bir örnek var hiç tanışmadım, bu yüzden makalede bu vakayı kaçırdım Kesirli-rasyonel fonksiyonların integralleri, şimdi bunu atlayacağım. Hala böyle bir integralle karşılaşırsanız, ders kitabına bakın - orada her şey basit. Karşılaşma olasılığı sıfıra düşen materyali (basit olanları bile) dahil etmenin uygun olduğunu düşünmüyorum.
Karmaşık trigonometrik fonksiyonların entegrasyonu
Çoğu örnek için "karmaşık" sıfatı yine büyük ölçüde koşulludur. Yüksek kuvvetlerdeki teğetler ve kotanjantlarla başlayalım. Kullanılan çözme yöntemleri açısından bakıldığında, teğet ve kotanjant hemen hemen aynı şeydir, bu yüzden teğet hakkında daha fazla konuşacağım, bu da integrali çözmek için gösterilen yöntemin kotanjant için de geçerli olduğunu ima ediyor.
Yukarıdaki derste inceledik evrensel trigonometrik ikame Trigonometrik fonksiyonların belirli türdeki integrallerini çözmek için. Evrensel trigonometrik ikamenin dezavantajı, kullanımının çoğu zaman zor hesaplamalara sahip hantal integrallerle sonuçlanmasıdır. Ve bazı durumlarda evrensel trigonometrik ikameden kaçınılabilir!
Başka bir kanonik örneği ele alalım: Birin integralinin sinüse bölümü:
Örnek 17
Belirsiz integrali bulun
Burada evrensel trigonometrik ikameyi kullanabilir ve cevaba ulaşabilirsiniz, ancak daha rasyonel bir yol var. Her adım için yorumlarla birlikte eksiksiz bir çözüm sunacağım:

(1) Çift açının sinüsü için trigonometrik formülü kullanırız.
(2) Yapay bir dönüşüm gerçekleştiriyoruz: Paydayı bölüp ile çarpıyoruz.
(3) Paydadaki iyi bilinen formülü kullanarak kesri teğete dönüştürürüz.
(4) Fonksiyonu diferansiyel işaretin altına getiriyoruz.
(5) İntegrali alın.
Kendi başınıza çözebileceğiniz birkaç basit örnek:
Örnek 18
Belirsiz integrali bulun
Not: İlk adım indirgeme formülünü kullanmak olmalıdır. ![]() ve önceki örneğe benzer eylemleri dikkatlice gerçekleştirin.
ve önceki örneğe benzer eylemleri dikkatlice gerçekleştirin.
Örnek 19
Belirsiz integrali bulun
Aslında bu çok basit bir örnek.
Dersin sonunda çözümleri ve cevapları tamamlayın.
Artık kimsenin integrallerle sorunu olmayacağını düşünüyorum: ![]() vesaire.
vesaire.
Yöntemin fikri nedir? Buradaki fikir, yalnızca teğetleri ve teğet türevini integral halinde düzenlemek için dönüşümleri ve trigonometrik formülleri kullanmaktır. Yani, değiştirmekten bahsediyoruz: ![]() . Örnek 17-19'da aslında bu değiştirmeyi kullandık, ancak integraller o kadar basitti ki eşdeğer bir işlemle - fonksiyonu diferansiyel işaretin altına alarak - başardık.
. Örnek 17-19'da aslında bu değiştirmeyi kullandık, ancak integraller o kadar basitti ki eşdeğer bir işlemle - fonksiyonu diferansiyel işaretin altına alarak - başardık.
Daha önce de belirttiğim gibi benzer bir mantık kotanjant için de yapılabilir.
Yukarıdaki değişikliğin uygulanması için resmi bir önkoşul da vardır:
Kosinüs ve sinüsün kuvvetlerinin toplamı negatif bir tamsayı ÇİFT sayıdır, Örneğin:
integral için – negatif bir tamsayı ÇİFT sayı.
! Not : eğer integral YALNIZCA bir sinüs veya YALNIZCA bir kosinüs içeriyorsa, o zaman integral aynı zamanda negatif tek derece olarak da alınır (en basit durumlar Örnekler No. 17, 18'dedir).
Bu kuralı temel alan birkaç anlamlı göreve daha bakalım:
Örnek 20
Belirsiz integrali bulun
Sinüs ve kosinüs kuvvetlerinin toplamı: 2 – 6 = –4, negatif bir tamsayı ÇİFT sayıdır; bu, integralin teğetlere ve onun türevine indirgenebileceği anlamına gelir: 
(1) Paydayı dönüştürelim.
(2) İyi bilinen formülü kullanarak şunu elde ederiz:
(3) Paydayı dönüştürelim.
(4) Formülü kullanıyoruz ![]() .
.
(5) Fonksiyonu diferansiyel işaretin altına getiriyoruz.
(6) Değiştirme işlemini gerçekleştiriyoruz. Daha deneyimli öğrenciler değiştirme işlemini gerçekleştiremeyebilir, ancak yine de teğeti bir harfle değiştirmek daha iyidir - kafanın karışma riski daha azdır.
Örnek 21
Belirsiz integrali bulun
Bu kendi başınıza çözebileceğiniz bir örnektir.
Orada bekleyin, şampiyonluk turları başlamak üzere =)
Çoğu zaman integrand bir "karmaşık nokta" içerir:
Örnek 22
Belirsiz integrali bulun ![]()
Bu integral başlangıçta bir teğet içerir ve bu da hemen zaten tanıdık bir düşünceye yol açar:

Her şey yukarıda tartışıldığı için yapay dönüşümü en başta ve geri kalan adımları yorumsuz bırakacağım.
Kendi çözümünüz için birkaç yaratıcı örnek:
Örnek 23
Belirsiz integrali bulun ![]()
Örnek 24
Belirsiz integrali bulun ![]()
Evet, elbette, sinüs ve kosinüsün güçlerini düşürebilir ve evrensel trigonometrik ikameyi kullanabilirsiniz, ancak teğetler aracılığıyla gerçekleştirilirse çözüm çok daha verimli ve daha kısa olacaktır. Dersin sonunda tam çözüm ve cevaplar
İntegralleri çözmek kolay bir iştir, ancak yalnızca seçilmiş birkaç kişi için. Bu makale integralleri anlamayı öğrenmek isteyen ancak onlar hakkında hiçbir şey bilmeyen veya neredeyse hiçbir şey bilmeyenler içindir. İntegral... Neden gerekli? Nasıl hesaplanır? Belirli ve belirsiz integraller nelerdir? İntegral için bildiğiniz tek kullanım, ulaşılması zor yerlerden yararlı bir şey elde etmek için integral simgesi şeklinde bir tığ işi kanca kullanmaksa, o zaman hoş geldiniz! İntegralleri nasıl çözeceğinizi ve neden onsuz yapamayacağınızı öğrenin.
"İntegral" kavramını inceliyoruz
Entegrasyon Eski Mısır'da biliniyordu. Elbette modern haliyle değil ama yine de. O zamandan bu yana matematikçiler bu konu üzerine pek çok kitap yazdılar. Özellikle kendilerini öne çıkardılar Newton Ve Leibniz ama şeylerin özü değişmedi. İntegraller sıfırdan nasıl anlaşılır? Mümkün değil! Bu konuyu anlamak için yine de matematiksel analizin temelleri hakkında temel bilgiye ihtiyacınız olacak. İntegralleri anlamak için gerekli olan bilgiler zaten bloğumuzda mevcut.
Belirsiz integral
Biraz fonksiyonumuz olsun f(x) .
Belirsiz integral fonksiyonu f(x) bu fonksiyon denir F(x) türevi fonksiyona eşit olan f(x) .
Başka bir deyişle, bir integral ters türev veya ters türevdir. Bu arada, makalemizde nasıl olduğunu okuyun.

Tüm sürekli fonksiyonlar için bir antiderivatif mevcuttur. Ayrıca, sabit bir farklılık gösteren fonksiyonların türevleri çakıştığından, antiderivatife sıklıkla sabit bir işaret eklenir. İntegrali bulma sürecine entegrasyon denir.
Basit örnek:

Temel fonksiyonların ters türevlerini sürekli hesaplamamak için bunları bir tabloya koymak ve hazır değerleri kullanmak uygundur:

Belirli integral
İntegral kavramıyla uğraşırken sonsuz küçük niceliklerle uğraşıyoruz. İntegral, bir şeklin alanını, düzgün olmayan bir cismin kütlesini, düzensiz hareket sırasında kat edilen mesafeyi ve çok daha fazlasını hesaplamaya yardımcı olacaktır. Bir integralin sonsuz sayıda sonsuz küçük terimin toplamı olduğu unutulmamalıdır.
Örnek olarak, bir fonksiyonun grafiğini hayal edin. Bir fonksiyonun grafiğiyle sınırlanan bir şeklin alanı nasıl bulunur?

İntegral kullanma! Fonksiyonun koordinat eksenleri ve grafiği ile sınırlanan eğrisel yamuğu sonsuz küçük parçalara bölelim. Bu şekilde şekil ince sütunlara bölünecektir. Sütunların alanlarının toplamı yamuğun alanı olacaktır. Ancak böyle bir hesaplamanın yaklaşık bir sonuç vereceğini unutmayın. Ancak segmentler ne kadar küçük ve dar olursa hesaplama da o kadar doğru olacaktır. Bunları uzunluğu sıfıra yakın olacak kadar azaltırsak, bölümlerin alanlarının toplamı şeklin alanına yönelecektir. Bu belirli bir integraldir ve şu şekilde yazılır:

a ve b noktalarına integralin sınırları denir.
 Bari Alibasov ve "İntegral" grubu
Bari Alibasov ve "İntegral" grubu Bu arada! Okuyucularımız için şimdi %10 indirim var.
Aptallar için integral hesaplama kuralları
Belirsiz integralin özellikleri
Belirsiz bir integral nasıl çözülür? Burada örnekleri çözerken işinize yarayacak belirsiz integralin özelliklerine bakacağız.
- İntegralin türevi integrale eşittir:

- Sabit, integral işaretinin altından çıkarılabilir:

- Toplamın integrali, integrallerin toplamına eşittir. Bu aynı zamanda fark için de geçerlidir:
Belirli bir integralin özellikleri
- Doğrusallık:

- İntegral sınırları değiştirilirse integralin işareti değişir:

- Şu tarihte: herhangi puan A, B Ve İle:

Belirli bir integralin bir toplamın limiti olduğunu zaten öğrenmiştik. Ancak bir örneği çözerken belirli bir değer nasıl elde edilir? Bunun için Newton-Leibniz formülü var:

İntegral çözme örnekleri
Aşağıda belirsiz integralleri bulmanın birkaç örneğini ele alacağız. Çözümün inceliklerini kendiniz çözmenizi ve net olmayan bir şey varsa yorumlarda sorular sormanızı öneririz.

Materyali güçlendirmek için integrallerin pratikte nasıl çözüldüğüne dair bir video izleyin. İntegral hemen verilmezse umutsuzluğa kapılmayın. Öğrenciler için profesyonel bir servisle iletişime geçin; kapalı bir yüzey üzerindeki herhangi bir üçlü veya eğri integral sizin gücünüz dahilinde olacaktır.
Aşağıdaki formül denir parça formülüne göre entegrasyon belirsiz integralde:
Parçalara göre entegrasyon formülünü uygulamak için integralin iki faktöre bölünmesi gerekir. Bunlardan biri ile gösterilir sen geri kalanı ikinci faktöre atıfta bulunur ve ile gösterilir. dv. Sonra farklılaşma yoluyla buluruz du ve entegrasyon - işlev v. Aynı zamanda sen dv- integrandın kolaylıkla entegre edilebilecek bir parçası.
Parçalara göre entegrasyon yöntemini kullanmak ne zaman faydalıdır? O zaman ne zaman integral şunları içerir :
1) - logaritmik fonksiyonlar ve ters trigonometrik fonksiyonlar ("yay" önekiyle), daha sonra, parçalara göre uzun süreli entegrasyon deneyimine dayanarak, bu fonksiyonlar şu şekilde gösterilir: sen;
2) , , - sinüs, kosinüs ve üs ile çarpılır P(X) x'te rastgele bir polinomdur, bu durumda bu işlevler şu şekilde gösterilir: dv ve polinom bitti sen;
3) , , , , bu durumda parçalara göre entegrasyon iki kez uygulanır.
İlk durum örneğini kullanarak parçalar halinde integral alma yönteminin değerini açıklayalım. İntegral işaretinin altındaki ifadenin logaritmik bir fonksiyon içermesine izin verin (bu örnek 1 olacaktır). Parçalara göre entegrasyon kullanılarak, böyle bir integral, yalnızca cebirsel fonksiyonların (çoğunlukla bir polinom), yani logaritmik veya ters trigonometrik bir fonksiyon içermeyen integralinin hesaplanmasına indirgenir. Dersin başında verilen parçalara göre entegrasyon formülünün kullanılması
ilk terimde (integral olmadan) logaritmik bir fonksiyon ve ikinci terimde (integral işareti altında) logaritma içermeyen bir fonksiyon elde ederiz. Cebirsel bir fonksiyonun integrali, işareti altında logaritmik veya ters trigonometrik bir fonksiyonun ayrı ayrı veya cebirsel bir faktörle birlikte bulunduğu integralden çok daha basittir.
Böylece, kullanarak parça formüllerine göre entegrasyon İntegral hemen gerçekleştirilmez: belirli bir integralin bulunması, başka bir integralin bulunmasına indirgenir. Parçalara göre entegrasyon formülünün anlamı, uygulanması sonucunda yeni integralin tablo halinde çıkması veya en azından orijinalinden daha basit hale gelmesidir.
Parçalara göre entegrasyon yöntemi, iki fonksiyonun çarpımını ayırt etmek için formülün kullanılmasına dayanır:
o zaman formda yazılabilir
dersin en başında verildi.
Fonksiyonu entegre ederek bulurken v bunun için sonsuz bir antiderivatif fonksiyon kümesi elde edilir. Parçalara göre entegrasyon formülünü uygulamak için bunlardan herhangi birini ve dolayısıyla keyfi bir sabite karşılık gelen olanı alabilirsiniz. İLE, sıfıra eşit. Bu nedenle fonksiyonu bulurken v keyfi sabit İLE girilmemelidir.
Parçalara göre entegrasyon yönteminin çok özel bir uygulaması vardır: İntegral işareti altındaki fonksiyonların derecesini azaltmak gerektiğinde antiderivatif fonksiyonları bulmak için tekrarlayan formüller türetmek için kullanılabilir. Derecenin azaltılması, örneğin sinüs ve kosinüs gibi fonksiyonlar için ikinciden büyük kuvvetlere ve bunların çarpımlarına yönelik tablo halinde integraller olmadığında gereklidir. Tekrarlayan formül, bir dizinin bir sonraki üyesini önceki üye aracılığıyla bulmaya yönelik bir formüldür. Belirtilen durumlarda, derecenin kademeli olarak düşürülmesiyle hedefe ulaşılır. Yani, eğer integral sinüs üzeri x'in dördüncü kuvveti ise, o zaman kısmi integral alarak sinüs üzeri üçüncü kuvvet için bir formül bulabilirsiniz, vb. Bu dersin son paragrafı açıklanan göreve ayrılmıştır.
Entegrasyonu parçalara göre birlikte uygulama
Örnek 1. Parçalara göre entegrasyon yöntemini kullanarak belirsiz integrali bulun:
Çözüm. İntegral ifadesinde - zaten bildiğimiz gibi makul bir şekilde şu şekilde gösterilebilecek logaritma: sen. Biz buna inanıyoruz.
Şunu buluruz (teorik referansın açıklamasında daha önce belirtildiği gibi, ilk terimde (integral olmadan) hemen bir logaritmik fonksiyon ve ikinci terimde (integral işareti altında) logaritma içermeyen bir fonksiyon elde ederiz::

Ve yine logaritma...
Örnek 2. Belirsiz integrali bulun:
Çözüm. İzin vermek , .
Logaritma karede mevcuttur. Bu, karmaşık bir fonksiyon olarak farklılaştırılması gerektiği anlamına gelir. Buluyoruz
,
.
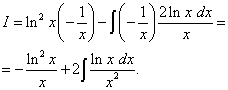
İkinci integrali tekrar parçalar halinde buluyoruz ve daha önce bahsedilen avantajı elde ediyoruz (ilk terimde (integral olmadan) logaritmik bir fonksiyon var ve ikinci terimde (integral işaretinin altında) bir fonksiyon içermeyen bir fonksiyon var) logaritma).
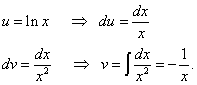

Orijinal integrali buluyoruz:

Örnek 3.
Çözüm. Arctanjant, logaritma gibi, şu şekilde daha iyi gösterilir: sen. Öyleyse izin ver.
Daha sonra ,
.
Parçalara göre entegrasyon formülünü uygulayarak şunu elde ederiz:
![]()
Bir değişkeni değiştirerek ikinci integrali buluruz.

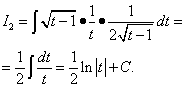
Değişkene geri dönelim X, alıyoruz
![]() .
.
Orijinal integrali buluyoruz:
![]() .
.
Örnek 4. Parçalara göre entegrasyon yöntemini kullanarak belirsiz integrali bulun:
Çözüm. Üssü şu şekilde belirtmek daha iyidir: dv. İntegrali iki faktöre ayırdık. Buna inanmak
Örnek 5. Parçalara göre entegrasyon yöntemini kullanarak belirsiz integrali bulun:
![]() .
.
Çözüm. İzin vermek , . Daha sonra , .
Parçalara göre entegrasyon formülünü (1) kullanarak şunları buluruz:
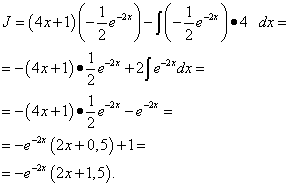
Örnek 6. Parçalara göre integral alarak belirsiz integrali bulun:
Çözüm. Üstel gibi sinüs de rahatlıkla şu şekilde gösterilebilir: dv. İzin vermek , .
Parçalara göre entegrasyon formülünü kullanarak şunları buluruz:
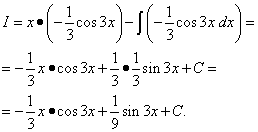
Tekrar parça parça entegrasyonu uyguluyoruz
Örnek 10. Parçalara göre integral alarak belirsiz integrali bulun:
![]() .
.
Çözüm. Tüm benzer durumlarda olduğu gibi, kosinüsü şu şekilde belirtmek uygundur: dv. ,'yi belirtiyoruz.
Daha sonra ![]() ,
.
,
.
Parçalara göre entegrasyon formülünü kullanarak şunu elde ederiz:
İkinci terime de parçalı integral uyguluyoruz. ,'yi belirtiyoruz.
Bu gösterimleri kullanarak söz konusu terimi entegre ederiz:

Şimdi gerekli integrali buluyoruz:

Parçalara göre entegrasyon yöntemiyle çözülebilen integraller arasında, teorik bölümde bahsedilen üç gruptan hiçbirine dahil olmayanlar da vardır; bunlar için pratikten şunu belirtmenin daha iyi olduğu bilinmektedir. sen ve ne aracılığıyla dv. Bu nedenle, bu durumlarda, “Parçalara göre entegrasyon yönteminin özü” paragrafında da verilen uygunluk hususunu kullanmanız gerekir: sen türev alma sırasında çok daha karmaşık hale gelmeyen integrandın bir parçası alınmalıdır, ancak dv- integrandın kolayca entegre edilebilecek bir parçası. Bu dersin son örneği böyle bir integralin çözümüdür.
Parçalara göre entegrasyon formülü şuna benzer:
.
Parçalara göre entegrasyon yöntemi bu formülün uygulanmasından oluşur. Pratik uygulamada u ve v'nin entegrasyon değişkeninin fonksiyonları olduğuna dikkat etmek önemlidir. İntegral değişkeninin x (integral gösterimin sonundaki d diferansiyel işaretinden sonraki sembol) olarak atanmasına izin verin. O halde u ve v, x'in fonksiyonlarıdır: u(x) ve v(x) .
Daha sonra
, .
Ve parçalara göre entegrasyon formülü şu şekli alır:
.
Yani integrand fonksiyonu iki fonksiyonun çarpımından oluşmalıdır:
,
bunlardan birini u olarak gösteririz: g(x) = u ve diğeri için integralin hesaplanması gerekir (daha kesin olarak antiderivatifin bulunması gerekir):
, o zaman dv = f(x) dx .
Bazı durumlarda f(x) = 1
.
,
Yani integralde
g(x) = u, x = v koyabiliriz.
Sürdürmek
;
.
Dolayısıyla bu yöntemde parçalara göre entegrasyon formülünün iki şekilde hatırlanması ve uygulanması gerekir:
Parçalara göre entegrasyonla hesaplanan integraller
Logaritmalar ve ters trigonometrik (hiperbolik) fonksiyonlar içeren integraller
Logaritmalar ve ters trigonometrik veya hiperbolik fonksiyonlar içeren integraller genellikle parçalara göre entegre edilir. Bu durumda logaritma veya ters trigonometrik (hiperbolik) fonksiyonları içeren kısım u, geri kalan kısım ise dv ile gösterilir.
, , , , , , .
Parçalara göre entegrasyon yöntemiyle hesaplanan bu tür integrallerin örnekleri şunlardır:
Bir polinom ile sin x, cos x veya e x'in çarpımını içeren integraller
, , ,
burada P(x), x'te bir polinomdur. İntegral alırken, P(x) polinomu u ve e ax dx ile gösterilir,çünkü balta dx veya günah baltası dx
- dv aracılığıyla.
, , .
İşte bu tür integrallerin örnekleri:
Parçalara göre entegrasyon yöntemini kullanarak integral hesaplama örnekleri
Logaritma ve ters trigonometrik fonksiyonlar içeren integral örnekleri
Örnek
İntegrali hesaplayın:
Detaylı çözüm
Burada integral bir logaritma içerir. Oyuncu değişikliği yapma sen =,
x olarak dv = x.
Daha sonra
,
.
2 dx
.
Daha sonra
.
Kalan integrali hesaplıyoruz:
Belirsiz integral tüm antiderivatiflerin kümesi olduğundan, hesaplamaların sonuna C sabitini eklemek gerekir. Ara hesaplamalara da eklenebilir, ancak bu yalnızca hesaplamaları karmaşık hale getirir.
Daha kısa çözüm
.Çözümü daha kısa bir versiyonda sunabilirsiniz. Bunu yapmak için u ve v ile değişiklik yapmanıza gerek yoktur ancak ikinci formdaki faktörleri gruplandırıp parçalara göre entegrasyon formülünü uygulayabilirsiniz.
Cevap
Logaritma ve ters trigonometrik fonksiyonlar içeren integral örnekleri
Örnek
.
Bir polinom ile sin x, cos x veya ex'in çarpımını içeren integral örnekleri
Çözüm
Diferansiyel işaretinin altındaki üssü tanıtalım:.
e - x dx = - e - x d(-x) = - d(e - x)
.
Parçalara göre integral alalım.
.
.
.
Parçalara göre entegrasyon yöntemini de kullanıyoruz.
Sonunda elimizde. Parçalara göre entegrasyon
- İntegrallerden birinin kolayca integrallenebildiği ve diğerinin türevlenebildiği belirli ve belirsiz integralleri çözmek için kullanılan bir yöntem. Hem belirsiz hem de belirli integralleri bulmak için oldukça yaygın bir yöntem. Kullanmanız gerektiğinde ana işaret, doğrudan entegre edilemeyen iki fonksiyonun çarpımından oluşan belirli bir fonksiyondur.
Formül
Bu yöntemi başarılı bir şekilde kullanabilmek için formülleri anlayıp öğrenmeniz gerekmektedir.
Belirsiz integralde parçalara göre entegrasyon formülü:
$$ \int udv = uv - \int vdu $$
Belirli bir integralde parçalara göre entegrasyon formülü:
$$ \int \limits_(a)^(b) udv = uv \bigg |_(a)^(b) - \int \limits_(a)^(b) vdu $$
Çözüm örnekleri
| Testler sırasında öğretmenler tarafından sıklıkla önerilen, parçalara göre entegrasyon çözümlerinin pratik örneklerini ele alalım. Lütfen integral sembolünün altında iki fonksiyonun çarpımının bulunduğunu unutmayın. Bu da bu yöntemin çözüme uygun olduğunun göstergesidir. |
| Örnek 1 |
| $ \int xe^xdx $ integralini bulun |
|
İntegralin iki fonksiyondan oluştuğunu görüyoruz; bunlardan biri farklılaştığında anında birliğe dönüşüyor, diğeri ise kolayca entegre olabiliyor. İntegrali çözmek için parçalara göre entegrasyon yöntemini kullanırız. $ u = x \rightarrow du=dx $ ve $ dv = e^x dx \rightarrow v=e^x $ olduğunu varsayalım. Bulunan değerleri ilk entegrasyon formülüne koyarız ve şunu elde ederiz: $$ \int xe^x dx = xe^x - \int e^x dx = xe^x - e^x + C $$ Sorununuzu çözemezseniz bize gönderin. Detaylı çözüm sunacağız. Hesaplamanın ilerlemesini görüntüleyebilecek ve bilgi alabileceksiniz. Bu, öğretmeninizden notunuzu zamanında almanıza yardımcı olacaktır! |
| Cevap |
|
$$ \int xe^x dx = xe^x - e^x + C $$ |
| Örnek 4 |
| $ \int \limits_0 ^1 (x+5) 3^x dx $ integralini hesaplayın |
| $ \int xe^xdx $ integralini bulun |
|
Önceki çözülmüş örneklere benzeterek, hangi fonksiyonun sorunsuz bir şekilde entegre edileceğini, hangilerinin farklılaştırılacağını bulacağız. $ (x+5) $'ın türevini alırsak bu ifadenin otomatik olarak birliğe dönüşeceğini lütfen unutmayın, bu da bizim avantajımıza olacaktır. Yani bunu yapıyoruz: $$ u=x+5 \rightarrow du=dx, dv=3^x dx \rightarrow v=\frac(3^x)(ln3) $$ Artık tüm bilinmeyen fonksiyonlar bulunmuştur ve belirli bir integral için parçalara göre entegrasyon için ikinci formüle yerleştirilebilir. $$ \int \limits_0 ^1 (x+5) 3^x dx = (x+5) \frac(3^x)(\ln 3) \bigg |_0 ^1 - \int \limits_0 ^1 \frac (3^x dx)(\ln 3) = $$ $$ = \frac(18)(\ln 3) - \frac(5)(\ln 3) - \frac(3^x)(\ln^2 3)\bigg| _0 ^1 = \frac(13)(\ln 3) - \frac(3)(\ln^2 3)+\frac(1)(\ln^2 3) = \frac(13)(\ln 3 )-\frac(4)(\ln^2 3) $$ |
| Cevap |
| $$ \int\limits_0 ^1 (x+5)3^x dx = \frac(13)(\ln 3)-\frac(4)(\ln^2 3) $$ |








