Belirli integral ve hesaplama yöntemleri. Kesin integral

Yamuk yöntemi

Ana makale:Yamuk yöntemi

Kısmi parçaların her birindeki fonksiyona sonlu değerlerden geçen bir doğru ile yaklaşılırsa yamuk yöntemi elde edilir.

Her segmentteki yamuğun alanı:

Her segmentteki yaklaşım hatası:

Nerede

Tüm entegrasyon aralığının eşit uzunlukta parçalara bölünmesi durumunda yamukların tam formülü:

Nerede

Yamuk formül hatası:

Nerede

Simpson'ın yöntemi.

İntegrand f(x) ikinci dereceden bir enterpolasyon polinomu ile değiştirilir P(x)– örneğin şekilde gösterildiği gibi üç düğümden geçen bir parabol ((1) – fonksiyon, (2) – polinom).

Entegrasyonun iki adımını ele alalım ( H= sabit = x i+1 – x i), yani üç düğüm x 0, x 1, x 2 Newton denklemini kullanarak bir parabol çiziyoruz:

İzin vermek z = x - x 0,
Daha sonra

Şimdi elde edilen ilişkiyi kullanarak bu aralıktaki integrali hesaplıyoruz:

.
İçin üniforma örgü Ve çift ​​adım sayısı n Simpson formülü şu şekli alır:

Burada , A integralin dördüncü türevinin sürekliliği varsayımı altında.

[düzenlemek] Arttırılmış doğruluk

Bir fonksiyonun tüm entegrasyon aralığı boyunca tek bir polinomla yaklaştırılması, kural olarak, integralin değerinin tahmin edilmesinde büyük bir hataya yol açar.

Hatayı azaltmak için entegrasyon segmenti parçalara bölünür ve her birinin üzerindeki integrali değerlendirmek için sayısal bir yöntem kullanılır.

Bölümlerin sayısı sonsuza yaklaştıkça, integralin tahmini, herhangi bir sayısal yöntem için analitik fonksiyonlar için gerçek değerine yönelir.

Yukarıdaki yöntemler, adımın yarıya indirilmesine yönelik basit bir prosedüre izin verir; her adım, işlev değerlerinin yalnızca yeni eklenen düğümlerde hesaplanmasını gerektirir. Hesaplama hatasını tahmin etmek için Runge kuralı kullanılır.

Runge kuralının uygulanması

düzenle]Belirli bir integralin hesaplanmasının doğruluğunun değerlendirilmesi

İntegral, seçilen formül (dikdörtgenler, yamuklar, Simpson parabolleri) kullanılarak adım sayısı n'ye eşit ve ardından adım sayısı 2n'ye eşit olacak şekilde hesaplanır. İntegralin değerinin 2n'ye eşit adım sayısıyla hesaplanmasındaki hata Runge formülü ile belirlenir:
, dikdörtgen ve yamuk formülleri ve Simpson formülü için.
Böylece integral, adım sayısının ardışık değerleri için hesaplanır; burada n 0, başlangıç ​​adım sayısıdır. Hesaplama işlemi, ε'nun belirtilen doğruluk olduğu bir sonraki N değeri için koşul sağlandığında sona erer.

Hata davranışının özellikleri.

Basitçe entegrasyon adım boyutunu azaltarak yüksek doğruluk elde edebileceksek neden farklı entegrasyon yöntemlerini analiz edelim? Bununla birlikte, son hatanın davranışının grafiğini göz önünde bulundurun R sayısal hesaplamanın sonuçları ve numaradan N aralığın bölümleri (yani, adım . Bölüm (1)'de, adım h'deki bir azalmaya bağlı olarak hata azalır. Ancak bölüm (2)'de, çok sayıda aritmetik işlemin sonucu olarak biriken hesaplama hatası hakim olmaya başlar. , her yöntemin kendine ait bir yöntemi var Rmin, birçok faktöre bağlıdır, ancak öncelikle yöntem hatasının önsel değerine bağlıdır R.

Romberg'in açıklayıcı formülü.

Romberg'in yöntemi, integralin değerini, bölüm sayısında çoklu bir artışla sıralı olarak hassaslaştırmaktan oluşur. Düzgün adımlarla yamuk formülü temel alınabilir H.
İntegrali bölüm sayısıyla gösterelim N= 1 olarak .
Adımı yarı yarıya azaltarak şunu elde ederiz: .
Adımı art arda 2 n kat azaltırsak, hesaplama için bir yineleme ilişkisi elde ederiz.

Uygulama değeri ortalama değer teoremleri belirli bir integralin değerini hesaplamadan niteliksel bir tahmin elde etme olasılığında yatmaktadır. Hadi formüle edelim : Bir fonksiyon bir aralıkta sürekli ise, o zaman bu aralığın içinde öyle bir nokta vardır ki .

Bu formül, karmaşık veya hantal bir fonksiyonun integralini kabaca tahmin etmek için oldukça uygundur. Formülü oluşturan tek nokta yaklaşık bir zorunluluktur bağımsız seçim noktalar En basit yolu - entegrasyon aralığının ortasını - seçersek (bazı ders kitaplarında önerildiği gibi), o zaman hata oldukça önemli olabilir. Daha doğru bir sonuç elde etmek için öneririz hesaplamayı aşağıdaki sırayla gerçekleştirin:

Aralıktaki bir fonksiyonun grafiğini oluşturun;

Fonksiyon grafiğinin kesilen kısımları eşit olacak şekilde dikdörtgenin üst sınırını çizin. alanı yaklaşık olarak eşit (yukarıdaki şekilde gösterilen şey tam olarak budur - iki eğrisel üçgen neredeyse aynıdır);

Şekilden belirleyin;

Ortalama değer teoremini kullanın.

Örnek olarak basit bir integrali hesaplayalım:

Kesin değer ;

Aralığın ortası için aynı zamanda yaklaşık bir değer de elde ederiz; açıkça yanlış sonuç;

Önerilere uygun olarak çizilen dikdörtgenin üst kenarı ile bir grafik oluşturarak yaklaşık değeri elde ederiz. Oldukça tatmin edici bir sonuç, hata %0,75'tir.

Yamuk formülü

Ortalama değer teoremini kullanan hesaplamaların doğruluğu, gösterildiği gibi, önemli ölçüde şunlara bağlıdır: görsel amaç puan çizelgesine göre. Nitekim aynı örnekte veya noktalarını seçerek integralin diğer değerlerini elde edebilirsiniz ve hata artabilir. Öznel faktörler, grafiğin ölçeği ve çizimin kalitesi sonucu büyük ölçüde etkiler. Bu kabul edilemez kritik hesaplamalarda, dolayısıyla ortalama değer teoremi yalnızca hızlı hesaplamalara uygulanır kalite integral tahminleri.

Bu bölümde yaklaşık integralin en popüler yöntemlerinden birini ele alacağız - yamuk formülü . Bu formülü oluşturmanın ana fikri, şekilde gösterildiği gibi eğrinin yaklaşık olarak kesikli bir çizgi ile değiştirilebileceği gerçeğine dayanmaktadır.

Kesinlik sağlamak için (ve şekle uygun olarak) integrasyon aralığının aşağıdakilere bölündüğünü varsayalım: eşit (bu isteğe bağlıdır, ancak çok kullanışlıdır) parçalar. Bu parçaların her birinin uzunluğu formülle hesaplanır ve denir. adım . Bölme noktalarının apsisleri, eğer verilmişse, formülle belirlenir; burada . Bilinen apsisleri kullanarak koordinatları hesaplamak kolaydır. Böylece,

Bu durum için yamuk formülüdür. Parantez içindeki ilk terimin, tüm ara koordinatların eklendiği başlangıç ​​ve son koordinatların yarı toplamı olduğuna dikkat edin. Entegrasyon aralığının isteğe bağlı sayıda bölümü için yamuk için genel formül şu forma sahiptir: karesel formüller: dikdörtgenler, Simpson, Gaussian, vb. Çeşitli şekillerdeki temel alanlarla eğrisel bir yamuğu temsil etme fikrine dayanırlar, bu nedenle yamuk formülüne hakim olduktan sonra benzer formülleri anlamak zor olmayacaktır. Pek çok formül yamuk formülü kadar basit değildir ancak az sayıda bölmeyle yüksek doğrulukta sonuçlar elde etmenize olanak sağlar.

Yamuk formülünü (veya benzerlerini) kullanarak, hem "gerçekleştirilemeyen" integralleri hem de karmaşık veya hantal fonksiyonların integrallerini pratikte gereken doğrulukla hesaplamak mümkündür.

Belirli bir integralle sürekli bir fonksiyondan F(X) son segmentte [ A, B] (burada ) bu segmentteki bazı antitürevlerinin artışıdır. (Genel olarak belirsiz integral konusunu tekrarlarsanız anlayış gözle görülür şekilde daha kolay olacaktır) Bu durumda notasyon kullanılır

Aşağıdaki grafiklerde görülebileceği gibi (antiderivatif fonksiyonun artışı ile gösterilmiştir), Belirli bir integral pozitif ya da negatif bir sayı olabilir(Anttürevin üst limitteki değeri ile alt limitteki değeri arasındaki fark olarak hesaplanır; F(B) - F(A)).

Sayılar A Ve B sırasıyla entegrasyonun alt ve üst sınırları olarak adlandırılır ve segment [ A, B] – entegrasyon segmenti.

Böylece eğer F(X) – bazı antiderivatif fonksiyonlar F(X), o zaman tanıma göre,

(38)

Eşitlik (38) denir Newton-Leibniz formülü . Fark F(B) – F(A) kısaca şu şekilde yazılır:

Bu nedenle Newton-Leibniz formülünü şu şekilde yazacağız:

(39)

Belirli integralin, hesaplanırken integralin hangi antitürevinin alındığına bağlı olmadığını kanıtlayalım. İzin vermek F(X) ve F( X) integralin keyfi antitürevleridir. Bunlar aynı fonksiyonun ters türevleri olduğundan sabit bir terimle farklılık gösterirler: Ф( X) = F(X) + C. Bu yüzden

Bu, segmentte şunu belirler: [ A, B] fonksiyonun tüm ters türevlerinin artışları F(X) eşleştir.

Bu nedenle, belirli bir integrali hesaplamak için integralin herhangi bir antitürevini bulmak gerekir; İlk önce belirsiz integrali bulmanız gerekir. Devamlı İLE sonraki hesaplamalara dahil edilmemiştir. Daha sonra Newton-Leibniz formülü uygulanır: üst limitin değeri ters türev fonksiyonuna yerleştirilir B , ayrıca - alt sınırın değeri A ve fark hesaplanır F(b) - F(a) . Ortaya çıkan sayı belirli bir integral olacaktır..

Şu tarihte: A = B tanım gereği kabul edildi

Örnek 1.

Çözüm. İlk önce belirsiz integrali bulalım:

Newton-Leibniz formülünün antiderivatife uygulanması

(saatte İLE= 0), şunu elde ederiz

Ancak belirli bir integral hesaplanırken antiderivatifi ayrı ayrı bulmak değil, integrali hemen (39) formuna yazmak daha iyidir.

Örnek 2. Belirli integrali hesaplayın

Çözüm. Formül kullanma

Belirli integralin özellikleri

Teorem 2.Belirli integralin değeri, integral değişkeninin tanımına bağlı değildir, yani

(40)

İzin vermek F(X) – için antiderivatif F(X). İçin F(T) antiderivatif aynı fonksiyondur F(T), burada bağımsız değişken yalnızca farklı şekilde belirtilir. Buradan,

Formül (39)'a göre son eşitlik, integrallerin eşitliği anlamına gelir.

Teorem 3.Sabit faktör belirli integralin işaretinden çıkarılabilir, yani

(41)

Teorem 4.Sonlu sayıda fonksiyonun cebirsel toplamının belirli integrali, bu fonksiyonların belirli integrallerinin cebirsel toplamına eşittir, yani

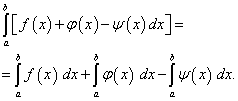(42)

Teorem 5.Bir integral parçası parçalara ayrılırsa, parçanın tamamı üzerindeki belirli integral, parçaları üzerindeki belirli integrallerin toplamına eşittir, yani Eğer

(43)

Teorem 6.İntegral limitleri yeniden düzenlenirken belirli integralin mutlak değeri değişmez, yalnızca işareti değişir, yani

(44)

Teorem 7(ortalama değer teoremi). Belirli bir integral, integral parçasının uzunluğu ile integralin içindeki bir noktadaki değerinin çarpımına eşittir., yani

(45)

Teorem 8.İntegralin üst sınırı alt sınırdan büyükse ve integral negatif değilse (pozitif), o zaman belirli integral de negatif değildir (pozitif), yani. Eğer

Teorem 9.İntegralin üst sınırı alt sınırdan büyükse ve fonksiyonlar sürekli ise eşitsizlik

dönem dönem entegre edilebilir, yani

(46)

Belirli integralin özellikleri, integrallerin doğrudan hesaplanmasını basitleştirmeyi mümkün kılar.

Örnek 5. Belirli integrali hesaplayın

Teorem 4 ve 3'ü kullanarak ve antitürevleri - tablo integralleri (7) ve (6) bulurken, şunu elde ederiz:

Değişken üst limitli belirli integral

İzin vermek F(X) – segmentte sürekli [ A, B] işlevi ve F(X) onun terstürevidir. Belirli integrali düşünün

(47)

Ve aracılığıyla T entegrasyon değişkeni üst sınırla karıştırılmayacak şekilde belirlenir. Değiştiğinde X belirli integral (47) de değişir, yani. entegrasyonun üst sınırının bir fonksiyonudur X ile gösterdiğimiz F(X), yani.

(48)

Fonksiyonun olduğunu kanıtlayalım F(X) için bir ters türevdir F(X) = F(T). Aslında farklılaşan F(X), elde ederiz

Çünkü F(X) – için antiderivatif F(X), A F(A) sabit bir değerdir.

İşlev F(X) – sonsuz sayıda antiderivatiften biri F(X), yani X = A sıfıra gider. Bu ifade, (48) eşitliğini koyarsak elde edilir. X = A ve önceki paragraftaki Teorem 1'i kullanın.

Belirli integrallerin parçalara göre entegrasyon yöntemi ve değişken değişimi yöntemiyle hesaplanması

tanım gereği nerede, F(X) – için antiderivatif F(X). İntegraldeki değişkeni değiştirirsek

o zaman formül (16)'ya uygun olarak şunu yazabiliriz:

Bu ifadede

için antiderivatif fonksiyon

Aslında ona göre türevi karmaşık fonksiyonların türevlenmesi kuralı, eşittir

α ve β değişkenin değerleri olsun T, bunun için fonksiyon

değerleri buna göre alır A Ve B, yani

Ancak Newton-Leibniz formülüne göre fark F(B) – F(A) Orada

Teorem. Eğer fonksiyon f(x) aralıkta integrallenebilir [ a, b], Nerede A< b ve herkes için x ∈ eşitsizlik geçerli

Teoremdeki eşitsizlikler kullanılarak belirli integral tahmin edilebilir; anlamının kapsandığı sınırları gösterir. Bu eşitsizlikler belirli integralin bir tahminini ifade eder.

Teorem [Ortalama Teoremi]. Eğer fonksiyon f(x) aralıkta integrallenebilir [ a, b] ve herkes için x ∈ eşitsizlikler giderildi m ≤ f(x) ≤ M, O

Nerede m ≤ μ ≤ M.

Yorum. Fonksiyonun olması durumunda f(x) aralıkta süreklidir [ a, b], teoremden eşitlik şu şekli alır:

Nerede c ∈. Sayı μ=f(c) Bu formülle tanımlanana denir ortalama değer işlevler f(x) segmentte [ a, b] Bu eşitlik aşağıdakilere sahiptir geometrik anlamı: sürekli bir çizgiyle sınırlanan kavisli bir yamuğun alanı y=f(x) (f(x) ≤ 0), aynı tabana ve yüksekliğe sahip bir dikdörtgenin alanına, bu doğru üzerindeki bir noktanın koordinatına eşittir.

Sürekli bir fonksiyonun antiderivatifinin varlığı

İlk olarak üst limiti değişken olan integral kavramını tanıtıyoruz.

Fonksiyona izin ver f(x) aralıkta integrallenebilir [ a, b] O zaman sayı ne olursa olsun X itibaren [ a, b], işlev f(x) aralıkta integrallenebilir [ a, b] Bu nedenle aralıkta [ a, b] fonksiyon tanımlı

buna değişken üst limitli integral denir.

Teorem. İntegral aralıkta sürekli ise [ a, b], bu durumda değişken üst limitli belirli bir integralin türevi vardır ve bu limit için integralin değerine eşittir, yani

Sonuçlar. Değişken bir üst limite sahip belirli bir integral, sürekli bir integralin antiderivatiflerinden biridir. Başka bir deyişle, bir aralıkta sürekli olan herhangi bir fonksiyonun bir antiderivatifi vardır.

Not 1. Eğer fonksiyon f(x) aralıkta integrallenebilir [ a, b] ise, üst limiti değişken olan integral, bu segmentte sürekli olan üst limitin bir fonksiyonudur. Aslında, St.2'den ve sahip olduğumuz ortalama değer teoreminden

Not 2. Değişken üst limitli integral, birçok yeni fonksiyonun tanımında kullanılır, örneğin, . Bu işlevler temel değildir; daha önce belirtildiği gibi, belirtilen integrallerin ters türevleri temel işlevler aracılığıyla ifade edilmez.

Entegrasyonun temel kuralları

Newton-Leibniz formülü

Herhangi iki antiderivatif fonksiyon olduğundan f(x) bir sabit kadar farklılık gösteriyorsa, önceki teoreme göre herhangi bir antiderivatifin olduğu iddia edilebilir. Φ(x) segmentte sürekli [ a, b] işlevler f(x) benziyor

Nerede C- biraz sabit.

Bu formülde varsayarsak x=a Ve x=b, st.1 belirli integralleri kullanarak şunu buluruz:

Bu eşitlikler ilişkiyi ima eder

buna denir Newton-Leibniz formülü.

Böylece aşağıdaki teoremi kanıtladık:

Teorem. Sürekli bir fonksiyonun belirli integrali, üst ve alt entegrasyon limitleri için antitürevlerinden herhangi birinin değerleri arasındaki farka eşittir.

Newton-Leibniz formülü şu şekilde yeniden yazılabilir:

Belirli bir integraldeki değişkeni değiştirme

Teorem. Eğer

• işlev f(x) aralıkta süreklidir [ a, b];
• çizgi segmenti [ a, b] fonksiyon değerlerinin kümesidir φ(t), segmentte tanımlanmış α ≤ t ≤ β ve üzerinde sürekli bir türev bulunan;
• φ(α)=a, φ(β)=b

o halde formül doğrudur

Parçalara göre entegrasyon formülü

Teorem. Eğer işlevler u=u(x), v=v(x) aralıkta sürekli türevler var [ a, b] ise formül geçerlidir

Daha önce belirli bir integrali, integralin antiderivatifinin değerlerindeki fark olarak değerlendirmiştik. İntegralin, entegrasyon aralığında bir ters türevine sahip olduğu varsayılmıştır.

Antiderivatifin temel fonksiyonlarla ifade edilmesi durumunda varlığından emin olabiliriz. Ancak böyle bir ifade yoksa, o zaman bir antiderivatifin varlığı sorusu açık kalır ve karşılık gelen belirli integralin var olup olmadığını bilmiyoruz.

Geometrik değerlendirmeler, örneğin y=e^(-x^2) fonksiyonu için antiderivatifi temel fonksiyonlarla ifade etmenin imkansız olmasına rağmen, integralin \textstyle(\int\limits_(a)^(b)e^(-x^2)\,dx) vardır ve x ekseni, y=e^(-x^2) fonksiyonunun grafiği ve x=a,~ x=b düz çizgileriyle sınırlı olan şeklin alanına eşittir (Şekil 6). ). Ancak daha titiz bir analizle, alan kavramının gerekçelendirilmesi gerektiği ve bu nedenle bir antiderivatifin ve belirli bir integralin varlığına ilişkin soruları çözerken ona güvenilemeyeceği ortaya çıkıyor.

Hadi bunu kanıtlayalım Bir aralıkta sürekli olan herhangi bir fonksiyonun bu aralıkta bir ters türevi vardır ve dolayısıyla bu parça üzerinde belirli bir integrali var. Bunu yapmak için belirli integral kavramına karşı bir antitürevin varlığı varsayımına dayanmayan farklı bir yaklaşıma ihtiyacımız var.

Önce bazılarını kuralım belirli bir integralin özellikleri, antiderivatifin değerleri arasındaki fark olarak anlaşılır.

Belirli integrallerin tahminleri

Teorem 1. y=f(x) fonksiyonunun aralıkta sınırlı olmasına izin verin ve m=\min_(x\in)f(x) Ve M=\max_(x\in)f(x) y=f(x) fonksiyonunun sırasıyla en küçük ve en büyük değerleri üzerindedir ve bu segmentte y=f(x) fonksiyonunun bir antiderivatifi vardır. Daha sonra

m(b-a)\leqslant \int\limits_(a)^(b)f(x)\,dx\leqslant M(b-a).

Kanıt. F(x), parça üzerindeki y=f(x) fonksiyonunun ters türevlerinden biri olsun. Daha sonra

\int\limits_(a)^(b)f(x)\,dx=\Bigl.(F(x))\Bigr|_(a)^(b)=F(b)-F(a).

Lagrange teoremine göre F(b)-F(a)=F"(c)(b-a), burada bir \int\limits_(a)^(b)f(x)\,dx=f(c)(b-a).

Koşula göre, segmentteki x'in tüm değerleri için aşağıdaki eşitsizlik geçerlidir: m\leqslant f(x)\leqslant M, Bu yüzden m\leqslant f(c)\leqslant M ve bu nedenle

m(b-a)\leqslant f(c)(b-a)\leqslant M(b-a), yani m(b-a)\leqslant \int\limits_(a)^(b)f(x)\,dx\leqslant M(b-a),

Q.E.D.

Çift eşitsizlik (1), belirli integralin değeri için yalnızca çok kaba bir tahmin verir. Örneğin bir doğru parçası üzerinde y=x^2 fonksiyonunun değerleri 1 ile 25 arasındadır ve bu nedenle eşitsizlikler meydana gelir.

4=1\cdot(5-1)\leqslant \int\limits_(1)^(5)x^2\,dx\leqslant 25\cdot(5-1)=100.

Daha doğru bir tahmin elde etmek için segmenti noktalarla birkaç parçaya bölün a=x_0 ve eşitsizlik (1) her parçaya uygulanır. Eşitsizlik segmentte geçerliyse, o zaman

m_k\cdot\Delta x_k\leqslant \int\limits_(x_k)^(x_(k+1)) f(x)\,dx\leqslant M_k\cdot \Delta x_k\,

burada \Delta x_k farkı (x_(k+1)-x_k), yani parçanın uzunluğunu belirtir. Bu eşitsizlikleri 0'dan n-1'e kadar tüm k değerleri için yazıp topladığımızda şunu elde ederiz:

\sum_(k=0)^(n-1)(m_k\cdot\Delta x_k) \leqslant \sum_(k=0)^(n-1) \int\limits_(x_k)^(x_(k+1) ))f(x)\,dx\leqslant \sum_(k=0)^(n-1) (M_k\cdot \Delta x_k),

Ancak belirli bir integralin toplama özelliğine göre, parçanın tüm kısımları üzerindeki integrallerin toplamı, bu parça üzerindeki integrale eşittir, yani.

\sum_(k=0)^(n-1) \int\limits_(x_k)^(x_(k+1))f(x)\,dx= \int\limits_a)^(b)f(x) \,dx\,.

Araç,

\sum_(k=0)^(n-1)(m_k\cdot\Delta x_k) \leqslant \sum_(k=0)^(n-1) \int\limits_(a)^(b)f(x) )\,dx\leqslant \sum_(k=0)^(n-1) (M_k\cdot \Delta x_k)

Örneğin, bir doğru parçasını her birinin uzunluğu 0,4 olan 10 eşit parçaya bölerseniz, o zaman kısmi bir parça üzerinde eşitsizlik geçerli

(1+0,\!4k)^2\leqslant x^2\leqslant \bigl(1+0,\!4(k+1)\bigr)^2

Bu nedenle elimizde:

0,\!4\sum_(k=0)^(9)(1+0,\!4k)^2\leqslant \int\limits_(1)^(5)x^2\,dx\leqslant 0, \!4\sum_(k=0)^(9)\bigl(1+0,\!4(k+1)\bigr)^2.

Hesaplayarak şunu elde ederiz: 36,\!64\leqslant \int\limits_(1)^(5) x^2\,dx\leqslant 46,\!24. Bu tahmin daha önce elde edilenlerden çok daha doğrudur 4\leqslant\int\limits_(1)^(5)x^2\,dx\leqslant100.

İntegralin daha da doğru bir tahminini elde etmek için, segmenti 10'a değil, örneğin 100 veya 1000 parçaya bölmeniz ve karşılık gelen toplamları hesaplamanız gerekir. Elbette bu integralin terstürevi kullanılarak hesaplanması daha kolaydır:

\int\limits_(1)^(5)x^2\,dx= \left.(\frac(x^3)(3))\right|_(1)^(5)= \frac(1) (3)(125-1)= \frac(124)(3)\,.

Ancak antitürevin ifadesi bizim için bilinmiyorsa, o zaman eşitsizlikler (2), integralin değerini aşağıdan ve yukarıdan tahmin etmeyi mümkün kılar.

Bölen sayı olarak belirli integral

Eşitsizlikte (2) yer alan m_k ve M_k sayıları, eşitsizlik her bir parça üzerinde geçerli olduğu sürece keyfi olarak seçilebilir. m_k\leqslant f(x)\leqslant M_k. Parçanın belirli bir bölümü için integralin en doğru tahmini, M_k'yi mümkün olan tüm değerlerin en küçüğü ve m_k'yi en büyüğü olarak alırsak elde edilir. Bu, m_k olarak segment üzerindeki y=f(x) fonksiyonunun değerlerinin tam alt sınırını ve M_k olarak aynı segment üzerindeki bu değerlerin tam üst sınırını almamız gerektiği anlamına gelir:

m_k=\inf_(x\in)f(x),\qquad M_k=\sup_(x\in)f(x).

Eğer y=f(x) parça üzerinde sınırlı bir fonksiyonsa, o zaman parçaların her birinde de sınırlı olur ve dolayısıyla bunun için m_k ve sayıları bulunur. M_k,~ 0\leqslant k\leqslant n-1. Bu m_k ve M_k sayıları seçimiyle, toplamlar \textstyle(\toplam\limits_(k=0)^(n-1)m_k\Delta x_k) Ve \textstyle(\toplam\limits_(k=0)^(n-1)M_k\Delta x_k) belirli bir P bölümü için y=-f(x) fonksiyonunun sırasıyla alt ve üst Darboux integral toplamları denir:

a=x_0

bölüm Bu toplamları sırasıyla s_(fP) ve S_(fP) olarak göstereceğiz ve eğer y=f(x) fonksiyonu sabitse o zaman basitçe s_P ve S_P olur.

Eşitsizlik (2) şu anlama gelir: bir aralıkta sınırlı bir y=f(x) fonksiyonunun bu aralıkta bir ters türevi varsa, o zaman belirli bir integral, sırasıyla tüm alt ve üst Darboux toplamlarından oluşan \(s_p\) ve \(S_P\) sayısal kümelerini ayırır. aralığın tüm olası bölümleri P. Genel olarak konuşursak, bu iki kümeyi ayıran sayı benzersiz olmayabilir. Ancak aşağıda, en önemli fonksiyon sınıfları için (özellikle sürekli fonksiyonlar için) bunun benzersiz olduğunu göreceğiz.

Bu bize yeni bir tanım getirme olanağı sağlıyor. \textstyle(\int\limits_(a)^(b) f(x)\,dx), bir antiderivatif kavramına dayanmaz, ancak yalnızca Darboux toplamlarını kullanır.

Tanım. Bir aralıkla sınırlı bir y=f(x) fonksiyonu, eğer aralığın tüm olası bölümleri için oluşturulmuş alt ve üst Darboux toplamları kümelerini ayıran tek bir sayı varsa, bu aralıkta integrallenebilir olarak adlandırılır. Eğer y=f(x) fonksiyonu aralıkta integrallenebiliyorsa, bu kümeleri ayıran tek sayıya bu fonksiyonun aralık ve anlam üzerinden belirli integrali denir.

İntegrali tanımladık \textstyle(\int\limits_(a)^(b) f(x)\,dx) durum için b, sonra koyarız