Ders 3. Dinamiğin genel teoremleri
Maddi noktalar sisteminin dinamiği teorik mekaniğin önemli bir dalıdır. Burada esas olarak, sonlu sayıda serbestlik derecesine (sistemin konumunu belirleyen maksimum sayıda bağımsız parametreye) sahip mekanik sistemlerin (madde noktaları sistemleri) hareketi ile ilgili problemleri ele alıyoruz. Sistem dinamiğinin asıl görevi, katı bir cismin ve mekanik sistemlerin hareket yasalarının incelenmesidir.
Bir sistemin hareketini incelemeye yönelik en basit yaklaşım aşağıdakilerden oluşur: N Maddi noktaların belirlenmesi, sistemin her bir noktasının hareketlerinin dikkate alınmasına gelir. Bu durumda noktalar arasındaki etkileşim kuvvetleri de dahil olmak üzere sistemin her noktasına etki eden tüm kuvvetlerin belirlenmesi gerekir.
Newton'un ikinci yasasına (1.2) göre her noktanın ivmesini belirleyerek, her nokta için ikinci dereceden üç skaler diferansiyel hareket yasasını elde ederiz; 3 N Tüm sistem için diferansiyel hareket yasaları.
Sistemin her bir noktası için verilen kuvvetlere ve başlangıç koşullarına dayalı olarak mekanik bir sistemin hareket denklemlerini bulmak için, ortaya çıkan diferansiyel yasaların entegre edilmesi gerekir. Bu problem, evrensel çekim yasasına göre (iki cisim problemi) yalnızca etkileşim kuvvetlerinin etkisi altında hareket eden iki maddi nokta durumunda bile zordur ve etkileşen üç nokta durumunda (üç cisim problemi) son derece zordur. ).
Bu nedenle çözülebilir denklemlere yol açacak ve mekanik bir sistemin hareketi hakkında fikir verecek problemlerin çözümüne yönelik yöntemlerin bulunması gerekmektedir. Diferansiyel hareket yasalarının bir sonucu olan genel dinamik teoremleri, entegrasyon sırasında ortaya çıkan karmaşıklıktan kaçınmamıza ve gerekli sonuçları elde etmemize olanak tanır.
3. 1. Genel notlar
Mekanik sistemin noktalarını indekslerle numaralandıracağız Ben, J, k vb. tüm değerlerin içinden geçen 1, 2, 3… N, Nerede N – sistemin nokta sayısı. İlgili fiziksel büyüklükler k nokta, noktayla aynı indeksle gösterilir. Örneğin, sırasıyla yarıçap vektörünü ve hızı ifade edin k bu nokta.
Sistemin her noktasına iki kaynaklı kuvvetler etki eder: Birincisi, kaynakları sistemin dışında bulunan kuvvetler. harici kuvvetler ve belirlenmiş; ikincisi, belirli bir sistemin diğer noktalarından gelen kuvvetlere denir. dahili kuvvetler ve belirlenmiş. İç kuvvetler Newton'un üçüncü yasasını karşılar. Herhangi bir durumda tüm mekanik sisteme etki eden iç kuvvetlerin en basit özelliklerini ele alalım.
İlk mülk. Sistemin tüm iç kuvvetlerinin geometrik toplamı (iç kuvvetlerin ana vektörü) sıfıra eşittir.
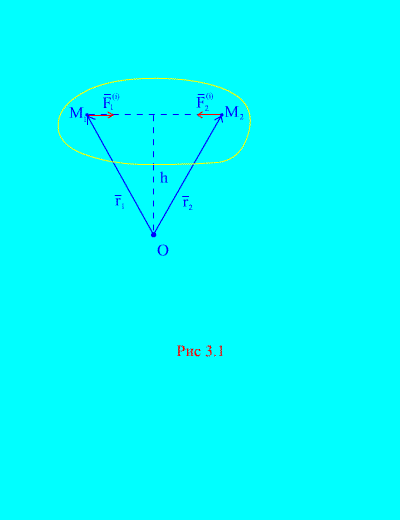
Aslında, sistemin herhangi iki keyfi noktasını ele alırsak, örneğin ve (Şekil 3.1), o zaman onlar için ![]() , Çünkü etki ve tepki kuvvetleri her zaman büyüklük bakımından eşit olup, etkileşen noktaları birbirine bağlayan bir etki çizgisi boyunca ters yönde etki eder. İç kuvvetlerin ana vektörü, etkileşen noktaların kuvvet çiftlerinden oluşur, bu nedenle
, Çünkü etki ve tepki kuvvetleri her zaman büyüklük bakımından eşit olup, etkileşen noktaları birbirine bağlayan bir etki çizgisi boyunca ters yönde etki eder. İç kuvvetlerin ana vektörü, etkileşen noktaların kuvvet çiftlerinden oluşur, bu nedenle
![]() (3.1)
(3.1)
İkinci mülk. Uzaydaki herhangi bir noktaya göre tüm iç kuvvetlerin momentlerinin geometrik toplamı sıfıra eşittir.
Kuvvetlerin momentlerinden ve noktaya göreli bir sistem düşünelim. HAKKINDA(Şekil 3.1). İtibaren (Şekil 3.1). bu açık
![]() ,
,
Çünkü her iki kuvvet de aynı kollara ve vektör momentlerinin zıt yönlerine sahiptir. Bir noktaya göre iç kuvvetlerin asal momenti HAKKINDA bu tür ifadelerin vektör toplamından oluşur ve sıfıra eşittir. Buradan,
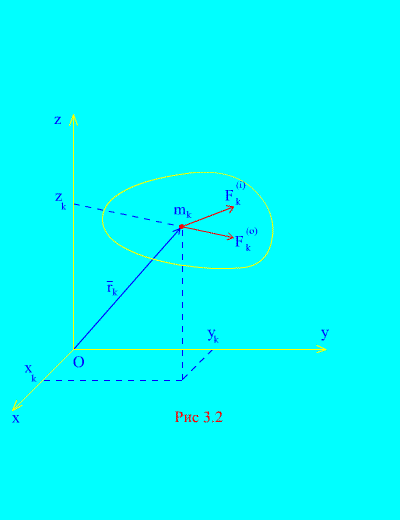
Aşağıdakilerden oluşan bir mekanik sisteme dış ve iç kuvvetler etki etsin. N puan (Şekil 3.2). Dış kuvvetlerin bileşkesi ve tüm iç kuvvetlerin bileşkesi sistemin her noktasına uygulanırsa, o zaman herhangi bir nokta için k Sistemin 3. noktasında diferansiyel hareket denklemleri çizilebilir. Bu tür denklemlerin toplamı olacak N:
ve sabit koordinat eksenleri üzerindeki projeksiyonlarda 3 N:
![]() (3.4)
(3.4)
Vektör denklemleri (3.3) veya eşdeğer skaler denklemler (3.4), tüm sistemin maddi noktalarının diferansiyel hareket yasalarını temsil eder. Tüm noktalar bir düzleme veya bir düz çizgiye paralel hareket ederse, ilk durumda denklemlerin (3.4) sayısı şu şekilde olacaktır: 2 N, saniyede N.

Örnek 1.İki kütle birbirine bir bloğun üzerine atılan uzatılamaz bir kabloyla bağlanır (Şekil 3.3). Sürtünme kuvvetlerinin yanı sıra blok ve kablonun kütlesinin de ihmal edilmesi, yüklerin hareketi ve kablo gerginliği yasasını belirler.
Çözüm. Sistem aynı eksene paralel hareket eden (uzatılamaz bir kabloyla birbirine bağlanan) iki malzeme gövdesinden oluşur. X. Diferansiyel hareket yasalarını eksene izdüşümlerde yazalım X herkes için.
Sağ ağırlığın ivmeyle düşmesine izin verin, sonra sol ağırlık ivmeyle yükselecektir. Kendimizi zihinsel olarak bağlantıdan (kablodan) kurtarır ve onu tepkilerle değiştiririz. (Şekil 3.3). Cisimlerin serbest olduğunu kabul ederek, eksene izdüşümü halinde hareketin diferansiyel yasalarını çizelim. X(bu, iplik gerginliklerinin iç kuvvetler olduğu ve yüklerin ağırlığının dış kuvvetler olduğu anlamına gelir):
Ve (gövdeler uzatılamaz bir kabloyla bağlı olduğundan) elde ederiz
İvme ve kablo gerilimi için bu denklemlerin çözülmesi T, alıyoruz
 .
.
Kablodaki gerilimin karşılık gelen yükün yer çekimi kuvvetine eşit olmadığını unutmayın.
3. 2. Kütle merkezinin hareketine ilişkin teorem
Düzlemdeki katı bir cismin ve mekanik sistemin oldukça karmaşık hareket edebildiği bilinmektedir. Bir cismin ve mekanik bir sistemin hareketiyle ilgili ilk teoreme şu şekilde ulaşılabilir: a k.-l atın. birbirine tutturulmuş birçok katı cisimden oluşan bir nesne. Bir parabolde uçacağı açıktır. Bu, noktanın hareketi incelenirken ortaya çıktı. Ancak artık nesne bir nokta değildir. Bir parabol içinde hareket eden belirli bir etkili merkez etrafında uçuşu sırasında döner ve sallanır. Karmaşık nesnelerin hareketiyle ilgili ilk teorem, belirli bir etkili merkezin, hareket eden bir nesnenin kütle merkezi olduğunu söylüyor. Kütle merkezinin mutlaka vücudun içinde olması gerekmez; onun dışında bir yerde bulunabilir.
Teorem. Mekanik bir sistemin kütle merkezi, sisteme etki eden tüm dış kuvvetlerin uygulandığı, tüm sistemin kütlesine eşit kütleye sahip maddi bir nokta olarak hareket eder.
Teoremi kanıtlamak için diferansiyel hareket yasalarını (3.3) aşağıdaki biçimde yeniden yazıyoruz:
![]() (3.5)
(3.5)
Nerede N – sistemin nokta sayısı.
Denklemleri terim terim toplayalım:
 (A)
(A)
Mekanik sistemin kütle merkezinin seçilen koordinat sistemine göre konumu formül (2.1) ile belirlenir:  Nerede M– sistemin kütlesi. Daha sonra eşitliğin sol tarafına (a) yazılacaktır.
Nerede M– sistemin kütlesi. Daha sonra eşitliğin sol tarafına (a) yazılacaktır.
Eşitliğin (a) sağ tarafındaki ilk toplam, dış kuvvetlerin ana vektörüne eşittir ve sonuncusu, iç kuvvetlerin özelliği gereği sıfıra eşittir. Daha sonra eşitlik (a), (b) dikkate alınarak yeniden yazılacaktır.
![]() , (3.6)
, (3.6)
onlar. Sistemin kütlesi ile kütle merkezinin ivmesinin çarpımı, sisteme etki eden tüm dış kuvvetlerin geometrik toplamına eşittir.
Denklem (3.6)'dan iç kuvvetlerin kütle merkezinin hareketini doğrudan etkilemediği sonucu çıkar. Ancak bazı durumlarda sisteme uygulanan dış kuvvetlerin ortaya çıkmasına neden olurlar. Böylece, bir arabanın tahrik tekerleklerini dönmeye iten iç kuvvetler, tekerlek jantına uygulanan bir dış yapışma kuvvetinin jant üzerinde etkili olmasına neden olur.
Örnek 2. Dikey bir düzlemde bulunan mekanizma, yatay ve pürüzsüz bir düzlem üzerine monte edilir ve yüzeye sağlam bir şekilde sabitlenmiş çubuklarla ona bağlanır. İLE Ve L (Şekil 3.4).
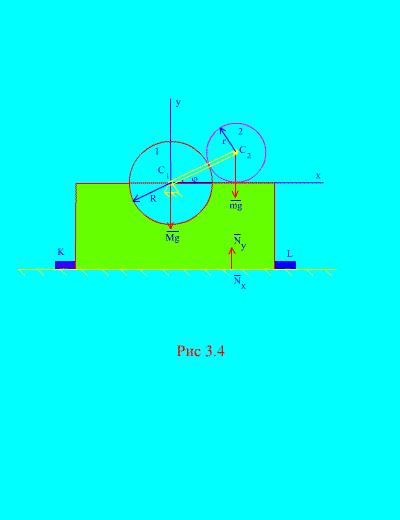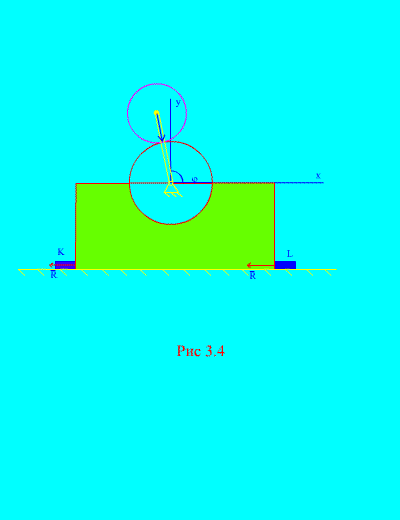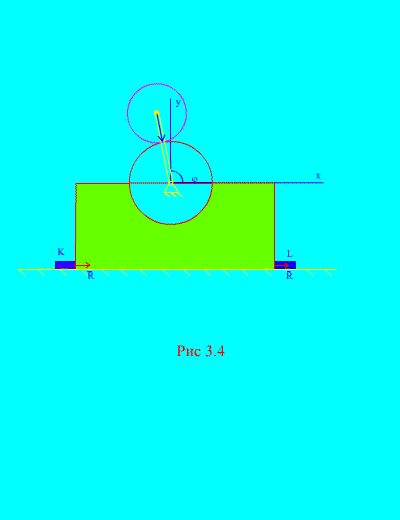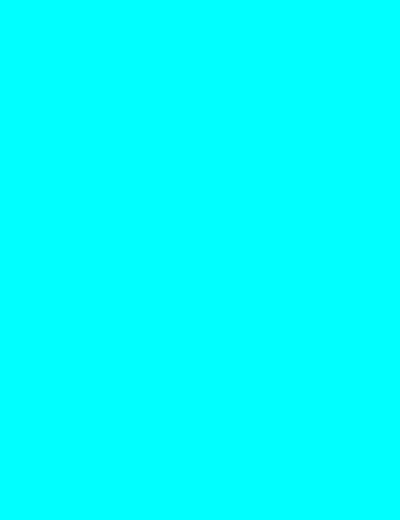
Disk 1 yarıçapı R hareketsiz. Disk 2 kütlesi M ve yarıçap R bir kranka bağlı, uzunluk R+ R noktada C2. Krank sabit bir hızla dönüyor
Açısal hız. Başlangıçta krank sağ yatay pozisyondaydı. Krankın kütlesini ihmal ederek, çerçevenin ve tekerleğin (1) toplam kütlesi şuna eşitse, çubuklara etkiyen maksimum yatay ve düşey kuvvetleri belirleyin: M. Ayrıca çubukların yokluğunda mekanizmanın davranışını da göz önünde bulundurun.
Çözüm. Sistem iki kütleden oluşur ( N=2 ): çerçeveli ve hareketli diskli sabit disk 1 2. Ekseni yönlendirin en sabit diskin ağırlık merkezi boyunca dikey olarak yukarı doğru, eksen X– yatay düzlem boyunca.
Kütle merkezinin (3.6) hareketine ilişkin teoremi koordinat biçiminde yazalım.
Bu sistemin dış kuvvetleri şunlardır: çerçevenin ve sabit diskin ağırlığı - Mg, hareketli disk ağırlığı – mg, - cıvataların toplam yatay reaksiyonu, - uçağın normal toplam reaksiyonu. Buradan,
Daha sonra hareket yasaları (b) yeniden yazılacaktır.
Mekanik sistemin kütle merkezinin koordinatlarını hesaplayalım:
 ; (G)
; (G)
şuradan görülebileceği gibi (Şekil 3.4), , , ![]() (krank açısı),
(krank açısı), ![]() . Bu ifadeleri (d)'de yerine koyarak ikinci türevlerin zamana göre hesaplanması T,'den bunu anlıyoruz
. Bu ifadeleri (d)'de yerine koyarak ikinci türevlerin zamana göre hesaplanması T,'den bunu anlıyoruz
 (D)
(D)
(c) ve (e)'yi (b)'de yerine koyarsak, şunu buluruz:

Çubuklara etki eden yatay basınç en büyük ve en az olduğunda çünkü = 1 buna göre, yani
![]()
![]()
Mekanizmanın yatay düzlemdeki basıncı en yüksek ve en düşük değerlere sahiptir. günah buna göre, yani
![]()
![]()
Aslında dinamiğin ilk problemi çözüldü: Sistemin kütle merkezinin (d) bilinen hareket denklemlerine göre, harekete dahil olan kuvvetler eski durumuna getirildi.
Barların yokluğunda k Ve L (Şekil 3.4) mekanizma yatay düzlemin üzerinde sıçramaya başlayabilir. Bu şu durumlarda gerçekleşecektir: olduğunda, mekanizmanın sıçradığı krankın açısal dönüş hızının eşitliği sağlaması gerektiği sonucu çıkar.
 .
.
3. 3. Kütle merkezinin hareketinin korunumu kanunu
Sisteme etki eden dış kuvvetlerin ana vektörü sıfıra eşitse; , sonra(3.6)kütle merkezinin ivmesinin sıfır olduğu, dolayısıyla kütle merkezinin hızının büyüklük ve yön bakımından sabit olduğu sonucu çıkar. Özellikle ilk anda kütle merkezi hareketsizse, dış kuvvetlerin ana vektörü sıfıra eşitken tüm zaman boyunca hareketsizdir.
Bu teoremden birkaç sonuç çıkar.
· İç kuvvetler tek başına sistemin kütle merkezinin hareketinin doğasını değiştiremez.
· Sisteme etki eden dış kuvvetlerin ana vektörü sıfır ise, kütle merkezi hareketsizdir veya düzgün ve doğrusal olarak hareket eder.
· Sistemin dış kuvvetlerinin ana vektörünün sabit bir eksene izdüşümü sıfıra eşitse, sistemin kütle merkezinin hızının bu eksene izdüşümü değişmez.
· Katı bir cisme uygulanan bir çift kuvvet, kütle merkezinin hareketini değiştiremez (yalnızca cismin kütle merkezi etrafında dönmesine neden olabilir).
Kütle merkezinin hareketinin korunumu yasasını gösteren bir örneği ele alalım.

Örnek 3.İki kütle, bir bloğun içinden atılan uzatılamaz bir iplikle birbirine bağlanır (Şekil 3.5) kütleli bir kama üzerine sabitlenmiş M. Kama düzgün bir yatay düzlem üzerinde durmaktadır. İlk anda sistem hareketsiz durumdaydı. İlk yük belirli bir yüksekliğe indirildiğinde kamanın düzlem boyunca yer değiştirmesini bulun N. Bloğun ve ipliğin kütlesini ihmal edin.
Çözüm. Yüklerle birlikte kamaya etki eden dış kuvvetler yerçekimidir ve Mg, ayrıca düzgün bir yatay yüzey N'nin normal reaksiyonunun yanı sıra,
İlk anda sistem hareketsiz olduğundan, .
Sistemin kütle merkezinin o andaki koordinatlarını hesaplayalım. T 1 yük ağırlaştığında G bir yüksekliğe inecek H.
Şu an için:
 ,
,
Nerede , , X– sırasıyla, g, g ağırlığındaki yüklerin kütle merkezinin ve kama ağırlığının koordinatları MG.
Kamanın zaman anında eksenin pozitif yönünde hareket ettiğini varsayalım. Öküz miktara göre L yükün ağırlığı belirli bir yüksekliğe düşerse N. O zaman şimdilik
Çünkü yükler kamayla birlikte hareket edecek L sağa doğru hareket edecek ve yük kama boyunca yukarı doğru hareket edecektir. O zamandan beri, hesaplamalardan sonra şunu elde ederiz:
 .
.
3.4. Sistem hareket miktarı
3.4.1. Sistem momentumunun hesaplanması
Maddi bir noktanın momentumu, noktanın kütlesi ile hız vektörünün çarpımına eşit bir vektör miktarıdır.
Momentum ölçüm birimi -
Mekanik bir sistemin momentumu, sistemin bireysel noktalarının momentumunun vektör toplamıdır;
Nerede N – sistemin nokta sayısı.
Mekanik bir sistemin momentumu sistemin kütlesi cinsinden ifade edilebilir. M ve kütle merkezinin hızı. Gerçekten mi,
onlar. Sistemin momentumu, tüm sistemin kütlesinin ve kütle merkezinin hızının çarpımına eşittir. Yön yön ile aynıdır (Şekil 3.6)

Dikdörtgen eksenlere yapılan projeksiyonlarda elimizdeki
burada , , sistemin kütle merkezinin hızının izdüşümleridir.
Burada M– mekanik sistemin kütlesi; sistem hareket ettiğinde değişmez.
Bu sonuçların özellikle katı cisimlerin hareket miktarlarının hesaplanmasında kullanılması uygundur.
Formül (3.7)'den, mekanik bir sistemin kütle merkezi sabit kalacak şekilde hareket etmesi durumunda sistemin momentumunun sıfıra eşit kalacağı açıktır.
3.4.2. Temel ve tam kuvvet darbesi
Bir kuvvetin zaman içinde maddi bir noktaya etkisi dt temel bir dürtü ile karakterize edilebilir. Zaman içindeki toplam kuvvet darbesi T, veya formülle belirlenen kuvvet darbesi
veya eksen koordinatları üzerine projeksiyonlarda
 (3.8a)
(3.8a)
Kuvvet darbesinin birimi.
3.4.3. Bir sistemin momentumundaki değişime ilişkin teorem
Sistemin noktalarına dış ve iç kuvvetler uygulansın. Daha sonra sistemin her noktası için diferansiyel hareket yasalarını (3.3) uygulayabiliriz, bunu aklımızda tutarak ![]() :
:
 .
.
Sistemin tüm noktalarını toplayarak şunu elde ederiz:
İç kuvvetlerin özelliği ve tanımı gereği ![]() sahibiz
sahibiz
 (3.9)
(3.9)
Bu denklemin her iki tarafını da çarparak dt Momentumdaki değişime ilişkin diferansiyel formda bir teorem elde ederiz:
![]() , (3.10)
, (3.10)
onlar. Mekanik bir sistemin diferansiyel momentumu, mekanik sistemin noktalarına etki eden tüm dış kuvvetlerin temel itkilerinin vektör toplamına eşittir.
Her iki tarafın (3.10) 0'dan zamana göre integralinin hesaplanması T, teoremi sonlu veya integral formda elde ederiz
 (3.11)
(3.11)
Koordinat eksenleri üzerindeki projeksiyonlarda sahip olacağımız
Mekanik bir sistemin momentumunun zamanla değişmesiT, aynı anda mekanik sistemin noktalarına etki eden dış kuvvetlerin tüm darbelerinin vektör toplamına eşittir.
Örnek 4. Yük ağırlığı M Bir kuvvetin etkisi altında dinlenme halindeyken eğik bir düzlemden aşağıya doğru iner F, zamanla orantılı: , burada (Şekil 3.7). Vücut bundan sonra hangi hızı kazanacak? T Hareketin başlamasından saniyeler sonra, yükün eğimli düzlemdeki kayma sürtünme katsayısı şuna eşitse: F.
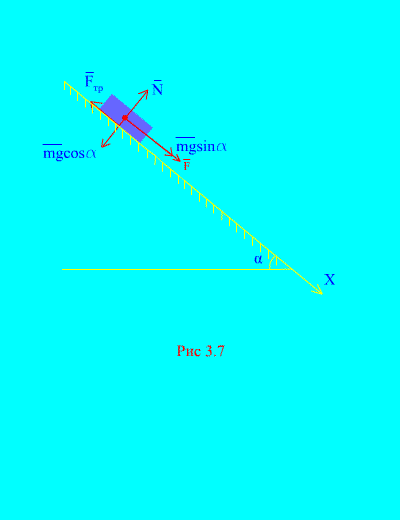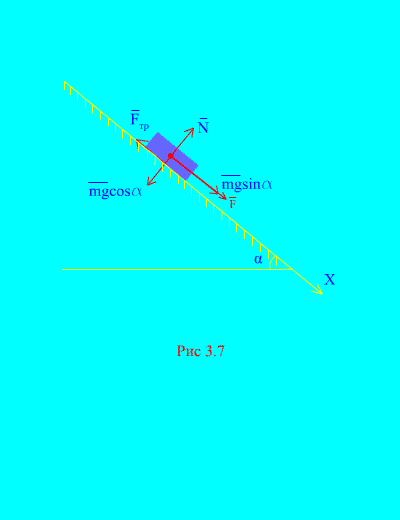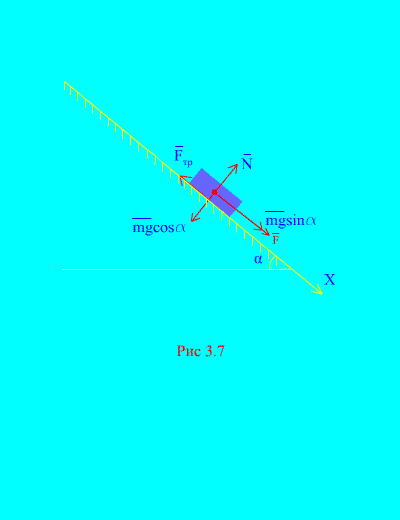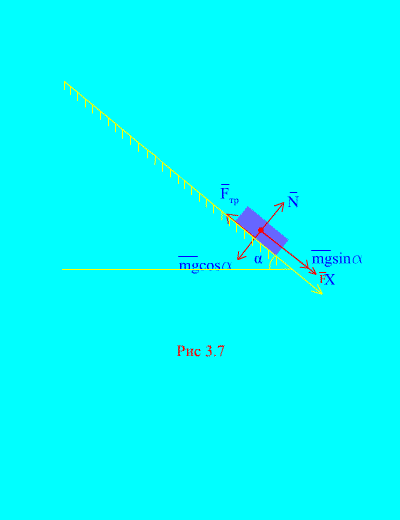
Çözüm. Yüke uygulanan kuvvetleri gösterelim: mg – yük yerçekimi kuvveti, N düzlemin normal tepkisidir, düzlem üzerindeki yükün kayma sürtünme kuvvetidir ve . Tüm kuvvetlerin yönü şekilde gösterilmiştir. (Şekil 3.7).
Ekseni yönlendirelim X eğik düzlem boyunca aşağıya doğru. Eksene izdüşümdeki momentumdaki (3.11) değişimle ilgili teoremi yazalım. X:
 (A)
(A)
Şarta göre çünkü zamanın ilk anında yük hareketsizdi. Tüm kuvvetlerin darbelerinin x eksenine izdüşümlerinin toplamı şuna eşittir:

Buradan,
 ,
,
 .
.
3.4.4. Momentumun korunumu yasaları
Korunum yasaları momentumdaki değişim teoreminin özel durumları olarak elde edilir. İki özel durum mümkündür.
· Sisteme uygulanan tüm dış kuvvetlerin vektör toplamı sıfıra eşitse; , o zaman aşağıdaki teoremden (3.9) , Ne ,
onlar. Sistemin dış kuvvetlerinin ana vektörü sıfır ise, sistemin hareket miktarı büyüklük ve yön bakımından sabittir.
· Dış kuvvetlerin ana vektörünün herhangi bir koordinat eksenine izdüşümü sıfıra eşitse, örneğin Ox, yani. ise momentumun bu eksene izdüşümü sabit bir değerdir.
Momentumun korunumu yasasının uygulanmasına ilişkin bir örneği ele alalım.

Örnek 5. Balistik sarkaç, uzun bir ip üzerinde asılı duran bir kütleye sahip bir cisimdir. (Şekil 3.8).
Hızla hareket eden bir kütle mermisi V ve sabit bir cisme çarparak sıkışıp kalır ve cisim sapar. Ceset yüksekliğe çıkarsa merminin hızı ne olurdu? H ?
Çözüm. Kurşunun sıkıştığı bedenin hız kazanmasına izin verin. Daha sonra, iki cismin etkileşimi sırasında momentumun korunumu yasasını kullanarak şunu yazabiliriz: ![]() .
.
Hız, mekanik enerjinin korunumu yasası kullanılarak hesaplanabilir  . Daha sonra . Sonuç olarak bulduk
. Daha sonra . Sonuç olarak bulduk
 .
.
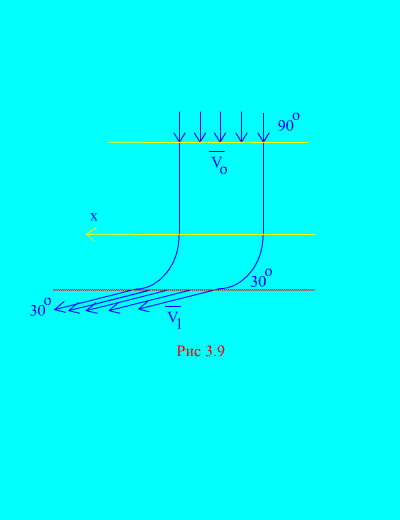
Örnek 6. Su sabit bir kanala giriyor (Şekil 3.9) yataya açılı hıza sahip değişken kesit; girişteki kanalın kesit alanı; Kanaldan çıkışta suyun hızı ufukla açı yapar.
Suyun kanal duvarlarında oluşturduğu reaksiyonun yatay bileşenini belirleyin. Suyun yoğunluğu  .
.
Çözüm. Kanal duvarlarının suya uyguladığı reaksiyonun yatay bileşenini belirleyeceğiz. Bu kuvvet istenilen kuvvete eşit büyüklükte ve zıt işaretlidir. (3.11a)’ya göre elimizde,
 . (A)
. (A)
T süresi boyunca kanala giren sıvı hacminin kütlesini hesaplıyoruz:
rAV 0 miktarına denir ikinci kütle - birim zamanda borunun herhangi bir bölümünden akan sıvının kütlesi.
Aynı sürede aynı miktarda su kanaldan çıkar. Başlangıç ve son hızlar durumda verilmiştir.
Sisteme (su) uygulanan dış kuvvetlerin yatay eksene izdüşümlerinin toplamını belirleyen eşitliğin (a) sağ tarafını hesaplayalım. Tek yatay kuvvet, ortaya çıkan duvar reaksiyonunun yatay bileşenidir. Rx. Bu kuvvet sabit su hareketi sırasında sabittir. Bu yüzden
 . (V)
. (V)
(b) ve (c)'yi (a)'da yerine koyarsak, şunu elde ederiz:
3.5. Sistemin kinetik momenti
3.5.1. Sistemin ana momentum anı

Merkez adı verilen bir A noktasına göre sistemin kütlesine sahip bir noktanın yarıçap vektörü olsun. (Şekil 3.10).
Bir noktanın momentumu (kinetik momenti) A merkezine göre vektör denir , formülle belirlenir
![]() . (3.12)
. (3.12)
Bu durumda vektör merkezden geçen düzleme dik olarak yönlendirilir A ve vektör .
Bir noktanın eksene göre momentumu (kinetik momenti) bir noktanın momentum momentinin bu eksen üzerinde seçilmiş herhangi bir merkeze göre bu eksene izdüşümüne denir.
Sistemin A merkezine göre ana momentum momenti (kinetik moment) miktar denir
 (3.13)
(3.13)
Sistemin eksene göre ana momentum momenti (kinetik moment) sistemin ana momentum momentinin bu eksen üzerinde seçilen herhangi birine göre bu eksen üzerindeki izdüşümüne denir. merkez ekseni.
3.5.2. Dönen katı bir cismin dönme eksenine göre kinetik momenti
Sabit noktayı hizalayalım HAKKINDA dönme ekseni üzerinde yatan vücut HAKKINDAz, koordinat sisteminin kökeni ile Ohooz eksenleri gövdeyle birlikte dönecek olan (Şekil 3.11). Vücudun bir noktasının koordinatların orijinine göre yarıçap vektörü olsun; eksen üzerindeki izdüşümü , , , ile gösterilecektir. Vücudun açısal hız vektörünün aynı eksenlerdeki izdüşümlerini 0, 0, () ile belirtiyoruz.
Belirli bir maddi nesneler sisteminin sabit bir koordinat sistemine göre hareketini ele alalım. Sistem özgür olmadığında, sisteme dayatılan bağlantıları atarsak ve onların eylemlerini karşılık gelen reaksiyonlarla değiştirirsek, serbest olarak düşünülebilir.
Sisteme uygulanan tüm kuvvetleri dış ve iç olarak ayıralım; her ikisi de atılan reaksiyonları içerebilir
bağlantılar. A noktasına göre dış kuvvetlerin ana vektörünü ve ana momentini gösterelim.
1. Momentumdaki değişime ilişkin teorem. Sistemin hareket miktarı ise (bkz.)
yani teorem geçerlidir: Sistemin momentumunun zamana göre türevi, tüm dış kuvvetlerin ana vektörüne eşittir.
Sistemin kütlesinin, kütle merkezinin hızının ifadesiyle vektör yerine koyarsak, denklem (4.1) farklı bir formda verilebilir:
Bu eşitlik, sistemin kütle merkezinin, kütlesi sistemin kütlesine eşit olan ve sistemin tüm dış kuvvetlerinin ana vektörüne geometrik olarak eşit bir kuvvetin uygulandığı maddi bir nokta gibi hareket etmesi anlamına gelir. Son ifadeye sistemin kütle merkezinin (atalet merkezi) hareketine ilişkin teorem denir.
O halde (4.1)'den momentum vektörünün büyüklük ve yön bakımından sabit olduğu sonucu çıkar. Bunu koordinat eksenine yansıtarak, sistemin çift tepe noktasının diferansiyel denklemleri olan üç skaler birinci integral elde ederiz:
Bu integrallere momentum integralleri denir. Kütle merkezinin hızı sabit olduğunda, yani düzgün ve doğrusal olarak hareket eder.
Dış kuvvetlerin ana vektörünün herhangi bir eksendeki, örneğin bir eksendeki izdüşümü sıfıra eşitse, o zaman bir birinci integralimiz olur veya ana vektörün iki izdüşümü sıfıra eşitse, o zaman iki tane vardır. Momentumun integralleri.
2. Açısal momentumdaki değişime ilişkin teorem. A'nın uzayda herhangi bir rastgele nokta (hareketli veya sabit) olmasına izin verin; bu noktanın, tüm hareket süresi boyunca sistemin herhangi bir spesifik maddi noktasıyla çakışması zorunlu değildir. Sabit bir koordinat sistemindeki hızını şu şekilde gösteririz: Bir malzeme sisteminin A noktasına göre kinetik momentindeki değişime ilişkin teorem şu şekildedir:
![]()
A noktası sabitse eşitlik (4.3) daha basit bir biçim alır:
Bu eşitlik, bir sistemin açısal momentumunun sabit bir noktaya göre değişimi hakkındaki teoremi ifade eder: Sistemin açısal momentumunun sabit bir noktaya göre hesaplanan zamana göre türevi, tüm dış kuvvetlerin göreceli temel momentine eşittir. bu noktaya.
O halde (4.4)'e göre açısal momentum vektörünün büyüklüğü ve yönü sabittir. Bunu koordinat eksenlerine yansıtarak, çift sistemin diferansiyel denklemlerinin skaler birinci integrallerini elde ederiz:
Bu integrallere momentum integralleri veya alan integralleri denir.
A noktası sistemin kütle merkezi ile çakışırsa, eşitliğin sağ tarafındaki ilk terim (4.3) kaybolur ve açısal momentumdaki değişime ilişkin teorem, aşağıdaki durumda olduğu gibi aynı yazı biçimine (4.4) sahip olur. sabit bir A noktası. Söz konusu durumda, eşitliğin (4.4) sol tarafındaki sistemin mutlak açısal momentumunun, sistemin eşit açısal momentumu ile değiştirilebileceğine dikkat edin (bkz. s. 4 § 3). kütle merkezine göre hareket halindedir.
Sistemin kütle merkezinden geçen sabit bir eksen veya sabit doğrultuda bir eksen olsun ve sistemin bu eksene göre kinetik momenti olsun. (4.4)'ten şu sonuç çıkıyor
eksene göre dış kuvvetlerin momenti nerede. Tüm hareket boyunca ilk integrale sahipsek
S.A. Chaplygin'in çalışmalarında, kinetik momentumdaki değişime ilişkin teoremin çeşitli genellemeleri elde edildi ve bunlar daha sonra yuvarlanan toplarla ilgili bir dizi problemi çözmek için uygulandı. Mekanik momentteki değişime ilişkin teoremin daha ileri genellemeleri ve bunların katı cisim dinamiği problemlerindeki uygulamaları çalışmalarda yer almaktadır. Bu çalışmaların ana sonuçları, sürekli olarak hareketli bir A noktasından geçen hareketli bir momentuma göre kinetik momentumun değişmesine ilişkin teorem ile ilgilidir. Bu eksen boyunca yönlendirilmiş bir birim vektör olsun. Eşitliğin (4.3) her iki tarafıyla skaler olarak çarpılıp terimi iki kısmına ekleyerek şunu elde ederiz:
Kinematik koşul karşılandığında
Denklem (4.5), (4.7)'den gelmektedir. Ve eğer (4.8) koşulu tüm hareket boyunca sağlanırsa, o zaman birinci integral (4.6) mevcuttur.
Sistemin bağlantıları idealse ve sanal yer değiştirmeler arasında sistemin eksen etrafında katı bir cisim olarak dönmesine izin veriyorsa ve o zaman reaksiyonların eksene göre ana momenti sıfıra eşitse ve ardından değer Denklemin (4.5) sağ tarafı tüm dış aktif kuvvetlerin eksene göre ana momentini temsil eder ve . Bu momentin sıfıra eşitliği ve (4.8) ilişkisinin geçerliliği, integralin (4.6) varlığı için yeterli koşulların dikkate alınması durumunda olacaktır.
Eksen yönü sabit ise (4.8) koşulu şu şekilde yazılacaktır:
![]()
Bu eşitlik, kütle merkezinin hızı ile A noktasının hızının eksen ve buna dik düzlem üzerindeki izdüşümlerinin paralel olduğu anlamına gelir. S.A. Chaplygin'in çalışmasında (4.9) yerine, X'in keyfi bir sabit değer olduğu daha az genel bir koşulun yerine getirilmesi gerekmektedir.
(4.8) koşulunun noktasının seçimine bağlı olmadığına dikkat edin. Aslında P eksen üzerinde keyfi bir nokta olsun. Daha sonra
ve bu nedenle
Sonuç olarak, Rézal'in (4.1) ve (4.4) denklemlerine ilişkin geometrik yorumuna dikkat çekiyoruz: vektörlerin uçlarının mutlak hız vektörleri ve sırasıyla, A noktasına göre tüm dış kuvvetlerin ana vektörüne ve ana momentine eşittir. .
Sorunların çözümünde sağlık sigortasının kullanılması bazı zorluklarla ilişkilidir. Bu nedenle, genellikle hareketin özellikleri ile kuvvetler arasında pratik uygulamaya daha uygun olan ek ilişkiler kurulur. Bu tür ilişkiler dinamiğin genel teoremleri. OMS'nin sonuçları olarak, özel olarak tanıtılan bazı hareket ölçümlerinin değişim hızı ile dış kuvvetlerin özellikleri arasında ilişkiler kurarlar.
Momentumdaki değişime ilişkin teorem. Maddi bir noktanın momentum vektörü (R. Descartes) kavramını tanıtalım (Şekil 3.4):
ben ben = tV G (3.9)
Pirinç. 3.4.
Sistem için konsepti tanıtıyoruz sistemin momentumunun ana vektörü geometrik toplam olarak:
Q = Y, m " V r
OZMS'ye uygun olarak: Xu, -^=i) veya X
TEKRAR) .
/w, = const değerini hesaba katarsak şunu elde ederiz: -Ym,!" = TEKRAR)
veya son haliyle
dO/di = A (E (3.11)
onlar. Sistemin momentum ana vektörünün zamana göre birinci türevi, dış kuvvetlerin ana vektörüne eşittir.
Kütle merkezinin hareketi ile ilgili teorem. Sistemin kütle merkezi konumu bağlı olan geometrik noktaya denir T, vesaire. sistemdeki kütlelerin /g/ dağılımından ve kütle merkezinin yarıçap vektörünün ifadesiyle belirlenir (Şekil 3.5):

Nerede gs - kütle merkezinin yarıçap vektörü.

Pirinç. 3.5.
Hadi arayalım = t sistemin kütlesi ile.İfadeyi çarptıktan sonra
(3.12)'yi paydaya uygulayarak ve sonucun her iki tarafının farklısını alarak
değerli bir eşitliğe sahip olacağız: g s t s = ^t.U. = 0 veya 0 = bu ABD.
Böylece sistemin ana momentum vektörü, sistemin kütlesi ile kütle merkezinin hızının çarpımına eşittir. Momentumdaki değişime ilişkin teoremi (3.11) kullanarak şunu elde ederiz:
t s dU s / dі = A (E) , veya
Formül (3.13) kütle merkezinin hareketine ilişkin teoremi ifade eder: Sistemin kütle merkezi, dış kuvvetlerin ana vektörünün etkilediği sistemin kütlesine sahip maddi bir nokta olarak hareket eder.
Açısal momentumdaki değişime ilişkin teorem. Maddi bir noktanın açısal momentumu kavramını, yarıçap vektörü ve momentumunun vektör çarpımı olarak tanıtalım:
ah'ya = bl X O, (3.14)
Nerede OI'ye - Maddi bir noktanın sabit bir noktaya göre momentum momenti HAKKINDA(Şekil 3.6).

Şimdi mekanik bir sistemin açısal momentumunu geometrik bir toplam olarak tanımlıyoruz:
К() = X ko, = ШУ, ? Ç-15>
(3.15)'in türevini alarak şunu elde ederiz:
Ґ sn--- X ben U. + sen X ben
Hesaba katıldığında = U G U ben X sen ben sen= 0 ve formül (3.2) ile şunu elde ederiz:
сіК а /с1ї - ї 0 .
(3.6)'daki ikinci ifadeye dayanarak, sonunda sistemin açısal momentumundaki değişime ilişkin bir teorem elde edeceğiz:
Mekanik bir sistemin sabit bir O merkezine göre momentum momentinin birinci zaman türevi, bu sisteme etki eden dış kuvvetlerin aynı merkeze göre ana momentine eşittir.
İlişkiyi (3.16) türetirken, şu varsayıldı: HAKKINDA- sabit nokta. Bununla birlikte, diğer bazı durumlarda ilişkinin (3.16) biçiminin, özellikle düzlemsel harekette moment noktasının kütle merkezinde, hızların veya ivmelerin anlık merkezinde seçilmesi durumunda değişmeyeceği gösterilebilir. Ayrıca eğer nokta HAKKINDA Hareketli bir maddesel noktaya çakışırsa, bu nokta için yazılan eşitlik (3.16) 0 = 0 özdeşliğine dönüşecektir.
Kinetik enerjideki değişime ilişkin teorem. Mekanik bir sistem hareket ettiğinde sistemin hem “dış” hem de iç enerjisi değişir. İç kuvvetlerin özellikleri, ana vektör ve ana moment, ana vektördeki ve ivme sayısının ana momentindeki değişimi etkilemiyorsa, o zaman sistemin enerji durumuna ilişkin süreçlerin değerlendirilmesine iç kuvvetler dahil edilebilir. Bu nedenle, bir sistemin enerjisindeki değişiklikleri değerlendirirken, iç kuvvetlerin de uygulandığı bireysel noktaların hareketlerini dikkate almak gerekir.
Maddi bir noktanın kinetik enerjisi miktar olarak tanımlanır.
T^tuTsg. (3.17)
Mekanik bir sistemin kinetik enerjisi, sistemin maddi noktalarının kinetik enerjilerinin toplamına eşittir:
dikkat et ki T > 0.
Kuvvetin gücünü, kuvvet vektörü ile hız vektörünün skaler çarpımı olarak tanımlayalım:

Çoğu zaman, bir mekanik sistemin hareketinin önemli özelliklerini, diferansiyel hareket denklemleri sisteminin entegrasyonuna başvurmadan tanımlamak mümkündür. Bu, genel dinamik teoremlerinin uygulanmasıyla elde edilir.
5.1. Temel kavramlar ve tanımlar
Dış ve iç kuvvetler. Mekanik bir sistemdeki bir noktaya etki eden herhangi bir kuvvet mutlaka ya aktif bir kuvvettir ya da bir birleşme reaksiyonudur. Sistemin noktalarına etki eden kuvvetlerin tamamı farklı iki sınıfa ayrılabilir: dış kuvvetler ve iç kuvvetler (e ve i endeksleri - Latince externus - dış ve internus - iç kelimelerinden). Dış kuvvetler, söz konusu sistemin parçası olmayan noktalardan ve cisimlerden bir sistemin noktalarına etki eden kuvvetlerdir. Söz konusu sistemin noktaları ve gövdeleri arasındaki etkileşim kuvvetlerine iç denir.
Bu bölüm, araştırmacı tarafından incelenen mekanik sisteme hangi malzeme noktalarının ve gövdelerinin dahil edildiğine bağlıdır. Sistemin bileşimini ek noktalar ve gövdeler ekleyerek genişletirseniz, önceki sistem için dışsal olan bazı kuvvetler, genişletilmiş sistem için içsel hale gelebilir.
İç kuvvetlerin özellikleri. Bu kuvvetler sistemin parçaları arasındaki etkileşim kuvvetleri olduğundan, etki-tepki aksiyomuna göre organize edilmiş “ikili” olarak tüm iç kuvvetler sistemine girerler. Bu “iki”nin her birinin güçlü yanları vardır
ana vektör ve keyfi bir merkeze göre ana moment sıfıra eşittir. Tüm iç kuvvetler sistemi yalnızca “ikililerden” oluştuğuna göre, o zaman
1) iç kuvvetler sisteminin ana vektörü sıfırdır,
2) iç kuvvetler sisteminin keyfi bir noktaya göre ana momenti sıfıra eşittir.
Sistemin kütlesi, sistemi oluşturan tüm noktaların ve cisimlerin mk kütlelerinin aritmetik toplamıdır:
Kütle merkezi Mekanik bir sistemin (atalet merkezi), yarıçap vektörü ve koordinatları formüllerle belirlenen geometrik bir C noktasıdır.
sistemi oluşturan noktaların yarıçap vektörleri ve koordinatları nerededir?
Düzgün bir yerçekimi alanında bulunan katı bir cisim için, kütle merkezinin ve ağırlık merkezinin konumları çakışır; diğer durumlarda bunlar farklı geometrik noktalardır.
Atalet referans sistemi ile birlikte öteleme hareketi yapan ataletsiz bir referans sistemi de sıklıkla eş zamanlı olarak değerlendirilir. Koordinat eksenleri (König eksenleri), C orijini sürekli olarak mekanik sistemin kütle merkeziyle çakışacak şekilde seçilir. Tanıma uygun olarak kütle merkezi Koenig eksenlerinde sabittir ve koordinatların başlangıç noktasında yer alır.
Sistemin eylemsizlik momenti bir eksene göre, sistemin tüm noktalarının mk kütlelerinin çarpımlarının eksene olan mesafelerinin kareleriyle toplamına eşit bir skaler miktardır:
![]()
Mekanik sistem katı bir cisim ise 12'yi bulmak için formülü kullanabilirsiniz.

yoğunluk nerede, vücudun kapladığı hacim.
Kütle merkezinin hareketi ile ilgili teorem. Mekanik bir sistemin diferansiyel hareket denklemleri. Mekanik bir sistemin kütle merkezinin hareketi ile ilgili teorem. Kütle merkezinin hareketinin korunumu kanunu.
Momentumdaki değişime ilişkin teorem. Maddi bir noktanın hareket miktarı. Temel kuvvet dürtüsü. Sonlu bir süre için kuvvet darbesi ve bunun koordinat eksenlerine yansıması. Diferansiyel ve sonlu formlarda maddi bir noktanın momentumundaki değişime ilişkin teorem.
Mekanik bir sistemin hareket miktarı; sistemin kütlesi ve kütle merkezinin hızı aracılığıyla ifadesi. Diferansiyel ve sonlu formlarda mekanik bir sistemin momentumundaki değişime ilişkin teorem. Mekanik momentumun korunumu kanunu
(Cisim kavramı ve değişken kütleli bir nokta. Meshchersky denklemi. Tsiolkovsky formülü.)
Açısal momentumdaki değişime ilişkin teorem. Maddi bir noktanın merkeze ve eksene göre momentum momenti. Maddi bir noktanın açısal momentumundaki değişime ilişkin teorem. Merkezi güç. Merkezi bir kuvvet durumunda maddi bir noktanın açısal momentumunun korunumu. (Sektör hızı kavramı. Alanlar kanunu.)
Mekanik bir sistemin merkeze ve eksene göre temel momentum momenti veya kinetik momenti. Dönen katı bir cismin dönme eksenine göre kinetik momenti. Mekanik bir sistemin kinetik momentindeki değişime ilişkin teorem. Mekanik bir sistemin açısal momentumunun korunumu yasası. (Kütle merkezine göre göreceli hareket halindeki mekanik bir sistemin kinetik momentindeki değişime ilişkin teorem.)
Kinetik enerjideki değişime ilişkin teorem. Maddi bir noktanın kinetik enerjisi. Temel kuvvet işi; temel çalışmanın analitik ifadesi. Bir kuvvetin uygulandığı noktanın son yer değiştirmesi üzerinde yaptığı iş. Yer çekimi işi, elastik kuvvet ve yer çekimi kuvveti. Diferansiyel ve sonlu formlarda maddi bir noktanın kinetik enerjisindeki değişime ilişkin teorem.
Mekanik bir sistemin kinetik enerjisi. Öteleme hareketi sırasında, sabit bir eksen etrafında dönme sırasında ve genel hareket durumunda (özellikle düzlemsel paralel hareket sırasında) katı bir cismin kinetik enerjisini hesaplamak için formüller. Diferansiyel ve sonlu formlarda mekanik bir sistemin kinetik enerjisindeki değişime ilişkin teorem. Katı bir cisimde iç kuvvetlerin yaptığı işin toplamı sıfıra eşittir. Sabit bir eksen etrafında dönen katı bir cisme uygulanan iş ve kuvvetlerin gücü.
Güç alanı kavramı. Potansiyel kuvvet alanı ve kuvvet fonksiyonu. Kuvvet projeksiyonlarının kuvvet fonksiyonu aracılığıyla ifadesi. Eşit potansiyele sahip yüzeyler. Bir kuvvetin potansiyel kuvvet alanındaki bir noktanın son yer değiştirmesi üzerindeki işi. Potansiyel enerji. Potansiyel kuvvet alanlarına örnekler: düzgün yerçekimi alanı ve yerçekimi alanı. Mekanik enerjinin korunumu kanunu.
Katı cisim dinamiği. Katı bir cismin öteleme hareketinin diferansiyel denklemleri. Katı bir cismin sabit bir eksen etrafında dönmesi için diferansiyel denklem. Fiziksel sarkaç. Katı bir cismin düzlemsel hareketinin diferansiyel denklemleri.
D'Alembert ilkesi. Maddi bir nokta için D'Alembert ilkesi; eylemsizlik kuvveti. Mekanik bir sistem için D'Alembert ilkesi. Rijit bir cismin noktalarının atalet kuvvetlerinin merkeze getirilmesi; Atalet kuvvetlerinin ana vektörü ve ana momenti.
(Sert bir gövdenin sabit bir eksen etrafında dönmesi sırasında rulmanların dinamik reaksiyonlarının belirlenmesi. Dönme ekseninin gövdenin ana atalet ekseni olması durumu.)
Olası hareketler ilkesi ve dinamiğin genel denklemi. Mekanik bir sisteme uygulanan bağlantılar. Maddi bir noktanın ve mekanik sistemin olası (veya sanal) hareketleri. Sistemin serbestlik derecesi sayısı. İdeal bağlantılar. Olası hareketler ilkesi. Dinamiğin genel denklemi.
Genelleştirilmiş koordinatlarda bir sistemin hareket denklemleri (Lagrange denklemleri). Sistemin genelleştirilmiş koordinatları; genelleştirilmiş hızlar Temel işin genelleştirilmiş koordinatlarda ifadesi. Genelleştirilmiş Kuvvetler ve Hesapları; potansiyeli olan kuvvetler durumu. Genelleştirilmiş koordinatlarda bir sistemin dengesi için koşullar. Bir sistemin genelleştirilmiş koordinatlarda diferansiyel hareket denklemleri veya 2. tür Lagrange denklemleri. Potansiyel kuvvetler durumunda Lagrange denklemleri; Lagrange fonksiyonu (kinetik potansiyel).
Denge kararlılığı kavramı. Sistemin kararlı denge konumuna yakın bir serbestlik derecesine sahip mekanik bir sistemin küçük serbest titreşimleri ve özellikleri.
Etki teorisinin unsurları. Etki fenomeni. Darbe kuvveti ve darbe dürtüsü. Bir darbe kuvvetinin maddi bir nokta üzerindeki etkisi. Mekanik bir sistemin çarpma anında momentumundaki değişime ilişkin teorem. Vücudun sabit bir yüzeye doğrudan merkezi etkisi; elastik ve elastik olmayan etkiler. Darbe geri kazanım katsayısı ve deneysel olarak belirlenmesi. İki cismin doğrudan merkezi etkisi. Carnot teoremi.
KAYNAKÇA
Temel
Butenin N.V., Lunts Ya-L., Merkin D.R. Teorik mekaniğin dersi. T. 1, 2. M., 1985 ve önceki basımlar.
Dobronravov V.V., Nikitin N.N. Teorik mekaniğin dersi. M., 1983.
Starzhinsky V. M. Teorik mekanik. M., 1980.
Targ S.M. Teorik mekanikte kısa ders. M., 1986 ve önceki basımlar.
Yablonsky A.A., Nikiforova V.M. Teorik mekaniğin dersi. Bölüm 1. M., 1984 ve önceki basımlar.
Yablonsky A.A. Teorik mekaniğin dersi. Bölüm 2. M., 1984 ve önceki basımlar.
Meshchersky I.V. Teorik mekanikle ilgili problemlerin toplanması. M., 1986 ve önceki basımlar.
Teorik mekanikle ilgili problemlerin toplanması/Ed. K. S. Kolesnikova. M., 1983.
Ek olarak
Bat M.I., Dzhanelidze G.Yu., Kelzon A.S.Örnekler ve problemlerde teorik mekanik. Parça 1, 2. M., 1984 ve önceki basımlar.
Teorik mekanikle ilgili problemlerin toplanması/5razhnichen/so N.A., Kan V.L., Mintzberg B.L. ve diğerleri, M., 1987.
Novozhilov I.V., Zatsepin M.F. Teorik mekanikte tipik bilgisayar tabanlı hesaplamalar. M., 1986,
Teorik mekanikte kurs ödevleri için ödevlerin toplanması / Ed. A. A. Yablonsky. M., 1985 ve önceki basımlar (problem çözme örneklerini içerir).








