Your aim:know methods for proving inequalities and be able to apply them.
Concept of inequality proof . Some inequalities become true numerical inequality in front of everyone acceptable values variables or on some given set of variable values. For example, inequalities A 2 ³0, ( A–b) 2 ³ 0 ,a 2 +b 2 +c 2 " ³ 0 are true for any real values variables, and the inequality ³ 0 – for any real non-negative values A. Sometimes the problem of proving an inequality arises.
To prove an inequality means to show that this inequality turns into a true numerical inequality for all admissible values of the variables or for a given set of values of these variables.
Methods for proving inequalities. notice, that general method there is no proof of inequalities. However, some of them can be specified.
1. A method for estimating the sign of the difference between the left and right sides of an inequality. The difference between the left and right sides of the inequality is compiled and it is established whether this difference is positive or negative for the considered values of the variables (for non-strict inequalities it is necessary to establish whether this difference is non-negative or non-positive).
Example 1. For any real numbers A And b there is inequality
a 2 +b 2³ 2 ab. (1)
Proof. Let's make up the difference between the left and right sides of the inequality:
a 2 +b 2 – 2ab = a 2 – 2ab + b 2 = (a–b) 2 .
Since the square of any real number is a non-negative number, then ( a–b) 2 ³ 0, which means a 2 +b 2³ 2 ab for any real numbers A And b. Equality in (1) occurs if and only if a = b.
Example 2. Prove that if A³ 0 and b³ 0, then ³ , i.e. arithmetic mean of non-negative real numbers A And b no less than their geometric mean.
Proof. If A³ 0 and b³ 0, then
³ 0. So, ³ .
2. Deductive method proofs of inequalities. The essence of this method is as follows: using a series of transformations, the required inequality is derived from some known (reference) inequalities. For example, the following inequalities can be used as reference: A 2 ³ 0 for any aÎ R ; (a–b) 2 ³ 0 for any A And bÎ R ; (A 2 + b 2) ³ 2 ab for any a, bÎ R ; ³ at A ³ 0, b ³ 0.
Example 3. Prove that for any real numbers A And b there is inequality
A 2 + b 2 + With 2³ ab + bc + ac.
Proof. From the true inequalities ( a–b) 2 ³ 0, ( b – c) 2 ³ 0 and ( c – a) 2 ³ 0 it follows that A 2 + b 2³ 2 ab, b 2 + c 2³ 2 bc, c 2 + a 2³ 2 ac. Adding all three inequalities term by term and dividing both sides of the new one by 2, we obtain the required inequality.
The original inequality can be proved using the first method. Indeed, A 2 + b 2 + With 2 –ab – bc – ac = 0,5(2A 2 + 2b 2 + 2With 2 – 2ab – 2bc – 2ac) = = 0,5((a–b) 2 + (a–c) 2 + (b–c) 2)³ 0.
Difference between A 2 + b 2 + With 2 and ab + bc + ac greater than or equal to zero, which means that A 2 + b 2 + With 2³ ab + bc + ac(equality is true if and only if a = b = c).
3. Estimation method for proving inequalities.
Example 4. Prove inequality
+ + + … + >
Proof. It is easy to see that the left side of the inequality contains 100 terms, each of which is no less. In this case they say that left side the inequalities can be estimated from below as follows:
+ + + … + > = 100 = .
4. Full induction method. The essence of the method is to consider all special cases covering the condition of the problem as a whole.
Example 5. Prove that if x > ï atï , That x > y.
Proof. There are two possible cases:
A) at³ 0 ; thenï atï = y, and by condition x >ï atï . Means, x > y;
b) at< 0; thenï atï > y and by condition x >ï atï means x > y.
Practical part
Task 0. Take Blank sheet paper and on it write down the answers to all the oral exercises given below. Then check your answers against the answers or summary instructions at the end of this educational element in the “Your Assistant” section.
Oral exercises
1. Compare the sum of the squares of two unequal numbers and their double product.
2. Prove the inequality:
A) ![]() ;
;
b) ![]() ;
;
V) ![]() ;
;
3. It is known that. Prove that .
4. It is known that. Prove that .
Exercise 1. That more:
a) 2 + 11 or 9; d) + or;
b) or + ; e) – or;
c) + or 2; e) + 2 or + ?
Task 2. Prove that for any real x there is an inequality:
a) 3( x+ 1) + x– 4(2 + x) < 0; г) 4x 2 + 1 ³ 4 x;
b) ( x+ 2)(x+ 4) > (x+ 1)(x+ 5); e) ³ 2 x;
V) ( x– 2) 2 > x(x- 4); e) l + 2 x 4 > x 2 + 2x 3 .
Task 3. Prove that:
A) x 3 + 1³ x 2 + x, If x³ –1;
b) x 3 + 1 £ x 2 + x, If x£ –1 .
Task 4. Prove that if a ³ 0, b³ 0, With³ 0, d³ 0, then
(a 2 + b 2)(c 2 + d 2) ³ ( ac + bd) 2 .
Task 5. Prove the inequality by isolating perfect square:
A) x 2 – 2xy + 9y 2 ³ 0;
b) x 2 + y 2 + 2³2( x+y);
at 10 x 2 + 10xy + 5y 2 + 1 > 0;
G) x 2 – xy + y 2 ³ 0 ;
d) x 2 + y 2 + z 2 + 3³ 2( x + y + z);
e) ( x+ l)( x – 2y + l) + y 2 ³ 0 .
Task 6. Prove that:
A) x 2 + 2y 2 + 2xy + 6y+ l0 > 0 ;
b) x 2 + y 2 – 2xy + 2x – 2at + 1 > 0;
at 3 x 2 + y 2 + 8x+ 4y – 2xy + 22 ³ 0;
G) x 2 + 2xy+ 3y 2 + 2x + 6y + 3 > 0.
Task 7. Prove that if n³ k³ 1, then k(n–k+ 1) ³ n.
Task 8. Prove that if 4 A + 2b= 1, then a 2 + b 2³ .
Define Values A And b, at which equality occurs.
Task 9. Prove the inequality:
A) X 3 + at 3³ X 2 at + xy 2 at x³ 0 and y ³ 0;
b) X 4 + at 4³ X 3 at + xy 3 for any x And at;
V) X 5 + at 5³ X 4 at + xy 4 at x³ 0 and y ³ 0;
G) x n + y n ³ x n-1 y + xy n-1 at x³ 0 and y ³ 0.
Methods for proving inequalities.
Solving inequalities. Equivalent inequalities.
Interval method. Systems of inequalities.
Proof of inequalities. There are several proof methodsinequalities. We will look at them using the example of inequality:
Where a – positive number.
1). Using a known or previously proven inequality.
It is known that ( a– 1 )² 0 .
2). Estimating the sign of the difference between the parts of the inequality .
Consider the difference between the left and right sides:
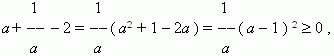
Moreover, equality occurs only when
a = 1 .3). Proof by contradiction.
Let's assume the opposite:a, we get: a 2 + 1 < 2 a, i.e.
a 2 + 1 – 2 a < 0 , or ( a– 1 ) 2 < 0, which is not true. (Why?) .
The resulting contradiction proves the validity of
The inequality in question.
4). Indefinite inequality method.
The inequality is called uncertain if he has a sign\/ or /\ ,
those. when we don't know which waythis sign should be turned
to get a fair inequality.
The same rules apply here asand with ordinary inequalities.
Consider the undefined inequality:
Multiplying both sides of the inequality bya, we get: a 2 + 1 \/ 2 a, i.e.
A 2 + 1 – 2 a \/ 0 , or ( a– 1) 2 \/ 0 , but here we already know how to turn
Sign \/ to get the correct inequality (How?). Turning it
IN in the right direction along the entire chain of inequalities from bottom to top, we
we obtain the required inequality.
Solving inequalities. Two inequalities containing the same unknowns are called equivalent , if they are valid for the same values of these unknowns. The same definition is used for the equivalence of two systems of inequalities. Solving inequalities is the process of moving from one inequality to another that is equivalent to an inequality. For this purpose they are used basic properties of inequalities(cm. ). In addition, replacing any expression with another identical to the given one can be used. Inequalities may be algebraic( containing only polynomials) And transcendental(for example logarithmic ortrigonometric). We will look at one very important method here,often used in solving algebraic inequalities
Interval method. Solve inequality: ( x – 3)( x – 5) < 2( x – 3). Here we cannot divide both sides of the inequality by (x – 3), since we do not know the sign of this binomial (it contains the unknown x ). Therefore we will rescheduleall terms of the inequality to the left side:
(x – 3)( x – 5) – 2( x – 3) < 0 ,
let's factorize it:
(x – 3)( x – 5 – 2) < 0 ,
and we get: ( x – 3)( x – 7) < 0. Теперь определим знак произведения в левой части неравенства в различных числовых интервалах. Заметим, что x= 3 and x = 7 - roots of this expression. Therefore, the entire number line will be divided by theseroots into the following three intervals:
In the interval I(x < 3 ) both factors are negative, therefore, their work positively; V interval II (3 < x< 7 ) first multiplier(x– 3 ) is positive, and the second ( x – 7 ) is negative, so their work negative; in the intervalIII(x> 7) both factors are positive, therefore, their work also positively. Now all that remains is to choose the interval in which our product negative. This is the intervalII, therefore, the solution to the inequality: 3 < x< 7. Last expression- the so-called double inequality. It means thatx must be both greater than 3 and less than 7.
EXAMPLE Solve the following inequality using the interval method:
(x – 1)(x – 2)(x – 3) … (x –100) > 0 .
Solution. The roots of the left side of the inequality are obvious: 1, 2, 3, …, 100.
They break number axis for 101 intervals:
Since the number of parentheses on the left side even(equals 100), then
At x < 1, когда все множители отрицательны, их произведение
Positively. When passing through the root there is a change
Sign of the work. Therefore, at the next interval, inside
Which product is positive, will be (2, 3), then (4, 5),
Then (6, 7), ... , (98, 99) and finally, x >100.
Thus, this inequality has a solution:
x < 1, 2 < x < 3, 4 < x < 5 ,…, x >100.
So, to solve an algebraic inequality, I need to move it allmembers to the left (orright side) and solvethe corresponding equation. After plot the found roots on the number axis; as a result, it is divided into a certain number of intervals. At the last stage of the solution, you need to determine what sign the polynomial has inside each of these intervals, and select the required intervals in accordance with the sign of the inequality being solved.
Note that most transcendental inequalities are reduced to an algebraic inequality by replacing the unknown. It must be solved with respect to the new unknown, and then, by reverse substitution, find a solution to the original inequality.
Systems of inequalities. To solve a system of inequalities, it is necessary to solve each of them and combine their solutions. This combination leads to one of the two possible cases: either the system has a solution or it doesn’t.
Example 1. Solve the system of inequalities:

Solution. Solution of the first inequality:
x < 4 ; а второго: x > 6.Thus, this system of inequalities has no solution.
(Why?)
Example 2. Solve the system of inequalities:
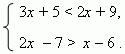
Solution: The first inequality, as before, gives:x < 4; но решение
The second inequality in this example:x > 1.
Thus, the solution to the system of inequalities: 1< x < 4.
Educational institution: Municipal Educational Institution Lyceum No. 1, Komsomolsk-on-Amur
Head: Budlyanskaya Natalya Leonidovna
If you would like to participate in great life, then fill your head with mathematics while you have the opportunity. She will then provide you with great assistance in all your work. (M.I. Kalinin)

Representation of the left side of the inequality as a sum of non-negative terms (the right side is 0) using identities.
Example 1. Prove that for any xϵR
Proof . 1 way.
2 way.
for a quadratic function which means its positivity for any real X.

Example 2. Prove that for any x and y
Proof. Example 3. Prove that Proof. Example 4. Prove that for any a and b Proof.

2. The opposite method
Here is a good example of using this method. Prove that for a, b ϵ R. Proof. Let's pretend that. But this clearly proves that our assumption is incorrect. C.T.D.

Example 5.Prove that for any numbers A, B, C the following inequality is true:
Proof. Obviously, it is enough to establish this inequality for non-negative A, B And WITH, since we will have the following relationship: ,
which is the rationale for the original inequality .

Now let there be such non-negative numbers A, B And WITH, for which the inequality holds , which is impossible under any real A, B And WITH. The assumption made above is refuted, which is proved by the original inequality under study.

Using the properties of the quadratic trinomial
The method is based on the property of non-negativity of a quadratic trinomial if And. Example 6. Prove that Proof. Let be, a=2, 2>0 =>

Example 7. Prove that for any real x and y the inequality holds Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
Proof . 1 way.
2 way.
for a quadratic function which means its positivity for any real X.

Example 2. Prove that for any x and y
Proof. Example 3. Prove that Proof. Example 4. Prove that for any a and b Proof.

2. The opposite method
Here is a good example of using this method. Prove that for a, b ϵ R. Proof. Let's pretend that. But this clearly proves that our assumption is incorrect. C.T.D.

Example 5.Prove that for any numbers A, B, C the following inequality is true:
Proof. Obviously, it is enough to establish this inequality for non-negative A, B And WITH, since we will have the following relationship: ,
which is the rationale for the original inequality .

Now let there be such non-negative numbers A, B And WITH, for which the inequality holds , which is impossible under any real A, B And WITH. The assumption made above is refuted, which is proved by the original inequality under study.

Using the properties of the quadratic trinomial
The method is based on the property of non-negativity of a quadratic trinomial if And. Example 6. Prove that Proof. Let be, a=2, 2>0 =>

Example 7. Prove that for any real x and y the inequality holds Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
2 way.
for a quadratic function which means its positivity for any real X.

Example 2. Prove that for any x and y
Proof. Example 3. Prove that Proof. Example 4. Prove that for any a and b Proof.

2. The opposite method
Here is a good example of using this method. Prove that for a, b ϵ R. Proof. Let's pretend that. But this clearly proves that our assumption is incorrect. C.T.D.

Example 5.Prove that for any numbers A, B, C the following inequality is true:
Proof. Obviously, it is enough to establish this inequality for non-negative A, B And WITH, since we will have the following relationship: ,
which is the rationale for the original inequality .

Now let there be such non-negative numbers A, B And WITH, for which the inequality holds , which is impossible under any real A, B And WITH. The assumption made above is refuted, which is proved by the original inequality under study.

Using the properties of the quadratic trinomial
The method is based on the property of non-negativity of a quadratic trinomial if And. Example 6. Prove that Proof. Let be, a=2, 2>0 =>

Example 7. Prove that for any real x and y the inequality holds Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
for a quadratic function which means its positivity for any real X.

Example 2. Prove that for any x and y
Proof. Example 3. Prove that Proof. Example 4. Prove that for any a and b Proof.

2. The opposite method
Here is a good example of using this method. Prove that for a, b ϵ R. Proof. Let's pretend that. But this clearly proves that our assumption is incorrect. C.T.D.

Example 5.Prove that for any numbers A, B, C the following inequality is true:
Proof. Obviously, it is enough to establish this inequality for non-negative A, B And WITH, since we will have the following relationship: ,
which is the rationale for the original inequality .

Now let there be such non-negative numbers A, B And WITH, for which the inequality holds , which is impossible under any real A, B And WITH. The assumption made above is refuted, which is proved by the original inequality under study.

Using the properties of the quadratic trinomial
The method is based on the property of non-negativity of a quadratic trinomial if And. Example 6. Prove that Proof. Let be, a=2, 2>0 =>

Example 7. Prove that for any real x and y the inequality holds Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
which means its positivity for any real X.

Example 2. Prove that for any x and y
Proof. Example 3. Prove that Proof. Example 4. Prove that for any a and b Proof.

2. The opposite method
Here is a good example of using this method. Prove that for a, b ϵ R. Proof. Let's pretend that. But this clearly proves that our assumption is incorrect. C.T.D.

Example 5.Prove that for any numbers A, B, C the following inequality is true:
Proof. Obviously, it is enough to establish this inequality for non-negative A, B And WITH, since we will have the following relationship: ,
which is the rationale for the original inequality .

Now let there be such non-negative numbers A, B And WITH, for which the inequality holds , which is impossible under any real A, B And WITH. The assumption made above is refuted, which is proved by the original inequality under study.

Using the properties of the quadratic trinomial
The method is based on the property of non-negativity of a quadratic trinomial if And. Example 6. Prove that Proof. Let be, a=2, 2>0 =>

Example 7. Prove that for any real x and y the inequality holds Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.

Example 2. Prove that for any x and y
Proof. Example 3. Prove that Proof. Example 4. Prove that for any a and b Proof.

2. The opposite method
Here is a good example of using this method. Prove that for a, b ϵ R. Proof. Let's pretend that. But this clearly proves that our assumption is incorrect. C.T.D.

Example 5.Prove that for any numbers A, B, C the following inequality is true:
Proof. Obviously, it is enough to establish this inequality for non-negative A, B And WITH, since we will have the following relationship: ,
which is the rationale for the original inequality .

Now let there be such non-negative numbers A, B And WITH, for which the inequality holds , which is impossible under any real A, B And WITH. The assumption made above is refuted, which is proved by the original inequality under study.

Using the properties of the quadratic trinomial
The method is based on the property of non-negativity of a quadratic trinomial if And. Example 6. Prove that Proof. Let be, a=2, 2>0 =>

Example 7. Prove that for any real x and y the inequality holds Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
Proof. Example 3. Prove that Proof. Example 4. Prove that for any a and b Proof.

2. The opposite method
Here is a good example of using this method. Prove that for a, b ϵ R. Proof. Let's pretend that. But this clearly proves that our assumption is incorrect. C.T.D.

Example 5.Prove that for any numbers A, B, C the following inequality is true:
Proof. Obviously, it is enough to establish this inequality for non-negative A, B And WITH, since we will have the following relationship: ,
which is the rationale for the original inequality .

Now let there be such non-negative numbers A, B And WITH, for which the inequality holds , which is impossible under any real A, B And WITH. The assumption made above is refuted, which is proved by the original inequality under study.

Using the properties of the quadratic trinomial
The method is based on the property of non-negativity of a quadratic trinomial if And. Example 6. Prove that Proof. Let be, a=2, 2>0 =>

Example 7. Prove that for any real x and y the inequality holds Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
Proof. Example 4. Prove that for any a and b Proof.

2. The opposite method
Here is a good example of using this method. Prove that for a, b ϵ R. Proof. Let's pretend that. But this clearly proves that our assumption is incorrect. C.T.D.

Example 5.Prove that for any numbers A, B, C the following inequality is true:
Proof. Obviously, it is enough to establish this inequality for non-negative A, B And WITH, since we will have the following relationship: ,
which is the rationale for the original inequality .

Now let there be such non-negative numbers A, B And WITH, for which the inequality holds , which is impossible under any real A, B And WITH. The assumption made above is refuted, which is proved by the original inequality under study.

Using the properties of the quadratic trinomial
The method is based on the property of non-negativity of a quadratic trinomial if And. Example 6. Prove that Proof. Let be, a=2, 2>0 =>

Example 7. Prove that for any real x and y the inequality holds Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
Proof.

2. The opposite method
Here is a good example of using this method. Prove that for a, b ϵ R. Proof. Let's pretend that. But this clearly proves that our assumption is incorrect. C.T.D.

Example 5.Prove that for any numbers A, B, C the following inequality is true:
Proof. Obviously, it is enough to establish this inequality for non-negative A, B And WITH, since we will have the following relationship: ,
which is the rationale for the original inequality .

Now let there be such non-negative numbers A, B And WITH, for which the inequality holds , which is impossible under any real A, B And WITH. The assumption made above is refuted, which is proved by the original inequality under study.

Using the properties of the quadratic trinomial
The method is based on the property of non-negativity of a quadratic trinomial if And. Example 6. Prove that Proof. Let be, a=2, 2>0 =>

Example 7. Prove that for any real x and y the inequality holds Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
Prove that for a, b ϵ R. Proof. Let's pretend that. But this clearly proves that our assumption is incorrect. C.T.D.

Example 5.Prove that for any numbers A, B, C the following inequality is true:
Proof. Obviously, it is enough to establish this inequality for non-negative A, B And WITH, since we will have the following relationship: ,
which is the rationale for the original inequality .

Now let there be such non-negative numbers A, B And WITH, for which the inequality holds , which is impossible under any real A, B And WITH. The assumption made above is refuted, which is proved by the original inequality under study.

Using the properties of the quadratic trinomial
The method is based on the property of non-negativity of a quadratic trinomial if And. Example 6. Prove that Proof. Let be, a=2, 2>0 =>

Example 7. Prove that for any real x and y the inequality holds Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
Let's pretend that. But this clearly proves that our assumption is incorrect. C.T.D.

Example 5.Prove that for any numbers A, B, C the following inequality is true:
Proof. Obviously, it is enough to establish this inequality for non-negative A, B And WITH, since we will have the following relationship: ,
which is the rationale for the original inequality .

Now let there be such non-negative numbers A, B And WITH, for which the inequality holds , which is impossible under any real A, B And WITH. The assumption made above is refuted, which is proved by the original inequality under study.

Using the properties of the quadratic trinomial
The method is based on the property of non-negativity of a quadratic trinomial if And. Example 6. Prove that Proof. Let be, a=2, 2>0 =>

Example 7. Prove that for any real x and y the inequality holds Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
C.T.D.

Example 5.Prove that for any numbers A, B, C the following inequality is true:
Proof. Obviously, it is enough to establish this inequality for non-negative A, B And WITH, since we will have the following relationship: ,
which is the rationale for the original inequality .

Now let there be such non-negative numbers A, B And WITH, for which the inequality holds , which is impossible under any real A, B And WITH. The assumption made above is refuted, which is proved by the original inequality under study.

Using the properties of the quadratic trinomial
The method is based on the property of non-negativity of a quadratic trinomial if And. Example 6. Prove that Proof. Let be, a=2, 2>0 =>

Example 7. Prove that for any real x and y the inequality holds Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
Proof. Obviously, it is enough to establish this inequality for non-negative A, B And WITH, since we will have the following relationship: ,
which is the rationale for the original inequality .

Now let there be such non-negative numbers A, B And WITH, for which the inequality holds , which is impossible under any real A, B And WITH. The assumption made above is refuted, which is proved by the original inequality under study.

Using the properties of the quadratic trinomial
The method is based on the property of non-negativity of a quadratic trinomial if And. Example 6. Prove that Proof. Let be, a=2, 2>0 =>

Example 7. Prove that for any real x and y the inequality holds Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
,
which is the rationale for the original inequality .

Now let there be such non-negative numbers A, B And WITH, for which the inequality holds , which is impossible under any real A, B And WITH. The assumption made above is refuted, which is proved by the original inequality under study.

Using the properties of the quadratic trinomial
The method is based on the property of non-negativity of a quadratic trinomial if And. Example 6. Prove that Proof. Let be, a=2, 2>0 =>

Example 7. Prove that for any real x and y the inequality holds Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
, which is impossible under any real A, B And WITH. The assumption made above is refuted, which is proved by the original inequality under study.

Using the properties of the quadratic trinomial
The method is based on the property of non-negativity of a quadratic trinomial if And. Example 6. Prove that Proof. Let be, a=2, 2>0 =>

Example 7. Prove that for any real x and y the inequality holds Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
And. Example 6. Prove that Proof. Let be, a=2, 2>0 =>

Example 7. Prove that for any real x and y the inequality holds Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
Proof. Let be, a=2, 2>0 =>

Example 7. Prove that for any real x and y the inequality holds Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
=>

Example 7. Prove that for any real x and y the inequality holds Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
Proof. Consider the left-hand side of the inequality as a quadratic trinomial with respect to X: , a>0, D D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
D= => P(x)>0 And true for any real values X And u.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.

Example 8. Prove that for any real values of x and y. Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
Proof. Let
, This means that for any real at and inequality is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
is satisfied for any real X And u.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.

Method of introducing new variables or substitution method
Example 9. Prove that for any non-negative numbers x, y, z Proof. Let us use the correct inequality for, . We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
. We obtain the inequality under study

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.

Using function properties.
Example 10. Let's prove the inequality for any a and b. Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
Proof. Let's consider 2 cases: If a=b then true
Moreover, equality is achieved only when a=b=0. 2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
If a=b then true
2)If , on R => ()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
()* ()>0, which proves the inequality

Example 11. Let us prove that for any
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
Proof. on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
on R. If, then the signs of the numbers coincide, which means the difference under study is positive =>

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.

Application of the method of mathematical induction
This method is used to prove inequalities regarding natural numbers. Example 12. Prove that for any nϵN
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
Let's check the truth of the statement when
- (right) 2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
Let's check the truth of the statement when
2) Assume the truth of the statement when (k>1)

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.

3) Let's prove the truth of the statement when n=k+1. Let's compare and: We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
We have: Conclusion: the statement is true for anyone nϵN.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.

Using remarkable inequalities
Theorem on averages (Cauchy's inequality)
Cauchy–Bunyakovsky inequality
Bernoulli's inequality
Let us consider each of the listed inequalities separately.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.

Application of the mean value theorem (Cauchy inequality)
The arithmetic mean of several non-negative numbers is greater than or equal to their geometric mean , Where The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.
The equal sign is achieved if and only if Let's consider special cases of this theorem:

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.

Let n=2, then
Let n=2, a>0, then
Let n=3, then
Example 13. Prove that for all non-negative a,b,c the inequality holds Proof.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.

Cauchy-Bunyakovsky inequality
The Cauchy-Bunyakovsky inequality states that for any; the ratio is valid The proven inequality has a geometric interpretation. For n=2,3 it expresses the well-known fact that the scalar product of two vectors on the plane and in space does not exceed the product of their lengths. For n=2 the inequality has the form: . For n=3 we get

Example 14.

Example 14.
Proof. Let us write the inequality under study in the following form:
This is a obviously true inequality, since it is a special case of the Cauchy–Bunyakovsky inequality.
Example 15. Prove that for any a,b,c ϵ R the following inequality holds:
Proof. It is enough to write this inequality in the form
and refer to the Cauchy–Bunyakovsky inequality.

Bernoulli's inequality
Bernoulli's inequality states that if x>-1, then for all natural values of n the following inequality holds: The inequality can be used for expressions of the form In addition, a very large group of inequalities can be easily proven using Bernoulli's theorem.

In addition, a very large group of inequalities can be easily proven using Bernoulli's theorem.

Example 16.
Proof. Putting x=0.5 and applying Bernoulli's theorem to express
We obtain the required inequality.
Example 17. Prove that for any n ϵ N
Proof.
by Bernoulli's theorem, as required. 
David Gilbert was asked about one of his former students. “Oh, so-and-so?” Hilbert remembered. “He became a poet. He had too little imagination for mathematics.

MOU Grishino-Slobodskaya secondary school
Module program
"Methods for proving inequalities"
as part of an elective course
"Behind the Pages of a Mathematics Textbook"
for students in grades 10-11
Compiled by:
mathematic teacher
Pankova E.Yu
Explanatory note
“Mathematics is called a tautological science: in other words, mathematicians are said to spend time proving that objects are equal to themselves. This statement is highly inaccurate for two reasons. Firstly, mathematics, despite its inherent scientific language, is not science; rather, it can be called art. Secondly The main results of mathematics are more often expressed by inequalities rather than equalities.”
Inequalities are used constantly in the practical work of mathematicians. They are used to obtain a number of interesting and important extremal properties of “symmetrical” figures: square, cube, equilateral triangle, as well as to prove the convergence of iterative processes and calculate some limits. The role of inequalities is also important in various issues of natural science and technology.
Problems on proving inequalities are the most difficult and interesting of the traditional ones. Proving inequalities requires the true ingenuity and creativity that makes mathematics the exciting subject that it is.
Teaching proofs plays a big role in the development of deductive-mathematical thinking and general thinking abilities of students. How to teach schoolchildren to independently prove inequalities? The answer is: only by considering many techniques and methods of evidence and applying them regularly.
The ideas used to prove inequalities are almost as varied as the inequalities themselves. In specific situations, general methods often lead to ugly solutions. But only a few schoolchildren succeed in combining several “basic” inequalities in a non-obvious way. And, besides, nothing prevents the student in each specific case from looking for a better solution than that obtained by the general method. For this reason, proof of inequalities is often relegated to the realm of art. And like any art, there are technical techniques here, the range of which is very wide and it is very difficult to master them all, but every teacher should strive to expand the mathematical tools available to him.
This module is recommended for students in grades 10-11. Not all possible methods for proving inequalities are discussed here (the method of replacing a variable, proving inequalities using a derivative, the method of research and generalization, and the ordering technique are not covered). You can offer to consider other methods at the second stage (for example, in 11th grade), if this module of the course arouses interest among students, and also based on the success of mastering the first part of the course.
|
Equations and inequalities with a parameter. |
||
|
Methods for proving inequalities. |
||
|
Equations and inequalities containing an unknown under the modulus sign. |
||
|
Systems of inequalities with two variables. |
"Behind the Pages of a Mathematics Textbook"
"Methods for proving inequalities"
|
Introduction. |
||
|
Proof of inequalities based on definition. |
||
|
Method mathematical induction. |
||
|
Application of classical inequalities. |
||
|
Graphic method. |
||
|
The opposite method. |
||
|
A technique for considering inequalities with respect to one of the variables. |
||
|
The idea of strengthening. |
||
|
Lesson - control. |
Lesson 1. Introduction.
Proving inequalities is a fascinating and challenging topic in elementary mathematics. The lack of a unified approach to the problem of proving inequalities leads to the search for a number of techniques suitable for proving inequalities certain types. This elective course will cover the following methods for proving inequalities:
Repetition:
Prove some properties.
Classic inequalities:
1)
 (Cauchy inequality)
(Cauchy inequality)
2)

3)

4)

Historical reference:
Inequality (1) is named after the French mathematician Auguste Cauchy. Number  called arithmetic mean numbers a and b;
called arithmetic mean numbers a and b;
number  called geometric mean numbers a and b. Thus, an inequality means that the arithmetic mean of two positive numbers is not less than their geometric mean.
called geometric mean numbers a and b. Thus, an inequality means that the arithmetic mean of two positive numbers is not less than their geometric mean.
Additionally:
Consider several mathematical sophisms with inequalities.
Mathematical sophistry- an amazing statement, the proof of which contains invisible and sometimes quite subtle errors.
Sophisms are false results obtained through reasoning that only seem correct, but necessarily contain one or another error.
Example:
Four is over twelve
Lesson 2. Proof of inequalities based on definition.
The essence of this method is as follows: in order to establish the validity of the inequalities F(x,y,z)>S(x,y,z) make up the difference F(x,y,z)-S(x,y,z) and prove that it is positive. Using this method, one often isolates a square, a cube of a sum or difference, or an incomplete square of a sum or difference. This helps determine the sign of the difference.
Example.
Prove the inequality (x+y)(x+y+2cosx)+2  2sin 2 x
2sin 2 x
Proof:
Consider the difference (x+y)(x+y+2cosx)+2- 2sin 2 x =(x+y)(x+y+2cosx)+2cos 2 x=(x+y)(x+y+2cosx) + cos 2 x +cos 2 x= (x+y) 2 +2(x+y)cosx+ cos 2 x +cos 2 x=((x+y)+cosx) 2 + cos 2 x 0.
Prove inequality:
1.ab(a+b)+bc(b+c)+ac(a+c) 6abc
3.
4. >2x-20
>2x-20
5.

6.(a+b)(b+c)(c+a) 8abc
7.
Lesson 3. Method of mathematical induction.
When proving inequalities that include integers often resort to the method of mathematical induction. The method is as follows:
1) check the truth of the theorem for n=1;
2) we assume that the theorem is true for some n=k, and based on this assumption we prove the truth of the theorem for n=k+1;
3) based on the first two steps and the principle of mathematical induction, we conclude that the theorem is true for any n.
Example.
Prove inequality
Proof:
1) for n=2 the inequality is true:
2) Let the inequality be true for n=k i.e.  (*)
(*)
Let us prove that the inequality is true for n=k+1, i.e.  .
.  Let's multiply both sides of the inequality (*) by
Let's multiply both sides of the inequality (*) by
we obtain 3) From item 1. and item 2 we conclude that the inequality is true for any n.
Prove inequality:
1)
2)
3)
4)
5)
6) .
.
Assignments for work in the classroom and at home
Lesson4. Application of classical inequalities.
Example.
Prove inequality:
Proof:
The essence of this method is as follows: using a series of transformations, the required inequality is derived using some classical inequalities. As support inequality  .
.
we use
 Let us reduce this inequality to the following form:
Let us reduce this inequality to the following form:
, Then  Let us reduce this inequality to the following form:
Let us reduce this inequality to the following form:
Prove inequality:
But =
2)
 1)(p+2)(q+2)(p+q)16pq (the inequality is used for proof)
1)(p+2)(q+2)(p+q)16pq (the inequality is used for proof)
(for docs inequality is used)
4)
 3) (a+b)(b+c)(c+a) 8abc (the inequality is used for proof)
3) (a+b)(b+c)(c+a) 8abc (the inequality is used for proof)
(for the doc, inequality is used).
Lesson 5. Graphic method.
The proof of inequalities by the graphical method is as follows: if we prove the inequality f(x)>g(x)(f(x)
1) build graphs of the functions y=f(x) and y=g(x);
Example.
Prove inequality:
2) if the graph of the function y=f(x) is located above (below) the graph of the function y=g(x), then the inequality being proved is true.  cosx
cosx
Proof:
,x0

Let us construct graphs of the functions y=cosx and
It is clear from the graph that at x0 the graph of the function y=cosx lies above the graph of the function y=.
Prove inequality:
1)
5)
Assignments for work in the classroom and at home.
Lesson 6. The opposite method
Example.
Prove inequality:
Proof:
The essence of this method is as follows: let you need to prove the truth of the inequality F(x,y,z) S(x,y,z)(1). They assume the opposite, i.e. that for at least one set of variables the inequality F(x,y,z) S(x,y,z) (2) is true. Using the properties of inequalities, transformations of inequality (2) are performed. If as a result of these transformations a false inequality is obtained, then this means that the assumption that inequality (2) is true is incorrect, and therefore inequality (1) is true.
Let's assume the opposite, i.e.  Let us square both sides of the inequality and obtain , from which
Let us square both sides of the inequality and obtain , from which
 and onwards
and onwards
. But this contradicts Cauchy's inequality. This means that our assumption is incorrect, that is, the inequality is true. Assignments for work in the classroom and at home.
Lesson9. Lesson - control of students' knowledge. This lesson can be done in pairs or if class in groups. At the end of the lesson, each student must be assessed. This is the credit form for this course. It is not recommended to conduct a test on this topic because the proof of inequalities, as already mentioned in the explanatory note, belongs to the field of art. At the beginning, students are asked to determine the method for proving the proposed inequalities. If students have difficulties, the teacher tells them the rational method, warning the group that this, of course, will affect their grade.
Work in pairs.
Examples of tasks.
________________________________________________________________
Prove inequality:
1. (method of mathematical induction)
(method of mathematical induction)
2. (a-priory)
(a-priory)
Module. Equations and inequalities with parameters. ... properties, formulation and proof theorems, derivation of formulas... the simplest inequalities. 7. Know how to use method intervals...
Open Olympiad program and mathematics preparation requirements for 9th grade students
ProgramConcept module real number. Arithmetic and geometric definitions module. Disclosure modules. ... inequalities. Proof inequalities. Solving linear, quadratic, fractional rational problems inequalities with one variable. Solution inequalities ...
Elective program in mathematics for 8th grade
ProgramDemonstrate methods proof a little more complex inequalities with this simple inequalities? So, in this ministerial program ...








