Peringkat Taylor melakukan servis cara yang efektif untuk mempelajari fungsi analitik dalam lingkaran zol Untuk mempelajari fungsi analitik dalam domain ring, ternyata dimungkinkan untuk membangun ekspansi pangkat positif dan negatif (z - zq) dalam bentuk generalisasi ekspansi Taylor. Deret (1), yang dipahami sebagai penjumlahan dua deret, disebut deret Laurent. Jelas bahwa daerah konvergensi deret (1) adalah bagian umum daerah konvergensi masing-masing deret (2). Mari kita temukan dia. Luas konvergensi deret pertama adalah lingkaran yang jari-jarinya ditentukan oleh rumus Cauchy-Hadamard. Di dalam lingkaran konvergensi, deret (3) konvergen ke fungsi analitik, dan pada lingkaran mana pun yang berjari-jari lebih kecil, deret tersebut konvergen. secara mutlak dan seragam. Baris kedua adalah seri kekuatan relatif terhadap suatu variabel, Deret (5) konvergen di dalam lingkaran konvergensinya ke fungsi analitik variabel kompleks m-*oo, dan dalam lingkaran mana pun yang berjari-jari lebih kecil konvergen secara absolut dan seragam, yang berarti luas konvergensi deret (4) adalah bagian luar lingkaran - Jika maka ada wilayah umum konvergensi deret (3) dan (4) - cincin melingkar yang deret (1) konvergen ke fungsi analitik. Terlebih lagi, di ring mana pun, ia menyatu secara mutlak dan seragam. Contoh 1. Tentukan luas konvergensi deret rad Laurent Titik-titik tunggal terisolasi dan klasifikasinya M Luas konvergensi baris pertama adalah bagian luar lingkaran dan luas konvergensi baris kedua adalah di dalam lingkaran Jadi, seri ini konvergen dalam lingkaran Teorema 15. Setiap fungsi f(z), bernilai tunggal dan apolitis dalam lingkaran melingkar dapat direpresentasikan dalam lingkaran ini sebagai jumlah dari deret konvergen, yang koefisien Cnnya ditentukan dan dihitung secara unik sesuai dengan rumus dimana 7p adalah lingkaran berjari-jari m Mari kita pasang R di dalam ring titik sembarang z. Mari kita buat lingkaran dengan pusat di titik r, yang jari-jarinya memenuhi pertidaksamaan dan pertimbangkan cincin Po yang baru teorema integral Cauchy untuk domain terhubung perkalian yang kita miliki. Kami mentransformasikan secara terpisah masing-masing integral dalam jumlah (8). Untuk semua titik £ sepanjang lingkaran 7d* hubungan de jumlah deret konvergen seragam 1 1 terpenuhi. Oleh karena itu, pecahan ^ dapat direpresentasikan dalam vi- / "/ Dengan mengalikan kedua bagian dengan fungsi kontinu (O dan melakukan integrasi suku demi suku sepanjang lingkaran, kita memperoleh bahwa kita melakukan transformasi integral kedua dengan cara yang sedikit berbeda. Untuk semua titik £ pada lingkaran ir>, hubungan berikut berlaku sebagai jumlah dari deret yang konvergen seragam. Mengalikan kedua bagian dengan fungsi kontinu) dan mengintegrasikan suku-suku di sepanjang lingkaran 7/, kita memperoleh bahwa Perhatikan bahwa integral dalam rumus (10) dan (12) adalah fungsi analitik dalam lingkaran melingkar. Oleh karena itu, menurut teorema Cauchy, nilai integral yang bersesuaian tidak akan berubah jika kita mengganti lingkaran 7/r dan 7r/ dengan lingkaran mana pun. Hal ini memungkinkan kita untuk menggabungkan rumus (10) dan (12), Mengganti integral pada ruas kanan rumus (8) dengan ekspresi masing-masing (9) dan (11), kita memperoleh pemuaian yang diinginkan Karena z - titik sewenang-wenang ring, maka deret (14) konvergen ke fungsi f(z) di mana saja di ring ini, dan di sembarang ring deret tersebut konvergen ke fungsi ini secara mutlak dan seragam. Sekarang mari kita buktikan bahwa penguraian bentuk (6) adalah unik. Mari kita asumsikan bahwa ada satu pemuaian lagi. Maka di mana pun di dalam ring R kita akan mempunyai Pada lingkaran, deret (15) konvergen secara seragam. Mari kita kalikan kedua ruas persamaan (di mana m adalah bilangan bulat tetap, dan integrasikan kedua deret suku demi suku. Hasilnya, kita peroleh di ruas kiri, dan di ruas kanan - Sch. Jadi, (4, = St. Sejak M - nomor sewenang-wenang, maka persamaan terakhir membuktikan keunikan dekomposisi. Deret (6) yang koefisiennya dihitung dengan menggunakan rumus (7), disebut deret Laurent dari fungsi f(z) pada ring kekuatan negatif disebut bagian yang benar dari deret Laurent, dan dengan bagian negatif - bagiannya bagian utama. Rumus (7) untuk koefisien deret Laurent jarang digunakan dalam praktik, karena biasanya memerlukan perhitungan yang rumit. Biasanya, jika memungkinkan, ekspansi Taylor yang sudah jadi digunakan fungsi dasar. Berdasarkan keunikan penguraiannya, cara hukum apapun akan membuahkan hasil yang sama. Contoh 2. Perhatikan perluasan fungsi deret Laurent berbagai bidang, menerima Fuiscia /(g) memiliki dua poin tunggal: . Oleh karena itu, terdapat tiga daerah annular yang berpusat di titik r = 0. Pada masing-masing daerah tersebut, fungsi /(r) bersifat analitik: a) lingkaran adalah cincin, bagian luar lingkaran (Gbr. 27). Mari kita cari perluasan Laurent dari fungsi /(z) di masing-masing wilayah ini. Mari kita nyatakan /(z) sebagai jumlah pecahan dasar a) Lingkaran Kita transformasikan relasi (16) dengan menggunakan rumus jumlah suku-sukunya perkembangan geometri, kita peroleh Substitusikan pemuaian yang ditemukan ke dalam rumus (17): Pemuaian ini adalah deret Taylor dari fungsi /(z). b) Gelanggang untuk fungsi -r tetap konvergen pada gelanggang ini, karena Deret (19) untuk fungsi j^j untuk |z| > 1 menyimpang. Oleh karena itu, kita transformasikan fungsi /(z) sebagai berikut: sekali lagi menerapkan rumus (19), kita memperoleh bahwa Deret ini konvergen untuk. Substitusikan ekspansi (18) dan (21) ke dalam relasi (20), kita peroleh c) Bagian luar lingkaran untuk fungsi -z untuk |z| > 2 divergen, dan deret (21) untuk fungsi- Mari kita nyatakan fungsi /(z) dalam bentuk berikut: /<*>Dengan menggunakan rumus (18) dan (19), kita memperoleh OR 1 Contoh ini menunjukkan bahwa untuk fungsi yang sama f(z) ekspansi Laurent, secara umum, memiliki jenis yang berbeda untuk cincin yang berbeda. Contoh 3. Carilah perluasan deret Laurent ke-8 dari suatu fungsi Deret Laurent Titik-titik singular terisolasi dan klasifikasinya dalam domain cincin A Kita menggunakan representasi fungsi f(z) dalam bentuk berikut: dan mentransformasikan suku kedua Menggunakan rumus jumlah suku suatu barisan geometri, kita peroleh Dengan mensubstitusi ekspresi yang ditemukan ke dalam rumus (22), kita memiliki Contoh 4. Perluas fungsi deret Laurent di titik zq = 0. Untuk kompleks apa pun kita punya Letakkan Ini pemuaian berlaku untuk sembarang titik z Ф 0. In dalam hal ini daerah annular mewakili seluruh bidang kompleks dengan satu titik yang dibuang z - 0. Daerah ini dapat didefinisikan dengan hubungan berikut: Fungsi ini bersifat analitis pada daerah Dari rumus (13) untuk koefisien deret Laurent, dengan menggunakan persamaan yang sama dengan penalaran seperti pada paragraf sebelumnya, maka diperoleh pertidaksamaan Kouiw. jika fungsi f(z) dibatasi pada lingkaran, dimana M adalah konstanta), maka titik-titik tunggal terisolasi Titik zo disebut titik tunggal terisolasi dari fungsi f(z) jika terdapat lingkungan cincin dari titik tersebut ( himpunan ini kadang-kadang disebut lingkungan tertusuk titik 2o), yang fungsinya f(z) bersifat unik dan analitik. Pada titik zo itu sendiri, fungsinya tidak terdefinisi atau tidak ambigu dan analitik. Tergantung pada perilaku fungsi /(r) ketika mendekati titik zo, ada tiga jenis yang dibedakan: poin tunggal. Suatu titik tunggal terisolasi dikatakan: 1) dapat dilepas jika terdapat titik berhingga 2) pymusach jika 3) titik tunggal esensial jika fungsi f(z) tidak mempunyai limit pada Tipe titik tunggal terisolasi berkaitan erat dengan sifat perluasan fungsi Laurent dengan pusat tertusuk. Teorema 16. Suatu titik tunggal terisolasi z0 dari suatu fungsi f(z) adalah titik tunggal yang dapat dipindahkan jika dan hanya jika perluasan Laurent dari fungsi f(z) di lingkungan titik zo tidak mengandung bagian utama, yaitu, memiliki bentuk Biarkan zo menjadi titik tunggal yang dapat dilepas. Maka ada yang berhingga, oleh karena itu, fungsi f(z) dibatasi pada lingkungan prokologis dari titik z. Kita tentukan Berdasarkan pertidaksamaan Cauchy Karena p dapat dipilih menjadi kecil secara sembarang, maka semua koefisien berpangkat negatif (z). - 20) sama dengan nol: Sebaliknya, misalkan perluasan fungsi Laurent /(r) di lingkungan titik zq hanya memuat bagian yang benar, yaitu berbentuk (23) dan oleh karena itu, adalah Taylor. Sangat mudah untuk melihat bahwa untuk z -* z0 fungsi /(z) mempunyai nilai limit: Teorema 17. Titik tunggal terisolasi zq dari fungsi f(z) dapat dipindahkan jika dan hanya jika fungsi J(z) adalah dibatasi di beberapa lingkungan tertusuk pada titik zq, Zgmechai tidak. Misalkan r adalah titik tunggal yang dapat dipindahkan dari fungsi /(r). Dengan asumsi kita mendapatkan bahwa fungsi /(r) bersifat analitik pada suatu lingkaran yang berpusat di titik r. Ini menentukan nama titik - yang dapat dilepas. Teorema 18. Titik tunggal terisolasi zq dari suatu fungsi f(z) adalah kutub jika dan hanya jika Ekspansi Laurent dari fungsi f(z) di lingkungan suatu titik mengandung sejumlah suku bukan nol yang berhingga (dan positif), yaitu berbentuk 4 Misalkan z0 adalah sebuah kutub. Sejak itu ada lingkungan titik z0 yang tertusuk di mana fungsinya f(z) adalah analitik dan bukan nol. Kemudian di lingkungan ini ditentukan fungsi analitik dan Akibatnya, titik zq adalah titik tunggal yang dapat dipindahkan (nol) dari fungsi tersebut atau di mana h(z) adalah fungsi analitik, h(z0) Φ 0. Maka h(zo) Φ 0 juga bersifat analitik, maka fungsi u bersifat analitik di lingkungan titik zq, dan oleh karena itu, dari situ kita peroleh bahwa Sekarang mari kita asumsikan bahwa fungsi f(z) mempunyai perluasan bentuk (24) di lingkungan tertusuk titik zо. Artinya di lingkungan ini fungsi f(z) bersifat analitik bersama dengan fungsinya. Untuk fungsi g(z) pemuaiannya valid, dari situ terlihat bahwa zq merupakan titik tunggal yang dapat dipindahkan dari fungsi g(z) dan ada adalah fakta sederhana lainnya. Titik Zq merupakan kutub dari fungsi f(z) jika dan hanya jika fungsi g(z) = yj dapat diperluas ke fungsi analitik di sekitar titik zq dengan menetapkan g(z0) = 0. Orde dari kutub fungsi f(z) disebut orde nol dari fungsi jfa. Dari Teorema 16 dan 18 berikut ini pernyataan selanjutnya. Teorema 19. Suatu titik tunggal terisolasi pada dasarnya adalah tunggal jika dan hanya jika bagian utama dari ekspansi Laurent di lingkungan tertusuk titik ini mengandung banyak suku bukan nol yang tak terhingga. Contoh 5. Titik tunggal dari fungsi tersebut adalah zo = 0. Kita mempunyai Deret Laurent Titik tunggal terisolasi dan klasifikasinya Oleh karena itu, zo = O adalah titik tunggal yang dapat dipindahkan. Perluasan fungsi /(z) menjadi deret Laurent di lingkungan sekitar titik nol hanya berisi bagian yang benar: Contoh7. /(z) = Titik tunggal fungsi f(z) adalah zq = 0. Mari kita perhatikan perilaku fungsi ini pada sumbu nyata dan sumbu imajiner: pada sumbu nyata di x 0, pada sumbu imajiner Oleh karena itu, tidak berhingga maupun batas tak terbatas f(z) tidak ada untuk z -* 0. Artinya, titik r = 0 pada dasarnya merupakan titik singular dari fungsi f(z). Mari kita cari perluasan Laurent dari fungsi f(z) di sekitar titik nol. Untuk setiap kompleks C kita mempunyai Set. Kemudian ekspansi Laurent berisi setan nomor akhir suku dengan pangkat negatif z.
Model dijelaskan oleh sistem dua otonom persamaan diferensial.
Bidang fase. Potret fase. metode isoklin. Isoklin utama. Keberlanjutan keadaan stabil. Sistem linier. Jenis titik tunggal: simpul, pelana, fokus, tengah. Contoh: reaksi kimia pesanan pertama.
Hasil yang paling menarik pada pemodelan kualitatif sifat-sifat sistem biologis diperoleh dengan menggunakan model dua persamaan diferensial yang memungkinkan penelitian kualitatif menggunakan metode tersebut bidang fase. Pertimbangkan sistem dua persamaan diferensial biasa yang otonom pandangan umum
(4.1)
P(x,y), Q(x,y)- fungsi berkelanjutan, didefinisikan di area tertentu G Bidang Euclidean ( x, y ‑ Koordinat Kartesius) dan memiliki turunan kontinu di wilayah ini dengan urutan tidak lebih rendah dari yang pertama.
Wilayah G bisa tidak terbatas atau terbatas. Jika variabel x, kamu memiliki arti biologis tertentu (konsentrasi zat, jumlah spesies), paling sering suatu wilayah G mewakili kuadran positif dari setengah bidang kanan:
0 £ X< ¥ ,0 £ kamu< ¥ .
Konsentrasi zat atau jumlah spesies juga dapat dibatasi dari atas oleh volume wadah atau luas habitat. Maka rentang variabelnya berbentuk:
0 £ X< x 0 , 0 £ kamu< y 0 .
Variabel x, kamu perubahan waktu sesuai dengan sistem persamaan (4.1), sehingga setiap keadaan sistem berhubungan dengan sepasang nilai variabel ( x, kamu).
|
|
 |
Sebaliknya, setiap pasangan variabel ( x, kamu) sesuai dengan keadaan tertentu dari sistem.
Pertimbangkan sebuah bidang dengan sumbu koordinat di mana nilai-nilai variabel diplot x, y. Setiap poin M bidang ini sesuai dengan keadaan sistem tertentu. Bidang ini disebut bidang fase dan mewakili totalitas semua keadaan sistem. Titik M(x,y) disebut titik representasi atau representasi.
Membiarkan masuk momen awal waktu t=t 0 koordinat titik yang mewakili M 0 (X(T 0), kamu(T 0)). Di setiap saat berikutnya T titik representasi akan bergeser sesuai dengan perubahan nilai variabel X(T), kamu(T). Pengumpulan poin M(X(T), kamu(t)) pada bidang fase, yang posisinya sesuai dengan keadaan sistem dalam proses perubahan variabel seiring waktu x(t), kamu(t) menurut persamaan (4.1), disebut lintasan fase.
Keseluruhan lintasan fase untuk nilai awal variabel yang berbeda memberikan “potret” sistem yang mudah terlihat. Konstruksi potret fase memungkinkan Anda menarik kesimpulan tentang sifat perubahan variabel x, kamu tanpa pengetahuan solusi analitis sistem persamaan asli(4.1).
Untuk menggambarkan potret fase, perlu dibuat bidang vektor arah lintasan sistem di setiap titik bidang fase. Mengatur kenaikanD t>0,kami mendapatkan kenaikan yang sesuai D X Dan D kamu dari ekspresi:
D x=P(x,y)D T,
D kamu=Q(x,kamu)D T.
Arah vektor mati/dx pada titik ( x, kamu) bergantung pada tanda fungsinya P(x, y), Q(x, y) dan dapat diberikan dalam tabel:
|
P(x,y)>0,Q(x,y)>0 |
|
|
P(x,y)<0,Q(x,y)<0 |
|
|
P(x,y)>0,Q(x,y)<0 |
|
|
P(x,y)<0,Q(x,y)>0 |
|
.(4.2)
Solusi untuk persamaan ini kamu = kamu(x, c), atau secara implisit F(x, y)=c, Di mana Dengan– konstanta integrasi, memberikan keluarga kurva integral dari persamaan (4.2) - lintasan fase sistem (4.1) di pesawat x, kamu.
metode isoklin
Untuk membuat potret fase yang mereka gunakan metode isoklin - garis digambar pada bidang fase yang memotong kurva integral pada satu sudut tertentu. Persamaan isoklin dapat dengan mudah diperoleh dari (4.2). Ayo taruh
Di mana A– nilai konstan tertentu. Arti A mewakili garis singgung dari sudut kemiringan garis singgung lintasan fasa dan dapat mengambil nilai dari –¥ ke + ¥ . Menggantikannya mati/dx dalam (4.2) kuantitas A kita memperoleh persamaan isoklin:
.(4.3)
Persamaan (4.3) mendefinisikan di setiap titik pada bidang suatu garis singgung unik terhadap kurva integral yang bersesuaian, dengan pengecualian pada titik di mana P(x,y)= 0, Q (x, y) = 0 , yang arah garis singgungnya menjadi tidak pasti, karena nilai turunannya menjadi tidak pasti:
.
Titik ini merupakan titik potong semua isoklin - poin khusus. Di dalamnya, turunan waktu dari variabel-variabel secara bersamaan menghilang X Dan kamu.
Jadi, pada suatu titik tunggal, laju perubahan variabel adalah nol. Akibatnya, titik tunggal persamaan diferensial lintasan fase (4.2) bersesuaian dengan keadaan stasioner sistem(4.1), dan koordinatnya merupakan nilai stasioner variabel x, kamu.
Yang menarik adalah isoklin utama:
dy/dx=0, P(x, y)=0 – isoklin garis singgung horizontal dan
hari/dx=¥ , Q(x, y)=0 – isoklin garis singgung vertikal.
Dengan membuat isoklin utama dan mencari titik potongnya (x,y), yang koordinatnya memenuhi syarat:
dengan demikian kita akan menemukan titik potong semua isoklin bidang fase, di mana arah garis singgung lintasan fase tidak pasti. Ini - titik tunggal, yang sesuai keadaan stasioner sistem(Gbr. 4.2).
Sistem (4.1) mempunyai keadaan stasioner yang sama banyaknya dengan jumlah titik potong isoklin utama pada bidang fase.
Setiap lintasan fase berhubungan dengan serangkaian pergerakan sistem dinamis, melewati keadaan yang sama dan berbeda satu sama lain hanya pada awal penghitungan waktu.
 |
|
Jika kondisi teorema Cauchy terpenuhi, maka melalui setiap titik dalam ruang x, y, t hanya ada satu kurva integral. Hal yang sama juga berlaku, karena otonomi, untuk lintasan fase: lintasan fase tunggal melewati setiap titik pada bidang fase.
Stabilitas Keadaan Stabil
Biarkan sistem berada dalam keadaan setimbang.
Kemudian titik representasi terletak pada salah satu titik tunggal sistem, yang menurut definisinya:
.
Stabil atau tidaknya suatu titik tunggal ditentukan oleh keluar atau tidaknya titik yang mewakilinya dengan penyimpangan kecil dari keadaan stasionernya. Sehubungan dengan sistem dua persamaan, pengertian kestabilan dalam bahasae, Dterlihat seperti ini.
Keadaan setimbang dikatakan stabil jika pada rentang tertentu terjadi penyimpangan dari keadaan setimbang (e )Anda dapat menentukan areanya D (e ), mengelilingi keadaan setimbang dan mempunyai sifat tidak ada lintasan yang dimulai di dalam wilayah tersebut D , tidak akan pernah mencapai perbatasan e . (Gbr. 4.4)
 |
|
Untuk sistem kelas besar - sistem yang kasar – yang sifat perilakunya tidak berubah dengan sedikit perubahan bentuk persamaan, informasi tentang jenis perilaku di sekitar keadaan stasioner dapat diperoleh dengan mengkaji bukan yang asli, melainkan yang disederhanakan. dilinearisasi sistem.
Sistem linier.
Pertimbangkan sistem dua persamaan linear:
.(4.4)
Di Sini a, b, c, d- konstanta, x, kamu- Koordinat kartesius pada bidang fase.
Kami akan mencari solusi umum dalam bentuk:
.(4.5)
Mari kita substitusikan ekspresi ini ke (4.4) dan kurangi sebesar e aku T:
(4.6)
Sistem persamaan aljabar (4.6) dengan yang tidak diketahui A, B memiliki solusi bukan nol hanya jika determinannya, yang terdiri dari koefisien-koefisien yang tidak diketahui, sama dengan nol:
.
Memperluas determinan ini, kita memperoleh persamaan karakteristik sistem:
.(4.7)
Menyelesaikan persamaan ini memberikan nilai eksponenaku 1,2 , yang memungkinkan nilai bukan nol A Dan B solusi persamaan (4.6). Makna-makna tersebut adalah
.(4.8)
Jika ekspresi radikalnya negatif, makaaku 1,2 bilangan konjugasi kompleks. Mari kita asumsikan bahwa kedua akar persamaan (4.7) mempunyai bagian real bukan nol dan tidak ada akar ganda. Kemudian solusi umum sistem (4.4) dapat direpresentasikan sebagai kombinasi linier eksponensial dengan eksponenaku 1 , aku 2 :
(4.9)
Untuk menganalisis sifat kemungkinan lintasan sistem pada bidang fase, kami menggunakan transformasi koordinat homogen linier, yang akan mengarahkan sistem ke bentuk kanonik:
,(4.10)
memungkinkan representasi yang lebih mudah pada bidang fase dibandingkan dengan sistem asli (4.4). Mari kita perkenalkan koordinat baruξ , η sesuai dengan rumus:
(4.1)
Dari pembelajaran aljabar linier diketahui bahwa pada kasus pertidaksamaan ke nol bagian realnyaaku 1 , aku 2 sistem asli (4.4) selalu dapat diubah menggunakan transformasi (4.11) ke bentuk kanonik (4.10) dan perilakunya pada bidang fase dapat dipelajariξ , η . Mari kita pertimbangkan berbagai kasus yang mungkin muncul di sini.
Akar λ 1 , λ 2 – sah dan bertanda sama
Dalam hal ini koefisien transformasinya nyata, kita berpindah dari bidang nyatax, yke bidang nyata ξ, η. Membagi persamaan kedua (4.10) dengan persamaan pertama, kita peroleh:
.(4.12)
Mengintegrasikan persamaan ini, kami menemukan:
Dimana .(4.13)
Mari kita sepakat untuk memahami dengan λ 2 akar persamaan karakteristik dengan modulus besar, yang tidak melanggar keumuman penalaran kita. Kemudian, karena dalam kasus ini akar-akarnya λ 1 , λ 2 – sah dan bertanda sama,A>1 , dan kita berhadapan dengan kurva integral tipe parabola.
Semua kurva integral (kecuali sumbu η , yang sesuai dengan ) sentuh di titik asal sumbu ξ, yang juga merupakan kurva integral persamaan (4.11). Asal koordinat adalah titik khusus.
Sekarang mari kita cari tahu arah pergerakan titik yang mewakili sepanjang lintasan fase. Jika λ 1 , λ 2 maka negatif, seperti dapat dilihat dari persamaan (4.10), |ξ|, |η| menurun seiring berjalannya waktu. Titik yang mewakili mendekati asal koordinat, namun tidak pernah mencapainya. Jika tidak, hal ini akan bertentangan dengan teorema Cauchy, yang menyatakan bahwa hanya satu lintasan fase yang melewati setiap titik pada bidang fase.
Titik khusus yang dilalui kurva integral, seperti keluarga parabola 
melewati titik asal dan disebut node (Gbr. 2). 4.5)
Keadaan keseimbangan tipe simpul di λ 1 , λ 2 < 0 adalah Lyapunov stabil, karena titik yang mewakili bergerak sepanjang semua kurva integral menuju titik asal koordinat. Ini simpul stabil. Jika λ 1 , λ 2 > 0, lalu |ξ|, |η| meningkat seiring waktu dan titik yang mewakili menjauh dari titik asal koordinat. Dalam hal ini, poin spesialnya– simpul tidak stabil .
Di bidang fase x, kamu sifat kualitatif umum dari perilaku kurva integral akan dipertahankan, tetapi garis singgung kurva integral tidak akan bertepatan dengan sumbu koordinat. Sudut kemiringan garis singgung ini akan ditentukan oleh rasio koefisiennya α , β , γ , δ dalam persamaan (4.11).
Akar λ 1 , λ 2 – sah dan memiliki tanda yang berbeda.
Konversi dari koordinat x, y ke koordinat ξ, η lagi nyata. Persamaan variabel kanonik kembali berbentuk (4.10), tetapi sekarang bertanda λ 1 , λ 2 berbeda. Persamaan lintasan fase memiliki bentuk:
Dimana ,(4.14)
Mengintegrasikan (4.14), kami menemukan
(4.15)
Ini persamaan tersebut mendefinisikan sekumpulan kurva bertipe hiperbolik, yang kedua sumbu koordinatnya– asimtot (pada A=1 kita akan memiliki keluarga hiperbola sama sisi). Sumbu koordinat dalam hal ini juga merupakan kurva integral– ini akan menjadi satu-satunya kurva integral yang melewati titik asal. Setiapyang terdiri dari lintasan tiga fasa: dari dua gerakan menuju keadaan setimbang (atau dari keadaan setimbang) dan dari keadaan setimbang. Semua kurva integral lainnya– adalah hiperbola yang tidak melewati titik asal (Gbr. 4.6) Poin khusus ini disebut "pelana ». Garis datar di dekat pelana gunung berperilaku serupa dengan lintasan fase di sekitar pelana.
Mari kita perhatikan sifat pergerakan titik yang mewakili sepanjang lintasan fase dekat keadaan setimbang. Misalkan,λ 1 >0 , λ 2<0 . Kemudian titik representasi ditempatkan pada sumbu ξ , akan menjauh dari titik asal, dan ditempatkan pada sumbu η – akan mendekati asal koordinat tanpa batas waktu, tanpa mencapainya dalam waktu yang terbatas. Dimanapun titik yang mewakili berada pada momen awal (kecuali titik tunggal dan titik pada asimtot η =0), ia pada akhirnya akan menjauh dari keadaan setimbang, meskipun awalnya ia bergerak sepanjang salah satu kurva integral menuju titik tunggal.
Jelas sekali titik tunggal seperti pelana selalu tidak stabil . Hanya di bawah kondisi awal yang dipilih secara khusus di asimtotη =0 sistem akan mendekati keadaan setimbang. Namun, hal ini tidak bertentangan dengan pernyataan tentang ketidakstabilan sistem. Jika kita menghitung, bahwa semua keadaan awal sistem pada bidang fase mempunyai kemungkinan yang sama, maka peluang keadaan awal yang berhubungan dengan pergerakan searah Ke titik tunggal sama dengan nol. Oleh karena itu, setiap gerakan nyata akan mengeluarkan sistem dari keadaan setimbang.Kembali ke koordinatx, kamu,kita akan memperoleh gambaran kualitatif yang sama tentang sifat pergerakan lintasan di sekitar titik asal koordinat.
Batas antara kasus simpul dan pelana yang dipertimbangkan adalah kasusnya Kapan salah satu indikator karakteristik, misalnya λ 1 , menghilang, yang terjadi ketika determinan sistem– ekspresi iklan-bc=0(lihat rumus 4.8 ). Dalam hal ini, koefisien ruas kanan persamaan (4.4) sebanding satu sama lain:
dan sistem mempunyai keadaan setimbang di semua titik garis:
Kurva integral yang tersisa adalah kelompok garis lurus sejajar dengan koefisien sudut , di mana titik-titik yang mewakili mendekati keadaan setimbang atau menjauh darinya, bergantung pada tanda akar kedua dari persamaan karakteristik λ 2 = iklan+d.(Gbr.4.7 ) Dalam hal ini, koordinat keadaan setimbang bergantung pada nilai awal variabel.
Akar λ 1 , λ 2 – kompleksmengkonjugasikan
Dalam hal ini, sungguhX Dan kamu kami akan melakukannya mempunyai konjugat kompleks ξ , η (4.10) . Namun, dengan memperkenalkan transformasi perantara lainnya, dalam hal ini juga dimungkinkan untuk mereduksi pertimbangan menjadi transformasi homogen linier nyata. Ayo taruh:
(4.16)
Di mana a,b, Dan kamu,v – nilai-nilai aktual. Dapat ditunjukkan bahwa transformasi darix, y Ke kamu,v berdasarkan asumsi kita, adalah nyata, linier, homogen dengan determinan yang berbeda dari nol. Berdasarkan persamaan(4.10, 4.16) kita punya:
Di mana
(4.17)
Membagi persamaan kedua dengan persamaan pertama, kita mendapatkan:
yang lebih mudah untuk diintegrasikan, jika kita pergi ke sistem koordinat kutub (R, φ ) . Setelah substitusi kita dapatkan dari mana:
.(4.18)
Jadi, pada bidang fasekamu, vkita berhadapan dengan keluarga spiral logaritmik, yang masing-masing memilikinyatitik asimtotik di titik asal.Titik tunggal, yaitu titik asimtotik dari semua kurva integral yang berbentuk spiral, bersarang di masing-masingteman, itu namanya fokus ( Gambar 4.8 ) .
Mari kita perhatikan sifat pergerakan titik yang mewakili sepanjang lintasan fase. Mengalikan persamaan pertama (4.17) dengankamu, dan yang kedua aktif ay dan menambahkan, kita mendapatkan:
Di mana
Membiarkan A 1 < 0 (A 1 = Ulangλ ) . Titik yang mewakili kemudian terus menerus mendekati titik asal koordinat tanpa mencapainya pada waktu yang terbatas. Ini berarti bahwa lintasan fase berbentuk spiral dan berhubungan dengan osilasi teredam variabel. Ini - fokus yang stabil .
Dalam kasus fokus stabil, seperti dalam kasus simpul stabil, tidak hanya kondisi Lyapunov yang terpenuhi, tetapi juga persyaratan yang lebih ketat. Yaitu, untuk setiap penyimpangan awal, sistem akan, seiring berjalannya waktu, kembali sedekat yang diinginkan ke posisi setimbang. Stabilitas seperti itu, di mana simpangan awal tidak hanya tidak bertambah, tetapi juga peluruhan, cenderung ke nol, disebut stabilitas mutlak .
Jika dalam rumus (4.18) A 1 >0 , maka titik yang mewakili menjauh dari titik asal, dan kita berhadapan dengan fokus tidak stabil . Saat berpindah dari pesawatkamu,vke bidang faseX, kamuspiral juga akan tetap spiral, tetapi akan berubah bentuk.
Sekarang mari kita pertimbangkan kasus kapanA 1
=0
. Lintasan fase di pesawatkamu, vakan ada lingkaran 
yang ada di pesawatx, ysesuai dengan elips:
Jadi, kapansebuah 1=0 melalui titik khususx= 0, kamu= 0 tidak ada kurva integral yang melewatinya. Titik tunggal terisolasi yang dekat dengan kurva integral merupakan kurva tertutup, khususnya elips yang saling menempel dan melingkupi titik tunggal, disebut pusat.
Jadi, enam jenis keadaan setimbang mungkin terjadi, bergantung pada sifat akar persamaan karakteristik (4.7). Tampilan lintasan fase pada bidang x, kamu untuk enam kasus ini ditunjukkan pada Gambar. 4.9.
Beras. 4.9.Jenis potret fase di sekitar keadaan stasioner untuk sistem persamaan linier (4.4).
Kelima jenis keadaan setimbang bersifat kasar; karakternya tidak berubah dengan perubahan yang cukup kecil di ruas kanan persamaan (4.4). Dalam hal ini, perubahan tidak hanya pada ruas kanan, tetapi juga pada turunan orde pertamanya haruslah kecil. Keadaan keseimbangan keenam – pusat – tidaklah kasar. Dengan perubahan kecil pada parameter sisi kanan persamaan, fokusnya menjadi stabil atau tidak stabil.
Diagram bifurkasi
Mari kita perkenalkan notasi berikut:
.
(4.11)
Maka persamaan karakteristiknya akan ditulis sebagai:
.
(4.12)
Misalkan sebuah bidang dengan koordinat kartesius berbentuk persegi panjang S , D dan tandai di atasnya area yang sesuai dengan satu atau beberapa jenis keadaan setimbang, yang ditentukan oleh sifat akar persamaan karakteristik
.(4.13)
Syarat kestabilan keadaan setimbang adalah adanya bagian nyata negatif dari yaku 1 dan aku 2 . Syarat perlu dan cukup untuk itu adalah terpenuhinya kesenjanganS > 0, D > 0 . Pada diagram (4.15), kondisi ini sesuai dengan titik-titik yang terletak pada kuartal pertama bidang parameter. Suatu titik tunggal akan menjadi fokus jikaaku 1 dan aku 2 kompleks. Kondisi ini sesuai dengan titik-titik pada bidang yang dituju , itu. titik antara dua cabang parabolaS 2 = 4 D. Poin poros S = 0, D>0, sesuai dengan keadaan keseimbangan tipe pusat. Juga,aku 1 dan aku 2 - sah, tetapi tandanya berbeda, mis. titik tunggal akan menjadi pelana jika D<0, dll. Hasilnya, kita mendapatkan diagram partisi bidang parameter S, D, ke dalam area yang sesuai dengan berbagai jenis keadaan keseimbangan.
Beras. 4.10. Diagram bifurkasi
untuk sistem persamaan linear 4.4
Jika koefisien sistem linier a, b, c, d bergantung pada parameter tertentu, maka ketika parameter ini berubah maka nilainya juga akan berubahS , D . Saat melintasi batas, karakter potret fase berubah secara kualitatif. Oleh karena itu, batas-batas seperti itu disebut batas bifurkasi - di sisi berlawanan dari batas tersebut, sistem memiliki dua potret fase yang berbeda secara topologi dan, karenanya, dua jenis perilaku yang berbeda.
Diagram menunjukkan bagaimana perubahan tersebut dapat terjadi. Jika kita mengecualikan kasus-kasus khusus - asal koordinat - maka mudah untuk melihat bahwa pelana dapat berubah menjadi simpul yang stabil atau tidak stabil ketika melintasi sumbu ordinat. Simpul yang stabil dapat masuk ke dalam pelana atau ke dalam fokus yang stabil, dll. Perhatikan bahwa transisi simpul stabil - fokus stabil dan simpul tidak stabil - fokus tidak stabil bukanlah percabangan, karena topologi ruang fase tidak berubah. Kita akan membahas lebih lanjut tentang topologi ruang fase dan transisi bifurkasi di Kuliah 6.
Selama transisi bifurkasi, sifat stabilitas suatu titik tunggal berubah. Misalnya, fokus yang stabil melalui pusat dapat berubah menjadi fokus yang tidak stabil. Percabangan ini disebut Percabangan Andronov-Hopf dengan nama ilmuwan yang mempelajarinya. Selama percabangan dalam sistem nonlinier ini, lahirlah siklus batas, dan sistem menjadi berosilasi sendiri (lihat Kuliah 8).
Contoh. Sistem reaksi kimia linier
Zat X mengalir dari luar dengan kecepatan tetap, berubah menjadi zat Y dan dengan kecepatan sebanding dengan konsentrasi zat Y, dikeluarkan dari bidang reaksi. Semua reaksi berorde satu, kecuali masuknya zat dari luar, yang berorde nol. Skema reaksinya terlihat seperti:
(4.14)
dan dijelaskan oleh sistem persamaan:
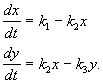(4.15)
Kita memperoleh konsentrasi stasioner dengan menyamakan ruas kanan dengan nol:
.(4.16)
Mari kita perhatikan potret fase sistem. Mari kita bagi persamaan kedua sistem (4.16) dengan persamaan pertama. Kami mendapatkan:
.(4.17)
Persamaan (4.17) menentukan perilaku variabel pada bidang fase. Mari kita membuat potret fase sistem ini. Pertama, mari kita menggambar isoklin utama pada bidang fase. Persamaan isoklin garis singgung vertikal:
Persamaan isoklin garis singgung horizontal:
Titik tunggal (keadaan stasioner) terletak pada perpotongan isoklin utama.
Sekarang mari kita tentukan pada sudut berapa sumbu koordinat berpotongan dengan kurva integral.
Jika x= 0, lalu.
Jadi, garis singgung dari garis singgung kurva integral kamu=kamu(x), memotong sumbu ordinat x=0, bernilai negatif pada setengah bidang atas (ingat bahwa variabel x, kamu memiliki nilai konsentrasi, dan oleh karena itu kita hanya tertarik pada kuadran kanan atas bidang fase). Dalam hal ini, garis singgung sudut singgung bertambah seiring bertambahnya jarak dari titik asal.
Pertimbangkan porosnya kamu= 0. Pada titik di mana sumbu ini memotong kurva integral, kurva tersebut dijelaskan oleh persamaan
Pada garis singgung kemiringan kurva integral yang melintasi sumbu absis adalah positif dan meningkat dari nol hingga tak terhingga seiring bertambahnya X.
Pada .
Kemudian, dengan peningkatan lebih lanjut, garis singgung sudut kemiringan berkurang nilai absolutnya, tetap negatif dan cenderung -1 pada X ® ¥ . Mengetahui arah garis singgung kurva integral pada isoklin utama dan sumbu koordinat, mudah untuk membuat gambaran keseluruhan lintasan fasa.
 |
|
Mari kita tentukan sifat kestabilan titik tunggal menggunakan metode Lyapunov. Penentu karakteristik sistem berbentuk:
.
Memperluas determinannya, kita memperoleh persamaan karakteristik sistem: , yaitu. Akar persamaan karakteristik keduanya negatif. Akibatnya, keadaan stasioner sistem adalah simpul yang stabil. Dalam hal ini, konsentrasi zat X cenderung keadaan stasioner selalu monoton, konsentrasi zat Y dapat melewati min atau maks. Mode osilasi tidak mungkin dilakukan dalam sistem seperti itu.
Konsep dan definisi dasar:
Titik nol dari fungsi analitik f(z) adalah titik “a” yang f(a)=0.
Nol berorde “n” dari suatu fungsi f(z) adalah titik “a” jika fn(a)¹0.
Titik tunggal “a” disebut titik tunggal terisolasi dari suatu fungsi f(z) jika terdapat lingkungan titik tersebut yang tidak memiliki titik tunggal selain “a”.
Ada tiga jenis titik tunggal terisolasi: .
1 titik tunggal yang dapat dilepas;
3 poin pada dasarnya tunggal.
Jenis titik tunggal yang ditemukan dapat ditentukan berdasarkan perilaku suatu fungsi tertentu pada titik tunggal yang ditemukan, serta dari bentuk deret Laurent yang diperoleh untuk fungsi tersebut di sekitar titik tunggal yang ditemukan.
Menentukan tipe titik tunggal berdasarkan perilaku fungsi pada titik tersebut.
1. Poin tunggal yang dapat dilepas.
Titik tunggal terisolasi a dari suatu fungsi f(z) disebut dapat dipindahkan jika terdapat limit yang berhingga.
2.Tiang.
Titik tunggal terisolasi a dari suatu fungsi f(z) disebut kutub jika 
.
3. Pada dasarnya poin tunggal.
Titik tunggal terisolasi a dari suatu fungsi f(z) disebut titik tunggal pada dasarnya jika tidak ada yang berhingga maupun tak terhingga.
Hubungan berikut terjadi antara nol dan kutub suatu fungsi.
Agar titik a menjadi kutub orde n dari fungsi f(Z), titik ini perlu dan cukup menjadi orde nol n untuk fungsi tersebut.
Jika n=1 kutubnya disebut sederhana.
Definisi: Titik tunggal terisolasi yang sifatnya tidak ambigu disebut:
a) dapat dilepas jika bagian utama dari pembusukannya hilang;
b) tiang, jika bagian utamanya memuat sejumlah suku yang berhingga;
c) suatu titik pada hakikatnya tunggal jika bagian utamanya memuat jumlah yang tak terbatas anggota.
a) Jadi, di sekitar titik tunggal yang dapat dipindahkan, pemuaiannya berbentuk:
menyatakan fungsi di semua titik lingkaran |z-a| Di pusat z=a persamaan tersebut tidak benar, karena fungsi di z=a mempunyai diskontinuitas dan ruas kanannya kontinu. Jika nilai fungsi di tengah diubah, sehingga sama dengan nilai di ruas kanan, maka celah tersebut akan dihilangkan - oleh karena itu dinamakan - dapat dilepas. b) Di sekitar kutub berorde m, pemuaian deret Laurent berbentuk: c) Di sekitar tiang sederhana Pengurangan dan rumus untuk menghitungnya. Residu fungsi analitik f(z) pada titik tunggal terisolasi z 0 adalah bilangan kompleks yang sama dengan nilai integral Sisa fungsi f(z) pada titik tunggal terisolasi z 0 dilambangkan dengan simbol Res f(z 0) atau Res (f(z); z 0). Dengan demikian, Res f(z 0)= Jika kita memasukkan n=-1 ke dalam rumus (22.15.1), kita mendapatkan: C -1 = atau Res f(z 0)= C -1 , itu. sisa fungsi f(z) terhadap titik tunggal z 0 sama dengan koefisien suku pertama dengan eksponen negatif pada perluasan fungsi f(z) pada deret Laurent. Perhitungan pemotongan. Titik tunggal beraturan atau dapat dilepas. Jelasnya, jika z=z 0 adalah titik tunggal beraturan atau titik tunggal yang dapat dipindahkan dari fungsi f(z), maka Res f(z 0)=0 (ekspansi Laurent dalam kasus ini tidak memiliki bagian utama, jadi c-1=0) . Tiang. Biarkan titik z 0 menjadi kutub sederhana dari fungsi f(z). Maka deret Laurent untuk fungsi f(z) di sekitar titik z 0 berbentuk: Dari sini Oleh karena itu, meneruskan persamaan ini ke limit di z --z 0, kita peroleh Jawabannya f(z0)= Pada dasarnya poin khusus. Jika titik z 0 pada dasarnya adalah titik singular dari fungsi f(z), maka untuk menghitung sisa fungsi pada titik ini, koefisien c-1 pada perluasan fungsi deret Laurent biasanya ditentukan secara langsung. Klasifikasi peristiwa. Jumlah, produk peristiwa, propertinya, representasi grafis. Acara dibagi menjadi: 1. Acak 2. Dapat diandalkan 3. Tidak mungkin Dapat diandalkan adalah peristiwa yang pasti terjadi dalam kondisi tertentu (malam menyusul pagi). Peristiwa acak adalah peristiwa yang mungkin terjadi atau tidak terjadi (lulus ujian). Peristiwa mustahil adalah peristiwa yang tidak akan terjadi pada kondisi tertentu (mengeluarkan pensil hijau dari kotak yang hanya berisi pensil merah). Poin tunggal dalam matematika. 1) Titik tunggal suatu kurva yang ditentukan oleh persamaan F ( x, kamu) = 0, - titik M 0 ( x 0 , kamu 0), yang kedua turunan parsial dari fungsi F ( x, kamu) menuju ke nol: Jika tidak semua turunan parsial kedua dari fungsi F ( x, kamu) pada titik M 0 sama dengan nol, maka O.t. Jika, bersamaan dengan hilangnya turunan pertama di titik M0, semua turunan kedua, tetapi tidak semua turunan ketiga, hilang, maka persamaan tersebut disebut rangkap tiga, dan seterusnya. Saat mempelajari struktur kurva di dekat O.t ganda, tanda ekspresi memainkan peran penting Jika Δ > 0, maka ruang terbuka tersebut disebut terisolasi; misalnya pada tikungan kamu 2 - x 4 + 4x 2= 0 titik asal koordinat adalah O. t. beras. 1
). Jika Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4= 0 titik asal koordinat adalah nodal O. t. beras. 2
). Jika = 0, maka titik umum kurva tersebut terisolasi atau dicirikan oleh fakta bahwa cabang-cabang kurva yang berbeda mempunyai garis singgung yang sama pada titik ini, misalnya: a) titik puncak jenis pertama - cabang-cabang yang berbeda dari kurva tersebut terletak pada sisi berlawanan dari garis singgung persekutuan dan membentuk suatu titik, seperti kurva kamu 2 - x 3= 0 (lihat beras. 3
,A); b) titik puncak jenis ke-2 - cabang-cabang kurva yang berbeda terletak di satu sisi garis singgung persekutuan, seperti kurva
(kamu - x 2)2 - x 5= 0 (lihat beras. 3
, B); c) titik sentuh diri (untuk kurva kamu 2 - x 4= 0 titik asal adalah titik sentuhan diri; (cm. beras. 3
, V). Selain O. t. yang disebutkan, ada banyak O. t. misalnya, titik asimtotik adalah titik puncak spiral dengan jumlah putaran yang tak terhingga (lihat. beras. 4
), titik terminasi, titik sudut, dll. 2) Titik tunggal persamaan diferensial adalah titik di mana pembilang dan penyebut ruas kanan persamaan diferensial hilang secara bersamaan (Lihat Persamaan Diferensial) dimana P dan Q merupakan fungsi terdiferensiasi kontinyu. Dengan asumsi O. t. terletak di titik asal koordinat dan menggunakan rumus Taylor (Lihat rumus Taylor), kita dapat merepresentasikan persamaan (1) dalam bentuk di mana P 1 ( x, kamu) dan Pertanyaan 1 ( x, kamu) - sangat kecil sehubungan dengan Yaitu, jika λ 1 ≠ λ 2 dan λ 1 λ 2 > 0 atau λ 1 = λ 2, maka O. t. semua kurva integral yang melalui titik-titik di lingkungan simpul yang cukup kecil masuk ke dalamnya. Jika λ 1 ≠ λ 2 dan λ 1 λ 2 i β, α ≠ 0 dan β ≠ 0, maka titik umumnya adalah fokus; semua kurva integral yang melalui titik-titik di lingkungan fokus yang cukup kecil mewakili spiral dengan jumlah putaran yang tak terhingga di lingkungan fokus yang kecil. Jika, akhirnya, λ 1,2 = ± Sayaβ, β ≠ 0, maka karakter O. t. tidak ditentukan oleh suku linier saja pada perluasan P ( x, kamu) dan Q ( x, kamu), seperti halnya dalam semua kasus di atas; di sini O.t. dapat menjadi fokus atau pusat, atau dapat bersifat lebih kompleks. Di sekitar pusat, semua kurva integral tertutup dan memuat pusat di dalamnya. Jadi, misalnya titik (0, 0) adalah simpul persamaan pada" = 2kamu/x(λ 1 = 1, λ 2 = 2; lihat beras. 5
, a) dan kamu" = kamu/x(λ 1 = λ 2 = 1; lihat beras. 5
, b), pelana untuk persamaan kamu" = -y/x(λ 1 = -1, λ 2 = 1 ; cm. beras. 6
), fokus persamaan kamu" =(x + kamu) /
(x - kamu) (λ 1 = 1 - Saya, λ 2 = 1 + Saya; cm. beras. 7
) dan pusat persamaan kamu" = -x/kamu(λ 1 = -Saya, λ 2 = Saya; cm. beras. 8
). Jika x, y) dan Q ( x, kamu) analitis, lingkungan O. t. orde tinggi dapat dibagi menjadi beberapa wilayah: D 1 - diisi dengan kurva integral, kedua ujungnya termasuk dalam O. t. salah satu ujungnya termasuk dalam O. t. (daerah parabola), dan D 3 - daerah yang dibatasi oleh dua kurva integral yang termasuk dalam teori umum, di antaranya terdapat kurva integral tipe hiperbolik (daerah hiperbolik) (lihat. beras. 9
). Jika tidak ada kurva integral yang termasuk dalam suatu titik umum, maka titik umum tersebut disebut titik bertipe stabil. Lingkungan osilator stabil terdiri dari kurva integral tertutup yang mengandung osmosis di dalamnya, di antaranya terdapat spiral (lihat Gambar. beras. 10
). Studi tentang persamaan diferensial, yaitu studi tentang perilaku kelompok kurva integral di sekitar persamaan diferensial, merupakan salah satu cabang teori kualitatif persamaan diferensial dan memainkan peran penting dalam penerapannya, khususnya dalam pertanyaan. stabilitas gerak (karya A.M. Lyapunov a, A. Poincare, dll.). 3) Titik tunggal dari fungsi analitik bernilai tunggal adalah titik di mana analitik fungsi tersebut dilanggar (lihat Fungsi analitik). Jika ada lingkungan O.t. A, bebas dari O. t. lainnya, lalu tunjuk A disebut terisolasi O. t A- teori umum yang terisolasi dan terdapat a yang terbatas disebut teori umum yang dapat dilepas. Dengan mengubah definisi suatu fungsi di titik a secara tepat (atau mendefinisikannya kembali pada titik ini, jika fungsi di titik tersebut tidak terdefinisi sama sekali), yaitu dengan berasumsi F(A)= b, adalah mungkin untuk mencapai hal itu A akan menjadi titik biasa dari fungsi yang dikoreksi. Misalnya, titik z= 0 adalah O.t. yang dapat dilepas untuk fungsi f 1 ( z) = F(z), Jika z≠ 0, dan F 1 (0), = 1, titik z= 0 adalah titik biasa [ F 1 (z) bersifat analitik pada intinya z= 0]. Jika A- O. t. dan a yang terisolasi disebut kutub atau titik tunggal yang tidak esensial dari suatu fungsi F(z), jika deret Laurent) berfungsi F(z) di sekitar O. t yang terisolasi tidak mengandung pangkat negatif z - sebuah, Jika A- O. t. yang dapat dilepas, berisi sejumlah derajat negatif yang terbatas z - sebuah, Jika A- tiang (dalam hal ini urutan tiang R didefinisikan sebagai derajat tertinggi dari a - suatu titik yang pada dasarnya istimewa. Misalnya saja untuk fungsinya dot z= 0 adalah kutub keteraturan R, untuk fungsi dot z= 0 pada dasarnya adalah titik tunggal. Pada batas lingkaran konvergensi suatu deret pangkat, paling sedikit harus terdapat satu O.t. fungsi yang diwakili dalam lingkaran ini oleh data seri kekuatan. Semua titik batas domain keberadaan fungsi analitik unik (batas alami) adalah batas fungsi tersebut. Jadi, semua titik pada lingkaran satuan | z| = 1 spesial untuk fungsi tersebut Untuk fungsi analitik multinilai, konsep “O. T." lebih sulit. Selain O. t., dalam masing-masing lembar permukaan Riemann suatu fungsi (yaitu, O. t. elemen analitik bernilai tunggal), setiap titik cabang juga merupakan O. t. Titik-titik cabang terisolasi dari permukaan Riemann (yaitu titik-titik cabang yang di beberapa lingkungannya tidak ada fungsi O.t. lainnya di daun mana pun) diklasifikasikan sebagai berikut. Jika a adalah titik cabang terisolasi dengan orde berhingga dan terdapat a berhingga, maka disebut kutub kritis. Jika A- titik cabang terisolasi dengan urutan tak terbatas dan a disebut O.t transendental. Semua titik cabang terisolasi lainnya disebut titik kritis yang pada dasarnya tunggal. Contoh: titik z= 0 adalah titik kritis biasa dari fungsi f ( z) = catatan z dan titik kritis tunggal dari fungsi tersebut F (z) = dosa ln z. Setiap masalah umum, kecuali masalah yang dapat dihilangkan, merupakan hambatan bagi kelanjutan analitis, yaitu kelanjutan analitis sepanjang kurva yang melewati masalah umum yang tidak dapat direduksi tidak mungkin dilakukan. Ensiklopedia Besar Soviet. - M.: Ensiklopedia Soviet.
1969-1978
.
Poin di sini. Lihat juga titik tunggal (persamaan diferensial). Ciri atau singularitas dalam matematika adalah suatu titik di mana suatu objek matematika (biasanya suatu fungsi) tidak terdefinisi atau mempunyai perilaku yang tidak beraturan (misalnya, suatu titik di mana ... ... Wikipedia Fungsi analitik adalah titik di mana kondisi analitik dilanggar. Jika fungsi analitik f(z) diberikan di lingkungan tertentu dari titik z0 di mana saja... Ensiklopedia fisik Fungsi analitik adalah titik di mana analitik fungsi tersebut dilanggar... Kamus Ensiklopedis Besar titik tunggal- - [Ya.N.Luginsky, M.S.Fezi Zhilinskaya, Yu.S.Kabirov. Kamus Teknik Elektro dan Teknik Tenaga Inggris-Rusia, Moskow, 1999] Topik Teknik Elektro, Konsep Dasar EN Titik Tunggal ... Panduan Penerjemah Teknis 1) Fungsi analitik f(z) adalah hambatan bagi kelanjutan analitik suatu elemen fungsi f(z) dari variabel kompleks z sepanjang suatu jalur pada bidang variabel ini. Biarkan fungsi analitik f(z) didefinisikan oleh beberapa... ... Ensiklopedia Matematika Fungsi analitik, titik di mana analitik fungsi dilanggar. * * * TITIK TUNGGAL TITIK TUNGGAL suatu fungsi analitik, titik di mana analitik fungsi tersebut dilanggar... Kamus Ensiklopedis titik tunggal- ypatingasis tugas statusas T sritis automatika atitikmenys: engl. titik tunggal vok. tunggalärer Punkt, m rus. titik tunggal, f pranc. titik khusus, m; point singulier, m … Automatikos terminų žodynas titik tunggal- ypatingasis taškas statusas T sritis fizika atitikmenys: engl. titik tunggal vok. tunggalärer Punkt, m rus. titik tunggal, f pranc. titik singulier, m … Fizikos terminų žodynas Membiarkan zq adalah titik tunggal dari fungsi /(r), t.s. f(z) tetapi bersifat analitik pada saat ini (khususnya, hal ini mungkin tidak dapat didefinisikan pada saat ini). Jika ada lingkungan yang tertusuk seperti itu intinya zq (yaitu himpunan O z - zq f(z) adalah aialitik, maka zo ditelepon titik tunggal yang terisolasi fungsi f(z). Definisi ini tetap sama dalam kasus zn = oo, jika yodium ditusuk di sekitar titik tersebut zq = oo mengerti set z> SAYA -
bagian luar lingkaran yang berpusat di titik asal. Dengan kata lain, poin khusus zq dikatakan terisolasi jika terdapat lingkungan titik tersebut yang di dalamnya terdapat titik-titik tunggal lain selainnya zq. Sepanjang pembahasan berikut ini kita hanya mempertimbangkan titik-titik tunggal yang memiliki karakter unik (fungsi f(z) diasumsikan tidak ambigu). Tergantung pada perilaku fungsinya f(z) pada z -> zq Ada tiga jenis titik tunggal. Titik tunggal yang terisolasi fungsi zq f(z) ditelepon: 1) titik tunggal yang dapat dilepas, jika ada batas yang terbatas 2) tiang, jika ada batasan 3) pada dasarnya poin khusus, Jika f(z) tidak mempunyai limit yang terbatas dan tidak terbatas pada z-> zq. Contoh 26.1. Mari kita tunjukkan bahwa ketiga jenis titik tunggal terwujud. Mari kita pertimbangkan F(z)= Poin zq = 0 terisolasi poin khusus dari fungsi ini. Dengan menggunakan rumus (22.12), kita memperoleh pemuaian dari situlah terdapat lim fi(z)= 1. Oleh karena itu zq = 0 adalah adalah titik tunggal yang dapat dipindahkan dari fungsi tersebut fi(z). Fungsi f'j(z) =---memiliki tiang pada suatu titik zo= 1 karena 2
R" X Sekarang mari kita pertimbangkan fungsinya )з(z)= e 1 ^ r dan tunjukkan itu zo = O pada dasarnya adalah titik tunggal dari fungsi ini. Saat berusaha z ke nol sepanjang sumbu real batas kiri dan kanan fungsi /z (z) berbeda: lim Dengan 1 / 1
=
0, lim s 1 /* = os. Oleh karena itu, x->0-0 x->0+O Apa f: saya (z) tidak mempunyai limit berhingga atau tak terhingga pada 2 ->
Oh, itu. zq = O pada dasarnya adalah titik tunggal dari fungsi ini. (Perhatikan bahwa seiring dengan kecenderungan intinya z - iy ke nol sepanjang fungsi sumbu imajiner tidak memiliki batas sama sekali.) Tentu saja ada titik-titik tunggal yang tidak terisolasi. Misalnya. fungsi tersebut memiliki kutub di titik-titiknya z n = -, N= ±1, ±2,... Karena itu, Zq = 0 adalah titik tunggal yang tidak terisolasi dari fungsi ini: di lingkungan mana pun (sekecil apa pun) titik ini terdapat titik tunggal lainnya g hal.
Membiarkan zo- titik tunggal terisolasi yang terbatas dari suatu fungsi f(z). Kemudian f(z) serupa di beberapa lingkungan tertusuk pada titik 0 Zo zo lingkungan ini dapat dianggap sebagai cincin dengan jari-jari dalam r = 0. Berdasarkan Teorema 25.1, pada lingkungan yang ditinjau fungsinya f(z) dapat diperluas menjadi deret Laurent (25.2). Kami akan menunjukkan bahwa perilaku fungsi di 2 -> zq (yaitu jenis titik tunggal zo) tergantung pada jenis bagian utama perluasan (25.2); Keadaan ini menjelaskan asal usul istilah “bagian utama”. Teorema 2G.2. Suatu titik tunggal terisolasi zo dari suatu fungsi f(z) dapat dipindahkan jika dan hanya jika pemuaian Lorapov di lingkungan tertusuk titik ini mempunyai oid itu. hanya terdiri dari bagian yang benar, dan semua koefisien bagian utama sama dengan poin. Bukti. 1. Biarkan zo- titik tunggal yang dapat dilepas. Mari kita buktikan perluasan fungsi Laurent f(z) memiliki bentuk (26.1). Sejak poin khusus zo dilepas, maka ada yang terbatas batas batas f(z) = SEBUAH. Karena itu, f(z) dibatasi di beberapa lingkungan tertusuk pada titik 0 z - zq jadi, itu. )(z) untuk semua orang z dari sekitar ini. Ayo ambil apa saja R. U р /?|, dan gunakan rumus (25.3) untuk koefisien deret Laurent: Untuk koefisien bagian utama muai n =- 1,-2,... Untuk nilai seperti itu N kita punya hal ~ hal-e 0 pada R-> 0. Karena nilainya R bisa dipilih sembarang kecil, kalau begitu Tuan~" bisa sekecil yang diinginkan. Sejak |s t,| ^ Tuan~hal dan c„ tidak bergantung pada p, maka c„ = 0 at Dan= - 1, -2,..., yang perlu dibuktikan. 2. Sekarang mari kita asumsikan bahwa ekspansi Laurent mempunyai bentuk (26.1). Deret (26.1) merupakan deret pangkat dan. oleh karena itu, ia menyatu tidak hanya di area yang tertusuk, tetapi juga di seluruh sekitarnya z-zq termasuk intinya jadi; jumlahnya S(z) bersifat analitik di z dan S(z) = )(z) pada 0 z - zo R. Oleh karena itu ada batas yang terbatas )(z)= Pt 5(g) = 5(th) - Oleh karena itu, titik tunggal zq Z->Zo Z-*Zo dapat dilepas. Teorema tersebut telah terbukti. Komentar. Dari pembuktian teorema tersebut dapat disimpulkan bahwa dalam lingkungan tertusuk 0 z - zo dari titik tunggal yang dapat dipindahkan fungsinya f(z) bertepatan dengan fungsi 5(r), yang bersifat analitik di seluruh lingkungan z - zo. Oleh karena itu, jika kita menetapkan /(th) = S(zq), kemudian, tanpa mengubah nilai fungsi f(z) di titik mana pun dari lingkungan yang tertusuk, kami akan menjadikan fungsi ini analitik di Go, yaitu. Mari kita “menghilangkan” fitur tersebut. Ini menjelaskan istilah “fitur yang dapat dilepas”. Adalah wajar untuk menganggap titik-titik tersebut sebagai titik-titik biasa, dan bukan titik-titik tunggal dari suatu fungsi f(z).
Misalnya saja fungsinya Pada contoh 26.1 ditunjukkan bahwa Pm Nr) = 1. yaitu. titik tunggal zq = 0 dapat dilepas. Dengan menetapkan /i(0) = 1, kita menghilangkan singularitas dan memperoleh fungsi analitik pada titik tersebut zq = 0 (dan seluruh bidang C). Mari kita mengkarakterisasi kutub dalam istilah ekspansi Laurent. Teorema 26.3. Titik tunggal terisolasi Zo dari suatu fungsi f(z) adalah kutub jika dan hanya jika, ketika bagian utama dari ekspansi Laurent dengan pusat Zq hanya memiliki sejumlah perbedaan yang terbatas dari nol koefisien dengan n: Bukti. 1. Biarkan zq - tiang, mis. batas/( z) = oo. Mari kita buktikan perluasan fungsi Laurent f(z) memiliki bentuk (2G.2). Sejak lim f(z)= oo. lalu ada lingkungan titik yang tertusuk ki zq. di mana f(z) bersifat analitik dan tidak memiliki angka nol. Lalu fungsinya g(z) = 1 /f(z) juga akan menjadi analitik di lingkungan yang tertusuk ini, dan lim g(z)= 0. Oleh karena itu, Zo dapat dilepas *-? *0 titik tunggal dari fungsi tersebut g(z). Mari kita definisikan g(z) pada intinya zo, menempatkan g(zo)=
0. Lalu g(z) akan menjadi analitik di seluruh lingkungan titik (tidak tertembus). z 0 , Dan z 0 akan menjadi nol terisolasinya. Mari kita nyatakan dengan N multiplisitas (urutan) dari nol ini. Seperti yang ditunjukkan pada §23, di sekitar titik tersebut fungsi zq g(z) dapat direpresentasikan dalam bentuk (lihat (23.2)) Dan (z$)f 0 dan kamu>(z) bersifat analitik di beberapa lingkungan intinya zo- Karena ip(z) kontinu pada suatu titik zo Dan g>(zo) Ф 0" lalu ip(z) tidak memiliki angka nol di beberapa lingkungan pada titik ini. Oleh karena itu fungsi 1 /-p(z) juga akan bersifat analitik di lingkungan ini dan, oleh karena itu, berkembang di dalamnya dalam deret Taylor: Membuka tanda kurung dan mengubah sebutan koefisien, kami menulis ekspansi terakhir dalam bentuk dimana c_jv = 1>o f 0. Jadi, bagian utama perluasan fungsi Laurent /(r) hanya memuat sejumlah suku berhingga; kita telah sampai pada persamaan yang diinginkan (26.2). 2. Masukkan titik-titik di lingkungan yang tertusuk th fungsi )(z) diwakili oleh ekspansi Laurent (26.2) (untuk bentuk yang lebih rinci, lihat (26.3)), bagian utamanya hanya berisi sejumlah suku yang terbatas, dan Dengan- D" F 0. Hal itu perlu dibuktikan Zq - tiang fungsi f(z). Mengalikan persamaan (26.3) dengan (G - G o) iV , kita mendapatkan fungsinya Deret pada (26.4) adalah deret pangkat yang konvergen ke fungsi analitik tidak hanya pada titik yang tertusuk, tetapi juga pada seluruh lingkungan titik tersebut. Zq. Oleh karena itu fungsinya jam(z) akan menjadi analitik dalam lingkungan ini jika kita mendefinisikannya lebih jauh dengan menempatkan h(zo)= s_dg F 0. Lalu Jadi titik th merupakan kutub dan Teorema 26.3 terbukti. Multiplisitas (urutan) fungsi nol g(z)= 1//(g) dipanggil pesanan tiang fungsi ke /(r). Jika N- urutan kutub th, lalu g(z)= (g - Zo) N ip(z), dan (pergi) F 0, dan seperti ditunjukkan pada bagian pertama pembuktian Teorema 26.3, perluasan fungsi /(r) mempunyai bentuk (26.3), dimana c_/v F 0. Sebaliknya jika /(r) diperluas menjadi deret (26.3) dan e-i F 0, lalu t.s. N- urutan kutub fungsi /(r). Dengan demikian, urutan kutub fungsi zq/(G) sama dengan bilangan koefisien bukan nol tertinggi dari bagian utama ekspansi Laurent di lingkungan tertusuk titik zq(yaitu sama dengan angka ini N, apa s_dg F 0 dan Sp= 0 jam N > N). Mari kita buktikan pernyataan berikut, yang sesuai untuk aplikasi. Akibat wajar 26.4. Titik zq merupakan kutub orde N fiksi/(G) saat itu dan hanya kapan/(G) dapat diwakilkan dalam bentuk dimana h(z) adalah fungsi analitik di sekitar titik th dan h(zo) f 0. Bukti. Fungsi cp(z) = l/jam(z) bersifat analitik di beberapa lingkungan titik h. Kondisi Akibat wajar 26.4 setara dengan yang berikut: Itu sebabnya zq -
multiplisitas nol N fungsi g(z). dan oleh karena itu merupakan kutub multiplisitas N fungsi /(2). II Contoh 26.5. Temukan titik tunggal terisolasi dari suatu fungsi Solusi: Titik-titik di mana (z 2
+ 1 )(z+ Z) 2 = 0. Jika z 2
aku- 1 = 0, lalu 2 = ±g Jika (z 4- 3) 2 = 0, maka z= -3. Oleh karena itu fungsi tersebut mempunyai tiga titik tunggal z= g, 22 = -g, Z3
=
- 3. Pertimbangkan z: G - tiang orde pertama (kami menggunakan Akibat wajar 26.4). Dapat dibuktikan dengan cara serupa bahwa 22 = -Saya juga tiang orde pertama. Untuk 2z kita memiliki: Mari kita lanjutkan dengan mempertimbangkan poin-poin yang pada dasarnya tunggal. Teorema 26.6. Suatu titik tunggal terisolasi zq dari suatu fungsi f(z) pada dasarnya tunggal jika dan hanya jika bagian utama dari ekspansi Laurent dengan pusat zq memiliki banyak perbedaan yang tak terhingga. nol, koefisien dari p. Bukti. Teorema 26.6 mengikuti langsung dari Teorema 26.2 dan 26.3. Memang kalau intinya zq pada dasarnya istimewa, maka bagian utama dari ekspansi Laurent tidak boleh ada atau mengandung jumlah suku yang terbatas (jika tidak, intinya Zq bisa dilepas atau di tiang). Oleh karena itu, jumlah suku pada bagian utama harus tidak terbatas. Sebaliknya, jika bagian utama memuat suku-suku yang tak terhingga banyaknya, maka Zq tidak dapat berupa suatu titik yang dapat dilepas maupun suatu tiang. Oleh karena itu, poin ini pada dasarnya istimewa. Menurut definisi tersebut, suatu titik yang pada dasarnya tunggal dicirikan oleh fakta bahwa fungsi /(2) tidak mempunyai limit yang terbatas maupun tidak terbatas untuk z ->zq. Gagasan yang lebih lengkap tentang betapa tidak teraturnya perilaku suatu fungsi di sekitar titik tunggal diberikan oleh teorema berikut. Teorema 26.7 (teorema Sokhotsky). Jika zq penting bagi orang, titik dari fungsi f(z), lalu untuk siapa pun bilangan kompleks
aku, termasuk A= Oh, ada barisan titik z n sedemikian rupa sehingga z n -> zo dan batas f(zn) = A. p->os Bukti. Mari kita pertimbangkan dulu kasusnya SEBUAH = oo. Pada bagian pertama pembuktian Teorema 2G.2 kita menetapkan bahwa jika f(z) dibatasi pada suatu lingkungan tertusuk dari titik r, maka semua koefisien c", n = - 1,- 2,... bagian utama sama dengan nol (dan, oleh karena itu, singularitas di go dapat dihilangkan). Karena dengan syarat th merupakan titik tunggal esensial, maka di setiap lingkungan titik th yang tertusuk, fungsi f(r) tidak terbatas. Mari kita ambil lingkungan yang kuat 0 Z sedemikian rupa f(zi) > 1 (jika |/(r)| z - zo I/2 ada benarnya z-2
, di mana |/(yy)| > 2, dst.: di lingkungan tertusuk O 71.
Jelas bahwa r„ -e go dan lim /(r“) = oo. Jadi, dalam kasus A = oo, Teorema 26.7 terbukti. Biarkan sekarang Sebuah f oo. Mari kita asumsikan terlebih dahulu bahwa ada lingkungan yang tertusuk 0 = -Y y----
akan bersikap analitis di lingkungan yang tertusuk ini dan, akibatnya, /(G) - A Akibatnya, go adalah titik tunggal terisolasi dari fungsi Φ(r). Kami akan menunjukkannya padamu. bahwa r pada dasarnya adalah titik tunggal dari Φ(r). Ini mungkin tidak benar. Lalu ada limit lim Ф(r), berhingga atau tak terhingga. Sebentar /(r) = A + , maka ada juga Hsh /(r), yang bertentangan dengan kondisi tersebut F(g) ~ :-*z 0 Saya melihat teoremanya. Jadi, r0 pada dasarnya adalah titik singular dari fungsi Φ(r). Berdasarkan pembuktian di atas, terdapat barisan titik-titik r n sedemikian rupa sehingga r n th dan lim Ф(rn) = oo. Dari sini Kami telah membuktikan pernyataan yang diperlukan dengan asumsi bahwa /(r) FA di beberapa lingkungan titik jalan yang tertusuk- Sekarang mari kita asumsikan bahwa ini salah, yaitu. di lingkungan titik kecil mana pun yang tertusuk secara sewenang-wenang, ada titik seperti itu G", itu /(r") = L. Lalu untuk apa saja N di lingkungan yang tertusuk 0 f(z u) = А. Jadi, pernyataan yang diinginkan benar N-yuo dalam semua kasus, dan Teorema 26.7 terbukti. Menurut Teorema 26.7 (Sokhotsky), di setiap lingkungan tertusuk (yang sangat kecil) dari suatu titik yang pada dasarnya tunggal, fungsi /(r) mengambil nilai yang mendekati bilangan mana pun dari perluasan bidang kompleks DENGAN. Untuk mempelajari titik tunggal terisolasi, perluasan fungsi dasar dasar Taylor yang sudah diketahui sering kali berguna. Contoh 2G.8. Tentukan jenis titik tunggal zq = 0 untuk fungsi tersebut Terselesaikan dan e. Mari kita perluas pembilang dan penyebutnya menjadi deret Taylor pangkat g z alih-alih r dan mengurangkan 1, kita mendapatkan Dengan menggunakan (22.12), kita memperoleh perluasan penyebutnya: Deret dalam perluasan ini bertemu di seluruh bidang kompleks €. Kita punya dan /2(2) merupakan anaritik di lingkungan titik tersebut zo = 0 (dan bahkan di seluruh bidang) dan /2(20) F 0, lalu jam(z) juga analitik di beberapa lingkungan titik gF 0. Menurut Akibat wajar 26.4, intinya Zo = 0 adalah tiang keteraturan tidak=4. II Contoh 26.9. Temukan titik tunggal suatu fungsi f(z)= sin j - dan tentukan tipenya. R e in e i e. Fungsi tersebut mempunyai satu titik tunggal berhingga zq = 1. Di titik lain dari C fungsinya w =--- analitis; maka fungsinya sin w akan bersifat analitis. Mengganti - alih-alih r ke dalam perluasan sinus (22.12), kita mendapatkan Kami mengalami dekomposisi fungsi dosa- menjadi deret Laurent di lingkungan tertusuk titik 2o = 1. Karena pemuaian yang dihasilkan mengandung banyak suku dengan pangkat negatif (r - 1) yang tak terhingga, maka zq = 1 pada dasarnya adalah titik tunggal (dalam hal ini, perluasan Laurent hanya terdiri dari bagian utama, dan bagian beraturan tidak ada). Perhatikan bahwa sifat singularitas dalam kasus ini dapat ditentukan langsung dari definisinya, tanpa menggunakan perluasan deret. Memang ada barisan (r",) dan (2") yang konvergen zo= 1, dan sedemikian rupa f(z"n)= 1, /(2") = 0 (sebutkan sendiri barisan tersebut). Jadi, f(z) tidak memiliki batas di z -> 1 dan karena itu titik zq - 1 pada dasarnya istimewa. Mari kita perkenalkan konsep perluasan fungsi Laurent di lingkungan suatu titik Zq = 00 dan pertimbangkan hubungan antara perluasan dan sifat singularitas pada titik ini. Perhatikan bahwa definisi titik tunggal terisolasi dan tipenya (dapat dilepas, kutub, atau pada dasarnya tunggal) terbawa ke kasus ini zq = oc tanpa perubahan. Tapi Teorema 26.2. 26.3 dan 26.6, terkait dengan sifat ekspansi Laurent, perlu diubah. Intinya adalah anggota cn(z- 2o) hal. N= -1,-2,..., bagian utama, mendefinisikan “ketidakteraturan” fungsi di dekatnya titik akhir Zq, karena 2 cenderung oo, mereka akan berperilaku “benar” (cenderung 0). Sebaliknya, anggota bagian yang benar dengan N= 1,2,... akan cenderung oo; mereka menentukan sifat fitur di Zq = oo. Oleh karena itu, bagian utama dari perluasan di sekitar oo akan terdiri dari istilah dengan kekuatan positif P, dan yang benar - dengan yang negatif. Mari kita perkenalkan variabel baru w = 1/2. Fungsi televisi = 1/2, diperpanjang sehingga u(oo) = 0, satu-ke-satu dan memetakan lingkungan secara konformal z > R poin zq = 00 di sekitar |w| wq = 0. Jika fungsinya f(z) analitik di lingkungan yang tertusuk R z Zq = oc, maka fungsinya G(w) = f(l/w) akan menjadi analitik di lingkungan besar 0 wo = 0. Karena pada 2 -> oo akan ada w-> 0, lalu Itu sebabnya G(w) ada pada intinya wq = 0 adalah fitur yang bertipe sama dengan f(z) pada intinya Zq = 00. Mari kita perluas fungsi G(w) menjadi deret Laurent di lingkungan tertusuk titik wo = 0: Jumlah di sisi kanan (26.5) masing-masing mewakili bagian reguler dan utama dari perluasan. Mari beralih ke variabel z, menggantikan w = 1/z: Menunjuk N= -A*, 6* = 6_„ = hal dan memperhatikan itu G(l/z) = f(z), kita dapatkan Dekomposisi (2G.G) disebut Ekspansi Laurent dari fungsi f(z) di lingkungan titik zq yang tertusuk= oo. Jumlah pertama dalam (2G.6) disebut bagian yang tepat, dan jumlah kedua adalah bagian utama dari dekomposisi ini. Karena jumlah ini sesuai dengan bagian yang benar dan utama dari pemuaian (26.5), maka analogi Teorema 26.2, 26.3 dan 26.6 berlaku untuk pemuaian (26.6). Jadi, teorema berikut merupakan analogi dari Teorema 26.2. Teorema 26.10. Titik tunggal yang terisolasiZq -
sistem operasi (fungsi/(G) dapat dilepas jika dan hanya jika ekspansi Laurent di lingkungan tertusuk pada titik ini mempunyai bentuk
t.s. hanya terdiri dari bagian yang benar. Mari kita masukkan /(oo) = bersama. Fungsi didefinisikan oleh deret (26.7) yang konvergen di lingkungan tersebut z > R titik 2o = oc, disebut analitis pada titik z o = oo. (Perhatikan bahwa definisi ini setara dengan analitik fungsi G(w) pada titik wo = 0.) Contoh 26.11. Selidiki titik tunggal zq = oo dari fungsi tersebut Karena limitnya terbatas, maka zo = oo adalah titik tunggal yang dapat dipindahkan dari fungsi /(r). Jika kita memasukkan /(oo) = lim J(z)= 0, maka f(z) akan menjadi analitis tik pada intinya Zo= os. Mari kita tunjukkan cara mencari pemuaian yang sesuai (26.7). Mari beralih ke variabel w = 1 fz. Mengganti z= 1 /?е, kita dapat (persamaan terakhir berlaku di lingkungan tertusuk titik wо = 0, namun kita akan mendefinisikan lebih lanjut (7(0) = 0). Fungsi yang dihasilkan memiliki titik tunggal w =±saya, w =-1/3, dan pada intinya Wq = 0 bersifat analitik. Fungsi terungkap G(w) sedikit demi sedikit w(seperti yang dilakukan pada Contoh 25.7) dan mensubstitusikannya ke dalam deret pangkat yang dihasilkan w = 1/z, kita dapat memperoleh perluasan (26.7) dari fungsi tersebut f(z).
Teorema 26.3 untuk kasus ini zo= oo akan ditulis ulang dalam bentuk berikut. Teorema 26.12. Titik tunggal yang terisolasi th = os fungsi f(z) adalah kutub jika dan hanya jika bagian utama dari ekspansi Laurent (26.6) hanya memiliki sejumlah koefisien bukan nol yang terbatas Dengan": Di sini deretnya adalah bagian beraturan, dan polinomial dalam tanda kurung adalah bagian utama dari perluasannya. Multiplisitas kutub dalam oc didefinisikan sebagai multiplisitas kutub wq = 0 fungsi G(z). Sangat mudah untuk melihat bahwa banyaknya kutub bertepatan dengan jumlahnya N di (26.8). Q p | (saya 2 + 1)(z+3) 2 Tugas. Tunjukkan bahwa fungsinya f(z) =--
-- sudah masuk titik zo = oo tiang pesanan 3. Teorema 26.6 tentang suatu titik yang pada dasarnya tunggal dapat ditulis ulang untuk kasus tersebut zo= hampir kata demi kata, dan kami tidak membahasnya secara detail.
, diambil dalam arah positif sepanjang lingkaran L dengan pusat di titik z 0 terletak di domain analitik dari fungsi f(z) (yaitu di ring 0<|z-z0| . (22.15.1)
p = 2, 3, …)
Lihat apa itu “Titik tunggal” di kamus lain:
dan tentukan jenisnya.
