¿Cómo se denota la unidad imaginaria del número? Sobre la cuestión de la interpretación y el nombre.

Unidad imaginaria

Unidad imaginaria- un número complejo cuyo cuadrado es igual a menos uno.

En matemáticas y física, la unidad imaginaria se designa como latina. i o j. Le permite ampliar el campo de los números reales al campo de los números complejos. Definición precisa Depende del método de esta extensión.

La razón principal para introducir la unidad imaginaria es que no todos ecuación polinómica F(X) = 0 con coeficientes reales tiene soluciones en el campo de los números reales. Por ejemplo, la ecuación X 2 + 1 = 0 no tiene raíces reales. Sin embargo, si asumimos que las raíces son números complejos, entonces esta ecuación, como cualquier otra ecuación polinómica tiene solución.

La afirmación de que la unidad imaginaria es la “raíz cuadrada de −1” no es del todo correcta, porque −1 tiene dos aritméticas raíces cuadradas, uno de los cuales puede designarse como i, y el otro como - i.

Definición

Una unidad imaginaria es un número cuyo cuadrado es igual a −1. De este modo i es la solución de la ecuación
o
si definimos i Por lo tanto, la consideraremos una variable desconocida (“imaginaria”, “imaginaria”), entonces la segunda solución de la ecuación será: i, que se puede comprobar mediante sustitución.

Quién lo abrió y cuándo: El matemático italiano Gerolamo Cardano, amigo de Leonardo da Vinci, en 1545.

Al número i no se le puede llamar constante ni siquiera real. Los libros de texto la describen como una cantidad que, cuando se eleva al cuadrado, da menos uno. En otras palabras, es el lado del cuadrado con área negativa. En realidad esto no sucede. Pero a veces también puedes beneficiarte de lo irreal.

La historia del descubrimiento de esta constante es la siguiente. El matemático Gerolamo Cardano, mientras resolvía ecuaciones con cubos, introdujo la unidad imaginaria. Esto fue sólo un truco auxiliar: no había i en las respuestas finales: los resultados que la contenían se descartaron. Pero más tarde, tras examinar más de cerca su "basura", los matemáticos intentaron ponerla en práctica: multiplicar y dividir. numeros regulares por unidad imaginaria, suma los resultados entre sí y sustitúyelos en nuevas fórmulas. Así nació la teoría de los números complejos.

La desventaja es que lo “real” no se puede comparar con lo “irreal”: no funcionará decir que el mayor es una unidad imaginaria o 1. Por otro lado, prácticamente no quedan ecuaciones sin solución si utilizas números complejos. Por lo tanto, con cálculos complejos, es más conveniente trabajar con ellos y "limpiar" las respuestas solo al final. Por ejemplo, para descifrar una tomografía cerebral, no se puede prescindir de i.

Así es exactamente como los físicos tratan los campos y las ondas. Incluso se puede considerar que todos existen en un espacio complejo y que lo que vemos es sólo una sombra de los procesos “reales”. Mecánica cuántica, donde tanto el átomo como la persona son ondas, hace que esta interpretación sea aún más convincente.

El número i le permite resumir las principales constantes y acciones matemáticas en una fórmula. La fórmula es la siguiente: eπi+1 = 0, y algunos dicen que un conjunto tan condensado de reglas matemáticas puede enviarse a los extraterrestres para convencerlos de nuestra inteligencia.

Las expresiones de la forma que aparecen al resolver ecuaciones cuadráticas y cúbicas comenzaron a llamarse "imaginarias" en Siglos XVI-XVII Sin embargo, incluso para muchos científicos destacados del siglo XVII, la esencia algebraica y geométrica de las cantidades imaginarias no parecía clara. Leibniz, por ejemplo, escribió: “El Espíritu de Dios encontró en este milagro del análisis la salida más sutil, un monstruo del mundo de las ideas, una esencia dual situada entre el ser y el no ser, a la que llamamos raíz imaginaria de lo negativo. unidad."

Durante mucho tiempo no estuvo claro si todas las operaciones con números complejos conducían a resultados complejos o si, por ejemplo, extraer una raíz podría conducir al descubrimiento de algún nuevo tipo de números. El problema de expresar raíces de grados. norte de numero dado se resolvió en las obras de Moivre (1707) y Cotes (1722).

El símbolo fue propuesto por Euler (1777, publicado en 1794), quien tomó la primera letra de la palabra latina para ello. imaginario. Él difundió todo características estándar, incluido el logaritmo, en el dominio complejo. Euler también expresó en 1751 la idea de que el cuerpo de los números complejos es algebraicamente cerrado. D'Alembert (1747) llegó a la misma conclusión, pero el primero prueba estricta Este hecho pertenece a Gauss (1799). Gauss introdujo el término "número complejo" en un uso generalizado en 1831, aunque el término se había utilizado anteriormente en el mismo sentido. matemático francés Lázaro Carnot en 1803.

La interpretación geométrica de los números complejos y sus operaciones apareció por primera vez en la obra de Wessel (1799). Los primeros pasos en esta dirección los dio Wallis (Inglaterra) en 1685. Moderno representación geométrica, a veces llamado “diagrama de Argand”, entró en uso después de la publicación en 1806 y 1814 del trabajo de J. R. Argand, que repetía de forma independiente las conclusiones de Wessel.

Modelo aritmético de números complejos como pares. numeros reales fue construido por Hamilton (1837); esto demostró la consistencia de sus propiedades. Hamilton también propuso una generalización de los números complejos: los cuaterniones, cuyo álgebra no es conmutativa.

Considere la ecuación cuadrática incompleta:

X 2 = a,

Dónde A es una cantidad conocida. La solución de esta ecuación se puede escribir como:
Hay tres casos posibles aquí:

1).	Si un = 0, entonces x = 0.
2).	Si A – numero positivo, entonces su raíz cuadrada tiene dos significados: uno positivo y otro negativo; por ejemplo la ecuación X 2 = 25 tiene dos raíces: 5 y – 5. Esto suele escribirse como raíz con doble signo:
3).	Si A es un número negativo, entonces esta ecuación no tiene soluciones entre los números positivos y negativos que conocemos, porque la segunda potencia de cualquier número es el número no negativo. Pero si queremos obtener soluciones a la ecuación X 2 = a También por valores negativos A, nos vemos obligados a introducir números de un nuevo tipo: numeros imaginarios . De este modo, imaginario el numero se llama cuya segunda potencia es un número negativo. Según esta definición de números imaginarios podemos definir y imaginario unidad:

Entonces para la ecuación X 2 = – 25 obtenemos dos imaginario raíz:

Sustituyendo ambas raíces en nuestra ecuación, obtenemos la identidad. A diferencia de los números imaginarios, todos los demás números (positivos y negativos, enteros y fraccionarios, racionales e irracionales) se llaman válido o numeros reales . La suma de un número real y uno imaginario se llama Número complejo y se designa:

a + b i ,

Dónde a, b- numeros reales, i– unidad imaginaria.

Para obtener más información sobre números complejos, consulte la sección "Números complejos".

Ejemplos de números complejos: 3 + 4 i, 7 – 13.6 i , 0 + 25 i = 25 i , 2 + i.

Potencias de unidad imaginaria.

Grados i repetido en un bucle:

Que se puede escribir para cualquier grado en la forma:

Dónde norte- cualquier número entero.

De aquí:
Dónde mod 4 representa el resto cuando se divide por 4.

números reales al campo de los números complejos. La definición exacta depende del método de extensión.

La razón para introducir una unidad imaginaria es que no toda ecuación polinómica $f(x)=0$ con coeficientes reales tiene soluciones en el campo de los números reales. Entonces, la ecuación $x^2 + 1 = 0$ no tiene raíces reales. Sin embargo, resulta que cualquier ecuación polinómica con coeficientes complejos tiene solución integral- “Teorema fundamental del álgebra”.

Históricamente, la unidad imaginaria se introdujo por primera vez para resolver la ecuación cúbica real: a menudo, si había tres raíces reales, para obtener dos de ellas, la fórmula de Cardano requería sacar la raíz cúbica en números complejos.

Definición

Una unidad imaginaria es un número cuyo cuadrado es −1. Aquellos. $i$ es una de las soluciones de la ecuación

$x^2 + 1 = 0,$ o $x^2 = -1.$

Y luego su segunda solución a la ecuación será $-i$ , que se verifica por sustitución.

Potencias de unidad imaginaria.

Grados $i$ repetido en un bucle:

$\ldots$ $yo^(-3) = yo$ $yo^(-2) = -1$ $yo^(-1) = -yo$ $yo^0 = 1$ $yo^1 = yo$ $yo^2 = -1$ $yo^3 = -yo$ $yo^4 = 1$ $\ldots$

Que se puede escribir para cualquier grado en la forma:

$yo^(4n) = 1$ $yo^(4n+1) = yo$ $yo^(4n+2) = -1$ $yo^(4n+3) = -yo.$

Dónde norte- cualquier número entero.

De aquí: $i^n = i^(n \bmod 4)$ Dónde mod 4 es el resto cuando se divide por 4.

Número $yo^yo$ es real:

$i^i=(e^((i\pi/2)i))=e^(i^2\pi/2)=e^(-\pi/2)=0(,)20787957635\ldots$

Factorial

Factorial de unidad imaginaria i se puede definir como el valor de la función gamma a partir del argumento 1 + i :

$¡i! = \Gamma(1+i) \aproximadamente 0,4980 - 0,1549i.$

$|yo!| = \sqrt(\pi \over \sinh(\pi)) \aprox 0.521564... .$

Raíces de la unidad imaginaria

En el campo de los números complejos, la raíz norte-ésimo grado tiene norte decisiones. En plano complejo las raíces de la unidad imaginaria están en los vértices de un n-gón regular inscrito en un círculo de radio unitario.

$u_k=\cos (\frac((\frac(\pi)(2)) + 2\pi k)(n)) +i\ \sin (\frac((\frac(\pi)(2)) + 2\pi k)(n)), \quad k=0,1,...,n-1$

Esto se desprende de la fórmula de Moivre y del hecho de que la unidad imaginaria se puede representar en forma trigonométrica:

$i=\cos\ (\frac(\pi)(2)) + i\ \sin\ (\frac(\pi)(2))$

En particular, $\sqrt(i ) = \left$\frac(1 + i)(\sqrt(2));\ \frac(-1 - i)(\sqrt(2)) \right$$ Y $\sqrt(i ) = \left$-i;\ \frac(i + (\sqrt(3)))(2);\ \frac(i - (\sqrt(3)))(2) \right $$

Además, las raíces de una unidad imaginaria se pueden representar en forma exponencial:

$u_k=e^(\frac((\frac(\pi)(2) + 2\pi k) i)(n) ), \quad k=0,1,...,n-1$

Otras unidades imaginarias

En la construcción de Cayley-Dixon (o en las álgebras de Clifford), puede haber varias “unidades de expansión imaginarias”, y/o su cuadrado puede ser ="+1" o incluso ="0". Pero en este caso pueden aparecer divisores cero y hay otras propiedades que difieren de las propiedades del complejo “i”. Por ejemplo, hay tres unidades imaginarias anticonmutativas en el cuerpo cuaternión y también hay infinitas soluciones a la ecuación " $x^2 = -1$ ».

Sobre la cuestión de la interpretación y el nombre.

Gauss también argumentó que si las cantidades 1, −1 y √−1 no se llamaran, respectivamente, unidades positivas, negativas e imaginarias, sino directas, inversas y secundarias, entonces la gente no tendría la impresión de que existe algún tipo de conexión con estos números. secreto oscuro. Según Gauss, la representación geométrica da una nueva luz a la verdadera metafísica de los números imaginarios. Fue Gauss quien introdujo el término “números complejos” (a diferencia de los “números imaginarios” de Descartes) y usó el símbolo i para denotar √−1.

Maurice Kline, “Matemáticas. Pérdida de certeza." Capítulo VII. Desarrollo ilógico: serias dificultades en el umbral del siglo XIX.

Designaciones

Designación común $i$ , pero en ingeniería de radio la unidad imaginaria suele denotarse $j$ para no confundirse con la designación de corriente instantánea: $yo = yo(t)$ .

Ver también

Números duales y números dobles.

Escribe una reseña sobre el artículo "Unidad imaginaria"

Notas

Enlaces

Unidad imaginaria // Gran Enciclopedia Soviética: [en 30 volúmenes] / cap. ed. A. M. Prójorov. - 3ª edición. -M. : enciclopedia soviética, 1969-1978.



poderes de mil

Antiguos números rusos

Otras potencias de diez

potencias de doce

otro entero

Otros números

Extracto que caracteriza la Unidad Imaginaria

Varios comerciantes se agolparon alrededor del oficial.
- ¡Eh! ¡Es una pérdida de tiempo mentir! - dijo uno de ellos, delgado, con rostro severo. “Cuando te cortas la cabeza, no lloras por tu cabello”. ¡Toma lo que quieras! “Y agitó la mano con un gesto enérgico y se volvió de lado hacia el oficial.
"Es bueno para ti, Ivan Sidorich, hablar", dijo enojado el primer comerciante. - De nada, señoría.
- ¡Qué debería decir! – gritó el hombre delgado. "Tengo cien mil productos en tres tiendas aquí". ¿Podrás salvarlo cuando el ejército se haya ido? Eh gente el poder de dios¡No lo dobles con las manos!
“Por favor, señoría”, dijo el primer comerciante, inclinándose. El oficial se quedó desconcertado y la indecisión se reflejaba en su rostro.
- ¡Y a mi que me importa! - gritó de repente y caminó con pasos rápidos hacia adelante por la fila. En una tienda abierta se escucharon golpes y maldiciones, y mientras el oficial se acercaba, un hombre con un abrigo gris y la cabeza rapada saltó por la puerta.
Este hombre, inclinándose, pasó corriendo junto a los comerciantes y al oficial. El oficial atacó a los soldados que se encontraban en la tienda. Pero en ese momento se escucharon gritos terribles de una gran multitud en el puente Moskvoretsky y el oficial salió corriendo a la plaza.
- ¿Qué ha pasado? ¿Qué ha pasado? - preguntó, pero su compañero ya galopaba hacia los gritos, pasando por San Basilio el Bendito. El oficial montó y cabalgó tras él. Cuando se acercó al puente, vio dos cañones retirados de los ágiles, infantería caminando por el puente, varios carros caídos, varios caras asustadas y las caras risueñas de los soldados. Cerca de los cañones había un carro tirado por dos. Detrás del carro, cuatro galgos con cuello se apiñaban detrás de las ruedas. Había una montaña de cosas en el carro, y en lo más alto, junto a la silla de los niños, estaba sentada una mujer con las piernas vueltas boca abajo, gritando estridentemente y desesperadamente. Los camaradas dijeron al oficial que los gritos de la multitud y los chillidos de la mujer se produjeron porque el general Ermolov, que se abalanzó sobre esta multitud, al enterarse de que los soldados se estaban dispersando entre las tiendas y una multitud de residentes bloqueaban el puente, ordenó disparar. para ser retirado de los limbers y se le dio el ejemplo de que dispararía al puente. La multitud, derribando los carros, aplastándose unos a otros, gritando desesperadamente, apiñándose, despejó el puente y las tropas avanzaron.

Mientras tanto, la ciudad misma estaba vacía. Casi no había nadie en las calles. Las puertas y las tiendas estaban todas cerradas; Aquí y allá, cerca de las tabernas, se escuchaban gritos solitarios o cantos de borrachos. Nadie conducía por las calles y rara vez se escuchaban pasos de peatones. En Povarskaya reinaba un silencio absoluto y un desierto. En el enorme patio de la casa de los Rostov había restos de heno y excrementos de un tren de transporte, y no se veía ni una sola persona. En la casa de Rostov, que conservaba todas sus cosas buenas, había dos personas en el gran salón. Se trataba del conserje Ignat y del cosaco Mishka, nieto de Vasilich, que permaneció en Moscú con su abuelo. Mishka abrió el clavicordio y lo tocó con un dedo. El conserje, con los brazos en jarras y sonriendo alegremente, estaba de pie frente a un gran espejo.
- ¡Eso es inteligente! ¿A? ¡Tío Ignacio! - dijo el niño, de repente comenzando a golpear las teclas con ambas manos.
- ¡Mirar! - Respondió Ignat, maravillándose de cómo su rostro sonreía cada vez más en el espejo.
- ¡Desvergonzado! ¡Realmente, descarado! – detrás de ellos habló la voz de Mavra Kuzminishna, que entró silenciosamente. - Eka, de cuernos gruesos, enseña los dientes. ¡Acepta esto! Allí no todo está ordenado, Vasilich cae al suelo. ¡Dale tiempo!
Ignat, ajustándose el cinturón, dejó de sonreír, bajó los ojos sumisamente y salió de la habitación.
“Tía, lo haré con calma”, dijo el niño.
- Te daré uno ligero. ¡Pequeño tirador! – gritó Mavra Kuzminishna, levantándole la mano. - Ve y prepara un samovar para el abuelo.
Mavra Kuzminishna, sacudiéndose el polvo, cerró el clavicordio y, suspirando profundamente, salió de la sala y cerró la puerta principal.
Al salir al patio, Mavra Kuzminishna pensó adónde debería ir ahora: ¿debería tomar té en la dependencia de Vasilich o ordenar lo que aún no había sido ordenado en la despensa?
Se escucharon pasos rápidos en la calle tranquila. Los pasos se detuvieron en la puerta; El pestillo empezó a golpear bajo la mano que intentaba abrirlo.
Mavra Kuzminishna se acercó a la puerta.
- ¿A quién necesitas?
- Conde, Conde Ilya Andreich Rostov.
- ¿Quién eres?
- Soy un oficial. "Me gustaría ver", dijo la voz rusa agradable y señorial.
Mavra Kuzminishna abrió la puerta. Y un oficial de cara redonda, de unos dieciocho años, con un rostro parecido al de los Rostov, entró en el patio.
- Nos fuimos, padre. “Ayer nos dignamos partir a las vísperas”, dijo afectuosamente Mavra Kuzmipishna.
El joven oficial, de pie en la puerta, como si dudara entre entrar o no, chasqueó la lengua.
“¡Ay, qué vergüenza!”, dijo. - Ojalá lo hubiera hecho ayer... ¡Ay, qué lástima!..
Mientras tanto, Mavra Kuzminishna examinó cuidadosa y comprensivamente los rasgos familiares de la raza Rostov en el rostro. hombre joven, y el abrigo hecho jirones, y las botas gastadas que llevaba.
- ¿Por qué necesitabas un recuento? - ella preguntó.
- Sí… ¡qué hacer! - dijo el oficial con molestia y agarró el portón, como si tuviera intención de irse. Se detuvo de nuevo, indeciso.
- ¿Lo ves? - dijo de repente. "Soy pariente del conde y él siempre ha sido muy amable conmigo". Entonces, ya ves (miró su capa y sus botas con una sonrisa amable y alegre), y estaba agotado y no había dinero; entonces quería preguntarle al Conde...
Mavra Kuzminishna no le dejó terminar.

Unidad imaginaria- normalmente un número complejo cuyo cuadrado es igual a −1 (menos uno). Sin embargo, también son posibles otras opciones: en la construcción de la duplicación según Cayley-Dixon o en el marco del álgebra según Clifford.

Para números complejos

En matemáticas y física, la unidad imaginaria se designa como latina. texvc o No se puede analizar la expresión (archivo ejecutable texvc . Le permite ampliar el campo de los números reales al campo de los números complejos. La definición exacta depende del método de extensión.

La razón para introducir una unidad imaginaria es que no toda ecuación polinómica No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración): f(x)=0 con coeficientes reales tiene soluciones en el campo de los números reales. Entonces, la ecuación No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración): x^2 + 1 = 0 no tiene raíces reales. Sin embargo, resulta que cualquier ecuación polinómica con coeficientes complejos tiene una solución compleja: el "Teorema fundamental del álgebra".

La afirmación de que la unidad imaginaria es la “raíz cuadrada de −1” no es precisa: después de todo, “−1” tiene dos raíces cuadradas, una de las cuales puede designarse como “i” y la otra como “−i”. No importa qué raíz se tome como unidad imaginaria: todas las igualdades seguirán siendo válidas si todas las “i” se reemplazan simultáneamente por “-i” y “-i” por “i”. Sin embargo, debido a esta ambigüedad, para evitar cálculos erróneos, no se debe utilizar la notación para No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración). a través del radical (como No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración): \sqrt(-1)).

Definición

Una unidad imaginaria es un número cuyo cuadrado es −1. Aquellos. No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración). es una de las soluciones de la ecuación

No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración): x^2 + 1 = 0, o No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración): x^2 = -1.

Y luego su segunda solución a la ecuación será No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración): -i, que se verifica por sustitución.

Potencias de unidad imaginaria.

Grados No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración). repetido en un bucle:

No se puede analizar la expresión (archivo ejecutable texvc No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración): i^(-3) = i No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración): i^(-2) = -1 No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración): i^(-1) = -i No se puede analizar la expresión (archivo ejecutable texvc extraviado; Ver matemáticas/README - ayuda con la configuración.): i^0 = 1 No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración): i^1 = i No se puede analizar la expresión (archivo ejecutable texvc extraviado; Ver matemáticas/README - ayuda con la configuración.): i^2 = -1 No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración): i^3 = -i No se puede analizar la expresión (archivo ejecutable texvc extraviado; Ver matemáticas/README - ayuda con la configuración.): i^4 = 1 No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración.): \ldots

Que se puede escribir para cualquier grado en la forma:

No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración): i^(4n) = 1 No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración): i^(4n+1) = i No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración): i^(4n+2) = -1 No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda sobre la configuración): i^(4n+3) = -i.

Dónde norte- cualquier número entero.

De aquí: No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración): i^n = i^(n \bmod 4) Dónde mod 4 es el resto cuando se divide por 4.

Número No se puede analizar la expresión (archivo ejecutable texvc extraviado; Ver matemáticas/README - ayuda con la configuración.): i^i es real:

No se puede analizar la expresión (archivo ejecutable texvc extraviado; Ver matemáticas/README - ayuda con la configuración.): i^i=(e^((i\pi/2)i))=e^(i^2\pi/2)=e^(-\pi/ 2 )=0(,)20787957635\ldots

Factorial

Factorial de unidad imaginaria i se puede definir como el valor de la función gamma a partir del argumento 1 + i :

No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración.): i! = \Gamma(1+i) \aproximadamente 0,4980 - 0,1549i. No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración.): |i!| = \sqrt(\pi \over \sinh(\pi)) \aprox 0.521564... .

Raíces de la unidad imaginaria

En el campo de los números complejos, la raíz norte-ésimo grado tiene norte decisiones. En el plano complejo, las raíces de la unidad imaginaria se ubican en los vértices de un n-gón regular inscrito en un círculo de radio unitario.

No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda sobre la configuración.): u_k=\cos (\frac((\frac(\pi)(2)) + 2\pi k)(n)) +i\ \sin (\frac( (\frac(\pi)(2)) + 2\pi k)(n)), \quad k=0,1,...,n-1

Esto se desprende de la fórmula de Moivre y del hecho de que la unidad imaginaria se puede representar en forma trigonométrica:

No se puede analizar la expresión (archivo ejecutable texvc extraviado; Ver matemáticas/README - ayuda con la configuración.): i=\cos\ (\frac(\pi)(2)) + i\ \sin\ (\frac(\pi)(2))

En particular, No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración.): \sqrt(i ) = \left$\frac(1 + i)(\sqrt(2));\ \frac(-1 - i)(\sqrt( 2 )) \bien$ Y No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración): \sqrt(i ) = \left$-i;\ \frac(i + (\sqrt(3)))(2);\ \frac(i - ( \sqrt (3)))(2) \derecha$

Además, las raíces de una unidad imaginaria se pueden representar en forma exponencial:

No se puede analizar la expresión (archivo ejecutable texvc extraviado; Ver matemáticas/README - ayuda con la configuración.): u_k=e^(\frac((\frac(\pi)(2) + 2\pi k) i)(n) ), \quad k=0,1 , ...,n-1

Otras unidades imaginarias

Sobre la cuestión de la interpretación y el nombre.

Gauss también argumentó que si las cantidades 1, −1 y √−1 no se llamaran, respectivamente, unidades positivas, negativas e imaginarias, sino directas, inversas y secundarias, entonces la gente no tendría la impresión de que alguna cosa lúgubre está asociada con estos números secretos. Según Gauss, la representación geométrica da una nueva luz a la verdadera metafísica de los números imaginarios. Fue Gauss quien introdujo el término “números complejos” (a diferencia de los “números imaginarios” de Descartes) y usó el símbolo i para denotar √−1.

Maurice Kline, “Matemáticas. Pérdida de certeza." Capítulo VII. Desarrollo ilógico: serias dificultades en el umbral del siglo XIX.

Designaciones

Designación común No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración)., pero en ingeniería de radio la unidad imaginaria suele denotarse No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración.): j para no confundirse con la designación de corriente instantánea: No se puede analizar la expresión (archivo ejecutable texvc extraviado; Consulte matemáticas/README para obtener ayuda con la configuración): i = i (t) .

Ver también

Números duales y números dobles.

Escribe una reseña sobre el artículo "Unidad imaginaria"

Notas

Enlaces

Unidad imaginaria // Gran Enciclopedia Soviética: [en 30 volúmenes] / cap. ed. A. M. Prójorov. - 3ª edición. -M. : Enciclopedia soviética, 1969-1978.

Ver esta plantilla

poderes de mil

Antiguos números rusos

Otras potencias de diez

potencias de doce

otro entero

Otros números

Extracto que caracteriza la Unidad Imaginaria

– Esto no se puede enseñar, Isidora. La gente debe tener necesidad de Luz, necesidad de Bien. Ellos mismos deben querer el cambio. Porque lo que se da por la fuerza, una persona instintivamente intenta rechazarlo rápidamente, sin siquiera intentar comprender nada. Pero estamos divagando, Isidora. ¿Quieres que continúe la historia de Radomir y Magdalena?
Asentí afirmativamente, lamentando profundamente en mi corazón no poder tener una conversación con él de manera tan simple y tranquila, sin preocuparme por lo que el destino me había deparado. últimos minutos mi vida lisiada y no pensar con horror en la desgracia que se cierne sobre Anna...
– La Biblia escribe mucho sobre Juan el Bautista. ¿Estaba realmente con Radomir y los Caballeros del Templo? Su imagen es tan asombrosamente buena que a veces uno dudaba de si John era la figura real. ¿Puedes responder, Norte?
Norte sonrió cálidamente, aparentemente recordando algo muy agradable y querido para él...
– John era sabio y amable, como un gran sol cálido... Era un padre para todos los que caminaban con él, su maestro y amigo... Era valorado, obedecido y amado. Pero nunca fue el joven e increíblemente guapo como solían pintarlo los artistas. John en ese momento ya era un hechicero anciano, pero todavía muy fuerte y persistente. Alto y de cabello gris, parecía más un poderoso guerrero épico que un joven increíblemente guapo y gentil. Llevaba muy pelo largo, así como todos los demás que están con Radomir.

Era Radan, era verdaderamente extraordinariamente guapo. Él, al igual que Radomir, vivió en Meteora desde muy joven, junto a su madre, la hechicera María. Recuerda, Isidora, cuántos cuadros hay en los que aparece María con dos bebés, casi de la misma edad. Por alguna razón, todos los artistas famosos los pintaron, tal vez sin siquiera entender QUIÉN representaba realmente su pincel... Y lo más interesante es que es a Radan a quien María mira en todas estas pinturas. Aparentemente incluso entonces, cuando aún era un bebé, Radan ya era tan alegre y atractivo como lo fue durante su corta vida...

Y sin embargo... incluso si los artistas pintaron a Juan en estas pinturas, ¿cómo pudo ese mismo Juan haber envejecido tan monstruosamente en el momento de su ejecución, llevada a cabo a petición de la caprichosa Salomé?... Después de todo, según el Biblia, esto sucedió incluso antes de la crucifixión de Cristo, lo que significa que Juan no debería haber tenido más de treinta años en ese momento. cuatro años! ¿Cómo pasó de ser un joven apuesto y de cabello dorado a un judío anciano y completamente poco atractivo?

- ¿Entonces el Mago John no murió, Sever? – pregunté alegremente. – ¿O murió de otra manera?..
“Desafortunadamente, al verdadero John realmente le cortaron la cabeza, Isidora, pero esto no sucedió debido a la mala voluntad de una mujer caprichosa y malcriada. La causa de su muerte fue la traición de un “amigo” judío en quien confiaba y en cuya casa vivió durante varios años...
- ¿Pero cómo es que no lo sintió? ¿Cómo no viste qué clase de “amigo” era este? – Me indigné.
– Probablemente sea imposible sospechar de cada persona, Isidora... Creo que ya les resultó bastante difícil confiar en alguien, porque todos tuvieron que adaptarse de alguna manera y vivir en ese país extranjero y desconocido, no lo olvides. Porque, desde los grandes y mal menor aparentemente intentaron elegir menos. Pero es imposible predecirlo todo, lo sabes muy bien, Isidora... La muerte del mago Juan se produjo después de la crucifixión de Radomir. Fue envenenado por un judío, en cuya casa vivía Juan en ese momento junto con la familia del difunto Jesús. Una noche, cuando toda la casa ya dormía, el dueño, hablando con John, le regaló su té favorito mezclado con un fuerte veneno de hierbas... A la mañana siguiente, nadie pudo entender lo que había sucedido. Según el propietario, John simplemente se durmió instantáneamente y nunca más se despertó... Su cuerpo fue encontrado por la mañana en su cama ensangrentada con... una cabeza cortada... Según el mismo propietario, los judíos eran muy Tenían miedo de John, porque lo consideraban un mago insuperable. Y para estar seguros de que nunca más resucitaría, lo decapitaron. La cabeza de Juan fue posteriormente comprada (!!!) de ellos y llevada con ellos por los Caballeros del Templo, logrando conservarla y llevarla al Valle de los Magos, para así darle a Juan al menos una tan pequeña, pero respeto digno y merecido, sin permitir que los judíos simplemente se burlen de él, haciendo algo por su cuenta rituales magicos. A partir de entonces, la cabeza de John estuvo siempre con ellos, dondequiera que estuvieran. Y por esta misma cabeza, doscientos años después, los Caballeros del Temple fueron acusados de culto criminal al Diablo... Recuerdas el último “caso de los Templarios” (Caballeros del Temple), ¿no?, Isidora. ? Fue allí donde fueron acusados de adorar a una “cabeza parlante”, lo que enfureció a todo el clero de la iglesia.

- Perdóname, Sever, pero ¿por qué los Caballeros del Templo no trajeron la cabeza de John aquí a Meteora? Porque, hasta donde tengo entendido, ¡todos ustedes lo amaban mucho! ¿Y cómo sabes todos estos detalles? No estabas con ellos, ¿verdad? ¿Quién te dijo todo esto?
- Nos contó todo esto. historia triste La bruja María, madre de Radan y Radomir...
– ¡¿María volvió contigo después de la ejecución de Jesús?!... Después de todo, hasta donde yo sé, ella estuvo con su hijo durante la crucifixión. ¿Cuándo volvió contigo? ¿Será posible que todavía esté viva?.. – pregunté conteniendo la respiración.

Sujeto: Unidad imaginaria , su grados. Complejo números.

Algebraico forma integral números.

Objetivos: ampliar el concepto de número, introducir el concepto de unidad imaginaria y sus potencias, el concepto Número complejo; considere la forma algebraica de un número complejo; Desarrollar la capacidad de generalizar los conocimientos adquiridos, promover el desarrollo. pensamiento lógico;

educar a los estudiantes actitud consciente al proceso de aprendizaje.

Plan ( cuestiones en estudio )

Números imaginarios. Definición de unidad imaginaria. Potencias de la unidad imaginaria.

Definición de número complejo.

forma algebraica Número complejo.

1.Números imaginarios

Definición. Un número cuyo cuadrado es -1 se llama unidad imaginaria y

denotado por і ; і 2 = -1

Definición. Números que tienen la forma b і , donde b es un número real, se llaman

números imaginarios.

Por ejemplo:

Se sabe que los números reales están representados por puntos en el eje OX. Los números imaginarios están representados por puntos en el eje OU y, por lo tanto, el eje OX se llama eje real, y el eje OU es el eje imaginario. El conjunto de los números imaginarios se corresponde uno a uno con el conjunto de los números reales.

Definición. Dos números imaginarios b 1 i Y b 2 i se llaman iguales si b 1 = b 2

Definición. Número imaginario (- bi ) llamado lo opuesto de un número imaginario b і .

Por ejemplo:
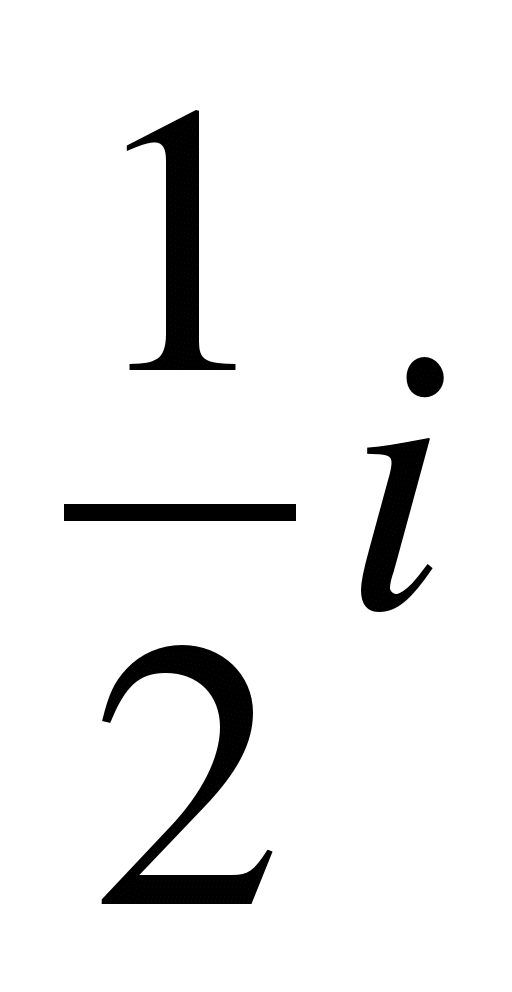Y
Y
.

Teorema. Cualquier potencia natural de un número. і se puede convertir a

uno de cuatro tipos 1; і ; -1; -і.

Prueba .

Considere la expresión і metro , donde metro - número natural. Está claro que son posibles cuatro casos:

1) metro = 4 k , k =1,2, ...

2) m=4k +1,k =0, 1,2,...

3) metro 4k +2, k = 0,1,2,...

4) metro = 4k +3, k =0,1,2, ....

Dejar metro = 4 k , Entonces і metro =і Alaska =(і A ) A =1 A =1

Dejarmetro =4 k +1, Entonces і metro = і Ak+1 = і Alaska yo=1yo=yo

Dejar metro = 4 k +2, Entoncesі metro =і Ak+2 = і Alaska і 2 = 1(-1)=-1

Dejarmetro =4 k +3, Entonces і metro

Ejemplo. Calcular el valor de una expresión.

Solución:

Comentario. Para calcular la potencia de una unidad imaginaria es conveniente utilizar la siguiente regla:

1) divide el exponente por 4;

2) reemplazar yo metro en yo R , donde p es el resto obtenido al dividir t entre 4, es decir, el número p se encuentra a partir de la igualdad t = 4k + p.

2. Números complejos

Definición. Un número complejo es un número que tiene la formaa+bi , donde a, b –

números reales, i es la unidad imaginaria. En este caso, el número "a" se llama

parte real de un número complejo, "b" - parte imaginaria

Número complejo.

Simbólicamente, las partes real e imaginaria de un número complejo se denotan de la siguiente manera:(reiniciar), (no lo hacen).

Estas designaciones se basan en las primeras letras. palabras latinas, que significa "real" e "Imaginaries", que significa "imaginario".

Comentario. A veces la parte imaginaria de un número complejo.z = A + b і llamado bi.

Definición. Dos números complejosz 1 = a 1 + b 1 i Yz 2 = A 2 + b 1 i se llaman iguales si

Rez 1 = Rez 2 , Soyz 1 = Soyz 2 .

Para los números complejos no existen conceptos de mayor y menor, es decir, los números complejos no son comparables.

Definición. Número complejo(-A- bi ) llamado lo opuesto de un número complejo

a+b.

Definición. Dos números complejos cuyas partes reales son iguales y cuyas partes imaginarias son iguales

parteslos opuestos se llaman números conjugados complejos y

están designados en consecuencia Y.

3. Forma algebraica de un número complejo. Acciones sobre números complejos dados en forma algebraica.

Número complejo representado como
llamado número complejo enforma algebraica .

Suma de números complejos

Definición. La suma de dos números complejos.
Y
llamado

Número complejo .

Entonces, (1)

Por lo tanto, para sumar dos números complejos, es necesario sumar sus partes reales, lo que da la parte real de la suma, y sumar las partes imaginarias, lo que da la parte imaginaria de la suma.

La suma de números conjugados siempre es real. número

eso es,
. (2)

Restar números complejos

Definición. La diferencia de dos números complejos.
Y
se llama

Número complejo
, que suma el número da un numero .

La resta de números complejos siempre es posible.

Teorema. Para cualquier número complejo
Y
siempre hay una diferencia
, que está determinado de forma única.

Así, para restar números complejos basta con restar sus partes reales y tomar su diferencia como la parte real de la diferencia, y también restar la parte imaginaria de la diferencia.

Resulta que (3)

La diferencia de dos números conjugados es siempre un número imaginario. ,

eso es,
(4)

Multiplicar números complejos

Definición. Producto de dos números complejos
y se llama tal número complejo, que está determinado por la fórmula: (5)

Para multiplicar números complejos, debes multiplicarlos según la regla para multiplicar polinomios, reemplazando por -1 y trae términos similares.

Al multiplicar números complejos, es mejor realizar una multiplicación directa. El producto de números conjugados siempre es Número Real Respuesta.

Preguntas de control:

1.Dar la definición de número complejo.

2.Formular la definición de unidad imaginaria.

3. Cómo encontrar el grado de una unidad imaginaria.

4.¿Qué números complejos se llaman iguales y conjugados?

5.Escribe una fórmula para encontrar una potencia arbitraria de una unidad imaginaria.

6. Da ejemplos de números puramente imaginarios.

7. Definir la suma, producto y cociente de dos números complejos.

Literatura

Escrito, D. T. Notas de conferencias sobre Matemáticas avanzadas: curso completo D.T. Escrito. – 9ª ed. – M.: Iris-press, 2009. 608 p.: enfermo. - (Educación más alta).

Lungu, K. N. Colección de problemas de matemáticas superiores. 1er año / K. N. Lungu, D. T. Pismenny, S. N. Fedin, Yu A. Shevchenko. – 7ª ed. – M.: Iris-press, 2008. 576 págs.: – (Educación superior).

Grigoriev V.P. Elementos de matemáticas superiores: un libro de texto para estudiantes. instituciones profe. educación / V. P. Grigoriev, Yu. – 10ª ed., borrada. – M. Centro editorial “Academia”, 2014. – 320 p.