Concepto de área
El concepto de área de cualquier figura geométrica, en particular un triángulo, estará asociado a una figura como un cuadrado. Para la unidad de área de cualquier figura geométrica tomaremos el área de un cuadrado cuyo lado es igual a uno. Para completar, recordemos dos propiedades básicas del concepto de áreas de figuras geométricas.
Propiedad 1: Si las figuras geométricas son iguales, entonces sus áreas también lo son.
Propiedad 2: Cualquier figura se puede dividir en varias figuras. Además, el área de la figura original es igual a la suma de las áreas de todas sus figuras constituyentes.
Veamos un ejemplo.
Ejemplo 1
Obviamente, uno de los lados del triángulo es una diagonal de un rectángulo, un lado del cual tiene una longitud de $5$ (ya que hay $5$ celdas) y el otro es $6$ (ya que hay $6$ celdas). Por tanto, el área de este triángulo será igual a la mitad de dicho rectángulo. El área del rectángulo es
Entonces el área del triángulo es igual a
Respuesta: $15$.
A continuación, consideraremos varios métodos para encontrar las áreas de triángulos, es decir, usando la altura y la base, usando la fórmula y el área de Heron. triangulo equilatero.
Cómo encontrar el área de un triángulo usando su altura y base
Teorema 1
El área de un triángulo se puede encontrar como la mitad del producto de la longitud de un lado por la altura de ese lado.
Matemáticamente se ve así
$S=\frac(1)(2)αh$
donde $a$ es la longitud del lado, $h$ es la altura dibujada hacia él.
Prueba.
Considere un triángulo $ABC$ en el que $AC=α$. Hacia este lado se dibuja la altura $BH$, que es igual a $h$. Vamos a construirlo hasta el cuadrado $AXYC$ como en la Figura 2.
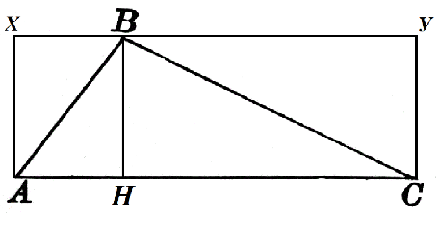
El área del rectángulo $AXBH$ es $h\cdot AH$, y el área del rectángulo $HBYC$ es $h\cdot HC$. Entonces
$S_ABH=\frac(1)(2)h\cdot AH$, $S_CBH=\frac(1)(2)h\cdot HC$
Por tanto, el área requerida del triángulo, según la propiedad 2, es igual a
$S=S_ABH+S_CBH=\frac(1)(2)h\cdot AH+\frac(1)(2)h\cdot HC=\frac(1)(2)h\cdot (AH+HC)=\ frac(1)(2)αh$
El teorema ha sido demostrado.
Ejemplo 2
Encuentra el área del triángulo en la siguiente figura si la celda tiene un área igual a uno
La base de este triángulo es igual a $9$ (ya que $9$ son $9$ cuadrados). La altura también es $9$. Entonces, por el teorema 1, obtenemos
$S=\frac(1)(2)\cdot 9\cdot 9=40.5$
Respuesta: $40,5$.
la fórmula de garza
Teorema 2
Si nos dan tres lados de un triángulo $α$, $β$ y $γ$, entonces su área se puede encontrar de la siguiente manera
$S=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
aquí $ρ$ significa el semiperímetro de este triángulo.
Prueba.
Considere la siguiente figura:
Por el teorema de Pitágoras, del triángulo $ABH$ obtenemos
Del triángulo $CBH$, según el teorema de Pitágoras, tenemos
$h^2=α^2-(β-x)^2$
$h^2=α^2-β^2+2βxx^2$
De estas dos relaciones obtenemos la igualdad
$γ^2-x^2=α^2-β^2+2βx-x^2$
$x=\frac(γ^2-α^2+β^2)(2β)$
$h^2=γ^2-(\frac(γ^2-α^2+β^2)(2β))^2$
$h^2=\frac((α^2-(γ-β)^2)((γ+β)^2-α^2))(4β^2)$
$h^2=\frac((α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α))(4β^2)$
Dado que $ρ=\frac(α+β+γ)(2)$, entonces $α+β+γ=2ρ$, lo que significa
$h^2=\frac(2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α))(4β^2)$
$h^2=\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2 )$
$h=\sqrt(\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2))$
$h=\frac(2)(β)\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
Por el teorema 1, obtenemos
$S=\frac(1)(2) βh=\frac(β)(2)\cdot \frac(2)(β) \sqrt(ρ(ρ-α)(ρ-β)(ρ-γ) )=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
Para determinar el área de un triángulo, puedes usar diferentes fórmulas. De todos los métodos, el más sencillo y utilizado es multiplicar la altura por la longitud de la base y luego dividir el resultado por dos. Sin embargo este método lejos de ser el único. A continuación puedes leer cómo encontrar el área de un triángulo usando diferentes fórmulas.
Por separado, veremos formas de calcular el área. tipos específicos triángulo: rectangular, isósceles y equilátero. Acompañamos cada fórmula con una breve explicación que te ayudará a comprender su esencia.
Métodos universales para encontrar el área de un triángulo.
Las fórmulas siguientes utilizan notación especial. Desciframos cada uno de ellos:
- a, b, c – las longitudes de los tres lados de la figura que estamos considerando;
- r es el radio del círculo que se puede inscribir en nuestro triángulo;
- R es el radio del círculo que se puede describir a su alrededor;
- α es la magnitud del ángulo formado por los lados b y c;
- β es la magnitud del ángulo entre a y c;
- γ es la magnitud del ángulo formado por los lados a y b;
- h es la altura de nuestro triángulo, bajada desde el ángulo α hasta el lado a;
- p – la mitad de la suma de los lados a, b y c.
Está lógicamente claro por qué puedes encontrar el área de un triángulo de esta manera. El triángulo se puede completar fácilmente hasta formar un paralelogramo, en el que un lado del triángulo actuará como diagonal. El área de un paralelogramo se encuentra multiplicando la longitud de uno de sus lados por el valor de la altura que se le dibuja. La diagonal divide este paralelogramo condicional en 2 triángulos idénticos. Por tanto, es bastante obvio que el área de nuestro triángulo original debe ser igual a la mitad del área de este paralelogramo auxiliar.
S=½ a b sen γ
Según esta fórmula, el área de un triángulo se encuentra multiplicando las longitudes de sus dos lados, es decir, a y b, por el seno del ángulo formado por ellos. Esta fórmula se deriva lógicamente de la anterior. Si bajamos la altura desde el ángulo β al lado b, entonces, según las propiedades de un triángulo rectángulo, cuando multiplicamos la longitud del lado a por el seno del ángulo γ, obtenemos la altura del triángulo, es decir, h .
El área de la figura en cuestión se encuentra multiplicando la mitad del radio del círculo que se puede inscribir en ella por su perímetro. Es decir, encontramos el producto del semiperímetro por el radio del círculo mencionado.
S= a b c/4R
Según esta fórmula, el valor que necesitamos lo podemos encontrar dividiendo el producto de los lados de la figura por 4 radios del círculo descrito a su alrededor.
Estas fórmulas son universales, ya que permiten determinar el área de cualquier triángulo (escaleno, isósceles, equilátero, rectangular). Esto también se puede hacer usando más cálculos complejos, en el que no nos detendremos en detalle.
Áreas de triángulos con propiedades específicas.

¿Cómo encontrar el área de un triángulo rectángulo? La peculiaridad de esta figura es que sus dos lados son al mismo tiempo sus alturas. Si a y b son catetos y c se convierte en la hipotenusa, entonces encontramos el área así:
Cómo encontrar el área triangulo isósceles? Tiene dos lados de longitud a y un lado de longitud b. En consecuencia, su área se puede determinar dividiendo por 2 el producto del cuadrado de lado a por el seno del ángulo γ.
¿Cómo encontrar el área de un triángulo equilátero? En él, la longitud de todos los lados es igual a a y la magnitud de todos los ángulos es α. Su altura es igual a la mitad del producto de la longitud del lado a y la raíz cuadrada de 3. Para encontrar el área triangulo regular, necesitas multiplicar el cuadrado del lado a por la raíz cuadrada de 3 y dividir por 4.
Concepto de área
El concepto de área de cualquier figura geométrica, en particular un triángulo, estará asociado a una figura como un cuadrado. Para la unidad de área de cualquier figura geométrica tomaremos el área de un cuadrado cuyo lado es igual a uno. Para completar, recordemos dos propiedades básicas del concepto de áreas de figuras geométricas.
Propiedad 1: Si las figuras geométricas son iguales, entonces sus áreas también lo son.
Propiedad 2: Cualquier figura se puede dividir en varias figuras. Además, el área de la figura original es igual a la suma de las áreas de todas sus figuras constituyentes.
Veamos un ejemplo.
Ejemplo 1
Obviamente, uno de los lados del triángulo es una diagonal de un rectángulo, un lado del cual tiene una longitud de $5$ (ya que hay $5$ celdas) y el otro es $6$ (ya que hay $6$ celdas). Por tanto, el área de este triángulo será igual a la mitad de dicho rectángulo. El área del rectángulo es
Entonces el área del triángulo es igual a
Respuesta: $15$.
A continuación, consideraremos varios métodos para encontrar las áreas de triángulos, es decir, usando la altura y la base, usando la fórmula de Heron y el área de un triángulo equilátero.
Cómo encontrar el área de un triángulo usando su altura y base
Teorema 1
El área de un triángulo se puede encontrar como la mitad del producto de la longitud de un lado por la altura de ese lado.
Matemáticamente se ve así
$S=\frac(1)(2)αh$
donde $a$ es la longitud del lado, $h$ es la altura dibujada hacia él.
Prueba.
Considere un triángulo $ABC$ en el que $AC=α$. Hacia este lado se dibuja la altura $BH$, que es igual a $h$. Vamos a construirlo hasta el cuadrado $AXYC$ como en la Figura 2.

El área del rectángulo $AXBH$ es $h\cdot AH$, y el área del rectángulo $HBYC$ es $h\cdot HC$. Entonces
$S_ABH=\frac(1)(2)h\cdot AH$, $S_CBH=\frac(1)(2)h\cdot HC$
Por tanto, el área requerida del triángulo, según la propiedad 2, es igual a
$S=S_ABH+S_CBH=\frac(1)(2)h\cdot AH+\frac(1)(2)h\cdot HC=\frac(1)(2)h\cdot (AH+HC)=\ frac(1)(2)αh$
El teorema ha sido demostrado.
Ejemplo 2
Encuentra el área del triángulo en la siguiente figura si la celda tiene un área igual a uno
La base de este triángulo es igual a $9$ (ya que $9$ son $9$ cuadrados). La altura también es $9$. Entonces, por el teorema 1, obtenemos
$S=\frac(1)(2)\cdot 9\cdot 9=40.5$
Respuesta: $40,5$.
la fórmula de garza
Teorema 2
Si nos dan tres lados de un triángulo $α$, $β$ y $γ$, entonces su área se puede encontrar de la siguiente manera
$S=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
aquí $ρ$ significa el semiperímetro de este triángulo.
Prueba.
Considere la siguiente figura:
Por el teorema de Pitágoras, del triángulo $ABH$ obtenemos
Del triángulo $CBH$, según el teorema de Pitágoras, tenemos
$h^2=α^2-(β-x)^2$
$h^2=α^2-β^2+2βxx^2$
De estas dos relaciones obtenemos la igualdad
$γ^2-x^2=α^2-β^2+2βx-x^2$
$x=\frac(γ^2-α^2+β^2)(2β)$
$h^2=γ^2-(\frac(γ^2-α^2+β^2)(2β))^2$
$h^2=\frac((α^2-(γ-β)^2)((γ+β)^2-α^2))(4β^2)$
$h^2=\frac((α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α))(4β^2)$
Dado que $ρ=\frac(α+β+γ)(2)$, entonces $α+β+γ=2ρ$, lo que significa
$h^2=\frac(2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α))(4β^2)$
$h^2=\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2 )$
$h=\sqrt(\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2))$
$h=\frac(2)(β)\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
Por el teorema 1, obtenemos
$S=\frac(1)(2) βh=\frac(β)(2)\cdot \frac(2)(β) \sqrt(ρ(ρ-α)(ρ-β)(ρ-γ) )=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
Un triangulo es asi figura geométrica, que consta de tres líneas que se conectan en puntos que no se encuentran en la misma línea. Los puntos de conexión de las líneas son los vértices del triángulo, que se designan en letras latinas(por ejemplo, A, B, C). Las líneas rectas que conectan un triángulo se llaman segmentos, que también suelen denotarse con letras latinas. Distinguir siguientes tipos triangulos:
- Rectangular.
- Obtuso.
- Angular agudo.
- Versátil.
- Equilátero.
- Isósceles.
Fórmulas generales para calcular el área de un triángulo.
Fórmula para el área de un triángulo en función de la longitud y la altura.
S= a*h/2,
donde a es la longitud del lado del triángulo cuyo área es necesario encontrar, h es la longitud de la altura trazada hasta la base.
la fórmula de garza
S=√р*(р-а)*(р-b)*(p-c),
donde √ es raíz cuadrada, p es el semiperímetro del triángulo, a,b,c es la longitud de cada lado del triángulo. El semiperímetro de un triángulo se puede calcular mediante la fórmula p=(a+b+c)/2.


Fórmula para el área de un triángulo según el ángulo y la longitud del segmento
S = (a*b*sin(α))/2,
Dónde b,c es la longitud de los lados del triángulo, sin(α) es el seno del ángulo entre los dos lados.


Fórmula para el área de un triángulo dado el radio del círculo inscrito y tres lados
S=p*r,
donde p es el semiperímetro del triángulo cuya área es necesario encontrar, r es el radio del círculo inscrito en este triángulo.


Fórmula para el área de un triángulo basada en tres lados y el radio del círculo circunscrito a su alrededor
S= (a*b*c)/4*R,
donde a,b,c es la longitud de cada lado del triángulo, R es el radio del círculo circunscrito alrededor del triángulo.


Fórmula para el área de un triángulo usando las coordenadas cartesianas de puntos
Las coordenadas cartesianas de puntos son coordenadas en el sistema xOy, donde x es la abscisa, y es la ordenada. sistema cartesiano Las coordenadas xOy en el plano se llaman mutuamente perpendiculares. ejes numéricos Ooh y Oy con comienzo común referencia en el punto O. Si las coordenadas de los puntos en este plano se dan en la forma A(x1, y1), B(x2, y2) y C(x3, y3), entonces puedes calcular el área del triángulo. usando la siguiente fórmula, que se obtiene de producto vectorial dos vectores.
S = |(x1 – x3) (y2 – y3) – (x2 – x3) (y1 – y3)|/2,
donde || significa módulo.


Cómo encontrar el área de un triángulo rectángulo
Un triángulo rectángulo es un triángulo cuyo ángulo mide 90 grados. Un triángulo sólo puede tener uno de esos ángulos.
Fórmula para el área de un triángulo rectángulo en dos lados
S=a*b/2,
donde a,b es la longitud de los catetos. Los catetos son los lados adyacentes a un ángulo recto.


Fórmula para el área de un triángulo rectángulo basada en la hipotenusa y el ángulo agudo
S = a*b*sen(α)/ 2,
donde a, b son los catetos del triángulo y sin(α) es el seno del ángulo en el que se cruzan las líneas a, b.


Fórmula para el área de un triángulo rectángulo basada en el lado y el ángulo opuesto
S = a*b/2*tg(β),
donde a, b son los catetos del triángulo, tan(β) es la tangente del ángulo en el que se conectan los catetos a, b.


Cómo calcular el área de un triángulo isósceles
Un triángulo isósceles es un triángulo que tiene dos lados iguales. Estos lados se llaman lados y el otro lado es la base. Para calcular el área de un triángulo isósceles, puedes utilizar una de las siguientes fórmulas.
Fórmula básica para calcular el área de un triángulo isósceles
S=h*c/2,
donde c es la base del triángulo, h es la altura del triángulo bajado hasta la base.


Fórmula de un triángulo isósceles basada en lado y base
S=(c/2)* √(a*a – c*c/4),
donde c es la base del triángulo, a es el tamaño de uno de los lados laterales del triángulo isósceles.


Cómo encontrar el área de un triángulo equilátero
Un triángulo equilátero es un triángulo en el que todos los lados son iguales. Para calcular el área de un triángulo equilátero, puedes utilizar la siguiente fórmula:
S = (√3*a*a)/4,
donde a es la longitud del lado del triángulo equilátero.


Las fórmulas anteriores le permitirán calcular el área requerida del triángulo. Es importante recordar que para calcular el área de triángulos es necesario considerar el tipo de triángulo y los datos disponibles que se pueden utilizar para el cálculo.
A veces en la vida hay situaciones en las que hay que ahondar en la memoria en busca de algo olvidado hace mucho tiempo. conocimiento escolar. Por ejemplo, necesita determinar el área de un terreno triangular, o ha llegado el momento de realizar otra renovación en un apartamento o casa privada, y necesita calcular cuánto material se necesitará para la superficie con forma triangular. Hubo un tiempo en el que podías resolver un problema de este tipo en un par de minutos, pero ahora estás tratando desesperadamente de recordar cómo determinar el área de un triángulo.
¡No te preocupes por eso! Después de todo, es bastante normal que el cerebro de una persona decida transferir conocimientos que no se han utilizado durante mucho tiempo a algún lugar remoto, del que a veces no es tan fácil extraerlos. Para que no tenga que luchar buscando conocimientos escolares olvidados para resolver tal problema, este artículo contiene varios metodos, que facilitan encontrar el área requerida del triángulo.
Es bien sabido que un triángulo es un tipo de polígono mínimamente limitado. numero posible lados En principio, cualquier polígono se puede dividir en varios triángulos conectando sus vértices con segmentos que no intersecan sus lados. Por tanto, conociendo el triángulo, puedes calcular el área de casi cualquier figura.
Entre todos los triángulos posibles que se presentan en la vida, se pueden distinguir los siguientes tipos particulares: y rectangular.
La forma más sencilla de calcular el área de un triángulo es cuando uno de sus ángulos es recto, es decir, en el caso de un triángulo rectángulo. Es fácil ver que es medio rectángulo. Por tanto, su área es igual a la mitad del producto de los lados que forman un ángulo recto entre sí.
Si conocemos la altura de un triángulo, caída desde uno de sus vértices hasta el lado opuesto, y la longitud de este lado, que se llama base, entonces el área se calcula como la mitad del producto de la altura por la base. Esto se escribe usando la siguiente fórmula:
S = 1/2*b*h, en el cual
S es el área requerida del triángulo;
b, h - respectivamente, la altura y la base del triángulo.
Es muy fácil calcular el área de un triángulo isósceles porque la altura dividirá el lado opuesto y se puede medir fácilmente. Si se determina el área, entonces conviene tomar como altura la longitud de uno de los lados que forman un ángulo recto.
Por supuesto, todo esto es bueno, pero ¿cómo determinar si uno de los ángulos de un triángulo es recto o no? Si el tamaño de nuestra figura es pequeño, entonces podemos utilizar una esquina de construcción, un triángulo de dibujo, una postal u otro objeto con forma rectangular.
Pero ¿y si tenemos un triangular? terreno? En este caso, proceda de la siguiente manera: cuente desde arriba del valor esperado ángulo recto de un lado la distancia es múltiplo de 3 (30 cm, 90 cm, 3 m), y del otro lado se mide una distancia en la misma proporción que es múltiplo de 4 (40 cm, 160 cm, 4 m) . Ahora necesitas medir la distancia entre puntos finales estos dos segmentos. Si el resultado es múltiplo de 5 (50 cm, 250 cm, 5 m), entonces podemos decir que el ángulo es recto.
Si se conoce la longitud de cada uno de los tres lados de nuestra figura, entonces el área del triángulo se puede determinar mediante la fórmula de Heron. Para que tenga una forma más sencilla se utiliza un nuevo valor, al que se le llama semiperímetro. Esta es la suma de todos los lados de nuestro triángulo, divididos por la mitad. Una vez calculado el semiperímetro, puedes comenzar a determinar el área mediante la fórmula:
S = raíz cuadrada (p (p-a)(p-b)(p-c)), donde
sqrt - raíz cuadrada;
p - valor del semiperímetro (p = (a+b+c)/2);
a, b, c - bordes (lados) del triángulo.
Pero ¿y si el triángulo tiene forma irregular? Hay dos formas posibles aquí. La primera es intentar dividir dicha figura en dos. triangulo rectángulo, cuya suma de áreas se calcula por separado y luego se suma. O, si se conoce el ángulo entre dos lados y el tamaño de estos lados, aplique la fórmula:
S = 0,5 * ab * senC, donde
a,b - lados del triángulo;
c es el tamaño del ángulo entre estos lados.
último caso en la práctica esto es raro, pero aún así en la vida todo es posible, por lo que la fórmula anterior no será superflua. ¡Buena suerte con tus cálculos!








