Sens spécial pour caractériser la distribution d'une variable aléatoire, ils possèdent des caractéristiques numériques appelées moments initiaux et centraux.
Le moment de départ k-ième commande αk(X) Variable aléatoire X k-ème puissance de cette quantité, c'est-à-dire
αk(X) = M(Xk) (6.8)
Formule (6.8) due à la définition de l'espérance mathématique pour divers Variables aléatoires a sa propre forme, à savoir pour une variable aléatoire discrète avec ensemble fini valeurs
pour une variable aléatoire continue
 , (6.10)
, (6.10)
Où F(X) - densité de distribution d'une variable aléatoire X.
Intégrale incorrecte dans la formule (6.10) se transforme en Intégrale définie sur un intervalle fini, si les valeurs d'une variable aléatoire continue n'existent que dans cet intervalle.
L'une des caractéristiques numériques introduites précédemment - l'espérance mathématique - n'est rien de plus que le moment initial du premier ordre, ou, comme on dit, le premier moment initial :
M(X) = α 1 (X).
Dans le paragraphe précédent, la notion de variable aléatoire centrée a été introduite HM(X). Si cette quantité est considérée comme la principale, alors les moments initiaux peuvent également être trouvés pour elle. Pour l'ampleur elle-même X ces moments seront dits centraux.
Moment central k-ième commande μk(X) Variable aléatoire X appelé espérance mathématique k-ième puissance de la variable aléatoire centrée, c'est-à-dire
μk(X) = M[(HM(X))k] (6.11)
Autrement dit, le point central k-ème ordre est l'espérance mathématique kème degré de déviation.
Moment central k le ème ordre pour une variable aléatoire discrète avec un ensemble fini de valeurs est trouvé par la formule :
![]() , (6.12)
, (6.12)
pour une variable aléatoire continue en utilisant la formule :
 (6.13)
(6.13)
À l'avenir, lorsqu'il deviendra clair de quel type de variable aléatoire nous parlons, nous ne l'écrirons pas dans la notation des moments initiaux et centraux, c'est-à-dire au lieu de αk(X) Et μk(X) on écrira simplement αk Et μk .
Il est évident que le moment central de premier ordre égal à zéro, puisqu'il ne s'agit que de l'espérance mathématique de l'écart, qui est égale à zéro selon ce qui a été prouvé précédemment, c'est-à-dire .
Il n’est pas difficile de comprendre que le moment central du second ordre d’une variable aléatoire X coïncide avec la variance de la même variable aléatoire, c'est-à-dire
De plus, il y a formules suivantes, reliant les moments initiaux et centraux :

Ainsi, les moments du premier et du deuxième ordre (espérance mathématique et dispersion) caractérisent les caractéristiques les plus importantes de la distribution : sa position et le degré de dispersion des valeurs. Pour plus Description détaillée les distributions sont des moments d’ordres supérieurs. Montrons-le.
Supposons que la distribution d'une variable aléatoire soit symétrique par rapport à son espérance mathématique. Alors tous les moments centraux d’ordre impair, s’ils existent, sont égaux à zéro. Ceci s'explique par le fait qu'en raison de la symétrie de la distribution pour chaque valeur positive quantités X − M(X) il existe un module égal Sens négatif, et les probabilités de ces valeurs sont égales. Par conséquent, la somme dans la formule (6.12) est constituée de plusieurs paires de termes de même ampleur mais de signe différent, qui s'annulent lors de la sommation. Ainsi, le montant total, c'est-à-dire le moment central de toute variable aléatoire discrète d’ordre impair est nul. De même, le moment central de tout ordre impair d’une variable aléatoire continue est égal à zéro, tout comme l’intégrale dans les limites symétriques d’une fonction impaire.
Il est naturel de supposer que si le moment central d’un ordre impair est différent de zéro, alors la distribution elle-même ne sera pas symétrique par rapport à son espérance mathématique. De plus, plus le moment central s’écarte de zéro, plus l’asymétrie de la distribution est grande. Prenons le moment central du plus petit ordre impair comme caractéristique de l'asymétrie. Puisque le moment central du premier ordre est nul pour les variables aléatoires ayant n’importe quelle distribution, il est préférable d’utiliser le moment central du troisième ordre à cette fin. Or, cet instant a la dimension d’un cube d’une variable aléatoire. Pour éliminer cet inconvénient et passer à une variable aléatoire sans dimension, divisez la valeur moment central par cube d'écart type.
Coefficient d'asymétrie Comme ou simplement asymétrie est appelé le rapport du moment central du troisième ordre au cube de l'écart type, c'est-à-dire
Parfois, l'asymétrie est appelée « asymétrie » et est désignée Sk ce qui vient de mot anglais biais - "oblique".
Si le coefficient d'asymétrie est négatif, alors sa valeur est fortement influencée par des termes négatifs (écarts) et la distribution aura asymétrie gauche, et le graphique de distribution (courbe) est plus plat à gauche de l'espérance mathématique. Si le coefficient est positif, alors asymétrie droite, et la courbe est plus plate à droite de l’espérance mathématique (Fig. 6.1).
 |
Comme il a été montré, pour caractériser l'étalement des valeurs d'une variable aléatoire autour de son espérance mathématique, on utilise le deuxième moment central, c'est-à-dire dispersion. Si ce moment est d'une grande importance valeur numérique, alors cette variable aléatoire a une grande dispersion de valeurs et la courbe de distribution correspondante a une forme plus plate que la courbe pour laquelle le deuxième moment central a valeur inférieure. Par conséquent, le deuxième moment central caractérise, dans une certaine mesure, la courbe de distribution « à sommet plat » ou « à sommet pointu ». Toutefois, cette caractéristique n’est pas très pratique. Le moment central du second ordre a la dimension égal au carré dimensions d'une variable aléatoire. Si nous essayons d'obtenir une quantité sans dimension en divisant la valeur du moment par le carré de l'écart type, alors pour toute variable aléatoire, nous obtenons : ![]() . Ainsi, ce coefficient ne peut être aucune caractéristique de la distribution d'une variable aléatoire. C'est la même chose pour toutes les distributions. Dans ce cas, vous pouvez utiliser le moment central quatrième commande.
. Ainsi, ce coefficient ne peut être aucune caractéristique de la distribution d'une variable aléatoire. C'est la même chose pour toutes les distributions. Dans ce cas, vous pouvez utiliser le moment central quatrième commande.
Excès Ek est la quantité déterminée par la formule
![]() (6.15)
(6.15)
L'aplatissement est principalement utilisé pour les variables aléatoires continues et sert à caractériser ce qu'on appelle la « raideur » de la courbe de distribution, ou autrement, comme déjà mentionné, à caractériser la courbe de distribution « à sommet plat » ou « à sommet pointu ». La courbe de distribution de référence est considérée comme la courbe distribution normale(ceci sera discuté en détail dans le prochain chapitre). Pour une variable aléatoire répartie sur loi normale, l’égalité est vraie. Par conséquent, un excès donné par la formule(6.15), sert de comparaison distribution donnée avec normal, dont l'aplatissement est égal à zéro.
Si un aplatissement positif est obtenu pour une variable aléatoire, alors la courbe de distribution de cette valeur présente un pic plus élevé que la courbe de distribution normale. Si l'aplatissement est négatif, alors la courbe a un sommet plus plat que la courbe de distribution normale (Fig. 6.2).
 |
Passons maintenant à types spécifiques lois de distribution de variables aléatoires discrètes et continues.
Les moments centraux sont appelés moments de distribution, lors du calcul desquels l'écart des options par rapport à la moyenne arithmétique est pris comme valeur initiale ces séries.
1. Calculez le moment central du premier ordre à l'aide de la formule :
2. Calculez le moment central du second ordre à l'aide de la formule :

où est la valeur du milieu des intervalles ;
Il s'agit d'une moyenne pondérée ;
Fi est le nombre de valeurs.
3. Calculez le moment central du troisième ordre à l'aide de la formule :

où est la valeur du milieu des intervalles ; - c'est la moyenne pondérée ; - fi-nombre de valeurs.
4. Calculez le moment central du quatrième ordre en utilisant la formule :

où est la valeur du milieu des intervalles ; - c'est la moyenne pondérée ; - fi-nombre de valeurs.
Calcul pour le tableau 3.2
Calcul pour le tableau 3.4
1. Calculez le moment central du premier ordre à l'aide de la formule (7.1) :
2. Calculez le moment central du second ordre à l'aide de la formule (7.2) :
3. Calculez le moment central du troisième ordre à l'aide de la formule (7.3) :
4. Calculez le moment central du quatrième ordre à l'aide de la formule (7.4) :
Calcul pour le tableau 3.6
1. Calculez le moment central du premier ordre à l'aide de la formule (7.1) :
2. Calculez le moment central du second ordre à l'aide de la formule (7.2) :
3. Calculez le moment central du troisième ordre à l'aide de la formule (7.3) :
4. Calculez le moment central du quatrième ordre à l'aide de la formule (7.4) :





Les moments d'ordres 1, 2, 3, 4 ont été calculés pour trois problèmes. Où le moment du troisième ordre est nécessaire pour calculer l'asymétrie, et le moment du quatrième ordre est nécessaire pour calculer l'aplatissement.
CALCUL DE L'ASYMÉTRIE DE DISTRIBUTION
Dans la pratique statistique, diverses distributions sont rencontrées. Il existe les types de courbes de distribution suivants :
· courbes à sommet unique : symétriques, modérément asymétriques et extrêmement asymétriques ;
· courbes multisommets.
En règle générale, les populations homogènes sont caractérisées par des distributions à un seul sommet. Multivertex indique l'hétérogénéité de la population étudiée. L'apparition de deux ou plusieurs sommets nécessite de regrouper les données afin d'identifier des groupes plus homogènes.
Trouver général la distribution consiste à évaluer son homogénéité, ainsi qu'à calculer des indicateurs d'asymétrie et d'aplatissement. Pour les distributions symétriques, les fréquences de deux options quelconques situées de manière égale des deux côtés du centre de distribution sont égales l'une à l'autre. La moyenne, le mode et la médiane calculés pour de telles distributions sont également égaux.
Dans une étude comparative de l'asymétrie de plusieurs distributions avec différentes unités de mesure, on calcule indicateur relatif asymétrie():


où est la moyenne pondérée ; Mo-mode; - dispersion pondérée quadratique moyenne ; Moi-médian.
Sa valeur peut être positive ou négative. Dans le premier cas nous parlons de sur l'asymétrie du côté droit, et dans le second - sur l'asymétrie du côté gauche.
Avec asymétrie du côté droit Mo>Me>x. Le plus largement utilisé (comme indicateur d'asymétrie) est le rapport du moment central du troisième ordre à l'écart type d'une série donnée au cube :
où est le moment central du troisième ordre ; -moyenne écart-type en cubes.
Application cet indicateur permet de déterminer non seulement l'ampleur de l'asymétrie, mais aussi de vérifier sa présence dans population. Il est généralement admis qu’une asymétrie supérieure à 0,5 (quel que soit son signe) est considérée comme significative ; s'il est inférieur à 0,25, alors il est insignifiant.
L’appréciation de l’importance relative est basée sur la moyenne erreur carrée, coefficient d'asymétrie (), qui dépend du nombre d'observations (n) et est calculé par la formule :

où n est le nombre d'observations.
Dans ce cas, l’asymétrie est importante et la répartition de la caractéristique dans la population est asymétrique. Sinon, l’asymétrie est insignifiante et sa présence peut être provoquée par des circonstances aléatoires.
Calcul pour le tableau 3.2 Regroupement de la population par moyenne mensuelle salaires, frotter.
Asymétrie importante du côté gauche.
Calcul pour le tableau 3.4 Regroupement de magasins par chiffre d'affaires au détail, en millions de roubles.
1. Déterminons les asymétries à l'aide de la formule (7.5) :
Asymétrie importante du côté droit.
Calcul pour le tableau 3.6 Regroupement des organismes de transport par chiffre d'affaires du transport de marchandises usage commun(millions de t.km)
1. Déterminons les asymétries à l'aide de la formule (7.5) :
Côté droit, légère asymétrie.
CALCUL DE KURTESS DE DISTRIBUTION
Pour les distributions symétriques, l'indice d'aplatissement () peut être calculé :

où est le moment central du quatrième ordre ; - écart type à la puissance quatrième.
Calcul pour le tableau 3.2 Regroupement de la population par salaire mensuel moyen, frotter.

Calcul pour le tableau 3.4 Regroupement de magasins par chiffre d'affaires au détail, en millions de roubles.
Calculons l'indicateur d'aplatissement à l'aide de la formule (7.7)

Distribution de pointe.
Calcul pour le tableau 3.6 Regroupement des organismes de transport par chiffre d'affaires fret des transports publics (millions de t.km)
Calculons l'indicateur d'aplatissement à l'aide de la formule (7.7)

Distribution à dessus plat.
ÉVALUATION DE L'HOMOGÉNÉITÉ DE LA POPULATION
Évaluation de l'homogénéité pour le tableau 3.2 Regroupement de la population par salaire mensuel moyen, frotter.
Il est à noter que si les indicateurs d'asymétrie et d'aplatissement caractérisent directement uniquement la forme de répartition de la caractéristique au sein de la population étudiée, leur définition n'a pas seulement une signification descriptive. Souvent, l'asymétrie et l'aplatissement fournissent certaines indications pour des recherches ultérieures sur le plan social - phénomènes économiques. Le résultat obtenu indique la présence d'une asymétrie significative en ampleur et de nature négative, il convient de noter que l'asymétrie est du côté gauche ; De plus, la population a une répartition plate.
Évaluation de l'homogénéité pour le tableau 3.4 Regroupement de magasins par chiffre d'affaires au détail, en millions de roubles.
Le résultat obtenu indique la présence d'une asymétrie significative en ampleur et de caractère positif, il convient de noter que l'asymétrie est du côté droit. Et la population a également une distribution à sommets nets.
Évaluation de l'homogénéité pour le tableau 3.6 Regroupement des organismes de transport par chiffre d'affaires fret des transports publics (millions de t.km)
Le résultat obtenu indique la présence d'une asymétrie insignifiante en ampleur et de nature positive, il convient de noter que l'asymétrie est du côté droit ; De plus, la population a une répartition à sommet plat.
Valeur attendue. Attente mathématique variable aléatoire discrète X, hôte numéro final valeurs Xje avec probabilités R.je, le montant s'appelle :
Attente mathématique variable aléatoire continue X s'appelle l'intégrale du produit de ses valeurs X sur la densité de distribution de probabilité F(X):
 (6b)
(6b)
Intégrale impropre (6 b) est supposé absolument convergent (sinon on dit que l’espérance mathématique M(X) n'existe pas). L'espérance mathématique caractérise valeur moyenne Variable aléatoire X. Sa dimension coïncide avec la dimension de la variable aléatoire.
Propriétés de l'espérance mathématique :
Dispersion. Variance Variable aléatoire X le numéro s'appelle :
L'écart est caractéristique de diffusion valeurs de variables aléatoires X par rapport à sa valeur moyenne M(X). La dimension de la variance est égale à la dimension de la variable aléatoire au carré. Sur la base des définitions de la variance (8) et de l'espérance mathématique (5) pour une variable aléatoire discrète et (6) pour une variable aléatoire continue, nous obtenons des expressions similaires pour la variance :
 (9)
(9)
Ici m = M(X).
Propriétés de dispersion :
Écart-type:
![]() (11)
(11)
Puisque la dimension de la moyenne écart carré identique à celui d’une variable aléatoire, il est plus souvent utilisé comme mesure de dispersion que de variance.
Moments de distribution. Les concepts d'espérance mathématique et de dispersion sont des cas particuliers de plus concept général pour les caractéristiques numériques des variables aléatoires – instants de distribution. Les moments de distribution d'une variable aléatoire sont présentés comme des attentes mathématiques de certaines fonctions simples d'une variable aléatoire. Alors, moment de la commande k par rapport au point X 0 est appelé l'espérance mathématique M(X–X 0 )k. Moments sur l'origine X= 0 sont appelés premiers instants et sont désignés :
![]() (12)
(12)
L'instant initial du premier ordre est le centre de la distribution de la variable aléatoire considérée :
![]() (13)
(13)
Moments sur le centre de distribution X= m sont appelés points centraux et sont désignés :
![]() (14)
(14)
De (7) il résulte que le moment central du premier ordre est toujours égal à zéro :
Les moments centraux ne dépendent pas de l'origine des valeurs de la variable aléatoire, puisque lorsqu'ils sont décalés de valeur constante AVEC son centre de distribution se décale de la même valeur AVEC, et l'écart par rapport au centre ne change pas : X – m = (X – AVEC) – (m – AVEC).
Maintenant, il est évident que dispersion- Ce moment central du deuxième ordre:
Asymétrie. Moment central du troisième ordre :
![]() (17)
(17)
sert à l'évaluation asymétries de distribution. Si la distribution est symétrique par rapport au point X= m, alors le moment central du troisième ordre sera égal à zéro (comme tous les moments centraux d'ordres impairs). Par conséquent, si le moment central du troisième ordre est différent de zéro, alors la distribution ne peut pas être symétrique. L'ampleur de l'asymétrie est évaluée à l'aide d'un modèle sans dimension coefficient d'asymétrie:
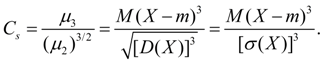 (18)
(18)
Le signe du coefficient d'asymétrie (18) indique une asymétrie du côté droit ou du côté gauche (Fig. 2).

Riz. 2. Types d'asymétrie de distribution.
Excès. Moment central du quatrième ordre :
![]() (19)
(19)
sert à évaluer ce qu'on appelle excès, qui détermine le degré d'inclinaison (pic) de la courbe de distribution près du centre de la distribution par rapport à la courbe de distribution normale. Puisque pour une distribution normale, la valeur prise comme kurtosis est :
 (20)
(20)
En figue. 3 montre des exemples de courbes de distribution avec différentes significations excès. Pour une distribution normale E= 0. Les courbes plus pointues que la normale ont un kurtosis positif, celles dont le sommet est plus plat ont un kurtosis négatif.

Riz. 3. Courbes de distribution avec différents degrés d'inclinaison (kurtosis).
Moments d'ordre supérieur dans les applications d'ingénierie statistiques mathématiques généralement pas utilisé.
Mode
discret une variable aléatoire est sa valeur la plus probable. Mode continu une variable aléatoire est sa valeur à laquelle la densité de probabilité est maximale (Fig. 2). Si la courbe de distribution a un maximum, alors la distribution est appelée unimodal. Si une courbe de distribution a plus d'un maximum, alors la distribution est appelée multimodal. Il existe parfois des distributions dont les courbes ont un minimum plutôt qu'un maximum. De telles distributions sont appelées anti-modal. DANS cas général le mode et l'espérance mathématique d'une variable aléatoire ne coïncident pas. Dans le cas particulier, pour modal, c'est à dire. ayant un mode de distribution symétrique et à condition qu'il y ait une espérance mathématique, cette dernière coïncide avec le mode et le centre de symétrie de la distribution.
Médian Variable aléatoire X- c'est sa signification Meh, pour lequel l'égalité est vraie : c'est-à-dire il est également probable que la variable aléatoire X sera moins ou plus Meh. Géométriquement médian est l'abscisse du point auquel l'aire sous la courbe de distribution est divisée en deux (Fig. 2). Dans le cas d'une distribution modale symétrique, la médiane, le mode et l'espérance mathématique sont les mêmes.
3.4. Moments d'une variable aléatoire.
Ci-dessus, nous avons pris connaissance des caractéristiques complètes du SV : la fonction de distribution et la série de distribution pour un SV discret, la fonction de distribution et la densité de probabilité pour un SV continu. Ces caractéristiques équivalentes deux à deux en termes de contenu informationnel sont les fonctions et décrire complètement le SV d'un point de vue probabiliste. Cependant, dans de nombreuses situations pratiques, il est soit impossible, soit inutile de caractériser une variable aléatoire de manière exhaustive. Il suffit souvent de préciser un ou plusieurs numérique paramètres qui décrivent dans une certaine mesure les principales caractéristiques de la distribution, et parfois trouver des caractéristiques exhaustives est, bien que souhaitable, trop difficile mathématiquement, et en opérant avec des paramètres numériques, nous nous limitons à des approximations, mais plus description simple. Les paramètres numériques spécifiés sont appelés caractéristiques numériques variables aléatoires et jouent un rôle majeur dans les applications de la théorie des probabilités à divers domaines scientifiques et technologiques, facilitant la solution des problèmes et permettant de présenter les résultats de la solution sous une forme simple et visuelle.
Les caractéristiques numériques les plus couramment utilisées peuvent être divisées en deux types : moments et caractéristiques de position. Il existe plusieurs types de moments, dont les deux plus couramment utilisés sont : primaire et centrale. D'autres types de moments, par ex. moments absolus, moments factoriels, nous ne considérons pas. Afin d'éviter l'utilisation d'une généralisation de l'intégrale - dite intégrale de Stieltjes, nous donnerons des définitions des moments séparément pour les SV continues et discrètes.
Définitions. 1. Le moment de départkSV discret du ème ordre s'appelle la quantité
Où F(X) est la densité de probabilité d'un SV donné.
3. Moment centralkSV discret du ème ordre s'appelle la quantité
Dans les cas où plusieurs SV sont simultanément envisagées, il convient, afin d'éviter les malentendus, d'indiquer l'identité du moment ; nous le ferons en indiquant la désignation du SV correspondant entre parenthèses, par exemple, ![]() , etc. Cette désignation ne doit pas être confondue avec la notation de la fonction, et la lettre entre parenthèses ne doit pas être confondue avec l'argument de la fonction. Les sommes et intégrales des membres droits des égalités (3.4.1 - 3.4.4) peuvent converger ou diverger selon la valeur k et distribution spécifique. Dans le premier cas, ils disent que le moment n'existe pas ou diverge, dans le second - quoi le moment existe ou converge. Si un SV discret a un nombre fini de valeurs finies ( N bien sûr), alors tous ses moments sont d'ordre fini k exister. À l'infini N, à partir de certains k et pour les ordres supérieurs, les moments d'un SV discret (à la fois initial et central) peuvent ne pas exister. Les moments d'une SV continue, comme le montrent les définitions, sont exprimés par des intégrales impropres, qui peuvent diverger à partir d'un certain k et pour les ordres supérieurs (à la fois initial et central). Les moments d’ordre zéro convergent toujours.
, etc. Cette désignation ne doit pas être confondue avec la notation de la fonction, et la lettre entre parenthèses ne doit pas être confondue avec l'argument de la fonction. Les sommes et intégrales des membres droits des égalités (3.4.1 - 3.4.4) peuvent converger ou diverger selon la valeur k et distribution spécifique. Dans le premier cas, ils disent que le moment n'existe pas ou diverge, dans le second - quoi le moment existe ou converge. Si un SV discret a un nombre fini de valeurs finies ( N bien sûr), alors tous ses moments sont d'ordre fini k exister. À l'infini N, à partir de certains k et pour les ordres supérieurs, les moments d'un SV discret (à la fois initial et central) peuvent ne pas exister. Les moments d'une SV continue, comme le montrent les définitions, sont exprimés par des intégrales impropres, qui peuvent diverger à partir d'un certain k et pour les ordres supérieurs (à la fois initial et central). Les moments d’ordre zéro convergent toujours.
Examinons plus en détail d'abord les moments initiaux, puis les moments centraux. D'un point de vue mathématique, le moment initial k-ème ordre est la « moyenne pondérée » k-ème degrés de valeurs SV ; dans le cas d'un SV discret, les poids sont les probabilités de valeurs ; dans le cas d'un SV continu, la fonction de poids est la densité de probabilité. De telles opérations sont largement utilisées en mécanique pour décrire la répartition des masses (moments statiques, moments d'inertie, etc.) ; Les analogies qui surviennent à cet égard sont discutées ci-dessous.
Pour une meilleure compréhension des instants initiaux, nous les considérons séparément pour des k. En théorie des probabilités, les moments d'ordres inférieurs sont les plus importants, c'est-à-dire à petit k, par conséquent, la considération doit être effectuée par ordre de valeurs croissantes k. Le moment initial d’ordre zéro est égal à
1, pour SV discret ;
 =1, pour SV continu,
=1, pour SV continu,
ceux. pour tout SV, il est égal à la même valeur - un, et ne contient donc aucune information sur les propriétés statistiques du SV.
Le moment initial du premier ordre (ou premier moment initial) est égal à
Pour SV discret ;
 , pour SV continu.
, pour SV continu.
Ce point est la caractéristique numérique la plus importante de tout SV, pour laquelle il existe plusieurs raisons interdépendantes. Premièrement, selon le théorème de Chebyshev (voir section 7.4), avec un nombre illimité de tests sur le SV, la moyenne arithmétique des valeurs observées tend (en un sens) vers , ainsi, pour tout SV, il s'agit d'un nombre caractéristique autour duquel se regroupent ses valeurs d’expérience. Deuxièmement, pour un CV continu, il est numériquement égal à X-ème coordonnée du centre de gravité du trapèze curviligne formé par la courbe F(X) (une propriété similaire se produit pour un SV discret), donc ce moment pourrait être appelé le « centre de gravité de la distribution ». Troisièmement, ce moment a des propriétés mathématiques remarquables, qui apparaîtront notamment au cours du cours, c'est pourquoi sa valeur est incluse dans les expressions des moments centraux (voir (3.4.3) et (3.4.4)).
L'importance de ce moment pour les problèmes théoriques et pratiques de la théorie des probabilités et ses propriétés mathématiques remarquables ont conduit au fait qu'en plus de la désignation et du nom « premier moment initial », d'autres désignations et noms sont utilisés dans la littérature, plus ou moins pratique et reflétant les propriétés mentionnées. Les noms les plus courants sont : valeur attendue, valeur moyenne, et notation : m, M[X], . On utilisera le plus souvent le terme « espérance mathématique » et la notation m; s'il y a plusieurs SV, on utilisera un indice indiquant l'identité de l'espérance mathématique, par exemple, m X , m oui etc.
Le moment initial du second ordre (ou deuxième moment initial) est égal à
Pour SV discret ;
 , pour SV continu ;
, pour SV continu ;
parfois on l'appelle carré moyen de la variable aléatoire et est désigné M.
Le moment initial du troisième ordre (ou troisième moment initial) est égal à
Pour SV discret ;
 , pour SV continu
, pour SV continu
parfois on l'appelle cube moyen d'une variable aléatoire et est désigné M[X 3 ].
Cela ne sert à rien de continuer à énumérer les points initiaux. Arrêtons-nous sur l'interprétation importante des moments d'ordre k>1. Laissez, avec SV X il y a aussi un SV Oui, et Y=X k (k=2, 3, ...). Cette égalité signifie que les variables aléatoires X Et Oui sont connectés de manière déterministe en ce sens que lorsque SV X prend la valeur X, NE Oui prend la valeur y = x k(à l'avenir, cette connexion de SV sera examinée plus en détail). Alors, d’après (3.4.1) et (3.4.2)
![]() =m oui
, k=2,
3, ...,
=m oui
, k=2,
3, ...,
c'est à dire. k Le ème moment initial de SV est égal à l'espérance mathématique k-ième puissance de cette variable aléatoire. Par exemple, le troisième moment initial de la longueur du bord d’un cube aléatoire est égal à l’espérance mathématique du volume du cube. La capacité de comprendre les moments comme certains attentes mathématiques- une autre facette de l'importance du concept d'espérance mathématique.
Passons à l'examen des points centraux. Puisque, comme cela apparaîtra clairement ci-dessous, les moments centraux sont exprimés sans ambiguïté à travers les moments initiaux et vice versa, la question se pose de savoir pourquoi les moments centraux sont nécessaires et pourquoi les moments initiaux ne suffisent pas. Considérons SV X(continu ou discret) et un autre SV Y, lié au premier comme Y = X + une, Où un 0 - non aléatoire nombre réel. Chaque valeur X Variable aléatoire X correspond à la valeur y=x+a Variable aléatoire Oui, donc la distribution de SV Oui aura la même forme (exprimée par le polygone de distribution dans le cas discret ou la densité de probabilité dans le cas continu) que la distribution SV X, mais décalé le long de l'axe des x du montant un. Par conséquent, les premiers instants de SV Oui différera des moments correspondants de SV X. Par exemple, il est facile de voir m oui =m X +un(des instants de plus ordre élevé sont liés par des relations plus complexes). Nous avons donc établi que les moments initiaux ne sont pas invariants par rapport au déplacement de la distribution dans son ensemble. Le même résultat sera obtenu si vous décalez non pas la distribution, mais le début de l'axe des x horizontalement d'un montant - un, c'est à dire. La conclusion équivalente est également valable : les moments initiaux ne sont pas invariants par rapport au décalage horizontal du début de l'axe des x.
Les moments centraux, destinés à décrire les propriétés des distributions qui ne dépendent pas de leur déplacement dans son ensemble, sont exempts de cet inconvénient. En effet, comme le montrent (3.4.3) et (3.4.4), lorsque la distribution dans son ensemble se déplace d'un montant un, ou, ce qui revient au même, décaler le début de l'axe des x du montant - un, toutes les valeurs X, avec les mêmes probabilités (dans le cas discret) ou la même densité de probabilité (dans le cas continu), changera de la quantité un, mais la quantité changera du même montant m, donc les valeurs des parenthèses à droite des égalités ne changeront pas. Ainsi, les moments centraux sont invariants par rapport au déplacement de la distribution dans son ensemble, ou, ce qui revient au même, par rapport au déplacement horizontal du début de l'axe des x. Ces moments recevaient le nom de « central » à l'époque où le premier moment initial était appelé « centre ». Il est utile de noter que le moment central de SV X peut être compris comme le moment initial correspondant de SV X 0 égal
|
X 0 =X-m X . |
NE X 0 est appelé centré(par rapport à SV X), et l'opération qui y conduit, c'est-à-dire soustraire son espérance mathématique à une variable aléatoire, est appelée centrage. Comme nous le verrons plus loin, cette notion et ce fonctionnement seront utiles tout au long du cours. Notez que le moment central de l'ordre k>1 peut être considéré comme l'espérance mathématique (moyenne) k-ème degré de SV centré : ![]() .
.
Considérons séparément les moments centraux des ordres inférieurs. Le moment central d’ordre zéro est égal à
 , pour les SV discrets ;
, pour les SV discrets ;
 , pour SV continu ;
, pour SV continu ;
c'est-à-dire pour n'importe quel SV et ne contient aucune information sur les propriétés statistiques de ce SV.
Le moment central du premier ordre (ou premier moment central) est égal à
pour SV discret ;
pour CB continu ; c'est-à-dire pour n'importe quel SV et ne contient aucune information sur les propriétés statistiques de ce SV.
Le moment central du deuxième ordre (ou deuxième moment central) est égal à
 , pour SV discret ;
, pour SV discret ;
 , pour SV continu.
, pour SV continu.
Comme cela apparaîtra clairement ci-dessous, ce point est l'un des plus importants de la théorie des probabilités, puisqu'il est utilisé comme caractéristique de la mesure de dispersion (ou dispersion) des valeurs SV, c'est pourquoi il est souvent appelé dispersion et est désigné D X. Notez que cela peut être compris comme le carré moyen du SV centré.
Le moment central du troisième ordre (troisième moment central) est égal à
Trouvons l'espérance mathématique X 2 :
M(X 2) = 1* 0, 6 + 4* 0, 2 + 25* 0, 19+ 10000* 0, 01 = 106, 15.
On voit ça M(X 2) bien plus M(X). C'est parce qu'après la mise au carré signification possible quantités X 2 correspondant à la valeur X=100 magnitude X, est devenu égal à 10 000, c'est-à-dire a augmenté de manière significative ; la probabilité de cette valeur est faible (0,01).
Ainsi, le passage de M(X)À M(X 2) a permis de mieux prendre en compte l'influence sur l'espérance mathématique de cette valeur possible, grande et faible probabilité. Bien entendu, si la valeur X avait plusieurs valeurs importantes et improbables, puis le passage à la valeur X 2, et encore plus aux quantités X 3 , X 4, etc., nous permettraient de « renforcer davantage le rôle » de ces valeurs importantes, mais improbables. C'est pourquoi il s'avère opportun de considérer l'espérance mathématique de l'ensemble degré positif variable aléatoire (non seulement discrète, mais aussi continue).
Moment initial de commande k Variable aléatoire X s'appelle l'espérance mathématique d'une quantité Xk :
vk = M(X).
En particulier,
v 1 =M(X),v 2 =M(X 2).
A l'aide de ces points, la formule de calcul de la variance D(X)=M(X 2)- [M(X)] 2 peut s'écrire ainsi :
D(X)=v 2 – . (*)
En plus des moments de la variable aléatoire X il est conseillé de considérer les moments de déviation X-M(X).
Le moment central d'ordre k d'une variable aléatoire X est l'espérance mathématique de la quantité(HM(X))k :
En particulier,
Les relations reliant les moments initiaux et centraux sont faciles à déduire. Par exemple, en comparant (*) et (***), on obtient
m 2 = v 2 – .
Il n'est pas difficile, à partir de la définition du moment central et en utilisant les propriétés de l'espérance mathématique, d'obtenir les formules :
m 3 = v 3 – 3v 2 v 1 + 2 ,
m 4 = v 4 – 4v 3 v 1 + 6v 2 + 3 .
Les moments d’ordre supérieur sont rarement utilisés.
Commentaire. Les points abordés ici sont appelés théorique. Contrairement aux moments théoriques, les moments calculés à partir de données d'observation sont appelés empirique. Les définitions des moments empiriques sont données ci-dessous (voir chapitre XVII, § 2).
Tâches
1. Les variances de deux variables aléatoires indépendantes sont connues : D(X) = 4,D(Oui)=3. Trouvez la variance de la somme de ces quantités.
représentant 7.
2. Variance d'une variable aléatoire X est égal à 5. Trouvez la variance des quantités suivantes : a) X-1; b) -2 X; V) ZH + 6.
représentant une) 5 ; b) 20 ; c) 45.
3. Valeur aléatoire X ne prend que deux valeurs : +C et -C, chacune avec une probabilité de 0,5. Trouvez la variance de cette quantité.
représentant AVEC 2 .
4. , connaissant la loi de sa distribution
| X | 0, 1 | |||
| P. | 0, 4 | 0, 2 | 0, 15 | 0, 25 |
représentant 67,6404.
5. Valeur aléatoire X peut prendre deux valeurs possibles : X 1 avec une probabilité de 0,3 et X 2 avec une probabilité de 0,7, et X 2 >x 1 . Trouver X 1 et X 2, sachant que M(X) = 2, 7i D(X) =0,21.
représentant X 1 = 2, X 2 = 3.
6. Trouver la variance d'une variable aléatoire X-nombre d'occurrences d'événements UN en deux tests indépendants, Si M(X) = 0, 8.
Note: Écrire loi binomiale distribution de probabilité du nombre d'occurrences d'un événement UN dans deux essais indépendants.
représentant 0, 48.
7. Un appareil composé de quatre appareils fonctionnant indépendamment est en cours de test. Les probabilités de panne de l'appareil sont les suivantes : R. 1 = 0,3; R. 2 = 0,4; p 3 = 0,5; R. 4 = 0,6. Trouvez l'espérance mathématique et la variance du nombre d'appareils défaillants.
représentant 1,8; 0,94.
8. Trouver la variance d'une variable aléatoire X- le nombre d'occurrences de l'événement dans 100 essais indépendants, dans chacun desquels la probabilité que l'événement se produise est de 0,7.
représentant 21.
9. Variance d'une variable aléatoire D(X) = 6,25. Trouver l'écart type s( X).
représentant 2, 5.
10. La variable aléatoire est spécifiée par la loi de distribution
| X | |||
| P. | 0, 1 | 0, 5 | 0, 4 |
Trouvez l'écart type de cette valeur.
représentant 2, 2.
11. La variance de chacune des 9 variables aléatoires mutuellement indépendantes distribuées de manière identique est égale à 36. Trouvez la variance de la moyenne arithmétique de ces variables.
représentant 4.
12. L'écart type de chacune des 16 variables aléatoires indépendantes les unes des autres distribuées de manière identique est de 10. Trouvez l'écart type de la moyenne arithmétique de ces variables.
représentant 2,5.
Chapitre neuf
LOI DES GRANDS NOMBRE
Remarques préliminaires
Comme on le sait déjà, il est impossible de prédire avec certitude à l'avance laquelle des valeurs possibles une variable aléatoire prendra à la suite du test ; cela dépend de nombreuses raisons aléatoires, qui ne peuvent être prises en compte. Il semblerait que puisque nous disposons d'informations très modestes sur chaque variable aléatoire dans ce sens, il est difficilement possible d'établir des modèles de comportement et des sommes suffisamment grand nombre Variables aléatoires. En fait, ce n'est pas vrai. Il s'avère que dans certaines conditions relativement larges, le comportement global d'un nombre suffisamment important de variables aléatoires perd presque son caractère aléatoire et devient naturel.
Pour la pratique, il est très important de connaître les conditions dans lesquelles l'action combinée de nombreuses causes aléatoires conduit à un résultat quasiment indépendant du hasard, puisqu'il permet de prévoir le déroulement des phénomènes. Ces conditions sont indiquées dans les théorèmes portant Nom commun loi grands nombres. Ceux-ci incluent les théorèmes de Chebyshev et de Bernoulli (il existe d'autres théorèmes qui ne sont pas abordés ici). Le théorème de Chebyshev est le plus loi commune grands nombres, le théorème de Bernoulli est le plus simple. Pour prouver ces théorèmes, nous utiliserons l'inégalité de Chebyshev.
L'inégalité de Chebyshev
L'inégalité de Chebyshev est valable pour les variables aléatoires discrètes et continues. Par souci de simplicité, nous nous limitons à prouver cette inégalité pour des quantités discrètes.
Considérons une variable aléatoire discrète X, spécifié par la table de répartition :
| X | X 1 | X 2 | … | xn |
| p | p 1 | P. 2 | … | pn |
Fixons-nous pour tâche d'estimer la probabilité que l'écart d'une variable aléatoire par rapport à son espérance mathématique ne dépasse pas valeur absolue nombre positif e. Si e est suffisamment petit, alors nous estimerons la probabilité que X prendra des valeurs assez proches de son espérance mathématique. P. L. Chebyshev a prouvé une inégalité qui nous permet de donner l'estimation qui nous intéresse.
L'inégalité de Chebyshev. La probabilité que l'écart d'une variable aléatoire X par rapport à son espérance mathématique en valeur absolue soit inférieur à un nombre positif e n'est pas inférieure à 1-D(X)/e 2 :
R.(|X-M(X)|< e ) 1-D(X)/e 2 .
Preuve. Depuis les événements consistant en la mise en œuvre des inégalités |X-M(X)|
R.(|X-M(X)|< e )+R(|X-M(X)| e)= 1.
D’où la probabilité qui nous intéresse
R.(|X-M(X)|< e )= 1-R(|X-M(X)| e). (*)
Le problème se résume donc à calculer la probabilité R.(| HM(X)| e).
Écrivons l'expression de la variance de la variable aléatoire X:
D(X)= [X 1 -M(X)] 2 p 1 + [X 2 -M(X)] 2 p 2 +…+ [xn-M(X)]2p.n.
Bien évidemment, tous les termes de cette somme sont non négatifs.
Écartons les termes pour lesquels | x je-M(X)|<e(pour les durées restantes | xj-M(X)| e), En conséquence, le montant ne peut que diminuer. Acceptons de supposer, pour être précis, que k les premiers termes (sans perte de généralité, on peut supposer que dans le tableau de distribution les valeurs possibles sont numérotées exactement dans cet ordre). Ainsi,
D(X) [xk + 1 -M(X)] 2 p k + 1 + [xk + 2 -M(X)] 2 p k + z + ... +[xn-M(X)] 2 p.n.
Notez que les deux côtés de l'inégalité | xj - M(X)| e (j = k+1, k+ 2, ..., P.) sont positifs, donc en les mettant au carré, on obtient l'inégalité équivalente | xj - M(X)| 2 e 2 Utilisons cette remarque et, en remplaçant chacun des facteurs dans la somme restante | xj - M(X)| 2 au nombre e 2(dans ce cas l'inégalité ne peut qu'augmenter), on obtient
D(X) e 2 (rk+ 1 + p k + 2 + … + р n). (**)
D'après le théorème d'addition, la somme des probabilités rk+ 1 + p k + 2 + … + р n il y a une possibilité que X prendra une, quelle qu'elle soit, des valeurs xk + 1 , xk+ 2 ,....xp, et pour chacun d'entre eux, l'écart satisfait l'inégalité | xj - M(X)| e Il s'ensuit que le montant rk+ 1 + p k + 2 + … + р n exprime la probabilité
P.(|X - M(X)| e).
Cette considération nous permet de réécrire l’inégalité (**) comme suit :
D(X) et 2P(|X - M(X)| e),
P.(|X - M(X)| e)D(X) /e 2 (***)
En remplaçant (***) par (*), on obtient finalement
P.(|X - M(X)| <e) 1-D(X) /e 2 ,
Q.E.D.
Commentaire. L'inégalité de Chebyshev a une signification pratique limitée car elle donne souvent une estimation approximative et parfois triviale (sans intérêt). Par exemple, si D(X)>e 2 et donc D(X)/e 2 > 1 puis 1 -D(X)/e 2 < 0 ; Ainsi, dans ce cas, l’inégalité de Chebyshev indique seulement que la probabilité d’écart est non négative, ce qui est déjà évident puisque toute probabilité est exprimée par un nombre non négatif.
La signification théorique de l'inégalité de Chebyshev est très grande. Ci-dessous, nous utiliserons cette inégalité pour dériver le théorème de Chebyshev.
Théorème de Chebyshev
Théorème de Chebyshev. Si X 1 , X 2 ,…, X n, ...-variables aléatoires indépendantes par paires, et leurs variances sont uniformément limitées(ne dépasse pas un nombre constant C), alors peu importe la taille du nombre positif e, la probabilité d'inégalité
Autrement dit, dans les conditions du théorème
Ainsi, le théorème de Chebyshev stipule que si un nombre suffisamment grand de variables aléatoires indépendantes avec des variances limitées est considéré, alors l'événement peut être considéré comme presque fiable, consistant dans le fait que l'écart de la moyenne arithmétique des variables aléatoires par rapport à la moyenne arithmétique de leur les attentes mathématiques seront arbitrairement grandes en valeur absolue petites
Preuve. Introduisons une nouvelle variable aléatoire en considération - la moyenne arithmétique des variables aléatoires
=(X 1 +X 2 +…+Xn)/n.
Trouvons l'espérance mathématique . En utilisant les propriétés de l'espérance mathématique (le facteur constant peut être soustrait du signe de l'espérance mathématique, l'espérance mathématique de la somme est égale à la somme des espérances mathématiques des termes), on obtient
M ![]() =
=
![]() . (*)
. (*)
En appliquant l’inégalité de Chebyshev à la quantité, nous avons
En substituant le membre de droite (***) à l'inégalité (**) (c'est pourquoi cette dernière ne peut qu'être renforcée), on a
De là, en passant à la limite en , on obtient
Enfin, en tenant compte du fait que la probabilité ne peut pas dépasser un, on peut finalement écrire
Le théorème a été prouvé.
Ci-dessus, lors de la formulation du théorème de Chebyshev, nous avons supposé que les variables aléatoires avaient des attentes mathématiques différentes. En pratique, il arrive souvent que des variables aléatoires aient la même espérance mathématique. Évidemment, si l’on suppose encore une fois que les dispersions de ces quantités sont limitées, alors le théorème de Chebyshev leur sera applicable.
Notons l'espérance mathématique de chacune des variables aléatoires par UN; dans le cas considéré, la moyenne arithmétique des espérances mathématiques, comme il est facile de le constater, est également égale à UN. Nous pouvons formuler le théorème de Chebyshev pour le cas particulier considéré.
Si X 1 , X 2 , ..., HP...-variables aléatoires indépendantes par paires qui ont la même espérance mathématique a, et si les variances de ces variables sont uniformément limitées, alors peu importe la taille du nombre e> Ah, probabilité d'inégalité
![]()
sera aussi proche de l’unité que souhaité si le nombre de variables aléatoires est suffisamment grand.
En d’autres termes, dans les conditions du théorème, il y aura égalité

L'essence du théorème de Chebyshev
L'essence du théorème éprouvé est la suivante : bien que des variables aléatoires indépendantes individuelles puissent prendre des valeurs éloignées de leurs attentes mathématiques, la moyenne arithmétique d'un nombre suffisamment grand de variables aléatoires avec haute probabilité prend des valeurs proches d'une certaine nombre constant, à savoir au nombre ( M(X 1)+ M(X 2)+...+M(Xp))/P(ou au numéro UN dans un cas particulier). En d’autres termes, les variables aléatoires individuelles peuvent avoir un écart significatif et leur moyenne arithmétique est très petite.
Ainsi, on ne peut pas prédire avec certitude quelle valeur possible chacune des variables aléatoires prendra, mais on peut prédire quelle valeur prendra leur moyenne arithmétique.
Donc, moyenne arithmétique d'un nombre suffisamment grand de variables aléatoires indépendantes(dont les variances sont uniformément bornées) perd le caractère de variable aléatoire. Cela s'explique par le fait que les écarts de chaque valeur par rapport à ses attentes mathématiques peuvent être à la fois positifs et négatifs et, dans le sens arithmétique, ils s'annulent.
Le théorème de Chebyshev est valable non seulement pour les variables aléatoires discrètes, mais également pour les variables aléatoires continues ; il se trouve qu'elle est un exemple brillant, confirmant la validité de la doctrine du matérialisme dialectique sur le lien entre hasard et nécessité.








