Comment trouver les points extrêmes d'un exemple de fonction. Extremum d'une fonction de deux variables

En passant ces inégalités à la limite en Δ X→ 0 et en tenant compte du fait que la dérivée F "(X 0) existe, et donc la limite à gauche ne dépend pas de la façon dont Δ X→ 0, on obtient : à Δ X → 0 – 0 F"(X 0) ≥ 0 a à Δ X → 0 + 0 F"(X 0) ≤ 0. Depuis F"(X 0) définit un nombre, alors ces deux inégalités ne sont compatibles que si F"(X 0) = 0.

Le théorème éprouvé stipule que les points maximum et minimum ne peuvent être trouvés que parmi les valeurs de l'argument pour lesquelles la dérivée devient nulle.

Nous avons considéré le cas où une fonction a une dérivée en tous points d'un certain segment. Quelle est la situation dans les cas où la dérivée n’existe pas ? Regardons des exemples.

Exemples.

1. oui=|X|.

   La fonction n'a pas de dérivée au point X=0 (à ce stade le graphique de la fonction n'a pas de tangente définie), mais à ce stade la fonction a un minimum, puisque oui(0)=0, et pour tout X≠ 0oui > 0.



La fonction n'a pas de dérivée en X=0, puisqu'il tend vers l'infini à X=0. Mais à ce stade, la fonction atteint un maximum.



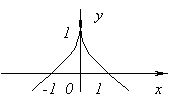
La fonction n'a pas de dérivée en X=0, puisque à X→0. A ce stade, la fonction n'a ni maximum ni minimum. Vraiment, f(x)=0 et à X<0f(x)<0, а при X>0f(x)>0.



Ainsi, d'après les exemples donnés et le théorème formulé, il ressort clairement qu'une fonction ne peut avoir un extremum que dans deux cas : 1) aux points où la dérivée existe et est égale à zéro ; 2) au point où la dérivée n'existe pas.

Cependant, si à un moment donné X 0 nous le savons f"(x 0 ) =0, alors on ne peut pas en conclure qu'au point X 0, la fonction a un extremum.

Par exemple. .



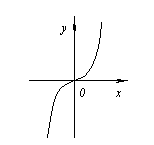
Mais point final X=0 n'est pas un point extremum, puisqu'à gauche de ce point les valeurs de la fonction sont situées en dessous de l'axe Bœuf, et à droite ci-dessus.

Les valeurs d'un argument du domaine d'une fonction auquel la dérivée de la fonction disparaît ou n'existe pas sont appelées points critiques.




De tout ce qui précède, il résulte que les points extrêmes de la fonction font partie des points critiques et, cependant, tous les points critiques ne sont pas des points extrêmes. Par conséquent, pour trouver l’extremum d’une fonction, vous devez trouver tous points critiques fonctions, puis examinez chacun de ces points séparément pour le maximum et le minimum. Le théorème suivant répond à cet objectif.

Théorème 2. (Condition suffisante pour l'existence d'un extremum.) Soit la fonction continue sur un intervalle contenant le point critique X 0, et est différentiable en tous les points de cet intervalle (sauf peut-être le point lui-même X 0). Si, en passant de gauche à droite par ce point, la dérivée change de signe de plus à moins, alors au point X = X La fonction 0 a un maximum. Si, en passant X 0 de gauche à droite, la dérivée change de signe de moins à plus, alors la fonction a un minimum à ce stade.

Ainsi, si

Preuve. Supposons d'abord qu'en passant par X 0 la dérivée change de signe du plus au moins, c'est-à-dire Devant tout le monde X, proche du point X 0 f "(x)> 0 pour X< x 0 , f "(x)< 0 pour x> x 0 . Appliquons le théorème de Lagrange à la différence f(x) - f(x 0 ) = f "(c)(x-x 0), où c est compris entre X Et X 0 .

1. Laisser X< x 0 . Alors c< x 0 et f"(c)> 0. C'est pourquoi f "(c)(x-x 0)< 0 et donc

   f(x) - f(x 0 )< 0, c'est-à-dire f(x)< f(x 0 ).

2. Laisser x > x 0 . Alors c>x 0 et f"(c)< 0. Moyens f "(c)(x-x 0)< 0. C'est pourquoi f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .

Ainsi, pour toutes les valeurs X assez près de X 0 f(x)< f(x 0 ) . Et cela signifie qu'au moment X La fonction 0 a un maximum.

La deuxième partie du théorème du minimum se démontre de la même manière.



Illustrons la signification de ce théorème dans la figure. Laisser f"(x 1 ) =0 et pour tout X, assez près de X 1, les inégalités sont satisfaites

f "(x)< 0 à X< x 1 , f "(x)> 0 à x> x 1 .

Puis à gauche du point X 1 la fonction augmente et diminue à droite, donc lorsque X = X 1 fonction va de croissante à décroissante, c'est-à-dire qu'elle a un maximum.

De même, nous pouvons considérer les points X 2 et X 3 .


Tout ce qui précède peut être schématiquement représenté dans l'image :

Règle d'étude de la fonction y=f(x) pour extremum

1. Trouver le domaine d'une fonction f(x).
2. Trouver la dérivée première d'une fonction f "(x).
3. Déterminez les points critiques pour cela :
   1. trouver les vraies racines de l'équation f "(x)=0;
   2. trouver toutes les valeurs X pour lequel la dérivée f "(x) n'existe pas.
4. Déterminez le signe de la dérivée à gauche et à droite du point critique. Puisque le signe de la dérivée reste constant entre deux points critiques, il suffit de déterminer le signe de la dérivée en un point à gauche et un point à droite du point critique.
5. Calculez la valeur de la fonction aux points extrêmes.

Exemples. Explorez les fonctions pour le minimum et le maximum.




VALEURS MAXIMUM ET MINIMUM D'UNE FONCTION SUR UN Segment

Le plus large la valeur d'une fonction sur un intervalle est la plus grande de toutes ses valeurs sur cet intervalle, et le plus petit– la plus petite de toutes ses valeurs.

Considérez la fonction y=f(x) continu sur le segment [ un B]. Comme on le sait, une telle fonction atteint ses valeurs maximale et minimale, soit à la limite du segment, soit à l'intérieur de celui-ci. Si la valeur la plus grande ou la plus petite d'une fonction est atteinte en un point interne du segment, alors cette valeur est le maximum ou le minimum de la fonction, c'est-à-dire qu'elle est atteinte aux points critiques.

Ainsi, nous obtenons ce qui suit règle pour trouver les valeurs les plus grandes et les plus petites d'une fonction sur un segment[ un B] :

1. Trouver tous les points critiques de la fonction dans l'intervalle ( un B) et calculez les valeurs de fonction à ces points.
2. Calculer les valeurs de la fonction aux extrémités du segment lorsque x = une, x = b.
3. Parmi toutes les valeurs obtenues, sélectionnez la plus grande et la plus petite.

Définition 1. Le point M(x 0 ; y 0) est appelé point maximum (minimum) de la fonction z = f(x; y) s'il existe un voisinage du point M tel que pour tous les points (x; y) de ce quartier l'inégalité suivante est vraie :

f(x 0 ; y 0)  f(x; y), .

Théorème 1 (une condition nécessaire à l'existence d'un extremum) . Si une fonction différentiable z = f(x; y) atteint un extremum au point M(x 0 ; y 0), alors ses dérivées partielles du premier ordre en ce point sont égales à zéro, c'est-à-dire
;

Les points auxquels les dérivées partielles sont égales à zéro sont appelés Stationnaire ou points critiques.

Théorème 2 (condition suffisante pour l'existence d'un extremum)

Soit la fonction z = f(x; y) :

a) défini dans un certain voisinage du point (x 0 ; y 0), dans lequel
Et
;

b) a des dérivées partielles continues du deuxième ordre à ce stade

;

Alors, si  = AC  B 2 > 0, alors au point (x 0 ; y 0) la fonction z = f(x; y) a un extremum, et si A< 0 (или С < 0) – максимум, если А >0 (ou C > 0) – minimum. Dans le cas  = AC  B 2< 0, функция z = f(x; y) экстремума не имеет. Если  = AC  B 2 = 0, то требуется дальнейшее исследование (сомнительный случай).

Exemple 1. Trouver l'extremum de la fonction z = x 2 + xy + y 2  3x  6y.

Solution. Trouvons les dérivées partielles du premier ordre :

Utilisons la condition nécessaire à l'existence d'un extremum :

En résolvant le système d'équations, on trouve les coordonnées x et y points fixes:x = 0; y = 3, c'est-à-dire M(0; 3).

Calculons les dérivées partielles du second ordre et trouvons leurs valeurs au point M.

UNE =
= 2 ; C =
= 2;

B =
.

Composons le discriminant  = AC  B 2 = 2  2  1 > 0, A = 2 > 0. Par conséquent, au point M(0 ; 3) la fonction donnée a un minimum. La valeur de la fonction à ce stade est z min = 9.

Trouver les extrema des fonctions

322. z = x 2 + y 2 + xy  4x  5y 323. z = y 3  x 3  3xy

324. z = x 2  2xy + 4y 3 325. z =
 y 2  x + 6 ans

326. z = x y (1  x  y) 327. z = 2xy  4x  2y

328. z = e  x/2 (x + y 2) 329. z = x 3 + 8y 3  6xy + 1

330. z = 3x 2 y  x 3  y 4 331. z = 3x + 6y  x 2  xy + y 2

Les valeurs les plus grandes et les plus petites d'une fonction de deux variables dans un domaine fermé

Pour trouver le plus grand Et moins valeurs de fonction dans zone fermée, nécessaire:

1) trouver les points critiques situés dans une zone donnée et calculer les valeurs de fonction en ces points ;

2) trouver les points critiques à la limite de la région et calculer le plus grand et plus petite valeur fonctions en eux;

3) parmi toutes les valeurs trouvées, sélectionnez la plus grande et la plus petite.

Exemple 2. Trouver les valeurs les plus grandes et les plus petites de la fonction z =
dans un cercle x 2 + y 2  1.

Solution. Trouvons les coordonnées des points critiques situés à l'intérieur de la région considérée, pour lesquelles nous calculons les dérivées partielles du premier ordre de la fonction z et les assimilons à zéro.

d'où x = 0, y = 0 et, donc, M(0; 0) est un point critique.

Calculons la valeur de la fonction z au point M(0; 0) : z(0; 0) = 2.

Trouvons les points critiques à la limite de la région - le cercle, donné par l'équation x 2 + y 2 = 1. En remplaçant y 2 = 1  x 2 dans la fonction z = z(x; y), nous obtenons une fonction d'une variable

z =
;

où x[1; 1].

Après avoir calculé la dérivée
et en l'assimilant à zéro, nous obtenons des points critiques sur la limite de la région x 1 = 0, x 2 = , x 3 =

Trouvons la valeur de la fonction z(x) =
aux points critiques et aux extrémités du segment [1 ; 1] : z(0) = ;
=;
; z(1) = ; z(1) =

Choisissons la plus grande et la plus petite parmi les valeurs de la fonction z aux points critiques situés à l'intérieur et sur la limite du cercle.

Donc z max. = z(0; 0) = 2

Avec ce service, vous pouvez trouver la plus grande et la plus petite valeur d'une fonction une variable f(x) avec la solution formatée dans Word. Si la fonction f(x,y) est donnée, il faut donc trouver l'extremum de la fonction de deux variables. Vous pouvez également trouver les intervalles des fonctions croissantes et décroissantes.

Règles de saisie des fonctions:

Condition nécessaire pour l'extremum d'une fonction d'une variable

Condition suffisante pour l'extremum d'une fonction d'une variable

F" 0 (x *) = 0
f"" 0 (x *) > 0

Alors le point x* est le point de minimum local (global) de la fonction.

Si au point x* la condition est remplie :

F" 0 (x *) = 0
f"" 0 (x*)< 0

Alors le point x * est un maximum local (global).

Exemple n°1. Trouvez les valeurs les plus grandes et les plus petites de la fonction : sur le segment.
Solution.

Le point critique est un x 1 = 2 (f’(x)=0). Ce point appartient au segment. (Le point x=0 n'est pas critique, puisque 0∉).
On calcule les valeurs de la fonction aux extrémités du segment et au point critique.
f(1)=9, f(2)= 5 / 2 , f(3)=3 8 / 81
Réponse : f min = 5 / 2 à x=2 ; f max =9 à x=1

Exemple n°2. En utilisant des dérivées d'ordre supérieur, trouvez l'extremum de la fonction y=x-2sin(x) .
Solution.
Trouvez la dérivée de la fonction : y’=1-2cos(x) . Trouvons les points critiques : 1-cos(x)=2, cos(x)=½, x=± π / 3 +2πk, k∈Z. On trouve y’’=2sin(x), calculer , ce qui veut dire x= π / 3 +2πk, k∈Z sont les points minimaux de la fonction ; , ce qui signifie x=- π / 3 +2πk, k∈Z sont les points maximum de la fonction.

Exemple n°3. Étudiez la fonction extremum au voisinage du point x=0.
Solution. Ici, il faut trouver les extrema de la fonction. Si l'extremum x=0, alors découvrez son type (minimum ou maximum). Si parmi les points trouvés il n'y a pas x = 0, alors calculez la valeur de la fonction f(x=0).
Il est à noter que lorsque la dérivée de chaque côté d'un point donné ne change pas de signe, la situations possibles même pour des fonctions différentiables : il peut arriver que pour un voisinage arbitrairement petit d'un côté du point x 0 ou des deux côtés, la dérivée change de signe. À ce stade, il est nécessaire d’utiliser d’autres méthodes pour étudier les fonctions à un niveau extrême.

Il s'agit d'une section plutôt intéressante des mathématiques que rencontrent absolument tous les élèves. classes de fin d'études et les étudiants. Cependant, tout le monde n’aime pas Matan. Certains ne peuvent même pas comprendre des choses de base comme une étude fonctionnelle apparemment standard. Cet article a pour but de corriger un tel oubli. Vous souhaitez en savoir plus sur l’analyse des fonctions ? Souhaitez-vous savoir ce que sont les points extremum et comment les trouver ? Alors cet article est fait pour vous.

Étudier le graphique d'une fonction

Tout d’abord, il convient de comprendre pourquoi il est nécessaire d’analyser le graphique. Exister fonctions simples, qui ne sera pas difficile à dessiner. Un exemple frappant Une parabole peut remplir une fonction similaire. Il ne sera pas difficile de dessiner un graphique. Tout ce qu'il faut, c'est l'aide conversion simple trouvez les nombres auxquels la fonction prend la valeur 0. Et en principe, c'est tout ce que vous devez savoir pour tracer un graphique d'une parabole.

Mais que se passe-t-il si la fonction que nous devons représenter graphiquement est beaucoup plus complexe ? Puisque les propriétés fonctions complexes ne sont pas évidents, il est nécessaire d'effectuer analyse complète. Ce n'est qu'après cela que la fonction peut être représentée graphiquement. Comment faire cela ? Vous pouvez trouver la réponse à cette question dans cet article.

Plan d'analyse fonctionnelle

La première chose à faire est de mener une étude superficielle de la fonction, au cours de laquelle nous trouvons le domaine de définition. Alors commençons dans l'ordre. Le domaine de définition est l'ensemble des valeurs par lesquelles la fonction est définie. En termes simples, ce sont les nombres qui peuvent être utilisés dans une fonction au lieu de x. Pour déterminer la portée, il suffit de consulter le dossier. Par exemple, il est évident que la fonction y (x) = x 3 + x 2 - x + 43 a un domaine de définition qui est l'ensemble des nombres réels. Eh bien, avec une fonction comme (x 2 - 2x)/x, tout est un peu différent. Puisque le nombre au dénominateur ne doit pas être égal à 0, le domaine de définition de cette fonction sera tout nombres réels, en plus de zéro.

Ensuite, vous devez trouver les soi-disant zéros de la fonction. Ce sont les valeurs d'argument auxquelles la fonction entière prend la valeur zéro. Pour ce faire, il est nécessaire d'assimiler la fonction à zéro, de la considérer en détail et d'effectuer quelques transformations. Prenons la fonction déjà familière y(x) = (x 2 - 2x)/x. Depuis cours scolaire on sait qu'une fraction est égale à 0 lorsque le numérateur égal à zéro. Par conséquent, nous rejetons le dénominateur et commençons à travailler avec le numérateur, en l'assimilant à zéro. Nous obtenons x 2 - 2x = 0 et mettons x entre parenthèses. D'où x (x - 2) = 0. En conséquence, nous constatons que notre fonction est égale à zéro lorsque x est égal à 0 ou 2.

Lors de l'étude du graphique d'une fonction, de nombreuses personnes rencontrent des problèmes sous forme de points extrêmes. Et c'est étrange. Après tout, les extrêmes sont tout à fait thème simple. Vous ne me croyez pas ? Voyez par vous-même en lisant cette partie article dans lequel nous parlerons des points minimum et maximum.

Tout d’abord, il convient de comprendre ce qu’est un extremum. Un extremum est la valeur limite qu'atteint une fonction sur un graphique. Il s'avère qu'il existe deux valeurs extrêmes : maximale et minimale. Pour plus de clarté, vous pouvez regarder l'image ci-dessus. Dans la zone étudiée, le point -1 est le maximum de la fonction y (x) = x 5 - 5x, et le point 1 est donc le minimum.

Ne confondez pas non plus les concepts. Les points extrêmes d'une fonction sont les arguments auxquels une fonction donnée devient valeurs extrêmes. À son tour, l’extremum est la valeur des minimums et des maximums d’une fonction. Par exemple, considérons à nouveau la figure ci-dessus. -1 et 1 sont les points extrema de la fonction, et 4 et -4 sont les extrema eux-mêmes.

Trouver des points extrêmes

Mais comment trouver les points extrêmes d’une fonction ? Tout est assez simple. La première chose à faire est de trouver la dérivée de l’équation. Disons que nous avons reçu la tâche : « Trouver les points extremum de la fonction y (x), x est l'argument pour plus de clarté, prenons la fonction y (x) = x 3 + 2x 2 + x + 54. Différencions et. obtenir l'équation suivante: 3x 2 + 4x + 1. En conséquence, nous avons obtenu une équation quadratique standard. Il ne reste plus qu’à l’assimiler à zéro et à trouver les racines. Depuis le discriminant Au dessus de zéro(D = 16 - 12 = 4), équation donnée est déterminé par deux racines. On les trouve et obtenons deux valeurs : 1/3 et -1. Ce seront les points extrêmes de la fonction. Mais comment déterminer qui est qui ? Quel point est le maximum et quel est le minimum ? Pour ce faire, vous devez prendre un point voisin et connaître sa valeur. Par exemple, prenons le nombre -2, qui est situé à gauche le long de la ligne de coordonnées partant de -1. Nous substituons cette valeur dans notre équation y(-2) = 12 - 8 + 1 = 5. En conséquence, nous obtenons nombre positif. Cela signifie que dans l'intervalle de 1/3 à -1, la fonction augmente. Ceci, à son tour, signifie que sur les intervalles allant de moins l'infini à 1/3 et de -1 à plus l'infini, la fonction diminue. Ainsi, on peut conclure que le nombre 1/3 est le point minimum de la fonction sur l'intervalle étudié, et -1 est le point maximum.

Il convient également de noter que l'examen d'État unifié nécessite non seulement de trouver des points extrêmes, mais également d'effectuer une sorte d'opération avec eux (addition, multiplication, etc.). C'est pour cette raison que cela vaut la peine de payer Attention particulière aux conditions du problème. Après tout, à cause de l'inattention, vous pouvez perdre des points.

Soit la fonction $z=f(x,y)$ définie dans un certain voisinage du point $(x_0,y_0)$. Ils disent que $(x_0,y_0)$ est un point maximum (local) si pour tous les points $(x,y)$ dans un voisinage du point $(x_0,y_0)$ l'inégalité $f(x,y) est satisfait< f(x_0,y_0)$. Если же для всех точек этой окрестности выполнено условие $f(x,y)>f(x_0,y_0)$, alors le point $(x_0,y_0)$ est appelé le point minimum (local).

Les points maximum et minimum sont souvent appelés terme général- points extrêmes.

Si $(x_0,y_0)$ est un point maximum, alors la valeur de la fonction $f(x_0,y_0)$ à ce stade est appelée le maximum de la fonction $z=f(x,y)$. En conséquence, la valeur de la fonction au point minimum est appelée le minimum de la fonction $z=f(x,y)$. Les minimums et les maximums d'une fonction sont unis par un terme commun - les extrema d'une fonction.

Algorithme d'étude de la fonction $z=f(x,y)$ pour extremum

1. Trouvez les dérivées partielles $\frac(\partial z)(\partial x)$ et $\frac(\partial z)(\partial y)$. Composer et résoudre le système d'équations $ \left \( \begin(aligned) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0 . \ end(aligned) \right.$. Les points dont les coordonnées satisfont au système spécifié sont appelés stationnaires.
2. Trouver $\frac(\partial^2z)(\partial x^2)$, $\frac(\partial^2z)(\partial x\partial y)$, $\frac(\partial^2z)(\partial y^2)$ et calculez la valeur de $\Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left( \frac (\partial^2z)(\partial x\partial y) \right)^2$ en chaque point stationnaire. Après cela, utilisez le schéma suivant :
   1. Si $\Delta > 0$ et $\frac(\partial^2z)(\partial x^2) > 0$ (ou $\frac(\partial^2z)(\partial y^2) > 0$), alors le point étudié est le point minimum.
   2. Si $\Delta > 0$ et $\frac(\partial^2z)(\partial x^2)< 0$ (или $\frac{\partial^2z}{\partial y^2} < 0$), то в исследуемая точка есть точкой максимума.
   3. Si $\Delta< 0$, то в расматриваемой стационарной точке экстремума нет.
   4. Si $\Delta = 0$, alors rien de précis ne peut être dit sur la présence d'un extremum ; requis recherche supplémentaire.

Remarque (souhaitable pour une compréhension plus complète du texte) : afficher\masquer

Si $\Delta > 0$, alors $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\ partiel^2z)(\partial x\partial y) \right)^2 > 0$. Et il s'ensuit que $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2) > \left(\frac(\partial^2z) ( \partial x\partial y)\right)^2 ≥ 0$. Ceux. $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2) > 0$. Si le produit de certaines quantités est supérieur à zéro, alors ces quantités sont du même signe. Autrement dit, si $\frac(\partial^2z)(\partial x^2) > 0$, alors $\frac(\partial^2z)(\partial y^2) > 0$. En bref, si $\Delta > 0$ alors les signes de $\frac(\partial^2z)(\partial x^2)$ et $\frac(\partial^2z)(\partial y^2)$ coïncident .

Exemple n°1

Examinez la fonction $z=4x^2-6xy-34x+5y^2+42y+7$ pour son extremum.

$$ \frac(\partial z)(\partial x)=8x-6y-34; \frac(\partial z)(\partial y)=-6x+10y+42. $$

$$ \left \( \begin(aligned) & 8x-6y-34=0;\\ & -6x+10y+42=0. \end(aligned) \right. $$

Réduisons chaque équation de ce système de 2$ et déplaçons les nombres vers la droite des équations :

$$ \left \( \begin(aligned) & 4x-3y=17;\\ & -3x+5y=-21. \end(aligned) \right. $$

Nous avons obtenu un système d'équations algébriques linéaires. Dans cette situation, il me semble plus pratique d’utiliser la méthode Cramer pour résoudre le système résultant.

$$ \begin(aligné) & \Delta=\left| \begin(array) (cc) 4 & -3\\ -3 & 5 \end(array)\right|=4\cdot 5-(-3)\cdot (-3)=20-9=11;\ \& \Delta_x=\gauche| \begin(array) (cc) 17 & -3\\ -21 & 5 \end(array)\right|=17\cdot 5-(-3)\cdot (-21)=85-63=22;\ \& \Delta_y=\gauche| \begin(array) (cc) 4 & 17\\ -3 & -21 \end(array)\right|=4\cdot (-21)-17\cdot (-3)=-84+51=-33 .\end(aligned) \\ x=\frac(\Delta_(x))(\Delta)=\frac(22)(11)=2; \; y=\frac(\Delta_(y))(\Delta)=\frac(-33)(11)=-3. $$

Les valeurs $x=2$, $y=-3$ sont les coordonnées du point stationnaire $(2;-3)$.

$$ \frac(\partial^2 z)(\partial x^2)=8; \frac(\partial^2 z)(\partial y^2)=10; \frac(\partial^2 z)(\partial x \partial y)=-6. $$

Calculons la valeur de $\Delta$ :

$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \partial x\partial y) \right)^2= 8\cdot 10-(-6)^2=80-36=44. $$

Puisque $\Delta > 0$ et $\frac(\partial^2 z)(\partial x^2) > 0$, alors selon le point $(2;-3)$ est le point minimum de la fonction $ z$. On trouve le minimum de la fonction $z$ en substituant dans fonction donnée coordonnées du point $(2;-3)$ :

$$ z_(min)=z(2;-3)=4\cdot 2^2-6\cdot 2 \cdot (-3)-34\cdot 2+5\cdot (-3)^2+42\ cdot (-3)+7=-90. $$

Répondre: $(2;-3)$ - point minimum ; $z_(min)=-90$.

Exemple n°2

Examinez la fonction $z=x^3+3xy^2-15x-12y+1$ pour son extremum.

Nous suivrons ce qui précède. Tout d’abord, trouvons les dérivées partielles du premier ordre :

$$ \frac(\partial z)(\partial x)=3x^2+3y^2-15; \frac(\partial z)(\partial y)=6xy-12. $$

Créons un système d'équations $ \left \( \begin(aligned) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0. \end(aligné) \right.$ :

$$ \left \( \begin(aligned) & 3x^2+3y^2-15=0;\\ & 6xy-12=0. \end(aligned) \right. $$

Réduisons la première équation de 3 et la seconde de 6.

$$ \left \( \begin(aligned) & x^2+y^2-5=0;\\ & xy-2=0. \end(aligned) \right. $$

Si $x=0$, alors la deuxième équation nous mènera à une contradiction : $0\cdot y-2=0$, $-2=0$. D'où la conclusion : $x\neq 0$. Ensuite à partir de la deuxième équation nous avons : $xy=2$, $y=\frac(2)(x)$. En remplaçant $y=\frac(2)(x)$ dans la première équation, nous aurons :

$$ x^2+\left(\frac(2)(x) \right)^2-5=0;\\ x^2+\frac(4)(x^2)-5=0;\\ x^4-5x^2+4=0. $$

Je suis bi équation quadratique. Nous effectuons le remplacement $t=x^2$ (c'est-à-dire que $t > 0$) :

$$ t^2-5t+4=0;\\ \begin(aligné) & D=(-5)^2-4\cdot 1 \cdot 4=9;\\ & t_1=\frac(-(- 5)-\sqrt(9))(2)=\frac(5-3)(2)=1;\\ & t_2=\frac(-(-5)+\sqrt(9))(2)= \frac(5+3)(2)=4.\end(aligné) $$

Si $t=1$, alors $x^2=1$. On a donc deux valeurs de $x$ : $x_1=1$, $x_2=-1$. Si $t=4$, alors $x^2=4$, c'est-à-dire $x_3=2$, $x_4=-2$. En rappelant que $y=\frac(2)(x)$, on obtient :

\begin(aligné) & y_1=\frac(2)(x_1)=\frac(2)(1)=2;\\ & y_2=\frac(2)(x_2)=\frac(2)(-1 )=-2;\\ & y_3=\frac(2)(x_3)=\frac(2)(2)=1;\\ & y_4=\frac(2)(x_4)=\frac(2)( -2)=-1. \end(aligné)

Nous avons donc quatre points stationnaires : $M_1(1;2)$, $M_2(-1;-2)$, $M_3(2;1)$, $M_4(-2;-1)$. Ceci termine la première étape de l’algorithme.

Commençons maintenant par l'algorithme. Trouvons les dérivées partielles du second ordre :

$$ \frac(\partial^2 z)(\partial x^2)=6x; \frac(\partial^2 z)(\partial y^2)=6x; \frac(\partial^2 z)(\partial x \partial y)=6y. $$

Trouvons $\Delta$ :

$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \partial x\partial y) \right)^2= 6x\cdot 6x-(6y)^2=36x^2-36y^2=36(x^2-y^2). $$

Nous allons maintenant calculer la valeur de $\Delta$ en chacun des points stationnaires précédemment trouvés. Commençons par le point $M_1(1;2)$. À ce stade, nous avons : $\Delta(M_1)=36(1^2-2^2)=-108$. Depuis $\Delta(M_1)< 0$, то согласно в точке $M_1$ экстремума нет.

Examinons le point $M_2(-1;-2)$. À ce stade, nous avons : $\Delta(M_2)=36((-1)^2-(-2)^2)=-108$. Depuis $\Delta(M_2)< 0$, то согласно в точке $M_2$ экстремума нет.

Examinons le point $M_3(2;1)$. A ce stade, nous obtenons :

$$ \Delta(M_3)=36(2^2-1^2)=108;\;\; \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3)=6\cdot 2=12. $$

Puisque $\Delta(M_3) > 0$ et $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3) > 0$, alors selon $M_3(2; 1)$ est le point minimum de la fonction $z$. On trouve le minimum de la fonction $z$ en substituant les coordonnées du point $M_3$ dans la fonction donnée :

$$ z_(min)=z(2;1)=2^3+3\cdot 2\cdot 1^2-15\cdot 2-12\cdot 1+1=-27. $$

Reste à explorer le point $M_4(-2;-1)$. A ce stade, nous obtenons :

$$ \Delta(M_4)=36((-2)^2-(-1)^2)=108;\;\; \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_4)=6\cdot (-2)=-12. $$

Puisque $\Delta(M_4) > 0$ et $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_4)< 0$, то согласно $M_4(-2;-1)$ есть точкой максимума функции $z$. Максимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_4$:

$$ z_(max)=z(-2;-1)=(-2)^3+3\cdot (-2)\cdot (-1)^2-15\cdot (-2)-12\cdot (-1)+1=29. $$

L’étude extremum est terminée. Il ne reste plus qu'à écrire la réponse.

Répondre:

• $(2;1)$ - point minimum, $z_(min)=-27$ ;
• $(-2;-1)$ - point maximum, $z_(max)=29$.

Note

Calculer la valeur $\Delta$ dans cas général ce n'est pas nécessaire, car nous ne nous intéressons qu'au signe, et non signification spécifique ce paramètre. Par exemple, pour l'exemple n°2 considéré ci-dessus, au point $M_3(2;1)$ nous avons $\Delta=36\cdot(2^2-1^2)$. Ici, il est évident que $\Delta > 0$ (puisque les deux facteurs $36$ et $(2^2-1^2)$ sont positifs) et il est possible de ne pas trouver de valeur spécifique de $\Delta$. Certes, pour les calculs standards, cette remarque est inutile - là, ils vous obligent à ramener les calculs à un nombre :)

Exemple n°3

Examinez la fonction $z=x^4+y^4-2x^2+4xy-2y^2+3$ pour son extremum.

Nous suivrons. Tout d’abord, trouvons les dérivées partielles du premier ordre :

$$ \frac(\partial z)(\partial x)=4x^3-4x+4y; \frac(\partial z)(\partial y)=4y^3+4x-4y. $$

Créons un système d'équations $ \left \( \begin(aligned) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0. \end(aligné) \right.$ :

$$ \left \( \begin(aligned) & 4x^3-4x+4y=0;\\ & 4y^3+4x-4y=0. \end(aligned) \right. $$

Réduisons les deux équations de 4$ :

$$ \left \( \begin(aligned) & x^3-x+y=0;\\ & y^3+x-y=0. \end(aligned) \right. $$

Ajoutons la première équation à la seconde et exprimons $y$ en termes de $x$ :

$$ y^3+x-y+(x^3-x+y)=0;\\ y^3+x^3=0; y^3=-x^3 ; y=-x. $$

En substituant $y=-x$ dans la première équation du système, nous aurons :

$$ x^3-x-x=0;\\ x^3-2x=0;\\ x(x^2-2)=0. $$

À partir de l'équation résultante, nous avons : $x=0$ ou $x^2-2=0$. De l'équation $x^2-2=0$, il s'ensuit que $x=-\sqrt(2)$ ou $x=\sqrt(2)$. Ainsi, trois valeurs de $x$ sont trouvées, à savoir : $x_1=0$, $x_2=-\sqrt(2)$, $x_3=\sqrt(2)$. Puisque $y=-x$, alors $y_1=-x_1=0$, $y_2=-x_2=\sqrt(2)$, $y_3=-x_3=-\sqrt(2)$.

La première étape de la solution est terminée. Nous avons trois points stationnaires : $M_1(0;0)$, $M_2(-\sqrt(2),\sqrt(2))$, $M_3(\sqrt(2),-\sqrt(2))$ .

Commençons maintenant par l'algorithme. Trouvons les dérivées partielles du second ordre :

$$ \frac(\partial^2 z)(\partial x^2)=12x^2-4; \frac(\partial^2 z)(\partial y^2)=12y^2-4; \frac(\partial^2 z)(\partial x \partial y)=4. $$

Trouvons $\Delta$ :

$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \partial x\partial y) \right)^2= (12x^2-4)(12y^2-4)-4^2=\\ =4(3x^2-1)\cdot 4(3y^2 -1)-16=16(3x^2-1)(3y^2-1)-16=16\cdot((3x^2-1)(3y^2-1)-1). $$

Nous allons maintenant calculer la valeur de $\Delta$ en chacun des points stationnaires précédemment trouvés. Commençons par le point $M_1(0;0)$. À ce stade, nous avons : $\Delta(M_1)=16\cdot((3\cdot 0^2-1)(3\cdot 0^2-1)-1)=16\cdot 0=0$. Puisque $\Delta(M_1) = 0$, des recherches supplémentaires sont nécessaires, car rien de précis ne peut être dit sur la présence d'un extremum au point considéré. Laissons ce point de côté pour l'instant et passons à d'autres points.

Examinons le point $M_2(-\sqrt(2),\sqrt(2))$. A ce stade, nous obtenons :

\begin(aligné) & \Delta(M_2)=16\cdot((3\cdot (-\sqrt(2))^2-1)(3\cdot (\sqrt(2))^2-1)- 1)=16\cdot 24=384;\\ & \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_2)=12\cdot (-\sqrt(2) )^2-4=24-4=20. \end(aligné)

Puisque $\Delta(M_2) > 0$ et $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_2) > 0$, alors selon $M_2(-\ sqrt(2),\sqrt(2))$ est le point minimum de la fonction $z$. On trouve le minimum de la fonction $z$ en substituant les coordonnées du point $M_2$ dans la fonction donnée :

$$ z_(min)=z(-\sqrt(2),\sqrt(2))=(-\sqrt(2))^4+(\sqrt(2))^4-2(-\sqrt( 2))^2+4\cdot (-\sqrt(2))\sqrt(2)-2(\sqrt(2))^2+3=-5. $$

De la même manière que pour le point précédent, nous examinons le point $M_3(\sqrt(2),-\sqrt(2))$. A ce stade, nous obtenons :

\begin(aligné) & \Delta(M_3)=16\cdot((3\cdot (\sqrt(2))^2-1)(3\cdot (-\sqrt(2))^2-1)- 1)=16\cdot 24=384;\\ & \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3)=12\cdot (\sqrt(2)) ^2-4=24-4=20. \end(aligné)

Puisque $\Delta(M_3) > 0$ et $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3) > 0$, alors selon $M_3(\sqrt (2),-\sqrt(2))$ est le point minimum de la fonction $z$. On trouve le minimum de la fonction $z$ en substituant les coordonnées du point $M_3$ dans la fonction donnée :

$$ z_(min)=z(\sqrt(2),-\sqrt(2))=(\sqrt(2))^4+(-\sqrt(2))^4-2(\sqrt(2 ))^2+4\cdot \sqrt(2)(-\sqrt(2))-2(-\sqrt(2))^2+3=-5. $$

Il est temps de revenir au point $M_1(0;0)$, auquel $\Delta(M_1) = 0$. Selon cela, des recherches supplémentaires sont nécessaires. Cette phrase évasive signifie "faites ce que vous voulez" :). Méthode générale Il n’existe pas de solution à de telles situations, et cela est compréhensible. Si une telle méthode existait, elle aurait été incluse depuis longtemps dans tous les manuels scolaires. En attendant, nous devons chercher approche spécialeà chaque point auquel $\Delta = 0$. Eh bien, examinons le comportement de la fonction au voisinage du point $M_1(0;0)$. Notons immédiatement que $z(M_1)=z(0;0)=3$. Supposons que $M_1(0;0)$ soit le point minimum. Ensuite, pour tout point $M$ d'un certain voisinage du point $M_1(0;0)$ nous obtenons $z(M) > z(M_1)$, c'est-à-dire $z(M) > 3$. Que se passe-t-il si un quartier contient des points auxquels $z(M)< 3$? Тогда в точке $M_1$ уж точно не будет минимума.

Considérons les points pour lesquels $y=0$, c'est-à-dire points de la forme $(x,0)$. À ces points, la fonction $z$ prendra les valeurs suivantes :

$$ z(x,0)=x^4+0^4-2x^2+4x\cdot 0-2\cdot 0^2+3=x^4-2x^2+3=x^2(x ^2-2)+3. $$

Dans tous les quartiers suffisamment petits $M_1(0;0)$ nous avons $x^2-2< 0$, посему $x^2(x^2-2) < 0$, откуда следует $x^2(x^2-2)+3 < 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z < 3$, посему точка $M_1(0;0)$ не может быть точкой минимума.

Mais peut-être que le point $M_1(0;0)$ est le point maximum ? Si tel est le cas, alors pour tout point $M$ d'un certain voisinage du point $M_1(0;0)$ nous obtenons $z(M)< z(M_1) $, т.е. $z(M) < 3$. А вдруг любая окрестность содержит точки, в которых $z(M) >3$ ? Alors il n'y aura certainement pas de maximum au point $M_1$.

Considérons les points pour lesquels $y=x$, c'est-à-dire points de la forme $(x,x)$. À ces points, la fonction $z$ prendra les valeurs suivantes :

$$ z(x,x)=x^4+x^4-2x^2+4x\cdot x-2\cdot x^2+3=2x^4+3. $$

Puisque dans n'importe quel voisinage du point $M_1(0;0)$ nous avons $2x^4 > 0$, alors $2x^4+3 > 3$. Conclusion : tout voisinage du point $M_1(0;0)$ contient des points pour lesquels $z > 3$, donc le point $M_1(0;0)$ ne peut pas être un point maximum.

Le point $M_1(0;0)$ n'est ni un point maximum ni un point minimum. Conclusion : $M_1$ n'est pas du tout un point extrême.

Répondre: $(-\sqrt(2),\sqrt(2))$, $(\sqrt(2),-\sqrt(2))$ sont les points minimaux de la fonction $z$. Aux deux points $z_(min)=-5$.