Qëllimi juaj:të njohë metodat për vërtetimin e pabarazive dhe të jetë në gjendje t'i zbatojë ato.
Koncepti i provës së pabarazisë . Disa pabarazi bëhen të vërteta pabarazia numerike para të gjithëve vlerat e pranueshme variablave ose në një grup të caktuar vlerash të ndryshueshme. Për shembull, pabarazitë A 2 ³0, ( A–b) 2 ³ 0 , a 2 +b 2 + c 2 " ³ 0 janë të vërteta për çdo vlerat reale variablat dhe pabarazia ³ 0 – për çdo vlerë reale jo negative A. Ndonjëherë lind problemi i vërtetimit të një pabarazie.
Të provosh një pabarazi do të thotë të tregosh atë kjo pabarazi shndërrohet në një pabarazi numerike të vërtetë për të gjitha vlerat e pranueshme të variablave ose në një grup të caktuar vlerash të këtyre variablave.
Metodat për vërtetimin e pabarazive. vini re, se metodë e përgjithshme nuk ka asnjë provë të pabarazive. Megjithatë, disa prej tyre mund të specifikohen.
1. Një metodë për vlerësimin e shenjës së ndryshimit midis anës së majtë dhe të djathtë të një pabarazie. Bëhet dallimi midis anës së majtë dhe të djathtë të pabarazisë dhe përcaktohet nëse ky ndryshim është pozitiv apo negativ për vlerat e konsideruara të variablave (për pabarazitë jo strikte është e nevojshme të përcaktohet nëse ky ndryshim është jo- negative ose jo pozitive).
Shembulli 1. Për çdo numër real A Dhe b ka pabarazi
a 2 +b 2³ 2 ab. (1)
Dëshmi. Le të bëjmë ndryshimin midis anës së majtë dhe të djathtë të pabarazisë:
a 2 +b 2 – 2ab = a 2 – 2ab + b 2 = (a–b) 2 .
Që nga sheshi i ndonjë numër realështë një numër jo negativ, atëherë ( a–b) 2 ³ 0, që do të thotë a 2 +b 2³ 2 ab për çdo numër real A Dhe b. Barazia në (1) ndodh nëse dhe vetëm nëse a = b.
Shembulli 2. Vërtetoni se nëse A³ 0 dhe b³ 0, pastaj ³ , d.m.th. mesatarja aritmetike e numrave realë jonegativë A Dhe b jo më pak se mesatarja e tyre gjeometrike.
Dëshmi. Nëse A³ 0 dhe b³ 0, atëherë
³ 0. Pra, ³ .
2. Metoda deduktive provat e pabarazive. Thelbi i kësaj metode është si vijon: duke përdorur një seri transformimesh, pabarazia e kërkuar rrjedh nga disa pabarazi të njohura (referenca). Për shembull, pabarazitë e mëposhtme mund të përdoren si referencë: A 2 ³ 0 për çdo aÎ R ; (a–b) 2 ³ 0 për çdo A Dhe bÎ R ; (A 2 + b 2) ³ 2 ab për çdo a, bÎ R ; ³ në A ³ 0, b ³ 0.
Shembulli 3. Vërtetoni se për çdo numër real A Dhe b ka pabarazi
A 2 + b 2 + Me 2³ ab + bc + ac.
Dëshmi. Nga pabarazitë e vërteta ( a–b) 2 ³ 0, ( b – c) 2 ³ 0 dhe ( c – a) 2 ³ 0 rrjedh se A 2 + b 2³ 2 ab, b 2 + c 2³ 2 para Krishtit, c 2 + a 2³ 2 ac. Duke i mbledhur të tre pabarazitë term pas termi dhe duke pjesëtuar të dyja anët e një të reje me 2, marrim pabarazinë e kërkuar.
Pabarazia origjinale mund të vërtetohet duke përdorur metodën e parë. Me të vërtetë, A 2 + b 2 + Me 2 –ab – bc – ac = 0,5(2A 2 + 2b 2 + 2Me 2 – 2ab - 2para Krishtit - 2ac) = = 0,5((a–b) 2 + (a–c) 2 + (b–c) 2)³ 0.
Dallimi midis A 2 + b 2 + Me 2 dhe ab + bc + ac më i madh ose i barabartë me zero, që do të thotë se A 2 + b 2 + Me 2³ ab + bc + ac(barazia është e vërtetë nëse dhe vetëm nëse a = b = c).
3. Metoda e vlerësimit për vërtetimin e pabarazive.
Shembulli 4. Vërtetoni pabarazinë
+ + + … + >
Dëshmi. Është e lehtë të shihet se ana e majtë e pabarazisë përmban 100 terma, secili prej të cilëve nuk është më pak. Në këtë rast ata thonë se ana e majte pabarazitë mund të vlerësohen nga më poshtë si më poshtë:
+ + + … + > = 100 = .
4. Metoda e induksionit të plotë. Thelbi i metodës është të merren parasysh të gjitha rastet e veçanta që mbulojnë gjendjen e problemit në tërësi.
Shembulli 5. Vërtetoni se nëse x > ï nëï , Se x > y.
Dëshmi. Ka dy raste të mundshme:
A) në³ 0 ; pastaj unë nëï = y, dhe sipas kushteve x >ï nëï . Do të thotë, x > y;
b) në< 0; pastaj unë nëï > y dhe sipas kushteve x >ï nëï do të thotë x > y.
Pjesa praktike
Detyra 0. Merrni Fletë e zbrazët letër dhe në të shënoni përgjigjet e të gjitha ushtrimeve me gojë të dhëna më poshtë. Pastaj kontrolloni përgjigjet tuaja kundrejt përgjigjeve ose udhëzimeve përmbledhëse në fund të kësaj element edukativ në seksionin "Asistenti juaj".
Ushtrime me gojë
1. Krahasoni shumën e katrorëve të dy numrave të pabarabartë dhe produktin e dyfishtë të tyre.
2. Vërtetoni pabarazinë:
A) ![]() ;
;
b) ![]() ;
;
V) ![]() ;
;
3. Dihet se. Vërtetoni atë.
4. Dihet se. Vërtetoni atë.
Ushtrimi 1. Më shumë:
a) 2 + 11 ose 9; d) + ose;
b) ose + ; e) – ose;
c) + ose 2; e) + 2 ose + ?
Detyra 2. Vërtetoni këtë me të vërtetë x ka një pabarazi:
a) 3( x+ 1) + x– 4(2 + x) < 0; г) 4x 2 + 1 ³ 4 x;
b) ( x+ 2)(x+ 4) > (x+ 1)(x+ 5); e) ³ 2 x;
V) ( x– 2) 2 > x(x- 4); e) l + 2 x 4 > x 2 + 2x 3 .
Detyra 3. Vërtetoni se:
A) x 3 + 1³ x 2 + x, Nëse x³ –1;
b) x 3 + 1 £ x 2 + x, Nëse x£ -1 .
Detyra 4. Vërtetoni se nëse a ³ 0, b³ 0, Me³ 0, d³ 0, atëherë
(a 2 + b 2)(c 2 + d 2) ³ ( ac + bd) 2 .
Detyra 5. Vërtetoni pabarazinë duke izoluar katror i përsosur:
A) x 2 – 2xy + 9y 2 ³ 0;
b) x 2 + y 2 + 2³2( x+y);
në 10 x 2 + 10xy + 5y 2 + 1 > 0;
G) x 2 – xy + y 2 ³ 0 ;
d) x 2 + y 2 + z 2 + 3³ 2( x + y + z);
e) ( x+ l)( x - 2y + l) + y 2 ³ 0 .
Detyra 6. Vërtetoni se:
A) x 2 + 2y 2 + 2xy + 6y+ l0 > 0 ;
b) x 2 + y 2 – 2xy + 2x – 2në + 1 > 0;
në 3 x 2 + y 2 + 8x+ 4y - 2xy + 22 ³ 0;
G) x 2 + 2xy+ 3y 2 + 2x + 6y + 3 > 0.
Detyra 7. Vërtetoni se nëse n³ k³ 1, atëherë k(n–k+ 1) ³ n.
Detyra 8. Vërtetoni se nëse 4 A + 2b= 1, atëherë a 2 + b 2³ .
Përcaktoni vlerat A Dhe b, në të cilën ndodh barazia.
Detyra 9. Vërtetoni pabarazinë:
A) X 3 + në 3³ X 2 në + xy 2 në x³ 0 dhe y ³ 0;
b) X 4 + në 4³ X 3 në + xy 3 për çdo x Dhe në;
V) X 5 + në 5³ X 4 në + xy 4 në x³ 0 dhe y ³ 0;
G) x n + y n ³ x n-1 y + xy n-1 në x³ 0 dhe y ³ 0.
Metodat për vërtetimin e pabarazive.
Zgjidhja e pabarazive. Pabarazitë ekuivalente.
Metoda e intervalit. Sistemet e pabarazive.
Vërtetimi i pabarazive. Ka disa metoda provashpabarazitë. Ne do t'i shikojmë ato duke përdorur shembullin e pabarazisë:
Ku a – numër pozitiv.
1). Përdorimi i një pabarazie të njohur ose të provuar më parë.
dihet se ( a– 1 )² 0 .
2). Vlerësimi i shenjës së diferencës ndërmjet pjesëve të pabarazisë .
Konsideroni ndryshimin midis anës së majtë dhe të djathtë:
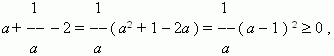
Për më tepër, barazia ndodh vetëm kur
a = 1 .3). Vërtetimi me kontradiktë.
Le të supozojmë të kundërtën:a, marrim: a 2 + 1 < 2 a, dmth.
a 2 + 1 – 2 a < 0 , ose ( a– 1 ) 2 < 0, gjë që nuk është e vërtetë. (Pse?) .
Kontradikta që rezulton vërteton vlefshmërinë e
Pabarazia në fjalë.
4). Metoda e pabarazisë së pacaktuar.
Pabarazia quhet i pasigurt nëse ai ka një shenjë\/ ose /\ ,
ato. kur nuk e dimë se në cilën rrugëkjo shenjë duhet të kthehet
për të marrë një pabarazi të drejtë.
Të njëjtat rregulla zbatohen këtu sidhe me pabarazi të zakonshme.
Merrni parasysh pabarazinë e papërcaktuar:
Duke shumëzuar të dyja anët e pabarazisë mea, marrim: a 2 + 1 \/ 2 a, dmth.
A 2 + 1 – 2 a \/ 0 , ose ( a– 1) 2 \/ 0 , por këtu ne tashmë dimë si të kthehemi
Shenja \/ për të marrë pabarazinë e saktë (Si?). Duke e kthyer atë
NË në drejtimin e duhur përgjatë gjithë zinxhirit të pabarazive nga poshtë lart, ne
marrim pabarazinë e kërkuar.
Zgjidhja e pabarazive. Quhen dy pabarazi që përmbajnë të njëjtat të panjohura ekuivalente , nëse janë të vlefshme për të njëjtat vlera të këtyre të panjohurave. I njëjti përkufizim përdoret për ekuivalencën e dy sistemeve të pabarazive. Zgjidhja e pabarazive është procesi i kalimit nga një pabarazi në tjetrën që është ekuivalente me një pabarazi. Për këtë qëllim ato përdoren vetitë themelore të pabarazive(cm. ). Përveç kësaj, mund të përdoret zëvendësimi i çdo shprehjeje me një tjetër që është identike me atë të dhënë. Pabarazitë mund të jenë algjebrike( që përmban vetëm polinomet) Dhe transcendentale(për shembull logaritmike osetrigonometrike). Këtu do të shohim një metodë shumë të rëndësishme,përdoret shpesh në zgjidhje algjebrike pabarazitë
Metoda e intervalit. Zgjidhja e pabarazisë: ( x – 3)( x – 5) < 2( x – 3). Këtu nuk mund t'i ndajmë të dyja anët e pabarazisë me (x – 3), pasi ne nuk e dimë shenjën e këtij binomi (përmban të panjohurën x ). Prandaj ne do të ricaktojmëtë gjithë termat e pabarazisë në anën e majtë:
(x – 3)( x – 5) – 2( x – 3) < 0 ,
le ta faktorizojmë:
(x – 3)( x – 5 – 2) < 0 ,
dhe ne marrim: ( x – 3)( x – 7) < 0. Теперь определим знак произведения в левой части неравенства в различных числовых интервалах. Заметим, что x= 3 dhe x = 7 - rrënjët e kësaj shprehjeje. Prandaj, e gjithë boshti numerik do të ndahet me këtorrënjët në tre intervalet e mëposhtme:
Në intervalin I(x < 3 ) të dy faktorët janë negativë, pra, të tyre puna pozitivisht; V intervali II (3 < x< 7 ) shumëzuesi i parë(x– 3 ) është pozitive, dhe e dyta ( x - 7) është negative, pra e tyre puna negativ; në intervalIII(x> 7) të dy faktorët janë pozitivë, pra, të tyre punë gjithashtu pozitivisht. Tani mbetet vetëm të zgjedhim intervalin në të cilin produkti ynë negativ. Ky është intervaliII, pra, zgjidhja e pabarazisë: 3 < x< 7. Shprehja e fundit- i ashtuquajturi pabarazi e dyfishtë. Do të thotë sex duhet të jetë më i madh se 3 dhe më i vogël se 7.
SHEMBULL Zgjidheni pabarazinë e mëposhtme duke përdorur metodën e intervalit:
(x – 1)(x – 2)(x – 3) … (x –100) > 0 .
Zgjidhja Rrënjët e anës së majtë të pabarazisë janë të dukshme: 1, 2, 3, ..., 100.
Ata thyejnë boshti numerik për 101 intervale:
Meqenëse numri i kllapave në anën e majtë madje(e barabartë 100), atëherë
Në x < 1, когда все множители отрицательны, их произведение
Pozitivisht. Kur kalon nëpër rrënjë ka një ndryshim
Shenja e veprës. Prandaj, në intervalin tjetër, brenda
Cili produkt është pozitiv, do të jetë (2, 3), pastaj (4, 5),
Pastaj (6, 7), ... , (98, 99) dhe në fund, x >100.
Kështu, kjo pabarazi ka një zgjidhje:
x < 1, 2 < x < 3, 4 < x < 5 ,…, x >100.
Kështu që, për të zgjidhur një pabarazi algjebrike, Më duhet t'i lëviz të gjithaanëtarët në të majtë (oseanën e djathtë) dhe zgjidhekuacionin përkatës. Pas vizatoni rrënjët e gjetura në boshtin e numrave; si rezultat, ai ndahet në një numër të caktuar intervalesh. Në fazën e fundit të zgjidhjes, duhet të përcaktoni se çfarë shenje ka polinomi brenda secilit prej këtyre intervaleve dhe të zgjidhni intervalet e kërkuara në përputhje me shenjën e pabarazisë që zgjidhet.
Vini re se shumica e pabarazive transcendentale reduktohen në një pabarazi algjebrike duke zëvendësuar të panjohurën. Duhet të zgjidhet në lidhje me të panjohurën e re, dhe më pas, me zëvendësim të kundërt, të gjendet një zgjidhje për pabarazinë fillestare.
Sistemet e pabarazive. Për të zgjidhur një sistem pabarazish, është e nevojshme të zgjidhet secili prej tyre dhe të kombinohen zgjidhjet e tyre. Ky kombinim çon në një nga të dy rastet e mundshme: ose sistemi ka një zgjidhje ose nuk ka.
Shembulli 1. Zgjidheni sistemin e pabarazive:

Zgjidhja e pabarazisë së parë:
x < 4 ; а второго: x > 6.Kështu, ky sistem pabarazish nuk ka zgjidhje.
(Pse?)
Shembulli 2. Zgjidheni sistemin e pabarazive:
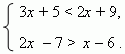
Zgjidhja: Pabarazia e parë, si më parë, jep:x < 4; но решение
Pabarazia e dytë në këtë shembull:x > 1.
Kështu, zgjidhja e sistemit të pabarazive: 1< x < 4.
Institucioni arsimor: Institucioni Arsimor Komunal Liceu Nr. 1, Komsomolsk-on-Amur
Kreu: Budlyanskaya Natalya Leonidovna
Nëse dëshironi të merrni pjesë në jetë e madhe, pastaj mbushe kokën me matematikë sa të kesh mundësi. Më pas ajo do t'ju ofrojë ndihmë të madhe në të gjithë punën tuaj. (M.I. Kalinin)

Paraqitja e anës së majtë të pabarazisë si një shumë e termave jonegativë (ana e djathtë është 0) duke përdorur identitete.
Shembulli 1. Vërtetoni këtë për çdo xϵR
Dëshmi . 1 mënyrë.
Metoda 2.
për një funksion kuadratik që do të thotë pozitiviteti i saj për çdo real X.

Shembulli 2. Vërtetoni se për çdo x dhe y
Dëshmi. Shembulli 3. Vërtetoni këtë Dëshmi. Shembulli 4. Vërtetoni se për çdo a dhe b Dëshmi.

2. Metoda e kundërt
Këtu është një shembull i mirë i përdorimit të kësaj metode. Vërtetoni se për a, b ϵ R. Dëshmi. Le të pretendojmë se. Por kjo dëshmon qartë se supozimi ynë është i pasaktë. C.T.D.

Shembulli 5.Vërtetoni se për çdo numër A, B, C pabarazia e mëposhtme është e vërtetë:
Dëshmi. Natyrisht, mjafton të vendoset kjo pabarazi për jonegative A, B Dhe ME, pasi do të kemi marrëdhënien e mëposhtme: ,
që është arsyetimi për pabarazinë fillestare .

Tani le të ketë numra të tillë jo negativë A, B Dhe ME, për të cilën vlen pabarazia , e cila është e pamundur nën çdo real A, B Dhe ME. Supozimi i bërë më sipër është hedhur poshtë, gjë që vërtetohet nga pabarazia origjinale në studim.

Përdorimi i vetive të trinomit kuadratik
Metoda bazohet në vetinë e jonegativitetit të një trinomi kuadratik nëse Dhe. Shembulli 6. Vërtetoni këtë Dëshmi. Le te jete, a=2, 2>0 =>

Shembulli 7. Vërtetoni se për çdo x dhe y real pabarazia vlen Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Dëshmi . 1 mënyrë.
Metoda 2.
për një funksion kuadratik që do të thotë pozitiviteti i saj për çdo real X.

Shembulli 2. Vërtetoni se për çdo x dhe y
Dëshmi. Shembulli 3. Vërtetoni këtë Dëshmi. Shembulli 4. Vërtetoni se për çdo a dhe b Dëshmi.

2. Metoda e kundërt
Këtu është një shembull i mirë i përdorimit të kësaj metode. Vërtetoni se për a, b ϵ R. Dëshmi. Le të pretendojmë se. Por kjo dëshmon qartë se supozimi ynë është i pasaktë. C.T.D.

Shembulli 5.Vërtetoni se për çdo numër A, B, C pabarazia e mëposhtme është e vërtetë:
Dëshmi. Natyrisht, mjafton të vendoset kjo pabarazi për jonegative A, B Dhe ME, pasi do të kemi marrëdhënien e mëposhtme: ,
që është arsyetimi për pabarazinë fillestare .

Tani le të ketë numra të tillë jo negativë A, B Dhe ME, për të cilën vlen pabarazia , e cila është e pamundur nën çdo real A, B Dhe ME. Supozimi i bërë më sipër është hedhur poshtë, gjë që vërtetohet nga pabarazia origjinale në studim.

Përdorimi i vetive të trinomit kuadratik
Metoda bazohet në vetinë e jonegativitetit të një trinomi kuadratik nëse Dhe. Shembulli 6. Vërtetoni këtë Dëshmi. Le te jete, a=2, 2>0 =>

Shembulli 7. Vërtetoni se për çdo x dhe y real pabarazia vlen Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Metoda 2.
për një funksion kuadratik që do të thotë pozitiviteti i saj për çdo real X.

Shembulli 2. Vërtetoni se për çdo x dhe y
Dëshmi. Shembulli 3. Vërtetoni këtë Dëshmi. Shembulli 4. Vërtetoni se për çdo a dhe b Dëshmi.

2. Metoda e kundërt
Këtu është një shembull i mirë i përdorimit të kësaj metode. Vërtetoni se për a, b ϵ R. Dëshmi. Le të pretendojmë se. Por kjo dëshmon qartë se supozimi ynë është i pasaktë. C.T.D.

Shembulli 5.Vërtetoni se për çdo numër A, B, C pabarazia e mëposhtme është e vërtetë:
Dëshmi. Natyrisht, mjafton të vendoset kjo pabarazi për jonegative A, B Dhe ME, pasi do të kemi marrëdhënien e mëposhtme: ,
që është arsyetimi për pabarazinë fillestare .

Tani le të ketë numra të tillë jo negativë A, B Dhe ME, për të cilën vlen pabarazia , e cila është e pamundur nën çdo real A, B Dhe ME. Supozimi i bërë më sipër është hedhur poshtë, gjë që vërtetohet nga pabarazia origjinale në studim.

Përdorimi i vetive të trinomit kuadratik
Metoda bazohet në vetinë e jonegativitetit të një trinomi kuadratik nëse Dhe. Shembulli 6. Vërtetoni këtë Dëshmi. Le te jete, a=2, 2>0 =>

Shembulli 7. Vërtetoni se për çdo x dhe y real pabarazia vlen Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
për një funksion kuadratik që do të thotë pozitiviteti i saj për çdo real X.

Shembulli 2. Vërtetoni se për çdo x dhe y
Dëshmi. Shembulli 3. Vërtetoni këtë Dëshmi. Shembulli 4. Vërtetoni se për çdo a dhe b Dëshmi.

2. Metoda e kundërt
Këtu është një shembull i mirë i përdorimit të kësaj metode. Vërtetoni se për a, b ϵ R. Dëshmi. Le të pretendojmë se. Por kjo dëshmon qartë se supozimi ynë është i pasaktë. C.T.D.

Shembulli 5.Vërtetoni se për çdo numër A, B, C pabarazia e mëposhtme është e vërtetë:
Dëshmi. Natyrisht, mjafton të vendoset kjo pabarazi për jonegative A, B Dhe ME, pasi do të kemi marrëdhënien e mëposhtme: ,
që është arsyetimi për pabarazinë fillestare .

Tani le të ketë numra të tillë jo negativë A, B Dhe ME, për të cilën vlen pabarazia , e cila është e pamundur nën çdo real A, B Dhe ME. Supozimi i bërë më sipër është hedhur poshtë, gjë që vërtetohet nga pabarazia origjinale në studim.

Përdorimi i vetive të trinomit kuadratik
Metoda bazohet në vetinë e jonegativitetit të një trinomi kuadratik nëse Dhe. Shembulli 6. Vërtetoni këtë Dëshmi. Le te jete, a=2, 2>0 =>

Shembulli 7. Vërtetoni se për çdo x dhe y real pabarazia vlen Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
që do të thotë pozitiviteti i saj për çdo real X.

Shembulli 2. Vërtetoni se për çdo x dhe y
Dëshmi. Shembulli 3. Vërtetoni këtë Dëshmi. Shembulli 4. Vërtetoni se për çdo a dhe b Dëshmi.

2. Metoda e kundërt
Këtu është një shembull i mirë i përdorimit të kësaj metode. Vërtetoni se për a, b ϵ R. Dëshmi. Le të pretendojmë se. Por kjo dëshmon qartë se supozimi ynë është i pasaktë. C.T.D.

Shembulli 5.Vërtetoni se për çdo numër A, B, C pabarazia e mëposhtme është e vërtetë:
Dëshmi. Natyrisht, mjafton të vendoset kjo pabarazi për jonegative A, B Dhe ME, pasi do të kemi marrëdhënien e mëposhtme: ,
që është arsyetimi për pabarazinë fillestare .

Tani le të ketë numra të tillë jo negativë A, B Dhe ME, për të cilën vlen pabarazia , e cila është e pamundur nën çdo real A, B Dhe ME. Supozimi i bërë më sipër është hedhur poshtë, gjë që vërtetohet nga pabarazia origjinale në studim.

Përdorimi i vetive të trinomit kuadratik
Metoda bazohet në vetinë e jonegativitetit të një trinomi kuadratik nëse Dhe. Shembulli 6. Vërtetoni këtë Dëshmi. Le te jete, a=2, 2>0 =>

Shembulli 7. Vërtetoni se për çdo x dhe y real pabarazia vlen Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.

Shembulli 2. Vërtetoni se për çdo x dhe y
Dëshmi. Shembulli 3. Vërtetoni këtë Dëshmi. Shembulli 4. Vërtetoni se për çdo a dhe b Dëshmi.

2. Metoda e kundërt
Këtu është një shembull i mirë i përdorimit të kësaj metode. Vërtetoni se për a, b ϵ R. Dëshmi. Le të pretendojmë se. Por kjo dëshmon qartë se supozimi ynë është i pasaktë. C.T.D.

Shembulli 5.Vërtetoni se për çdo numër A, B, C pabarazia e mëposhtme është e vërtetë:
Dëshmi. Natyrisht, mjafton të vendoset kjo pabarazi për jonegative A, B Dhe ME, pasi do të kemi marrëdhënien e mëposhtme: ,
që është arsyetimi për pabarazinë fillestare .

Tani le të ketë numra të tillë jo negativë A, B Dhe ME, për të cilën vlen pabarazia , e cila është e pamundur nën çdo real A, B Dhe ME. Supozimi i bërë më sipër është hedhur poshtë, gjë që vërtetohet nga pabarazia origjinale në studim.

Përdorimi i vetive të trinomit kuadratik
Metoda bazohet në vetinë e jonegativitetit të një trinomi kuadratik nëse Dhe. Shembulli 6. Vërtetoni këtë Dëshmi. Le te jete, a=2, 2>0 =>

Shembulli 7. Vërtetoni se për çdo x dhe y real pabarazia vlen Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Dëshmi. Shembulli 3. Vërtetoni këtë Dëshmi. Shembulli 4. Vërtetoni se për çdo a dhe b Dëshmi.

2. Metoda e kundërt
Këtu është një shembull i mirë i përdorimit të kësaj metode. Vërtetoni se për a, b ϵ R. Dëshmi. Le të pretendojmë se. Por kjo dëshmon qartë se supozimi ynë është i pasaktë. C.T.D.

Shembulli 5.Vërtetoni se për çdo numër A, B, C pabarazia e mëposhtme është e vërtetë:
Dëshmi. Natyrisht, mjafton të vendoset kjo pabarazi për jonegative A, B Dhe ME, pasi do të kemi marrëdhënien e mëposhtme: ,
që është arsyetimi për pabarazinë fillestare .

Tani le të ketë numra të tillë jo negativë A, B Dhe ME, për të cilën vlen pabarazia , e cila është e pamundur nën çdo real A, B Dhe ME. Supozimi i bërë më sipër është hedhur poshtë, gjë që vërtetohet nga pabarazia origjinale në studim.

Përdorimi i vetive të trinomit kuadratik
Metoda bazohet në vetinë e jonegativitetit të një trinomi kuadratik nëse Dhe. Shembulli 6. Vërtetoni këtë Dëshmi. Le te jete, a=2, 2>0 =>

Shembulli 7. Vërtetoni se për çdo x dhe y real pabarazia vlen Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Dëshmi. Shembulli 4. Vërtetoni se për çdo a dhe b Dëshmi.

2. Metoda e kundërt
Këtu është një shembull i mirë i përdorimit të kësaj metode. Vërtetoni se për a, b ϵ R. Dëshmi. Le të pretendojmë se. Por kjo dëshmon qartë se supozimi ynë është i pasaktë. C.T.D.

Shembulli 5.Vërtetoni se për çdo numër A, B, C pabarazia e mëposhtme është e vërtetë:
Dëshmi. Natyrisht, mjafton të vendoset kjo pabarazi për jonegative A, B Dhe ME, pasi do të kemi marrëdhënien e mëposhtme: ,
që është arsyetimi për pabarazinë fillestare .

Tani le të ketë numra të tillë jo negativë A, B Dhe ME, për të cilën vlen pabarazia , e cila është e pamundur nën çdo real A, B Dhe ME. Supozimi i bërë më sipër është hedhur poshtë, gjë që vërtetohet nga pabarazia origjinale në studim.

Përdorimi i vetive të trinomit kuadratik
Metoda bazohet në vetinë e jonegativitetit të një trinomi kuadratik nëse Dhe. Shembulli 6. Vërtetoni këtë Dëshmi. Le te jete, a=2, 2>0 =>

Shembulli 7. Vërtetoni se për çdo x dhe y real pabarazia vlen Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Dëshmi.

2. Metoda e kundërt
Këtu është një shembull i mirë i përdorimit të kësaj metode. Vërtetoni se për a, b ϵ R. Dëshmi. Le të pretendojmë se. Por kjo dëshmon qartë se supozimi ynë është i pasaktë. C.T.D.

Shembulli 5.Vërtetoni se për çdo numër A, B, C pabarazia e mëposhtme është e vërtetë:
Dëshmi. Natyrisht, mjafton të vendoset kjo pabarazi për jonegative A, B Dhe ME, pasi do të kemi marrëdhënien e mëposhtme: ,
që është arsyetimi për pabarazinë fillestare .

Tani le të ketë numra të tillë jo negativë A, B Dhe ME, për të cilën vlen pabarazia , e cila është e pamundur nën çdo real A, B Dhe ME. Supozimi i bërë më sipër është hedhur poshtë, gjë që vërtetohet nga pabarazia origjinale në studim.

Përdorimi i vetive të trinomit kuadratik
Metoda bazohet në vetinë e jonegativitetit të një trinomi kuadratik nëse Dhe. Shembulli 6. Vërtetoni këtë Dëshmi. Le te jete, a=2, 2>0 =>

Shembulli 7. Vërtetoni se për çdo x dhe y real pabarazia vlen Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Vërtetoni se për a, b ϵ R. Dëshmi. Le të pretendojmë se. Por kjo dëshmon qartë se supozimi ynë është i pasaktë. C.T.D.

Shembulli 5.Vërtetoni se për çdo numër A, B, C pabarazia e mëposhtme është e vërtetë:
Dëshmi. Natyrisht, mjafton të vendoset kjo pabarazi për jonegative A, B Dhe ME, pasi do të kemi marrëdhënien e mëposhtme: ,
që është arsyetimi për pabarazinë fillestare .

Tani le të ketë numra të tillë jo negativë A, B Dhe ME, për të cilën vlen pabarazia , e cila është e pamundur nën çdo real A, B Dhe ME. Supozimi i bërë më sipër është hedhur poshtë, gjë që vërtetohet nga pabarazia origjinale në studim.

Përdorimi i vetive të trinomit kuadratik
Metoda bazohet në vetinë e jonegativitetit të një trinomi kuadratik nëse Dhe. Shembulli 6. Vërtetoni këtë Dëshmi. Le te jete, a=2, 2>0 =>

Shembulli 7. Vërtetoni se për çdo x dhe y real pabarazia vlen Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Le të pretendojmë se. Por kjo dëshmon qartë se supozimi ynë është i pasaktë. C.T.D.

Shembulli 5.Vërtetoni se për çdo numër A, B, C pabarazia e mëposhtme është e vërtetë:
Dëshmi. Natyrisht, mjafton të vendoset kjo pabarazi për jonegative A, B Dhe ME, pasi do të kemi marrëdhënien e mëposhtme: ,
që është arsyetimi për pabarazinë fillestare .

Tani le të ketë numra të tillë jo negativë A, B Dhe ME, për të cilën vlen pabarazia , e cila është e pamundur nën çdo real A, B Dhe ME. Supozimi i bërë më sipër është hedhur poshtë, gjë që vërtetohet nga pabarazia origjinale në studim.

Përdorimi i vetive të trinomit kuadratik
Metoda bazohet në vetinë e jonegativitetit të një trinomi kuadratik nëse Dhe. Shembulli 6. Vërtetoni këtë Dëshmi. Le te jete, a=2, 2>0 =>

Shembulli 7. Vërtetoni se për çdo x dhe y real pabarazia vlen Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
C.T.D.

Shembulli 5.Vërtetoni se për çdo numër A, B, C pabarazia e mëposhtme është e vërtetë:
Dëshmi. Natyrisht, mjafton të vendoset kjo pabarazi për jonegative A, B Dhe ME, pasi do të kemi marrëdhënien e mëposhtme: ,
që është arsyetimi për pabarazinë fillestare .

Tani le të ketë numra të tillë jo negativë A, B Dhe ME, për të cilën vlen pabarazia , e cila është e pamundur nën çdo real A, B Dhe ME. Supozimi i bërë më sipër është hedhur poshtë, gjë që vërtetohet nga pabarazia origjinale në studim.

Përdorimi i vetive të trinomit kuadratik
Metoda bazohet në vetinë e jonegativitetit të një trinomi kuadratik nëse Dhe. Shembulli 6. Vërtetoni këtë Dëshmi. Le te jete, a=2, 2>0 =>

Shembulli 7. Vërtetoni se për çdo x dhe y real pabarazia vlen Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Dëshmi. Natyrisht, mjafton të vendoset kjo pabarazi për jonegative A, B Dhe ME, pasi do të kemi marrëdhënien e mëposhtme: ,
që është arsyetimi për pabarazinë fillestare .

Tani le të ketë numra të tillë jo negativë A, B Dhe ME, për të cilën vlen pabarazia , e cila është e pamundur nën çdo real A, B Dhe ME. Supozimi i bërë më sipër është hedhur poshtë, gjë që vërtetohet nga pabarazia origjinale në studim.

Përdorimi i vetive të trinomit kuadratik
Metoda bazohet në vetinë e jonegativitetit të një trinomi kuadratik nëse Dhe. Shembulli 6. Vërtetoni këtë Dëshmi. Le te jete, a=2, 2>0 =>

Shembulli 7. Vërtetoni se për çdo x dhe y real pabarazia vlen Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
,
që është arsyetimi për pabarazinë fillestare .

Tani le të ketë numra të tillë jo negativë A, B Dhe ME, për të cilën vlen pabarazia , e cila është e pamundur nën çdo real A, B Dhe ME. Supozimi i bërë më sipër është hedhur poshtë, gjë që vërtetohet nga pabarazia origjinale në studim.

Përdorimi i vetive të trinomit kuadratik
Metoda bazohet në vetinë e jonegativitetit të një trinomi kuadratik nëse Dhe. Shembulli 6. Vërtetoni këtë Dëshmi. Le te jete, a=2, 2>0 =>

Shembulli 7. Vërtetoni se për çdo x dhe y real pabarazia vlen Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
, e cila është e pamundur nën çdo real A, B Dhe ME. Supozimi i bërë më sipër është hedhur poshtë, gjë që vërtetohet nga pabarazia origjinale në studim.

Përdorimi i vetive të trinomit kuadratik
Metoda bazohet në vetinë e jonegativitetit të një trinomi kuadratik nëse Dhe. Shembulli 6. Vërtetoni këtë Dëshmi. Le te jete, a=2, 2>0 =>

Shembulli 7. Vërtetoni se për çdo x dhe y real pabarazia vlen Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Dhe. Shembulli 6. Vërtetoni këtë Dëshmi. Le te jete, a=2, 2>0 =>

Shembulli 7. Vërtetoni se për çdo x dhe y real pabarazia vlen Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Dëshmi. Le te jete, a=2, 2>0 =>

Shembulli 7. Vërtetoni se për çdo x dhe y real pabarazia vlen Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
=>

Shembulli 7. Vërtetoni se për çdo x dhe y real pabarazia vlen Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Dëshmi. Konsideroni anën e majtë të pabarazisë si një trinom kuadratik në lidhje me X: , a>0, D D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
D= => P(x)>0 Dhe e vërtetë për çdo vlerë reale X Dhe u.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.

Shembulli 8. Vërtetoni këtë për çdo vlerë reale të x dhe y. Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Dëshmi. Le
, Kjo do të thotë se për çdo të vërtetë në dhe pabarazia është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
është i kënaqur për çdo të vërtetë X Dhe u.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.

Metoda e futjes së variablave të reja ose metoda e zëvendësimit
Shembulli 9. Vërtetoni se për çdo numër jonegativ x, y, z Dëshmi. Le të përdorim pabarazinë e saktë për, . Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
. Marrim pabarazinë në studim

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.

Përdorimi i vetive të funksionit.
Shembulli 10. Le të vërtetojmë pabarazinë për çdo a dhe b. Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Dëshmi. Le të shqyrtojmë 2 raste: Nëse a=b atëherë e vërtetë
Për më tepër, barazia arrihet vetëm kur a=b=0. 2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Nëse a=b atëherë e vërtetë
2) Nëse , në R => ()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
()* ()>0, që vërteton pabarazinë

Shembulli 11. Le ta vërtetojmë këtë për cilindo
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Dëshmi. në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
në R. Nëse, atëherë shenjat e numrave përkojnë, që do të thotë se diferenca në studim është pozitive =>

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.

Zbatimi i metodës së induksionit matematik
Kjo metodë përdoret për të vërtetuar pabarazitë në lidhje me numrat natyrorë. Shembulli 12. Vërtetoni se për çdo nϵN
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Le të kontrollojmë të vërtetën e deklaratës kur
- (djathtas) 2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Le të kontrollojmë të vërtetën e deklaratës kur
2) Supozoni vërtetësinë e pohimit kur (k>1)

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.

3) Të vërtetojmë vërtetësinë e pohimit kur n=k+1. Le të krahasojmë dhe: Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Ne kemi: Përfundim: deklarata është e vërtetë për këdo nϵN.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.

Përdorimi i pabarazive të dukshme
Teorema mbi mesataret (pabarazia e Cauchy)
Pabarazia Cauchy–Bunyakovsky
Pabarazia e Bernulit
Le të shqyrtojmë secilën nga pabarazitë e listuara veç e veç.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.

Zbatimi i teoremës së vlerës mesatare (pabarazia Cauchy)
Mesatarja aritmetike e disa numrave jonegativë është më e madhe ose e barabartë me mesataren e tyre gjeometrike , Ku Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.
Shenja e barazimit arrihet nëse dhe vetëm nëse Le të shqyrtojmë raste të veçanta të kësaj teoreme:

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.

Le të jetë n=2, atëherë
Le të jetë n=2, a>0, atëherë
Le të jetë n=3, atëherë
Shembulli 13. Vërtetoni se për të gjitha jonegativet a,b,c vlen pabarazia Dëshmi.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.

Pabarazia Cauchy-Bunyakovsky
Pabarazia Cauchy-Bunyakovsky thotë se për çdo; raporti është i vlefshëm Pabarazia e provuar ka një interpretim gjeometrik. Për n=2,3 shpreh faktin e njohur se prodhimi skalar i dy vektorëve në rrafsh dhe në hapësirë nuk e kalon prodhimin e gjatësive të tyre. Për n=2 mosbarazimi ka formën: . Për n=3 marrim

Shembulli 14.

Shembulli 14.
Dëshmi. Le të shkruajmë pabarazinë në studim në formën e mëposhtme:
Kjo është padyshim një pabarazi e vërtetë, pasi është një rast i veçantë i pabarazisë Cauchy-Bunyakovsky.
Shembulli 15. Vërtetoni se për çdo a,b,c ϵ R vlen pabarazia e mëposhtme:
Dëshmi. Mjafton ta shkruajmë këtë pabarazi në formë
dhe referojuni pabarazisë Cauchy–Bunyakovsky.

Pabarazia e Bernulit
Pabarazia e Bernulit thotë se nëse x>-1, atëherë për të gjitha vlerat natyrore të n-së vlen pabarazia e mëposhtme: Pabarazia mund të përdoret për shprehjet e formës Përveç kësaj, një grup shumë i madh i pabarazive mund të vërtetohet lehtësisht duke përdorur teoremën e Bernulit.

Përveç kësaj, një grup shumë i madh i pabarazive mund të vërtetohet lehtësisht duke përdorur teoremën e Bernulit.

Shembulli 16.
Dëshmi. Duke vënë x=0.5 dhe duke zbatuar teoremën e Bernulit për të shprehur
Ne marrim pabarazinë e kërkuar.
Shembulli 17. Vërtetoni se për çdo n ϵ N
Dëshmi.
sipas teoremës së Bernulit, siç kërkohet. 
David Gilbert u pyet për një prej tij ish studentë. “Oh, filani?” Ai u bë poet.

MOU Shkolla e mesme Grishino-Slobodskaya
Programi i modulit
"Metodat për vërtetimin e pabarazive"
si pjesë e një lënde me zgjedhje
"Pas faqeve të një teksti matematike"
për nxënësit e klasave 10-11
Përpiluar nga:
mësues i matematikës
Pankova E.Yu
Shënim shpjegues
“Matematika quhet shkencë tautologjike: me fjalë të tjera, thuhet se matematikanët shpenzojnë kohë duke vërtetuar se objektet janë të barabartë me veten e tyre. Kjo deklaratë është shumë e pasaktë për dy arsye. Së pari, matematika, pavarësisht nga e natyrshme e saj gjuha shkencore, nuk është shkencë; përkundrazi, mund të quhet art. Së dyti Rezultatet kryesore të matematikës shprehen më shpesh me pabarazi sesa me barazi.
Pabarazitë përdoren vazhdimisht në punën praktike të matematikanëve. Ato përdoren për të marrë një sërë vetive ekstreme interesante dhe të rëndësishme të figurave "simetrike": katror, kub, trekëndësh barabrinjës, si dhe për të vërtetuar konvergjencën e proceseve përsëritëse dhe për të llogaritur disa kufij. Roli i pabarazive është gjithashtu i rëndësishëm në çështje të ndryshme të shkencës dhe teknologjisë natyrore.
Problemet për vërtetimin e pabarazive janë më të vështirat dhe më interesantet nga ato tradicionale. Provimi i pabarazive kërkon zgjuarsi të vërtetë, krijimtarinë që e bën matematikën lëndën emocionuese që është.
Mësimi i provave luan një rol të madh në zhvillimin e të menduarit deduktiv-matematikor dhe aftësive të të menduarit të përgjithshëm të nxënësve. Si t'i mësoni nxënësit e shkollave të provojnë në mënyrë të pavarur pabarazitë? Përgjigja është: vetëm duke marrë parasysh shumë teknika dhe metoda të provës dhe duke i zbatuar ato rregullisht.
Idetë e përdorura për të vërtetuar pabarazitë janë pothuajse po aq të ndryshme sa edhe vetë pabarazitë. Në situata specifike, metodat e përgjithshme shpesh çojnë në zgjidhje të shëmtuara. Por vetëm disa nxënës ia dalin të ndërthurin disa pabarazi “themelore” në një mënyrë jo të dukshme. Dhe, përveç kësaj, asgjë nuk e pengon studentin në çdo rast specifik të kërkojë një zgjidhje më të mirë se ajo e marrë me metodën e përgjithshme. Për këtë arsye, prova e pabarazive shpesh zhvendoset në fushën e artit. Dhe si çdo art, këtu ka teknika teknike, diapazoni i të cilave është shumë i gjerë dhe është shumë e vështirë t'i zotërosh të gjitha, por çdo mësues duhet të përpiqet të zgjerojë mjetet matematikore që ka në dispozicion.
Ky modul rekomandohet për nxënësit e klasave 10-11. Këtu nuk diskutohen të gjitha metodat e mundshme për vërtetimin e pabarazive (metoda e zëvendësimit të një ndryshoreje, vërtetimi i pabarazive duke përdorur një derivat, metoda e kërkimit dhe përgjithësimit dhe teknika e renditjes nuk janë përfshirë). Ju mund të ofroni të konsideroni metoda të tjera në fazën e dytë (për shembull, në klasën e 11-të), nëse ky modul i kursit ngjall interes tek studentët, dhe gjithashtu bazuar në suksesin e zotërimit të pjesës së parë të kursit.
|
Ekuacionet dhe pabarazitë me një parametër. |
||
|
Metodat për vërtetimin e pabarazive. |
||
|
Ekuacionet dhe pabarazitë që përmbajnë një të panjohur nën shenjën e modulit. |
||
|
Sistemet e pabarazive me dy ndryshore. |
"Pas faqeve të një teksti matematike"
"Metodat për vërtetimin e pabarazive"
|
Prezantimi. |
||
|
Vërtetimi i pabarazive bazuar në përkufizim. |
||
|
Metoda induksioni matematik. |
||
|
Zbatimi i pabarazive klasike. |
||
|
Metoda grafike. |
||
|
Metoda e kundërt. |
||
|
Një teknikë për shqyrtimin e pabarazive në lidhje me një nga variablat. |
||
|
Ideja e forcimit. |
||
|
Mësimi - kontrolli. |
Mesimi 1. Prezantimi.
Vërtetimi i pabarazive është një temë magjepsëse dhe sfiduese në matematikën fillore. Mungesa e një qasjeje të unifikuar ndaj problemit të vërtetimit të pabarazive çon në kërkimin e një numri teknikash të përshtatshme për vërtetimin e pabarazive lloje të caktuara. Ky lëndë zgjedhore do të mbulojë metodat e mëposhtme për vërtetimin e pabarazive:
Përsëritje:
Provoni disa veti.
Pabarazitë klasike:
1)
 (Pabarazia cauchy)
(Pabarazia cauchy)
2)

3)

4)

Referenca historike:
Pabarazia (1) është emëruar sipas matematikanit francez Auguste Cauchy. Numri  thirrur mesatare aritmetike numrat a dhe b;
thirrur mesatare aritmetike numrat a dhe b;
numri  thirrur mesatare gjeometrike numrat a dhe b. Kështu, një pabarazi do të thotë që mesatarja aritmetike e dy numrave pozitivë nuk është më e vogël se mesatarja e tyre gjeometrike.
thirrur mesatare gjeometrike numrat a dhe b. Kështu, një pabarazi do të thotë që mesatarja aritmetike e dy numrave pozitivë nuk është më e vogël se mesatarja e tyre gjeometrike.
Për më tepër:
Konsideroni disa sofizma matematikore me pabarazi.
Sofia matematikore- një deklaratë e mahnitshme, prova e së cilës fsheh gabime të padukshme dhe ndonjëherë mjaft delikate.
Sofizmat janë rezultate të rreme të marra përmes arsyetimit që vetëm duken të sakta, por detyrimisht përmbajnë një ose një gabim tjetër.
Shembull:
Katër është mbi dymbëdhjetë
Mësimi 2. Vërtetimi i pabarazive bazuar në përkufizim.
Thelbi i kësaj metode është si vijon: për të përcaktuar vlefshmërinë e pabarazive F(x,y,z)>S(x,y,z) përbëjnë diferencën F(x,y,z)-S( x,y,z) dhe provoni se është pozitive. Duke përdorur këtë metodë, njeriu shpesh izolon një katror, një kub të një shume ose ndryshimi, ose një katror jo të plotë të një shume ose ndryshimi. Kjo ndihmon në përcaktimin e shenjës së ndryshimit.
Shembull.
Vërtetoni pabarazinë (x+y)(x+y+2cosx)+2  2 mëkat 2x
2 mëkat 2x
Dëshmi:
Merrni parasysh ndryshimin (x+y)(x+y+2cosx)+2- 2sin 2 x =(x+y)(x+y+2cosx)+2cos 2 x=(x+y)(x+y+2cosx ) + cos 2 x +cos 2 x= (x+y) 2 +2(x+y)cosx+ cos 2 x +cos 2 x=((x+y)+cosx) 2 + cos 2 x 0.
Vërtetoni pabarazinë:
1.ab(a+b)+bc(b+c)+ac(a+c) 6abc
3.
4. > 2x-20
> 2x-20
5.

6.(a+b)(b+c)(c+a) 8abc
7.
Mësimi 3. Metoda e induksionit matematik.
Kur vërtetohen pabarazitë që përfshijnë numra të plotë shpesh përdorin metodën e induksionit matematik. Metoda është si më poshtë:
1) kontrolloni vërtetësinë e teoremës për n=1;
2) supozojmë se teorema është e vërtetë për disa n=k, dhe bazuar në këtë supozim vërtetojmë vërtetësinë e teoremës për n=k+1;
3) bazuar në dy hapat e parë dhe parimin e induksionit matematik, konkludojmë se teorema është e vërtetë për çdo n.
Shembull.
Vërtetoni pabarazinë
Dëshmi:
1) për n=2 pabarazia është e vërtetë:
2) Le të jetë e vërtetë pabarazia për n=k d.m.th.  (*)
(*)
Le të vërtetojmë se pabarazia është e vërtetë për n=k+1, d.m.th.  .
.  Le të shumëzojmë të dyja anët e pabarazisë (*) me
Le të shumëzojmë të dyja anët e pabarazisë (*) me
marrim 3) Nga pika 1. dhe pika 2 konkludojmë se pabarazia është e vërtetë për çdo n.
Vërtetoni pabarazinë:
1)
2)
3)
4)
5)
6) .
.
Detyrat për punë në klasë dhe në shtëpi
Mësimi 4. Zbatimi i pabarazive klasike.
Shembull.
Vërtetoni pabarazinë:
Dëshmi:
Thelbi i kësaj metode është si vijon: duke përdorur një seri transformimesh, pabarazia e kërkuar nxirret duke përdorur disa pabarazi klasike. Si mbështesin pabarazinë  .
.
ne përdorim
 Le ta zvogëlojmë këtë pabarazi në formën e mëposhtme:
Le ta zvogëlojmë këtë pabarazi në formën e mëposhtme:
, Pastaj  Le ta zvogëlojmë këtë pabarazi në formën e mëposhtme:
Le ta zvogëlojmë këtë pabarazi në formën e mëposhtme:
Vërtetoni pabarazinë:
Por =
2)
 1)(p+2)(q+2)(p+q)16pq (pabarazia përdoret për vërtetim)
1)(p+2)(q+2)(p+q)16pq (pabarazia përdoret për vërtetim)
(për dokumente përdoret pabarazia)
4)
 3) (a+b)(b+c)(c+a) 8abc (pabarazia përdoret për vërtetim)
3) (a+b)(b+c)(c+a) 8abc (pabarazia përdoret për vërtetim)
(për dokumentin përdoret pabarazia).
Mësimi 5. Metoda grafike.
Vërtetimi i mosbarazimeve me metodën grafike është si më poshtë: nëse vërtetojmë pabarazinë f(x)>g(x)(f(x)
1) të ndërtojmë grafikë të funksioneve y=f(x) dhe y=g(x);
Shembull.
Vërtetoni pabarazinë:
2) nëse grafiku i funksionit y=f(x) ndodhet mbi (poshtë) grafikun e funksionit y=g(x), atëherë pabarazia që vërtetohet është e vërtetë.  cosx
cosx
Dëshmi:
, x0

Le të ndërtojmë grafikët e funksioneve y=cosx dhe
Nga grafiku shihet qartë se në x0 grafiku i funksionit y=cosx qëndron mbi grafikun e funksionit y=.
Vërtetoni pabarazinë:
1)
5)
Detyrat për punë në klasë dhe në shtëpi.
Mësimi 6. Metoda e kundërt
Shembull.
Vërtetoni pabarazinë:
Dëshmi:
Thelbi i kësaj metode është si vijon: le t'ju duhet të provoni vërtetësinë e pabarazisë F(x,y,z) S(x,y,z)(1). Ata supozojnë të kundërtën, që do të thotë se për të paktën një grup variablash pabarazia F(x,y,z) S(x,y,z) (2) është e vërtetë. Duke përdorur vetitë e inekuacioneve, kryhen shndërrimet e pabarazisë (2). Nëse si rezultat i këtyre transformimeve fitohet një pabarazi e rreme, atëherë kjo do të thotë se supozimi se pabarazia (2) është e vërtetë është e pasaktë, dhe për rrjedhojë pabarazia (1) është e vërtetë.
Le të supozojmë të kundërtën, d.m.th.  Le të katrorë të dy anët e pabarazisë dhe të marrë , nga e cila
Le të katrorë të dy anët e pabarazisë dhe të marrë , nga e cila
 dhe në vazhdim
dhe në vazhdim
. Por kjo bie ndesh me pabarazinë e Cauchy. Kjo do të thotë se supozimi ynë është i pasaktë, domethënë pabarazia është e vërtetë për detyrat në klasë dhe në shtëpi.
Mësimi 9. Mësimi - kontrolli i njohurive të nxënësve. Ky mësim mund të bëhet në çifte ose nëse klasë në grupe. Në fund të orës së mësimit, çdo nxënës duhet të vlerësohet. Ky është formulari i kredisë për këtë kurs. Nuk rekomandohet kryerja e testeve për këtë temë sepse vërtetimi i pabarazive, siç është përmendur tashmë në shënimin shpjegues, i përket fushës së artit. Në fillim, nxënësve u kërkohet të përcaktojnë metodën e vërtetimit të pabarazive të propozuara. Nëse nxënësit kanë ndonjë vështirësi, mësuesi u tregon metodën racionale, duke paralajmëruar grupin se kjo, natyrisht, do të ndikojë në notën e tyre.
Punë në çift.
Shembuj detyrash.
________________________________________________________________
Vërtetoni pabarazinë:
1. (metoda e induksionit matematik)
(metoda e induksionit matematik)
2. (a-parësore)
(a-parësore)
Moduli. Ekuacionet dhe pabarazitë me parametra. ... vetitë, formulimi dhe provë teorema, nxjerrja e formulave... më e thjeshta pabarazitë. 7. Di të përdorin metodë intervale...
Programi i Olimpiadës së Hapur dhe kërkesat e përgatitjes së matematikës për nxënësit e klasave të 9-ta
ProgramiKoncepti modul numër real. Aritmetike dhe përkufizimet gjeometrike modul. Zbulimi modulet. ... pabarazitë. Dëshmi pabarazitë. Zgjidhja e problemeve racionale lineare, kuadratike, thyesore pabarazitë me një variabël. Zgjidhje pabarazitë ...
Program me zgjedhje në matematikë për klasën e 8-të
ProgramiDemonstroni metodat provë pak më komplekse pabarazitë me këtë të thjeshtë pabarazitë? Pra, në këtë ministror program ...








