Gjeni ekstremin e funksionit. Rritja, zvogëlimi dhe ekstremi i një funksioni

Çfarë është një ekstrem i një funksioni dhe cili është kushti i nevojshëm për një ekstrem?

Ekstremumi i një funksioni është maksimumi dhe minimumi i funksionit.

Kusht paraprak Maksimumi dhe minimumi (ekstremi) i një funksioni janë si më poshtë: nëse funksioni f(x) ka një ekstrem në pikën x = a, atëherë në këtë pikë derivati ​​është ose zero, ose i pafund, ose nuk ekziston.

Ky kusht është i nevojshëm, por jo i mjaftueshëm. Derivati ​​në pikën x = a mund të shkojë në zero, në pafundësi ose të mos ekzistojë pa funksionin të ketë një ekstrem në këtë pikë.

Si është gjendje e mjaftueshme ekstremi i funksionit (maksimumi apo minimal)?

Kushti i parë:

Nëse, në afërsi të mjaftueshme me pikën x = a, derivati ​​f?(x) është pozitiv në të majtë të a dhe negativ në të djathtë të a, atëherë në pikën x = a funksioni f(x) ka maksimale

Nëse, në afërsi të mjaftueshme me pikën x = a, derivati ​​f?(x) është negativ në të majtë të a dhe pozitiv në të djathtë të a, atëherë në pikën x = a funksioni f(x) ka minimale me kusht që funksioni f(x) këtu të jetë i vazhdueshëm.

Në vend të kësaj, mund të përdorni kushtin e dytë të mjaftueshëm për ekstremin e një funksioni:

Le të zhduket në pikën x = a derivati ​​i parë f?(x); nëse derivati ​​i dytë f??(a) është negativ, atëherë funksioni f(x) ka një maksimum në pikën x = a, nëse është pozitiv, atëherë ka një minimum.

Cila është pika kritike e një funksioni dhe si ta gjejmë atë?

Kjo është vlera e argumentit të funksionit në të cilin funksioni ka një ekstrem (d.m.th. maksimum ose minimal). Për ta gjetur ju duhet gjeni derivatin funksioni f?(x) dhe, duke e barazuar atë me zero, zgjidhin ekuacionin f?(x) = 0. Rrënjët e këtij ekuacioni, si dhe ato pika në të cilat derivati ​​i këtij funksioni nuk ekziston, janë pika kritike, d.m.th., vlerat e argumentit në të cilat mund të ketë një ekstrem. Ato mund të identifikohen lehtësisht duke parë grafiku derivat: ne jemi të interesuar për ato vlera të argumentit në të cilat grafiku i funksionit kryqëzon boshtin e abshisave (boshti Ox) dhe ato në të cilat grafiku pëson ndërprerje.

Për shembull, le të gjejmë ekstremi i një parabole.

Funksioni y(x) = 3x2 + 2x - 50.

Derivati ​​i funksionit: y?(x) = 6x + 2

Zgjidheni ekuacionin: y?(x) = 0

6x + 2 = 0, 6x = -2, x = -2/6 = -1/3

NË në këtë rast pika kritike është x0=-1/3. Është me këtë vlerë argumenti që ka funksioni ekstreme. ndaj tij gjeni, zëvendësoni numrin e gjetur në shprehje për funksionin në vend të "x":

y0 = 3*(-1/3)2 + 2*(-1/3) - 50 = 3*1/9 - 2/3 - 50 = 1/3 - 2/3 - 50 = -1/3 - 50 = -50.333.

Si të përcaktohet maksimumi dhe minimumi i një funksioni, d.m.th. vlerat e tij më të mëdha dhe më të vogla?

Nëse shenja e derivatit kur kalon pikë kritike x0 ndryshon nga "plus" në "minus", atëherë x0 është pikë maksimale; nëse shenja e derivatit ndryshon nga minus në plus, atëherë x0 është pikë minimale; nëse shenja nuk ndryshon, atëherë në pikën x0 nuk ka as maksimum dhe as minimum.

Për shembullin e konsideruar:

Marrim një vlerë arbitrare të argumentit në të majtë të pikës kritike: x = -1

Në x = -1, vlera e derivatit do të jetë y?(-1) = 6*(-1) + 2 = -6 + 2 = -4 (d.m.th. shenja është "minus").

Tani marrim një vlerë arbitrare të argumentit në të djathtë të pikës kritike: x = 1

Në x = 1, vlera e derivatit do të jetë y(1) = 6*1 + 2 = 6 + 2 = 8 (d.m.th. shenja është "plus").

Siç mund ta shihni, derivati ​​ndryshoi shenjën nga minus në plus kur kalonte nëpër pikën kritike. Kjo do të thotë që në vlerën kritike x0 kemi një pikë minimale.

Më i madhi dhe vlera më e vogël funksionet në interval(në një segment) gjenden duke përdorur të njëjtën procedurë, vetëm duke marrë parasysh faktin se, ndoshta, jo të gjitha pikat kritike do të qëndrojnë brenda intervalit të specifikuar. Ato pika kritike që janë jashtë intervalit duhet të përjashtohen nga shqyrtimi. Nëse ka vetëm një pikë kritike brenda intervalit, ajo do të ketë një maksimum ose një minimum. Në këtë rast, për të përcaktuar vlerat më të mëdha dhe më të vogla të funksionit, marrim parasysh edhe vlerat e funksionit në skajet e intervalit.

Për shembull, le të gjejmë vlerat më të mëdha dhe më të vogla të funksionit

y(x) = 3sin(x) - 0.5x

në intervale:

Pra, derivati ​​i funksionit është

y?(x) = 3cos(x) - 0,5

Ne zgjidhim ekuacionin 3cos(x) - 0,5 = 0

cos(x) = 0,5/3 = 0,16667

x = ±arccos(0,16667) + 2πk.

Ne gjejmë pika kritike në intervalin [-9; 9]:

x = arccos(0.16667) - 2π*2 = -11.163 (nuk përfshihet në interval)

x = -arccos(0.16667) - 2π*1 = -7.687

x = arccos (0,16667) - 2π*1 = -4,88

x = -arccos(0,16667) + 2π*0 = -1,403

x = arccos (0,16667) + 2π*0 = 1,403

x = -arccos(0,16667) + 2π*1 = 4,88

x = arccos (0,16667) + 2π*1 = 7,687

x = -arccos(0.16667) + 2π*2 = 11.163 (nuk përfshihet në interval)

Ne gjejmë vlerat e funksionit në vlerat kritike argumenti:

y (-7,687) = 3cos(-7,687) - 0,5 = 0,885

y(-4,88) = 3cos(-4,88) - 0,5 = 5,398

y (-1,403) = 3cos(-1,403) - 0,5 = -2,256

y (1,403) = 3cos (1,403) - 0,5 = 2,256

y (4,88) = 3cos (4,88) - 0,5 = -5,398

y (7,687) = 3cos (7,687) - 0,5 = -0,885

Mund të shihet se në intervalin [-9; 9] vlerën më të lartë funksioni ka në x = -4.88:

x = -4,88, y = 5,398,

dhe më i vogli - në x = 4.88:

x = 4,88, y = -5,398.

Në intervalin [-6; -3] kemi vetëm një pikë kritike: x = -4.88. Vlera e funksionit në x = -4.88 është e barabartë me y = 5.398.

Gjeni vlerën e funksionit në fund të intervalit:

y(-6) = 3cos(-6) - 0,5 = 3,838

y(-3) = 3cos(-3) - 0,5 = 1,077

Në intervalin [-6; -3] kemi vlerën më të madhe të funksionit

y = 5,398 në x = -4,88

vlera më e vogël -

y = 1,077 në x = -3

Si të gjeni pikat e lakimit të një grafiku funksioni dhe të përcaktoni anët konvekse dhe konkave?

Për të gjetur të gjitha pikat e lakimit të drejtëzës y = f(x), duhet të gjeni derivatin e dytë, ta barazoni me zero (zgjidhni ekuacionin) dhe të provoni të gjitha ato vlera të x për të cilat derivati ​​i dytë është zero, e pafundme ose nuk ekziston. Nëse, kur kalon nëpër njërën nga këto vlera, derivati ​​i dytë ndryshon shenjën, atëherë grafiku i funksionit ka një lakim në këtë pikë. Nëse nuk ndryshon, atëherë nuk ka asnjë kthesë.

Rrënjët e ekuacionit f? (x) = 0, si dhe pikat e mundshme të ndërprerjes së funksionit dhe derivatit të dytë, ndajnë domenin e përkufizimit të funksionit në një numër intervalesh. Konveksiteti në secilin interval të tyre përcaktohet nga shenja e derivatit të dytë. Nëse derivati ​​i dytë në një pikë të intervalit në studim është pozitiv, atëherë drejtëza y = f(x) është konkave lart, dhe nëse negative, atëherë poshtë.

Si të gjejmë ekstremet e një funksioni të dy ndryshoreve?

Për të gjetur ekstremin e funksionit f(x,y), të diferencueshëm në domenin e specifikimit të tij, ju duhet:

1) gjeni pikat kritike, dhe për këtë - zgjidhni sistemin e ekuacioneve

fх? (x,y) = 0, fу? (x,y) = 0

2) për çdo pikë kritike P0(a;b) hetoni nëse shenja e diferencës mbetet e pandryshuar

për të gjitha pikat (x;y) mjaftueshëm afër P0. Nëse diferenca mbetet shenjë pozitive, atëherë në pikën P0 kemi një minimum, nëse negativ, atëherë kemi një maksimum. Nëse diferenca nuk ruan shenjën e saj, atëherë nuk ka ekstrem në pikën P0.

Ekstremat e funksionit përcaktohen në mënyrë të ngjashme për më shumë argumentet.

Ku mund të gjeni faqen zyrtare të Inspektoratit Shtetëror të Punës në Rajonin Bryansk në internet
www.rostrud.ru - faqja zyrtare e Rostrud - Shërbimi Federal mbi punën dhe punësimin Referenca e Rostrud - 8-800-707-88-41 Dërgoni një apel elektronik në Rostrud (adresa e emailit: [email i mbrojtur]) git77.rostrud.ru &mda

Ku mund të gjeni informacione për futbollin spanjoll?
Primera Division (Spanjisht: Primera División) është një ligë profesioniste futbolli në Spanjë (Spanjisht: Liga de Fútbol Profesional, LFP), e njohur gjithashtu thjesht si Primera, ose La Liga (Spanjisht: La Liga), është një turne profesionist futbolli.

Cila është monedha zyrtare e Rusisë
Emri i shtetit Emri - para/këmbë monedhë Australia Dollar/cent Australian Austri Shiling Austriak/grosz - euro Azerbajxhan Manat Shqipëri Lek/kindarka Algjeri Dinar/centimo algjerian Argjentinë Argjentinë austral/centavo Afganistan Afganistan/pul Bangladesh Taka/pais Belgjikë franga/centimo belg - euro Bullgari Lev/stotinka

Cilët njerëz të famshëm vdiqën më 2 nëntor
2 Nëntori është dita e 306-të e vitit (307 in vite të brishtë) V Kalendari Gregorian. Deri në fund të vitit kanë mbetur edhe 59 ditë Festat 2 Nëntor Kombëtar: Ishujt e Virgjër (SHBA) - Dita e Lirisë; Bjellorusia - Gjyshërit (Dita e Kujtesës); Liberi - Dita e Falenderimeve; Meksikë, Poloni, Po

Cilat janë prapashtesat formuese zero?
Çfarë është prapashtesa zero është një prapashtesë që nuk shprehet me tinguj në të folur ose me shkronja në të shkruar, por me ndihmën e së cilës formohen fjalë të reja. Metoda e formimit të fjalëve duke përdorur një prapashtesë zero në disa manuale quhet pa prapashtesë, dhe në të tjera - prapashtesë zero. Prapashtesa zero tregohet grafikisht nga &Osla

Kush është një qiramarrës spirancë?
Anchor qiramarrës - qiramarrës kryesor në qendra tregtare, duke tërhequr blerësit drejt tij. Një nga shenjat më të rëndësishme"spirancat" konsiderojnë njohjen e saj midis klientëve, gjë që presupozon promovimin dhe ekzistencën e markës në formatin e një dyqani të veçantë - shitje me pakicë në rrugë, për shembull, si Zara, M-video

Cili është emri i faqes zyrtare të Akademisë Ekonomike Ruse. G.V. Plekhanov (REA)
Më poshtë janë faqet zyrtare të internetit të kryesore universitetet shtetërore Moskë: Moskovski universiteti shtetëror me emrin M.V. Akademia Lomonosov e Zyrës së Prokurorit të Përgjithshëm Federata Ruse Akademia Shtetërore shërbim zjarrfikës Akademia EMERCOM e Rusisë ekonomia kombëtare nën Qeverinë e Akademisë së Punës të Federatës Ruse (ANH) dhe marrëdhëniet shoqërore(ATiSO) Akademik

Cilat festa festohen më 16 maj
16 maji është dita e 136-të e vitit (e 137-ta në vitin e brishtë) sipas kalendarit gregorian. Deri në fund të vitit kanë mbetur edhe 229 ditë. Ngjarjet dhe festat e festuara më 16 maj: Dita Botërore e Përkujtimit të Personave që vdiqën nga SIDA; Dita e Biografëve; Apara Ekadashi në Indi. Ngjarjet fetare Ortodoksia: Dita e Shën Theodosius Pechersk; Nga

Cila është gjeografia e shpërndarjes së barërave të këqija?
Pelin Ambrosia Vjetore, në fund të pranverës. Biologjia dhe morfologjia Kërcelli është 20-200 cm i gjatë, i drejtë, i degëzuar në mënyrë panikulare, në majë, me pubesencë të dobët ose mjaft të fortë. Rrënja është me rrënjë, depërton në tokë deri në një thellësi prej 4 m. Gjethet janë 4-15 cm të gjata, jeshile të errët sipër, pothuajse glabrous, gri-jeshile poshtë, me qime të dendura-pubescent; sipërme

Cilat janë kafshët poikilotermike?
Kafshët poikilotermike janë kafshë me gjak të ftohtë, kafshë me një temperaturë të brendshme të paqëndrueshme të trupit që ndryshon në varësi të temperaturës mjedisi i jashtëm. Kafshët poikilotermike përfshijnë të gjithë jovertebrorët, dhe vertebrorët përfshijnë peshqit, amfibët dhe zvarranikët. Temperatura e trupit të kafshëve poikilotermike është zakonisht vetëm 1-20C më e lartë se temperatura e ambientit

Si të bëni tërheqjet në mënyrë korrekte
tërheqje - ushtrim bazë për muskujt e krahëve, shpinës dhe gjoksit. Tërhiqe lart është ushtrim kyç, duke zhvilluar forcën. Tërheqjet mund të bëhen në çdo kohë dhe pothuajse kudo, ato nuk kërkojnë ndonjë pajisje të veçantë ose të shkoni në palestër, gjë që është shumë e rëndësishme. Tërheqjet në shirit janë më së shumti ushtrim efektiv në

Siç mund ta shihni, kjo shenjë e një ekstremi të një funksioni kërkon ekzistencën e një derivati ​​të paktën në rendin e dytë në pikë.

Shembull.

Gjeni ekstremin e funksionit.

Zgjidhje.

Le të fillojmë me fushën e përkufizimit:

Le të dallojmë funksionin origjinal:

x=1, domethënë kjo është një pikë e ekstremit të mundshëm. Gjejmë derivatin e dytë të funksionit dhe llogarisim vlerën e tij në:

x = 1 x=1 Prandaj, me kushtin e dytë të mjaftueshëm për një ekstrem, - pikë maksimale. Pastaj

- funksioni maksimal.

Ilustrim grafik.

Përgjigje:

Kushti i tretë i mjaftueshëm për ekstremin e një funksioni. Lëreni funksionin y=f(x) ka derivate deri në n -rendi i -te fqinjesise se pikes dhe derivateve deri n+1

Shembull.

-rendit në vetë pikën. Le të jetë. .

Zgjidhje.

Gjeni pikat ekstreme të funksionit

Funksioni origjinal është një funksion racional i tërësishëm;

Le të dallojmë funksionin: Derivati ​​shkon në zero në

Prandaj, këto janë pika të ekstremit të mundshëm. Le të përdorim kushtin e tretë të mjaftueshëm për një ekstrem.

Ne gjejmë derivatin e dytë dhe llogarisim vlerën e tij në pikat e ekstremit të mundshëm (do të heqim llogaritjet e ndërmjetme): Rrjedhimisht, është pika maksimale (për shenjën e tretë të mjaftueshme të ekstremit që kemi n=1

Dhe). Për të zbuluar natyrën e pikave

gjejmë derivatin e tretë dhe llogarisim vlerën e tij në këto pika: Prandaj, a është pika e lakimit të funksionit ( n=1

Mbetet të merremi me çështjen. Gjejmë derivatin e katërt dhe llogarisim vlerën e tij në këtë pikë:

Prandaj, është pika minimale e funksionit.

- funksioni maksimal.

Ilustrim grafik.

Pika maksimale është pika minimale e funksionit.

10. Ekstrema e një funksioni Përkufizimi i një ekstremi

Thirret funksioni y = f(x). në rritje (në rënie) në një interval të caktuar, nëse për x 1< x 2 выполняется неравенство (f(x 1) < f (x 2) (f(x 1) >f (x 2)).

Nëse funksioni i diferencueshëm y = f(x) rritet (zvogëlohet) në një interval, atëherë derivati ​​i tij në këtë interval f " (x)  0

(f " (x)  0).

Pika x O thirrur pikë maksimale lokale (minimale) funksioni f(x), nëse ka një fqinjësi të pikës x O, për të gjitha pikat e të cilave mosbarazimi f(x) ≤ f(x о) (f(x) ≥ f(x о)) është i vërtetë.

Quhen pikët maksimale dhe minimale pika ekstreme, dhe vlerat e funksionit në këto pika janë të tij ekstremet.

Pikat ekstreme

Kushtet e nevojshme për një ekstrem. Nëse pika x Oështë një pikë ekstreme e funksionit f(x), atëherë ose f " (x o) = 0, ose f (x o) nuk ekziston. Pika të tilla quhen kritike, dhe vetë funksioni përcaktohet në pikën kritike. Ekstrema e një funksioni duhet kërkuar ndër pikat e tij kritike.

Kushti i parë i mjaftueshëm. Le x O- pika kritike. Nëse f "(x) kur kalon nëpër një pikë x O ndryshon shenjën plus në minus, pastaj në pikë x O funksioni ka një maksimum, përndryshe ka një minimum. Nëse, gjatë kalimit nëpër pikën kritike, derivati ​​nuk ndryshon shenjë, atëherë në pikën x O nuk ka ekstrem.

Kushti i dytë i mjaftueshëm. Le të ketë funksioni f(x) një derivat f " (x) në afërsi të pikës x O dhe derivati ​​i dytë në vetë pikën x O. Nëse f "(x o) = 0, >0 (<0), то точка x Oështë pika minimale (maksimale) lokale e funksionit f(x). Nëse =0, atëherë duhet të përdorni kushtin e parë të mjaftueshëm ose të përdorni derivate më të lartë.

Në një segment, funksioni y = f(x) mund të arrijë vlerën e tij minimale ose maksimale qoftë në pikat kritike ose në skajet e segmentit.

Shembulli 3.22. Gjeni ekstremin e funksionit f(x) = 2x 3 - 15x 2 + 36x - 14.

Zgjidhje. Meqenëse f "(x) = 6x 2 - 30x +36 = 6(x‑2)(x - 3), atëherë pikat kritike të funksionit x 1 = 2 dhe x 2 = 3. Ekstrema mund të jetë vetëm në Pra, kur kalon në pikën x 1 = 2, derivati ​​ndryshon shenjën e tij nga plus në minus, atëherë në këtë pikë funksioni ka një maksimum kur kalon në pikën x 2 = 3 në plus, pra në pikën x 2 = 3 funksioni ka një minimum, pasi kemi llogaritur vlerat e funksionit në pikat x 1 = 2 dhe x 2 = 3, gjejmë ekstremin e funksionit: maksimumi f(. 2) = 14 dhe minimumi f(3) = 13.

Konsideroni grafikun e një funksioni të vazhdueshëm Lëreni funksionin treguar në figurë.

Vlera e funksionit në një pikë x 1 do të jetë më i madh se vlerat e funksionit në të gjitha pikat fqinje si në të majtë ashtu edhe në të djathtë të x 1. Në këtë rast themi se funksioni ka në pikë x 1 maksimumi. Në pikën x Funksioni 3 padyshim gjithashtu ka një maksimum. Nëse marrim parasysh pikën x 2, atëherë vlera e funksionit në të është më e vogël se të gjitha vlerat fqinje. Në këtë rast themi se funksioni ka në pikë x 2 minimumi. Po kështu për pikën x 4 .

Funksioni Lëreni funksionin në pikën x 0 ka maksimale, nëse vlera e funksionit në këtë pikë është më e madhe se vlerat e tij në të gjitha pikat e një intervali që përmban pikën x 0, d.m.th. nëse ekziston një fqinjësi e tillë e një pike x 0, që është për të gjithë x≠x 0 , që i përket kësaj lagjeje, pabarazia qëndron f(x)<f(x 0 ) .

Funksioni Lëreni funksionin ka minimale në pikën x 0 , nëse ekziston një fqinjësi e tillë e një pike x 0 , kjo është për të gjithë x≠x 0 që i përket kësaj lagjeje, qëndron pabarazia f(x)>f(x 0.

Pikat në të cilat funksioni arrin maksimumin dhe minimumin e tij quhen pika ekstreme, dhe vlerat e funksionit në këto pika quhen ekstreme të funksionit.

Le t'i kushtojmë vëmendje faktit që një funksion i përcaktuar në një segment mund të arrijë maksimumin dhe minimumin e tij vetëm në pikat e përfshira brenda segmentit në shqyrtim.

Vini re se nëse një funksion ka një maksimum në një pikë, kjo nuk do të thotë se në atë pikë funksioni ka vlerën më të madhe në të gjithë domenin e përkufizimit. Në figurën e diskutuar më sipër, funksioni në pikë x 1 ka një maksimum, megjithëse ka pika në të cilat vlerat e funksionit janë më të mëdha se në pikë x 1 . Në veçanti, f(x 1) < f(x 4) d.m.th. minimumi i funksionit është më i madh se maksimumi. Nga përkufizimi i maksimumit rezulton vetëm se kjo është vlera më e madhe e funksionit në pika mjaft afër pikës maksimale.

Teorema 1. (Kushti i domosdoshëm për ekzistencën e një ekstremi.) Nëse funksioni i diferencueshëm Lëreni funksionin ka në pikën x=x 0 ekstrem, atëherë derivati ​​i tij në këtë pikë bëhet zero.

Dëshmi. Le, për definicion, në pikën x Funksioni 0 ka një maksimum. Pastaj, për ngritje mjaft të vogla Δ x ne kemi f(x 0 + Δ x) 0 ) , d.m.th. Por pastaj

Duke kaluar në këto pabarazi në kufirin në Δ x→ 0 dhe duke marrë parasysh se derivati f "(x 0) ekziston, dhe për këtë arsye kufiri në të majtë nuk varet nga mënyra se si Δ x→ 0, marrim: në Δ x → 0 – 0 f"(x 0) ≥ 0 a në Δ x → 0 + 0 f"(x 0) ≤ 0. Meqenëse f"(x 0) përcakton një numër, atëherë këto dy pabarazi janë të pajtueshme vetëm nëse f"(x 0) = 0.

Teorema e provuar thotë se pikat maksimale dhe minimale mund të gjenden vetëm midis atyre vlerave të argumentit në të cilat derivati ​​bëhet zero.

Shqyrtuam rastin kur një funksion ka një derivat në të gjitha pikat e një segmenti të caktuar. Cila është situata në rastet kur derivati ​​nuk ekziston? Le të shohim shembuj.

Shembuj.

1. y=|x|.

   Funksioni nuk ka derivat në pikë x=0 (në këtë pikë grafiku i funksionit nuk ka një tangjente të përcaktuar), por në këtë pikë funksioni ka një minimum, pasi y(0)=0, dhe për të gjitha x≠ 0y > 0.



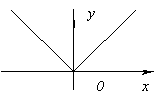
Funksioni nuk ka derivat në x=0, pasi shkon në pafundësi në x=0. Por në këtë pikë funksioni ka një maksimum.



Funksioni nuk ka derivat në x=0, pasi në x→0. Në këtë pikë funksioni nuk ka as një maksimum dhe as një minimum. Vërtet, f(x)=0 dhe në x<0f(x)<0, а при x>0f(x)>0.



Kështu, nga shembujt e dhënë dhe nga teorema e formuluar, del qartë se një funksion mund të ketë një ekstrem vetëm në dy raste: 1) në pikat ku derivati ​​ekziston dhe është i barabartë me zero; 2) në pikën ku derivati ​​nuk ekziston.

Megjithatë, nëse në një moment x 0 ne e dimë këtë f" (x 0 ) =0, atëherë nuk mund të konkludohet nga kjo se në pikën x 0 funksioni ka një ekstrem.

Për shembull. .



Por periudha x=0 nuk është një pikë ekstreme, pasi në të majtë të kësaj pike vlerat e funksionit janë të vendosura poshtë boshtit kau, dhe në të djathtë sipër.

Quhen vlerat e një argumenti nga fusha e një funksioni në të cilin derivati ​​i funksionit zhduket ose nuk ekziston. pikat kritike.




Nga të gjitha sa më sipër, rezulton se pikat ekstreme të funksionit janë ndër pikat kritike, dhe, megjithatë, jo çdo pikë kritike është një pikë ekstreme. Prandaj, për të gjetur ekstremin e një funksioni, duhet të gjeni të gjitha pikat kritike të funksionit dhe më pas të ekzaminoni secilën prej këtyre pikave veçmas për maksimumin dhe minimumin. Teorema e mëposhtme i shërben këtij qëllimi.

Teorema 2. (Kusht i mjaftueshëm për ekzistencën e një ekstremi.) Le të jetë funksioni i vazhdueshëm në një interval që përmban pikën kritike x 0, dhe është i diferencueshëm në të gjitha pikat e këtij intervali (përveç, ndoshta, vetë pikës x 0). Nëse, kur lëviz nga e majta në të djathtë përmes kësaj pike, derivati ​​ndryshon shenjën nga plus në minus, atëherë në pikën x = x Funksioni 0 ka një maksimum. Nëse, kur kaloni x 0 nga e majta në të djathtë, derivati ​​ndryshon shenjën nga minus në plus, atëherë funksioni ka një minimum në këtë pikë.

Kështu, nëse

Dëshmi. Së pari, le të supozojmë se kur kalojmë x 0 derivati ​​ndryshon shenjën nga plus në minus, d.m.th. para të gjithëve x, afër pikës x 0 f "(x)> 0 për x< x 0 , f" (x)< 0 për x>x 0 . Le të zbatojmë teoremën e Lagranzhit për ndryshimin f(x) - f(x 0 ) = f "(c) (x- x 0), ku c shtrihet mes x Dhe x 0 .

1. Le x< x 0 . Pastaj c< x 0 dhe f "(c)> 0. Kjo është arsyeja pse f "(c) (x- x 0)< 0 dhe prandaj

   f(x) - f(x 0 )< 0, d.m.th. f(x)< f(x 0 ).

2. Le x > x 0 . Pastaj c>x 0 dhe f" (c)< 0. Mjetet f "(c) (x- x 0)< 0. Kjo është arsyeja pse f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .

Kështu, për të gjitha vlerat x mjaft afër x 0 f(x)< f(x 0 ) . Dhe kjo do të thotë se në pikën x Funksioni 0 ka një maksimum.

Pjesa e dytë e teoremës minimale vërtetohet në mënyrë të ngjashme.



Le të ilustrojmë kuptimin e kësaj teoreme në figurë. Le f" (x 1 ) =0 dhe për cilindo x, mjaft afër x 1, pabarazitë janë të kënaqura

f" (x)< 0 në x< x 1 , f "(x)> 0 në x>x 1 .

Pastaj në të majtë të pikës x 1 funksioni rritet dhe zvogëlohet në të djathtë, pra, kur x = x 1 funksion shkon nga rritja në zvogëlim, domethënë ka një maksimum.

Në mënyrë të ngjashme, ne mund të shqyrtojmë pikat x 2 dhe x 3 .


Të gjitha sa më sipër mund të përshkruhen skematikisht në foto:

Rregulla për studimin e funksionit y=f(x) për ekstremin

1. Gjeni domenin e një funksioni f(x).
2. Gjeni derivatin e parë të një funksioni f" (x).
3. Përcaktoni pikat kritike për këtë:
   1. gjeni rrënjët reale të ekuacionit f" (x)=0;
   2. gjeni të gjitha vlerat x për të cilat derivati f" (x) nuk ekziston.
4. Përcaktoni shenjën e derivatit majtas dhe djathtas të pikës kritike. Meqenëse shenja e derivatit mbetet konstante ndërmjet dy pikave kritike, mjafton të përcaktohet shenja e derivatit në një pikë në të majtë dhe një pikë në të djathtë të pikës kritike.
5. Llogaritni vlerën e funksionit në pikat ekstreme.

Shembuj. Eksploroni funksionet për minimumin dhe maksimumin.




VLERA MAKSIMALE DHE MË E VOGLA E NJË FUNKSIONI NË NJË Segment

Më i madhi vlera e një funksioni në një interval është më e madhja nga të gjitha vlerat e tij në këtë interval, dhe më i vogli– më e vogla nga të gjitha vlerat e saj.

Merrni parasysh funksionin Lëreni funksionin e vazhdueshme në segmentin [ a, b]. Siç dihet, një funksion i tillë arrin vlerat e tij maksimale dhe minimale, qoftë në kufirin e segmentit ose brenda tij. Nëse vlera më e madhe ose më e vogël e një funksioni arrihet në një pikë të brendshme të segmentit, atëherë kjo vlerë është maksimumi ose minimumi i funksionit, domethënë arrihet në pikat kritike.

Kështu, marrim sa vijon rregull për gjetjen e vlerave më të mëdha dhe më të vogla të një funksioni në një segment a, b] :

1. Gjeni të gjitha pikat kritike të funksionit në intervalin ( a, b) dhe llogaritni vlerat e funksionit në këto pika.
2. Llogaritni vlerat e funksionit në skajet e segmentit kur x = a, x = b.
3. Nga të gjitha vlerat e marra, zgjidhni më të madhin dhe më të voglin.

Hyrje

Në shumë fusha të shkencës dhe në aktivitete praktike, shpesh duhet të merret me problemin e gjetjes së ekstremit të një funksioni. Fakti është se shumë teknikë, ekonomikë etj. proceset modelohen nga një funksion ose disa funksione që varen nga variablat - faktorë që ndikojnë në gjendjen e fenomenit që modelohet. Kërkohet të gjendet ekstremi i funksioneve të tilla për të përcaktuar gjendjen optimale (racionale) dhe kontrollin e procesit. Pra, në ekonomi, problemet e minimizimit të kostove ose maksimizimit të fitimeve shpesh zgjidhen - problemi mikroekonomik i kompanisë. Në këtë punim, ne nuk marrim parasysh çështjet e modelimit, por konsiderojmë vetëm algoritme për kërkimin e ekstremeve të funksioneve në versionin më të thjeshtë, kur nuk vendosen kufizime mbi variablat (optimizimi i pakushtëzuar), dhe ekstremi kërkohet vetëm për një funksion objektiv.

EKSTREMA E FUNKSIONIT

Konsideroni grafikun e një funksioni të vazhdueshëm Lëreni funksionin treguar në figurë. Vlera e funksionit në një pikë x 1 do të jetë më i madh se vlerat e funksionit në të gjitha pikat fqinje si në të majtë ashtu edhe në të djathtë të x 1. Në këtë rast themi se funksioni ka në pikë x 1 maksimumi. Në pikën x Funksioni 3 padyshim gjithashtu ka një maksimum. Nëse marrim parasysh pikën x 2, atëherë vlera e funksionit në të është më e vogël se të gjitha vlerat fqinje. Në këtë rast themi se funksioni ka në pikë x 2 minimumi. Po kështu për pikën x 4 .

Funksioni Lëreni funksionin në pikën x 0 ka maksimale, nëse vlera e funksionit në këtë pikë është më e madhe se vlerat e tij në të gjitha pikat e një intervali që përmban pikën x 0, d.m.th. nëse ekziston një fqinjësi e tillë e një pike x 0, që është për të gjithë x ≠x 0 , që i përket kësaj lagjeje, pabarazia qëndron f(x) <f(x 0 ) .

Funksioni Lëreni funksionin ka minimale në pikën x 0 , nëse ekziston një fqinjësi e tillë e një pike x 0 , kjo është për të gjithë x ≠x 0 që i përket kësaj lagjeje, qëndron pabarazia f(x) >f(x 0 .

Pikat në të cilat funksioni arrin maksimumin dhe minimumin e tij quhen pika ekstreme, dhe vlerat e funksionit në këto pika quhen ekstreme të funksionit.

Le t'i kushtojmë vëmendje faktit që një funksion i përcaktuar në një segment mund të arrijë maksimumin dhe minimumin e tij vetëm në pikat e përfshira brenda segmentit në shqyrtim.

Vini re se nëse një funksion ka një maksimum në një pikë, kjo nuk do të thotë se në atë pikë funksioni ka vlerën më të madhe në të gjithë domenin e përkufizimit. Në figurën e diskutuar më sipër, funksioni në pikë x 1 ka një maksimum, megjithëse ka pika në të cilat vlerat e funksionit janë më të mëdha se në pikë x 1 . Në veçanti, f (x 1) < f (x 4) d.m.th. minimumi i funksionit është më i madh se maksimumi. Nga përkufizimi i maksimumit rezulton vetëm se kjo është vlera më e madhe e funksionit në pika mjaft afër pikës maksimale.

Teorema 1. (Një kusht i domosdoshëm për ekzistencën e një ekstremi.) Nëse funksioni i diferencueshëm Lëreni funksionin ka në pikën x=x 0 ekstrem, atëherë derivati ​​i tij në këtë pikë bëhet zero.

Dëshmi. Le, për definicion, në pikën x Funksioni 0 ka një maksimum. Pastaj, për ngritje mjaft të vogla Δ x ne kemi f(x 0 + Δ x) 0 ) , d.m.th.

Por pastaj

Duke kaluar në këto pabarazi në kufirin në Δ x→ 0 dhe duke marrë parasysh se derivati f "(x 0) ekziston, dhe për këtë arsye kufiri në të majtë nuk varet nga mënyra se si Δ x→ 0, marrim: në Δ x → 0 – 0 f" (x 0) ≥ 0 a në Δ x → 0 + 0 f" (x 0) ≤ 0. Meqenëse f" (x 0) përcakton një numër, atëherë këto dy pabarazi janë të pajtueshme vetëm nëse f" (x 0) = 0.

Teorema e provuar thotë se pikat maksimale dhe minimale mund të gjenden vetëm midis atyre vlerave të argumentit në të cilat derivati ​​bëhet zero.

Shqyrtuam rastin kur një funksion ka një derivat në të gjitha pikat e një segmenti të caktuar. Cila është situata në rastet kur derivati ​​nuk ekziston? Le të shohim shembuj.

y =|x |.

Funksioni nuk ka derivat në pikë x=0 (në këtë pikë grafiku i funksionit nuk ka një tangjente të përcaktuar), por në këtë pikë funksioni ka një minimum, pasi y(0)=0, dhe për të gjitha x ≠ 0y > 0.

nuk ka derivat në x=0, pasi shkon në pafundësi në x=0. Por në këtë pikë funksioni ka një maksimum. nuk ka derivat në x=0, pasi në x→0. Në këtë pikë funksioni nuk ka as një maksimum dhe as një minimum. Vërtet, f(x)=0 dhe në x <0f(x) <0, а при x >0f(x) >0.

Kështu, nga shembujt e dhënë dhe nga teorema e formuluar, del qartë se një funksion mund të ketë një ekstrem vetëm në dy raste: 1) në pikat ku derivati ​​ekziston dhe është i barabartë me zero; 2) në pikën ku derivati ​​nuk ekziston.

Megjithatë, nëse në një moment x 0 ne e dimë këtë f" (x 0 ) =0, atëherë nuk mund të konkludohet nga kjo se në pikën x 0 funksioni ka një ekstrem.

Për shembull.

.

Por periudha x=0 nuk është një pikë ekstreme, pasi në të majtë të kësaj pike vlerat e funksionit janë të vendosura poshtë boshtit kau, dhe në të djathtë sipër.

Quhen vlerat e një argumenti nga fusha e një funksioni në të cilin derivati ​​i funksionit zhduket ose nuk ekziston. pikat kritike .

Nga të gjitha sa më sipër, rezulton se pikat ekstreme të funksionit janë ndër pikat kritike, dhe, megjithatë, jo çdo pikë kritike është një pikë ekstreme. Prandaj, për të gjetur ekstremin e një funksioni, duhet të gjeni të gjitha pikat kritike të funksionit dhe më pas të ekzaminoni secilën prej këtyre pikave veçmas për maksimumin dhe minimumin. Teorema e mëposhtme i shërben këtij qëllimi.

Teorema 2. (Një kusht i mjaftueshëm për ekzistencën e një ekstremi.) Le të jetë funksioni i vazhdueshëm në një interval që përmban pikën kritike x 0, dhe është i diferencueshëm në të gjitha pikat e këtij intervali (përveç, ndoshta, vetë pikës x 0). Nëse, kur lëviz nga e majta në të djathtë përmes kësaj pike, derivati ​​ndryshon shenjën nga plus në minus, atëherë në pikën x = x Funksioni 0 ka një maksimum. Nëse, kur kaloni x 0 nga e majta në të djathtë, derivati ​​ndryshon shenjën nga minus në plus, atëherë funksioni ka një minimum në këtë pikë.

Kështu, nëse

f" (x)>0 në x <x 0 dhe f" (x)< 0 në x>x 0, atëherë x 0 – pikë maksimale;

në x <x 0 dhe f "(x)> 0 në x>x 0, atëherë x 0 - pikë minimale.

Dëshmi. Së pari, le të supozojmë se kur kalojmë x 0 derivati ​​ndryshon shenjën nga plus në minus, d.m.th. para të gjithëve x, afër pikës x 0 f "(x)> 0 për x< x 0 , f" (x)< 0 për x>x 0 . Le të zbatojmë teoremën e Lagranzhit për ndryshimin f(x) - f(x 0 ) = f "(c) (x- x 0), ku c shtrihet mes x Dhe x 0 .

Le x< x 0 . Pastaj c< x 0 dhe f "(c)> 0. Kjo është arsyeja pse f "(c) (x- x 0)< 0 dhe prandaj

f(x) - f(x 0 )< 0, d.m.th. f(x)< f(x 0 ).

Le x > x 0 . Pastaj c>x 0 dhe f" (c)< 0. Mjetet f "(c) (x- x 0)< 0. Kjo është arsyeja pse f(x) - f(x 0 ) <0,т.е.f(x) < f(x 0 ) .

Kështu, për të gjitha vlerat x mjaft afër x 0 f(x) < f(x 0 ) . Dhe kjo do të thotë se në pikën x Funksioni 0 ka një maksimum.

Pjesa e dytë e teoremës minimale vërtetohet në mënyrë të ngjashme.

Le të ilustrojmë kuptimin e kësaj teoreme në figurë. Le f" (x 1 ) =0 dhe për cilindo x, mjaft afër x 1, pabarazitë janë të kënaqura

f" (x)< 0 në x< x 1 , f "(x)> 0 në x>x 1 .

Pastaj në të majtë të pikës x 1 funksioni rritet dhe zvogëlohet në të djathtë, pra, kur x = x 1 funksion shkon nga rritja në zvogëlim, domethënë ka një maksimum.

Në mënyrë të ngjashme, ne mund të shqyrtojmë pikat x 2 dhe x 3 .

Të gjitha sa më sipër mund të përshkruhen skematikisht në foto:

Rregulla për studimin e funksionit y=f(x) për ekstremin

Gjeni domenin e një funksioni f(x).

Gjeni derivatin e parë të një funksioni f" (x) .

Përcaktoni pikat kritike për këtë:

gjeni rrënjët reale të ekuacionit f" (x) =0;

gjeni të gjitha vlerat x për të cilat derivati f" (x) nuk ekziston.

Përcaktoni shenjën e derivatit majtas dhe djathtas të pikës kritike. Meqenëse shenja e derivatit mbetet konstante ndërmjet dy pikave kritike, mjafton të përcaktohet shenja e derivatit në një pikë në të majtë dhe një pikë në të djathtë të pikës kritike.

Llogaritni vlerën e funksionit në pikat ekstreme.

Ky është një seksion mjaft interesant i matematikës, me të cilin ndeshen absolutisht të gjithë të diplomuarit dhe studentët. Megjithatë, jo të gjithë e pëlqejnë matanin. Disa nuk mund të kuptojnë as gjërat themelore si një studim funksioni në dukje standard. Ky artikull synon të korrigjojë një shkelje të tillë. Dëshironi të mësoni më shumë rreth analizës së funksionit? Dëshironi të dini se cilat janë pikat ekstreme dhe si t'i gjeni ato? Atëherë ky artikull është për ju.

Studimi i grafikut të një funksioni

Së pari, ia vlen të kuptoni pse duhet të analizoni fare grafikun. Ka funksione të thjeshta që nuk janë të vështira për t'u vizatuar. Një shembull i mrekullueshëm i një funksioni të tillë është një parabolë. Nuk do të jetë e vështirë të vizatoni një grafik. Gjithçka që nevojitet është, duke përdorur një transformim të thjeshtë, për të gjetur numrat në të cilët funksioni merr vlerën 0. Dhe në parim, kjo është gjithçka që duhet të dini për të vizatuar një grafik të një parabole.

Por, çka nëse funksioni që na duhet të grafikojmë është shumë më kompleks? Meqenëse vetitë e funksioneve komplekse nuk janë mjaft të dukshme, është e nevojshme të kryhet një analizë e tërë. Vetëm pas kësaj funksioni mund të përshkruhet grafikisht. Si ta bëni këtë? Përgjigjen për këtë pyetje mund ta gjeni në këtë artikull.

Plani i analizës së funksionit

Gjëja e parë që duhet të bëjmë është të bëjmë një studim sipërfaqësor të funksionit, gjatë të cilit gjejmë domenin e përkufizimit. Pra, le të fillojmë me radhë. Fusha e përkufizimit është grupi i vlerave me të cilat përcaktohet funksioni. E thënë thjesht, këta janë numrat që mund të përdoren në një funksion në vend të x. Për të përcaktuar shtrirjen, thjesht duhet të shikoni rekordin. Për shembull, është e qartë se funksioni y (x) = x 3 + x 2 - x + 43 ka një fushë përkufizimi që është bashkësia e numrave realë. Epo, me një funksion si (x 2 - 2x)/x gjithçka është pak më ndryshe. Meqenëse numri në emërues nuk duhet të jetë i barabartë me 0, domeni i përcaktimit të këtij funksioni do të jenë të gjithë numrat realë përveç zeros.

Tjetra, ju duhet të gjeni të ashtuquajturat zero të funksionit. Këto janë vlerat e argumenteve në të cilat i gjithë funksioni merr vlerën zero. Për ta bërë këtë, është e nevojshme të barazoni funksionin me zero, ta konsideroni atë në detaje dhe të kryeni disa transformime. Le të marrim funksionin tashmë të njohur y(x) = (x 2 - 2x)/x. Nga kursi i shkollës dimë se një thyesë është e barabartë me 0 kur numëruesi është i barabartë me zero. Prandaj, ne e hedhim poshtë emëruesin dhe fillojmë të punojmë me numëruesin, duke e barazuar atë me zero. Marrim x 2 - 2x = 0 dhe vendosim x jashtë kllapave. Prandaj x (x - 2) = 0. Si rezultat, ne gjejmë se funksioni ynë është i barabartë me zero kur x është i barabartë me 0 ose 2.

Kur studiojnë grafikun e një funksioni, shumë njerëz hasin probleme në formën e pikave ekstreme. Dhe është e çuditshme. Në fund të fundit, ekstremet janë një temë mjaft e thjeshtë. Nuk më besoni? Shihni vetë duke lexuar këtë pjesë të artikullit, në të cilin do të flasim për pikët minimale dhe maksimale.

Së pari, ia vlen të kuptoni se çfarë është një ekstrem. Një ekstrem është vlera kufi që arrin një funksion në një grafik. Rezulton se ekzistojnë dy vlera ekstreme - maksimale dhe minimale. Për qartësi, mund të shikoni foton e mësipërme. Në zonën e studiuar, pika -1 është maksimumi i funksionit y (x) = x 5 - 5x, dhe pika 1, në përputhje me rrethanat, është minimumi.

Gjithashtu, mos i ngatërroni konceptet. Pikat ekstreme të një funksioni janë ato argumente në të cilat një funksion i caktuar fiton vlera ekstreme. Nga ana tjetër, ekstremi është vlera e minimumeve dhe maksimaleve të një funksioni. Për shembull, merrni përsëri figurën e mësipërme. -1 dhe 1 janë pikat ekstreme të funksionit, dhe 4 dhe -4 janë vetë ekstremet.

Gjetja e pikave ekstreme

Por si i gjeni pikat ekstreme të një funksioni? Gjithçka është mjaft e thjeshtë. Gjëja e parë që duhet të bëni është të gjeni derivatin e ekuacionit. Le të themi se kemi marrë detyrën: “Gjeni pikat ekstreme të funksionit y (x), x është argumenti për qartësi, le të marrim funksionin y (x) = x 3 + 2x 2 + x + 54. Të dallojmë dhe. merrni ekuacionin e mëposhtëm: 3x 2 + 4x + 1. Si rezultat, ne kemi një ekuacion standard kuadratik, që duhet bërë më pas është ta barazojmë atë me zero dhe të gjejmë rrënjët meqenëse diskriminuesi është më i madh se zero = 16 - 12 = 4), ky ekuacion përcaktohet nga dy rrënjë dhe i marrim ato: 1/3 dhe -1. Megjithatë, si mund të përcaktoni është kush është maksimumi dhe cila është minimumi Për ta bërë këtë, duhet të merrni pikën fqinje dhe të merrni numrin -2, i cili ndodhet në të majtë përgjatë vijës së koordinatave? 1. Zëvendësoni këtë vlerë në ekuacionin tonë y(-2) = 12 - 8 + 1 = 5. Si rezultat, ne marrim një numër pozitiv Kjo do të thotë se në intervalin nga 1/3 në -1. Kjo, nga ana tjetër, do të thotë që në intervalet nga minus pafundësi në 1/3 dhe nga -1 në plus pafundësi funksioni zvogëlohet. Kështu, mund të konkludojmë se numri 1/3 është pika minimale e funksionit në intervalin e studiuar, dhe -1 është pika maksimale.

Vlen gjithashtu të theksohet se Provimi i Unifikuar i Shtetit kërkon jo vetëm gjetjen e pikëve ekstreme, por edhe kryerjen e një lloj operacioni me to (shtim, shumëzim, etj.). Është për këtë arsye që ia vlen t'i kushtohet vëmendje e veçantë kushteve të problemit. Në fund të fundit, për shkak të pavëmendjes, ju mund të humbni pikë.