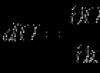Combinatorics is a branch of mathematics devoted to solving problems of choosing and arranging elements of a certain set in accordance with given rules. Combinatorics studies combinations and permutations of objects, the arrangement of elements that has given properties. A common question in combinatorial problems ah: in how many ways….
Combinatorial problems also include problems of constructing magic squares, decoding and encoding problems.
The birth of combinatorics as a branch of mathematics is associated with the works of the great 17th century French mathematicians Blaise Pascal (1623–1662) and Pierre Fermat (1601–1665) on the theory gambling. These works contained principles for determining the number of combinations of elements finite set. Since the 50s of the 20th century, interest in combinatorics has been revived due to the rapid development of cybernetics.
The basic rules of combinatorics are sum rule And rule works.
- Sum Rule
If some element A can be selected n ways, and element B can be selected m ways, then the choice “either A or B” can be made n+ m ways.
For example, If there are 5 apples and 6 pears on a plate, then one fruit can be chosen in 5 + 6 = 11 ways.
- Product rule
If element A can be selected n ways, and element B can be selected m ways, then a pair A and B can be selected n m ways.
For example, if there are 2 different envelopes and 3 different stamps, then you can choose the envelope and stamp in 6 ways (2 3 = 6).
The product rule is also true when considering elements of several sets.
For example, if there are 2 different envelopes, 3 different stamps and 4 different postcards, then you can choose the envelope, stamp and postcard in 24 ways (2 3 4 = 24).
Product of all natural numbers from 1 to n inclusive is called n - factorial and is denoted by the symbol n!
n! = 1 2 3 4 … n.
For example, 5! = 1 2 3 4 5 = 120.
For example, if there are 3 balls - red, blue and green, then you can put them in a row in 6 ways (3 2 1 = 3! = 6).
Sometimes a combinatorial problem is solved by constructing tree possible options .
For example, let's decide previous task about 3 balls by constructing a tree.
Workshop on solving problems in combinatorics.
CHALLENGES and solutions
1. There are 6 apples, 5 pears and 4 plums in a vase. How many options are there for choosing one fruit?
Answer: 15 options.
2. How many options are there for purchasing one rose if they sell 3 scarlet, 2 scarlet and 4 yellow roses?
Answer: 9 options.
3. Five roads lead from city A to city B, and three roads lead from city B to city C. How many paths through B lead from A to C?
![]()
Answer: 15 ways.
4. In how many ways can you make a pair of one vowel and one consonant of the word “shawl”?
vowels: a, o – 2 pcs.
consonants: p, l, t, k – 4 pcs.Answer: 8 ways.
5. How many dance couples can be made from 8 boys and 6 girls?
Answer: 48 pairs.
6. There are 4 first courses and 7 second courses in the dining room. How many different two-course lunch options can you order?
Answer: 28 options.
7. How many different double digit numbers can it be made using the numbers 1, 4 and 7 if the numbers can be repeated?
1 digit – 3 ways
2 digit – 3 ways
3 digit – 3 waysAnswer: 9 different two-digit numbers.
8. How many different three-digit numbers can be made using the numbers 3 and 5, if the numbers can be repeated?
1 digit – 2 ways
2nd digit – 2 ways
3rd digit – 2 waysAnswer: 8 different numbers.
9. How many different two-digit numbers can be made from the digits 0, 1, 2, 3, if the digits can be repeated?
1 digit – 3 ways
2 digit – 4 waysAnswer: 12 different numbers.
10. How many three-digit numbers are there in which all digits are even?
Even numbers – 0, 2, 4, 6, 8.
1 digit – 4 ways
2 digit – 5 ways
3 digit – 5 waysAnswer: There are 100 numbers.
11. How many even three-digit numbers are there?
1 digit – 9 ways (1, 2, 3, 4, 5, 6, 7, 8, 9)
2nd digit – 10 ways (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
3rd digit – 5 ways (0, 2, 4, 6, 8)9 10 5 = 450
Answer: There are 450 numbers.
12. How many different three-digit numbers can be made from three different numbers 4, 5, 6?
1 digit – 3 ways
2nd digit – 2 ways
3rd digit – 1st wayAnswer: 6 different numbers.
13. In how many ways can the vertices of a triangle be designated using the letters A, B, C, D?
1 top – 4 ways
2nd top – 3 ways
3rd top – 2 waysAnswer: 24 ways.
14. How many different three-digit numbers can be made from the digits 1, 2, 3, 4, 5, provided that not a single digit is repeated?
1 digit – 5 ways
2 digit – 4 ways
3 digit – 3 waysAnswer: 60 different numbers.
15. How many different three-digit numbers less than 400 can be made from the digits 1, 3, 5, 7, 9, if any of these digits can be used only once?
1 digit – 2 ways
2 digit – 4 ways
3 digit – 3 waysAnswer: 24 different numbers.
16. In how many ways can you make a flag consisting of three horizontal stripes? various colors, if there is material in six colors?
1 lane – 6 ways
2 lane – 5 ways
3 lane – 4 waysAnswer: 120 ways.
17. 8 people are selected from the class who have best results on the run. In how many ways can they be made into a team of three people to participate in the relay?
1 person – 8 ways
2 people – 7 ways
3 people – 6 waysAnswer: 336 ways.
18. On Thursday in the first grade there should be four lessons: writing, reading, mathematics and physical education. How many different schedule options can you create for this day?
1 lesson – 4 ways
Lesson 2 – 3 ways
Lesson 3 – 2 ways
Lesson 4 – method 14 3 2 1 = 24
Answer: 24 options.
19. In the fifth grade, 8 subjects are studied. How many different schedule options can be created for Monday, if there should be 5 lessons on this day and all the lessons are different?
1 lesson – 8 options
Lesson 2 – 7 options
Lesson 3 – 6 options
Lesson 4 – 5 options
Lesson 5 – 4 options8 7 6 5 4 = 6720
Answer: 6720 options.
20. The code for the safe is made up of five different numbers. How many different options for creating a cipher?
1 digit – 5 ways
2 digit – 4 ways
3 digit – 3 ways
4 digit – 2 ways
5 digit – 1 way5 4 3 2 1 = 120
Answer: 120 options.
21. In how many ways can 6 people be seated at a table with 6 cutlery?
6 5 4 3 2 1 = 720
Answer: 720 ways.
22. How many variants of seven-digit telephone numbers can be formed if you exclude numbers starting with zero and 9?
1 digit – 8 ways
2 digit – 10 ways
3 digit – 10 ways
4 digit – 10 ways
5 digit – 10 ways
6 digit – 10 ways
7 digit – 10 ways8 10 10 10 10 10 10 = 8.000.000
Answer: 8,000,000 options.
23. telephone exchange serves subscribers whose telephone numbers consist of 7 digits and begin with 394. How many subscribers is this station designed for?
Phone number 394
10 10 10 10 = 10.000
Answer: 10,000 subscribers.
24. There are 6 pairs of gloves various sizes. In how many ways can one glove be selected from them? left hand and one glove for right hand so these gloves come in different sizes?
Left gloves - 6 ways
Right gloves - 5 ways (6th glove is the same size as the left one)Answer: 30 ways.
25. The numbers 1, 2, 3, 4, 5 make up five-digit numbers in which all the digits are different. How many of these even numbers?
5th digit – 2 ways (two even digits)
4 digit – 4 ways
3 digit – 3 ways
2nd digit – 2 ways
1 digit – 1 way2 4 3 2 1 = 48
Answer: 48 even numbers.
26. How many four-digit numbers are there, made up of odd digits and divisible by 5?
Odd numbers – 1, 3, 5, 7, 9.
Of these, they are divided into 5 – 5.
4 digit – 1 way (digit 5)
3 digit – 4 ways
2 digit – 3 ways
1 digit – 2 ways1 4 3 2 = 24
Answer: 24th.
27. How many exist five digit numbers, whose third digit is 7, the last digit is even?
1 digit – 9 ways (all except 0)
2 digit – 10 ways
3 digit – 1 way (digit 7)
4 digit – 10 ways
5 digit – 5 ways (0, 2, 4, 6, 8)9 10 1 10 5 = 4500
Answer: 4500 numbers.
28. How many six-digit numbers are there in which the second digit is 2, the fourth is 4, the sixth is 6, and all the rest are odd?
1 digit – 5 options (from 1, 3, 5, 7, 9)
2 digit – 1 option (digit 2)
3rd digit – 5 options
4 digit – 1 option (digit 4)
5 digit – 5 options
6 digit – 1 option (digit 6)5 1 5 1 5 1 = 125
Answer: 125 numbers.
29.How many different numbers less than a million can be written using the numbers 8 and 9?
Single digits – 2
Double digits – 2 2 = 4
Three-digit numbers – 2 2 2 = 8
Four-digit numbers – 2 2 2 2 =16
Five-digit – 2 2 2 2 2 = 32
Six-digit – 2 2 2 2 2 2 = 64Total: 2 + 4 + 8 + 16 + 32 + 64 = 126
Answer: 126 numbers.
30. There are 11 people in the football team. You need to choose a captain and his deputy. In how many ways can this be done?
Captain - 11 ways
Deputy - 10 waysAnswer: 110 ways.
31.There are 30 people in the class. In how many ways can you choose the headman and the person responsible for travel tickets?
Headman - 30 ways
Answer. for tickets - 29 waysAnswer: 870 ways.
32. 12 boys, 10 girls and 2 teachers are participating in the hike. How many options for groups of three people on duty (1 boy, 1 girl, 1 teacher) can be formed?
12 10 2 = 240
Answer: 240 ways.
33. How many combinations of four letters of the Russian alphabet (there are only 33 letters in the alphabet) can be made, provided that 2 adjacent letters are different?
Task 1. Eight students shook hands. How many handshakes were there?
Solution. A “subset” consisting of two students (m=2) participates in the handshake, while the entire set of students is 8 people (n=8). Since the order is not important in the handshake process, we choose a formula for the number of combinations:
Task. In how many ways can a three-color striped flag be made from five pieces of material of different colors?
Solution. The order is important, since rearranging the matter within the three-color flag indicates different countries. Therefore, we choose the formula for the number of placements without repetitions, where the set of pieces of matter is n = 5, and the subset of colors is m = 3:
![]()
Task 2. How many dictionaries must be published to be able to translate from any of the six languages into any of them?
Solution. The set includes 6 languages n=6. Since translation is a relationship between two languages, then m = 2, and the order is important, since, for example, Russian-English and English-Russian dictionaries have various applications. Therefore, we choose placements without repetitions:
![]()
Task 3. How many options are there for creating a schedule for Monday if students have 9 subjects, and on Monday there are 4 pairs of classes, and the subjects are not repeated?
Solution. a) For students, the order is not important, so we choose the formula for the number of combinations:
![]()
b) For teachers, order is important, so we choose a placement formula without repetition:
![]()
Task 4. In how many ways can nine books be arranged on a bookshelf, among which is a three-volume book by A.S. Pushkin?
Solution.
Since the three volumes included in a three-volume set must stand side by side, and in increasing order of number to the right, we consider them as one element of a given set, in which there are 6 more elements. Therefore, we choose permutations without repetitions in a set containing seven elements:
P 7 = 7! = 5040
Task 5. In how many ways can you assign three people on duty in a group of 30 people?
Solution.
a) If their role in the duty process is the same, then the order is not important, so we choose combinations without repetition:
From 3 30 = 30! / 3!27! = 4060
b) If the order is important, i.e. during their duty functional responsibilities are different, then using the placement formula without repetition we have:
And 3 30 = 30! / 27! = 24360
Task 6. How many six-digit telephone numbers are there for which: a) any digits are possible; b) are all numbers different?
Solution.
a) 1. Since any digits are possible in a six-digit dialing of a telephone number, any of the 10 digits from 0 to 9 can appear in each of the six places. It is necessary to select from all possible ten digits only those six that will be used for six-digit telephone numbers. Since the order of the digits in recording telephone numbers is important, using the placement formula with repetitions we have:
A 10 6 = 10 6 = 1000000
2. As you know, there are no six-digit numbers starting with zero, so you need to count their number and subtract it from the total number of combinations. We will find the number of numbers whose first digit is 0 using the placement formula with repetitions, “fixing” zero, i.e. in each of the other five possible places any of the ten digits from
0 to 9. Then the number of such combinations:
A 10 5 = 10 5 = 100000
3. The total number of six-digit telephone numbers, which can have any, including repeating, digits, is equal to the difference:
A 10 6 – A 10 5 = 10 6 – 10 5 = 1000000 – 100000 = 900000
b) 1. Now let all the numbers in a six-digit set be different. Of all the possible ten digits, it is necessary to select only those six that are used for six-digit telephone numbers, and no digit is repeated. Then, according to the placement formula without repetitions, we have:
And 10 6 = 10! / (10 – 6)! = 5x6x7x8x9x10 = 151200
2. Since there are no six-digit numbers starting with zero, you need to count their number and subtract it from the total number of combinations. We will find the number of numbers whose first digit is 0 using the placement formula without repetitions, “fixing zero”, i.e. in each of the five remaining possible places there may be numbers from 0 to 9. Then we will find the number of such combinations using the placement formula without repetition. We have:
And 10 5 = 10! / (10-5)! = 6x7x8x9x10 = 30240
3. The total number of six-digit telephone numbers that cannot have repeating digits is equal to the difference:
A 10 6 – A 10 5 = 10 6 – 10 5 = 151200 – 30240 = 120960
Task 7. In how many ways can a delegation of three people be selected, choosing them among four married couples, if:
a) the delegation includes any three of these eight people;
b) the delegation must consist of two women and one man;
Does the delegation not include members of the same family?
Solution.
a) The order is not important:
From 8 3 = 8! / 3! 5! = 56
b) Let's choose two women from the available 4 C 4 2 ways and one man from the 4 C 4 1 ways. According to the product rule ( And man, And two women) we have C 4 2 x C 4 1 = 24.
c) From four families, we select 3 members of the delegation in four ways (since C 4 3 = 4! / 3!1! = 4). But in each family there are two ways to select a member of the delegation. According to the product rule C 4 3 x2x2x2 = 4x8 =32.
Task 8. The college has 2,000 students. Is it possible to say that at least two of them have the same initials of both first and last names?
Solution.
There are 33 letters in the Russian alphabet, of which ъ, ь, ы, й cannot be used, so n = 33-4 = 29. Each of the 29 letters can be an initial And name, And surnames. According to the product rule 29x29 = 841< 2000. Значит может быть лишь 841 различных вариантов, и среди 2000 студентов обязательно будут совпадения.
Combinatorics is a branch of mathematics that studies questions about how many different combinations, subject to certain conditions, can be made from given objects. The basics of combinatorics are very important for estimating the probabilities of random events, because They allow us to calculate the fundamentally possible number of different scenarios for the development of events.
Basic formula of combinatorics
Let there be k groups of elements, and i-th group consists of n i elements. Let's select one element from each group. Then total number The N ways in which such a choice can be made is determined by the relation N=n 1 *n 2 *n 3 *...*n k .
Example 1. Let us explain this rule with a simple example. Let there be two groups of elements, and the first group consists of n 1 elements, and the second - of n 2 elements. How many different pairs of elements can be made from these two groups, such that the pair contains one element from each group? Let's say we took the first element from the first group and, without changing it, went through all possible pairs, changing only the elements from the second group. There can be n 2 such pairs for this element. Then we take the second element from the first group and also make all possible pairs for it. There will also be n 2 such pairs. Since there are only n 1 elements in the first group, the total possible options will be n 1 *n 2 .
Example 2. How many three-digit even numbers can be made from the digits 0, 1, 2, 3, 4, 5, 6, if the digits can be repeated?
Solution: n 1 =6 (because you can take any number from 1, 2, 3, 4, 5, 6 as the first digit), n 2 =7 (because you can take any number from 0 as the second digit , 1, 2, 3, 4, 5, 6), n 3 =4 (since any number from 0, 2, 4, 6 can be taken as the third digit).
So, N=n 1 *n 2 *n 3 =6*7*4=168.
In the case when all groups consist of the same number elements, i.e. n 1 =n 2 =...n k =n we can assume that each selection is made from the same group, and the element after selection is returned to the group. Then the number of all selection methods is n k . This method of selection in combinatorics is called samples with return.
Example 3. How many four-digit numbers can be made from the digits 1, 5, 6, 7, 8?
Solution. For each digit of a four-digit number there are five possibilities, which means N=5*5*5*5=5 4 =625.
Consider a set consisting of n elements. In combinatorics this set is called general population.
Number of placements of n elements by m
Definition 1. Accommodation from n elements by m in combinatorics any ordered set from m various elements selected from the population in n elements.
Example 4. Different arrangements of three elements (1, 2, 3) by two will be the sets (1, 2), (2, 1), (1, 3), (3, 1), (2, 3), (3, 2 ). Placements may differ from each other both in elements and in their order.
The number of placements in combinatorics is denoted by A n m and is calculated by the formula:
Comment: n!=1*2*3*...*n (read: “en factorial”), in addition, it is assumed that 0!=1.
Example 5. How many two-digit numbers are there in which the tens digit and the units digit are distinct and odd?
Solution: because If there are five odd digits, namely 1, 3, 5, 7, 9, then this task comes down to selecting and placing two of the five different digits in two different positions, i.e. specified numbers will:
Definition 2. Combination from n elements by m in combinatorics any unordered set from m various elements, selected from the general population in n elements.
Example 6. For the set (1, 2, 3), the combinations are (1, 2), (1, 3), (2, 3).
Number of combinations of n elements, m each
The number of combinations is denoted by C n m and is calculated by the formula:
![]()
Example 7. In how many ways can a reader choose two books out of six available?
Solution: The number of methods is equal to the number of combinations of six books of two, i.e. equals:
![]()
Permutations of n elements
Definition 3. Permutation from n elements are called any ordered set these elements.
Example 7a. All possible permutations of a set consisting of three elements (1, 2, 3) are: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), ( 3, 2, 1), (3, 1, 2).
The number of different permutations of n elements is denoted by P n and is calculated by the formula P n =n!.
Example 8. In how many ways can seven books by different authors be arranged in one row on a shelf?
Solution: this problem is about the number of permutations seven different books. There are P 7 =7!=1*2*3*4*5*6*7=5040 ways to arrange the books.
Discussion. We see that the number of possible combinations can be calculated by different rules(permutations, combinations, placements) and the result will be different, because The calculation principle and the formulas themselves are different. Looking carefully at the definitions, you will notice that the result depends on several factors simultaneously.
Firstly, from how many elements we can combine their sets (how large population elements).
Secondly, the result depends on the size of the sets of elements we need.
Finally, it is important to know whether the order of the elements in the set is significant to us. Let us explain the last factor using the following example.
Example 9. On parent meeting 20 people are present. How many different composition options are there? parent committee, if 5 people should enter it?
Solution: In this example, we are not interested in the order of names on the committee list. If, as a result, the same people turn out to be part of it, then in meaning for us this is the same option. Therefore, we can use the formula to calculate the number combinations of 20 elements 5 each.
Things will be different if each committee member is initially responsible for a specific area of work. Then, with the same list composition of the committee, there are possibly 5 within it! options permutations that matter. The number of different (both in composition and area of responsibility) options is determined in this case by the number placements of 20 elements 5 each.
Self-test tasks
1. How many three-digit even numbers can be made from the digits 0, 1, 2, 3, 4, 5, 6, if the digits can be repeated?
2. How many five-digit numbers are there that are read the same from left to right and from right to left?
3. There are ten subjects in the class and five lessons a day. In how many ways can you create a schedule for one day?
4. In how many ways can 4 delegates be selected for a conference if there are 20 people in the group?
5. In how many ways can eight different letters be placed in eight different envelopes, if only one letter is placed in each envelope?
6. A commission consisting of two mathematicians and six economists should be composed of three mathematicians and ten economists. In how many ways can this be done?
Topic “Solving combinatorial problems”
Target: continue to develop the skills to solve the simplest combinatorial problems of practical content; consider other ways to solve combinatorial problems ( Multiplication rule; table)
Tasks:
Educational:
Contribute to:
generalization and systematization of students’ knowledge and skills on the topic
By the end of the lesson, students should be able to:
find possible combinations, composed of numbers, words, objects that meet the conditions of the task.
Educational:
Contribute to:
formation cognitive interest to the subject;
formation conscious attitude to work.
Educational:
Contribute to:
development mathematical thinking And logical speech students;
development of the ability to independently choose a solution method and the ability to justify the choice.
Mathematics is everywhere -
Just look at it
And I’ll have a lot of examples right away
You will find around you...
The epigraph to our lesson will be poetic lines, reading which determine the purpose of today's lesson - (to prove, to make sure that knowledge of mathematics is necessary in any human activity)
Today we will conduct research and prove that mathematics is all around us.
November 4 is a holiday. How many of you can tell what this holiday is called? (Day national unity)
Show slide #1 (Almost 4 centuries ago in early November militia led by the merchant Minin and governor Pozharsky, drove the Polish interventionists from Moscow and marked the beginning of the end of the so-called Time of Troubles. The militia of Minin and Pozharsky is unique in that it is the only example in Russian history when the fate of the country and state was decided by the people themselves, without the participation of the authorities as such. The people donated their last pennies to armament and went to liberate the land and restore order in the capital. Our great-great-great-great-great-grandfathers went to fight for the land many times, and they won.Then all classes, all nationalities, villages, cities and metropolises united. This day is rightly called the Day of National Unity. There was no other day like this in Russian history).
One of the symbols Russian state is the flag.
(read information about the flag)
!!!(Give to children, work in pairs)
Flag - a panel, usually rectangular in shape, raised on a special mast (flagpole)
August 22, 1991, emergency session Supreme Council The RSFSR decided to consider “a cloth of............., ………….., ……………. stripes” the official national flag of Russia.
(after the children fill out, ask what happened and listen to the answers)
Slide No. 1
!!! How many of you know what each color means?
- red color - symbolizes energy, strength, blood shed for the Fatherland.
- blue– the color of faith (the color of the Mother of God, under whose protection Russia is);
- white– means freedom and independence;
Let's find out how many flags there are in the world, consisting of 3 horizontal stripes of white, red and blue:
Task: 1.Read the problem.
- What topic does it belong to? this task? (comb.rear)
Oral survey.
What problems are called combinatorial?
What is combinatorics?
Can combinatorics help in real life?
In what games do we use combinatorics?
What methods of solving combinatorial problems do you know? (enumeration of options, tree of options,)
Solution:
Method - enumeration (let them draw - prepare rectangles)
2.method: Tree of options.
Now we will look at two more ways to solve combinatorial problems: a) the multiplication rule;
b) using a table.
3.way - Multiplication rule
In how many ways can each strip be selected?
1 lane - 3 ways
2 lane - 2 ways
3 lane - 1 way
Basic rule of the work:
If the first element in a combination can be selected A ways, after which the second element – b ways, then the total number of combinations will be equal to a x b .
3 ∙ 2 ∙ 1 = 6
Answer: 6 ways
TO
WITH
B
TO
KS
KB
WITH
SK
SB
B
BC
BS
Method: Options tableLet's write down the names of the stripes in the flag: KSB; BKS; KBS; SBC; BSK SKB.
Is there a State Flag of the Russian Federation among these flags?
What other states use for their national flag such symbolism?
It turns out that there are states where the flags have the same colors and the same arrangement.
( Answer: Slovakia, Slovenia, Croatia, Serbia)
Answer: Slovakia, Slovenia, Croatia, Serbia)
Student performances:
Slovakia, Slovenia, Croatia, Serbia are Slavic states, the colors white, red, blue symbolize general beginning Slavs
Flags of European countries where the colors are found: white, blue, red - these are the Netherlands and France.

Flag of Slovakia

Flag of Slovenia

Flag of Croatia

Flag of Serbia
Teacher: Guys, our lesson is coming to an end.
Do you think we achieved the goal of the lesson today, why?
What was difficult in the lesson and why?
In addition, students are asked to answer 3 quick questions:
In today's lesson I was... (easy, usually, difficult)
New material I... (I have learned and can apply, I have learned and find it difficult to apply, I have not learned)
My self-esteem for the lesson...
Lesson summary- Sinkway.
Combinatorics
Interesting, unknown.
Study, understand, sort through.
Present in all areas.
Variability.
5) Homework:
Tasks
One rather famous musketeer has 3 elegant hats, 4 wonderful cloaks and 2 pairs of great boots. How many costume options can he create?
There are 11 people on the football team. It is necessary to select a captain and his deputy. In how many ways can this be done?
How many different two-digit numbers can be made using the numbers 1, 4, 7, if the numbers are repeated
How many different three-digit numbers can be made from the numbers 1, 2, 3, 4, 5, provided that no number is repeated?
How many different two-digit numbers can be made from the numbers 0, 1, 2, 3 if the numbers: a) can be repeated; b) cannot be repeated?
The safe code consists of five different numbers. How many different options for creating a cipher?
1) a) How many two-digit numbers can be made from the numbers 1, 3, 5, 7, 9?
b) How many two-digit numbers can be made from the numbers 1, 3, 5, 7, 9, provided that the numbers should not be repeated.
2) Create a problem about your class.
3) Several countries decided to use symbols for their national flag in the form of 3 horizontal stripes of different widths, different colors– white, blue, red. How many countries can use such symbols, provided that each country has its own flag?
In how many ways can 6 people be seated at a table with 6 cutlery?
In the fifth grade, 8 subjects are studied. How many different schedule options can be created for Monday, if there should be 5 lessons on this day and all the lessons are different?
How many possible seven-digit phone numbers can be created if you exclude numbers starting with 0 and 9?
Application:
Task 1:
Flag - a panel, usually rectangular in shape, raised on a special mast (flagpole)
The national flag is one of the state……………..
On August 22, 1991, an emergency session of the Supreme Council of the RSFSR decided to consider the “cloth of ..................., ……………., …………… stripes” as official national flag of Russia.
Task 2
1. Read the problem.
Problem: (solution in notebook)
How many flags are there made up of three horizontal stripes of the same width and different colors - white, red and blue?
1.Repeat the names of the components of the division action;
Where each component is located.
2. Complete any three tasks from the list above, using any solution method.
Reflection:
1.Today on in the lesson I was …………. (easy, usually, difficult)
2. I… (learned and can apply the new material, learned and find it difficult to apply, did not learn)
3.My self-esteem for the lesson...