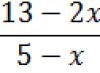Consider the following equations:
1. 2*x + 3*y = 15;
2. x 2 + y 2 = 4;
4. 5*x 3 + y 2 = 8.
Each of the equations presented above is an equation with two variables. Many points coordinate plane, whose coordinates turn the equation into a correct numerical equality, is called graph of an equation in two unknowns.
Graphing an Equation in Two Variables
Equations with two variables have a wide variety of graphs. For example, for the equation 2*x + 3*y = 15 the graph will be a straight line, for the equation x 2 + y 2 = 4 the graph will be a circle with radius 2, the graph of the equation y*x = 1 will be a hyperbola, etc.
Whole equations with two variables also have such a concept as degree. This degree is determined in the same way as for an entire equation with one variable. To do this, bring the equation to the form when left side there is a polynomial standard view, and the right one is zero. This is done through equivalent transformations.
Graphical method for solving systems of equations
Let's figure out how to solve systems of equations that will consist of two equations with two variables. Let's consider a graphical method for solving such systems.
Example 1. Solve the system of equations:
( x 2 + y 2 = 25
(y = -x 2 + 2*x + 5.
Let's construct graphs of the first and second equations in the same coordinate system. The graph of the first equation will be a circle with a center at the origin and radius 5. The graph of the second equation will be a parabola with branches going down.
All points on the graphs will each satisfy their own equation. We need to find points that will satisfy both the first and second equations. Obviously, these will be the points where these two graphs intersect.
Using our figure we find approximate values coordinates at which these points intersect. We get the following results:
A(-2.2;-4.5), B(0;5), C(2.2;4.5), D(4,-3).
This means that our system of equations has four solutions.
x1 ≈ -2.2; y1 ≈ -4.5;
x2 ≈ 0; y2 ≈ 5;
x3 ≈ 2.2; y3 ≈ 4.5;
x4 ≈ 4,y4 ≈ -3.
If we substitute these values into the equations of our system, we can see that the first and third solutions are approximate, and the second and fourth are exact. Graphical method often used to estimate the number of roots and their approximate boundaries. Solutions are often approximate rather than accurate.
Video tutorial " Graphic method solutions of systems of equations" presents educational material to master this topic. Material contains general concept about solving a system of equations, as well as detailed explanation using an example of how a system of equations is solved graphically.
The visual aid uses animation to make constructions more convenient and understandable, as well as different ways discharge important concepts and details for an in-depth understanding of the material and better memorization.
The video lesson begins by introducing the topic. Students are reminded what a system of equations is and what systems of equations they were already familiar with in 7th grade. Previously, students had to solve systems of equations of the form ax+by=c. Deepening the concept of solving systems of equations and in order to develop the ability to solve them, this video lesson examines the solution of a system consisting of two equations of the second degree, as well as one equation of the second degree, and the second of the first degree. We are reminded of what solving a system of equations is. The definition of a solution to a system as a pair of values of variables that reverse its equations when substituted into a correct equality is displayed on the screen. In accordance with the definition of the system solution, the task is specified. It is displayed on the screen to remember that solving a system means finding suitable solutions or proving their absence.

It is proposed to master a graphical method for solving a certain system of equations. Application this method is considered using the example of solving a system consisting of the equations x 2 +y 2 =16 and y=-x 2 +2x+4. Graphic solution The system begins by plotting each of these equations. Obviously, the graph of the equation x 2 + y 2 = 16 will be a circle. The points belonging to a given circle are the solution to the equation. Next to the equation, a circle of radius 4 with center O at the origin is constructed on the coordinate plane. The graph of the second equation is a parabola, the branches of which are lowered down. This parabola corresponding to the graph of the equation is constructed on the coordinate plane. Any point belonging to a parabola, is a solution to the equation y=-x 2 +2x+4. It is explained that the solution to a system of equations is points on the graphs that simultaneously belong to the graphs of both equations. This means that the intersection points of the constructed graphs will be solutions to the system of equations.

It is noted that the graphical method consists of finding the approximate value of the coordinates of points located at the intersection of two graphs, which reflect the set of solutions to each equation of the system. The figure shows the coordinates of the found intersection points of the two graphs: A, B, C, D[-2;-3.5]. These points are solutions to a system of equations found graphically. You can check their correctness by substituting them into the equation and obtaining a fair equality. After substituting the points into the equation, it is clear that some of the points give exact value solutions, and the part represents the approximate value of the solution to the equation: x 1 =0, y 1 =4; x 2 =2, y 2 ≈3.5; x 3 ≈3.5, y 3 = -2; x 4 = -2, y 4 ≈-3.5.

The video tutorial explains in detail the essence and application of the graphical method of solving a system of equations. This makes it possible to use it as a video tutorial in an algebra lesson at school when studying this topic. The material will also be useful for self-study students and can help explain the topic during distance learning.
In this lesson we will look at solving systems of two equations in two variables. First, let's look at the graphical solution of a system of two linear equations and the specifics of the set of their graphs. Next, we will solve several systems using the graphical method.
Topic: Systems of equations
Lesson: Graphical method for solving a system of equations
Consider the system
A pair of numbers that is simultaneously a solution to both the first and second equations of the system is called solving a system of equations.
Solving a system of equations means finding all its solutions, or establishing that there are no solutions. We have looked at the graphs of the basic equations, let's move on to considering systems.
Example 1. Solve the system ![]()
Solution:
These are linear equations, the graph of each of them is a straight line. The graph of the first equation passes through the points (0; 1) and (-1; 0). The graph of the second equation passes through the points (0; -1) and (-1; 0). The lines intersect at the point (-1; 0), this is the solution to the system of equations ( Rice. 1).
The solution to the system is a pair of numbers. Substituting this pair of numbers into each equation, we obtain the correct equality.
We got the only solution linear system.
Recall that when solving a linear system, the following cases are possible:
the system has a unique solution - the lines intersect,
the system has no solutions - the lines are parallel,
the system has an infinite number of solutions - the straight lines coincide.
We have reviewed special case systems when p(x; y) and q(x; y) are linear expressions of x and y.
Example 2. Solve a system of equations ![]()
Solution:
The graph of the first equation is a straight line, the graph of the second equation is a circle. Let's build the first graph by points (Fig. 2).
The center of the circle is at point O(0; 0), the radius is 1.

The graphs intersect at point A(0; 1) and point B(-1; 0).
Example 3. Solve the system graphically
Solution: Let's build a graph of the first equation - it is a circle with a center at t.O(0; 0) and radius 2. The graph of the second equation is a parabola. It is shifted upward by 2 relative to the origin, i.e. its vertex is point (0; 2) (Fig. 3).

Graphs have one common point- t. A(0; 2). It is the solution to the system. Let's plug a couple of numbers into the equation to check if it's correct.
Example 4. Solve the system
Solution: Let's build a graph of the first equation - this is a circle with a center at t.O(0; 0) and radius 1 (Fig. 4).

Let's plot the function This is a broken line (Fig. 5).

Now let's move it 1 down along the oy axis. This will be the graph of the function
Let's place both graphs in the same coordinate system (Fig. 6).

We get three intersection points - point A(1; 0), point B(-1; 0), point C(0; -1).
We looked at the graphical method for solving systems. If you can plot a graph of each equation and find the coordinates of the intersection points, then this method is quite sufficient.
But often the graphical method makes it possible to find only an approximate solution of the system or answer the question about the number of solutions. Therefore, other methods are needed, more accurate, and we will deal with them in the following lessons.
1. Mordkovich A.G. and others. Algebra 9th grade: Textbook. For general education Institutions.- 4th ed. - M.: Mnemosyne, 2002.-192 p.: ill.
2. Mordkovich A.G. and others. Algebra 9th grade: Problem book for students educational institutions/ A. G. Mordkovich, T. N. Mishustina and others - 4th ed. - M.: Mnemosyne, 2002.-143 p.: ill.
3. Makarychev Yu. N. Algebra. 9th grade: educational. for general education students. institutions / Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, I. E. Feoktistov. — 7th ed., rev. and additional - M.: Mnemosyne, 2008.
4. Alimov Sh.A., Kolyagin Yu.M., Sidorov Yu.V. Algebra. 9th grade. 16th ed. - M., 2011. - 287 p.
5. Mordkovich A. G. Algebra. 9th grade. In 2 hours. Part 1. Textbook for students of general education institutions / A. G. Mordkovich, P. V. Semenov. — 12th ed., erased. - M.: 2010. - 224 p.: ill.
6. Algebra. 9th grade. In 2 parts. Part 2. Problem book for students of general education institutions / A. G. Mordkovich, L. A. Aleksandrova, T. N. Mishustina and others; Ed. A. G. Mordkovich. — 12th ed., rev. - M.: 2010.-223 p.: ill.
1. College.ru section on mathematics ().
2. Internet project “Tasks” ().
3. Educational portal“I WILL SOLVE THE USE” ().
1. Mordkovich A.G. and others. Algebra 9th grade: Problem book for students of general education institutions / A. G. Mordkovich, T. N. Mishustina, etc. - 4th ed. - M.: Mnemosyne, 2002.-143 p.: ill. No. 105, 107, 114, 115.
Entry level
Solving equations, inequalities, systems using function graphs. Visual guide (2019)
Many tasks that we are used to calculating purely algebraically can be solved much easier and faster; using function graphs will help us with this. You say “how so?” draw something, and what to draw? Believe me, sometimes it is more convenient and easier. Let's get started? Let's start with the equations!
Graphical solution of equations
Graphical solution of linear equations
As you already know, the graph of a linear equation is a straight line, hence the name of this type. Linear equations are quite easy to solve algebraically - we transfer all the unknowns to one side of the equation, everything we know to the other and voila! We found the root. Now I'll show you how to do it graphically.
So you have the equation:
How to solve it?
Option 1, and the most common one is to move the unknowns to one side and the knowns to the other, we get:
Now let's build. What did you get?
What do you think is the root of our equation? That's right, the coordinate of the intersection point of the graphs is:

Our answer is
That's the whole wisdom of the graphic solution. As you can easily check, the root of our equation is a number!
As I said above, this is the most common option, close to algebraic solution, but you can solve it differently. For consideration alternative solution Let's return to our equation:
This time we will not move anything from side to side, but will construct the graphs directly, as they are now:
Built? Let's see!

What is the solution this time? That's right. The same thing - the coordinate of the intersection point of the graphs:

And, again, our answer is.
As you can see, with linear equations everything is extremely simple. It's time to look at something more complex... For example, graphical solution of quadratic equations.
Graphical solution of quadratic equations
So, now let's start solving the quadratic equation. Let's say you need to find the roots of this equation:
Of course, you can now start counting through the discriminant, or according to Vieta’s theorem, but many people make mistakes when multiplying or squaring, especially if the example is with large numbers, and, as you know, you won’t have a calculator for the exam... Therefore, let’s try to relax a little and draw while solving this equation.
Find solutions graphically given equation Can in various ways. Let's look at the different options, and you can choose which one you like best.
Method 1. Directly
We simply build a parabola using this equation:
To do this quickly, I'll give you one little hint: It is convenient to start the construction by determining the vertex of the parabola. The following formulas will help determine the coordinates of the vertex of a parabola:
You will say “Stop! The formula for is very similar to the formula for finding the discriminant,” yes, it is, and this is a huge disadvantage of “directly” constructing a parabola to find its roots. However, let's count to the end, and then I'll show you how to do it much (much!) easier!
Did you count? What coordinates did you get for the vertex of the parabola? Let's figure it out together:
Exactly the same answer? Well done! And now we already know the coordinates of the vertex, but to construct a parabola we need more... points. How many minimum points do you think we need? Right, .
You know that a parabola is symmetrical about its vertex, for example:

Accordingly, we need two more points on the left or right branch of the parabola, and in the future we will symmetrically reflect these points on the opposite side:

Let's return to our parabola. For our case, period. We need two more points, so we can take positive ones, or we can take negative ones? Which points are most convenient for you? It’s more convenient for me to work with positive ones, so I’ll calculate at and.
Now we have three points, and we can easily construct our parabola by reflecting two last points relative to its top:

What do you think is the solution to the equation? That's right, points at which, that is, and. Because.
And if we say that, it means that it must also be equal, or.
Just? We have finished solving the equation in a complex graphical way, or there will be more!
Of course, you can check our answer algebraically - you can calculate the roots using Vieta's theorem or Discriminant. What did you get? The same? You see! Now let's look at a very simple graphic solution, I'm sure you'll really like it!
Method 2. Divided into several functions
Let’s take our same equation: , but we’ll write it a little differently, namely:
Can we write it like this? We can, since the transformation is equivalent. Let's look further.
Let's construct two functions separately:
- - the schedule is simple parabola, which you can easily build even without defining the vertex using formulas and drawing up a table to determine other points.
- - the graph is a straight line, which you can just as easily construct by estimating the values in your head without even resorting to a calculator.
Built? Let's compare with what I got:

Do you think that in in this case are the roots of the equation? Right! The coordinates obtained by the intersection of two graphs and, that is:

Accordingly, the solution to this equation is:
What do you say? Agree, this method of solution is much easier than the previous one and even easier than looking for roots through a discriminant! If so, try solving the following equation using this method:
What did you get? Let's compare our graphs:

The graphs show that the answers are:
Did you manage? Well done! Now let's look at the equations a little more complicated, namely, the solution mixed equations, that is, equations containing functions of different types.
Graphical solution of mixed equations
Now let's try to solve the following:
Of course, we can bring everything to common denominator, find the roots of the resulting equation, not forgetting to take into account the ODZ, but again, we will try to solve it graphically, as we did in all previous cases.
This time let's build the following 2 graphs:
- - the graph is a hyperbola
- - the graph is a straight line, which you can easily construct by estimating the values in your head without even resorting to a calculator.
Realized it? Now start building.
Here's what I got:

Looking at this picture, tell me what are the roots of our equation?
That's right, and. Here's the confirmation:

Try plugging our roots into the equation. Did it work?
That's right! Agree, solving such equations graphically is a pleasure!
Try to solve the equation graphically yourself:
I'll give you a hint: move part of the equation to right side, so that on both sides there are the simplest functions to construct. Did you get the hint? Take action!
Now let's see what you got:
Respectively:
- - cubic parabola.
- - ordinary straight line.
Well, let's build:

As you wrote down long ago, the root of this equation is - .
Having decided this large number examples, I’m sure you realized how easy and quick it is to solve equations graphically. It's time to figure out how to solve systems in this way.
Graphic solution of systems
Graphically solving systems is essentially no different from graphically solving equations. We will also build two graphs, and their intersection points will be the roots of this system. One graph is one equation, the second graph is another equation. Everything is extremely simple!
Let's start with the simplest thing - solving systems of linear equations.
Solving systems of linear equations
Let's say we have the following system:
First, let's transform it so that on the left there is everything that is connected with, and on the right - everything that is connected with. In other words, let’s write these equations as a function in our usual form:
Now we just build two straight lines. What is the solution in our case? Right! The point of their intersection! And here you need to be very, very careful! Think about it, why? Let me give you a hint: we are dealing with a system: in the system there is both, and... Got the hint?
That's right! When solving a system, we must look at both coordinates, and not just as when solving equations! Another important point- write them down correctly and not confuse where we have the meaning and where the meaning is! Did you write it down? Now let's compare everything in order:

And the answers: and. Do a check - substitute the found roots into the system and make sure whether we solved it correctly graphically?
Solving systems of nonlinear equations
What if, instead of one straight line, we have quadratic equation? It's okay! You just build a parabola instead of a straight line! Don't believe me? Try solving the following system:
What's our next step? That’s right, write it down so that it’s convenient for us to build graphs:
And now it’s all a matter of small things - build it quickly and here’s your solution! We are building:

Did the graphs turn out the same? Now mark the solutions of the system in the figure and correctly write down the identified answers!
Did you do everything? Compare with my notes:

Is everything right? Well done! You're already clicking similar tasks like nuts! If so, let’s give you a more complicated system:
What are we doing? Right! We write the system so that it is convenient to build:
I’ll give you a little hint, since the system looks very complicated! When constructing graphs, build them “more”, and most importantly, do not be surprised by the number of intersection points.
So, let's go! Exhaled? Now start building!
So how? Beautiful? How many intersection points did you get? I have three! Let's compare our graphs:

Also? Now carefully write down all the solutions of our system:
Now look at the system again:
Can you imagine that you solved this in just 15 minutes? Agree, mathematics is still simple, especially when looking at an expression you are not afraid to make a mistake, but just take it and solve it! You're great!
Graphical solution of inequalities
Graphical solution of linear inequalities
After last example You can handle everything! Now exhale - compared to the previous sections, this one will be very, very easy!
We will start, as usual, with a graphical solution linear inequality. For example, this one:
First, let's carry out the simplest transformations - open the brackets full squares and give similar terms:
The inequality is not strict, therefore it is not included in the interval, and the solution will be all points that are to the right, since more, more, and so on:

Answer:
That's it! Easily? Let's solve a simple inequality with two variables:
Let's draw a function in the coordinate system.

Did you get such a schedule? Now let’s look carefully at what inequality we have there? Less? This means we paint over everything that is to the left of our straight line. What if there were more? That's right, then we would paint over everything that is to the right of our straight line. It's simple.

All solutions of this inequality"shaded" orange. That's it, the inequality with two variables is solved. This means that the coordinates of any point from the shaded area are the solutions.
Graphical solution of quadratic inequalities
Now we will understand how to graphically solve quadratic inequalities.
But before we get down to business, let's review some material regarding the quadratic function.
What is the discriminant responsible for? That’s right, for the position of the graph relative to the axis (if you don’t remember this, then definitely read the theory about quadratic functions).
In any case, here's a little reminder for you:

Now that we have refreshed all the material in our memory, let's get down to business - solve the inequality graphically.
I’ll tell you right away that there are two options for solving it.
Option 1
We write our parabola as a function:
Using the formulas, we determine the coordinates of the vertex of the parabola (exactly the same as when solving quadratic equations):
Did you count? What did you get?
Now let's take two more different points and calculate for them:
Let's start building one branch of the parabola:

We symmetrically reflect our points onto another branch of the parabola:

Now let's return to our inequality.
We need it to be less than zero, respectively:

Since in our inequality the sign is strictly less than, then endpoints we exclude - “prick out”.
Answer:
Long way, right? Now I will show you a simpler version of the graphical solution using the example of the same inequality:
Option 2

We return to our inequality and mark the intervals we need:

Agree, it's much faster.
Let us now write down the answer:
Let's consider another solution that simplifies the algebraic part, but the main thing is not to get confused.
Multiply the left and right sides by:
Try to solve the following yourself quadratic inequality in any way you like: .
Did you manage?
Look how my graph turned out:

Answer: .
Graphical solution of mixed inequalities
Now let's move on to more complex inequalities!
How do you like this:
It's creepy, isn't it? Honestly, I have no idea how to solve this algebraically... But it’s not necessary. Graphically there is nothing complicated about this! The eyes are afraid, but the hands are doing!
The first thing we will start with is by constructing two graphs:
I won’t write out a table for each one - I’m sure you can do it perfectly on your own (wow, there are so many examples to solve!).
Did you paint it? Now build two graphs.
Let's compare our drawings?

Is it the same with you? Great! Now let's arrange the intersection points and use color to determine which graph we should have larger in theory, that is. Look what happened in the end:

Now let’s just look at where our selected graph is higher than the graph? Feel free to take a pencil and paint over this area! She will be the solution to our complex inequality!

At what intervals along the axis is we located higher than? Right, . This is the answer!
Well, now you can handle any equation, any system, and even more so any inequality!
BRIEFLY ABOUT THE MAIN THINGS
Algorithm for solving equations using function graphs:
- Let's express it through
- Let's define the function type
- Let's build graphs of the resulting functions
- Let's find the intersection points of the graphs
- Let’s write the answer correctly (taking into account the ODZ and inequality signs)
- Let's check the answer (substitute the roots into the equation or system)
For more information about constructing function graphs, see the topic “”.