Significado especial para caracterizar la distribución de una variable aleatoria, tienen características numéricas llamadas momentos inicial y central.
El momento inicial k-ésimo orden α k(X) variable aleatoria X k-ésima potencia de esta cantidad, es decir
α k(X) = METRO(X k) (6.8)
Fórmula (6.8) debido a la definición de expectativa matemática para varios variables aleatorias tiene su propia forma, es decir, para una variable aleatoria discreta con conjunto finito valores
para una variable aleatoria continua
 , (6.10)
, (6.10)
Dónde F(X) - densidad de distribución de una variable aleatoria X.
Integral impropia en la fórmula (6.10) se convierte en integral definida durante un intervalo finito, si los valores de una variable aleatoria continua existen solo en este intervalo.
Una de las características numéricas introducidas anteriormente, la expectativa matemática, no es más que el momento inicial de primer orden o, como dicen, el primer momento inicial:
METRO(X) = α 1 (X).
En el párrafo anterior se introdujo el concepto de variable aleatoria centrada. HM(X). Si esta cantidad se considera la principal, entonces también se pueden encontrar sus momentos iniciales. Por la magnitud misma X Estos momentos se llamarán centrales.
Momento central k-ésimo orden mk(X) variable aleatoria X llamada expectativa matemática k-ésima potencia de la variable aleatoria centrada, es decir
mk(X) = METRO[(HM(X))k] (6.11)
En otras palabras, el punto central k-ésimo orden es la expectativa matemática k grado de desviación.
Momento central k El orden de una variable aleatoria discreta con un conjunto finito de valores se encuentra mediante la fórmula:
![]() , (6.12)
, (6.12)
para una variable aleatoria continua usando la fórmula:
 (6.13)
(6.13)
En el futuro, cuando quede claro de qué tipo de variable aleatoria estamos hablando, no la escribiremos en la notación de los momentos inicial y central, es decir, en lugar de α k(X) Y mk(X) simplemente escribiremos α k Y mk .
Es obvio que el momento central de primer orden igual a cero, ya que esta no es más que la expectativa matemática de la desviación, la cual es igual a cero según lo demostrado anteriormente, es decir .
No es difícil entender que el momento central de segundo orden de una variable aleatoria X coincide con la varianza de la misma variable aleatoria, es decir
Además, hay siguientes fórmulas, conectando los momentos inicial y central:

Así, los momentos de primer y segundo orden (esperanza matemática y dispersión) caracterizan las características más importantes de la distribución: su posición y el grado de dispersión de los valores. Para más Descripción detallada Las distribuciones son momentos de órdenes superiores. Mostrémoslo.
Supongamos que la distribución de una variable aleatoria es simétrica con respecto a su expectativa matemática. Entonces todos los momentos centrales de orden impar, si existen, son iguales a cero. Esto se explica por el hecho de que debido a la simetría de la distribución para cada valor positivo cantidades X − METRO(X) hay un módulo igual significado negativo, y las probabilidades de estos valores son iguales. En consecuencia, la suma de la fórmula (6.12) consta de varios pares de términos iguales en magnitud pero de diferente signo, que se cancelan entre sí al realizar la suma. Por tanto, el importe total, es decir el momento central de cualquier variable aleatoria discreta de orden impar es cero. De manera similar, el momento central de cualquier orden impar de una variable aleatoria continua es igual a cero, al igual que la integral en límites simétricos de una función impar.
Es natural suponer que si el momento central de un orden impar es diferente de cero, entonces la distribución en sí no será simétrica con respecto a su expectativa matemática. Además, cuanto más difiere el momento central de cero, mayor es la asimetría en la distribución. Tomemos el momento central del orden impar más pequeño como una característica de la asimetría. Dado que el momento central de primer orden es cero para variables aleatorias que tienen cualquier distribución, es mejor utilizar el momento central de tercer orden para este propósito. Sin embargo, este momento tiene la dimensión de un cubo de una variable aleatoria. Para deshacerse de este inconveniente y pasar a una variable aleatoria adimensional, divida el valor momento central por cubo de desviación estándar.
Coeficiente de asimetría Como o simplemente asimetría se llama relación entre el momento central de tercer orden y el cubo de la desviación estándar, es decir
A veces la asimetría se llama "asimetría" y se designa S k de que viene palabra inglesa sesgado - "oblicuo".
Si el coeficiente de asimetría es negativo, entonces su valor está fuertemente influenciado por términos negativos (desviaciones) y la distribución tendrá asimetría izquierda, y el gráfico de distribución (curva) es más plano a la izquierda de la expectativa matemática. Si el coeficiente es positivo, entonces asimetría derecha, y la curva es más plana a la derecha de la expectativa matemática (figura 6.1).
 |
Como se ha mostrado, para caracterizar la dispersión de los valores de una variable aleatoria en torno a su expectativa matemática, se utiliza el segundo momento central, es decir dispersión. Si este momento es de gran importancia. valor numérico, entonces esta variable aleatoria tiene una gran dispersión de valores y la curva de distribución correspondiente tiene una forma más plana que la curva para la cual tiene el segundo momento central bajo valor. Por lo tanto, el segundo momento central caracteriza, en cierta medida, la curva de distribución de “parte superior plana” o “de parte superior aguda”. Sin embargo, esta característica no es muy conveniente. El momento central de segundo orden tiene la dimensión igual al cuadrado Dimensiones de una variable aleatoria. Si intentamos obtener una cantidad adimensional dividiendo el valor del momento por el cuadrado de la desviación estándar, entonces para cualquier variable aleatoria obtenemos: ![]() . Por tanto, este coeficiente no puede ser ninguna característica de la distribución de una variable aleatoria. Es lo mismo para todas las distribuciones. En este caso, puedes utilizar el momento central. cuarto orden.
. Por tanto, este coeficiente no puede ser ninguna característica de la distribución de una variable aleatoria. Es lo mismo para todas las distribuciones. En este caso, puedes utilizar el momento central. cuarto orden.
Exceso Ek es la cantidad determinada por la fórmula
![]() (6.15)
(6.15)
La curtosis se utiliza principalmente para variables aleatorias continuas y sirve para caracterizar la llamada "inclinación" de la curva de distribución o, como ya se mencionó, para caracterizar la curva de distribución de "parte superior plana" o "de parte superior aguda". Se considera que la curva de distribución de referencia es la curva distribución normal(Esto se discutirá en detalle en el próximo capítulo). Para una variable aleatoria distribuida sobre ley normal, se mantiene la igualdad. Por lo tanto, el exceso dado por la fórmula(6.15), sirve para comparación distribución dada con normal, cuya curtosis es igual a cero.
Si se obtiene una curtosis positiva para alguna variable aleatoria, entonces la curva de distribución de este valor tiene más picos que la curva de distribución normal. Si la curtosis es negativa, entonces la curva tiene una parte superior más plana en comparación con la curva de distribución normal (Fig. 6.2).
 |
Pasemos ahora a tipos específicos Leyes de distribución de variables aleatorias discretas y continuas.
Los momentos centrales se denominan momentos de distribución, al calcular cuál se toma como valor inicial la desviación de las opciones de la media aritmética. estas series.
1. Calcule el momento central de primer orden usando la fórmula:
2. Calcule el momento central de segundo orden usando la fórmula:

¿Dónde está el valor de la mitad de los intervalos?
Este es un promedio ponderado;
Fi es el número de valores.
3. Calcule el momento central de tercer orden usando la fórmula:

¿Dónde está el valor de la mitad de los intervalos? - este es el promedio ponderado; - fi-número de valores.
4. Calcule el momento central de cuarto orden usando la fórmula:

¿Dónde está el valor de la mitad de los intervalos? - este es el promedio ponderado; - fi-número de valores.
Cálculo para la tabla 3.2
Cálculo para la tabla 3.4
1. Calcule el momento central de primer orden usando la fórmula (7.1):
2. Calcule el momento central de segundo orden usando la fórmula (7.2):
3. Calcule el momento central de tercer orden usando la fórmula (7.3):
4. Calcule el momento central de cuarto orden usando la fórmula (7.4):
Cálculo para la tabla 3.6
1. Calcule el momento central de primer orden usando la fórmula (7.1):
2. Calcule el momento central de segundo orden usando la fórmula (7.2):
3. Calcule el momento central de tercer orden usando la fórmula (7.3):
4. Calcule el momento central de cuarto orden usando la fórmula (7.4):





Se calcularon momentos de orden 1, 2, 3, 4 para tres problemas. Donde se necesita el momento de tercer orden para calcular la asimetría y el momento de cuarto orden para calcular la curtosis.
CÁLCULO DE ASIMETRÍA DE DISTRIBUCIÓN
En la práctica estadística, se encuentran varias distribuciones. Existen los siguientes tipos de curvas de distribución:
· curvas de un solo vértice: simétricas, moderadamente asimétricas y extremadamente asimétricas;
· curvas multivértices.
Las poblaciones homogéneas, por regla general, se caracterizan por distribuciones de un solo vértice. Multivértice indica la heterogeneidad de la población en estudio. La aparición de dos o más vértices hace necesario reagrupar los datos para identificar grupos más homogéneos.
Averiguar general La distribución implica evaluar su homogeneidad, así como calcular indicadores de asimetría y curtosis. Para distribuciones simétricas, las frecuencias de dos opciones cualesquiera que estén ubicadas igualmente a ambos lados del centro de distribución son iguales entre sí. La media, la moda y la mediana calculadas para dichas distribuciones también son iguales.
En un estudio comparativo de la asimetría de varias distribuciones con diferentes unidades de medida, se calcula indicador relativo asimetría():


¿Dónde está el promedio ponderado? Mo-moda; - dispersión ponderada cuadrática media; Yo-mediana.
Su valor puede ser positivo o negativo. En el primer caso estamos hablando acerca de sobre la asimetría del lado derecho, y en el segundo, sobre la asimetría del lado izquierdo.
Con asimetría del lado derecho Mo>Me >x. El más utilizado (como indicador de asimetría) es la relación entre el momento central de tercer orden y la desviación estándar de una serie determinada al cubo:
¿Dónde está el momento central de tercer orden? -promedio Desviación Estándar cubicado.
Solicitud este indicador permite determinar no solo la magnitud de la asimetría, sino también verificar su presencia en población. Generalmente se acepta que una asimetría superior a 0,5 (independientemente del signo) se considera significativa; si es inferior a 0,25, entonces es insignificante.
La evaluación de la materialidad se basa en el promedio error cuadrado, coeficiente de asimetría (), que depende del número de observaciones (n) y se calcula mediante la fórmula:

donde n es el número de observaciones.
En este caso, la asimetría es significativa y la distribución de la característica en la población es asimétrica. De lo contrario, la asimetría es insignificante y su presencia puede deberse a circunstancias aleatorias.
Cálculo para la tabla 3.2 Agrupación de la población por promedio mensual salarios, frotar.
Asimetría significativa del lado izquierdo.
Cálculo para la tabla 3.4 Agrupación de tiendas por volumen de negocios minorista, millones de rublos.
1. Determinemos las asimetrías usando la fórmula (7.5):
Asimetría significativa del lado derecho.
Cálculo para la tabla 3.6 Agrupación de organizaciones de transporte por volumen de negocios de transporte de mercancías. uso común(millones de t.km)
1. Determinemos las asimetrías usando la fórmula (7.5):
Del lado derecho, ligera asimetría.
CÁLCULO DE KURTESS DE DISTRIBUCIÓN
Para distribuciones simétricas, el índice de curtosis () se puede calcular:

¿Dónde está el momento central de cuarto orden? - desviación estándar a la cuarta potencia.
Cálculo para la tabla 3.2 Agrupación de la población por salario medio mensual, frotar.

Cálculo para la tabla 3.4 Agrupación de tiendas por volumen de negocios minorista, millones de rublos.
Calculemos el indicador de curtosis usando la fórmula (7.7)

Distribución de picos.
Cálculo para la tabla 3.6 Agrupación de organizaciones de transporte por facturación de mercancías del transporte público (millones de t.km)
Calculemos el indicador de curtosis usando la fórmula (7.7)

Distribución superior plana.
EVALUACIÓN DE LA HOMOGENEIDAD DE LA POBLACIÓN
Evaluación de homogeneidad para la tabla 3.2 Agrupación de la población por salario medio mensual, frotar.
Cabe señalar que, aunque los indicadores de asimetría y curtosis caracterizan directamente sólo la forma de distribución de la característica dentro de la población estudiada, su definición no tiene sólo un significado descriptivo. A menudo, la asimetría y la curtosis proporcionan ciertas indicaciones para futuras investigaciones sociales. fenómenos económicos. El resultado obtenido indica la presencia de asimetría significativa en magnitud y de naturaleza negativa; cabe señalar que la asimetría es del lado izquierdo; Además, la población tiene una distribución plana.
Evaluación de homogeneidad para la tabla 3.4 Agrupación de tiendas por volumen de negocios minorista, millones de rublos.
El resultado obtenido indica la presencia de asimetría significativa en magnitud y de carácter positivo, cabe señalar que la asimetría es del lado derecho; Y también la población tiene una distribución de vértice agudo.
Evaluación de homogeneidad para el cuadro 3.6 Agrupación de organizaciones de transporte por facturación de mercancías del transporte público (millones de t.km)
El resultado obtenido indica la presencia de asimetría de magnitud insignificante y de carácter positivo; cabe señalar que la asimetría es del lado derecho; Además, la población tiene una distribución achatada.
Valor esperado. Expectativa matemática variable aleatoria discreta X, anfitrión numero final valores Xi con probabilidades Ri, la cantidad se llama:
Expectativa matemática variable aleatoria continua X se llama integral del producto de sus valores X sobre la densidad de distribución de probabilidad F(X):
 (6b)
(6b)
Integral impropia (6 b) se supone que es absolutamente convergente (de lo contrario, dicen que la expectativa matemática METRO(X) no existe). La expectativa matemática caracteriza valor promedio variable aleatoria X. Su dimensión coincide con la dimensión de la variable aleatoria.
Propiedades de la expectativa matemática:
Dispersión. Diferencia variable aleatoria X el numero se llama:
La varianza es característica de dispersión valores de variables aleatorias X en relación con su valor medio METRO(X). La dimensión de la varianza es igual a la dimensión de la variable aleatoria al cuadrado. Con base en las definiciones de varianza (8) y expectativa matemática (5) para una variable aleatoria discreta y (6) para una variable aleatoria continua, obtenemos expresiones similares para la varianza:
 (9)
(9)
Aquí metro = METRO(X).
Propiedades de dispersión:
Desviación Estándar:
![]() (11)
(11)
Dado que la dimensión del promedio desviación cuadrada Al igual que el de una variable aleatoria, se utiliza más a menudo como medida de dispersión que de varianza.
Momentos de distribución. Los conceptos de expectativa matemática y dispersión son casos especiales de más concepto general para características numéricas de variables aleatorias – momentos de distribución. Los momentos de distribución de una variable aleatoria se introducen como expectativas matemáticas de algunas funciones simples de una variable aleatoria. Entonces, momento de orden. k relativo al punto X 0 se llama expectativa matemática METRO(X–X 0 )k. Momentos sobre el origen. X= 0 se llaman momentos iniciales y son designados:
![]() (12)
(12)
El momento inicial de primer orden es el centro de la distribución de la variable aleatoria considerada:
![]() (13)
(13)
Momentos sobre el centro de distribución. X= metro son llamados puntos centrales y son designados:
![]() (14)
(14)
De (7) se deduce que el momento central de primer orden es siempre igual a cero:
Los momentos centrales no dependen del origen de los valores de la variable aleatoria, ya que al desplazarse por valor constante CON su centro de distribución se desplaza en el mismo valor CON, y la desviación del centro no cambia: X – metro = (X – CON) – (metro – CON).
Ahora es obvio que dispersión- Este momento central de segundo orden:
Asimetría. Momento central de tercer orden:
![]() (17)
(17)
sirve para evaluación asimetrías de distribución. Si la distribución es simétrica con respecto al punto X= metro, entonces el momento central de tercer orden será igual a cero (como todos los momentos centrales de órdenes impares). Por tanto, si el momento central de tercer orden es distinto de cero, entonces la distribución no puede ser simétrica. La magnitud de la asimetría se evalúa utilizando un modelo adimensional. coeficiente de asimetría:
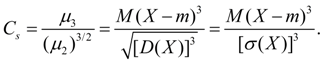 (18)
(18)
El signo del coeficiente de asimetría (18) indica asimetría del lado derecho o izquierdo (Fig. 2).

Arroz. 2. Tipos de asimetría de distribución.
Exceso. Momento central de cuarto orden:
![]() (19)
(19)
sirve para evaluar el llamado exceso, que determina el grado de inclinación (pico) de la curva de distribución cerca del centro de la distribución en relación con la curva de distribución normal. Ya que para una distribución normal, el valor tomado como curtosis es:
 (20)
(20)
En la Fig. 3 muestra ejemplos de curvas de distribución con diferentes significados exceso. Para distribución normal mi= 0. Las curvas que son más puntiagudas de lo normal tienen una curtosis positiva, las que son más planas tienen una curtosis negativa.

Arroz. 3. Curvas de distribución con distintos grados de inclinación (curtosis).
Momentos de orden superior en aplicaciones de ingeniería. estadística matemática normalmente no se utiliza.
Moda
discreto una variable aleatoria es su valor más probable. Moda continuo una variable aleatoria es su valor en el que la densidad de probabilidad es máxima (Fig. 2). Si la curva de distribución tiene un máximo, entonces la distribución se llama unimodal. Si una curva de distribución tiene más de un máximo, entonces la distribución se llama multimodal. A veces hay distribuciones cuyas curvas tienen un mínimo en lugar de un máximo. Estas distribuciones se denominan antimodal. EN caso general la moda y la expectativa matemática de una variable aleatoria no coinciden. En el caso especial, para modal, es decir. teniendo una distribución moda, simétrica y siempre que exista una expectativa matemática, esta última coincide con la moda y centro de simetría de la distribución.
Mediana variable aleatoria X- este es su significado Bueno, para lo cual se cumple la igualdad: es decir es igualmente probable que la variable aleatoria X será menos o más Bueno. Geométricamente mediana es la abscisa del punto en el que el área bajo la curva de distribución se divide por la mitad (Fig. 2). En el caso de una distribución modal simétrica, la mediana, la moda y la expectativa matemática son las mismas.
3.4. Momentos de una variable aleatoria.
Arriba nos familiarizamos con las características integrales del SV: la función de distribución y la serie de distribución para un SV discreto, la función de distribución y la densidad de probabilidad para un SV continuo. Estas características equivalentes por pares en términos de contenido de información son funciones y describir completamente el SV desde un punto de vista probabilístico. Sin embargo, en muchas situaciones prácticas es imposible o innecesario caracterizar una variable aleatoria de manera exhaustiva. A menudo basta con especificar uno o más numérico parámetros que hasta cierto punto describen las características principales de la distribución y, a veces, encontrar características exhaustivas es, aunque deseable, demasiado difícil matemáticamente, y operando con parámetros numéricos, estamos limitados a aproximarnos, pero más descripción sencilla. Los parámetros numéricos especificados se llaman características numéricas variables aleatorias y juegan un papel importante en las aplicaciones de la teoría de la probabilidad a diversos campos de la ciencia y la tecnología, facilitando la solución de problemas y permitiendo que los resultados de la solución se presenten de forma sencilla y visual.
Las características numéricas más utilizadas se pueden dividir en dos tipos: momentos y características de posición. Existen varios tipos de momentos, de los cuales los dos más utilizados son: primaria y central. Otros tipos de momentos, p.e. momentos absolutos, momentos factoriales, no consideramos. Para evitar el uso de una generalización de la integral, la llamada integral de Stieltjes, daremos definiciones de momentos por separado para SV continuas y discretas.
Definiciones. 1. El momento inicialk-ésimo orden SV discreto se llama cantidad
Dónde F(X) es la densidad de probabilidad de un SV dado.
3. Momento centralk-ésimo orden SV discreto se llama cantidad
En los casos en que se estén considerando varios SV al mismo tiempo, es conveniente, para evitar malentendidos, indicar la identidad del momento; Esto lo haremos indicando entre paréntesis la designación del SV correspondiente, por ejemplo, ![]() , etc. Esta designación no debe confundirse con la notación de función, y la letra entre paréntesis no debe confundirse con el argumento de la función. Las sumas e integrales en los lados derechos de las igualdades (3.4.1 - 3.4.4) pueden converger o divergir según el valor k y distribución específica. En el primer caso dicen que el momento no existe o diverge, en el segundo - que momento existe o converge. Si un SV discreto tiene un número finito de valores finitos ( norte por supuesto), entonces todos sus momentos son de orden finito k existir. En infinito norte, a partir de algunos k y para órdenes superiores, los momentos de un SV discreto (tanto inicial como central) pueden no existir. Los momentos de un SV continuo, como se desprende de las definiciones, se expresan mediante integrales impropias, que pueden divergir a partir de un cierto k y para órdenes superiores (simultáneamente inicial y central). Los momentos de orden cero siempre convergen.
, etc. Esta designación no debe confundirse con la notación de función, y la letra entre paréntesis no debe confundirse con el argumento de la función. Las sumas e integrales en los lados derechos de las igualdades (3.4.1 - 3.4.4) pueden converger o divergir según el valor k y distribución específica. En el primer caso dicen que el momento no existe o diverge, en el segundo - que momento existe o converge. Si un SV discreto tiene un número finito de valores finitos ( norte por supuesto), entonces todos sus momentos son de orden finito k existir. En infinito norte, a partir de algunos k y para órdenes superiores, los momentos de un SV discreto (tanto inicial como central) pueden no existir. Los momentos de un SV continuo, como se desprende de las definiciones, se expresan mediante integrales impropias, que pueden divergir a partir de un cierto k y para órdenes superiores (simultáneamente inicial y central). Los momentos de orden cero siempre convergen.
Consideremos con más detalle primero los momentos iniciales y luego los centrales. Desde un punto de vista matemático, el momento inicial k-ésimo orden es el “promedio ponderado” k-ésimos grados de valores SV; en el caso de un SV discreto, las ponderaciones son las probabilidades de los valores; en el caso de un SV continuo, la función de ponderación es la densidad de probabilidad. Operaciones de este tipo se utilizan mucho en mecánica para describir la distribución de masas (momentos estáticos, momentos de inercia, etc.); Las analogías que surgen a este respecto se analizan a continuación.
Para una mejor comprensión de los momentos iniciales, los consideraremos por separado para determinados k. En la teoría de la probabilidad, los momentos de órdenes inferiores son los más importantes, es decir, en los momentos pequeños. k, por lo tanto, la consideración debe realizarse en orden de valores crecientes. k. El momento inicial de orden cero es igual a
1, para SV discreto;
 =1, para SV continuo,
=1, para SV continuo,
aquellos. para cualquier SV es igual al mismo valor: uno y, por lo tanto, no contiene ninguna información sobre las propiedades estadísticas del SV.
El momento inicial de primer orden (o primer momento inicial) es igual a
Para SV discreto;
 , para SV continuo.
, para SV continuo.
Este punto es la característica numérica más importante de cualquier SV, por lo que existen varias razones interrelacionadas. En primer lugar, según el teorema de Chebyshev (ver sección 7.4), con un número ilimitado de pruebas en el SV, la media aritmética de los valores observados tiende (en cierto sentido) a , por lo tanto, para cualquier SV, este es un número característico en torno al cual se agrupan sus valores en torno a la experiencia. En segundo lugar, para un CV continuo es numéricamente igual a X-ésima coordenada del centro de gravedad del trapecio curvilíneo formado por la curva F(X) (una propiedad similar ocurre para un SV discreto), por lo que este momento podría denominarse “centro de gravedad de la distribución”. En tercer lugar, este momento tiene propiedades matemáticas notables, que quedarán claras a lo largo del curso, en particular, por lo que su valor se incluye en las expresiones para los momentos centrales (ver (3.4.3) y (3.4.4)).
La importancia de este momento para los problemas teóricos y prácticos de la teoría de la probabilidad y sus notables propiedades matemáticas han llevado a que, además de la designación y el nombre "primer momento inicial", en la literatura se utilicen otras designaciones y nombres, más o menos conveniente y que refleje las propiedades mencionadas. Los nombres más comunes son: valor esperado, valor promedio y notación: metro, METRO[X], . Usaremos con mayor frecuencia el término “expectativa matemática” y la notación metro; si hay varios SV, usaremos un subíndice que indique la identidad de la expectativa matemática, por ejemplo, metro X , metro y etc.
El momento inicial de segundo orden (o segundo momento inicial) es igual a
Para SV discreto;
 , para SV continuo;
, para SV continuo;
a veces se llama cuadrado medio de la variable aleatoria y es designado METRO.
El momento inicial de tercer orden (o tercer momento inicial) es igual a
Para SV discreto;
 , para SV continuo
, para SV continuo
a veces se llama cubo promedio de una variable aleatoria y es designado METRO[X 3 ].
No tiene sentido seguir enumerando los puntos iniciales. Detengámonos en la importante interpretación de los momentos de orden. k>1. Vamos, junto con SV X también hay un SV Y, y Y=X k (k=2, 3, ...). Esta igualdad significa que las variables aleatorias X Y Y están conectados deterministamente en el sentido de que cuando SV X adquiere el valor X, NE Y adquiere el valor y=x k(En el futuro, esta conexión SV se considerará con más detalle). Entonces, según (3.4.1) y (3.4.2)
![]() =metro y
, k=2,
3, ...,
=metro y
, k=2,
3, ...,
es decir. k El momento inicial de SV es igual a la expectativa matemática. k-ésima potencia de esta variable aleatoria. Por ejemplo, el tercer momento inicial de la longitud del borde de un cubo aleatorio es igual a la expectativa matemática del volumen del cubo. La capacidad de entender momentos como ciertos. expectativas matemáticas- otra faceta de la importancia del concepto de expectativa matemática.
Pasemos a considerar los puntos centrales. Dado que, como quedará claro más adelante, los momentos centrales se expresan inequívocamente a través de momentos iniciales y viceversa, surge la pregunta de por qué los momentos centrales son necesarios y por qué los momentos iniciales no son suficientes. Consideremos SV X(continua o discreta) y otra SV Y, relacionada con la primera como Y=X+a, Dónde a 0 - no aleatorio Número Real. cada valor X variable aleatoria X corresponde al valor y=x+a variable aleatoria Y, por lo tanto la distribución de SV Y tendrá la misma forma (expresada por el polígono de distribución en el caso discreto o la densidad de probabilidad en el caso continuo) que la distribución SV X, pero desplazado a lo largo del eje x en la cantidad a. En consecuencia, los momentos iniciales de SV Y diferirá de los momentos correspondientes de SV X. Por ejemplo, es fácil ver metro y =metro X +a(momentos más alto orden están conectados por relaciones más complejas). Así que hemos establecido que los momentos iniciales no son invariantes con respecto al desplazamiento de la distribución en su conjunto. Se obtendrá el mismo resultado si no desplaza la distribución, sino el comienzo del eje x horizontalmente en una cantidad: a, es decir. La conclusión equivalente también es válida: los momentos iniciales no son invariantes con respecto al desplazamiento horizontal del inicio del eje x.
Los momentos centrales, destinados a describir aquellas propiedades de las distribuciones que no dependen de su desplazamiento en su conjunto, están libres de este inconveniente. De hecho, como puede verse en (3.4.3) y (3.4.4), cuando la distribución en su conjunto se desplaza una cantidad a, o, lo que es lo mismo, desplazando el inicio del eje x en la cantidad - a, todos los valores X, con las mismas probabilidades (en el caso discreto) o la misma densidad de probabilidad (en el caso continuo), cambiará en la cantidad a, pero la cantidad cambiará en la misma cantidad metro, por lo que los valores de los paréntesis en el lado derecho de las igualdades no cambiarán. De este modo, los momentos centrales son invariantes respecto al desplazamiento de la distribución en su conjunto, o, lo que es lo mismo, respecto al desplazamiento horizontal del inicio del eje x. Estos momentos recibieron el nombre de “central” en aquellos días en que el primer momento inicial se llamaba “centro”. Es útil señalar que el momento central de SV X puede entenderse como el momento inicial correspondiente de SV X 0 igual
|
X 0 =x-m X . |
nordeste X 0 se llama centrado(en relación con SV X), y la operación que conduce a ella, es decir, restar su expectativa matemática de una variable aleatoria, se llama centrado. Como veremos más adelante, este concepto y esta operación nos serán de utilidad a lo largo del curso. Nótese que el momento central del orden k>1 puede considerarse como la expectativa matemática (promedio) k-ésimo grado de SV centrado: ![]() .
.
Consideremos por separado los momentos centrales de los órdenes inferiores. El momento central de orden cero es igual a
 , para SV discretos;
, para SV discretos;
 , para SV continuo;
, para SV continuo;
es decir, para cualquier SV y no contiene ninguna información sobre las propiedades estadísticas de este SV.
El momento central de primer orden (o primer momento central) es igual a
para SV discreto;
para CB continuo; es decir, para cualquier SV y no contiene ninguna información sobre las propiedades estadísticas de este SV.
El momento central de segundo orden (o segundo momento central) es igual a
 , para SV discreto;
, para SV discreto;
 , para SV continuo.
, para SV continuo.
Como quedará claro a continuación, este punto es uno de los más importantes en la teoría de la probabilidad, ya que se utiliza como una característica de la medida de dispersión (o dispersión) de los valores de SV, por lo que a menudo se le llama dispersión y es designado D X. Tenga en cuenta que esto puede entenderse como el cuadrado medio del SV centrado.
El momento central de tercer orden (tercer momento central) es igual a
Encontremos la expectativa matemática. X 2 :
METRO(X 2) = 1* 0, 6 + 4* 0, 2 + 25* 0, 19+ 10000* 0, 01 = 106, 15.
Vemos eso METRO(X 2) mucho más METRO(X). Esto se debe a que después de elevar al cuadrado posible significado cantidades X 2 correspondiente al valor X=100 magnitud X, se volvió igual a 10.000, es decir aumentó significativamente; la probabilidad de este valor es baja (0,01).
Así, la transición de METRO(X)A METRO(X 2) permitió tener mejor en cuenta la influencia en la expectativa matemática de ese valor posible, que es grande y tiene una probabilidad baja. Por supuesto, si el valor X tenía varios valores grandes e improbables, entonces la transición al valor X 2, y más aún a las cantidades X 3 , X 4, etc., nos permitirían “fortalecer aún más el papel” de estos valores importantes, pero poco probables, posibles. Por eso resulta aconsejable considerar la expectativa matemática del conjunto grado positivo variable aleatoria (no solo discreta, sino también continua).
Momento inicial de orden k variable aleatoria X se llama expectativa matemática de una cantidad Xk:
v k = M(X).
En particular,
v 1 = METRO(X), v 2 = METRO(X 2).
Usando estos puntos, la fórmula para calcular la varianza D(X)= METRO(X 2)- [METRO(X)] 2 se puede escribir así:
D(X)=v 2 – . (*)
Además de los momentos de la variable aleatoria. X es aconsejable considerar momentos de desviación XM(X).
El momento central de orden k de una variable aleatoria X es la esperanza matemática de la cantidad(HM(X))k:
En particular,
Las relaciones que conectan los momentos inicial y central se derivan fácilmente. Por ejemplo, comparando (*) y (***), obtenemos
metro 2 = v 2 – .
No es difícil, a partir de la definición del momento central y utilizando las propiedades de la expectativa matemática, obtener las fórmulas:
metro 3 = v 3 – 3v 2 v 1 + 2 ,
metro 4 = v 4 – 4v 3 v 1 + 6v 2 + 3 .
Rara vez se utilizan momentos de orden superior.
Comentario. Los puntos aquí discutidos se denominan teórico. A diferencia de los momentos teóricos, los momentos que se calculan a partir de datos de observación se denominan empírico. A continuación se dan definiciones de momentos empíricos (véase el capítulo XVII, § 2).
Tareas
1. Se conocen las varianzas de dos variables aleatorias independientes: D(X) = 4, D(Y)=3. Encuentra la varianza de la suma de estas cantidades.
Reps. 7.
2. Varianza de una variable aleatoria X es igual a 5. Encuentre la varianza de las siguientes cantidades: a) X-1; segundo) -2 X; V) Z H + 6.
Reps. a) 5; segundo) 20; c) 45.
3. Valor aleatorio X toma sólo dos valores: +C y -C, cada uno con una probabilidad de 0,5. Encuentra la varianza de esta cantidad.
Reps. CON 2 .
4. , conociendo la ley de su distribución
| X | 0, 1 | |||
| PAG | 0, 4 | 0, 2 | 0, 15 | 0, 25 |
Reps. 67,6404.
5. Valor aleatorio X puede tomar dos valores posibles: X 1 con probabilidad 0,3 y X 2 con probabilidad 0,7, y X 2 >x 1 . Encontrar X 1 y X 2, sabiendo que METRO(X) = 2, 7i D(X) =0,21.
Reps. X 1 = 2, X 2 = 3.
6. Encuentra la varianza de una variable aleatoria. X-número de ocurrencias de eventos A en dos pruebas independientes, Si METRO(X) = 0, 8.
Nota. Escribir ley binomial distribución de probabilidad del número de ocurrencias de un evento A en dos ensayos independientes.
Reps. 0, 48.
7. Se está probando un dispositivo que consta de cuatro dispositivos que funcionan de forma independiente. Las probabilidades de falla del dispositivo son las siguientes: R 1 = 0,3; R 2 = 0,4; pag 3 = 0,5; R 4 = 0,6. Encuentre la expectativa matemática y la varianza del número de dispositivos fallidos.
Reps. 1,8; 0,94.
8. Encuentra la varianza de una variable aleatoria. X- el número de ocurrencias del evento en 100 ensayos independientes, en cada uno de los cuales la probabilidad de que ocurra el evento es 0,7.
Reps. 21.
9. Varianza de una variable aleatoria D(X) = 6,25. Encuentre la desviación estándar s( X).
Reps. 2, 5.
10. La variable aleatoria está especificada por la ley de distribución.
| X | |||
| PAG | 0, 1 | 0, 5 | 0, 4 |
Encuentre la desviación estándar de este valor.
Reps. 2, 2.
11. La varianza de cada una de las 9 variables aleatorias mutuamente independientes distribuidas idénticamente es igual a 36. Encuentre la varianza de la media aritmética de estas variables.
Reps. 4.
12. La desviación estándar de cada una de las 16 variables aleatorias mutuamente independientes distribuidas idénticamente es 10. Encuentre la desviación estándar de la media aritmética de estas variables.
Reps. 2,5.
Capítulo Nueve
LEY DE LOS GRANDES NÚMEROS
Observaciones preliminares
Como ya se sabe, es imposible predecir con seguridad de antemano cuál de los posibles valores tomará una variable aleatoria como resultado de la prueba; Depende de muchas razones aleatorias que no se pueden tener en cuenta. Parecería que, dado que disponemos de información muy modesta sobre cada variable aleatoria en este sentido, es casi imposible establecer patrones de comportamiento y sumas suficientemente gran número variables aleatorias. Actualmente, esto no es verdad. Resulta que bajo ciertas condiciones relativamente amplias, el comportamiento global de un número suficientemente grande de variables aleatorias casi pierde su carácter aleatorio y se vuelve natural.
Para la práctica, es muy importante conocer las condiciones en las que la acción combinada de muchas causas aleatorias conduce a un resultado casi independiente del azar, ya que permite prever el curso de los fenómenos. Estas condiciones se indican en los teoremas que llevan nombre común ley números grandes. Estos incluyen los teoremas de Chebyshev y Bernoulli (hay otros teoremas que no se analizan aquí). El teorema de Chebyshev es el más ley común Para números grandes, el teorema de Bernoulli es el más simple. Para demostrar estos teoremas usaremos la desigualdad de Chebyshev.
La desigualdad de Chebyshev
La desigualdad de Chebyshev es válida para variables aleatorias discretas y continuas. Por simplicidad, nos limitamos a demostrar esta desigualdad para cantidades discretas.
Considere una variable aleatoria discreta X, especificado por la tabla de distribución:
| X | X 1 | X 2 | … | xn |
| pag | pag 1 | PAG 2 | … | pn |
Plantémonos la tarea de estimar la probabilidad de que la desviación de una variable aleatoria de su expectativa matemática no exceda valor absoluto numero positivo mi. Si e es lo suficientemente pequeño, entonces estimaremos la probabilidad de que X tomará valores bastante cercanos a su expectativa matemática. P. L. Chebyshev demostró una desigualdad que nos permite dar la estimación que nos interesa.
La desigualdad de Chebyshev. La probabilidad de que la desviación de una variable aleatoria X de su expectativa matemática en valor absoluto sea menor que un número positivo e no sea menor que 1-D(X)/mi 2 :
R(|X-M(X)|< e ) 1-D(X)/mi 2 .
Prueba. Desde eventos que consisten en la implementación de desigualdades. |X-M(X)|
R(|X-M(X)|< e )+R(|X-M(X)| mi)= 1.
De ahí la probabilidad que nos interesa
R(|X-M(X)|< e )= 1-R(|X-M(X)| mi). (*)
Por tanto, el problema se reduce a calcular la probabilidad. R(| HM(X)| mi).
Escribamos la expresión para la varianza de la variable aleatoria. X:
D(X)= [X 1 -METRO(X)] 2 pag 1 + [X 2 -METRO(X)] 2 pag 2 +…+ [xn -M(X)]2p.n.
Obviamente, todos los términos de esta suma no son negativos.
Descartemos aquellos términos para los cuales | xyo-METRO(X)|<mi(para los términos restantes | xj-METRO(X)| mi), Como resultado, la cantidad sólo puede disminuir. Aceptemos asumir, para mayor certeza, que el k los primeros términos (sin pérdida de generalidad, podemos suponer que en la tabla de distribución los valores posibles están numerados exactamente en este orden). De este modo,
D(X) [x k + 1 -METRO(X)] 2 p k + 1 + [x k + 2 -METRO(X)] 2 pag k + z + ... +[xn -M(X)] 2 p.n.
Tenga en cuenta que ambos lados de la desigualdad | xj - METRO(X)| mi (j = k+1, k+ 2, ..., PAG) son positivas, por lo tanto al elevarlas al cuadrado obtenemos la desigualdad equivalente | xj - METRO(X)| 2 mi 2 Usemos esta observación y, reemplazando cada uno de los factores en la suma restante | xj - METRO(X)| 2 en numero mi 2(en este caso la desigualdad sólo puede aumentar), obtenemos
D(X) mi 2 (rk+ 1 +pk+ 2 + … + r n). (**)
Según el teorema de la suma, la suma de las probabilidades rk+ 1 +pk+ 2 + … + r n existe la posibilidad de que X tomará uno, no importa cuál, valor x k + 1 , xk+ 2 ,....xp, y para cualquiera de ellos la desviación satisface la desigualdad | xj - METRO(X)| mi De ello se deduce que la cantidad rk+ 1 +pk+ 2 + … + r n expresa probabilidad
PAG(|X - METRO(X)| mi).
Esta consideración nos permite reescribir la desigualdad (**) de la siguiente manera:
D(X) mi 2 P(|X - METRO(X)| mi),
PAG(|X - METRO(X)| mi)D(X) /mi 2 (***)
Sustituyendo (***) en (*), finalmente obtenemos
PAG(|X - METRO(X)| <mi) 1- D(X) /mi 2 ,
Q.E.D.
Comentario. La desigualdad de Chebyshev tiene una importancia práctica limitada porque a menudo proporciona una estimación aproximada y a veces trivial (sin interés). Por ejemplo, si D(X)> e 2 y por lo tanto D(X)/mi 2 > 1 luego 1 - D(X)/mi 2 < 0; Así, en este caso, la desigualdad de Chebyshev sólo indica que la probabilidad de desviación no es negativa, y esto ya es obvio, ya que cualquier probabilidad se expresa mediante un número no negativo.
La importancia teórica de la desigualdad de Chebyshev es muy grande. A continuación usaremos esta desigualdad para derivar el teorema de Chebyshev.
teorema de chebyshev
El teorema de Chebyshev. Si X 1 , X 2 ,…, X n, ...-variables aleatorias independientes por pares, y sus varianzas están uniformemente acotadas(no exceda un número constante C), entonces no importa cuán pequeño sea el número positivo e, la probabilidad de desigualdad
En otras palabras, bajo las condiciones del teorema
Así, el teorema de Chebyshev establece que si se considera un número suficientemente grande de variables aleatorias independientes con varianzas limitadas, entonces se puede considerar casi confiable un evento que consiste en el hecho de que la desviación de la media aritmética de las variables aleatorias de la media aritmética de sus las expectativas matemáticas serán arbitrariamente grandes en valor absoluto pequeñas
Prueba. Introduzcamos una nueva variable aleatoria en consideración: la media aritmética de variables aleatorias.
=(X 1 +X 2 +…+X norte)/norte.
Encontremos la expectativa matemática. . Usando las propiedades de la expectativa matemática (el factor constante se puede sacar del signo de la expectativa matemática, la expectativa matemática de la suma es igual a la suma de las expectativas matemáticas de los términos), obtenemos
METRO ![]() =
=
![]() . (*)
. (*)
Aplicando la desigualdad de Chebyshev a la cantidad, tenemos
Sustituyendo el lado derecho (***) en la desigualdad (**) (razón por la cual esta última sólo puede fortalecerse), tenemos
De aquí, pasando al límite en , obtenemos
Finalmente, teniendo en cuenta que la probabilidad no puede exceder uno, finalmente podemos escribir
El teorema está demostrado.
Arriba, al formular el teorema de Chebyshev, asumimos que las variables aleatorias tienen expectativas matemáticas diferentes. En la práctica, sucede a menudo que las variables aleatorias tienen la misma expectativa matemática. Obviamente, si volvemos a suponer que las dispersiones de estas cantidades son limitadas, entonces el teorema de Chebyshev será aplicable a ellas.
Denotemos la expectativa matemática de cada una de las variables aleatorias por A; En el caso que nos ocupa, la media aritmética de las expectativas matemáticas, como es fácil de ver, también es igual a A. Podemos formular el teorema de Chebyshev para el caso particular que estamos considerando.
Si X 1 , X 2 , ..., hp...-variables aleatorias independientes por pares que tienen la misma expectativa matemática a, y si las varianzas de estas variables son uniformemente limitadas, entonces no importa cuán pequeño sea el número e>Oh, probabilidad de desigualdad
![]()
será tan cercano a la unidad como se desee si el número de variables aleatorias es lo suficientemente grande.
En otras palabras, bajo las condiciones del teorema habrá igualdad.

La esencia del teorema de Chebyshev.
La esencia del teorema probado es la siguiente: aunque las variables aleatorias independientes individuales pueden tomar valores alejados de sus expectativas matemáticas, la media aritmética de un número suficientemente grande de variables aleatorias con probabilidad alta toma valores cercanos a uno determinado numero constante, es decir, al número ( METRO(X 1)+ METRO(X 2)+...+M(Xp))/PAG(o al número A en un caso especial). En otras palabras, las variables aleatorias individuales pueden tener una dispersión significativa y su media aritmética es dispersamente pequeña.
Por lo tanto, no se puede predecir con seguridad qué valor posible tomará cada una de las variables aleatorias, pero sí se puede predecir qué valor tomará su media aritmética.
Entonces, media aritmética de un número suficientemente grande de variables aleatorias independientes(cuyas varianzas están uniformemente acotadas) pierde el carácter de variable aleatoria. Esto se explica por el hecho de que las desviaciones de cada valor de sus expectativas matemáticas pueden ser tanto positivas como negativas, y en la media aritmética se cancelan entre sí.
El teorema de Chebyshev es válido no sólo para variables aleatorias discretas, sino también continuas; ella resulta ser un ejemplo brillante, confirmando la validez de la doctrina del materialismo dialéctico sobre la conexión entre azar y necesidad.








