Gangguan misterius: sejarah fraktal dan area penerapannya. Fraktal dalam bilangan prima

Perkenalan

Konsep fraktal.................................................. ......................................................4

Sejarah munculnya fraktal…………………………………………………........6

Fraktal aljabar………………..…………………………….8

1. Kumpulan Maldebrod………………………………………...9

   Julia mengatur…………………………………………………11

   Kumpulan Newton (fraktal)…………………………………………………13

   Fraktal (gelembung) Halley………………………………………..14

Penerapan Praktis fraktal……………………………...15

Kesimpulan……………………………………………………………………….19

Daftar referensi……………………………………………………………...…20

Perkenalan

Bahasa sains berubah dengan cepat dunia modern. Sejarah perkembangan fisika sudah ada lebih dari satu abad. Selama ini, sejumlah besar fenomena alam yang beragam telah dipelajari, hukum dasar fisika telah ditemukan yang menjelaskan berbagai fakta eksperimental.

Sebagian besar sistem di alam menggabungkan dua sifat: pertama, mereka sangat besar, sering kali memiliki banyak segi, beragam dan kompleks, dan Kedua mereka terbentuk di bawah pengaruh sangat Bukan jumlah besar pola sederhana, dan berkembang lebih jauh, dengan menaati pola sederhana ini. Ini adalah yang paling banyak sistem yang berbeda, mulai dari kristal dan gugus saja (berbagai jenis akumulasi, seperti awan, sungai, gunung, benua, bintang), diakhiri dengan ekosistem dan objek biologis(dari daun pakis hingga otak manusia). Fraktal hanyalah objek seperti itu: di satu sisi, kompleks (mengandung banyak elemen tak terhingga), di sisi lain, dikonstruksi menurut sangat hukum sederhana. Berkat sifat ini, fraktal memiliki banyak kesamaan dengan banyak objek alam. Tapi fraktalnya lebih baik dibandingkan dengan objek alami fakta bahwa fraktal memiliki definisi matematis yang ketat dan dapat dideskripsikan serta dianalisis secara ketat. Oleh karena itu, teori fraktal memungkinkan untuk memprediksi laju pertumbuhan sistem perakaran tanaman, biaya tenaga kerja untuk mengeringkan rawa, ketergantungan massa jerami pada tinggi pucuk, dan masih banyak lagi. Ini adalah arah baru dalam matematika yang telah dibuat paradigma ilmiah sebuah revolusi yang signifikansinya sebanding dengan teori relativitas dan mekanika kuantum. Objek geometri fraktal dengan caranya sendiri penampilan sangat berbeda dari bentuk geometris “biasa” yang biasa kita gunakan. Faktanya, ini merupakan sebuah terobosan deskripsi matematika sistem yang untuk waktu yang lama tidak dapat dideskripsikan seperti itu.

Geometri fraktal tidak “murni” teori geometri. Ini lebih merupakan sebuah konsep tampilan baru pada hal-hal terkenal, restrukturisasi persepsi, memaksa peneliti untuk melihat dunia dengan cara baru.

Tujuan dari pekerjaan saya adalah untuk mengenal konsep "fraktal" dan variasinya "fraktal aljabar".

Konsep fraktal

Relatif baru-baru ini, dalam matematika, gambaran suatu benda muncul, lebih besar, namun mirip dengan garis. Beberapa ilmuwan merasa kesulitan untuk memahami konsep garis yang tidak memiliki lebar, sehingga mereka secara bertahap mulai mempelajarinya bentuk geometris dan struktur yang memiliki dimensi spasial pecahan. Kurva kontinu yang semua turunannya digantikan oleh kurva putus-putus atau sangat bergerigi. Contoh mencolok dari kurva tersebut adalah lintasan partikel Brown. Dari sinilah konsep fraktal muncul dalam sains.

Fraktal(lat. fractus - hancur, patah, patah) - kompleks sosok geometris, yang mempunyai sifat kemiripan diri, yaitu terdiri dari beberapa bagian yang masing-masing mirip dengan keseluruhan gambar (Gbr. 1). Lebih lanjut dalam arti luas Fraktal dipahami sebagai himpunan titik-titik dalam ruang Euclidean yang mempunyai dimensi metrik pecahan (dalam pengertian Minkowski atau Hausdorff) atau dimensi metrik.

Beras. 1
Perlu dicatat bahwa kata "fraktal" bukanlah istilah matematika dan tidak memiliki aturan yang berlaku umum definisi matematika. Ini dapat digunakan ketika gambar yang dimaksud memiliki salah satu properti berikut:

Ia memiliki struktur non-sepele di semua skala. Berbeda dengan bangun biasa (seperti lingkaran, elips, grafik fungsi lancar): Jika kita melihat pecahan kecil suatu bangun datar dengan skala yang sangat besar, maka akan terlihat seperti pecahan garis lurus. Untuk fraktal, peningkatan skala tidak menyebabkan penyederhanaan struktur; pada semua skala kita akan melihat gambaran yang sama rumitnya.

Apakah mirip dengan diri sendiri atau kira-kira mirip dengan diri sendiri.

Ini memiliki dimensi metrik pecahan.

Banyak objek di alam yang mempunyai sifat fraktal, misalnya pantai, awan, tajuk pohon, sistem peredaran darah dan sistem alveolar pada manusia atau hewan.
Fraktal, terutama di bidang pesawat, populer karena kombinasi keindahannya dengan kemudahan konstruksinya menggunakan komputer.

Sejarah fraktal

Studi tentang fraktal pada pergantian abad ke-19 dan ke-20 lebih bersifat episodik daripada sistematis, karena sebelumnya para ahli matematika terutama mempelajari objek-objek “baik” yang dapat dipelajari dengan menggunakan metode umum dan teori. Pada tahun 1872, matematikawan Jerman Karl Weierstrass membuat sebuah contoh fungsi berkelanjutan, yang tidak terdiferensiasi dimanapun, yaitu tidak mempunyai garis singgung pada salah satu titiknya. Namun konstruksinya sepenuhnya abstrak dan sulit dipahami. Oleh karena itu, pada tahun 1904, Helge von Koch dari Swedia menemukan kurva kontinu yang tidak memiliki garis singgung di mana pun, dan cukup mudah untuk digambar. Ternyata ia memiliki sifat fraktal. Salah satu varian dari kurva ini disebut “kepingan salju Koch”.
Ide kemiripan diri tokoh diangkat oleh orang Prancis Paul Pierre Levy, mentor masa depan Benoit Mandelbrot. Pada tahun 1938, artikelnya “Kurva dan permukaan bidang dan spasial yang terdiri dari bagian-bagian yang serupa dengan keseluruhan” diterbitkan, yang menggambarkan fraktal lain - kurva Levy C. Semua fraktal yang tercantum di atas secara kondisional dapat diklasifikasikan sebagai satu kelas fraktal konstruktif (geometris).
Kelas lainnya adalah fraktal dinamis (aljabar), yang mencakup himpunan Mandelbrot. Penelitian pertama ke arah ini dimulai pada awal abad ke-20 dan dikaitkan dengan nama matematikawan Perancis Gaston Julia dan Pierre Fatu. Pada tahun 1918, karya Julia diterbitkan dengan iterasi kompleks fungsi rasional, yang menggambarkan himpunan Julia, seluruh keluarga fraktal yang berkerabat dekat dengan himpunan Mandelbrot. Karya ini dianugerahi hadiah Akademi Perancis Namun, tidak terdapat satu pun ilustrasi di dalamnya, sehingga tidak mungkin untuk mengapresiasi keindahan objek yang terbuka

Ide pertama geometri fraktal muncul pada abad ke-19. Cantor, dengan menggunakan prosedur rekursif (berulang) sederhana, mengubah garis menjadi kumpulan titik-titik yang tidak terhubung (yang disebut Cantor Dust). Dia akan mengambil garis dan menghapus sepertiga bagian tengah dan kemudian mengulangi hal yang sama dengan bagian yang tersisa. (Gbr. 2)

Beras. 2

Peano menggambar jenis khusus garis.(Gbr. 3)

Beras. 3

Untuk menggambarnya, Peano menggunakan algoritma berikut.

Pada langkah pertama, ia mengambil sebuah garis lurus dan menggantinya dengan 9 ruas yang 3 kali lebih pendek dari panjang garis aslinya (bagian 1 dan 2 gambar). Kemudian dia melakukan hal yang sama pada setiap segmen garis yang dihasilkan. Dan seterusnya tanpa batas. Keunikan garis tersebut adalah memenuhi seluruh bidang. Telah dibuktikan bahwa untuk setiap titik pada bidang dapat dicari suatu titik milik garis Peano.

Kurva Peano dan debu Cantor melampaui objek geometris biasa. Mereka tidak mempunyai dimensi yang jelas. Debu Cantor sepertinya dibangun berdasarkan garis lurus satu dimensi, tetapi terdiri dari titik-titik (dimensi 0). Dan kurva Peano dibangun berdasarkan garis satu dimensi, dan hasilnya adalah sebuah bidang. Di banyak bidang ilmu pengetahuan lainnya, muncul masalah-masalah yang penyelesaiannya membuahkan hasil yang aneh, serupa dengan yang dijelaskan di atas ( gerak Brown, harga saham).

Hingga abad ke-20, data mengenai hal tersebut benda aneh, tanpa ada upaya untuk mensistematisasikannya. Sampai Benoit Mandelbrot, bapak geometri fraktal modern dan kata fraktal, mempelajarinya. Secara bertahap membandingkan fakta, ia sampai pada penemuan arah baru dalam matematika - geometri fraktal.

Untuk membayangkan fraktal dengan lebih jelas, mari kita perhatikan contoh yang diberikan dalam buku B. Mandelbrot “The Fractal Geometry of Nature”, yang telah menjadi buku klasik - “Berapa panjang pantai Inggris?” Jawaban atas pertanyaan ini tidak sesederhana kelihatannya. Itu semua tergantung pada panjang alat yang digunakan. Dengan mengukur pantai menggunakan penggaris kilometer, mereka memperoleh panjang tertentu. Namun, banyak teluk dan semenanjung kecil yang terlewatkan, yang ukurannya jauh lebih kecil dari penggaris yang diukur. Dengan memperkecil ukuran penggaris menjadi 1 meter, ternyata panjang pantai akan menjadi lebih panjang. Apabila mengukur panjang tepian menggunakan penggaris milimeter, dengan memperhatikan bagian-bagian yang lebih besar dari satu milimeter, maka panjangnya akan semakin besar. Akibatnya, jawaban atas pertanyaan yang tampaknya sederhana ini dapat membingungkan siapa pun - panjang pantai Inggris tidak ada habisnya.

Fraktal aljabar

Fraktal aljabar mendapatkan namanya karena dibuat berdasarkan basis rumus aljabar. Ada beberapa metode untuk memperoleh fraktal aljabar. Salah satu caranya adalah dengan menghitung fungsi secara berulang, dimanaz - bilangan kompleks, dan f adalah fungsi tertentu. Perhitungan fungsi ini berlanjut hingga kondisi tertentu terpenuhi. Dan jika kondisi ini terpenuhi, sebuah titik akan ditampilkan di layar. Dalam hal ini, nilai fungsi untuk poin yang berbeda bidang kompleks mungkin punya perilaku yang berbeda:

cenderung tak terbatas seiring berjalannya waktu;

cenderung 0;
mengambil beberapa nilai tetap dan tidak melampauinya;
perilakunya kacau, tanpa tren apa pun.

3.1 Himpunan Mandelbrot

Himpunan Mandelbrot (salah satu objek fraktal paling terkenal) pertama kali dibuat (secara visual menggunakan komputer) oleh Benoit Mandelbrot pada musim semi tahun 1980 di pusat penelitian Perusahaan IBM dinamai menurut namanya. Thomas J.Watson. Dan meskipun penelitian terhadap objek semacam itu dimulai pada abad terakhir, penemuan kumpulan ini dan peningkatan perangkat kerasnya merupakan hal yang penting grafik komputer V derajat yang menentukan mempengaruhi perkembangan geometri fraktal dan teori chaos. Jadi, apa himpunan Mandelbrot itu?

Pertimbangkan fungsi variabel kompleks. Ayo taruhdan pertimbangkan urutannya, di mana untuk apa pun. Barisan seperti itu dapat dibatasi (yaitu dapat terdapat r sedemikian sehingga untuk sembarang) atau “lari hingga tak terhingga” (yaitu untuk r > 0 apa pun yang ada). Himpunan Mandelbrot dapat didefinisikan sebagai himpunan bilangan kompleks c yang barisan tertentunya dibatasi. Sayangnya, hal itu tidak diketahui ekspresi analitis, yang memungkinkan c tertentu menentukan apakah ia termasuk dalam himpunan Mandelbrot atau tidak. Oleh karena itu, untuk membangun suatu himpunan, digunakan eksperimen komputer: mereka melihat himpunan titik-titik pada bidang kompleks dengan langkah tertentu, dan untuk setiap titik mereka melaksanakannya. sejumlah tertentu iterasi (temukan sejumlah anggota urutan) dan perhatikan “perilakunya”. (Gbr. 4).

Himpunan Mandelbrot terbukti terletak pada lingkaran dengan jari-jari r=2 dan berpusat di titik asal. Jadi, jika pada suatu langkah modulus suku berikutnya dari barisan tersebut melebihi 2, kita dapat segera menyimpulkan bahwa titik yang bersesuaian dengan c, yang mendefinisikan barisan ini, tidak termasuk dalam himpunan Mandelbrot.

Dengan mengurangi langkah pemindaian bilangan kompleks dan meningkatkan jumlah iterasi, kita dapat memperoleh gambar sedetail yang kita suka, namun selalu hanya perkiraan gambar dari himpunan tersebut.

Mari kita punya N warna, diberi nomor untuk kepastian dari 0 hingga N-1. Kita asumsikan, sekali lagi untuk kepastian, bahwa warna hitam mempunyai angka 0. Jika untuk suatu c tertentu setelah iterasi N-1 titiknya tidak melampaui lingkaran berjari-jari 2, kita asumsikan bahwa c termasuk dalam himpunan Mandelbrot dan catlah ini poin c berwarna hitam. Sebaliknya, jika pada langkah tertentu k (k Є ) titik berikutnya berada di luar lingkaran berjari-jari 2 (yaitu, pada langkah ke-k kita menyadari bahwa titik tersebut “melarikan diri”), kita akan mengecatnya dengan warna k.

Gambar indah diperoleh ketika pilihan yang bagus palet dan lingkungan himpunan (yaitu, di luar himpunan kita akan mendapatkan “titik berwarna”) (Gbr. 5, 6).

Beras. 4

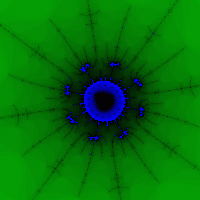
Beras. 5 Gambar. 6

3.2 Julia siap

Himpunan Julia, yang berkerabat dekat dengan himpunan Mandelbrot, dipelajari pada awal abad ke-20 oleh ahli matematika Gaston Julia dan Pierre Fatou (lihat). Pada tahun 1917-1919 Mereka memperoleh hasil mendasar terkait fungsi iterasi dari variabel kompleks. Secara umum, fakta ini perlu didiskusikan secara terpisah dan merupakan contoh yang mengesankan penelitian matematika, beberapa dekade lebih maju dari masanya (para ilmuwan hanya dapat membayangkan secara kasar seperti apa objek yang mereka pelajari!), namun kami hanya akan menjelaskan metode untuk menyusun himpunan Julia untuk fungsi variabel kompleks. Lebih tepatnya, kita akan membangun apa yang disebut. "mengisi set Julia".

Perhatikan sebuah persegi panjang (x 1 ;y 1 )-(X 2 ;y 2 ). Mari kita perbaiki konstanta c dan mulai melihat titik-titik persegi panjang yang dipilih dengan langkah tertentu. Untuk setiap titik, seperti dalam membangun himpunan Mandelbrot, kita akan melakukan serangkaian iterasi (daripada jumlah yang lebih besar iterasi, semakin akurat himpunan yang diperoleh). Jika setelah serangkaian iterasi titik tersebut tidak “melarikan diri” melampaui batas lingkaran berjari-jari 2, kita akan mengecatnya dengan warna hitam, sebaliknya dengan warna dari palet. (Gbr. 7, 8, 9, 10).

Beras. 7

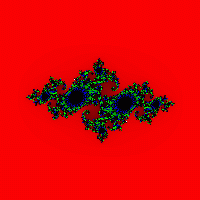
Gambar.8 Gambar. 9

Beras. 10

3.3 Kumpulan Newton (fraktal)

Jenis fraktal dinamis lainnya adalah fraktal Newton (disebut cekungan). (Gbr. 11). Rumus konstruksinya didasarkan pada metode solusi persamaan nonlinier, yang ditemukan oleh ahli matematika hebat pada abad ke-17. Melamar rumus umum Metode Newton zn+1 = zn - f (zn)/f"(zn), n=0, 1, 2… untuk menyelesaikan persamaan f (x)=0 polinomial zk-a, kita memperoleh barisan titik-titik : zn+1 = (k-1)znk/kznk-1, n=0, 1, 2... Memilih berbagai bilangan kompleks z0 sebagai perkiraan awal, kita akan memperoleh barisan yang konvergen ke akar-akar polinomial ini mempunyai tepat k akar, maka seluruh bidang tersebut dibagi menjadi k bagian – daerah tarikan akar.

Beras. 11

3.4 Fraktal (gelembung) Halley

Fraktal seperti itu diperoleh jika, sebagai aturan untuk membangun fraktal dinamis, rumus Halley digunakan untuk menemukan nilai perkiraan akar suatu fungsi. (Gbr. 12).

Metode ini terdiri dari serangkaian iterasi:

Ide metodenya hampir sama dengan yang digunakan untuk menggambar fraktal dinamis: kita ambil beberapa nilai awal(seperti biasa, yang kita bicarakan nilai variabel dan fungsi) dan terapkan rumus tersebut berkali-kali, sehingga diperoleh barisan angka. Hampir selalu konvergen ke salah satu angka nol dari fungsi tersebut (yaitu, nilai variabel di mana fungsi tersebut bernilai 0). Metode Halley, meskipun rumusnya rumit, berhasil lebih efektif dibandingkan metode tersebut : Urutan konvergen ke fungsi nol lebih cepat.

Beras. 12

Penerapan praktis fraktal

Fraktal menemukan segalanya penerapan yang lebih besar dalam sains. Alasan utama untuk ini adalah penjelasannya dunia nyata terkadang bahkan lebih baik daripada fisika atau matematika tradisional. Berikut beberapa contohnya.

Sistem komputer

Dari semua gambar yang dapat dibuat oleh komputer, hanya sedikit yang dapat bersaing dengan gambar fraktal yang sedang kita bicarakan tentang kecantikan sejati.

Paling penggunaan yang berguna Fraktal dalam ilmu komputer adalah kompresi data fraktal. Jenis kompresi ini didasarkan pada kenyataan bahwa dunia nyata digambarkan dengan baik oleh geometri fraktal. Pada saat yang sama, gambar dikompresi jauh lebih baik dibandingkan dengan metode konvensional (seperti jpeg atau gif). Keuntungan lain dari kompresi fraktal adalah ketika gambar diperbesar, tidak ada efek pikselasi (memperbesar ukuran titik ke ukuran yang mendistorsi gambar). Dengan kompresi fraktal, setelah diperbesar, gambar sering kali terlihat lebih baik dari sebelumnya.

Mekanika fluida

Studi tentang turbulensi arus telah diadaptasi dengan sangat baik

fraktal. Aliran turbulen bersifat kacau sehingga sulit untuk dimodelkan secara akurat. Dan di sini transisi ke representasi fraktal membantu, yang sangat memudahkan pekerjaan para insinyur dan fisikawan, memungkinkan mereka untuk lebih memahami dinamika aliran kompleks.

Dengan menggunakan fraktal, Anda juga dapat menyimulasikan api.

Bahan berpori terwakili dengan baik dalam bentuk fraktal karena memiliki geometri yang sangat kompleks. Ini digunakan dalam ilmu perminyakan.

Telekomunikasi

Untuk mengirimkan data jarak jauh, antena dengan

bentuk fraktal, yang sangat mengurangi ukuran dan beratnya. Fraktal digunakan untuk menggambarkan kelengkungan permukaan. Permukaan yang tidak rata ditandai dengan kombinasi dua fraktal yang berbeda.
Obat

Interaksi biosensori. Denyut jantung.
Biologi

Pemodelan proses chaos, khususnya saat mendeskripsikan model populasi.
Nanoteknologi

Dalam kasus nanoteknologi, fraktal juga berperan peran penting, karena, karena pengorganisasian mandiri secara hierarkis, banyak sistem nano memiliki dimensi non-integer, yaitu fraktal dalam sifat geometris, fisikokimia, atau fungsionalnya. Misalnya, contoh cemerlang sistem fraktal kimia adalah molekul "dendrimer » . (Gbr. 13)

Beras. 13

Literatur

Di antara karya sastra temukan yang memiliki sifat fraktal tekstual, struktural, atau semantik. Dalam fraktal teks, unsur-unsur teks berpotensi diulang tanpa henti (“Pendeta mempunyai seekor anjing...”, “Perumpamaan filsuf yang bermimpi bahwa ia adalah seekor kupu-kupu yang bermimpi bahwa ia adalah seorang filsuf yang bermimpi...” dan teks dengan ekstensi (“Rumah yang dia bangun Jack”)

Dalam fraktal struktural, skema teks berpotensi fraktal: karangan bunga soneta (15 puisi), karangan bunga soneta (211 puisi), karangan bunga soneta (2455 puisi).

Kesimpulan

Fraktal adalah objek dengan kompleksitas tak terbatas, memungkinkan Anda melihat detailnya dari dekat maupun dari jauh. Bumi -contoh klasik objek fraktal. Dari luar angkasa terlihat seperti bola. Jika kita mendekatinya, kita akan menemukan lautan, benua, garis pantai, dan barisan pegunungan. Mari kita lihat pegunungan lebih dekat - detail yang lebih halus akan terlihat: sebidang tanah di permukaan gunung, dalam skalanya, sama rumit dan tidak ratanya dengan gunung itu sendiri. Dan pembesaran yang lebih besar lagi akan memperlihatkan partikel-partikel kecil tanah, yang masing-masing merupakan objek fraktal.

Sebagai kesimpulan, saya ingin mengatakan bahwa setelah fraktal ditemukan, menjadi jelas bagi banyak ilmuwan bahwa bentuk geometri Euclidean lama yang baik jauh lebih rendah daripada kebanyakan objek alam karena tidak adanya ketidakteraturan, ketidakteraturan, dan ketidakpastian di dalamnya. Ada kemungkinan bahwa ide-ide baru dalam geometri fraktal akan membantu mempelajari banyak hal fenomena misterius alam sekitar. Saat ini, fraktal dengan cepat menyerang banyak bidang fisika, biologi, kedokteran, sosiologi, dan ekonomi. Metode pemrosesan gambar dan pengenalan pola yang menggunakan konsep-konsep baru memungkinkan peneliti untuk menerapkan peralatan matematika ini deskripsi kuantitatif jumlah yang sangat besar benda dan struktur alam.

Daftar literatur bekas

1. Pengenalan fraktal,

2. Zhikov V.V. Di set Julia. // Ilmu pengetahuan alam modern: Ensiklopedia: Dalam 10 jilid.T.1: Matematika. Mekanika. M., 2000.

3. Zhikov V.V. // Ilmu pengetahuan alam modern: Ensiklopedia: Dalam 10 jilid. Mekanika. M., 2000.

4. Mandelbrot B. Geometri alam fraktal. – M: Lembaga Penelitian Komputer, 2002.

5. Morozov A.D. Pengantar teori fraktal. -Moscow-Izhevsk: Institute of Computer Research, 2002, 160 halaman.

6. Fraktal dinamis (aljabar) // Elemen.. URL:http:// elemen. ru/ poster/ fraktal/ dinamis

7. Fraktal dinamis (aljabar) // Elemen.. URL:http:// elementy.ru/posters/fractals/Mandelbrot#nop

8. Fraktal aljabar // Fraktal.. URL:http://rusproject.narod.ru/article/fractals.htm

Kupu-kupu tentu saja tidak tahu apa-apa tentang ular. Tapi burung pemburu kupu-kupu tahu tentang mereka. Burung yang tidak mengenali ular dengan baik lebih mungkin...

Fraktal (Dinamis).

Fraktal jenis ini muncul ketika mempelajari sistem dinamis nonlinier (sesuai dengan namanya). Perilaku sistem seperti itu dapat dijelaskan secara kompleks fungsi nonlinier(polinomial) f(z). Mari kita ambil titik awal z0 pada bidang kompleks. Sekarang perhatikan barisan bilangan tak terhingga pada bidang kompleks, yang masing-masing diperoleh dari bilangan sebelumnya: z0, z1 = f(z0), z2 = f(z1), ... zn+1 = f(zn). Tergantung pada titik awal z0 barisan seperti itu dapat berperilaku berbeda: cenderung tak terhingga sebagai n → ∞; menyatu dengan beberapa orang titik akhir; secara siklis mengambil serangkaian nilai tetap; Opsi yang lebih kompleks juga dimungkinkan.

Jadi, setiap titik z pada bidang kompleks memiliki perilakunya sendiri selama iterasi fungsi f(z), dan seluruh bidang dibagi menjadi beberapa bagian. Selain itu, titik-titik yang terletak pada batas-batas bagian-bagian ini memiliki sifat-sifat berikut: dengan perpindahan kecil yang sewenang-wenang, sifat perilakunya berubah secara tajam (titik-titik tersebut disebut titik bifurkasi). Jadi, ternyata himpunan titik yang mempunyai satu jenis perilaku tertentu, serta himpunan titik bifurkasi, sering kali mempunyai sifat fraktal. Ini adalah himpunan Julia untuk fungsi f(z).

Himpunan Mandelbrot dibangun agak berbeda. Perhatikan fungsi fc(z) = z2 + c, dimana c adalah bilangan kompleks. Mari kita buat barisan fungsi ini dengan z0 = 0; bergantung pada parameter c, ia dapat menyimpang hingga tak terhingga atau tetap terbatas. Selain itu, semua nilai c yang barisan ini dibatasi membentuk himpunan Mandelbrot. Ini dipelajari secara rinci oleh Mandelbrot sendiri dan ahli matematika lainnya, yang menemukan banyak hal properti yang menarik dari orang banyak ini.

Terlihat bahwa definisi himpunan Julia dan Mandelbrot serupa satu sama lain. Faktanya, kedua rangkaian ini berkaitan erat. Yaitu, himpunan Mandelbrot adalah semua nilai parameter kompleks c yang himpunan Julia fc(z) terhubung (suatu himpunan disebut terhubung jika tidak dapat dibagi menjadi dua bagian yang terpisah-pisah, dengan beberapa syarat tambahan).

Ini yang paling banyak kelompok besar fraktal. Mereka diperoleh dengan menggunakan proses nonlinier di ruang berdimensi n. Proses dua dimensi adalah yang paling banyak dipelajari. Menafsirkan proses iteratif nonlinier sebagai sistem dinamis diskrit, seseorang dapat menggunakan terminologi teori sistem ini: potret fase, proses keadaan tunak, penarik, dll.

Diketahui bahwa sistem dinamis nonlinier mempunyai beberapa keadaan stabil. Keadaan di mana sistem dinamis menemukan dirinya sendiri setelah sejumlah iterasi tertentu bergantung pada keadaan awalnya. Oleh karena itu, setiap keadaan stabil (atau, seperti yang mereka katakan, penarik) memiliki wilayah keadaan awal tertentu, yang darinya sistem tersebut pasti akan masuk ke keadaan akhir yang sedang dipertimbangkan. Dengan demikian ruang fase sistem ini dibagi menjadi area daya tarik penarik. Jika ruang fasenya dua dimensi, maka warnai daerah tarik-menariknya warna yang berbeda, Anda dapat memperoleh potret fase warna dari sistem ini (proses berulang). Dengan mengubah algoritma pemilihan warna, Anda bisa mendapatkan pola fraktal yang kompleks dengan pola multiwarna yang aneh. Kejutan bagi ahli matematika adalah kemampuan untuk menghasilkan struktur non-trivial yang sangat kompleks menggunakan algoritma primitif.

Sebagai contoh, perhatikan himpunan Mandelbrot (lihat Gambar 3 dan Gambar 4). Algoritme konstruksinya cukup sederhana dan didasarkan pada ekspresi iteratif sederhana:

Z = Z[i] * Z[i] + C,

dimana Zi dan C adalah variabel kompleks. Iterasi dilakukan untuk setiap titik awal C dari wilayah persegi panjang atau persegi - bagian dari bidang kompleks. Proses iteratif berlanjut hingga Z[i] melampaui lingkaran berjari-jari 2 yang pusatnya terletak di titik (0,0), (artinya penariknya sistem dinamis berada di tak terhingga), atau setelah cukup jumlah besar iterasi (misalnya 200-500) Z[i] akan berkumpul di suatu titik pada lingkaran. Bergantung pada jumlah iterasi selama Z[i] tetap berada di dalam lingkaran, Anda dapat mengatur warna titik C (jika Z[i] tetap berada di dalam lingkaran untuk jumlah iterasi yang cukup besar, proses iterasi berhenti dan raster ini titik dicat hitam) .

Algoritma di atas memberikan perkiraan terhadap apa yang disebut himpunan Mandelbrot. Himpunan Mandelbrot berisi titik-titik yang, selama jumlah yang tak terbatas iterasi tidak mencapai tak terhingga (titik berwarna hitam). Titik-titik yang termasuk dalam batas himpunan (di sinilah letaknya struktur yang kompleks) pergi hingga tak terhingga untuk nomor akhir iterasi, dan titik-titik yang terletak di luar himpunan menjadi tak terhingga setelah beberapa iterasi (latar belakang putih).

Contoh fraktal aljabar:

• Mandelbrot siap
• Julia siap
• Fraktal Halley
• Fraktal Newton

Saya menemukan fraktal ini ketika saya sedang melihat interferensi gelombang di permukaan sungai. Gelombang bergerak menuju pantai, dipantulkan dan ditumpangkan pada dirinya sendiri. Apakah ada keteraturan dalam pola yang diciptakan gelombang? Mari kita coba menemukannya. Mari kita perhatikan bukan keseluruhan gelombang, tetapi hanya vektor geraknya. Mari kita buat “pantai” mulus untuk menyederhanakan percobaan.

Percobaan dapat dilakukan pada selembar kertas biasa dari buku catatan sekolah.

Atau menggunakan implementasi algoritma JavaScript.

Ambil persegi panjang dengan sisi q dan p. Mari kita kirim sinar (vektor) dari sudut ke sudut. Sinar bergerak ke salah satu sisi persegi panjang, dipantulkan dan terus berpindah ke sisi berikutnya. Hal ini berlanjut hingga sinar mengenai salah satu sudut yang tersisa. Jika ukuran sisi q dan p adalah bilangan koprima, maka diperoleh suatu pola (seperti yang akan kita lihat nanti, fraktal).

Pada gambar kita dapat melihat dengan jelas cara kerja algoritma ini.

Animasi GIF:

Hal yang paling menakjubkan adalah dengan sisi yang berbeda persegi panjang - kita mendapatkan pola yang berbeda.

Mengapa saya menyebut pola ini fraktal? Seperti yang Anda ketahui, “fraktal” adalah bangun datar yang memiliki sifat kesamaan diri. Sebagian gambar mengulangi keseluruhan gambar. Jika kita memperbesar dimensi sisi Q dan P secara signifikan, jelas bahwa pola-pola ini memiliki sifat kesamaan diri.

Mari kita coba meningkatkannya. Kami akan meningkatkannya dengan cara yang licik. Mari kita ambil contoh pola 17x29. Pola berikut akan menjadi: 29x(17+29=46), 46x(29+46=75)…
Satu sisi: F(n);
Sisi kedua: F(n+1)=F(n)+F(n-1);
17, 29, 46, 75, 121, 196, 317, 513, 830, 1343
Seperti bilangan Fibonacci, hanya saja anggota deret pertama dan kedua berbeda: F(0)=17, F(1)=29.

Jika sisi besar genap, hasilnya adalah pola berikut:

Jika sisi terpendeknya genap:

Jika kedua sisinya ganjil, kita mendapatkan pola simetris:

Tergantung pada bagaimana pancaran sinar dimulai:

atau

Saya akan mencoba menjelaskan apa yang terjadi pada persegi panjang ini.

Mari kita pisahkan persegi dari persegi panjang dan lihat apa yang terjadi di perbatasannya.

Sinar keluar pada titik yang sama dengan titik masuknya.

Pada saat yang sama, jumlah kotak yang dilewati sinar selalu genap.

Oleh karena itu, jika Anda memotong persegi dari persegi panjang, bagian fraktal yang tidak berubah akan tetap ada.

Jika Anda memisahkan kotak dari fraktal sebanyak mungkin, Anda bisa sampai ke “awal” fraktal.

Apakah ini terlihat seperti spiral Fibonacci?

Fraktal juga bisa didapat dari bilangan Fibonacci.

Dalam matematika, bilangan Fibonacci (Deret Fibonacci, Deret Fibonacci) adalah bilangan:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…
Menurut definisinya, dua digit pertama deret Fibonacci adalah 0 dan 1, dan setiap angka berikutnya sama dengan jumlah dua angka sebelumnya.
F(n)=F(n-1)+F(n-2)
F(0)=0, F(1)=1

Ayo pergi:

Seperti yang bisa kita lihat, semakin dekat rasio aspek mendekati rasio emas, semakin besar detail fraktalnya.

Dalam hal ini, fraktal mengulangi bagian fraktal, diperbesar sebesar .

Alih-alih menggunakan angka Fibonacci, Anda dapat menggunakan ukuran sisi irasional:

Kami mendapatkan fraktal yang sama.

Fraktal yang sama dapat diperoleh dalam bentuk persegi jika Anda memotret sinar pada sudut yang berbeda:

Apa yang bisa Anda katakan sebagai kesimpulan?
Kekacauan juga merupakan keteraturan. Dengan hukumnya sendiri. Urutan ini belum dipelajari, tetapi cukup dapat dipelajari. Dan seluruh keinginan ilmu pengetahuan adalah untuk menemukan pola-pola ini. Dan pada akhirnya menghubungkan potongan-potongan teka-teki untuk melihat gambaran besarnya.
Mari kita lihat permukaan sungai. Kalau dilempar batu, ombak akan datang. Lingkaran yang cukup menerima untuk dipelajari. Kecepatan, periode, panjang gelombang - semua ini dapat dihitung. Namun hingga gelombang mencapai pantai, ia tidak terpantul dan mulai tumpang tindih. Kita mendapat chaos (gangguan) yang sudah sulit dipelajari.
Bagaimana jika kita bergerak dari arah yang berlawanan? Sederhanakan perilaku gelombang sebanyak mungkin. Sederhanakan, temukan polanya, lalu coba gambarkan gambar penuh apa yang terjadi.
Apa yang bisa disederhanakan? Tentunya membuat permukaan reflektif menjadi lurus, tanpa lengkungan. Selanjutnya, alih-alih menggunakan gelombang itu sendiri, gunakan hanya vektor gerak gelombang. Pada prinsipnya, ini cukup untuk membangun algoritma sederhana dan mensimulasikan proses di komputer. Dan itu bahkan cukup untuk membuat “model” perilaku gelombang pada selembar kertas kotak-kotak biasa.
Apa hasilnya? Hasilnya, kita melihatnya di proses gelombang(riak yang sama di permukaan sungai) yang kita alami bukanlah kekacauan, melainkan hamparan fraktal (struktur serupa) di atas satu sama lain.

Mari kita pertimbangkan jenis gelombang lainnya. Seperti diketahui, gelombang elektromagnetik terdiri dari tiga vektor - vektor gelombang dan vektor listrik dan tegangan medan magnet. Seperti yang bisa kita lihat, jika Anda “menangkap” gelombang seperti itu daerah tertutup– dimana vektor-vektor ini berpotongan, kita mendapatkan struktur tertutup yang cukup jelas. Mungkin partikel elementer– apakah ini fraktal yang sama?

Semua fraktal dalam persegi panjang dari 1 hingga 80 (6723x6723 px):

Area tertutup dalam fraktal (6723x6723 px):

Hanya fraktal yang indah (4078x2518 px):