Reševanje enačb in neenačb z modulom pogosto povzroča težave. Vendar, če dobro razumete, kaj je absolutna vrednost števila, In kako pravilno razširiti izraze, ki vsebujejo znak modula, potem prisotnost v enačbi izraz pod znakom modula, preneha biti ovira za njegovo rešitev.

Malo teorije. Vsaka številka ima dve značilnosti: absolutna vrednostštevilo in njegov znak.

Na primer, število +5 ali preprosto 5 ima znak "+" in absolutno vrednost 5.

Število -5 ima znak "-" in absolutno vrednost 5.

Absolutni vrednosti števil 5 in -5 sta 5.

Absolutno vrednost števila x imenujemo modul števila in jo označujemo z |x|.

Kot vidimo, je modul števila enak samemu številu, če je to število večje ali enako nič, in to število z nasprotno znamenje, če je to število negativno.

Enako velja za vse izraze, ki se pojavijo pod znakom modula.

Pravilo razširitve modula izgleda takole:

|f(x)|= f(x), če je f(x) ≥ 0, in

|f(x)|= - f(x), če je f(x)< 0

Na primer |x-3|=x-3, če je x-3≥0 in |x-3|=-(x-3)=3-x, če je x-3<0.

Če želite rešiti enačbo, ki vsebuje izraz pod znakom modula, morate najprej razširite modul v skladu s pravilom razširitve modula.

Nato postane naša enačba ali neenakost v dve različni enačbi, ki obstajata na dveh različnih numeričnih intervalih.

Ena enačba obstaja na numeričnem intervalu, na katerem je izraz pod znakom modula nenegativen.

In druga enačba obstaja na intervalu, kjer je izraz pod znakom modula negativen.

Poglejmo preprost primer.

Rešimo enačbo:

|x-3|=-x 2 +4x-3

1. Odprimo modul.

|x-3|=x-3, če je x-3≥0, tj. če je x≥3

|x-3|=-(x-3)=3-x, če je x-3<0, т.е. если х<3

2. Dobili smo dva številska intervala: x≥3 in x<3.

Poglejmo, v katere enačbe se pretvori izvirna enačba na posameznem intervalu:

A) Za x≥3 |x-3|=x-3 in ima naša poškodba obliko:

Pozor! Ta enačba obstaja le na intervalu x≥3!

Odprimo oklepaje in predstavimo podobne izraze:

in reši to enačbo.

Ta enačba ima korenine:

x 1 =0, x 2 =3

Pozor! ker enačba x-3=-x 2 +4x-3 obstaja samo na intervalu x≥3, nas zanimajo le tisti koreni, ki pripadajo temu intervalu. Ta pogoj je izpolnjen le pri x 2 =3.

B) Pri x<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:

Pozor! Ta enačba obstaja samo na intervalu x<3!

Odprimo oklepaje in predstavimo podobne izraze. Dobimo enačbo:

x 1 =2, x 2 =3

Pozor! saj enačba 3-x=-x 2 +4x-3 obstaja le na intervalu x<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х 1 =2.

Torej: iz prvega intervala vzamemo samo koren x=3, iz drugega - koren x=2.

Točilkina Julija

Delo predstavlja različne metode za reševanje enačb z modulom.

Prenesi:

Predogled:

Občinska proračunska izobraževalna ustanova

"Srednja šola št. 59"

Enačbe z modulom

Abstraktno delo

Izvedeno Učenka 9A razreda

MBOU "Srednja šola št. 59" Barnaul

Točilkina Julija

Nadzornik

Zakharova Ljudmila Vladimirovna,

učiteljica matematike

MBOU "Srednja šola št. 59" Barnaul

Barnaul 2015

Uvod

Sem v devetem razredu. V tem študijskem letu me čaka zaključno spričevalo za osnovni šolski tečaj. Za pripravo na izpit smo kupili zbirko D. A. Maltseva Matematika. 9. razred. Pregledoval sem zbirko in odkril enačbe, ki vsebujejo ne samo enega, ampak tudi več modulov. Učiteljica je meni in mojim sošolcem razložila, da se takšne enačbe imenujejo enačbe »ugnezdenih modulov«. To ime se nam je zdelo nenavadno, rešitev pa je bila na prvi pogled precej zapletena. Tako se je pojavila tema za moje delo "Enačbe z modulom". Odločil sem se, da bom to temo preučil globlje, še posebej, ker mi bo koristila pri opravljanju izpitov ob koncu šolskega leta in mislim, da bo potrebna v 10. in 11. razredu. Vse našteto določa relevantnost teme, ki sem jo izbral.

Cilj dela:

Razmislite o različnih metodah za reševanje enačb z modulom.
Naučite se reševati enačbe, ki vsebujejo predznak absolutne vrednosti z različnimi metodami

Za delo na temi so bile oblikovane naslednje naloge:

Naloge:

Preučite teoretično gradivo na temo »Modul realno število».
Razmislite o metodah reševanja enačb in utrdite pridobljeno znanje z reševanjem nalog.
Uporabite pridobljeno znanje pri reševanju različnih enačb, ki vsebujejo znak modula v srednji šoli

Predmet študija:metode za reševanje enačb z modulom

Predmet študija:enačbe z modulom

Raziskovalne metode:

Teoretično : študij literature o temi raziskovanja;

Internet - informacije.

Analiza informacije, pridobljene s preučevanjem literature; rezultati, dobljeni z reševanjem enačb z modulom na različne načine.

Primerjava metod za reševanje enačb je predmet racionalnosti njihove uporabe pri reševanju različnih enačb z modulom.

"Začnemo razmišljati, ko nekaj zadenemo." Paul Valery.

1. Pojmi in definicije.

Koncept "modula" se pogosto uporablja v številnih delih šolskega tečaja matematike, na primer pri preučevanju absolutnih in relativnih napak približnega števila; v geometriji in fiziki se preučujeta pojma vektor in njegova dolžina (vektorski modul). Koncepti modula se uporabljajo pri predmetih višje matematike, fizike in tehničnih ved, ki se študirajo na visokošolskih ustanovah.

Beseda "modul" izhaja iz latinske besede "modulus", kar pomeni "mera". Ta beseda ima več pomenov in se ne uporablja le v matematiki, fiziki in tehnologiji, ampak tudi v arhitekturi, programiranju in drugih natančnih vedah.

Domneva se, da je izraz predlagal Cotes, Newtonov študent. Znak modula je v 19. stoletju uvedel Weierstrass.

V arhitekturi je modul začetna merska enota, določena za dano arhitekturno strukturo.

V tehniki je to izraz, ki se uporablja na različnih področjih tehnike, z njim označujemo različne koeficiente in količine, na primer modul elastičnosti, modul uprijema ...

V matematiki ima modul več pomenov, vendar ga bom obravnaval kot absolutno vrednost števila.

Definicija 1: Modul (absolutna vrednost) realnega števila A sama ta številka se imenuje, če A ≥0 ali nasprotno število – in če A modul nič enako nič.

Pri reševanju enačb z modulom je priročno uporabiti lastnosti modula.

Oglejmo si dokaze lastnosti 5,6,7.

Trditev 5. Enakost │ a+b │=│ a │+│ b │ drži, če av ≥ 0.

Dokaz. Dejansko po kvadriranju obeh strani te enakosti dobimo │ a+b │²=│ a │²+2│ ab │+│ c │²,

a²+ 2 ab+b²=a²+ 2│ ab │+ b², od koder je │ ab │= ab

In zadnja enakost bo veljala, ko pov ≥0.

Trditev 6. Enakost │ a-c │=│ a │+│ c │ velja, ko pov ≤0.

Dokaz. Za dokaz je dovolj v enakosti

│ а+в │=│ а │+│ в │ zamenjajte v z - в, potem je а· (- в ) ≥0, od koder je av ≤0.

Trditev 7. Enakost │ a │+│ b │= a+b izvedel pri a ≥0 in b ≥0.

Dokaz . Po obravnavanju štirih primerov a ≥0 in b ≥0; a ≥0 in c A v ≥0; A V a ≥0 in b ≥0.

(a-c) v ≥0.

Geometrijska interpretacija

|a| je razdalja na koordinatni premici od točke s koordinato A , do izvora.

|-a| |a|

A 0 a x

Geometrična razlaga pomena |a| jasno potrjuje, da |-a|=|a|

Če 0, potem sta na koordinatni premici dve točki a in –a, enako oddaljeni od nič, katerih modula sta enaka.

Če je a=0, potem na koordinatni premici |a| predstavljeno s točko 0.

Definicija 2: Enačba z modulom je enačba, ki vsebuje spremenljivko pod znakom absolutne vrednosti (pod znakom modula). Na primer: |x +3|=1

Definicija 3: Rešiti enačbo pomeni najti vse njene korenine ali dokazati, da korenin ni.

2. Metode rešitve

Iz definicije in lastnosti modula sledijo glavne metode za reševanje enačb z modulom:

"Razširitev" modula (tj. z uporabo definicije);
Uporaba geometrijskega pomena modula (lastnost 2);
Metoda grafične rešitve;
Uporaba ekvivalentnih transformacij (lastnosti 4.6);
Zamenjava spremenljivke (to uporablja lastnost 5).
Intervalna metoda.

Dovolj sem se odločil veliko število primerov, vendar vam v delu predstavljam le nekaj, po mojem mnenju tipičnih primerov, rešenih na različne načine, ker se ostali podvajajo in da bi razumeli, kako rešiti enačbe z modulom, ni treba upoštevajte vse rešene primere.

REŠEVANJE ENAČB | f(x)| = a

Razmislite o enačbi | f(x)| = a, a R

Enačbo te vrste je mogoče rešiti z definicijo modula:

če A potem enačba nima korenin.

Če je a= 0, potem je enačba enakovredna f(x)=0.

Če je a>0, potem je enačba ekvivalentna množici

Primer. Rešite enačbo |3x+2|=4.

rešitev.

|3x+2|=4, potem 3x+2=4,

3x+2= -4;

X=-2,

X=2/3

ODGOVOR: -2;2/3.

REŠEVANJE ENAČB Z UPORABO GEOMETRIJSKIH LASTNOSTI MODULA.

Primer 1. Rešite enačbo /x-1/+/x-3/=6.

rešitev.

Reševanje te enačbe pomeni iskanje vseh takih točk na numerični osi Ox, za vsako od katerih je vsota razdalj od nje do točk s koordinatama 1 in 3 enaka 6.

Niti ene točke iz segmentatega pogoja ne izpolnjuje, saj vsota navedenih razdalj je 2. Zunaj tega segmenta sta dve točki: 5 in -1.

1 1 3 5

Odgovor: -1;5

Primer 2. Reši enačbo |x 2 +x-5|+|x 2 +x-9|=10.

rešitev.

Označimo x 2 +x-5= a, potem / a /+/ a-4 /=10. Poiščimo točke na osi Ox tako, da je za vsako od njih vsota razdalj do točk s koordinatama 0 in 4 enaka 10. Temu pogoju zadostujeta -4 in 7.

3 0 4 7

Torej x 2 +x-5= 4 x 2 +x-5=7

X 2 +x-2=0 x 2 +x-12=0

X 1= 1, x 2= -2 x 1= -4, x 2= 3 Odgovor: -4;-2; 1; 3.

REŠEVANJE ENAČB | f(x)| = | g(x)|.

Ker | a |=|v |, če je a= v, potem enačba oblike | f(x)| = | g(x )| enakovreden celoti

Primer 1.

Reši enačbo | x –2| = |3 – x |.

rešitev.

Ta enačba je enakovredna dvema enačbama:

x – 2 = 3 – x (1) in x – 2 = –3 + x (2)

2 x = 5 –2 = –3 – napačno

X = 2,5 enačba nima rešitev.

ODGOVOR: 2.5.

Primer 2.

Reši enačbo |x 2 +3x-20|= |x 2 -3x+ 2|.

rešitev.

Ker sta obe strani enačbe nenegativni, torejkvadriranje je enakovredna transformacija:

(x 2 +3x-20) 2 = (x 2 -3x+2) 2

(x 2 +3x-20) 2 - (x 2 -3x+2) 2 =0,

(x 2 +3x-20-x 2 +3x-2) (x 2 +3x-20+x 2 -3x+2)=0,

(6x-22)(2x 2 -18)=0,

6x-22=0 ali 2x 2 -18=0;

X=22/6, x=3, x=-3.

X=11/3

Odgovor: -3; 3; 11/3.

REŠITEV ENAČB POGLEDA | f(x)| = g(x).

Razlika med tema enačbama in| f(x)| =a dejstvo, da je tudi desna stran spremenljivka. In lahko je pozitiven in negativen. Zato morate posebej preveriti, da je nenegativen, ker modul ne more biti enak negativnemu številu (lastnost№1 )

1 način

Rešitev enačbe | f(x)| = g(x ) zmanjša na nabor rešitev enačbin preverjanje pravičnosti neenakosti g(x )>0 za najdene vrednosti neznanke.

Metoda 2 (po definiciji modula)

Ker | f(x)| = g(x), če je f(x) = 0; | f(x)| = - f(x), če je f(x)

Primer.

Reši enačbo |3 x –10| = x – 2.

rešitev.

Ta enačba je enakovredna kombinaciji dveh sistemov:

ODGOVOR: 3; 4.

REŠITEV ENAČB OBLIKE |f 1 (x)|+|f 2 (x)|+…+|f n (x)|=g(x)

Rešitev tovrstnih enačb temelji na definiciji modula. Za vsako funkcijo f 1 (x), f 2 (x), …, f n (x) potrebno je najti definicijsko domeno, njene ničle in diskontinuitetne točke, pri čemer splošno definicijsko domeno razdelimo na intervale, v vsakem od katerih so funkcije f 1 (x), f 2 (x), …, f n (x) obdržijo svoj znak. Nato z uporabo definicije modula za vsako od najdenih področij dobimo enačbo, ki jo je treba rešiti na tem intervalu. Ta metoda dobil ime "intervalna metoda»

Primer.

Rešite enačbo |x-2|-3|x+4|=1.

rešitev.

Poiščimo točke, v katerih so submodularni izrazi enaki nič

x-2=0, x+4=0,

x=2; x=-4.

Razdelimo številsko premico na intervale x

Reševanje enačbe se zmanjša na rešitev treh sistemov:

ODGOVOR: -15, -1,8.

GRAFIČNA METODA ZA REŠEVANJE ENAČB, KI VSEBUJEJO ZNAK MODULA.

Grafični način reševanja enačb je približen, saj je natančnost odvisna od izbranega enotskega odseka, debeline svinčnika, kotov, pod katerimi se premice sekajo itd. Toda ta metoda vam omogoča, da ocenite, koliko rešitev ima dana enačba.

Primer. Grafično rešite enačbo |x - 2| + |x - 3| + |2x - 8| = 9

rešitev. Izdelajmo grafe funkcij v enem koordinatnem sistemu

y=|x - 2| + |x - 3| + |2x - 8| in y=9.

Za izdelavo grafa je potrebno to funkcijo upoštevati na vsakem intervalu (-∞; 2); [ 3/2 ; ∞ )

Odgovor: (- ∞ ; 4/3] [ 3/2 ; ∞ )

Metodo ekvivalentnih transformacij smo uporabili tudi pri reševanju enačb | f(x)| = | g(x)|.

ENAČBE S KOMPLEKSNIM MODULOM

Druga vrsta enačb so enačbe s "kompleksnim" modulom. Take enačbe vključujejo enačbe, ki imajo »module znotraj modula«. Enačbe te vrste je mogoče rešiti z različnimi metodami.

Primer 1.

Reši enačbo ||||x| – |–2| –1| –2| = 2.

rešitev.

Po definiciji modula imamo:

Rešimo prvo enačbo.

||| x |–2| –1| = 4

| x | – 2 = 5;

| x | = 7;

x = 7.

Rešimo drugo enačbo.

||| x | –2| –1| = 0,

|| x | –2| = 1,

| x | –2 = 1,

| x | = 3 in | x | = 1,

x = 3; x = 1.

Odgovor: 1; 3; 7.

Primer 2.

Reši enačbo |2 – |x + 1|| = 3.

rešitev.

Rešimo enačbo z uvedbo nove spremenljivke.

Naj | x + 1| = y, potem |2 – y | = 3, od tukaj

Naredimo obratno zamenjavo:

(1) | x + 1| = –1 – ni rešitev.

(2) | x + 1| = 5

ODGOVOR: –6; 4.

Primer3.

Koliko korenov ima enačba | 2 | x | -6 | = 5 - x?

rešitev. Rešimo enačbo z enakovrednimi shemami.

Enačba | 2 | x | -6 | = 5 je enakovreden sistemu:

A se izračuna v skladu z naslednjimi pravili:

Zaradi jedrnatosti so uporabljeni zapisi |a|. Torej, |10| = 10; - 1/3 = | 1 / 3 |; | -100| =100 itd.

Vsaka velikost X ustreza dokaj natančni vrednosti | X|. In to pomeni identiteta pri= |X| kompleti pri kot nekateri funkcija argumenta X.

Urnik to funkcije predstavljeno spodaj.

Za x > 0 |x| = x, in za x< 0 |x|= -x; v zvezi s tem je vrstica y = | x| pri x> 0 v kombinaciji z ravno črto y = x(simetrala prvega koordinatnega kota), in kdaj X< 0 - с прямой y = -x(simetrala drugega koordinatnega kota).

Ločeno enačbe vključi neznanke pod znak modul.

Poljubni primeri takih enačb - | X— 1| = 2, |6 — 2X| =3X+ 1 itd.

Reševanje enačb ki vsebuje neznanko pod znakom modula, temelji na dejstvu, da če je absolutna vrednost neznanega števila x enaka pozitivnemu številu a, potem je samo to število x enako a ali -a.

Na primer:, če | X| = 10, potem oz X=10 oz X = -10.

Razmislimo reševanje posameznih enačb.

Analizirajmo rešitev enačbe | X- 1| = 2.

Razširimo modul potem razlika X- 1 je lahko enako + 2 ali - 2. Če je x - 1 = 2, potem X= 3; če X- 1 = - 2, torej X= - 1. Naredimo zamenjavo in ugotovimo, da obe vrednosti izpolnjujeta enačbo.

Odgovori. Zgornja enačba ima dva korena: x 1 = 3, x 2 = - 1.

Analizirajmo rešitev enačbe | 6 — 2X| = 3X+ 1.

Po razširitev modula dobimo: ali 6 - 2 X= 3X+ 1 ali 6 - 2 X= - (3X+ 1).

V prvem primeru X= 1, v drugi pa X= - 7.

Pregled. pri X= 1 |6 — 2X| = |4| = 4, 3x+ 1 = 4; izhaja iz sodišča, X = 1 - korenina dano enačbe.

pri x = - 7 |6 — 2x| = |20| = 20, 3x+ 1= - 20; ker je 20 ≠ -20, torej X= - 7 ni koren podana enačba.

Odgovori. U enačba ima samo en koren: X = 1.

Enačbe te vrste so lahko rešiti in grafično.

Torej se odločimo Na primer, grafično enačba | X- 1| = 2.

Najprej bomo zgradili funkcijska grafika pri = |x- 1|. Najprej narišimo graf funkcije pri=X- 1:

Ta del tega grafične umetnosti, ki se nahaja nad osjo X Ne bomo ga spremenili. Za njo X- 1 > 0 in torej | X-1|=X-1.

Del grafa, ki se nahaja pod osjo X, upodobimo simetrično glede na to os. Ker za ta del X - 1 < 0 и соответственно |X - 1|= - (X - 1). Posledično linija(polna črta) in bo graf funkcije y = | X—1|.

Ta črta se bo sekala z naravnost pri= 2 v dveh točkah: M 1 z absciso -1 in M 2 z absciso 3. In v skladu s tem enačba | X- 1| =2 bosta dva korena: X 1 = - 1, X 2 = 3.

Srednja šola MBOU št. 17, Ivanovo

« Enačbe z modulom"
Metodološki razvoj

Sestavljeno

učiteljica matematike

Lebedeva N.V.

20010

Pojasnilo

Poglavje 1. Uvod

Oddelek 2. Osnovne lastnosti Oddelek 3. Geometrična razlaga koncepta modula števila Razdelek 4. Graf funkcije y = |x| Oddelek 5. Konvencije

Poglavje 2. Reševanje enačb, ki vsebujejo modul

Razdelek 1. Enačbe oblike |F(x)| = m (najenostavnejši) Razdelek 2. Enačbe oblike F(|x|) = m Razdelek 3. Enačbe oblike |F(x)| = G(x) Razdelek 4. Enačbe oblike |F(x)| = ± F(x) (najlepši) Razdelek 5. Enačbe oblike |F(x)| = |G(x)| Oddelek 6. Primeri rešitev nestandardne enačbe Razdelek 7. Enačbe oblike |F(x)| + |G(x)| = 0 Razdelek 8. Enačbe oblike |a 1 x ± b 1 | ± |a 2 x ± v 2 | ± …|a n x ± in n | = m Oddelek 9. Enačbe, ki vsebujejo več modulov

Poglavje 3. Primeri reševanja različnih enačb z modulom.

Oddelek 1. Trigonometrične enačbe Razdelek 2. Eksponentne enačbe Oddelek 3. Logaritemske enačbe Oddelek 4. Iracionalne enačbe Oddelek 5. Naloge povečana kompleksnost Odgovori na vaje Bibliografija

Pojasnilo.

Koncept absolutne vrednosti (modula) realnega števila je ena njegovih bistvenih značilnosti. Ta koncept je zelo razširjen v različnih delih fizikalnih, matematičnih in tehničnih znanosti. V praksi poučevanja matematičnih predmetov v srednjih šolah v skladu s programom Ministrstva za obrambo Ruske federacije se koncept "absolutne vrednosti števila" večkrat srečuje: v 6. razredu je definicija modula in predstavljen je njegov geometrijski pomen; v 8. razredu se oblikuje pojem absolutne napake, obravnava se rešitev najpreprostejših enačb in neenačb, ki vsebujejo modul, ter se preučujejo lastnosti aritmetičnega kvadratnega korena; v 11. razredu koncept najdemo v razdelku »Koren n- stopnja." Izkušnje poučevanja kažejo, da se učenci pogosto srečujejo s težavami pri reševanju nalog, ki zahtevajo poznavanje te snovi, in jih pogosto preskočijo, ne da bi jih začeli dokončati. Podobne naloge vsebujejo tudi besedila izpitnih nalog za predmete 9. in 11. razreda. Poleg tega so zahteve, ki jih univerze postavljajo diplomantom, drugačne, in sicer na višji ravni kot zahteve šolskega kurikuluma. Za življenje v sodobni družbi je zelo pomembno oblikovanje matematičnega načina razmišljanja, ki se kaže v določenih miselnih veščinah. V procesu reševanja problemov z moduli je potrebna sposobnost uporabe tehnik, kot so generalizacija in specifikacija, analiza, klasifikacija in sistematizacija ter analogija. Reševanje takšnih nalog vam omogoča, da preizkusite svoje znanje o glavnih delih šolskega tečaja, stopnjo logičnega razmišljanja in začetne raziskovalne sposobnosti. To delo je posvečeno enemu od razdelkov - reševanju enačb, ki vsebujejo modul. Sestavljena je iz treh poglavij. Prvo poglavje predstavlja osnovne koncepte in najpomembnejše teoretične premisleke. Drugo poglavje predlaga devet glavnih tipov enačb, ki vsebujejo modul, razpravlja o metodah za njihovo reševanje in preučuje primere različnih stopenj kompleksnosti. Tretje poglavje ponuja kompleksnejše in nestandardne enačbe (trigonometrične, eksponentne, logaritemske in iracionalne). Za vsako vrsto enačb so vaje za samostojno reševanje (odgovori in navodila so priloženi). Glavni namen tega dela je metodološka pomoč učiteljem pri pripravi na pouk in pri organizaciji izbirnih predmetov. Gradivo se lahko uporablja tudi kot učni pripomoček za srednješolce. Naloge, predlagane v delu, so zanimive in jih ni vedno enostavno rešiti, kar omogoča bolj zavestno izobraževalno motivacijo študentov, preverjanje njihovih sposobnosti in povečanje stopnje pripravljenosti diplomantov za vpis na univerze. Diferenciran izbor predlaganih vaj vključuje prehod z reproduktivne ravni obvladovanja gradiva na ustvarjalno, pa tudi priložnost, da se naučite, kako uporabiti svoje znanje pri reševanju nestandardnih problemov.

Poglavje 1. Uvod.

Oddelek 1. Določitev absolutne vrednosti .

Opredelitev : Absolutna vrednost (modul) realnega števila A nenegativno število imenujemo: A oz -A. Oznaka: │ A │ Vnos se glasi: “modul števila a” ali “absolutna vrednost števila a”

│ a, če je a > 0

│a│ = │ 0, če je a = 0 (1)

│ - in, če a
Primeri: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1
Razširi izrazni modul:
a) │x - 8│, če je x > 12 b) │2x + 3│, če je x ≤ -2 │x – 8│= x – 8 │ 2x + 3│= - 2x – 3
Oddelek 2. Osnovne lastnosti.
Razmislimo o osnovnih lastnostih absolutne vrednosti. Lastnost #1: Nasprotna števila imajo enaki moduli, tj. │а│=│- а│ Pokažimo, da je enakost pravilna. Zapišimo definicijo števila - A : │- a│= (2) Primerjajmo niza (1) in (2). Očitno je, da definicije absolutne vrednostištevilke A in - A ujemati se. torej │а│=│- а│
Z revidiranjem naslednje lastnosti Omejili se bomo na njihovo formulacijo, saj je njihov dokaz podan Lastnost #2: Absolutna vrednost zneska končno število realna števila ne presegajo vsote absolutnih vrednosti izrazov: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │+ … + │а n │ Lastnost #3: Absolutna vrednost razlike med dvema realnima številoma ne presega vsote njunih absolutnih vrednosti: │а - в│ ≤│а│+│в│ Lastnost #4: Absolutna vrednost produkta končnega števila realnih števil je enaka produktu absolutnih vrednosti faktorjev: │а·в│=│а│·│в│ Lastnost #5: Absolutna vrednost kvocienta realnih števil je enaka kvocientu njihovih absolutnih vrednosti:

Oddelek 3. Geometrična razlaga koncepta modula števila.

Vsako realno število lahko povežemo s točko na številski premici, ki bo geometrijska slika podano realno število. Vsaka točka na številski premici ustreza svoji oddaljenosti od izhodišča, tj. dolžina odseka od izhodišča do dane točke. Ta razdalja se vedno obravnava kot nenegativna vrednost. Zato bo dolžina ustreznega segmenta geometrijska interpretacija absolutna vrednost danega realnega števila

Predstavljena geometrijska ilustracija jasno potrjuje lastnost št. 1, tj. modula nasprotnih števil sta enaka. Od tu je enostavno razumljiva veljavnost enakosti: │х – а│= │а – x│. Tudi rešitev enačbe │х│= m, kjer je m ≥ 0, in sicer x 1,2 = ± m, postane bolj očitna. Primeri: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1

x 1,2 = 2; 4

Oddelek 4. Graf funkcije y = │х│

Domena te funkcije so vsa realna števila.

Oddelek 5. Konvencije.

V prihodnje bo pri obravnavi primerov reševanja enačb uporabljeno naslednje simboli: ( - znak sistema [ - znak celote Pri reševanju sistema enačb (neenačb) se najde presečišče rešitev enačb (neenačb), ki so vključene v sistem. Pri reševanju množice enačb (neenačb) se najde unija rešitev, vključenih v množico enačb (neenačb).

Poglavje 2. Reševanje enačb, ki vsebujejo modul.

V tem poglavju si bomo ogledali algebraične metode reševanje enačb, ki vsebujejo enega ali več modulov.

Razdelek 1. Enačbe oblike │F (x)│= m

Enačba te vrste se imenuje najenostavnejša. Ima rešitev, če in samo če je m ≥ 0. Po definiciji modula je izvirna enačba enakovredna nizu dveh enačb: │ F(x)│=m

Primeri:
№1. Rešite enačbo: │7х - 2│= 9

Odgovor: x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

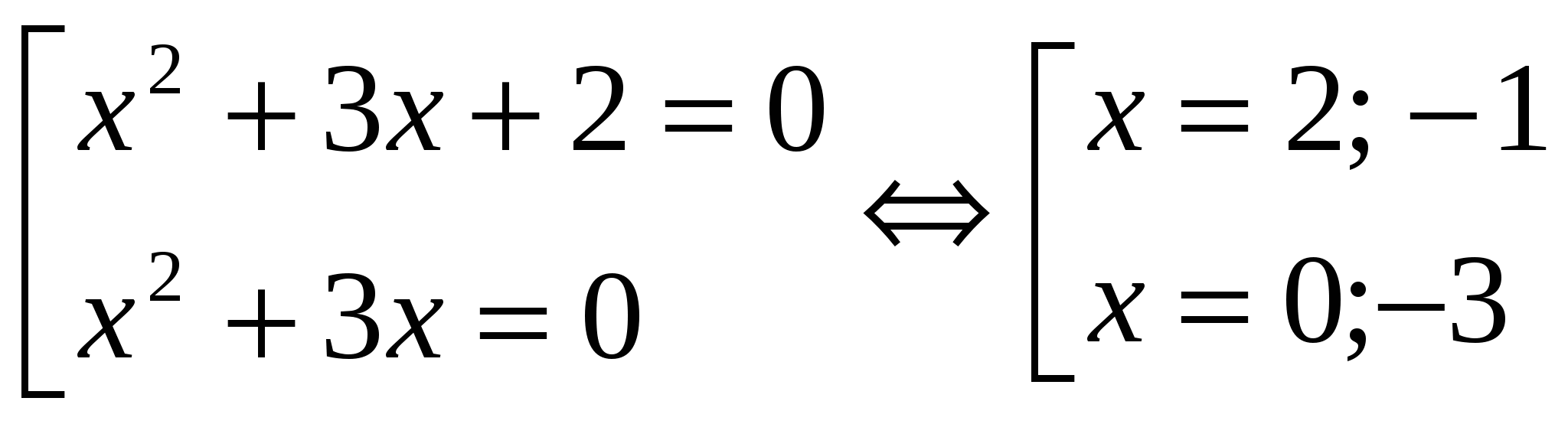x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Odgovor: vsota korenin je - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 pomeni x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – obe vrednosti izpolnjujeta pogoj m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Odgovor: število korenov enačbe 7. vaje:
№1. Rešite enačbo in navedite vsoto korenov: │х - 5│= 3 №2 . Rešite enačbo in označite manjši koren: │x 2 + x│= 0 №3 . Rešite enačbo in označite večji koren: │x 2 – 5x + 4│= 4 №4 .Reši enačbo in označi cela korenina: │2x 2 – 7x + 6│= 1 №5 .Rešite enačbo in označite število korenov: │x 4 – 13x 2 + 50│= 14

Oddelek 2. Enačbe oblike F(│х│) = m

Argument funkcije na levi strani je pod znakom modula in desni del ni odvisen od spremenljivke. Razmislimo o dveh načinih reševanja enačb te vrste. 1 način: Po definiciji absolutne vrednosti je prvotna enačba enakovredna kombinaciji dveh sistemov. V vsakem od njih je podmodularnemu izrazu naložen pogoj. F(│х│) =m

Ker je funkcija F(│x│) soda v celotnem definicijskem področju, sta korena enačb F(x) = m in F(- x) = m pari nasprotnih števil. Zato je dovolj, da rešimo enega od sistemov (pri obravnavanju primerov na ta način bo podana rešitev enega sistema). 2. način: Uporaba metode uvajanja nove spremenljivke. V tem primeru je uveden zapis │x│= a, kjer je a ≥ 0. Ta metoda manj voluminozen dizajn.
Primeri: №1 . Rešite enačbo: 3x 2 – 4│x│= - 1 Uporabimo uvedbo nove spremenljivke. Označimo │x│= a, kjer je a ≥ 0. Dobimo enačbo 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Vrnitev na prvotno spremenljivko: │ x│=1 in │х│= 1/3. Vsaka enačba ima dva korena. Odgovor: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Rešite enačbo: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2

Poiščimo rešitev prvega sistema populacije: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Upoštevajte, da x 2 ne izpolnjuje pogoj x ≥ 0. Rešitev drugi sistem bo število, nasprotni pomen x 1. Odgovor: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Rešimo enačbo: x 4 – │х│= 0 Označimo │х│= a, kjer je a ≥ 0. Dobimo enačbo a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Vrnitev na prvotno spremenljivko: │х│=0 in │х│= 1 x = 0; ± 1 Odgovor: x 1 = 0; X 2 = 1; X 3 = - 1.
vaje: №6. Rešite enačbo: 2│х│ - 4,5 = 5 – 3 / 8 │х│ №7 . Rešite enačbo, v odgovoru navedite število korenov: 3x 2 - 7│x│ + 2 = 0 №8 . Rešite enačbo, v odgovoru navedite celoštevilske rešitve: x 4 + │x│ - 2 = 0

Razdelek 3. Enačbe oblike │F(x)│ = G(x)

Desna stran enačbe te vrste je odvisna od spremenljivke in ima zato rešitev, če in samo če je desna stran funkcija G(x) ≥ 0. Izvirna enačba se lahko reši na dva načina: 1 način: Standard, ki temelji na razkritju modula na podlagi njegove definicije in je sestavljen iz enakovrednega prehoda na kombinacijo dveh sistemov. │ F(x)│ =G(X)

To metodo je mogoče racionalno uporabiti v primeru kompleksen izraz za funkcijo G(x) in manj kompleksne – za funkcijo F(x), saj se predpostavlja, da se neenačbe rešujejo s funkcijo F(x). 2. način: Sestavljen je iz prehoda na enakovredni sistem, v katerem je na desni strani naložen pogoj. │ F(x)│= G(x)

Ta metoda je primernejša za uporabo, če je izraz za funkcijo G(x) manj kompleksen kot za funkcijo F(x), saj je predpostavljena rešitev neenačbe G(x) ≥ 0. Poleg tega je v primeru več modulov, je priporočljivo uporabiti drugo možnost. Primeri: №1. Rešite enačbo: │x + 2│= 6 -2x

(1 način) Odgovor: x = 1 1 / 3 №2.
│x 2 – 2x - 1│= 2 (x + 1)

(2 način) Odgovor: Produkt korenin je 3.
№3. Rešite enačbo in v odgovoru navedite vsoto korenin:
│x - 6│= x 2 - 5x + 9

Odgovor: vsota korenin je 4.
vaje: №9. │x + 4│= - 3x №10. Rešite enačbo, navedite število rešitev v odgovoru:│x 2 + x - 1│= 2x – 1 №11 . Rešite enačbo, v odgovoru označite zmnožek korenov:│x + 3│= x 2 + x – 6

Razdelek 4. Enačbe oblike │F(x)│= F(x) in │F(x)│= - F(x)

Enačbe te vrste se včasih imenujejo "najlepše". Ker je desna stran enačb odvisna od spremenljivke, rešitve obstajajo, če in samo če je desna stran nenegativna. Zato so izvirne enačbe enakovredne neenačbam:
│F(x)│= F(x) F(x) ≥ 0 in │F(x)│= - F(x) F(x) Primeri: №1 . Rešite enačbo, v odgovoru navedite manjši koren celega števila: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Odgovor: x = 1№2. Rešite enačbo, v odgovoru navedite dolžino intervala: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Odgovor: dolžina vrzeli je 6.№3 . Rešite enačbo in navedite število celih rešitev v vašem odgovoru: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Odgovor: 4 celotne rešitve.№4 . Reši enačbo in jo navedi v odgovoru največji koren:
│4 – x -

│= 4 – x –

x 2 – 5x + 5 = 0 D = 5 x 1,2 =

≈ 1,4

Odgovor: x = 3.

vaje: №12. Rešite enačbo, v odgovoru označite cel koren: │x 2 + 6x + 8│= x 2 + 6x + 8 №13. Rešite enačbo, v odgovoru navedite število celih rešitev: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. Rešite enačbo, navedite celo število, ki ni koren enačbe:

Razdelek 5. Enačbe oblike │F(x)│= │G(x)│

Ker sta obe strani enačbe nenegativni, rešitev vključuje upoštevanje dveh primerov: submodularni izrazi so enakega ali nasprotnega predznaka. Zato je prvotna enačba enakovredna kombinaciji dveh enačb: │ F(x)│= │ G(x)│

Primeri: №1. Rešite enačbo, v odgovoru navedite cel koren: │x + 3│=│2x - 1│

Odgovor: cel koren x = 4.№2. Reši enačbo: │ x – x 2 - 1│=│2x – 3 – x 2 │

Odgovor: x = 2.№3 . Rešite enačbo in v odgovoru označite produkt korenin:

Korenske enačbe 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Odgovor: produkt korenin je – 0,25. vaje: №15 . Rešite enačbo in v odgovoru navedite celotno rešitev: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16. Rešite enačbo, v odgovoru označite manjši koren:│5x - 3│=│7 - x│ №17 . Rešite enačbo in v odgovoru navedite vsoto korenin:

Oddelek 6. Primeri reševanja nestandardnih enačb

IN ta del Upoštevali bomo primere nestandardnih enačb, pri reševanju katerih se absolutna vrednost izraza razkrije z definicijo. Primeri:

№1. Rešite enačbo, v odgovoru navedite vsoto korenov: x · │x│- 5x – 6 = 0
Odgovor: vsota korenin je 1 №2. . Rešite enačbo, v odgovoru označite manjši koren: x 2 - 4x ·
- 5 = 0
Odgovor: manjši koren x = - 5. №3. Reši enačbo:

Odgovor: x = -1. vaje: №18. Rešite enačbo in označite vsoto korenov: x · │3x + 5│= 3x 2 + 4x + 3
№19. Reši enačbo: x 2 – 3x =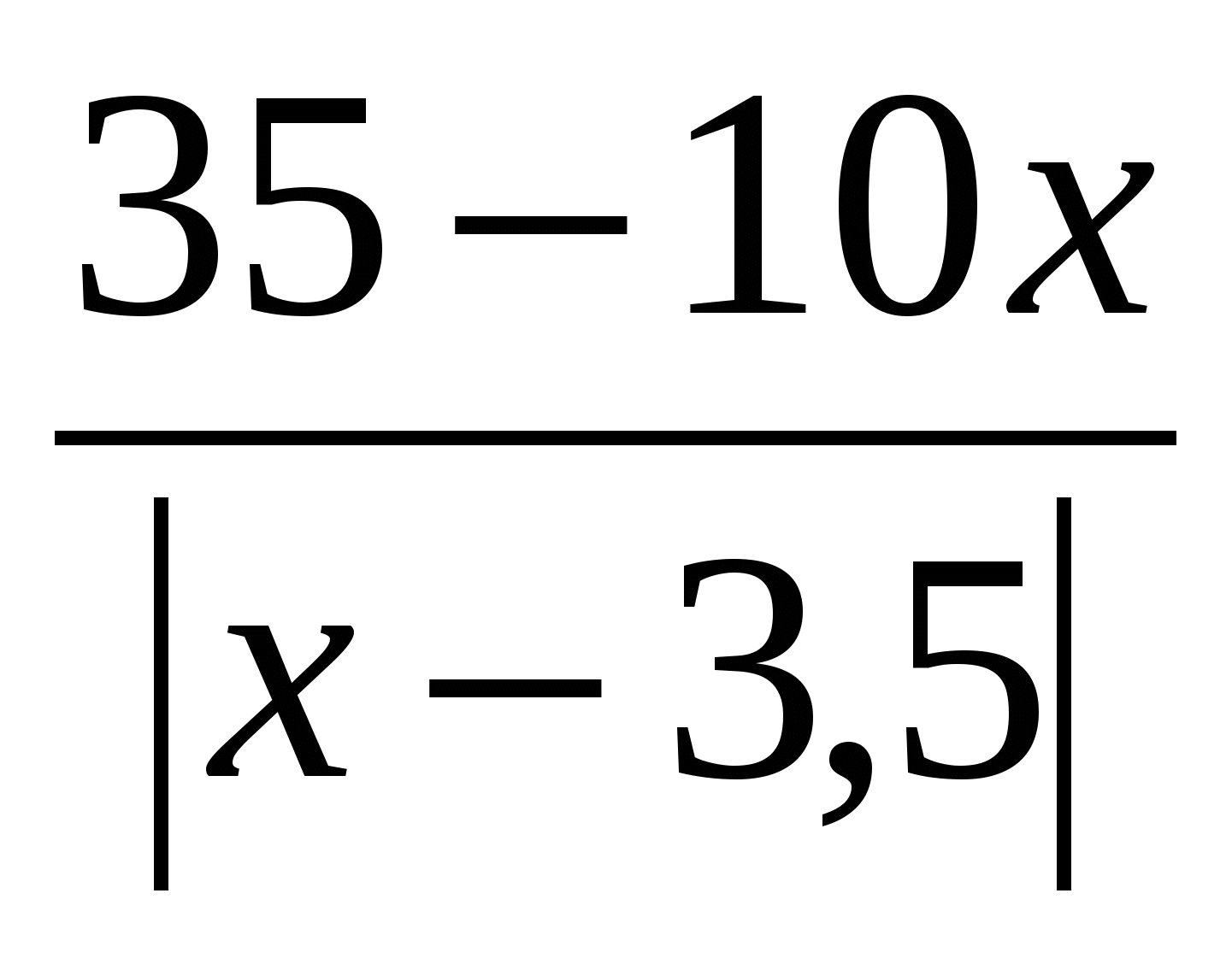

№20. Reši enačbo:

Razdelek 7. Enačbe oblike │F(x)│+│G(x)│=0

Lahko opazimo, da je na levi strani enačbe te vrste vsota nenegativnih količin. Zato ima izvirna enačba rešitev, če in samo če sta oba člena enaka nič hkrati. Enačba je enakovredna sistemu enačb: │ F(x)│+│ G(x)│=0
Primeri: №1 . Reši enačbo:

Odgovor: x = 2. №2. Reši enačbo: Odgovor: x = 1. vaje: №21. Reši enačbo: №22 . Rešite enačbo in v odgovoru navedite vsoto korenin: №23 . Rešite enačbo in v odgovoru označite število rešitev:

Oddelek 8. Enačbe oblike │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m

Za reševanje tovrstnih enačb se uporablja intervalna metoda. Če jo rešimo z zaporedno širitvijo modulov, dobimo n sklopov sistemov, kar je zelo okorno in neprijetno. Oglejmo si algoritem intervalne metode: 1). Poiščite vrednosti spremenljivk X, pri katerem je vsak modul enak nič (ničle submodularnih izrazov):

2). Najdene vrednosti označite na številski premici, ki je razdeljena na intervale (število intervalov je enako n+1 ) 3). Ugotovite, s kakšnim znakom je vsak modul razkrit v vsakem od dobljenih intervalov (pri reševanju lahko uporabite številsko premico in na njej označite znake) 4). Prvotna enačba je enakovredna agregatu n+1 sistemov, v vsakem od katerih je navedena pripadnost spremenljivke X enega od intervalov. Primeri: №1 . Rešite enačbo in v odgovoru označite največji koren:

1). Poiščimo ničle submodularnih izrazov: x = 2; x = -3 2). Označimo najdene vrednosti na številski premici in ugotovimo, s kakšnim znakom je vsak modul razkrit na dobljenih intervalih:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)

- ni rešitev Enačba ima dva korena. Odgovor: največji koren x = 2. №2. Rešite enačbo in v svoj odgovor vnesite celoten koren:

1). Poiščimo ničle submodularnih izrazov: x = 1,5; x = - 1 2). Označimo najdene vrednosti na številski premici in določimo, s kakšnim znakom je vsak modul razkrit na dobljenih intervalih: x + 1 x + 1 x + 1 - + +
-1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).

Najnovejši sistem nima rešitev, zato ima enačba dva korena. Pri reševanju enačbe bodite pozorni na znak »-« pred drugim modulom. Odgovor: cel koren x = 7. №3. Rešite enačbo, v odgovoru navedite vsoto korenov: 1). Poiščimo ničle submodularnih izrazov: x = 5; x = 1; x = - 2 2). Označimo najdene vrednosti na številski premici in določimo, s kakšnim znakom je vsak modul razkrit v nastalih intervalih: x – 5 x – 5 x – 5 x – 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).

Enačba ima dva korena x = 0 in 2. Odgovor: vsota korenin je 2. №4 . Reši enačbo: 1). Poiščimo ničle submodularnih izrazov: x = 1; x = 2; x = 3. 2). Ugotovimo, s kakšnim predznakom je vsak modul razkrit na dobljenih intervalih. 3).

Združimo rešitve prvega trije sistemi. Odgovor: ; x = 5.
vaje: №24. Reši enačbo:

№25. Rešite enačbo in v odgovoru navedite vsoto korenin: №26. Rešite enačbo in v odgovoru označite manjši koren: №27. Rešite enačbo in v odgovoru označite večji koren:

Oddelek 9. Enačbe, ki vsebujejo več modulov

Enačbe, ki vsebujejo več modulov, predvidevajo prisotnost absolutnih vrednosti v submodularnih izrazih. Osnovno načelo za reševanje enačb te vrste je zaporedno razkritje modulov, začenši z "zunanjim". Med reševanjem se uporabljajo tehnike, obravnavane v razdelkih št. 1, št. 3.

Primeri: №1. Reši enačbo:
Odgovor: x = 1; - enajst. №2. Reši enačbo:
Odgovor: x = 0; 4; - 4. №3. Rešite enačbo in v odgovoru označite produkt korenin:
Odgovor: produkt korenin je – 8. №4. Reši enačbo:
Označimo enačbe populacije (1) in (2) in razmislite o rešitvi za vsako od njih posebej zaradi lažjega načrtovanja. Ker obe enačbi vsebujeta več kot en modul, je primerneje izvesti enakovreden prehod na množice sistemov. (1)

(2)

odgovor:
vaje: №36. Rešite enačbo, v odgovoru navedite vsoto korenov: 5 │3x-5│ = 25 x №37. Rešite enačbo, če je korenin več, v odgovoru navedite vsoto korenin: │x + 2│ x – 3x – 10 = 1 №38. Rešite enačbo: 3 │2x -4│ = 9 │x│ №39. Rešite enačbo in v odgovoru navedite število korenov: 2 │ sin x│ = √2 №40 . Rešite enačbo in v odgovoru navedite število korenin:

Oddelek 3. Logaritemske enačbe.

Preden rešimo naslednje enačbe, je treba pregledati lastnosti logaritmov in logaritemska funkcija. Primeri: №1. Rešite enačbo, v odgovoru navedite zmnožek korenov: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1

Primer 1: če je x ≥ - 1, potem je log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – izpolnjuje pogoj x ≥ - 1 2 primer: če je x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – izpolnjuje pogoj x - 1
Odgovor: produkt korenin je – 15.
№2. Rešite enačbo, v odgovoru navedite vsoto korenov: lg
O.D.Z.

Odgovor: vsota korenov je 0,5.
№3. Reši enačbo: log 5
O.D.Z.

Odgovor: x = 9. №4. Rešite enačbo: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Uporabimo formulo za premik na drugo bazo. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Poiščemo ničle submodularnih izrazov: x = 25; x = Te številke delijo površino sprejemljive vrednosti na tri intervale, zato je enačba enakovredna kombinacija treh sistemi
odgovor :)