Ta spletni matematični kalkulator vam bo pomagal rešiti enačbo ali neenačbo z moduli. Program za reševanje enačb in neenačb z moduli ne le daje odgovor na problem, ampak vodi podrobna rešitev z obrazložitvijo, tj. prikazuje postopek pridobivanja rezultata.

Ta program je lahko koristen za srednješolce v srednjih šolah kot priprave na testi in izpite, pri preverjanju znanja pred enotnim državnim izpitom, da starši nadzorujejo rešitev številnih problemov iz matematike in algebre. Ali pa vam je morda predrago najeti mentorja ali kupiti nove učbenike? Ali pa želite le opraviti čim hitreje? Domača naloga pri matematiki ali algebri? V tem primeru lahko uporabite tudi naše programe s podrobnimi rešitvami.

Tako lahko izvajate lastno usposabljanje in/ali svoje usposabljanje. mlajši bratje ali sester, medtem ko se stopnja izobrazbe na področju problemov, ki se rešujejo, povečuje.

|x| ali abs(x) - modul x

Vnesite enačbo ali neenačbo z moduli

Rešite enačbo ali neenačbo

Ugotovljeno je bilo, da nekateri skripti, potrebni za rešitev te težave, niso bili naloženi in program morda ne bo deloval.
Morda imate omogočen AdBlock.
V tem primeru ga onemogočite in osvežite stran.

JavaScript je onemogočen v vašem brskalniku.
Da se rešitev prikaže, morate omogočiti JavaScript.
Tukaj so navodila, kako omogočiti JavaScript v brskalniku.

Ker Veliko ljudi je pripravljenih rešiti problem, vaša zahteva je v čakalni vrsti.
Čez nekaj sekund se spodaj prikaže rešitev.
Prosim počakaj sek...

Če ti opazil napako v rešitvi, potem lahko o tem pišete v obrazcu za povratne informacije.
Ne pozabi navedite, katero nalogo ti se odloči kaj vnesite v polja.

Naše igre, uganke, emulatorji:

Malo teorije.

Enačbe in neenačbe z moduli

V osnovnem šolskem tečaju algebre lahko naletite na najpreprostejše enačbe in neenačbe z moduli. Za njihovo rešitev lahko uporabite geometrijska metoda, ki temelji na dejstvu, da je \(|x-a| \) razdalja na številski premici med točkama x in a: \(|x-a| = \rho (x;\; a)\). Če želite na primer rešiti enačbo \(|x-3|=2\), morate najti točke na številski premici, ki so oddaljene od točke 3 na razdalji 2. Takšni točki sta dve: \(x_1=1 \) in \(x_2=5\) .

Reševanje neenačbe \(|2x+7|

Toda glavni način reševanja enačb in neenakosti z moduli je povezan s tako imenovanim "razkritjem modula po definiciji":
če \(a \geq 0 \), potem \(|a|=a \);
if \(a Praviloma se enačba (neenačba) z moduli reducira na množico enačb (neenačb), ki ne vsebujejo znaka modula.

Poleg zgornje definicije se uporabljajo naslednje izjave:
1) Če je \(c > 0\), potem je enačba \(|f(x)|=c \) enakovredna naboru enačb: \(\left[\begin(array)(l) f(x )=c \\ f(x)=-c \end(matrika)\desno.
2) Če \(c > 0 \), potem je neenakost \(|f(x)| 3) Če \(c \geq 0 \), potem je neenakost \(|f(x)| > c \) enakovreden nizu neenakosti: \(\left[\begin(array)(l) f(x) c \end(array)\right. \)
4) Če sta obe strani neenakosti \(f(x) PRIMER 1. Rešite enačbo \(x^2 +2|x-1| -6 = 0\).

Če \(x-1 \geq 0\), potem \(|x-1| = x-1\) in podana enačba prevzame obliko
\(x^2 +2(x-1) -6 = 0 \Desna puščica x^2 +2x -8 = 0 \).
Če je \(x-1 \(x^2 -2(x-1) -6 = 0 \desna puščica x^2 -2x -4 = 0 \).
Zato je treba dano enačbo obravnavati ločeno v vsakem od obeh navedenih primerov.
1) Naj \(x-1 \geq 0 \), tj. \(x\geq 1\). Iz enačbe \(x^2 +2x -8 = 0\) najdemo \(x_1=2, \; x_2=-4\). Pogoj \(x \geq 1 \) je izpolnjen samo z vrednostjo \(x_1=2\).
2) Naj \(x-1 Odgovor: \(2; \;\; 1-\sqrt(5) \)

PRIMER 2. Rešite enačbo \(|x^2-6x+7| = \frac(5x-9)(3)\).

Prvi način(razširitev modula po definiciji).
Z razmišljanjem kot v 1. primeru pridemo do zaključka, da je treba dano enačbo obravnavati ločeno, če sta izpolnjena dva pogoja: \(x^2-6x+7 \geq 0 \) ali \(x^2-6x+7

1) Če je \(x^2-6x+7 \geq 0 \), potem \(|x^2-6x+7| = x^2-6x+7 \) in dana enačba ima obliko \(x ^2 -6x+7 = \frac(5x-9)(3) \Desna puščica 3x^2-23x+30=0 \). Ko se je to odločil kvadratna enačba, dobimo: \(x_1=6, \; x_2=\frac(5)(3) \).
Ugotovimo, ali vrednost \(x_1=6\) izpolnjuje pogoj \(x^2-6x+7 \geq 0\). Če želite to narediti, zamenjajmo določeno vrednost V kvadratna neenakost. Dobimo: \(6^2-6 \cdot 6+7 \geq 0 \), tj. \(7 \geq 0 \) je prava neenakost. To pomeni, da je \(x_1=6\) koren dane enačbe.
Ugotovimo, ali vrednost \(x_2=\frac(5)(3)\) izpolnjuje pogoj \(x^2-6x+7 \geq 0\). To naredite tako, da navedeno vrednost nadomestite s kvadratno neenakostjo. Dobimo: \(\left(\frac(5)(3) \right)^2 -\frac(5)(3) \cdot 6 + 7 \geq 0 \), tj. \(\frac(25)(9) -3 \geq 0 \) je nepravilna neenakost. To pomeni, da \(x_2=\frac(5)(3)\) ni koren dane enačbe.

2) Če \(x^2-6x+7 Vrednost \(x_3=3\) izpolnjuje pogoj \(x^2-6x+7 Vrednost \(x_4=\frac(4)(3) \) ne izpolnjuje pogoj \ (x^2-6x+7 Torej ima dana enačba dva korena: \(x=6, \; x=3 \).

Drugi način.Če je podana enačba \(|f(x)| = h(x) \), potem z \(h(x) \(\left[\begin(array)(l) x^2-6x+7 = \frac (5x-9)(3) \\ x^2-6x+7 = -\frac(5x-9)(3) \end(matrika)\desno \)
Obe enačbi sta bili rešeni zgoraj (z uporabo prve metode reševanja dane enačbe), njuni koreni so naslednji: \(6,\; \frac(5)(3),\; 3,\; \frac(4 )(3)\). Pogoj \(\frac(5x-9)(3) \geq 0 \) teh štirih vrednosti izpolnjujeta samo dve: 6 in 3. To pomeni, da ima dana enačba dva korena: \(x=6 , \; x=3 \ ).

Tretji način(grafični).
1) Zgradimo graf funkcije \(y = |x^2-6x+7| \). Najprej sestavimo parabolo \(y = x^2-6x+7\). Imamo \(x^2-6x+7 = (x-3)^2-2 \). Graf funkcije \(y = (x-3)^2-2\) lahko dobite iz grafa funkcije \(y = x^2\), tako da ga premaknete za 3 merilne enote v desno (vzdolž os x) in 2 merilni enoti navzdol ( vzdolž osi y). Premica x=3 je os parabole, ki nas zanima. Kot kontrolne točke za natančnejše risanje je priročno vzeti točko (3; -2) - vrh parabole, točko (0; 7) in točko (6; 7), ki je simetrična glede na os parabole. .
Če želite zdaj sestaviti graf funkcije \(y = |x^2-6x+7| \), morate pustiti nespremenjene tiste dele konstruirane parabole, ki ne ležijo pod osjo x, in zrcaliti tisti del parabole. parabolo, ki leži pod osjo x glede na os x.
2) Zgradimo graf linearna funkcija\(y = \frac(5x-9)(3)\). Za kontrolne točke je priročno vzeti točke (0; –3) in (3; 2).

Pomembno je, da se točka x = 1,8 presečišča premice z abscisno osjo nahaja desno od levega presečišča parabole z abscisno osjo - to je točka \(x=3-\ sqrt(2) \) (ker \(3-\sqrt(2 ) 3) Sodeč po risbi se grafa sekata v dveh točkah - A(3; 2) in B(6; 7). Če zamenjamo abscisi teh točke x = 3 in x = 6 v dano enačbo, se prepričamo, da je v drugem primeru dosežena pravilna numerična enakost. To pomeni, da je bila naša hipoteza potrjena - enačba ima dva korena: x = 3 in x = 6. Odgovor: 3;

Komentiraj. Grafična metoda kljub vsej svoji eleganci ni zelo zanesljiv. V obravnavanem primeru je delovalo samo zato, ker so koreni enačbe cela števila.

PRIMER 3. Rešite enačbo \(|2x-4|+|x+3| = 8\)

Prvi način
Izraz 2x–4 postane 0 v točki x = 2, izraz x + 3 pa postane 0 v točki x = –3. Ti dve točki delita številsko premico na tri intervale: \(x

Razmislite o prvem intervalu: \((-\infty; \; -3) \).
Če x Upoštevajte drugi interval: \([-3; \; 2) \).
Če \(-3 \leq x Upoštevajte tretji interval: \( [ 3/2 ; ∞ )

Metoda ekvivalentne transformacije uporabljali tudi pri reševanju enačb | f(x)| = | g(x)|.

ENAČBE S KOMPLEKSNIM MODULOM

Druga vrsta enačb so enačbe s "kompleksnim" modulom. Take enačbe vključujejo enačbe, ki imajo »module znotraj modula«. Enačbe te vrste je mogoče rešiti z uporabo različne metode.

Primer 1.

Reši enačbo ||||x| – |–2| –1| –2| = 2.

rešitev.

Po definiciji modula imamo:

Rešimo prvo enačbo.

||| x |–2| –1| = 4

| x | – 2 = 5;

| x | = 7;

x = 7.

Rešimo drugo enačbo.

||| x | –2| –1| = 0,

|| x | –2| = 1,

| x | –2 = 1,

| x | = 3 in | x | = 1,

x = 3; x = 1.

Odgovor: 1; 3; 7.

Primer 2.

Rešite enačbo |2 – |x + 1|| = 3.

rešitev.

Rešimo enačbo z uvedbo nove spremenljivke.

Naj | x + 1| = y, potem |2 – y | = 3, od tukaj

Naredimo obratno zamenjavo:

(1) | x + 1| = –1 – ni rešitev.

(2) | x + 1| = 5

ODGOVOR: –6; 4.

Primer3.

Koliko korenov ima enačba | 2 | x | -6 | = 5 - x?

rešitev. Rešimo enačbo z enakovrednimi shemami.

Enačba | 2 | x | -6 | = 5 je enakovreden sistemu:

Srednja šola MBOU št. 17, Ivanovo

« Enačbe z modulom"
Metodološki razvoj

Sestavljeno

učiteljica matematike

Lebedeva N.V.

20010

Pojasnilo

Poglavje 1. Uvod

Oddelek 2. Osnovne lastnosti Oddelek 3. Geometrična razlaga koncepta modula števila Razdelek 4. Graf funkcije y = |x| Oddelek 5. Konvencije

Poglavje 2. Reševanje enačb, ki vsebujejo modul

Razdelek 1. Enačbe oblike |F(x)| = m (najenostavnejši) Razdelek 2. Enačbe oblike F(|x|) = m Razdelek 3. Enačbe oblike |F(x)| = G(x) Razdelek 4. Enačbe oblike |F(x)| = ± F(x) (najlepši) Razdelek 5. Enačbe oblike |F(x)| = |G(x)| Oddelek 6. Primeri rešitev nestandardne enačbe Razdelek 7. Enačbe oblike |F(x)| + |G(x)| = 0 Razdelek 8. Enačbe oblike |a 1 x ± b 1 | ± |a 2 x ± b 2 | ± …|a n x ± in n | = m Razdelek 9. Enačbe, ki vsebujejo več modulov

Poglavje 3. Primeri reševanja različnih enačb z modulom.

Oddelek 1. Trigonometrične enačbe Oddelek 2. Eksponentne enačbe Oddelek 3. Logaritemske enačbe Oddelek 4. Iracionalne enačbe Oddelek 5. Naloge povečana kompleksnost Odgovori na vaje Bibliografija

Pojasnilo.

Koncept absolutne vrednosti (modula) realnega števila je ena njegovih bistvenih značilnosti. Ta koncept je zelo razširjen v različnih delih fizikalnih, matematičnih in tehničnih znanosti. V praksi poučevanja matematičnih predmetov v Srednja šola v skladu s programom Ministrstva za obrambo Ruske federacije se koncept "absolutne vrednosti števila" večkrat srečuje: v 6. razredu se uvaja definicija modula in njegov geometrijski pomen; v 8. razredu se pojem oblikuje absolutna napaka, obravnava se rešitev najpreprostejših enačb in neenačb, ki vsebujejo modul, preučujejo se lastnosti aritmetike kvadratni koren; v 11. razredu koncept najdemo v razdelku »Koren n- stopnja." Izkušnje poučevanja kažejo, da se učenci pogosto srečujejo s težavami pri reševanju nalog, ki zahtevajo poznavanje te snovi, in jih pogosto preskočijo, ne da bi jih začeli reševati. V besedilih izpitne naloge Podobne naloge so vključene tudi za tečaje 9. in 11. razreda. Poleg tega so zahteve, ki jih univerze postavljajo diplomantom, različne, in sicer bolj visoka stopnja kot zahteve šolskega kurikuluma. Za življenje v moderna družba Zelo pomembno je razviti matematični stil razmišljanja, ki se kaže v določenih mentalnih veščinah. V procesu reševanja problemov z moduli je potrebna sposobnost uporabe tehnik, kot so generalizacija in specifikacija, analiza, klasifikacija in sistematizacija ter analogija. Reševanje takšnih nalog vam omogoča, da preizkusite svoje znanje o glavnih razdelkih šolski tečaj, raven logično razmišljanje, začetne raziskovalne sposobnosti. to delo je namenjen enemu od razdelkov - reševanju enačb, ki vsebujejo modul. Sestavljen je iz tri poglavja. Prvo poglavje predstavlja osnovne koncepte in najpomembnejše teoretične premisleke. Drugo poglavje predlaga devet glavnih vrst enačb, ki vsebujejo modul, razpravlja o metodah za njihovo reševanje in preučuje primere različne ravni težave. Tretje poglavje ponuja kompleksnejše in nestandardne enačbe (trigonometrične, eksponentne, logaritemske in iracionalne). Za vsako vrsto enačbe obstajajo vaje za neodvisna odločitev(odgovori in navodila so priloženi). Glavni namen tega dela je zagotoviti metodološka pomoč učiteljev pri pripravah na pouk in organizaciji izbirnih predmetov. Material se lahko uporablja tudi kot učna pomoč za srednješolce. Naloge, ponujene v delu, so zanimive in jih ni vedno enostavno rešiti, kar vam omogoča učna motivacijaštudente, da se bolj zavedajo, preizkusijo svoje sposobnosti in izboljšajo stopnjo pripravljenosti maturantov za vpis na univerze. Diferenciran izbor predlaganih vaj vključuje prehod z reproduktivne ravni obvladovanja gradiva na ustvarjalno, pa tudi priložnost, da se naučite, kako uporabiti svoje znanje pri reševanju nestandardnih problemov.

Poglavje 1. Uvod.

Oddelek 1. Določitev absolutne vrednosti .

Opredelitev : Absolutna vrednost (modul) realnega števila A klical nenegativno število: A oz -A. Oznaka: │ A │ Vnos se glasi: “modul števila a” ali “absolutna vrednost števila a”

│ a, če je a > 0

│a│ = │ 0, če je a = 0 (1)

│ - in če a
Primeri: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1
Razširi izrazni modul:
a) │x - 8│, če je x > 12 b) │2x + 3│, če je x ≤ -2 │x – 8│= x – 8 │ 2x + 3│= - 2x – 3
Oddelek 2. Osnovne lastnosti.
Razmislimo o osnovnih lastnostih absolutne vrednosti. Lastnost #1: Nasprotna števila imajo enaki moduli, tj. │а│=│- а│ Pokažimo, da je enakost resnična. Zapišimo definicijo števila - A : │- a│= (2) Primerjajmo niza (1) in (2). Očitno so definicije absolutnih vrednosti števil A in - A ujemati se. torej │а│=│- а│
Z revidiranjem naslednje lastnosti Omejili se bomo na njihovo formulacijo, saj je njihov dokaz podan Lastnost #2: Absolutna vrednost zneska končno število realna števila ne presegajo vsote absolutnih vrednosti izrazov: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │+ … + │а n │ Lastnost #3: Absolutna vrednost razlike med dvema realnima številoma ne presega vsote njunih absolutnih vrednosti: │а - в│ ≤│а│+│в│ Lastnost #4: Absolutna vrednost produkta končnega števila realnih števil je enaka produktu absolutnih vrednosti faktorjev: │а·в│=│а│·│в│ Lastnost #5: Absolutna vrednost kvocienta realnih števil je enaka kvocientu njihovih absolutnih vrednosti:

Oddelek 3. Geometrična razlaga koncepta modula števila.

Vsako realno število lahko povežemo s točko na številski premici, kar bo geometrijska slika podano realno število. Vsaka točka na številski premici ustreza svoji oddaljenosti od izhodišča, tj. dolžina odseka od izhodišča do dane točke. Ta razdalja se vedno obravnava kot nenegativna vrednost. Zato bo dolžina ustreznega segmenta geometrijska interpretacija absolutna vrednost danega realnega števila

Predstavljena geometrijska ilustracija jasno potrjuje lastnost št. 1, tj. moduli nasprotna števila so enaki. Od tu je enostavno razumljiva veljavnost enakosti: │х – а│= │а – x│. Tudi rešitev enačbe │х│= m, kjer je m ≥ 0, in sicer x 1,2 = ± m, postane bolj očitna. Primeri: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1

x 1,2 = 2; 4

Oddelek 4. Graf funkcije y = │х│

Domena te funkcije so vsa realna števila.

Oddelek 5. Konvencije.

V prihodnje bo pri obravnavi primerov reševanja enačb uporabljeno naslednje simboli: ( - znak sistema [ - znak celote Pri reševanju sistema enačb (neenačb) se najde presečišče rešitev enačb (neenačb), ki so vključene v sistem. Pri reševanju množice enačb (neenačb) se najde unija rešitev, vključenih v množico enačb (neenačb).

Poglavje 2. Reševanje enačb, ki vsebujejo modul.

V tem poglavju si bomo ogledali algebraične metode reševanje enačb, ki vsebujejo enega ali več modulov.

Razdelek 1. Enačbe oblike │F (x)│= m

Enačba te vrste se imenuje najenostavnejša. Ima rešitev, če in samo če je m ≥ 0. Po definiciji modula je izvirna enačba enakovredna nizu dveh enačb: │ F(x)│=m

Primeri:
№1. Rešite enačbo: │7х - 2│= 9

Odgovor: x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

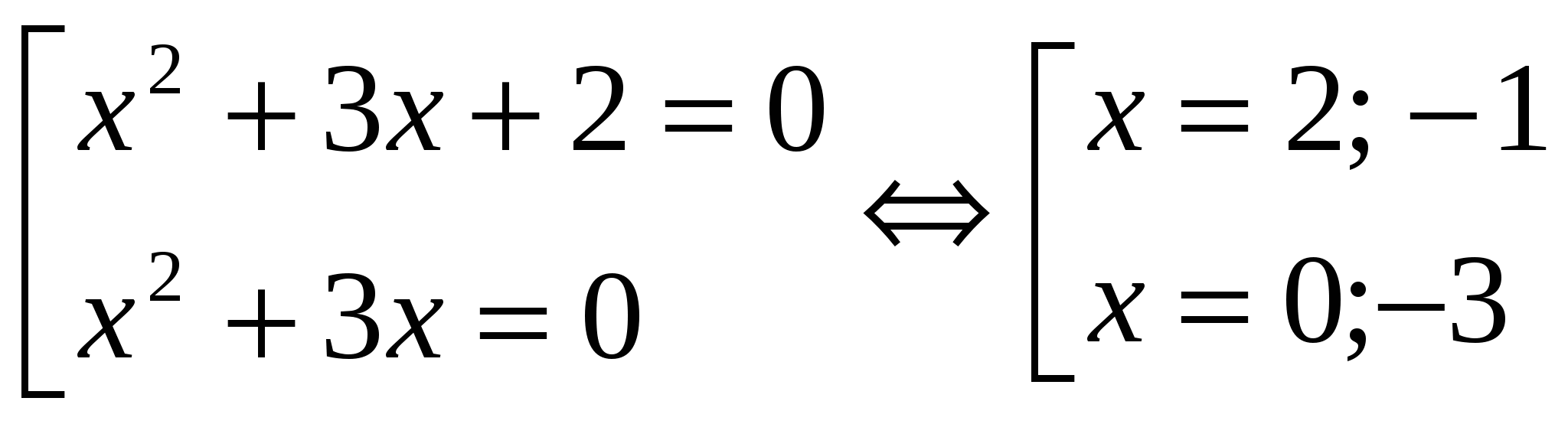x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Odgovor: vsota korenin je - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 pomeni x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – obe vrednosti izpolnjujeta pogoj m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Odgovor: število korenov enačbe 7. vaje:
№1. Rešite enačbo in navedite vsoto korenov: │х - 5│= 3 №2 . Rešite enačbo in označite manjši koren: │x 2 + x│= 0 №3 . Rešite enačbo in označite večji koren: │x 2 – 5x + 4│= 4 №4 .Reši enačbo in označi cela korenina: │2x 2 – 7x + 6│= 1 №5 .Rešite enačbo in označite število korenov: │x 4 – 13x 2 + 50│= 14

Oddelek 2. Enačbe oblike F(│х│) = m

Argument funkcije na levi strani je pod znakom modula, desna stran pa je neodvisna od spremenljivke. Razmislimo o dveh načinih reševanja enačb te vrste. 1 način: Po definiciji absolutne vrednosti je prvotna enačba enakovredna kombinaciji dveh sistemov. V vsakem od njih je submodularnemu izrazu naložen pogoj. F(│х│) =m

Ker je funkcija F(│x│) soda v celotnem definicijskem področju, sta korena enačb F(x) = m in F(- x) = m pari nasprotnih števil. Zato je dovolj, da rešimo enega od sistemov (pri obravnavanju primerov na ta način bo podana rešitev enega sistema). 2. način: Uporaba metode uvajanja nove spremenljivke. V tem primeru je uveden zapis │x│= a, kjer je a ≥ 0. Ta metoda manj voluminozen dizajn.
Primeri: №1 . Rešite enačbo: 3x 2 – 4│x│= - 1 Uporabimo uvedbo nove spremenljivke. Označimo │x│= a, kjer je a ≥ 0. Dobimo enačbo 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Vrnitev na prvotno spremenljivko: │ x│=1 in │х│= 1/3. Vsaka enačba ima dva korena. Odgovor: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Rešite enačbo: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2

Poiščimo rešitev prvega sistema populacije: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Upoštevajte, da x 2 ne izpolnjuje pogoj x ≥ 0. Rešitev drugi sistem bo število, nasprotni pomen x 1. Odgovor: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Rešimo enačbo: x 4 – │х│= 0 Označimo │х│= a, kjer je a ≥ 0. Dobimo enačbo a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Vrnitev na prvotno spremenljivko: │х│=0 in │х│= 1 x = 0; ± 1 Odgovor: x 1 = 0; X 2 = 1; X 3 = - 1.
vaje: №6. Rešite enačbo: 2│х│ - 4,5 = 5 – 3 / 8 │х│ №7 . Rešite enačbo, v odgovoru navedite število korenov: 3x 2 - 7│x│ + 2 = 0 №8 . Rešite enačbo, v odgovoru navedite celoštevilske rešitve: x 4 + │x│ - 2 = 0

Razdelek 3. Enačbe oblike │F(x)│ = G(x)

Desna stran enačbe te vrste je odvisna od spremenljivke in ima zato rešitev, če in samo če je desna stran funkcija G(x) ≥ 0. Izvirno enačbo je mogoče rešiti na dva načina : 1 način: Standard, ki temelji na razkritju modula na podlagi njegove definicije in je sestavljen iz enakovrednega prehoda na kombinacijo dveh sistemov. │ F(x)│ =G(X)

To metodo je mogoče racionalno uporabiti v primeru kompleksen izraz za funkcijo G(x) in manj kompleksne – za funkcijo F(x), saj se predpostavlja, da se neenačbe rešujejo s funkcijo F(x). 2. način: Sestavljen je iz prehoda na enakovredni sistem, v katerem je na desni strani naložen pogoj. │ F(x)│= G(x)

Ta metoda je primernejša za uporabo, če je izraz za funkcijo G(x) manj kompleksen kot za funkcijo F(x), saj je predpostavljena rešitev neenačbe G(x) ≥ 0. Poleg tega je v primeru več modulov, je priporočljivo uporabiti drugo možnost. Primeri: №1. Rešite enačbo: │x + 2│= 6 -2x

(1 način) Odgovor: x = 1 1 / 3 №2.
│x 2 – 2x - 1│= 2 (x + 1)

(2 način) Odgovor: Produkt korenin je 3.
№3. Rešite enačbo in v odgovoru navedite vsoto korenin:
│x - 6│= x 2 - 5x + 9

Odgovor: vsota korenin je 4.
vaje: №9. │x + 4│= - 3x №10. Rešite enačbo, navedite število rešitev v odgovoru:│x 2 + x - 1│= 2x – 1 №11 . Rešite enačbo, v odgovoru označite zmnožek korenov:│x + 3│= x 2 + x – 6

Razdelek 4. Enačbe oblike │F(x)│= F(x) in │F(x)│= - F(x)

Enačbe te vrste včasih imenujemo "najlepše". Ker je desna stran enačb odvisna od spremenljivke, obstajajo rešitve, če in samo če je desna stran nenegativna. Zato so izvirne enačbe enakovredne neenačbam:
│F(x)│= F(x) F(x) ≥ 0 in │F(x)│= - F(x) F(x) Primeri: №1 . Rešite enačbo, v odgovoru navedite manjši koren celega števila: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Odgovor: x = 1№2. Rešite enačbo, v odgovoru navedite dolžino intervala: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Odgovor: dolžina vrzeli je 6.№3 . Rešite enačbo in navedite število celih rešitev v vašem odgovoru: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Odgovor: 4 celotne rešitve.№4 . Reši enačbo in jo navedi v odgovoru največji koren:
│4 – x -

│= 4 – x –

x 2 – 5x + 5 = 0 D = 5 x 1,2 =

≈ 1,4

Odgovor: x = 3.

vaje: №12. Rešite enačbo, v odgovoru označite cel koren: │x 2 + 6x + 8│= x 2 + 6x + 8 №13. Rešite enačbo, v odgovoru navedite število celih rešitev: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. Rešite enačbo, navedite celo število, ki ni koren enačbe:

Razdelek 5. Enačbe oblike │F(x)│= │G(x)│

Ker sta obe strani enačbe nenegativni, rešitev vključuje upoštevanje dveh primerov: submodularni izrazi so enakega ali nasprotnega predznaka. Zato je prvotna enačba enakovredna kombinaciji dveh enačb: │ F(x)│= │ G(x)│

Primeri: №1. Rešite enačbo, v odgovoru navedite cel koren: │x + 3│=│2x - 1│

Odgovor: cel koren x = 4.№2. Reši enačbo: │ x – x 2 - 1│=│2x – 3 – x 2 │

Odgovor: x = 2.№3 . Rešite enačbo in v odgovoru označite produkt korenin:

Korenske enačbe 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Odgovor: produkt korenin je – 0,25. vaje: №15 . Rešite enačbo in v odgovoru navedite celotno rešitev: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16. Rešite enačbo, v odgovoru označite manjši koren:│5x - 3│=│7 - x│ №17 . Rešite enačbo in v odgovoru navedite vsoto korenin:

Oddelek 6. Primeri reševanja nestandardnih enačb

IN ta del Upoštevali bomo primere nestandardnih enačb, pri reševanju katerih se absolutna vrednost izraza razkrije z definicijo. Primeri:

№1. Rešite enačbo, v odgovoru navedite vsoto korenov: x · │x│- 5x – 6 = 0
Odgovor: vsota korenin je 1 №2. . Rešite enačbo, v odgovoru označite manjši koren: x 2 - 4x ·
- 5 = 0
Odgovor: manjši koren x = - 5. №3. Reši enačbo:

Odgovor: x = -1. vaje: №18. Rešite enačbo in navedite vsoto korenov: x · │3x + 5│= 3x 2 + 4x + 3
№19. Reši enačbo: x 2 – 3x =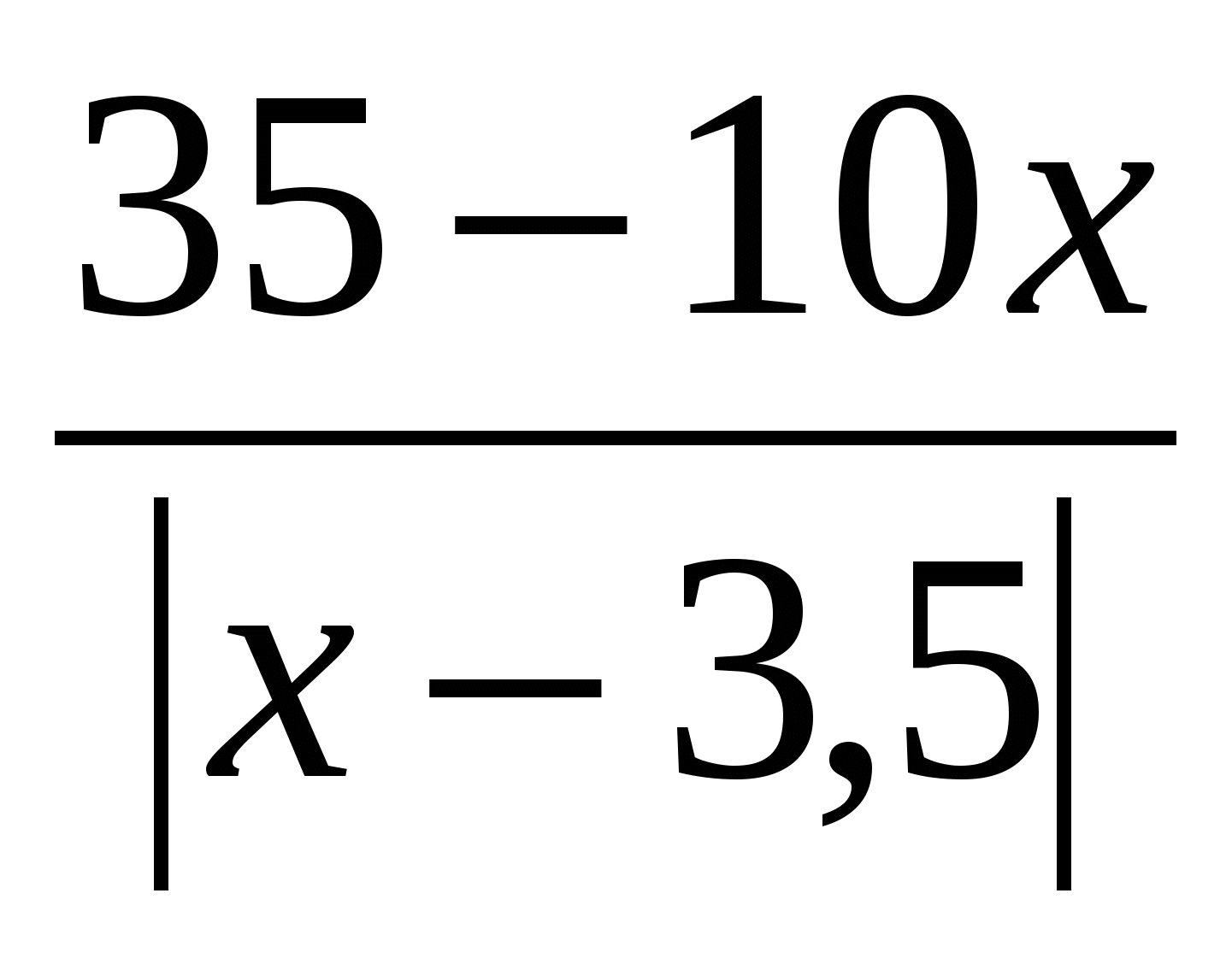

№20. Reši enačbo:

Razdelek 7. Enačbe oblike │F(x)│+│G(x)│=0

Z lahkoto opazimo, da je na levi strani enačbe te vrste vsota nenegativnih količin. Zato ima izvirna enačba rešitev, če in samo če sta oba člena enaka nič hkrati. Enačba je enakovredna sistemu enačb: │ F(x)│+│ G(x)│=0
Primeri: №1 . Reši enačbo:

Odgovor: x = 2. №2. Reši enačbo: Odgovor: x = 1. vaje: №21. Reši enačbo: №22 . Rešite enačbo in v odgovoru navedite vsoto korenin: №23 . Rešite enačbo in v odgovoru označite število rešitev:

Oddelek 8. Enačbe oblike │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m

Za reševanje tovrstnih enačb se uporablja intervalna metoda. Če jo rešimo z zaporedno širitvijo modulov, dobimo n sklopov sistemov, kar je zelo okorno in neprijetno. Oglejmo si algoritem intervalne metode: 1). Poišči vrednosti spremenljivk X, pri kateri vsak modul enako nič(ničle submodularnih izrazov):

2). Najdene vrednosti označite na številski premici, ki je razdeljena na intervale (število intervalov je enako n+1 ) 3). Ugotovite, s kakšnim znakom je vsak modul razkrit v vsakem od dobljenih intervalov (pri reševanju lahko uporabite številsko premico in na njej označite znake) 4). Prvotna enačba je enakovredna agregatu n+1 sistemov, v vsakem od katerih je navedena pripadnost spremenljivke X enega od intervalov. Primeri: №1 . Rešite enačbo in v odgovoru označite največji koren:

1). Poiščimo ničle submodularnih izrazov: x = 2; x = -3 2). Označimo najdene vrednosti na številski premici in določimo, s kakšnim znakom je vsak modul razkrit na nastalih intervalih:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)

- ni rešitev Enačba ima dva korena. Odgovor: največji koren x = 2. №2. Rešite enačbo in v svoj odgovor vnesite celoten koren:

1). Poiščimo ničle submodularnih izrazov: x = 1,5; x = - 1 2). Označimo najdene vrednosti na številski premici in določimo, s kakšnim znakom je vsak modul razkrit na dobljenih intervalih: x + 1 x + 1 x + 1 - + +
-1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).

Najnovejši sistem nima rešitev, zato ima enačba dva korena. Pri reševanju enačbe bodite pozorni na znak »-« pred drugim modulom. Odgovor: cel koren x = 7. №3. Rešite enačbo, v odgovoru navedite vsoto korenov: 1). Poiščimo ničle submodularnih izrazov: x = 5; x = 1; x = - 2 2). Označimo najdene vrednosti na številski premici in določimo, s kakšnim znakom je vsak modul razkrit v nastalih intervalih: x – 5 x – 5 x – 5 x – 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).

Enačba ima dva korena x = 0 in 2. Odgovor: vsota korenin je 2. №4 . Reši enačbo: 1). Poiščimo ničle submodularnih izrazov: x = 1; x = 2; x = 3. 2). Ugotovimo, s kakšnim predznakom je vsak modul razkrit na dobljenih intervalih. 3).

Združimo rešitve prvega trije sistemi. Odgovor: ; x = 5.
vaje: №24. Reši enačbo:

№25. Rešite enačbo in v odgovoru navedite vsoto korenin: №26. Rešite enačbo in v odgovoru označite manjši koren: №27. Rešite enačbo in v odgovoru označite večji koren:

Razdelek 9. Enačbe, ki vsebujejo več modulov

Enačbe, ki vsebujejo več modulov, predvidevajo prisotnost absolutnih vrednosti v submodularnih izrazih. Osnovno načelo reševanja enačb te vrste je zaporedno razkritje modulov, začenši z "zunanjim". Med reševanjem se uporabljajo tehnike, obravnavane v razdelkih št. 1, št. 3.

Primeri: №1. Reši enačbo:
Odgovor: x = 1; - enajst. №2. Reši enačbo:
Odgovor: x = 0; 4; - 4. №3. Rešite enačbo in v odgovoru označite produkt korenin:
Odgovor: produkt korenin je – 8. №4. Reši enačbo:
Označimo enačbe populacije (1) in (2) in razmislite o rešitvi za vsako od njih posebej zaradi lažjega načrtovanja. Ker obe enačbi vsebujeta več kot en modul, je primerneje izvesti enakovreden prehod na množice sistemov. (1)

(2)

odgovor:
vaje: №36. Rešite enačbo, v odgovoru navedite vsoto korenov: 5 │3x-5│ = 25 x №37. Rešite enačbo, če je korenin več, v odgovoru navedite vsoto korenin: │x + 2│ x – 3x – 10 = 1 №38. Rešite enačbo: 3 │2x -4│ = 9 │x│ №39. Rešite enačbo in v odgovoru navedite število korenov: 2 │ sin x│ = √2 №40 . Rešite enačbo in v odgovoru navedite število korenin:

Oddelek 3. Logaritemske enačbe.

Preden rešimo naslednje enačbe, je treba pregledati lastnosti logaritmov in logaritemska funkcija. Primeri: №1. Rešite enačbo, v odgovoru navedite zmnožek korenov: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1

Primer 1: če je x ≥ - 1, potem je log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – izpolnjuje pogoj x ≥ - 1 2 primer: če je x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – izpolnjuje pogoj x - 1
Odgovor: produkt korenin je – 15.
№2. Rešite enačbo, v odgovoru navedite vsoto korenin: lg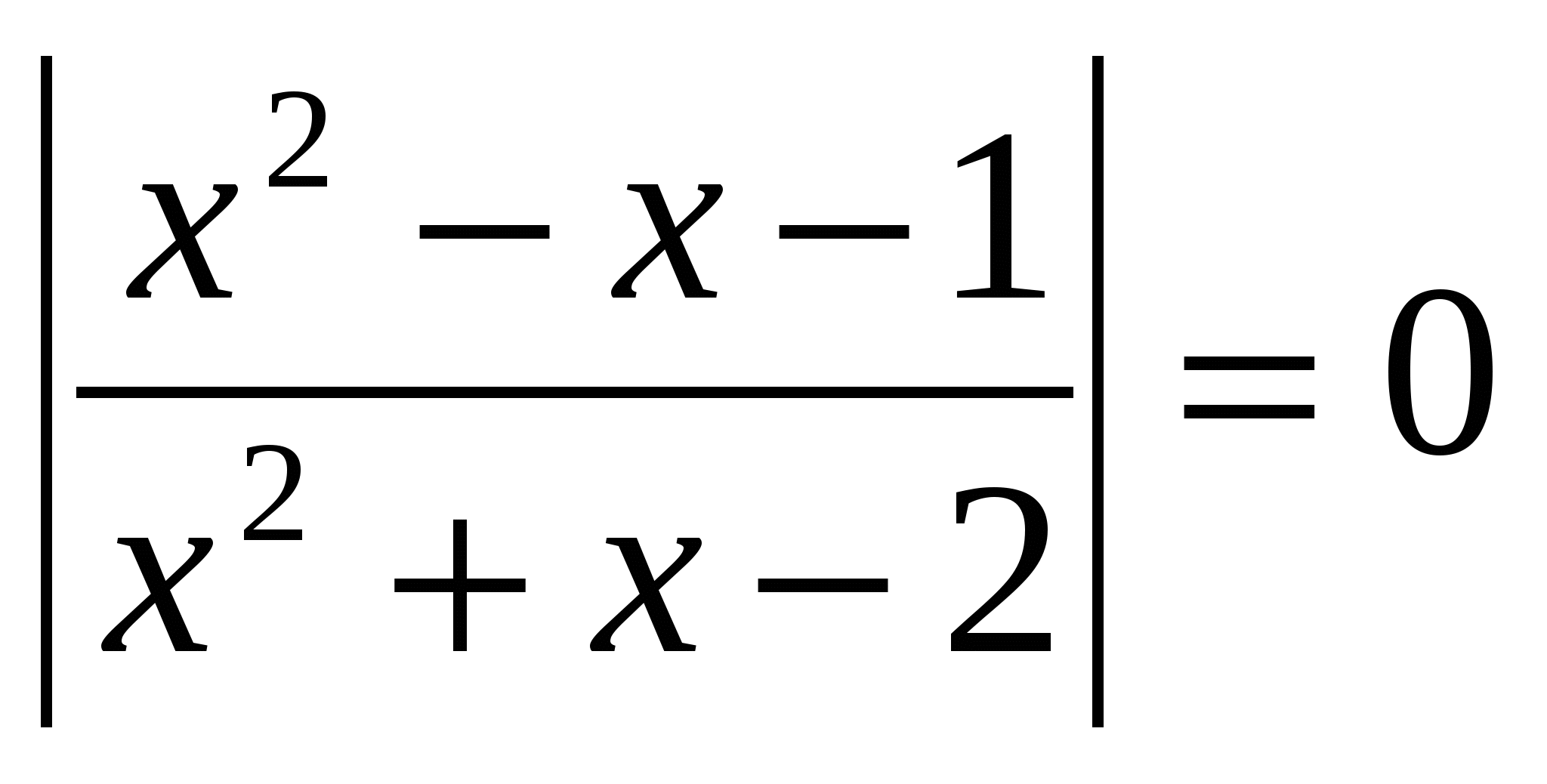
O.D.Z.

Odgovor: vsota korenov je 0,5.
№3. Reši enačbo: log 5
O.D.Z.

Odgovor: x = 9. №4. Rešite enačbo: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Uporabimo formulo za premik na drugo bazo. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Poiščemo ničle submodularnih izrazov: x = 25; x = Te številke delijo površino sprejemljive vrednosti na tri intervale, zato je enačba enakovredna kombinacija treh sistemi
odgovor :)