TRABAJO PRÁCTICO N°1
Sujeto: "Transformación de conceptos algebraicos, racionales, irracionales, expresiones de poder».
Objetivo del trabajo: aprenda a transformar expresiones algebraicas, racionales, irracionales y de potencias utilizando fórmulas de multiplicación abreviadas, propiedades básicas de raíces y potencias.
Información teórica.
RAÍCES DE GRADO NATURAL A PARTIR DEL NÚMERO, SUS PROPIEDADES.
Raíz norte – grados : , norte - exponente raíz, A - expresión radical
Si norte - número impar, entonces la expresión tiene sentido cuando A
Si norte - número par, entonces la expresión tiene sentido cuando
Raíz aritmética:
![]()
Raíz impar de un número negativo:
PROPIEDADES BÁSICAS DE LAS RAÍCES
La regla para extraer la raíz de un producto:
![]()
Regla para extraer una raíz de una raíz:
![]()
La regla para eliminar el multiplicador debajo del signo raíz:
Ingresando un multiplicador bajo el signo de la raíz:
![]() ,
,
El índice de la raíz y el índice de la expresión radical se pueden multiplicar por el mismo número.
![]()
La regla para elevar una raíz a una potencia.
GRADO CON INDICADOR NATURAL
= , a – la base del título,norte – exponente
Propiedades:
Al multiplicar potencias con las mismas bases, se suman los exponentes, pero la base permanece sin cambios.
![]()
Al dividir grados con las mismas bases, se restan los exponentes, pero la base permanece sin cambios.
![]()
Al elevar una potencia a una potencia, los exponentes se multiplican.
Al elevar el producto de dos números a una potencia, cada número se eleva a esa potencia y se multiplican los resultados.
![]()
Si el cociente de dos números se eleva a una potencia, entonces el numerador y el denominador se elevan a esta potencia y el resultado se divide entre sí.
GRADO CON INDICADOR ENTERO
![]()
Propiedades:
en r >0 > en r <0
7 . Para cualquier número racionalr Ys de la desigualdad > debería
> en a >1 en
Fórmulas de multiplicación abreviadas.

Ejemplo 1. Simplifica la expresión.
Apliquemos las propiedades de las potencias (multiplicando potencias con la misma base y división de poderes con la misma base):  .
.
Respuesta: 9m 7 .
Ejemplo 2. Reducir fracción:
Solución Entonces el dominio de definición de la fracción son todos los números excepto x ≠ 1 y x ≠ -2. ![]() .Al reducir la fracción, obtenemos .El dominio de definición de la fracción resultante: x ≠ -2, es decir más amplio que el rango de definición de la fracción original. Por tanto, las fracciones y son iguales para x ≠ 1 y x ≠ -2.
.Al reducir la fracción, obtenemos .El dominio de definición de la fracción resultante: x ≠ -2, es decir más amplio que el rango de definición de la fracción original. Por tanto, las fracciones y son iguales para x ≠ 1 y x ≠ -2.
Ejemplo 3. Reducir fracción: ![]()
Ejemplo 4. Simplificar: ![]()
Ejemplo 5.Simplificar: ![]()
Ejemplo 6. Simplificar: ![]()
Ejemplo 7. Simplificar: ![]()
Ejemplo 8. Simplificar: 
Ejemplo 9. Calcular: ![]() .
.
Solución.
Ejemplo 10. Simplifica la expresión:
Solución. 
Ejemplo 11.Reducir una fracción si
Solución. ![]() .
.
Ejemplo 12. Libérate de la irracionalidad en el denominador de una fracción
Solución. En el denominador tenemos irracionalidad de 2do grado, por lo tanto multiplicamos tanto el numerador como el denominador de la fracción por la expresión conjugada, es decir, la suma de los números y , luego en el denominador tenemos la diferencia de cuadrados, que elimina la irracionalidad.
OPCIÓN - I1. Simplifica la expresión:



 , donde a es un número racional,
b
- número natural
, donde a es un número racional,
b
- número natural
 ,
, 
5. Simplifica:
 ;
; 
 ,
,  ,
, 
 10. Sigue esta acción:
10. Sigue esta acción:
8. Reducir la fracción 

9. Toma acción 
OPCIÓN - II
1. Simplifica la expresión:

2. Encuentra el significado de la expresión:

3. Imagina un título con indicador fraccionario en forma de raíz

4. Liderar expresión especificada a la mente  , donde a es un número racional,
b
- número natural
, donde a es un número racional,
b
- número natural
 ,
, 
5. Simplifica:
 ;
; 
6. Reemplazar raíces aritméticas con potencias con exponente fraccionario.
 ,
,  ,
, 
7. Presentar la expresión como una fracción cuyo denominador no contiene signo de raíz.
 10. Sigue esta acción:
10. Sigue esta acción:
8. Reducir la fracción 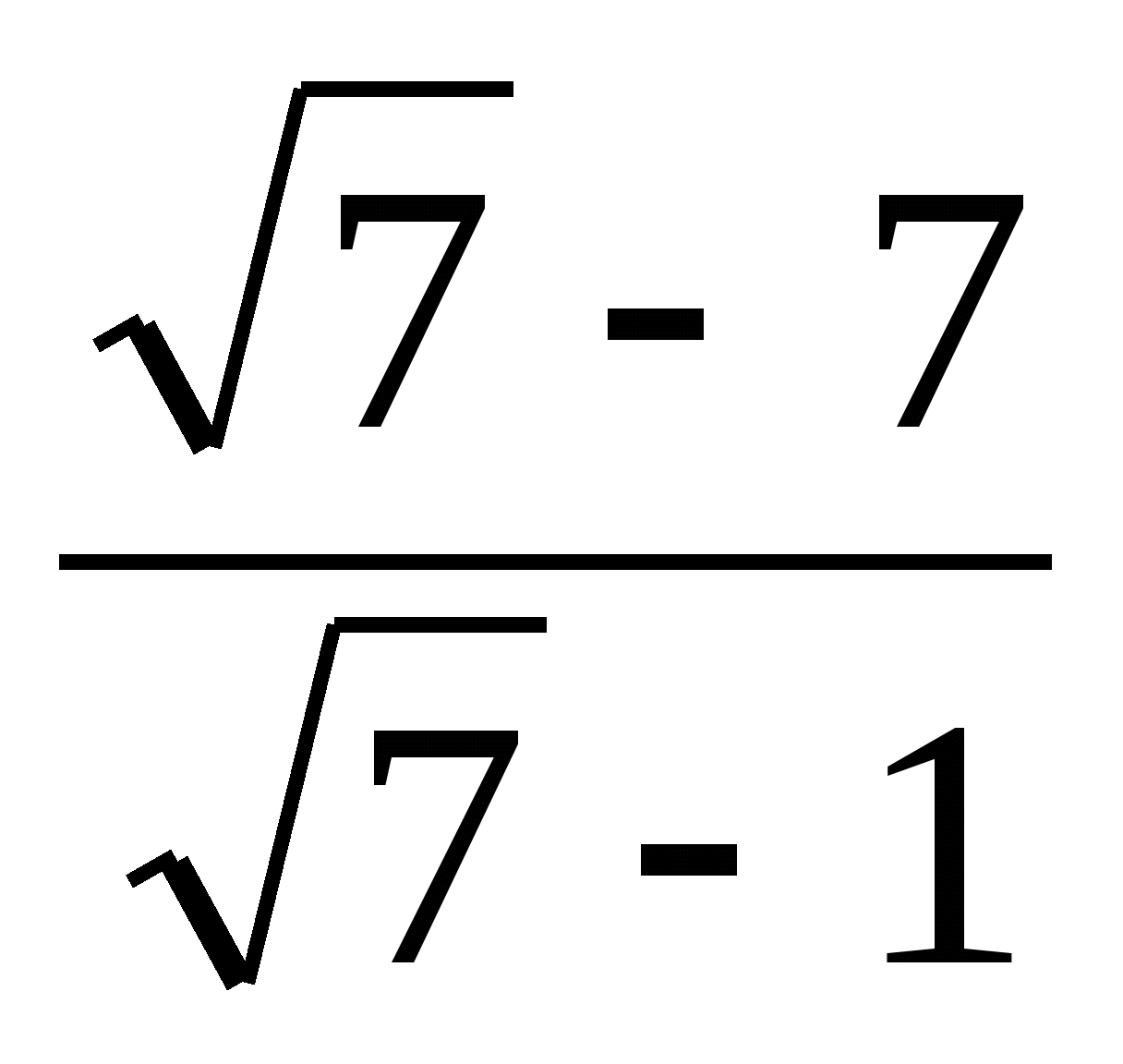

9. Toma acción 
1. Sigue esta acción:

2. Encuentra el significado de la expresión:

3. Representar una potencia con exponente fraccionario como raíz.

4. Reduzca la expresión especificada a la forma.  , donde a es un número racional,
b
- número natural
, donde a es un número racional,
b
- número natural
 ,
, 
5. Simplifica:
 ;
; 
6. Reemplazar raíces aritméticas con potencias con exponente fraccionario.
 ,
,  ,
, 
7. Presentar la expresión como una fracción cuyo denominador no contiene signo de raíz.
 10. Sigue esta acción:
10. Sigue esta acción:
8. Reducir la fracción 

9. Toma acción

OPCIÓN - IV
1. Sigue esta acción:

2. Encuentra el significado de la expresión:

3. Representar una potencia con exponente fraccionario como raíz.

 ,
, 
4. Reduzca la expresión especificada a la forma.  , donde a es un número racional,
b
- número natural
, donde a es un número racional,
b
- número natural
 ,
, 
5. Simplifica:
Expresiones irracionales y sus transformaciones.
La última vez que recordamos (o aprendimos, según quién) qué es , aprendió a extraer esas raíces, descubrió las propiedades básicas de las raíces pieza por pieza y decidió no ejemplos complejos con raíces.
Esta lección será una continuación de la anterior y estará dedicada a la transformación de los más diferentes expresiones que contiene todo tipo de raíces. Este tipo de expresiones se llaman irracional. Aquí aparecerán expresiones con letras, condiciones adicionales, cómo deshacerse de la irracionalidad en fracciones y algunas técnicas avanzadas para trabajar con raíces. Las técnicas que se discutirán en Esta lección, será una buena base para resolver Problemas con el examen estatal unificado(y no sólo) de casi cualquier nivel de complejidad. Entonces empecemos.
En primer lugar, duplicaré aquí. fórmulas básicas y propiedades de las raíces. Para no saltar de un tema a otro. Aquí están:
![]()
![]() en
en
![]()
Debes conocer estas fórmulas y poder aplicarlas. Y en ambas direcciones, de izquierda a derecha y de derecha a izquierda. En ellos se basa la solución a la mayoría de tareas con raíces de cualquier grado de complejidad. Empecemos por lo más sencillo por ahora: con aplicación directa fórmulas o sus combinaciones.
Fácil aplicación de fórmulas.
En esta parte se considerarán ejemplos sencillos e inofensivos, sin letras, condiciones adicionales ni otros trucos. Sin embargo, incluso en ellos, por regla general, hay opciones. Y cuanto más sofisticado sea el ejemplo, más opciones de este tipo habrá. Y un estudiante sin experiencia tiene el problema principal- ¿donde empezar? La respuesta aquí es simple: Si no sabes lo que necesitas, haz lo que puedas.. Siempre y cuando tus acciones estén en paz y armonía con las reglas de las matemáticas y no las contradigan). Por ejemplo, esta tarea:
Calcular:
Incluso en un ejemplo tan sencillo, hay varios caminos posibles hacia la respuesta.
La primera es simplemente multiplicar las raíces por la primera propiedad y extraer la raíz del resultado:
La segunda opción es esta: no lo tocamos, trabajamos con. Sacamos el factor de debajo del signo raíz y luego, de acuerdo con la primera propiedad. Como esto:
Puedes decidir todo lo que quieras. En cualquiera de las opciones, la respuesta es uno: ocho. Por ejemplo, es más fácil para mí multiplicar 4 y 128 y obtener 512, y la raíz cúbica se puede extraer fácilmente de este número. Si alguien no recuerda que 512 es 8 al cubo, entonces no importa: puedes escribir 512 como 2 9 (las primeras 10 potencias de dos, espero que lo recuerdes) y usar la fórmula para la raíz de la potencia. :
Otro ejemplo.
Calcular: .
Si trabajas de acuerdo con la primera propiedad (poner todo bajo una misma raíz), obtendrás un número considerable, del que luego se puede extraer la raíz, y tampoco el azúcar. Y no es un hecho que se extraiga exactamente). Por lo tanto, aquí es útil eliminar los factores de debajo de la raíz del número. Y aprovecha al máximo:
Y ahora todo está bien:
Todo lo que queda es escribir el ocho y el dos bajo una raíz (según la primera propiedad) y listo. :)
Ahora agreguemos algunas fracciones.
Calcular:
El ejemplo es bastante primitivo, pero también tiene opciones. Puedes usar el multiplicador para transformar el numerador y reducirlo con el denominador:

O puede utilizar inmediatamente la fórmula para dividir raíces:

Como vemos, de esta manera y de aquella, todo es correcto.) Si no tropiezas a mitad del camino y cometes un error. Aunque ¿dónde puedo equivocarme aquí?...
Veamos ahora lo más último ejemplo de tareaúltima lección:
Simplificar:
![]()
Un conjunto de raíces completamente inimaginable, e incluso anidadas. ¿Qué tengo que hacer? ¡Lo principal es no tener miedo! Aquí primero notamos debajo de las raíces los números 2, 4 y 32, potencias de dos. Lo primero que hay que hacer es reducir todos los números a dos: después de todo, cuanto más números idénticos en el ejemplo, cuantos menos diferentes, más sencillo). Comencemos por separado con el primer factor:
![]()
El número se puede simplificar reduciendo el dos bajo la raíz con el cuatro en el exponente de la raíz:
Ahora bien, según la raíz de la obra:
![]() .
.
En el número sacamos el dos como signo raíz:
Y nos ocupamos de la expresión usando la raíz de la fórmula raíz:
Entonces, el primer factor se escribirá así:
Las raíces anidadas desaparecieron, los números se hicieron más pequeños, lo que ya agrada. Es solo que las raíces son diferentes, pero lo dejaremos así por ahora. Si es necesario, los convertiremos a los mismos. Tomemos el segundo factor.)
Transformamos el segundo factor de forma similar, usando la fórmula de la raíz del producto y la raíz de la raíz. Cuando sea necesario, reducimos los indicadores utilizando la quinta fórmula:
Insertamos todo en ejemplo original y obtenemos:
Obtuvimos el producto de un montón de raíces completamente diferentes. Sería bueno reunirlos a todos en un solo indicador y luego ya veremos. Bueno, es muy posible. El mayor de los exponentes de la raíz es 12, y todos los demás (2, 3, 4, 6) son divisores del número 12. Por lo tanto, reduciremos todas las raíces de acuerdo con la quinta propiedad a un exponente: 12:
![]()
Contamos y obtenemos:
No obtuvimos un buen número, pero está bien. Se nos pidió simplificar expresión, no contar. ¿Simplificado? ¡Ciertamente! Y el tipo de respuesta (entero o no) ya no juega ningún papel aquí.
Algunas fórmulas de suma/resta y multiplicación abreviada
Desafortunadamente, fórmulas generales Para suma y resta de raíces no en matemáticas. Sin embargo, en las tareas se suelen encontrar estas acciones con arraigo. Aquí es necesario comprender que cualquier raíz es exactamente los mismos símbolos matemáticos que las letras en álgebra). Y se aplican las mismas técnicas y reglas a las raíces que a las letras: abrir paréntesis, traer otros similares, fórmulas de multiplicación abreviadas, etc.
Por ejemplo, para todos está claro que . Similar lo mismo Las raíces se pueden sumar/restar entre sí con bastante facilidad:
![]()
![]()
Si las raíces son diferentes, entonces buscamos una manera de hacerlas iguales: sumando/restando un multiplicador o usando la quinta propiedad. Si no se simplifica de ninguna manera, entonces quizás las transformaciones sean más astutas.
Veamos el primer ejemplo.
Encuentra el significado de la expresión: .
Las tres raíces, aunque cúbicas, son de diferente números. No se extraen puramente y se suman/restan entre sí. Por tanto, el uso de fórmulas generales no funciona aquí. ¿Qué tengo que hacer? Saquemos los factores en cada raíz. En cualquier caso, no será peor). Además, de hecho, no hay otras opciones:
Eso es, .
Esa es la solución. Aquí pasamos de diferentes raíces a las mismas con la ayuda quitando el multiplicador de debajo de la raíz. Y luego simplemente trajeron otros similares). Decidimos más.
Encuentra el valor de una expresión.:
Definitivamente no hay nada que puedas hacer con la raíz de diecisiete. Trabajamos de acuerdo con la primera propiedad: hacemos una raíz a partir del producto de dos raíces:
Ahora echemos un vistazo más de cerca. ¿Qué tenemos bajo el gran raíz cúbica? La diferencia es qua... ¡Pues claro! Diferencia de cuadrados:
Ahora solo queda extraer la raíz: .
Calcular:
Aquí tendrás que mostrar ingenio matemático.) Pensamos aproximadamente de la siguiente manera: “Entonces, en el ejemplo, el producto de las raíces. Debajo de una raíz está la diferencia y debajo de la otra está la suma. Muy similar a la fórmula de diferencia de cuadrados. Pero… ¡Las raíces son diferentes! El primero es cuadrado y el segundo es de cuarto grado... Sería bueno hacerlos iguales. Según la quinta propiedad, uno puede fácilmente raíz cuadrada hacer la raíz cuarta. Para ello basta con elevar al cuadrado la expresión radical”.
Si pensaste lo mismo, entonces estás a medio camino del éxito. ¡Absolutamente correcto! Convirtamos el primer factor en una cuarta raíz. Como esto:
![]()
Ahora ya no hay nada que hacer, pero tendrás que recordar la fórmula del cuadrado de la diferencia. Sólo cuando se aplica a las raíces. ¿Así que lo que? ¿Por qué las raíces son peores que otros números o expresiones? Construimos:
“Hmm, bueno, lo erigieron, ¿y qué? El rábano picante no es más dulce que el rábano. ¡Detener! ¿Y si sacas los cuatro que están debajo de la raíz? Entonces aparecerá la misma expresión que bajo la segunda raíz, sólo que con un menos, ¡y esto es exactamente lo que estamos tratando de lograr!
¡Bien! Tomemos cuatro:
![]() .
.
Y ahora, una cuestión de tecnología:
Así es como se desenredan los ejemplos complejos). Ahora es el momento de practicar con fracciones.
Calcular:
Está claro que hay que convertir el numerador. ¿Cómo? Usando la fórmula del cuadrado de la suma, por supuesto. ¿Tenemos otras opciones? :) Lo cuadramos, sacamos los factores, reducimos los indicadores (cuando sea necesario):
¡Guau! Obtuvimos exactamente el denominador de nuestra fracción). Esto significa que la fracción entera es obviamente igual a uno:

Otro ejemplo. Sólo que ahora pasamos a otra fórmula para la multiplicación abreviada).
Calcular:
Está claro que en la práctica se debe utilizar el cuadrado de la diferencia. Escribimos el denominador por separado y ¡vamos!
Sacamos los factores de debajo de las raíces:
![]()
Por eso,
Ahora todo lo malo se reduce magníficamente y resulta:

Bueno, llevémoslo al siguiente nivel. :)
Cartas y condiciones adicionales.
Las expresiones literales con raíces son algo más complicado que expresiones numéricas, y es una fuente inagotable Errores molestos y muy graves. Cerremos esta fuente.) Los errores surgen debido al hecho de que tales tareas a menudo involucran números y expresiones negativos. Se nos dan directamente en la tarea o se nos ocultan en cartas y condiciones adicionales. Y en el proceso de trabajar con raíces, debemos recordar constantemente que en las raíces grado par tanto debajo de la raíz misma como como resultado de la extracción de la raíz debe haber expresión no negativa. La fórmula clave en las tareas de este párrafo será la cuarta fórmula:
Con raices grado impar No hay preguntas: siempre se extrae todo allí, tanto los más como los menos. Y el inconveniente, en todo caso, se adelanta. Vayamos directo a las raíces incluso grados.) Por ejemplo, una tarea tan corta.
Simplificar: , Si .
Parecería que todo es sencillo. Simplemente resultará ser una X.) ¿Pero por qué entonces? Condición adicional ? En tales casos, es útil estimar con números. Puramente para mí.) Si, entonces x es obviamente un numero negativo. Menos tres, por ejemplo. O menos cuarenta. Dejar . ¿Puedes elevar menos tres a la cuarta potencia? ¡Ciertamente! El resultado es 81. ¿Es posible extraer la raíz cuarta de 81? ¿Por qué no? ¡Poder! Obtienes tres. Ahora analicemos toda nuestra cadena:
¿Qué vemos? La entrada fue un número negativo y la salida ya era positiva. Era menos tres, ahora es más tres.) Volvamos a las letras. Sin duda, módulo será exactamente x, pero solo x en sí es menos (¡por condición!), y el resultado de la extracción (en virtud de raíz aritmética!) debe ser más. ¿Cómo conseguir un plus? ¡Muy simple! Para hacer esto, basta con anteponer un número obviamente negativo a un signo menos). Y solución correcta tiene este aspecto:
Por cierto, si usáramos la fórmula, al recordar la definición de módulo, inmediatamente obtendríamos la respuesta correcta. Porque el
|x| = -x en x<0.
Saca el factor del signo raíz: , Dónde .
La primera mirada es a la expresión radical. Todo está bien aquí. En cualquier caso, no será negativo. Empecemos a extraer. Usando la fórmula de la raíz de un producto, extraemos la raíz de cada factor:
No creo que sea necesario explicar de dónde vienen los módulos). Ahora analicemos cada uno de los módulos.
Multiplicador | a | lo dejamos sin cambios: no tenemos ninguna condición para la cartaa. No sabemos si es positivo o negativo. Siguiente módulo |segundo 2 | se puede omitir con seguridad: en cualquier caso, la expresiónsegundo 2 no negativo. Pero sobre |c 3 | - ya hay un problema aquí.) Si, entonces c 3 <0. Стало быть, модуль надо раскрыть con un menos: | c 3 | = - c 3 . En total, la solución correcta sería:
Y ahora, el problema inverso. No es el más fácil, ¡te lo advierto de inmediato!
Ingrese un multiplicador bajo el signo de la raíz.: .
Si escribes inmediatamente la solución como esta
entonces tú cayó en una trampa. Este mala decisión! ¿Qué pasa?
Echemos un vistazo más de cerca a la expresión debajo de la raíz. Bajo la raíz del cuarto grado, como sabemos, debería haber no negativo expresión. De lo contrario, la raíz no tiene significado.) Por lo tanto, Y esto, a su vez, significa que y, por lo tanto, en sí mismo tampoco es positivo: .
Y el error aquí es que estamos introduciendo desde la raíz no positivo número: el cuarto grado lo convierte en no negativo y se obtiene el resultado incorrecto: a la izquierda hay un menos deliberado y a la derecha ya hay un más. Y ponlo en la raíz incluso grado tenemos el derecho sólo no negativo números o expresiones. Y deje el menos, si lo hay, delante de la raíz). ¿Cómo podemos identificar un factor no negativo en el número?, sabiendo que ella misma es completamente negativa? ¡Sí, exactamente lo mismo! Pon un menos.) Y para que nada cambie, compénsalo con otro menos. Como esto:
![]()
Y ahora ya no negativo Ingresamos tranquilamente el número (-b) debajo de la raíz de acuerdo con todas las reglas:
Este ejemplo muestra claramente que, a diferencia de otras ramas de las matemáticas, en las raíces la respuesta correcta no siempre se deriva automáticamente de las fórmulas. Debe pensar y tomar personalmente la decisión correcta). Especialmente debe tener más cuidado con las señales en ecuaciones y desigualdades irracionales.
Veamos la siguiente técnica importante al trabajar con raíces: deshacerse de la irracionalidad.
Eliminando la irracionalidad en fracciones.
Si la expresión contiene raíces, permítame recordarle que dicha expresión se llama expresión con irracionalidad. En algunos casos, puede resultar útil deshacerse de esta misma irracionalidad (es decir, de las raíces). ¿Cómo se puede eliminar la raíz? Nuestra raíz desaparece cuando... elevada a un poder. Con un indicador igual al indicador raíz o un múltiplo del mismo. Pero, si elevamos la raíz a una potencia (es decir, multiplicamos la raíz por sí misma el número requerido de veces), entonces la expresión cambiará. No es bueno.) Sin embargo, en matemáticas hay temas en los que la multiplicación es bastante sencilla. En fracciones, por ejemplo. Según la propiedad básica de una fracción, si el numerador y el denominador se multiplican (dividen) por el mismo número, el valor de la fracción no cambiará.
Digamos que nos dan esta fracción:
¿Es posible deshacerse de la raíz del denominador? ¡Poder! Para hacer esto, la raíz debe cortarse en cubos. ¿Qué nos falta en el denominador de un cubo lleno? Nos falta un multiplicador, es decir.. Entonces multiplicamos el numerador y el denominador de la fracción por

La raíz del denominador ha desaparecido. Pero... apareció en el numerador. No se puede hacer nada, así es el destino.) Esto ya no es importante para nosotros: nos pidieron que liberáramos el denominador de las raíces. ¿Liberado? Indudablemente.)
Por cierto, aquellos que ya se sienten cómodos con la trigonometría pueden haber prestado atención al hecho de que en algunos libros de texto y tablas, por ejemplo, designan de manera diferente: en algún lugar y en algún lugar. La pregunta es: ¿qué es lo correcto? Respuesta: ¡todo es correcto!) Si adivinas eso– esto es simplemente el resultado de la liberación de la irracionalidad en el denominador de la fracción. :)
¿Por qué deberíamos liberarnos de la irracionalidad en fracciones? ¿Qué diferencia hay si la raíz está en el numerador o en el denominador? La calculadora calculará todo de todos modos.) Bueno, para aquellos que no se separan de una calculadora, prácticamente no hay diferencia... Pero incluso contando con una calculadora, puedes prestar atención al hecho de que dividir en entero El número siempre es más conveniente y más rápido que en irracional. Y guardaré silencio sobre la división en columnas).
El siguiente ejemplo sólo confirmará mis palabras.
¿Cómo podemos eliminar aquí la raíz cuadrada del denominador? Si el numerador y el denominador se multiplican por la expresión, entonces el denominador será el cuadrado de la suma. La suma de los cuadrados del primer y segundo número nos dará números sin raíces, lo cual es muy agradable. Sin embargo... aparecerá doble producto el primer número al segundo, donde aún quedará la raíz de tres. No canaliza. ¿Qué tengo que hacer? ¡Recuerda otra fórmula maravillosa para la multiplicación abreviada! Donde no hay productos dobles, sino sólo cuadrados:
Una expresión que, cuando se multiplica por una determinada suma (o diferencia), produce diferencia de cuadrados, también llamado expresión conjugada. En nuestro ejemplo, la expresión conjugada será la diferencia. Entonces multiplicamos el numerador y el denominador por esta diferencia:
¿Qué puedo decir? Como resultado de nuestras manipulaciones, no sólo desapareció la raíz del denominador, ¡sino que la fracción desapareció por completo! :) Incluso con una calculadora, restar la raíz de tres de un tres es más fácil que calcular una fracción con la raíz en el denominador. Otro ejemplo.
Libérate de la irracionalidad en el denominador de una fracción:
¿Cómo salir de esto? Las fórmulas para la multiplicación abreviada con cuadrados no funcionan de inmediato: eliminar completamente las raíces no será posible debido a que esta vez nuestra raíz no es cuadrada, sino cúbico. Es necesario que la raíz se eleve de alguna manera hasta formar un cubo. Por tanto, se debe utilizar una de las fórmulas con cubos. ¿Cuál? Vamos a pensarlo. El denominador es la suma. ¿Cómo podemos lograr el cubo de la raíz? Multiplicar por diferencia al cuadrado parcial! Entonces aplicaremos la fórmula suma de cubos. Éste:
Como a tenemos tres, y como cualidad b– raíz cúbica de cinco:
Y nuevamente la fracción desapareció.) Tales situaciones en las que, cuando se libera de la irracionalidad en el denominador de una fracción, la fracción misma desaparece por completo junto con las raíces, ocurren muy a menudo. ¡Qué te parece este ejemplo!
Calcular:
![]()
¡Intenta sumar estas tres fracciones! ¡Sin errores! :) Un denominador común lo vale. ¿Y si intentáramos liberarnos de la irracionalidad en el denominador de cada fracción? Bueno, probemos:
¡Vaya, qué interesante! ¡Todas las fracciones desaparecieron! Completamente. Y ahora el ejemplo se puede solucionar de dos formas:
Sencillo y elegante. Y sin largos y tediosos cálculos. :)
Por eso es necesario poder realizar la operación de liberación de la irracionalidad en fracciones. En ejemplos tan sofisticados, es lo único que salva, sí.) Por supuesto, nadie canceló la atención. Hay tareas en las que se le pide que se deshaga de la irracionalidad en numerador. Estas tareas no son diferentes de las consideradas, solo el numerador se borra de la raíz).
Ejemplos más complejos
Queda por considerar algunas técnicas especiales para trabajar con raíces y practicar para desenredar no los ejemplos más simples. Y luego la información recibida será suficiente para resolver problemas con raíces de cualquier nivel de complejidad. Entonces, adelante.) Primero, averigüemos qué hacer con las raíces anidadas cuando la fórmula raíz a raíz no funciona. Por ejemplo, aquí tienes un ejemplo.
Calcular:
La raíz está debajo de la raíz... Además, debajo de las raíces está la suma o diferencia. Por lo tanto, la fórmula para la raíz de la raíz (con multiplicación de exponentes) está aquí. No funciona. Entonces es necesario hacer algo al respecto expresiones radicales: Simplemente no tenemos otras opciones. En tales ejemplos, la mayoría de las veces la raíz grande está cifrada. cuadrado perfecto alguna cantidad. O diferencias. ¡Y la raíz del cuadrado ya está perfectamente extraída! Y ahora nuestra tarea es descifrarlo.) Este descifrado se realiza maravillosamente a través de sistema de ecuaciones. Ahora verás todo por ti mismo.)
Entonces, bajo la primera raíz tenemos esta expresión:
¿Qué pasa si no acertaste? ¡Vamos a revisar! Lo elevamos al cuadrado usando la fórmula para el cuadrado de la suma:
Así es.) Pero... ¿De dónde saqué esta expresión? ¿Desde el cielo?
No.) Sinceramente, lo bajaremos un poco más. Usando simplemente esta expresión, muestro exactamente cómo los redactores de tareas cifran dichos cuadrados. :) ¿Cuánto es 54? Este suma de cuadrados del primer y segundo numero. Y ojo, ¡ya sin raíces! Y la raíz permanece en doble producto, que en nuestro caso es igual a . Por lo tanto, desentrañar tales ejemplos comienza con la búsqueda del doble producto. Si te desenredas con la selección habitual. Y, por cierto, sobre las señales. Aquí todo es sencillo. Si hay un más antes del doble, entonces el cuadrado de la suma. Si es un menos, entonces las diferencias.) Tenemos un más, es decir, el cuadrado de la suma.) Y ahora, el método analítico de decodificación prometido. A través del sistema.)
Entonces, debajo de nuestra raíz está claramente colgando la expresión (a+b) 2, y nuestra tarea es encontrar a Y b. En nuestro caso, la suma de cuadrados da 54. Entonces escribimos:
![]()
Ahora duplica el producto. Lo tenemos. Entonces lo anotamos:
Tenemos este sistema:
![]()
Resolvemos por el método de sustitución habitual. Expresamos a partir de la segunda ecuación, por ejemplo, y la sustituimos en la primera:

Resolvamos la primera ecuación:
Consiguió bicuadrado ecuación relativaa . Calculamos el discriminante:
Medio,
Obtuvimos hasta cuatro valores posibles.a. No tenemos miedo. Ahora eliminaremos todo lo innecesario). Si ahora calculamos los valores correspondientes para cada uno de los cuatro valores encontrados, obtendremos cuatro soluciones para nuestro sistema. Aquí están:
Y aquí surge la pregunta: ¿qué solución es la adecuada para nosotros? Vamos a pensarlo. Las soluciones negativas se pueden descartar de inmediato: al elevar al cuadrado, los menos se “quemarán” y toda la expresión radical no cambiará en su conjunto). Las dos primeras opciones permanecen. Puedes elegirlos de forma completamente arbitraria: reorganizar los términos aún no cambia la suma.) Sea, por ejemplo, , a .
En total, obtenemos el cuadrado de la siguiente suma bajo la raíz:
Todo está claro.)
No en vano describo el proceso de decisión con tanto detalle. Para dejar claro cómo se produce el descifrado). Pero hay un problema. El método analítico de decodificación, aunque fiable, es muy largo y engorroso: hay que resolver una ecuación bicuadrática, obtener cuatro soluciones para el sistema y luego seguir pensando cuáles elegir... ¿Preocupante? Estoy de acuerdo, es problemático. Este método funciona perfectamente en la mayoría de estos ejemplos. Sin embargo, muy a menudo puedes ahorrarte mucho trabajo y encontrar ambos números de forma creativa. Por selección.) ¡Sí, sí! Ahora, usando el ejemplo del segundo término (segunda raíz), mostraré una manera más fácil y rápida de aislar cuadrado lleno debajo de la raíz.
Entonces ahora tenemos esta raíz: ![]() .
.
Pensemos así: “Lo más probable es que debajo de la raíz haya un cuadrado completo encriptado. Una vez que hay un menos antes del doble, significa el cuadrado de la diferencia. La suma de los cuadrados del primer y segundo número nos da el número. 54. ¿Pero qué tipo de cuadrados son estos? 1 y 53? 49 y 5 ? Hay demasiadas opciones... No, es mejor empezar a desenredar con el doble de producto. NuestroSe puede escribir como . Una vez que el producto duplicado, luego inmediatamente descartamos los dos. Entonces candidatos para el puesto. a y b siguen siendo 7 y . ¿Qué pasa si son 14 y/2 ? Es posible. ¡Pero siempre empezamos con algo sencillo!” Entonces, dejemos, a. Revisémoslos para la suma de cuadrados:
¡Sucedió! Esto significa que nuestra expresión radical es en realidad el cuadrado de la diferencia:
A continuación se muestra una forma sencilla de evitar alterar el sistema. No siempre funciona, pero en muchos de estos ejemplos es suficiente. Entonces, debajo de las raíces hay cuadrados completos. Ya solo queda extraer correctamente las raíces y calcular el ejemplo:
Ahora veamos una tarea aún menos estándar sobre raíces).
Demuestre que el número A– número entero, si .
No se extrae nada directamente, se incrustan las raíces, e incluso en distintos grados… ¡Una pesadilla! Sin embargo, la tarea tiene sentido.) Por lo tanto, existe una clave para resolverla.) Y la clave aquí es esta. Considere nuestra igualdad
Cómo ecuación relativa A. ¡Sí Sí! Sería bueno deshacerse de las raíces. Nuestras raíces son cúbicas, así que elevamos al cubo ambos lados de la ecuación. Según la fórmula cubo de la suma:

Los cubos y las raíces cúbicas se cancelan entre sí, y debajo de cada raíz grande tomamos un paréntesis del cuadrado y colapsamos el producto de la diferencia y la suma en una diferencia de cuadrados:
Por separado, calculamos la diferencia de cuadrados bajo las raíces:
Las transformaciones idénticas de expresiones son una de las líneas de contenido del curso de matemáticas escolar. Las transformaciones idénticas se utilizan ampliamente para resolver ecuaciones, desigualdades, sistemas de ecuaciones y desigualdades. Además, transformaciones idénticas de expresiones contribuyen al desarrollo de la inteligencia, la flexibilidad y la racionalidad del pensamiento.
Los materiales propuestos están destinados a estudiantes de 8º grado e incluyen fundamentos teóricos. transformaciones de identidad racional y ir expresiones racionales, tipos de tareas para transformar dichas expresiones y el texto de la prueba.
1. Fundamentos teóricos de las transformaciones de identidad.
Las expresiones en álgebra son registros que consisten en números y letras conectados por signos de acción.
https://pandia.ru/text/80/197/images/image002_92.gif" width="77" height="21 src=">.gif" width="20" height="21 src="> – expresiones algebraicas.
Dependiendo de las operaciones se distinguen expresiones racionales e irracionales.
Las expresiones algebraicas se llaman racionales si se relacionan con las letras incluidas en ellas. A, b, Con, ... no se realizan otras operaciones excepto suma, multiplicación, resta, división y exponenciación.
Expresiones algebraicas que contienen operaciones para extraer la raíz de una variable o elevar una variable a grado racional, que no es un número entero, se denominan irracionales con respecto a esta variable.
Por transformación idéntica expresión dada se llama reemplazo de una expresión por otra, idénticamente igual a ella en algún conjunto.
Los siguientes hechos teóricos subyacen a transformaciones idénticas de expresiones racionales e irracionales.
1. Propiedades de los grados con exponente entero:
![]() , norte EN; A 1=A;
, norte EN; A 1=A;
, norte EN, A¹0; A 0=1, A¹0;
![]() , A¹0;
, A¹0;
, A¹0;
, A¹0;
, A¹0, b¹0;
![]() , A¹0, b¹0.
, A¹0, b¹0.
2. Fórmulas de multiplicación abreviadas:
Dónde A, b, Con– cualquier número real;
Dónde A¹0, X 1 y X 2 – raíces de la ecuación ![]() .
.
3. La principal propiedad de las fracciones y acciones sobre fracciones:
![]() , Dónde b¹0, Con¹0;
, Dónde b¹0, Con¹0;
; ![]() ;
;
4. Definición de raíz aritmética y sus propiedades:
![]() ; , b#0; https://pandia.ru/text/80/197/images/image026_24.gif" width="84" height="32">; ;
; , b#0; https://pandia.ru/text/80/197/images/image026_24.gif" width="84" height="32">; ; ![]() ,
,
Dónde A, b – números no negativos, norte EN, norte³2, metro EN, metro³2.
1. Tipos de ejercicios de conversión de expresiones
Existir Varios tipos Ejercicios sobre transformaciones idénticas de expresiones. primer tipo: La conversión que debe realizarse se especifica explícitamente.
Por ejemplo.
1. Representarlo como un polinomio.
Al realizar esta transformación utilizamos las reglas de multiplicación y resta de polinomios, la fórmula de multiplicación abreviada y reducción de términos semejantes.
2. Tenga en cuenta: ![]() .
.
Al realizar la transformación, utilizamos la regla de eliminación. multiplicador común detrás del paréntesis y 2 fórmulas de multiplicación abreviadas.
3. Reducir la fracción:
![]() .
.

Al realizar la transformación utilizamos la eliminación del factor común entre paréntesis, leyes conmutativas y contráctiles, 2 fórmulas de multiplicación abreviadas y operaciones sobre potencias.
4. Elimine el factor de debajo del signo raíz si A³0, b³0, Con³0: https://pandia.ru/text/80/197/images/image036_17.gif" width="432" height="27">
Usamos las reglas para acciones sobre raíces y la definición del módulo de un número.
5. Eliminar la irracionalidad en el denominador de una fracción. ![]() .
.
Segundo tipo Los ejercicios son ejercicios en los que se indica claramente la principal transformación que se debe realizar. En tales ejercicios, el requisito generalmente se formula de una de las siguientes formas: simplificar la expresión, calcular. Al realizar tales ejercicios, primero es necesario identificar qué y en qué orden se deben realizar las transformaciones para que la expresión adquiera una forma más compacta que la dada, o se obtenga un resultado numérico.
Por ejemplo
6. Simplifica la expresión:
Solución:
![]() .
.
Reglas utilizadas para operar fracciones algebraicas y fórmulas de multiplicación abreviadas.
7. Simplifica la expresión:
 .
.
Si A³0, b³0, A¹ b.
Usamos fórmulas de multiplicación abreviadas, reglas para sumar fracciones y multiplicar expresiones irracionales, la identidad https://pandia.ru/text/80/197/images/image049_15.gif" width="203" height="29">.
Usamos la operación de seleccionar un cuadrado completo, la identidad https://pandia.ru/text/80/197/images/image053_11.gif" width="132 height=21" height="21">, si .
Prueba:
Desde , entonces y o o o , es decir .
Usamos la condición y la fórmula para la suma de cubos.
Hay que tener en cuenta que las condiciones que conectan variables también se pueden especificar en ejercicios de los dos primeros tipos.
Por ejemplo.
10. Encuentra si .
Mantener su privacidad es importante para nosotros. Por este motivo, hemos desarrollado una Política de Privacidad que describe cómo usamos y almacenamos su información. Revise nuestras prácticas de privacidad y háganos saber si tiene alguna pregunta.
Recopilación y uso de información personal.
La información personal se refiere a datos que pueden usarse para identificar o contactar a una persona específica.
Es posible que se le solicite que proporcione su información personal en cualquier momento cuando se comunique con nosotros.
A continuación se muestran algunos ejemplos de los tipos de información personal que podemos recopilar y cómo podemos usar dicha información.
Qué información personal recopilamos:
- Cuando envía una solicitud en el sitio, podemos recopilar información diversa, incluyendo su nombre, número de teléfono, dirección Correo electrónico etc.
Cómo usamos tu información personal:
- Recogido por nosotros informacion personal nos permite comunicarnos con usted e informarle sobre ofertas únicas, promociones y otros eventos y próximos eventos.
- De vez en cuando, podemos utilizar su información personal para enviar avisos y comunicaciones importantes.
- También podemos utilizar información personal para fines internos como auditoría, análisis de datos y varios estudios con el fin de mejorar los servicios que brindamos y brindarle recomendaciones sobre nuestros servicios.
- Si participa en un sorteo de premios, concurso o promoción similar, podremos utilizar la información que proporcione para administrar dichos programas.
Divulgación de información a terceros
No revelamos la información que recibimos de usted a terceros.
Excepciones:
- Si es necesario, de conformidad con la ley, el procedimiento judicial, los procedimientos legales y/o en base a solicitudes públicas o solicitudes de agencias gubernamentales en el territorio de la Federación de Rusia: divulgar su información personal. También podemos divulgar información sobre usted si determinamos que dicha divulgación es necesaria o apropiada para fines de seguridad, cumplimiento de la ley u otros fines de importancia pública.
- En caso de una reorganización, fusión o venta, podemos transferir la información personal que recopilamos al tercero sucesor correspondiente.
Protección de información personal
Tomamos precauciones, incluidas las administrativas, técnicas y físicas, para proteger su información personal contra pérdida, robo y uso indebido, así como contra acceso no autorizado, divulgación, alteración y destrucción.
Respetando su privacidad a nivel de empresa
Para garantizar que su información personal esté segura, comunicamos estándares de privacidad y seguridad a nuestros empleados y aplicamos estrictamente las prácticas de privacidad.
El artículo revela el significado de las expresiones irracionales y las transformaciones con ellas. Consideremos el concepto mismo de expresiones irracionales, transformación y expresiones características.
Yandex.RTB R-A-339285-1
¿Qué son las expresiones irracionales?
Al introducir las raíces en la escuela, estudiamos el concepto de expresiones irracionales. Estas expresiones están estrechamente relacionadas con las raíces.
Definición 1
Expresiones irracionales son expresiones que tienen raíz. Es decir, se trata de expresiones que tienen radicales.
Residencia en esta definición, tenemos que x - 1, 8 3 3 6 - 1 2 3, 7 - 4 3 (2 + 3), 4 a 2 d 5: d 9 2 a 3 5 son todas expresiones de tipo irracional.
Al considerar la expresión x · x - 7 · x + 7 x + 3 2 · x - 8 3 encontramos que la expresión es racional. Las expresiones racionales incluyen polinomios y fracciones algebraicas. Los irracionales incluyen trabajar con expresiones logarítmicas o expresiones radicales.
Principales tipos de transformaciones de expresiones irracionales.
Al calcular tales expresiones, es necesario prestar atención al DZ. A menudo requieren transformaciones adicionales en forma de soportes de apertura, fundición miembros similares, grupos y así sucesivamente. La base de tales transformaciones son las operaciones con números. Las transformaciones de expresiones irracionales siguen un orden estricto.
Ejemplo 1
Transforma la expresión 9 + 3 3 - 2 + 4 · 3 3 + 1 - 2 · 3 3 .
Solución
Es necesario reemplazar el número 9 con una expresión que contenga la raíz. Entonces entendemos eso
81 + 3 3 - 2 + 4 3 3 + 1 - 2 3 3 = = 9 + 3 3 - 2 + 4 3 3 + 1 - 2 3 3
La expresión resultante tiene términos similares, así que realicemos casting y agrupación. Obtenemos
9 + 3 3 - 2 + 4 3 3 + 1 - 2 3 3 = = 9 - 2 + 1 + 3 3 + 4 3 3 - 2 3 3 = = 8 + 3 3 3
Respuesta: 9 + 3 3 - 2 + 4 3 3 + 1 - 2 3 3 = 8 + 3 3 3
Ejemplo 2
Presenta la expresión x + 3 5 2 - 2 · x + 3 5 + 1 - 9 como producto de dos irracionales usando fórmulas de multiplicación abreviadas.
Soluciones
x + 3 5 2 - 2 x + 3 5 + 1 - 9 = = x + 3 5 - 1 2 - 9
Representamos el 9 en la forma de 3 2, y aplicamos la fórmula de la diferencia de cuadrados:
x + 3 5 - 1 2 - 9 = x + 3 5 - 1 2 - 3 2 = = x + 3 5 - 1 - 3 x + 3 5 - 1 + 3 = = x + 3 5 - 4 x + 3 5 + 2
El resultado de transformaciones idénticas condujo al producto de dos expresiones racionales que era necesario encontrar.
Respuesta:
x + 3 5 2 - 2 x + 3 5 + 1 - 9 = = x + 3 5 - 4 x + 3 5 + 2
Puede realizar otras transformaciones que se aplican a expresiones irracionales.
Convertir una expresión radical
Lo importante es que la expresión bajo el signo raíz se puede reemplazar por otra que sea idénticamente igual a él. Esta afirmación permite trabajar con una expresión radical. Por ejemplo, 1 + 6 se puede sustituir por 7 o 2 · a 5 4 - 6 por 2 · a 4 · a 4 - 6 . Son idénticamente iguales, por lo que el reemplazo tiene sentido.
Cuando no hay un 1 diferente de a, donde una desigualdad de la forma a n = a 1 n es válida, entonces tal igualdad es posible sólo para a = a 1. Los valores de dichas expresiones son iguales a cualquier valor de las variables.
Usando propiedades raíz
Las propiedades de las raíces se utilizan para simplificar expresiones. Para aplicar la propiedad a · b = a · b, donde a ≥ 0, b ≥ 0, entonces de la forma irracional 1 + 3 · 12 se puede llegar a ser idénticamente igual a 1 + 3 · 12. Propiedad. . . un k norte 2 norte 1 = un norte 1 · norte 2 · , . . . , · n k , donde a ≥ 0 significa que x 2 + 4 4 3 se puede escribir en la forma x 2 + 4 24 .
Hay algunos matices a la hora de convertir expresiones radicales. Si hay una expresión, entonces - 7 - 81 4 = - 7 4 - 81 4 no podemos escribirla, ya que la fórmula a b n = a n b n sirve solo para a no negativo y b positivo. Si la propiedad se aplica correctamente, el resultado será una expresión de la forma 7 4 81 4 .
Para una transformación correcta se utilizan transformaciones de expresiones irracionales utilizando las propiedades de las raíces.
Ingresando un multiplicador bajo el signo de la raíz.
Definición 3Colocar debajo del signo raíz.– significa reemplazar la expresión B · C n, y B y C son algunos números o expresiones, donde n es un número natural mayor que 1, expresión igual, que tiene la forma B n · C n o - B n · C n .
Si simplificamos la expresión de la forma 2 x 3, luego de sumarla a la raíz, obtenemos 2 3 x 3. Tales transformaciones sólo son posibles después estudio detallado reglas para ingresar un multiplicador bajo el signo de la raíz.
Quitar el multiplicador de debajo del signo raíz
Si hay una expresión de la forma B n · C n , entonces se reduce a la forma B · C n , donde hay n impares , que toman la forma B · C n siendo n pares , siendo B y C algunos números y expresiones.
Es decir, si tomamos una expresión irracional de la forma 2 3 x 3, eliminamos el factor de debajo de la raíz, obtenemos la expresión 2 x 3. O x + 1 2 · 7 dará como resultado una expresión de la forma x + 1 · 7, que tiene otra notación de la forma x + 1 · 7.
Es necesario eliminar el factor de debajo de la raíz para simplificar la expresión y su conversión rápida.
Convertir fracciones que contienen raíces
Una expresión irracional puede ser como número natural, y en forma de fracción. Para convertir expresiones fraccionarias gran atención pagar a su denominador. Si tomamos una fracción de la forma (2 + 3) x 4 x 2 + 5 3, entonces el numerador tomará la forma 5 x 4 y, usando las propiedades de las raíces, encontramos que el denominador será x 2 + 5 6. La fracción original se puede escribir como 5 x 4 x 2 + 5 6.
Es necesario prestar atención al hecho de que es necesario cambiar el signo solo del numerador o solo del denominador. lo entendemos
X + 2 x - 3 x 2 + 7 4 = x + 2 x - (- 3 x 2 + 7 4) = x + 2 x 3 x 2 - 7 4
La reducción de una fracción se utiliza con mayor frecuencia al simplificar. lo entendemos
3 · x + 4 3 - 1 · x x + 4 3 - 1 3 reducir en x + 4 3 - 1 . Obtenemos la expresión 3 x x + 4 3 - 1 2.
Antes de la reducción, es necesario realizar transformaciones que simplifiquen la expresión y permitan factorizar. expresión compleja. Las fórmulas de multiplicación abreviadas se utilizan con mayor frecuencia.
Si tomamos una fracción de la forma 2 · x - y x + y, entonces es necesario introducir nuevas variables u = x y v = x, entonces la expresión dada cambiará de forma y se convertirá en 2 · u 2 - v 2 u + v. El numerador debe expandirse a polinomios según la fórmula, luego obtenemos que
2 · u 2 - v 2 u + v = 2 · (u - v) · u + v u + v = 2 · u - v . Después de realizar la sustitución inversa, llegamos a la forma 2 x - y, que es igual a la original.
Se permite la reducción a un nuevo denominador, luego es necesario multiplicar el numerador por un factor adicional. Si tomamos una fracción de la forma x 3 - 1 0, 5 · x, entonces la reducimos al denominador x. Para hacer esto, necesitas multiplicar el numerador y el denominador por la expresión 2 x, luego obtenemos la expresión x 3 - 1 0, 5 x = 2 x x x 3 - 1 0, 5 x 2 x = 2 x x 3 - 1 x .
Es necesario reducir fracciones o acercar otras similares solo a la ODZ de la fracción especificada. Cuando multiplicamos el numerador y el denominador por una expresión irracional, encontramos que nos deshacemos de la irracionalidad en el denominador.
Deshacerse de la irracionalidad en el denominador
Cuando una expresión se deshace de la raíz del denominador mediante transformación, se llama deshacerse de la irracionalidad. Veamos el ejemplo de una fracción de la forma x 3 3. Después de deshacernos de la irracionalidad, obtenemos una nueva fracción de la forma 9 3 x 3.
Transición de las raíces a los poderes
Las transiciones de raíces a potencias son necesarias para transformar rápidamente expresiones irracionales. Si consideramos la igualdad a m n = a m n , podemos ver que su uso es posible cuando a es un número positivo, m es un número entero y n es un número natural. Si consideramos la expresión 5 - 2 3, en caso contrario tenemos derecho a escribirla como 5 - 2 3. Estas expresiones son equivalentes.
Cuando la raíz tiene un número negativo o un número con variables, entonces la fórmula a m n = a m n no siempre es aplicable. Si necesita reemplazar dichas raíces (- 8) 3 5 y (- 16) 2 4 con potencias, entonces obtenemos que - 8 3 5 y - 16 2 4 mediante la fórmula a m n = a m n no trabajamos con a negativa. Para analizar en detalle el tema de las expresiones radicales y sus simplificaciones, es necesario estudiar el artículo sobre la transición del arraigo al poder y viceversa. Cabe recordar que la fórmula a m n = a m n no es aplicable a todas las expresiones de este tipo. Deshacerse de la irracionalidad contribuye a una mayor simplificación de la expresión, su transformación y solución.
Si nota un error en el texto, resáltelo y presione Ctrl+Enter








