Jūsų tikslas:žinoti nelygybių įrodinėjimo metodus ir mokėti juos taikyti.
Nelygybės įrodymo samprata . Kai kurios nelygybės tampa tiesa skaitinė nelygybė visų akivaizdoje priimtinos vertės kintamiesiems arba tam tikram kintamųjų reikšmių rinkiniui. Pavyzdžiui, nelygybės A 2 ³0, ( A–b) 2 ³ 0 ,a 2 +b 2 +c 2 " ³ 0 tinka bet kuriam tikrosios vertybės kintamieji ir nelygybė ³ 0 – bet kokioms realioms neneigiamoms reikšmėms A. Kartais iškyla nelygybės įrodymo problema.
Įrodyti nelygybę reiškia tai parodyti ši nelygybė virsta tikra skaitine nelygybe visoms leistinoms kintamųjų reikšmėms arba tam tikram šių kintamųjų verčių rinkiniui.
Nelygybių įrodinėjimo metodai. Atkreipkite dėmesį, kad bendras metodas nėra nelygybės įrodymų. Tačiau kai kuriuos iš jų galima nurodyti.
1. Metodas skirtumo tarp kairiosios ir dešiniosios nelygybės pusių ženklo įvertinimo. Suskaičiuojamas skirtumas tarp kairės ir dešinės nelygybės pusių ir nustatoma, ar šis skirtumas yra teigiamas ar neigiamas nagrinėjamoms kintamųjų reikšmėms (negriežtoms nelygybėms būtina nustatyti, ar šis skirtumas yra ne neigiamas ar ne teigiamas).
1 pavyzdys. Bet kokiems realiesiems skaičiams A Ir b yra nelygybė
a 2 +b 2³ 2 ab. (1)
Įrodymas. Suskaičiuokime skirtumą tarp kairės ir dešinės nelygybės pusių:
a 2 +b 2 – 2ab = a 2 – 2ab + b 2 = (a–b) 2 .
Kadangi kvadratas bet realus skaičius yra neneigiamas skaičius, tada ( a–b) 2 ³ 0, o tai reiškia a 2 +b 2³ 2 ab bet kokiems realiems skaičiams A Ir b. Lygybė (1) įvyksta tada ir tik tada a = b.
2 pavyzdys. Įrodykite, kad jei A³ 0 ir b³ 0, tada ³ , t.y. neneigiamų realiųjų skaičių aritmetinis vidurkis A Ir b ne mažesnis už jų geometrinį vidurkį.
Įrodymas. Jeigu A³ 0 ir b³ 0, tada
³ 0. Taigi, ³ .
2. Dedukcinis metodas nelygybių įrodymai.Šio metodo esmė tokia: naudojant transformacijų eilę, reikiama nelygybė išvedama iš kai kurių žinomų (referencinių) nelygybių. Pavyzdžiui, šios nelygybės gali būti naudojamos kaip nuoroda: A 2 ³ 0 už bet kurį aÎ R ; (a–b) 2 ³ 0 bet kuriai A Ir bÎ R ; (A 2 + b 2) ³ 2 ab bet kokiam a, bÎ R ; ³ at A ³ 0, b ³ 0.
3 pavyzdys. Įrodykite, kad bet kokie realieji skaičiai A Ir b yra nelygybė
A 2 + b 2 + Su 2³ ab + bc + ac.
Įrodymas. Iš tikrosios nelygybės ( a–b) 2 ³ 0, ( b – c) 2 ³ 0 ir ( c – a) 2 ³ 0 iš to išplaukia, kad A 2 + b 2³ 2 ab, b 2 + c 2³ 2 bc, c 2 + a 2³ 2 ak. Sudėjus visas tris nelygybes po dėmens ir padalijus abi naujosios puses iš 2, gauname reikiamą nelygybę.
Pradinė nelygybė gali būti įrodyta naudojant pirmąjį metodą. Tiesą sakant, A 2 + b 2 + Su 2 –ab – bc – ac = 0,5(2A 2 + 2b 2 + 2Su 2 – 2ab – 2bc – 2ac) = = 0,5((a–b) 2 + (a–c) 2 + (b–c) 2)³ 0.
Skirtumas tarp A 2 + b 2 + Su 2 ir ab + bc + ac didesnis už nulį arba lygus jam, o tai reiškia, kad A 2 + b 2 + Su 2³ ab + bc + ac(lygybė yra teisinga tada ir tik tada a = b = c).
3. Įvertinimo metodas nelygybėms įrodyti.
4 pavyzdys. Įrodykite nelygybę
+ + + … + >
Įrodymas. Nesunku pastebėti, kad kairėje nelygybės pusėje yra 100 terminų, kurių kiekvienas yra ne mažesnis. Šiuo atveju jie taip sako kairėje pusėje nelygybes galima įvertinti iš žemiau pateiktos formulės:
+ + + … + > = 100 = .
4. Pilnas indukcijos metodas. Metodo esmė yra atsižvelgti į visus specialius atvejus, apimančius visos problemos būklę.
5 pavyzdys. Įrodykite, kad jei x > ï adresuï , Tai x > y.
Įrodymas. Galimi du atvejai:
A) adresu³ 0 ; tada adresuï = y, ir pagal sąlygą x >ï adresuï . Reiškia, x > y;
b) adresu< 0; tada adresuï > y ir pagal sąlygą x >ï adresuï reiškia x > y.
Praktinė dalis
0 užduotis. Imk tuščias lapas popieriaus ir ant jo surašykite visų žemiau pateiktų žodinių pratimų atsakymus. Tada palyginkite savo atsakymus su atsakymais arba santraukos instrukcijomis šio straipsnio pabaigoje edukacinis elementas skiltyje „Jūsų padėjėjas“.
Burnos pratimai
1. Palyginkite dviejų nelygių skaičių ir jų dvigubos sandaugos kvadratų sumą.
2. Įrodykite nelygybę:
A) ![]() ;
;
b) ![]() ;
;
V) ![]() ;
;
3. Yra žinoma, kad. Įrodyk, kad.
4. Yra žinoma, kad. Įrodyk, kad.
1 užduotis. Dar daugiau:
a) 2 + 11 arba 9; d) + arba;
b) arba + ; e) – arba;
c) + arba 2; e) + 2 arba + ?
2 užduotis.Įrodykite, kad tai tikrai x yra nelygybė:
a) 3 ( x+ 1) + x– 4(2 + x) < 0; г) 4x 2 + 1 ³ 4 x;
b) ( x+ 2)(x+ 4) > (x+ 1)(x+ 5); e) ³ 2 x;
V) ( x– 2) 2 > x(x– 4); e) l + 2 x 4 > x 2 + 2x 3 .
3 užduotis.Įrodykite, kad:
A) x 3 + 1³ x 2 + x, Jeigu x³ –1;
b) x 3 + 1 £ x 2 + x, Jeigu x£ –1 .
4 užduotis.Įrodykite, kad jei a ³ 0, b³ 0, Su³ 0, d³ 0, tada
(a 2 + b 2)(c 2 + d 2) ³ ( ac + bd) 2 .
5 užduotis.Įrodykite nelygybę išskirdami tobulas kvadratas:
A) x 2 – 2xy + 9y 2³ 0;
b) x 2 + y 2 + 2³2 ( x+y);
c) 10 x 2 + 10xy + 5y 2 + 1 > 0;
G) x 2 – xy + y 2³ 0 ;
d) x 2 + y 2 + z 2 + 3³ 2 ( x + y + z);
e) ( x+ l)( x – 2y + l) + y 2³ 0 .
6 užduotis.Įrodykite, kad:
A) x 2 + 2y 2 + 2xy + 6y+ l0 > 0 ;
b) x 2 + y 2 – 2xy + 2x – 2adresu + 1 > 0;
c) 3 x 2 + y 2 + 8x+ 4y – 2xy + 22 ³ 0;
G) x 2 + 2xy+ 3y 2 + 2x + 6y + 3 > 0.
7 užduotis.Įrodykite, kad jei n³ k³ 1, tada k(n–k+ 1) ³ n.
8 užduotis.Įrodykite, kad jei 4 A + 2b= 1, tada a 2 + b 2³ .
Apibrėžkite vertybes A Ir b, kurioje atsiranda lygybė.
9 užduotis.Įrodykite nelygybę:
A) X 3 + adresu 3³ X 2 adresu + xy 2 val x³ 0 ir y ³ 0;
b) X 4 + adresu 4³ X 3 adresu + xy 3 už bet kurį x Ir adresu;
V) X 5 + adresu 5³ X 4 adresu + xy 4 val x³ 0 ir y ³ 0;
G) x n + y n ³ x n-1 m + xy n-1 val x³ 0 ir y ³ 0.
Nelygybių įrodinėjimo metodai.
Nelygybių sprendimas. Ekvivalentinės nelygybės.
Intervalinis metodas. Nelygybių sistemos.
Nelygybių įrodymas. Yra keletas įrodinėjimo būdųnelygybės. Pažvelgsime į juos naudodamiesi nelygybės pavyzdžiu:
Kur a – teigiamas skaičius.
1). Naudojant žinomą arba anksčiau įrodytą nelygybę.
Yra žinoma, kad ( a– 1 )² 0 .
2). Skirtumo tarp nelygybės dalių ženklo įvertinimas .
Apsvarstykite skirtumą tarp kairės ir dešinės pusės:
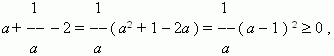
Be to, lygybė atsiranda tik tada, kai
a = 1 .3). Įrodymas prieštaravimu.
Tarkime, priešingai:a, gauname: a 2 + 1 < 2 a, t.y.
a 2 + 1 – 2 a < 0 , arba ( a– 1 ) 2 < 0, kas netiesa. (Kodėl?).
Atsiradęs prieštaravimas įrodo pagrįstumą
Aptariama nelygybė.
4). Neribotos nelygybės metodas.
Nelygybė vadinama neapibrėžtas jei jis turi ženklą\/ arba /\ ,
tie. kai nežinome į kurią pusęšis ženklas turėtų būti pasuktas
gauti teisingą nelygybę.
Čia galioja tos pačios taisyklės kaipir su įprastomis nelygybėmis.
Apsvarstykite neapibrėžtą nelygybę:
Abi nelygybės puses padauginus iša, gauname: a 2 + 1 \/ 2 a, t.y.
A 2 + 1 – 2 a \/ 0 , arba ( a– 1) 2 \/ 0 , bet čia jau žinome kaip pasukti
Pažymėkite \/, kad gautumėte teisingą nelygybę (Kaip?). Sukant jį
IN teisinga kryptimi išilgai visos nelygybių grandinės iš apačios į viršų, mes
gauname reikiamą nelygybę.
Nelygybių sprendimas. Vadinamos dvi nelygybės, turinčios tuos pačius nežinomuosius lygiavertis , jei jie galioja toms pačioms šių nežinomųjų vertėms. Tas pats apibrėžimas naudojamas dviejų nelygybių sistemų lygiavertiškumui. Nelygybių sprendimas yra perėjimo iš vienos nelygybės į kitą procesas, kuris yra lygiavertis nelygybei. Šiuo tikslu jie naudojami pagrindinės nelygybių savybės(cm. ). Be to, bet kurią išraišką galima pakeisti kita, kuri yra identiška nurodytai. Gali būti nelygybės algebrinė( kuriuose yra tik daugianariai) Ir transcendentinis(pvz logaritminis arbatrigonometrinis). Čia apžvelgsime vieną labai svarbų metodą,dažnai naudojamas sprendžiant algebrinė nelygybės
Intervalinis metodas. Išspręskite nelygybę: ( x – 3)( x – 5) < 2( x – 3). Čia negalime padalyti abiejų nelygybės pusių iš (x – 3), kadangi mes nežinome šio dvinario ženklo (jame yra nežinomasis x ). Todėl planuosime iš naujovisi nelygybės nariai į kairę pusę:
(x – 3)( x – 5) – 2( x – 3) < 0 ,
koeficientuokime:
(x – 3)( x – 5 – 2) < 0 ,
ir mes gauname :( x – 3)( x – 7) < 0. Теперь определим знак произведения в левой части неравенства в различных числовых интервалах. Заметим, что x= 3 ir x = 7 - šios išraiškos šaknys. Todėl visa skaičių eilutė bus padalinta iš šiųšaknys į šiuos tris intervalus:
Intervale aš(x < 3 ) abu veiksniai yra neigiami, todėl jų dirbti teigiamai; V intervalas II (3 < x< 7 ) pirmasis daugiklis(x– 3 ) yra teigiamas, o antrasis ( x – 7 ) yra neigiamas, todėl jų dirbti neigiamas; intervaleIII(x> 7) abu veiksniai yra teigiami, todėl jų dirbti taip pat teigiamai. Dabar belieka pasirinkti intervalą, kuriame mūsų gaminys neigiamas. Tai yra intervalasII, todėl nelygybės sprendimas: 3 < x< 7. Paskutinė išraiška- vadinamasis dviguba nelygybė. Tai reiškia, kadx turi būti didesnis nei 3 ir mažesnis nei 7.
PAVYZDYS Intervaliniu metodu išspręskite šią nelygybę:
(x – 1)(x – 2)(x – 3) … (x –100) > 0 .
Sprendimas Kairiosios nelygybės šaknys yra akivaizdžios: 1, 2, 3, …, 100.
Jie sulūžta skaičių ašis 101 intervalui:
Kadangi skliaustų skaičius kairėje pusėje net(lygus 100), tada
At x < 1, когда все множители отрицательны, их произведение
Teigiamai. Kai praeina per šaknį, vyksta pasikeitimas
Darbo ženklas. Todėl kitu intervalu, viduje
Kuris produktas yra teigiamas, bus (2, 3), tada (4, 5),
Tada (6, 7), ... , (98, 99) ir galiausiai, x >100.
Taigi ši nelygybė turi sprendimą:
x < 1, 2 < x < 3, 4 < x < 5 ,…, x >100.
Taigi, išspręsti algebrinę nelygybę, Man reikia visa tai perkeltinariai į kairę (arbadešinėje pusėje) ir išspręskiteatitinkama lygtis. Po to rastąsias šaknis nubraižykite skaičių ašyje; dėl to jis yra padalintas į tam tikrą intervalų skaičių. Paskutiniame sprendimo etape turite nustatyti, kokį ženklą turi daugianario kiekviename iš šių intervalų, ir pasirinkti reikiamus intervalus pagal sprendžiamos nelygybės ženklą.
Atkreipkite dėmesį, kad dauguma transcendentinių nelygybių redukuojama iki algebrinės nelygybės, pakeičiant nežinomąją. Jis turi būti išspręstas atsižvelgiant į naują nežinomybę, o tada, naudojant atvirkštinį pakeitimą, rasti pradinės nelygybės sprendimą.
Nelygybių sistemos. Norint išspręsti nelygybių sistemą, būtina išspręsti kiekvieną iš jų ir sujungti jų sprendimus. Šis derinys veda prie vienas iš dviejų galimi atvejai: arba sistema turi sprendimą, arba ne.
1 pavyzdys. Išspręskite nelygybių sistemą:

Pirmosios nelygybės sprendimas:
x < 4 ; а второго: x > 6.Taigi ši nelygybių sistema neturi sprendimo.
(Kodėl?)
2 pavyzdys. Išspręskite nelygybių sistemą:
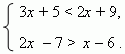
Sprendimas: Pirmoji nelygybė, kaip ir anksčiau, suteikia:x < 4; но решение
Antroji nelygybė šiame pavyzdyje:x > 1.
Taigi nelygybių sistemos sprendimas: 1< x < 4.
Mokymo įstaiga: Savivaldybės švietimo įstaiga licėjus Nr. 1, Komsomolskas prie Amūro
Vadovė: Budlyanskaya Natalya Leonidovna
Jei norite dalyvauti puikus gyvenimas, tada užpildykite galvą matematika, kol turėsite galimybę. Tada ji suteiks jums didelę pagalbą atliekant visus jūsų darbus. (M.I. Kalininas)

Kairiosios nelygybės pusės vaizdavimas kaip neneigiamų dėmenų suma (dešinė pusė lygi 0), naudojant tapatybes.
1 pavyzdys. Įrodykite, kad bet kuriam xϵR
Įrodymas . 1 būdas.
2 būdas.
kvadratinei funkcijai o tai reiškia jos pozityvumą bet kokiam tikram X.

2 pavyzdys. Įrodykite, kad bet kokiems x ir y
Įrodymas. 3 pavyzdys. Įrodyk tai Įrodymas. 4 pavyzdys. Įrodykite, kad bet kuriam a ir b atveju Įrodymas.

2. Priešingas metodas
Čia yra geras šio metodo naudojimo pavyzdys. Įrodykite, kad a, b ϵ R. Įrodymas. Tarkime, kad. Bet tai aiškiai įrodo, kad mūsų prielaida yra neteisinga. C.T.D.

5 pavyzdys.Įrodykite, kad bet kokiems skaičiams A, B, C yra teisinga ši nelygybė:
Įrodymas. Akivaizdu, kad pakanka nustatyti šią nelygybę neneigiamam A, B Ir SU, nes mūsų santykiai bus tokie: ,
kuri yra pradinės nelygybės pagrindimas .

Dabar tegul būna tokie neneigiami skaičiai A, B Ir SU, kuriam galioja nelygybė , o tai neįmanoma pagal jokią realybę A, B Ir SU. Aukščiau padaryta prielaida paneigiama, o tai įrodo pradinė tiriama nelygybė.

Naudojant kvadratinio trinalio savybes
Metodas pagrįstas kvadratinio trinalio neneigiamumo savybe, jei Ir. 6 pavyzdys. Įrodyk tai Įrodymas. Leiskite a=2, 2>0 =>

7 pavyzdys. Įrodykite, kad bet kokiam realiam x ir y nelygybė galioja Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
Įrodymas . 1 būdas.
2 būdas.
kvadratinei funkcijai o tai reiškia jos pozityvumą bet kokiam tikram X.

2 pavyzdys. Įrodykite, kad bet kokiems x ir y
Įrodymas. 3 pavyzdys. Įrodyk tai Įrodymas. 4 pavyzdys. Įrodykite, kad bet kuriam a ir b atveju Įrodymas.

2. Priešingas metodas
Čia yra geras šio metodo naudojimo pavyzdys. Įrodykite, kad a, b ϵ R. Įrodymas. Tarkime, kad. Bet tai aiškiai įrodo, kad mūsų prielaida yra neteisinga. C.T.D.

5 pavyzdys.Įrodykite, kad bet kokiems skaičiams A, B, C yra teisinga ši nelygybė:
Įrodymas. Akivaizdu, kad pakanka nustatyti šią nelygybę neneigiamam A, B Ir SU, nes mūsų santykiai bus tokie: ,
kuri yra pradinės nelygybės pagrindimas .

Dabar tegul būna tokie neneigiami skaičiai A, B Ir SU, kuriam galioja nelygybė , o tai neįmanoma pagal jokią realybę A, B Ir SU. Aukščiau padaryta prielaida paneigiama, o tai įrodo pradinė tiriama nelygybė.

Naudojant kvadratinio trinalio savybes
Metodas pagrįstas kvadratinio trinalio neneigiamumo savybe, jei Ir. 6 pavyzdys. Įrodyk tai Įrodymas. Leiskite a=2, 2>0 =>

7 pavyzdys. Įrodykite, kad bet kokiam realiam x ir y nelygybė galioja Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
2 būdas.
kvadratinei funkcijai o tai reiškia jos pozityvumą bet kokiam tikram X.

2 pavyzdys. Įrodykite, kad bet kokiems x ir y
Įrodymas. 3 pavyzdys. Įrodyk tai Įrodymas. 4 pavyzdys. Įrodykite, kad bet kuriam a ir b atveju Įrodymas.

2. Priešingas metodas
Čia yra geras šio metodo naudojimo pavyzdys. Įrodykite, kad a, b ϵ R. Įrodymas. Tarkime, kad. Bet tai aiškiai įrodo, kad mūsų prielaida yra neteisinga. C.T.D.

5 pavyzdys.Įrodykite, kad bet kokiems skaičiams A, B, C yra teisinga ši nelygybė:
Įrodymas. Akivaizdu, kad pakanka nustatyti šią nelygybę neneigiamam A, B Ir SU, nes mūsų santykiai bus tokie: ,
kuri yra pradinės nelygybės pagrindimas .

Dabar tegul būna tokie neneigiami skaičiai A, B Ir SU, kuriam galioja nelygybė , o tai neįmanoma pagal jokią realybę A, B Ir SU. Aukščiau padaryta prielaida paneigiama, o tai įrodo pradinė tiriama nelygybė.

Naudojant kvadratinio trinalio savybes
Metodas pagrįstas kvadratinio trinalio neneigiamumo savybe, jei Ir. 6 pavyzdys. Įrodyk tai Įrodymas. Leiskite a=2, 2>0 =>

7 pavyzdys. Įrodykite, kad bet kokiam realiam x ir y nelygybė galioja Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
kvadratinei funkcijai o tai reiškia jos pozityvumą bet kokiam tikram X.

2 pavyzdys. Įrodykite, kad bet kokiems x ir y
Įrodymas. 3 pavyzdys. Įrodyk tai Įrodymas. 4 pavyzdys. Įrodykite, kad bet kuriam a ir b atveju Įrodymas.

2. Priešingas metodas
Čia yra geras šio metodo naudojimo pavyzdys. Įrodykite, kad a, b ϵ R. Įrodymas. Tarkime, kad. Bet tai aiškiai įrodo, kad mūsų prielaida yra neteisinga. C.T.D.

5 pavyzdys.Įrodykite, kad bet kokiems skaičiams A, B, C yra teisinga ši nelygybė:
Įrodymas. Akivaizdu, kad pakanka nustatyti šią nelygybę neneigiamam A, B Ir SU, nes mūsų santykiai bus tokie: ,
kuri yra pradinės nelygybės pagrindimas .

Dabar tegul būna tokie neneigiami skaičiai A, B Ir SU, kuriam galioja nelygybė , o tai neįmanoma pagal jokią realybę A, B Ir SU. Aukščiau padaryta prielaida paneigiama, o tai įrodo pradinė tiriama nelygybė.

Naudojant kvadratinio trinalio savybes
Metodas pagrįstas kvadratinio trinalio neneigiamumo savybe, jei Ir. 6 pavyzdys. Įrodyk tai Įrodymas. Leiskite a=2, 2>0 =>

7 pavyzdys. Įrodykite, kad bet kokiam realiam x ir y nelygybė galioja Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
o tai reiškia jos pozityvumą bet kokiam tikram X.

2 pavyzdys. Įrodykite, kad bet kokiems x ir y
Įrodymas. 3 pavyzdys. Įrodyk tai Įrodymas. 4 pavyzdys. Įrodykite, kad bet kuriam a ir b atveju Įrodymas.

2. Priešingas metodas
Čia yra geras šio metodo naudojimo pavyzdys. Įrodykite, kad a, b ϵ R. Įrodymas. Tarkime, kad. Bet tai aiškiai įrodo, kad mūsų prielaida yra neteisinga. C.T.D.

5 pavyzdys.Įrodykite, kad bet kokiems skaičiams A, B, C yra teisinga ši nelygybė:
Įrodymas. Akivaizdu, kad pakanka nustatyti šią nelygybę neneigiamam A, B Ir SU, nes mūsų santykiai bus tokie: ,
kuri yra pradinės nelygybės pagrindimas .

Dabar tegul būna tokie neneigiami skaičiai A, B Ir SU, kuriam galioja nelygybė , o tai neįmanoma pagal jokią realybę A, B Ir SU. Aukščiau padaryta prielaida paneigiama, o tai įrodo pradinė tiriama nelygybė.

Naudojant kvadratinio trinalio savybes
Metodas pagrįstas kvadratinio trinalio neneigiamumo savybe, jei Ir. 6 pavyzdys. Įrodyk tai Įrodymas. Leiskite a=2, 2>0 =>

7 pavyzdys. Įrodykite, kad bet kokiam realiam x ir y nelygybė galioja Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.

2 pavyzdys. Įrodykite, kad bet kokiems x ir y
Įrodymas. 3 pavyzdys. Įrodyk tai Įrodymas. 4 pavyzdys. Įrodykite, kad bet kuriam a ir b atveju Įrodymas.

2. Priešingas metodas
Čia yra geras šio metodo naudojimo pavyzdys. Įrodykite, kad a, b ϵ R. Įrodymas. Tarkime, kad. Bet tai aiškiai įrodo, kad mūsų prielaida yra neteisinga. C.T.D.

5 pavyzdys.Įrodykite, kad bet kokiems skaičiams A, B, C yra teisinga ši nelygybė:
Įrodymas. Akivaizdu, kad pakanka nustatyti šią nelygybę neneigiamam A, B Ir SU, nes mūsų santykiai bus tokie: ,
kuri yra pradinės nelygybės pagrindimas .

Dabar tegul būna tokie neneigiami skaičiai A, B Ir SU, kuriam galioja nelygybė , o tai neįmanoma pagal jokią realybę A, B Ir SU. Aukščiau padaryta prielaida paneigiama, o tai įrodo pradinė tiriama nelygybė.

Naudojant kvadratinio trinalio savybes
Metodas pagrįstas kvadratinio trinalio neneigiamumo savybe, jei Ir. 6 pavyzdys. Įrodyk tai Įrodymas. Leiskite a=2, 2>0 =>

7 pavyzdys. Įrodykite, kad bet kokiam realiam x ir y nelygybė galioja Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
Įrodymas. 3 pavyzdys. Įrodyk tai Įrodymas. 4 pavyzdys. Įrodykite, kad bet kuriam a ir b atveju Įrodymas.

2. Priešingas metodas
Čia yra geras šio metodo naudojimo pavyzdys. Įrodykite, kad a, b ϵ R. Įrodymas. Tarkime, kad. Bet tai aiškiai įrodo, kad mūsų prielaida yra neteisinga. C.T.D.

5 pavyzdys.Įrodykite, kad bet kokiems skaičiams A, B, C yra teisinga ši nelygybė:
Įrodymas. Akivaizdu, kad pakanka nustatyti šią nelygybę neneigiamam A, B Ir SU, nes mūsų santykiai bus tokie: ,
kuri yra pradinės nelygybės pagrindimas .

Dabar tegul būna tokie neneigiami skaičiai A, B Ir SU, kuriam galioja nelygybė , o tai neįmanoma pagal jokią realybę A, B Ir SU. Aukščiau padaryta prielaida paneigiama, o tai įrodo pradinė tiriama nelygybė.

Naudojant kvadratinio trinalio savybes
Metodas pagrįstas kvadratinio trinalio neneigiamumo savybe, jei Ir. 6 pavyzdys. Įrodyk tai Įrodymas. Leiskite a=2, 2>0 =>

7 pavyzdys. Įrodykite, kad bet kokiam realiam x ir y nelygybė galioja Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
Įrodymas. 4 pavyzdys. Įrodykite, kad bet kuriam a ir b atveju Įrodymas.

2. Priešingas metodas
Čia yra geras šio metodo naudojimo pavyzdys. Įrodykite, kad a, b ϵ R. Įrodymas. Tarkime, kad. Bet tai aiškiai įrodo, kad mūsų prielaida yra neteisinga. C.T.D.

5 pavyzdys.Įrodykite, kad bet kokiems skaičiams A, B, C yra teisinga ši nelygybė:
Įrodymas. Akivaizdu, kad pakanka nustatyti šią nelygybę neneigiamam A, B Ir SU, nes mūsų santykiai bus tokie: ,
kuri yra pradinės nelygybės pagrindimas .

Dabar tegul būna tokie neneigiami skaičiai A, B Ir SU, kuriam galioja nelygybė , o tai neįmanoma pagal jokią realybę A, B Ir SU. Aukščiau padaryta prielaida paneigiama, o tai įrodo pradinė tiriama nelygybė.

Naudojant kvadratinio trinalio savybes
Metodas pagrįstas kvadratinio trinalio neneigiamumo savybe, jei Ir. 6 pavyzdys. Įrodyk tai Įrodymas. Leiskite a=2, 2>0 =>

7 pavyzdys. Įrodykite, kad bet kokiam realiam x ir y nelygybė galioja Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
Įrodymas.

2. Priešingas metodas
Čia yra geras šio metodo naudojimo pavyzdys. Įrodykite, kad a, b ϵ R. Įrodymas. Tarkime, kad. Bet tai aiškiai įrodo, kad mūsų prielaida yra neteisinga. C.T.D.

5 pavyzdys.Įrodykite, kad bet kokiems skaičiams A, B, C yra teisinga ši nelygybė:
Įrodymas. Akivaizdu, kad pakanka nustatyti šią nelygybę neneigiamam A, B Ir SU, nes mūsų santykiai bus tokie: ,
kuri yra pradinės nelygybės pagrindimas .

Dabar tegul būna tokie neneigiami skaičiai A, B Ir SU, kuriam galioja nelygybė , o tai neįmanoma pagal jokią realybę A, B Ir SU. Aukščiau padaryta prielaida paneigiama, o tai įrodo pradinė tiriama nelygybė.

Naudojant kvadratinio trinalio savybes
Metodas pagrįstas kvadratinio trinalio neneigiamumo savybe, jei Ir. 6 pavyzdys. Įrodyk tai Įrodymas. Leiskite a=2, 2>0 =>

7 pavyzdys. Įrodykite, kad bet kokiam realiam x ir y nelygybė galioja Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
Įrodykite, kad a, b ϵ R. Įrodymas. Tarkime, kad. Bet tai aiškiai įrodo, kad mūsų prielaida yra neteisinga. C.T.D.

5 pavyzdys.Įrodykite, kad bet kokiems skaičiams A, B, C yra teisinga ši nelygybė:
Įrodymas. Akivaizdu, kad pakanka nustatyti šią nelygybę neneigiamam A, B Ir SU, nes mūsų santykiai bus tokie: ,
kuri yra pradinės nelygybės pagrindimas .

Dabar tegul būna tokie neneigiami skaičiai A, B Ir SU, kuriam galioja nelygybė , o tai neįmanoma pagal jokią realybę A, B Ir SU. Aukščiau padaryta prielaida paneigiama, o tai įrodo pradinė tiriama nelygybė.

Naudojant kvadratinio trinalio savybes
Metodas pagrįstas kvadratinio trinalio neneigiamumo savybe, jei Ir. 6 pavyzdys. Įrodyk tai Įrodymas. Leiskite a=2, 2>0 =>

7 pavyzdys. Įrodykite, kad bet kokiam realiam x ir y nelygybė galioja Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
Tarkime, kad. Bet tai aiškiai įrodo, kad mūsų prielaida yra neteisinga. C.T.D.

5 pavyzdys.Įrodykite, kad bet kokiems skaičiams A, B, C yra teisinga ši nelygybė:
Įrodymas. Akivaizdu, kad pakanka nustatyti šią nelygybę neneigiamam A, B Ir SU, nes mūsų santykiai bus tokie: ,
kuri yra pradinės nelygybės pagrindimas .

Dabar tegul būna tokie neneigiami skaičiai A, B Ir SU, kuriam galioja nelygybė , o tai neįmanoma pagal jokią realybę A, B Ir SU. Aukščiau padaryta prielaida paneigiama, o tai įrodo pradinė tiriama nelygybė.

Naudojant kvadratinio trinalio savybes
Metodas pagrįstas kvadratinio trinalio neneigiamumo savybe, jei Ir. 6 pavyzdys. Įrodyk tai Įrodymas. Leiskite a=2, 2>0 =>

7 pavyzdys. Įrodykite, kad bet kokiam realiam x ir y nelygybė galioja Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
C.T.D.

5 pavyzdys.Įrodykite, kad bet kokiems skaičiams A, B, C yra teisinga ši nelygybė:
Įrodymas. Akivaizdu, kad pakanka nustatyti šią nelygybę neneigiamam A, B Ir SU, nes mūsų santykiai bus tokie: ,
kuri yra pradinės nelygybės pagrindimas .

Dabar tegul būna tokie neneigiami skaičiai A, B Ir SU, kuriam galioja nelygybė , o tai neįmanoma pagal jokią realybę A, B Ir SU. Aukščiau padaryta prielaida paneigiama, o tai įrodo pradinė tiriama nelygybė.

Naudojant kvadratinio trinalio savybes
Metodas pagrįstas kvadratinio trinalio neneigiamumo savybe, jei Ir. 6 pavyzdys. Įrodyk tai Įrodymas. Leiskite a=2, 2>0 =>

7 pavyzdys. Įrodykite, kad bet kokiam realiam x ir y nelygybė galioja Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
Įrodymas. Akivaizdu, kad pakanka nustatyti šią nelygybę neneigiamam A, B Ir SU, nes mūsų santykiai bus tokie: ,
kuri yra pradinės nelygybės pagrindimas .

Dabar tegul būna tokie neneigiami skaičiai A, B Ir SU, kuriam galioja nelygybė , o tai neįmanoma pagal jokią realybę A, B Ir SU. Aukščiau padaryta prielaida paneigiama, o tai įrodo pradinė tiriama nelygybė.

Naudojant kvadratinio trinalio savybes
Metodas pagrįstas kvadratinio trinalio neneigiamumo savybe, jei Ir. 6 pavyzdys. Įrodyk tai Įrodymas. Leiskite a=2, 2>0 =>

7 pavyzdys. Įrodykite, kad bet kokiam realiam x ir y nelygybė galioja Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
,
kuri yra pradinės nelygybės pagrindimas .

Dabar tegul būna tokie neneigiami skaičiai A, B Ir SU, kuriam galioja nelygybė , o tai neįmanoma pagal jokią realybę A, B Ir SU. Aukščiau padaryta prielaida paneigiama, o tai įrodo pradinė tiriama nelygybė.

Naudojant kvadratinio trinalio savybes
Metodas pagrįstas kvadratinio trinalio neneigiamumo savybe, jei Ir. 6 pavyzdys. Įrodyk tai Įrodymas. Leiskite a=2, 2>0 =>

7 pavyzdys. Įrodykite, kad bet kokiam realiam x ir y nelygybė galioja Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
, o tai neįmanoma pagal jokią realybę A, B Ir SU. Aukščiau padaryta prielaida paneigiama, o tai įrodo pradinė tiriama nelygybė.

Naudojant kvadratinio trinalio savybes
Metodas pagrįstas kvadratinio trinalio neneigiamumo savybe, jei Ir. 6 pavyzdys. Įrodyk tai Įrodymas. Leiskite a=2, 2>0 =>

7 pavyzdys. Įrodykite, kad bet kokiam realiam x ir y nelygybė galioja Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
Ir. 6 pavyzdys. Įrodyk tai Įrodymas. Leiskite a=2, 2>0 =>

7 pavyzdys. Įrodykite, kad bet kokiam realiam x ir y nelygybė galioja Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
Įrodymas. Leiskite a=2, 2>0 =>

7 pavyzdys. Įrodykite, kad bet kokiam realiam x ir y nelygybė galioja Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
=>

7 pavyzdys. Įrodykite, kad bet kokiam realiam x ir y nelygybė galioja Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
Įrodymas. Apsvarstykite kairę nelygybės pusę kaip kvadratinį trinarį, atsižvelgiant į X: , a>0, D D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
D= => P(x)>0 Ir tiesa bet kokioms tikroms vertybėms X Ir u.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.

8 pavyzdys. Įrodyk tai bet kokioms tikrosioms x ir y reikšmėms. Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
Įrodymas. Leiskite
, Tai reiškia, kad bet kokiam tikram adresu ir nelygybė yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
yra patenkintas bet kokiu tikru X Ir u.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.

Naujų kintamųjų įvedimo metodas arba pakeitimo metodas
9 pavyzdys. Įrodykite, kad bet kokiems neneigiamiems skaičiams x, y, z Įrodymas. Panaudokime teisingą nelygybę, . Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
. Gauname tiriamą nelygybę

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.

Funkcijos savybių naudojimas.
10 pavyzdys. Įrodykime nelygybę bet kuriam a ir b. Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
Įrodymas. Panagrinėkime 2 atvejus: Jei a = b, tada tiesa
Be to, lygybė pasiekiama tik tada, kai a=b=0. 2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
Jei a = b, tada tiesa
2) Jei , ant R => ()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
()* ()>0, kas įrodo nelygybę

11 pavyzdys. Įrodykime tai bet kuriam
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
Įrodymas. ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
ant R. Jei, tada skaičių ženklai sutampa, vadinasi, tiriamas skirtumas yra teigiamas =>

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.

Matematinės indukcijos metodo taikymas
Šis metodas naudojamas natūraliųjų skaičių nelygybėms įrodyti. 12 pavyzdys. Įrodykite, kad bet kuriam nϵN
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
Patikrinkime teiginio teisingumą kada
- (dešinėje) 2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
Patikrinkime teiginio teisingumą kada
2) Tarkime teiginio teisingumą kada (k>1)

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.

3) Įrodykime teiginio teisingumą, kai n=k+1. Palyginkime ir: Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
Turime: Išvada: teiginys tinka bet kam nϵN.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.

Naudojant nuostabias nelygybes
Teorema apie vidurkius (Cauchy nelygybė)
Koši – Bunyakovskio nelygybė
Bernulio nelygybė
Panagrinėkime kiekvieną iš išvardytų nelygybių atskirai.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.

Vidutinės vertės teoremos taikymas (Koši nelygybė)
Kelių neneigiamų skaičių aritmetinis vidurkis yra didesnis arba lygus jų geometriniam vidurkiui , Kur Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.
Lygybės ženklas pasiekiamas tada ir tik tada Panagrinėkime specialius šios teoremos atvejus:

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.

Tada tegul n=2
Tada tegul n=2, a>0
Tada tegul n=3
13 pavyzdys. Įrodykite, kad visiems neneigiamiems a,b,c galioja nelygybė Įrodymas.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.

Koši-Buniakovskio nelygybė
Koši-Bunyakovskio nelygybė teigia, kad bet kuriai; santykis galioja Įrodyta nelygybė turi geometrinį aiškinimą. Jei n=2,3 tai išreiškia gerai žinomą faktą, kad dviejų vektorių skaliarinė sandauga plokštumoje ir erdvėje neviršija jų ilgių sandaugos. Jei n=2 nelygybė yra tokia: . Jei n=3 gauname

14 pavyzdys.

14 pavyzdys.
Įrodymas. Parašykime tiriamą nelygybę tokia forma:
Tai akivaizdžiai tikra nelygybė, nes tai ypatingas Koši – Bunyakovskio nelygybės atvejis.
15 pavyzdys. Įrodykite, kad bet kuriai a,b,c ϵ R galioja ši nelygybė:
Įrodymas. Užtenka šią nelygybę parašyti formoje
ir nurodo Koši – Bunyakovskio nelygybę.

Bernulio nelygybė
Bernoulli nelygybė teigia, kad jei x>-1, tai visoms n natūralioms vertėms galioja ši nelygybė: Nelygybė gali būti naudojama formos išraiškoms Be to, naudojant Bernulio teoremą galima nesunkiai įrodyti labai didelę nelygybių grupę.

Be to, naudojant Bernulio teoremą galima nesunkiai įrodyti labai didelę nelygybių grupę.

16 pavyzdys.
Įrodymas. Įdėjimas x=0,5 ir taikant Bernulio teoremą išreikšti
Gauname reikiamą nelygybę.
17 pavyzdys. Įrodykite, kad bet kuriam n ϵ N
Įrodymas.
pagal Bernulio teoremą, kaip reikalaujama. 
Davidas Gilbertas buvo paklaustas apie vieną iš savo buvę mokiniai. „O, toks ir toks?“ – prisiminė Hilbertas: „Jis turėjo per mažai fantazijos matematikai.

SM Grišino-Slobodskajos vidurinė mokykla
Modulio programa
"Nelygybių įrodinėjimo metodai"
kaip pasirenkamojo kurso dalis
„Už matematikos vadovėlio puslapių“
10-11 klasių mokiniams
Sudarė:
matematikos mokytojas
Pankova E.Yu
Aiškinamasis raštas
„Matematika vadinama tautologiniu mokslu: kitaip tariant, matematikai skiria laiko įrodinėti, kad objektai yra lygūs jiems patiems. Šis teiginys yra labai netikslus dėl dviejų priežasčių. Pirma, matematika, nepaisant jos prigimties moksline kalba, nėra mokslas; veikiau tai galima vadinti menu. Antra Pagrindiniai matematikos rezultatai dažniau išreiškiami nelygybėmis, o ne lygybėmis“.
Praktiniame matematikų darbe nelygybės naudojamos nuolat. Jie naudojami norint gauti daugybę įdomių ir svarbių „simetriškų“ figūrų: kvadrato, kubo, lygiašonio trikampio savybių, taip pat įrodyti iteracinių procesų konvergenciją ir apskaičiuoti kai kurias ribas. Nelygybės vaidmuo taip pat svarbus įvairiuose gamtos mokslų ir technologijų klausimais.
Nelygybės įrodinėjimo problemos yra sunkiausios ir įdomiausios iš tradicinių. Nelygybėms įrodyti reikia tikro išradingumo ir kūrybiškumo, dėl kurių matematika yra tokia įdomi tema, kokia ji yra.
Įrodinėjimo mokymas vaidina didelį vaidmenį ugdant mokinių dedukcinį-matematinį mąstymą ir bendruosius mąstymo gebėjimus. Kaip išmokyti moksleivius savarankiškai įrodyti nelygybes? Atsakymas yra toks: tik apsvarstant daugybę įrodymų ir metodų bei reguliariai juos taikant.
Idėjos, naudojamos nelygybei įrodyti, yra beveik tokios pat įvairios, kaip ir pačios nelygybės. Konkrečiose situacijose bendrieji metodai dažnai veda prie negražių sprendimų. Tačiau tik nedaugeliui moksleivių pavyksta neakivaizdžiai sujungti kelias „pagrindines“ nelygybes. Be to, niekas netrukdo studentui kiekvienu konkrečiu atveju ieškoti geresnio sprendimo nei gautas bendruoju metodu. Dėl šios priežasties nelygybės įrodymas dažnai perkeliamas į meno sritį. O kaip ir bet kuriame mene, čia yra techninių technikų, kurių spektras labai platus ir jas visas labai sunku įvaldyti, tačiau kiekvienas mokytojas turėtų stengtis plėsti jam prieinamas matematines priemones.
Šis modulis rekomenduojamas 10-11 klasių mokiniams. Čia aptariami ne visi galimi nelygybių įrodinėjimo būdai (neaptariamas kintamojo pakeitimo metodas, nelygybių įrodinėjimas naudojant išvestinę, tyrimo ir apibendrinimo metodas, rikiavimo technika). Galite pasiūlyti apsvarstyti kitus metodus antrajame etape (pavyzdžiui, 11 klasėje), jei šis kurso modulis sukelia studentų susidomėjimą, taip pat remiantis sėkme įsisavinti pirmąją kurso dalį.
|
Lygtys ir nelygybės su parametru. |
||
|
Nelygybių įrodinėjimo metodai. |
||
|
Lygtys ir nelygybės, kurių modulio ženkle yra nežinomasis. |
||
|
Nelygybių sistemos su dviem kintamaisiais. |
„Už matematikos vadovėlio puslapių“
„Nelygybių įrodinėjimo metodai“
|
Įvadas. |
||
|
Nelygybių įrodymas remiantis apibrėžimu. |
||
|
Metodas matematinė indukcija. |
||
|
Klasikinių nelygybių taikymas. |
||
|
Grafinis metodas. |
||
|
Priešingas metodas. |
||
|
Metodas, skirtas įvertinti nelygybes vieno iš kintamųjų atžvilgiu. |
||
|
Idėja stiprinti. |
||
|
Pamoka – kontrolė. |
1 pamoka. Įvadas.
Nelygybių įrodinėjimas yra patraukli ir sudėtinga elementariosios matematikos tema. Vieningo požiūrio į nelygybių įrodinėjimo problemą nebuvimas skatina ieškoti daugybės metodų, tinkamų nelygybėms įrodyti. tam tikrų tipų. Šis pasirenkamasis kursas apims šiuos nelygybių įrodymo metodus:
Kartojimas:
Įrodykite kai kurias savybes.
Klasikinės nelygybės:
1)
 (Kauchy nelygybė)
(Kauchy nelygybė)
2)

3)

4)

Istorinė informacija:
Nelygybė (1) pavadinta prancūzų matematiko Auguste'o Cauchy vardu. Skaičius  paskambino aritmetinis vidurkis skaičiai a ir b;
paskambino aritmetinis vidurkis skaičiai a ir b;
numerį  paskambino geometrinis vidurkis skaičiai a ir b. Taigi nelygybė reiškia, kad dviejų teigiamų skaičių aritmetinis vidurkis yra ne mažesnis už jų geometrinį vidurkį.
paskambino geometrinis vidurkis skaičiai a ir b. Taigi nelygybė reiškia, kad dviejų teigiamų skaičių aritmetinis vidurkis yra ne mažesnis už jų geometrinį vidurkį.
Papildomai:
Apsvarstykite keletą matematinių sofizmų su nelygybėmis.
Matematinė sofitika– nuostabus teiginys, kurio įrodymas slepia nepastebimas ir kartais gana subtilias klaidas.
Sofizmai – tai klaidingi rezultatai, gauti samprotaujant, kurie tik atrodo teisingi, bet būtinai turi vieną ar kitą klaidą.
Pavyzdys:
Keturi yra daugiau nei dvylika
2 pamoka. Nelygybių įrodymas remiantis apibrėžimu.
Šio metodo esmė tokia: norint nustatyti nelygybių F(x,y,z)>S(x,y,z) teisingumą, sudaromas skirtumas F(x,y,z)-S( x,y,z) ir įrodyti, kad jis teigiamas. Taikant šį metodą, dažnai išskiriamas kvadratas, sumos ar skirtumo kubas arba nepilnas sumos ar skirtumo kvadratas. Tai padeda nustatyti skirtumo ženklą.
Pavyzdys.
Įrodykite nelygybę (x+y)(x+y+2cosx)+2  2sin 2x
2sin 2x
Įrodymas:
Apsvarstykite skirtumą (x+y)(x+y+2cosx)+2-2sin 2 x =(x+y)(x+y+2cosx)+2cos 2 x=(x+y)(x+y+2cosx ) + cos 2 x +cos 2 x= (x+y) 2 +2(x+y)cosx+ cos 2 x +cos 2 x=((x+y)+cosx) 2 + cos 2 x 0.
Įrodykite nelygybę:
1.ab(a+b)+bc(b+c)+ac(a+c) 6abc
3.
4. >2x-20
>2x-20
5.

6.(a+b)(b+c)(c+a) 8abc
7.
3 pamoka. Matematinės indukcijos metodas.
Įrodžius nelygybes, kurios apima natūraliuosius skaičius dažnai griebiasi matematinės indukcijos metodo. Metodas yra toks:
1) patikrinkite teoremos teisingumą, kai n=1;
2) darome prielaidą, kad teorema yra teisinga kai n=k, ir remdamiesi šia prielaida įrodome teoremos teisingumą, kai n=k+1;
3) remdamiesi pirmaisiais dviem žingsniais ir matematinės indukcijos principu, darome išvadą, kad teorema yra teisinga bet kuriam n.
Pavyzdys.
Įrodykite nelygybę
Įrodymas:
1) n=2 nelygybė yra teisinga:
2) Tegul nelygybė teisinga n=k t.y.  (*)
(*)
Įrodykime, kad nelygybė teisinga n=k+1, t.y.  .
.  Padauginkime abi nelygybės (*) puses iš
Padauginkime abi nelygybės (*) puses iš
gauname 3) Iš 1. ir 2 punkto darome išvadą, kad nelygybė teisinga bet kuriai n.
Įrodykite nelygybę:
1)
2)
3)
4)
5)
6) .
.
Užduotys darbui klasėje ir namuose
4 pamoka. Klasikinių nelygybių taikymas.
Pavyzdys.
Įrodykite nelygybę:
Įrodymas:
Šio metodo esmė yra tokia: naudojant transformacijų eilę, reikiama nelygybė išvedama naudojant kai kurias klasikines nelygybes. Kaip palaikyti nelygybę  .
.
mes naudojame
 Sumažinkime šią nelygybę iki tokios formos:
Sumažinkime šią nelygybę iki tokios formos:
, Tada  Sumažinkime šią nelygybę iki tokios formos:
Sumažinkime šią nelygybę iki tokios formos:
Įrodykite nelygybę:
Bet =
2)
 1)(p+2)(q+2)(p+q)16pq (nelygybė naudojama įrodymui)
1)(p+2)(q+2)(p+q)16pq (nelygybė naudojama įrodymui)
(dokumentams naudojama nelygybė)
4)
 3) (a+b)(b+c)(c+a) 8abc (nelygybė naudojama įrodymui)
3) (a+b)(b+c)(c+a) 8abc (nelygybė naudojama įrodymui)
(doc, naudojama nelygybė).
5 pamoka. Grafinis metodas.
Nelygybių įrodymas grafiniu metodu yra toks: jei įrodysime nelygybę f(x)>g(x)(f(x)
1) sudaryti funkcijų y=f(x) ir y=g(x) grafikus;
Pavyzdys.
Įrodykite nelygybę:
2) jei funkcijos y=f(x) grafikas yra aukščiau (žemiau) funkcijos y=g(x) grafiko, tai įrodoma nelygybė yra teisinga.  cosx
cosx
Įrodymas:
,x0

Sukurkime funkcijų y=cosx ir grafikus
Iš grafiko matyti, kad ties x0 funkcijos y=cosx grafikas yra aukščiau funkcijos y= grafiko.
Įrodykite nelygybę:
1)
5)
Užduotys darbui klasėje ir namuose.
6 pamoka. Priešingas metodas
Pavyzdys.
Įrodykite nelygybę:
Įrodymas:
Šio metodo esmė tokia: tereikia įrodyti nelygybės F(x,y,z) S(x,y,z)(1) teisingumą. Jie daro prielaidą priešingai, tai yra, kad bent vienai kintamųjų aibei nelygybė F(x,y,z) S(x,y,z) (2) yra teisinga. Naudojantis nelygybių savybėmis, atliekamos nelygybės (2) transformacijos. Jei dėl šių transformacijų gaunama klaidinga nelygybė, tai reiškia, kad prielaida, kad nelygybė (2) yra teisinga, yra neteisinga, taigi ir nelygybė (1) yra teisinga.
Tarkime priešingai, t.y.  Leiskite mums kvadratu abi nelygybės puses ir gauti , Iš kurių
Leiskite mums kvadratu abi nelygybės puses ir gauti , Iš kurių
 ir toliau
ir toliau
. Tačiau tai prieštarauja Cauchy nelygybei. Tai reiškia, kad mūsų prielaida yra neteisinga, tai yra, nelygybė yra teisinga: Užduotys darbui klasėje ir namuose.
9 pamoka. Pamoka – mokinių žinių kontrolė. Šią pamoką galima atlikti poromis arba jei klasė grupėmis. Pamokos pabaigoje kiekvienas mokinys turi būti įvertintas. Tai yra šio kurso įskaitos forma. Nerekomenduojama atlikti testo šia tema, nes nelygybių įrodymas, kaip jau minėta aiškinamajame rašte, priklauso meno sričiai. Pradžioje studentų prašoma nustatyti siūlomų nelygybių įrodinėjimo metodą. Jei mokiniams kyla sunkumų, mokytojas pasako jiems racionalų metodą, įspėdamas grupę, kad tai, žinoma, turės įtakos jų pažymiui.
Darbas poromis.
Užduočių pavyzdžiai.
________________________________________________________________
Įrodykite nelygybę:
1. (matematinės indukcijos metodas)
(matematinės indukcijos metodas)
2. (pagal apibrėžimą)
(pagal apibrėžimą)
Modulis. Lygtys ir nelygybės su parametrais. ... savybės, formuluotė ir įrodymas teoremos, formulių išvedimas... paprasčiausias nelygybės. 7. Žinokite, kaip naudotis metodas intervalai...
Atviros olimpiados programos ir matematikos pasiruošimo reikalavimai 9 klasės mokiniams
ProgramaKoncepcija modulis realus skaičius. Aritmetika ir geometriniai apibrėžimai modulis. Atskleidimas moduliai. ... nelygybės. Įrodymas nelygybės. Tiesinių, kvadratinių, trupmeninių racionalių uždavinių sprendimas nelygybės su vienu kintamuoju. Sprendimas nelygybės ...
Pasirenkamoji matematikos programa 8 klasei
ProgramaDemonstruoti metodus įrodymasšiek tiek sudėtingesnis nelygybės su šiuo paprastu nelygybės? Taigi šioje ministerijoje programa ...








