Un sistema ordenado de dos o tres ejes que se cruzan perpendicularmente entre sí con comienzo común referencia (origen) y una unidad común de longitud se llama sistema de coordenadas cartesiano rectangular .
Sistema de coordenadas cartesiano general (sistema de coordenadas afines) puede incluir ejes no necesariamente perpendiculares. En honor de matemático francés René Descartes (1596-1662) nombró precisamente un sistema de coordenadas en el que se mide una unidad de longitud común en todos los ejes y los ejes son rectos.
Sistema de coordenadas cartesianas rectangulares en un plano. tiene dos ejes y sistema de coordenadas cartesiano rectangular en el espacio - tres ejes. Cada punto en un plano o en el espacio está definido por un conjunto ordenado de coordenadas: números correspondientes a la unidad de longitud del sistema de coordenadas.
Tenga en cuenta que, como se desprende de la definición, existe un sistema de coordenadas cartesianas en línea recta, es decir, en una dimensión. La introducción de coordenadas cartesianas en una recta es una de las formas por las que cualquier punto de una recta se asocia a un número real bien definido, es decir, una coordenada.
El método de coordenadas, que surgió en las obras de René Descartes, marcó una reestructuración revolucionaria de todas las matemáticas. Se hizo posible interpretar ecuaciones algebraicas(o desigualdades) en forma de imágenes geométricas (gráficos) y, a la inversa, buscar una solución problemas geométricos utilizando fórmulas analíticas y sistemas de ecuaciones. Si, desigualdad z < 3 геометрически означает полупространство, лежащее ниже плоскости, параллельной Plano coordinado xoy y ubicado por encima de este plano por 3 unidades.
Usando el sistema de coordenadas cartesiano, la pertenencia de un punto a una curva dada corresponde al hecho de que los números X Y y satisfacer alguna ecuación. Por tanto, las coordenadas de un punto en un círculo con centro en un punto dado ( a; b) satisface la ecuación (X - a)² + ( y - b)² = R² .
Sistema de coordenadas cartesianas rectangulares en un plano.
Dos ejes perpendiculares en un plano con origen común y la misma forma unitaria de escala Sistema de coordenadas rectangular cartesiano en el plano. . Uno de estos ejes se llama eje. Buey, o eje x , el otro - el eje Oye, o eje y . Estos ejes también se denominan ejes de coordenadas. Denotemos por METROX Y METROy respectivamente, la proyección de un punto arbitrario METRO en el eje Buey Y Oye. ¿Cómo obtener proyecciones? pasemos por el punto METRO Buey. Esta recta corta al eje Buey en el punto METROX. pasemos por el punto METRO recta perpendicular al eje Oye. Esta recta corta al eje Oye en el punto METROy. Esto se muestra en la imagen de abajo.
X Y y puntos METRO llamaremos a los valores de los segmentos dirigidos en consecuencia omX Y omy. Los valores de estos segmentos dirigidos se calculan en consecuencia como X = X0 - 0 Y y = y0 - 0 . Coordenadas cartesianas X Y y puntos METRO abscisa Y ordenada . El hecho de que el punto METRO tiene coordenadas X Y y, se denota de la siguiente manera: METRO(X, y) .
Los ejes de coordenadas dividen el plano en cuatro. cuadrante , cuya numeración se muestra en la siguiente figura. También muestra la disposición de los signos de las coordenadas de los puntos según su ubicación en un cuadrante particular.
Además de las coordenadas rectangulares cartesianas en un plano, también se suele considerar el sistema de coordenadas polares. Sobre el método de transición de un sistema de coordenadas a otro - en la lección sistema de coordenadas polares .
Sistema de coordenadas cartesianas rectangulares en el espacio.
Las coordenadas cartesianas en el espacio se introducen en completa analogía con las coordenadas cartesianas en el plano.
Tres ejes mutuamente perpendiculares en el espacio ( ejes de coordenadas) con un comienzo común oh y con la misma unidad de escala forman Sistema de coordenadas rectangular cartesiano en el espacio. .
Uno de estos ejes se llama eje. Buey, o eje x , el otro - el eje Oye, o eje y , el tercer eje Onz, o aplicar eje . Dejar METROX, METROy METROz- proyecciones de un punto arbitrario METRO espacio en el eje Buey , Oye Y Onz respectivamente.
pasemos por el punto METRO BueyBuey en el punto METROX. pasemos por el punto METRO plano perpendicular al eje Oye. Este plano corta al eje Oye en el punto METROy. pasemos por el punto METRO plano perpendicular al eje Onz. Este plano corta al eje Onz en el punto METROz.
Coordenadas rectangulares cartesianas X , y Y z puntos METRO llamaremos a los valores de los segmentos dirigidos en consecuencia omX, omy Y omz. Los valores de estos segmentos dirigidos se calculan en consecuencia como X = X0 - 0 , y = y0 - 0 Y z = z0 - 0 .
Coordenadas cartesianas X , y Y z puntos METRO son llamados en consecuencia abscisa , ordenada Y aplicar .
Los ejes de coordenadas tomados en pares se encuentran en planos de coordenadas. xoy , yOz Y zOx .
Problemas sobre puntos en un sistema de coordenadas cartesiano
Ejemplo 1.
A(2; -3) ;
B(3; -1) ;
C(-5; 1) .
Encuentre las coordenadas de las proyecciones de estos puntos sobre el eje de abscisas.
Solución. Como se desprende de la parte teórica de esta lección, la proyección de un punto sobre el eje de abscisas se ubica sobre el propio eje de abscisas, es decir, el eje Buey, y por tanto tiene una abscisa igual a la abscisa del propio punto, y una ordenada (coordenada en el eje Oye, que el eje x corta en el punto 0), igual a cero. Entonces obtenemos las siguientes coordenadas de estos puntos en el eje x:
Ax(2;0);
Bx(3;0);
Cx (-5; 0).
Ejemplo 2. EN sistema cartesiano las coordenadas en el plano son puntos dados
A(-3; 2) ;
B(-5; 1) ;
C(3; -2) .
Encuentre las coordenadas de las proyecciones de estos puntos sobre el eje de ordenadas.
Solución. Como se desprende de la parte teórica de esta lección, la proyección de un punto sobre el eje de ordenadas se sitúa sobre el propio eje de ordenadas, es decir, el eje Oye, y por tanto tiene una ordenada igual a la ordenada del propio punto, y una abscisa (coordenada en el eje Buey, que el eje de ordenadas corta en el punto 0), que es igual a cero. Entonces obtenemos las siguientes coordenadas de estos puntos en el eje de ordenadas:
Ay(0;2);
By(0;1);
Cy(0;-2).
Ejemplo 3. En el sistema de coordenadas cartesiano, los puntos están dados en el plano.
A(2; 3) ;
B(-3; 2) ;
C(-1; -1) .
Buey .
Buey Buey Buey, tendrá la misma abscisa que el punto dado y una ordenada igual en valor absoluto ordenada de un punto dado y su signo opuesto. Entonces obtenemos las siguientes coordenadas de puntos simétricos a estos puntos con respecto al eje Buey :
A"(2; -3) ;
B"(-3; -2) ;
C"(-1; 1) .
Resuelva problemas utilizando el sistema de coordenadas cartesiano usted mismo y luego observe las soluciones.
Ejemplo 4. Determine en qué cuadrantes (cuartos, dibujando con cuadrantes, al final del párrafo "Sistema de coordenadas cartesianas rectangulares en un plano") se puede ubicar un punto METRO(X; y) , Si
1) xy > 0 ;
2) xy < 0 ;
3) X − y = 0 ;
4) X + y = 0 ;
5) X + y > 0 ;
6) X + y < 0 ;
7) X − y > 0 ;
8) X − y < 0 .
Ejemplo 5. En el sistema de coordenadas cartesiano, los puntos están dados en el plano.
A(-2; 5) ;
B(3; -5) ;
C(a; b) .
Encuentre las coordenadas de puntos simétricos a estos puntos con respecto al eje. Oye .
Sigamos resolviendo problemas juntos
Ejemplo 6. En el sistema de coordenadas cartesiano, los puntos están dados en el plano.
A(-1; 2) ;
B(3; -1) ;
C(-2; -2) .
Encuentre las coordenadas de puntos simétricos a estos puntos con respecto al eje. Oye .
Solución. Gira 180 grados alrededor del eje. Oye segmento direccional desde el eje Oye hasta este punto. En la figura, donde se indican los cuadrantes del plano, vemos que el punto simétrico al dado con respecto al eje Oye, tendrá la misma ordenada que el punto dado, y una abscisa igual en valor absoluto a la abscisa del punto dado y de signo opuesto. Entonces obtenemos las siguientes coordenadas de puntos simétricos a estos puntos con respecto al eje Oye :
A"(1; 2) ;
B"(-3; -1) ;
C"(2; -2) .
Ejemplo 7. En el sistema de coordenadas cartesiano, los puntos están dados en el plano.
A(3; 3) ;
B(2; -4) ;
C(-2; 1) .
Encuentre las coordenadas de puntos simétricos a estos puntos con respecto al origen.
Solución. Giramos el segmento dirigido que va desde el origen hasta el punto dado 180 grados alrededor del origen. En la figura, donde se indican los cuadrantes del plano, vemos que un punto simétrico al punto dado con respecto al origen de coordenadas tendrá una abscisa y una ordenada igual en valor absoluto a la abscisa y la ordenada del punto dado, pero opuesto en signo. Entonces obtenemos las siguientes coordenadas de puntos simétricos a estos puntos con respecto al origen:
A"(-3; -3) ;
B"(-2; 4) ;
C(2; -1) .
Ejemplo 8.
A(4; 3; 5) ;
B(-3; 2; 1) ;
C(2; -3; 0) .
Encuentra las coordenadas de las proyecciones de estos puntos:
1) en un avión oxi ;
2) en un avión Oxz ;
3) al avión Oyz ;
4) en el eje de abscisas;
5) en el eje de ordenadas;
6) en el eje de aplicación.
1) Proyección de un punto sobre un plano. oxi se sitúa en este plano mismo, y por tanto tiene una abscisa y ordenada iguales a la abscisa y ordenada de un punto dado, y una aplicada igual a cero. Entonces obtenemos las siguientes coordenadas de las proyecciones de estos puntos sobre oxi :
Axy (4; 3; 0);
Bxy (-3; 2; 0);
Cxy(2;-3;0).
2) Proyección de un punto sobre un plano. Oxz está situado en este plano mismo, y por tanto tiene una abscisa y una aplicación iguales a la abscisa y una aplicación de un punto dado, y una ordenada igual a cero. Entonces obtenemos las siguientes coordenadas de las proyecciones de estos puntos sobre Oxz :
Axz (4; 0; 5);
Bxz (-3; 0; 1);
Cxz (2; 0; 0).
3) Proyección de un punto sobre un plano. Oyz se encuentra en este plano mismo, y por tanto tiene ordenada y aplicada iguales a la ordenada y aplicada de un punto dado, y una abscisa igual a cero. Entonces obtenemos las siguientes coordenadas de las proyecciones de estos puntos sobre Oyz :
Ayz(0; 3; 5);
Byz (0; 2; 1);
Cyz (0; -3; 0).
4) Como se desprende de la parte teórica de esta lección, la proyección de un punto sobre el eje de abscisas se ubica sobre el propio eje de abscisas, es decir, el eje Buey, y por lo tanto tiene una abscisa igual a la abscisa del punto mismo, y la ordenada y la aplicación de la proyección son iguales a cero (ya que los ejes de ordenadas y aplicación se cruzan con la abscisa en el punto 0). Obtenemos las siguientes coordenadas de las proyecciones de estos puntos sobre el eje de abscisas:
Ax (4; 0; 0);
Bx (-3; 0; 0);
Cx(2;0;0).
5) La proyección de un punto sobre el eje de ordenadas se sitúa sobre el propio eje de ordenadas, es decir, el eje Oye, y por lo tanto tiene una ordenada igual a la ordenada del punto mismo, y la abscisa y la aplicación de la proyección son iguales a cero (ya que los ejes de abscisa y aplicación se cruzan con el eje de ordenadas en el punto 0). Obtenemos las siguientes coordenadas de las proyecciones de estos puntos sobre el eje de ordenadas:
Ay(0; 3; 0);
By (0; 2; 0);
Cy(0;-3;0).
6) La proyección de un punto sobre el eje del aplicador se sitúa en el propio eje del aplicador, es decir, el eje Onz, y por lo tanto tiene una aplicación igual a la aplicación del punto mismo, y la abscisa y la ordenada de la proyección son iguales a cero (ya que los ejes de abscisas y ordenadas se cruzan con el eje de la aplicación en el punto 0). Obtenemos las siguientes coordenadas de las proyecciones de estos puntos sobre el eje aplicado:
Az (0; 0; 5);
Bz (0; 0; 1);
Cz(0; 0; 0).
Ejemplo 9. En el sistema de coordenadas cartesiano, los puntos se dan en el espacio.
A(2; 3; 1) ;
B(5; -3; 2) ;
C(-3; 2; -1) .
Encuentre las coordenadas de puntos simétricos a estos puntos con respecto a:
1) avión oxi ;
2) aviones Oxz ;
3) aviones Oyz ;
4) ejes de abscisas;
5) ejes de ordenadas;
6) aplicar ejes;
7) origen de coordenadas.
1) “Mover” el punto al otro lado del eje oxi oxi, tendrá una abscisa y una ordenada iguales a la abscisa y la ordenada de un punto dado, y una aplicación igual en magnitud a la aplicada de un punto dado, pero de signo opuesto. Entonces, obtenemos las siguientes coordenadas de puntos simétricos a los datos relativos al plano. oxi :
A"(2; 3; -1) ;
B"(5; -3; -2) ;
C"(-3; 2; 1) .
2) “Mover” el punto al otro lado del eje Oxz a la misma distancia. En la figura que muestra el espacio de coordenadas, vemos que un punto simétrico a uno dado con respecto al eje Oxz, tendrá una abscisa y una aplicación iguales a la abscisa y una aplicación de un punto dado, y una ordenada igual en magnitud a la ordenada de un punto dado, pero de signo opuesto. Entonces, obtenemos las siguientes coordenadas de puntos simétricos a los datos relativos al plano. Oxz :
A"(2; -3; 1) ;
B"(5; 3; 2) ;
C"(-3; -2; -1) .
3) “Mover” el punto al otro lado del eje Oyz a la misma distancia. En la figura que muestra el espacio de coordenadas, vemos que un punto simétrico a uno dado con respecto al eje Oyz, tendrá una ordenada y una aplicada iguales a la ordenada y una aplicada de un punto dado, y una abscisa igual en valor a la abscisa de un punto dado, pero de signo opuesto. Entonces, obtenemos las siguientes coordenadas de puntos simétricos a los datos relativos al plano. Oyz :
A"(-2; 3; 1) ;
B"(-5; -3; 2) ;
C"(3; 2; -1) .
Por analogía con puntos simétricos en el plano y puntos en el espacio simétricos a los datos relativos a los planos, observamos que en el caso de simetría con respecto a algún eje del sistema de coordenadas cartesiano en el espacio, la coordenada en el eje con respecto al cual se da la simetría será conservará su signo, y las coordenadas de los otros dos ejes serán las mismas en términos absolutos, el mismo valor que las coordenadas de un punto dado, pero de signo opuesto.
4) La abscisa conservará su signo, pero la ordenada y la aplicada cambiarán de signo. Entonces, obtenemos las siguientes coordenadas de puntos simétricos a los datos relativos al eje de abscisas:
A"(2; -3; -1) ;
B"(5; 3; -2) ;
C"(-3; -2; 1) .
5) La ordenada conservará su signo, pero la abscisa y la aplicada cambiarán de signo. Entonces, obtenemos las siguientes coordenadas de puntos simétricos a los datos relativos al eje de ordenadas:
A"(-2; 3; -1) ;
B"(-5; -3; -2) ;
C"(3; 2; 1) .
6) La aplicada conservará su signo, pero la abscisa y la ordenada cambiarán de signo. Entonces, obtenemos las siguientes coordenadas de puntos simétricos a los datos relativos al eje de aplicación:
A"(-2; -3; 1) ;
B"(-5; 3; 2) ;
C"(3; -2; -1) .
7) Por analogía con la simetría en el caso de puntos en un plano, en el caso de simetría con respecto al origen de coordenadas, todas las coordenadas de un punto simétrico a este serán iguales en valor absoluto a las coordenadas de un punto dado, pero opuesto a ellos en signo. Entonces, obtenemos las siguientes coordenadas de puntos simétricos a los datos relativos al origen.
Instrucciones
Anote Operaciones matemáticas en forma de texto e ingréselo en el campo de consulta de búsqueda en pagina de inicio Sitio de Google si no puede utilizar la calculadora, pero tiene acceso a Internet. Este motor de búsqueda tiene una calculadora multifuncional incorporada, que es mucho más fácil de usar que cualquier otro. No hay una interfaz con botones: todos los datos deben ingresarse en forma de texto en un solo campo. Por ejemplo, si se sabe coordenadas puntos extremos segmento V sistema tridimensional coordenadas A(51.34 17.2 13.02) y A(-11.82 7.46 33.5), entonces coordenadas punto medio segmento C((51,34-11,82)/2 (17,2+7,46)/2 (13,02+33,5)/2). Al ingresar (51.34-11.82)/2 en el campo de consulta de búsqueda, luego (17.2+7.46)/2 y (13.02+33.5)/2, puede usar Google para obtener coordenadas C(19,76 12,33 23,26).
Ecuación estándar círculo te permite descubrir varios información importante sobre esta figura, por ejemplo, las coordenadas de su centro, la longitud del radio. En algunos problemas, por el contrario, parámetros dados necesitas crear una ecuación.
Instrucciones
Determina qué información tienes sobre el círculo según la tarea que se te ha asignado. Recuerda eso meta final Es la necesidad de determinar las coordenadas del centro, así como el diámetro. Todas sus acciones deben estar dirigidas a lograr este resultado en particular.
Utilice datos sobre la presencia de puntos de intersección con líneas de coordenadas u otras líneas. Tenga en cuenta que si el círculo pasa por el eje de abscisas, el segundo tendrá la coordenada 0, y si pasa por el eje de ordenadas, entonces el primero. Estas coordenadas te permitirán encontrar las coordenadas del centro del círculo y también calcular el radio.
No te olvides de las propiedades básicas de las secantes y tangentes. En particular, el teorema más útil es que en el punto de contacto el radio y la tangente forman un ángulo recto. Pero tenga en cuenta que es posible que le pidan que demuestre todos los teoremas utilizados durante el curso.
Resuelve los tipos más estándar para aprender a ver de inmediato cómo utilizar ciertos datos para la ecuación de un círculo. Entonces, además de las tareas ya mencionadas con directamente coordenadas dadas y aquellos en los que se da información sobre la presencia de puntos de intersección, para compilar la ecuación de un círculo, se puede utilizar el conocimiento sobre el centro del círculo, la longitud de la cuerda y en qué se encuentra esta cuerda.
Para resolver, construir triángulo isósceles, cuya base será acorde dado, A lados iguales– radios. Compile desde donde podrá encontrar fácilmente los datos necesarios. Para hacer esto, basta con usar la fórmula para encontrar la longitud de un segmento en un plano.
Vídeo sobre el tema.
Se entiende por círculo una figura que consta de muchos puntos en un plano equidistante de su centro. Distancia del centro a los puntos. círculo llamado radio.
Un sistema de coordenadas rectangular en un plano está formado por dos ejes de coordenadas X'X e Y'Y mutuamente perpendiculares. Los ejes de coordenadas se cruzan en el punto O, que se llama origen, se selecciona una dirección positiva en cada eje. La dirección positiva de los ejes (en un sistema de coordenadas diestro) se elige de modo que cuando se gira el eje X'X. en sentido antihorario 90°, su dirección positiva coincide con la dirección positiva del eje Y'Y. Los cuatro ángulos (I, II, III, IV) formados por los ejes coordenados X'X e Y'Y se denominan ángulos coordenados (ver Fig. 1).
La posición del punto A en el plano está determinada por dos coordenadas xey. La coordenada x es igual a la longitud del segmento OB, la coordenada y es igual a la longitud del segmento OC en las unidades de medida seleccionadas. Los segmentos OB y OC están definidos por líneas trazadas desde el punto A paralelas a los ejes Y'Y y X'X, respectivamente. La coordenada x se llama abscisa del punto A, la coordenada y se llama ordenada del punto A. Se escribe de la siguiente manera: A(x, y).
Si el punto A se encuentra en ángulo coordenado I, entonces el punto A tiene abscisa y ordenada positivas. Si el punto A se encuentra en el ángulo coordenado II, entonces el punto A tiene una abscisa negativa y una ordenada positiva. Si el punto A se encuentra en el ángulo coordenado III, entonces el punto A tiene abscisas y ordenadas negativas. Si el punto A se encuentra en el ángulo coordenado IV, entonces el punto A tiene una abscisa positiva y una ordenada negativa.
Sistema de coordenadas rectangulares en el espacio. está formado por tres ejes de coordenadas OX, OY y OZ mutuamente perpendiculares. Los ejes de coordenadas se cruzan en el punto O, que se llama origen, en cada eje se selecciona una dirección positiva, indicada por flechas, y una unidad de medida para los segmentos en los ejes. Las unidades de medida son las mismas para todos los ejes. OX - eje de abscisas, OY - eje de ordenadas, OZ - eje de aplicación. La dirección positiva de los ejes se elige de modo que cuando el eje OX se gira 90° en sentido antihorario, su dirección positiva coincida con la dirección positiva del eje OY, si esta rotación se observa desde la dirección positiva del eje OZ. Este sistema de coordenadas se llama diestro. Si pulgar mano derecha Tome la dirección X como la dirección X, el índice como la dirección Y y el del medio como la dirección Z, luego se forma un sistema de coordenadas a la derecha. Dedos similares de la mano izquierda forman el sistema de coordenadas izquierdo. Es imposible combinar los sistemas de coordenadas derecho e izquierdo para que coincidan los ejes correspondientes (ver Fig. 2).
La posición del punto A en el espacio está determinada por tres coordenadas x, y y z. La coordenada x es igual a la longitud del segmento OB, la coordenada y es la longitud del segmento OC, la coordenada z es la longitud del segmento OD en las unidades de medida seleccionadas. Los segmentos OB, OC y OD están definidos por planos trazados desde el punto A paralelos a los planos YOZ, XOZ y XOY, respectivamente. La coordenada x se llama abscisa del punto A, la coordenada y se llama ordenada del punto A, la coordenada z se llama aplicación del punto A. Se escribe de la siguiente manera: A(a, b, c).
orty
Un sistema de coordenadas rectangular (de cualquier dimensión) también se describe mediante un conjunto de vectores unitarios alineados con los ejes de coordenadas. El número de vectores unitarios es igual a la dimensión del sistema de coordenadas y todos son perpendiculares entre sí.
En el caso tridimensional, estos vectores unitarios suelen denominarse i j k o mi X mi y mi z. Además, en el caso de un sistema de coordenadas diestro, siguientes fórmulas con el producto cruzado de vectores:
- [i j]=k ;
- [j k]=i ;
- [k i]=j .
Historia
El sistema de coordenadas rectangulares fue introducido por primera vez por René Descartes en su obra "Discurso sobre el método" en 1637. Por lo tanto, el sistema de coordenadas rectangulares también se llama: sistema de coordenadas Cartesianas. El método de coordenadas para describir objetos geométricos sentó las bases. geometría analítica. Pierre Fermat también contribuyó al desarrollo del método de coordenadas, pero sus trabajos se publicaron por primera vez después de su muerte. Descartes y Fermat utilizaron el método de coordenadas sólo en el plano.
método de coordenadas para espacio tridimensional Fue utilizado por primera vez por Leonhard Euler en el siglo XVIII.
ver también
Enlaces
Fundación Wikimedia. 2010.
- sistema de coordenadas Cartesianas
- grado cartesiano
Vea qué son las “coordenadas cartesianas” en otros diccionarios:
COORDENADAS CARTESINAS- (Sistema de coordenadas cartesiano) un sistema de coordenadas en un plano o en el espacio, generalmente con ejes mutuamente perpendiculares y escalas iguales a lo largo de los ejes rectangulares. Coordenadas cartesianas. Lleva el nombre de R. Descartes... Gran diccionario enciclopédico
Coordenadas cartesianas- Un sistema de coordenadas formado por dos ejes perpendiculares. La posición de un punto en dicho sistema se forma utilizando dos números que determinan la distancia desde el centro de coordenadas a lo largo de cada uno de los ejes. Temas informativos... ... Guía del traductor técnico
Coordenadas cartesianas- (sistema de coordenadas cartesianas), un sistema de coordenadas en un plano o en el espacio, generalmente con ejes mutuamente perpendiculares y escalas iguales a lo largo de los ejes de coordenadas cartesianas rectangulares; Lleva el nombre de R. Descartes... diccionario enciclopédico
Coordenadas cartesianas- Dekarto koordinatės statusas T sritis Standartizacija ir metrologija apibrėžtis Tiesinė plokštumos arba erdvės koordinačių sistema. Joje ašių masteliai paprastai būna lygūs. atitikmenys: inglés. Coordenadas cartesianas vok. kartesische Koordinaten, f… Penkiakalbis aiškinamasis metrologijos terminų žodynas
Coordenadas cartesianas- Dekarto koordinatės statusas T sritis fizika atitikmenys: engl. Coordenadas cartesianas; coordenadas de cuadrícula vok. kartesische Koordinaten, f rus. Coordenadas cartesianas, f pranc. coordinadas cartésiennes, f … Fizikos terminų žodynas
COORDENADAS CARTESINAS- un método para determinar la posición de puntos en un plano por sus distancias a dos ejes rectos perpendiculares fijos. Este concepto ya se ve en Arquímedes y Apologis de Perga hace más de dos mil años e incluso entre los antiguos egipcios. Por primera vez esto... ... Enciclopedia Matemática
COORDENADAS CARTESINAS- Sistema de coordenadas cartesianas [llamado así por los franceses. filósofo y matemático R. Descartes (R. Descartes; 1596 1650)], un sistema de coordenadas en un plano o en el espacio, generalmente con ejes mutuamente perpendiculares y escalas iguales a lo largo de los ejes rectangulares D ... Gran Diccionario Politécnico Enciclopédico
COORDENADAS CARTESINAS- (Sistema de coordenadas cartesiano), un sistema de coordenadas en un plano o en el espacio, generalmente con ejes mutuamente perpendiculares y escalas iguales a lo largo de los ejes rectangulares. El nombre de R. Descartes... Ciencias Naturales. diccionario enciclopédico
COORDENADAS CARTESINAS- El sistema para posicionar cualquier punto que se encuentre en los huesos en relación con dos ejes que se cruzan en ángulo recto. Desarrollado por René Descartes, este sistema se convirtió en la base para métodos estándar representación grafica datos. Linea horizontal… … Diccionario en psicología
Coordenadas- Coordenadas. En el avión (izquierda) y en el espacio (derecha). COORDENADAS (del latín co juntos y ordinatus ordenados), números que determinan la posición de un punto en una recta, plano, superficie, en el espacio. Las coordenadas son distancias... Diccionario enciclopédico ilustrado
Definición 1. Eje numérico (recta numérica, recta de coordenadas) Ox es la recta en la que se selecciona el punto O origen (origen de coordenadas)(Fig.1), dirección
oh → X
catalogado como dirección positiva y se marca un segmento, cuya longitud se considera unidad de longitud.
Definición 2. Un segmento cuya longitud se toma como unidad de longitud se llama escala.
Cada punto en el eje numérico tiene una coordenada, que es Número Real. La coordenada del punto O es cero. La coordenada de un punto arbitrario A que se encuentra sobre el rayo Ox es igual a la longitud del segmento OA. La coordenada de un punto arbitrario A del eje numérico que no se encuentra en el rayo Ox es negativa y en valor absoluto es igual a la longitud del segmento OA.
Definición 3. Sistema de coordenadas cartesianas rectangulares Oxy en el plano. llamar a dos mutuamente perpendicular ejes numéricos Ox y Oy con la misma escala Y punto de referencia común en el punto O, y tal que la rotación desde el rayo Ox en un ángulo de 90° hasta el rayo Oy se realiza en la dirección en sentido anti-horario(Figura 2).
Nota. El sistema de coordenadas cartesiano rectangular Oxy, que se muestra en la Figura 2, se llama sistema correcto coordenadas, A diferencia de sistemas de coordenadas izquierdas, en el que la rotación del haz Ox formando un ángulo de 90° con respecto al haz Oy se realiza en el sentido de las agujas del reloj. En esta guía nosotros Solo consideramos sistemas de coordenadas diestros., sin especificarlo específicamente.
Si introducimos algún sistema de coordenadas cartesianas rectangulares Oxy en el plano, entonces cada punto del plano adquirirá dos coordenadas – abscisa Y ordenada, que se calculan de la siguiente manera. Sea A un punto arbitrario del plano. Dejemos caer perpendiculares desde el punto A. AUTOMÓVIL CLUB BRITÁNICO. 1 y AUTOMÓVIL CLUB BRITÁNICO. 2 a las rectas Ox y Oy, respectivamente (Fig. 3).
Definición 4. La abscisa del punto A es la coordenada del punto. A 1 en el eje numérico Ox, la ordenada del punto A es la coordenada del punto A 2 en el eje numérico Oy.
Designación Coordenadas (abscisas y ordenadas) del punto A en el sistema de coordenadas cartesiano rectangular Oxy (Fig.4) generalmente se denota A(X;y) o A = (X; y).
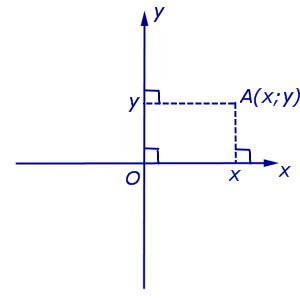
Nota. Punto O, llamado origen, tiene coordenadas oh(0 ; 0) .
Definición 5. En el sistema de coordenadas cartesiano rectangular Oxy eje numérico Ox se llama eje de abscisas y el eje numérico Oy se llama eje de ordenadas (Fig. 5).
Definición 6. Cada sistema de coordenadas cartesianas rectangular divide el plano en 4 cuartos (cuadrantes), cuya numeración se muestra en la Figura 5.
Definición 7. El plano en el que se da un sistema de coordenadas cartesianas rectangulares se llama Plano coordinado.
Nota. El eje de abscisas se especifica en el plano de coordenadas mediante la ecuación y= 0, el eje de ordenadas viene dado en el plano de coordenadas por la ecuación X = 0.
Declaración 1. Distancia entre dos puntos Plano coordinado
A 1 (X 1 ;y 1) Y A 2 (X 2 ;y 2)
calculado según la fórmula
Prueba . Considere la Figura 6.
| |A 1 A 2 | 2 = = (X 2 -X 1) 2 + (y 2 -y 1) 2 . | (1) |
Por eso,
Q.E.D.
Ecuación de un círculo en el plano coordenado.
Consideremos en el plano coordenado Oxy (Fig. 7) una circunferencia de radio R con centro en el punto A 0 (X 0 ;y 0) .
Coordenadas polares
el numero se llama radio polar puntos o primera coordenada polar. La distancia no puede ser negativa, por lo que el radio polar de cualquier punto es. La primera coordenada polar también se denota letra griega(“ro”), pero estoy acostumbrado a la versión latina y la usaré en el futuro.
el numero se llama ángulo polar punto dado o segunda coordenada polar. El ángulo polar normalmente varía dentro (el llamado valores de los ángulos principales). Sin embargo, es bastante aceptable utilizar el rango y, en algunos casos, existe una necesidad directa de considerar todos los valores de los ángulos desde cero hasta "más infinito". Por cierto, te recomiendo que te acostumbres a la medida en radianes de un ángulo, ya que se opera con grados en Matemáticas avanzadas considerado no comme il faut.
la pareja se llama coordenadas polares puntos Son fáciles de encontrar y valores específicos. Tangente ángulo agudo triángulo rectángulo - hay una relación lado opuesto al cateto adyacente: por lo tanto, el ángulo mismo: 
. Según el teorema de Pitágoras, el cuadrado de la hipotenusa igual a la suma cuadrados de catetos: por tanto, el radio polar:
De este modo, 
.
Un pingüino es bueno, pero una bandada es mejor: 
Esquinas orientadas negativamente 
Lo marqué con flechas por si acaso, por si algunos de los lectores aún no conocían esta orientación. Si lo deseas, puedes “atornillar” 1 vuelta (rad o 360 grados) a cada uno de ellos y, de paso, ponerte cómodo. valores de la tabla:
Pero la desventaja de estos ángulos orientados "tradicionalmente" es que están "torcidos" demasiado (más de 180 grados) en sentido antihorario. Anticipo la pregunta: “¿por qué hay escasez y por qué hay ángulos negativos? En matemáticas, el más corto y formas racionales. Bueno, desde el punto de vista de la física, la dirección de rotación suele ser de fundamental importancia: cada uno de nosotros intentó abrir la puerta tirando de la manija en la dirección incorrecta =)
El orden y la técnica de construir puntos en coordenadas polares.
Hermosas fotos Son hermosos, pero construirlos en el sistema de coordenadas polares es una tarea bastante laboriosa. No hay dificultades con puntos cuyos ángulos polares son 
, en nuestro ejemplo estos son puntos 
; Los valores que son múltiplos de 45 grados tampoco causan muchos problemas: . Pero, ¿cómo construir correcta y competentemente, digamos, un punto?
Necesitará una hoja de papel a cuadros, un lápiz y lo siguiente herramientas de dibujo: regla, compás, transportador. EN como último recurso, puedes arreglártelas con una sola regla, o incluso... ¡sin ella! Sigue leyendo y obtendrás otra prueba de que este país es invencible =)
Ejemplo 1
Construya un punto en el sistema de coordenadas polares.
Primero que nada, necesitas descubrir medida de gradoángulo Si el rincón no te resulta familiar o tienes dudas, siempre es mejor utilizar mesa o una fórmula general para convertir radianes a grados. Entonces nuestro ángulo es (o).
Dibujemos un sistema de coordenadas polares (vea el comienzo de la lección) y tomemos un transportador. Los propietarios de un instrumento redondo no tendrán dificultad para marcar 240 grados, pero con probabilidad alta Tendrás en tus manos una versión semicircular del dispositivo. Problema ausencia total transportador si tienes impresora y tijeras resuelto por artesanía.
Hay dos formas: dar la vuelta a la hoja y marcar 120 grados, o “atornillar” media vuelta y examinar esquina opuesta. Elijamos el método de adulto y hagamos una marca de 60 grados: 
O un transportador liliputiense o una jaula gigante =) Sin embargo, para medir un ángulo, la escala no es importante.
Con un lápiz, dibuje una línea recta delgada que pase por el poste y la marca hecha: 
Hemos resuelto el ángulo, ahora el radio polar es el siguiente. Toma una brújula y a lo largo de la línea Establecemos su solución en 3 unidades, la mayoría de las veces son, por supuesto, centímetros: 
Ahora coloque con cuidado la aguja en el poste y movimiento rotacional Hacemos una pequeña serifa (color rojo). Se construyó el punto requerido: 
Puedes prescindir de un círculo aplicando la regla directamente sobre la línea recta construida y midiendo 3 centímetros. Pero, como veremos más adelante, en problemas que involucran la construcción en un sistema de coordenadas polares una situación típica es cuando necesitas marcar dos o gran cantidad puntos con el mismo radio polar, por lo que es más eficiente endurecer el metal. En particular, en nuestro dibujo, al girar la pata de la brújula 180 grados, es fácil hacer una segunda muesca y construir un punto simétrico con respecto al polo. Usémoslo para trabajar en el material del siguiente párrafo:
Relación entre sistemas de coordenadas rectangulares y polares
Obviamente agreguemos al sistema de coordenadas polares, una cuadrícula de coordenadas "normal" y dibuja un punto en el dibujo: 
Siempre es útil tener en cuenta esta conexión al dibujar coordenadas polares. Aunque, quiera o no, se sugiere sin más indicios.
Establezcamos la relación entre coordenadas polares y cartesianas usando un ejemplo. punto específico. Consideremos triángulo rectángulo, en el que la hipotenusa es igual al radio polar: , y los catetos son iguales a las coordenadas “X” e “Y” del punto en el sistema de coordenadas cartesiano: 
.
El seno de un ángulo agudo es la razón entre el cateto opuesto y la hipotenusa: 
El coseno de un ángulo agudo es la relación entre el cateto adyacente y la hipotenusa: 
Al mismo tiempo, repetimos las definiciones de seno, coseno (y un poco antes de tangente) del plan de estudios de noveno grado de una escuela integral.
Agregue fórmulas de trabajo en su libro de referencia que expresen las coordenadas cartesianas de un punto a través de sus coordenadas polares; tendremos que lidiar con ellas más de una vez, y la próxima vez ahora mismo =)
Encontremos las coordenadas del punto en sistema rectangular coordenadas: 
De este modo:
Las fórmulas resultantes abren otra laguna en el problema de la construcción, cuando es posible prescindir de un transportador: primero encontramos las coordenadas cartesianas del punto (por supuesto, en el borrador), luego encontramos mentalmente el lugar correcto en el dibujo. y marca este punto. En etapa final Dibuja una línea recta delgada que pase por el punto construido y el poste. Como resultado, resulta que el ángulo supuestamente se midió con un transportador.
Es curioso que estudiantes muy desesperados puedan prescindir incluso de una regla y utilicen en su lugar el borde liso de un libro de texto, un cuaderno o libro de calificaciones– después de todo, los fabricantes de portátiles se preocuparon por las métricas, 1 celda = 5 milímetros.
Todo esto me recordó un chiste muy conocido en el que pilotos ingeniosos trazaban un rumbo a lo largo de un paquete de Belomor =) Aunque, bromas aparte, el chiste no está tan lejos de la realidad, recuerdo que en uno de los vuelos domésticos en Rusia Federación, todos los instrumentos de navegación del avión fallaron y la tripulación aterrizó con éxito el avión utilizando un vaso de agua normal, que mostraba el ángulo del avión con respecto al suelo. Y la pista de aterrizaje... aquí está, visible desde el parabrisas.
Usando el teorema de Pitágoras citado al comienzo de la lección, es fácil obtener fórmulas inversas: , por eso:
El ángulo "phi" en sí se expresa estándar a través del arcotangente, absolutamente igual que argumento de número complejo con todos sus problemas.
También es recomendable colocar el segundo grupo de fórmulas en tu equipaje de referencia.
Después análisis detallado vuelos con puntos individuales, pasemos a la continuación natural del tema:
Ecuación de una recta en coordenadas polares
Esencialmente, la ecuación de una línea en un sistema de coordenadas polares es función del radio polar desde el ángulo polar (argumento). En este caso, se tiene en cuenta el ángulo polar. en radianes(!) Y continuamente toma valores de a (a veces se debe considerar hasta el infinito, o en varios problemas por conveniencia desde hasta). Cada valor del ángulo “phi” que se incluye en dominio función, corresponde a un único valor del radio polar.
La función polar se puede comparar con una especie de radar: cuando un rayo de luz que emana de un polo gira en sentido antihorario y "detecta" (dibuja) una línea.
Un ejemplo estándar de una curva polar es Espiral de Arquímedes. La siguiente imagen la muestra. primera ronda– cuando el radio polar que sigue al ángulo polar toma valores de 0 a: 
Además, al cruzar el eje polar en el punto , la espiral continuará desenrollándose, alejándose infinitamente del polo. Pero casos similares en la práctica son bastante raros; más situación típica, cuando en todas las revoluciones posteriores “caminamos por la misma línea” que se obtuvo en el rango.
En el primer ejemplo nos encontramos con el concepto dominio de definición Función polar: dado que el radio polar no es negativo, aquí no se pueden considerar ángulos negativos.
! Nota : en algunos casos se acostumbra utilizar coordenadas polares generalizadas, donde el radio puede ser negativo, y estudiaremos brevemente este enfoque un poco más adelante
Además de la espiral de Arquímedes, hay muchas otras curvas famosas, pero, como dicen, nunca te cansas del arte, así que seleccioné ejemplos que se encuentran muy a menudo en tareas prácticas reales.
Primero, las ecuaciones y líneas más simples:
Una ecuación de la forma especifica la que emana del polo Rayo. De hecho, piénselo, si el valor del ángulo Siempre(sea lo que sea "er") constantemente, entonces ¿qué línea es?
Nota : en el sistema de coordenadas polares generalizado ecuación dada define una línea recta que pasa por el polo
Una ecuación de la forma determina... adivina la primera vez - si para cualquiera¿El radio del ángulo "phi" permanece constante? De hecho esta es la definición. círculo centrado en el polo del radio.
Por ejemplo, . Para mayor claridad, encontremos la ecuación de esta recta en un sistema de coordenadas rectangular. Utilizando la fórmula obtenida en el párrafo anterior, realizamos la sustitución:
Elevemos al cuadrado ambos lados:
– ecuación de un círculo con centro en el origen del radio 2, que es lo que había que comprobar.
Desde la creación y publicación del artículo. sobre la dependencia lineal y la independencia lineal de los vectores Recibí varias cartas de visitantes del sitio que hacían una pregunta del tipo: "existe un sistema de coordenadas rectangular simple y conveniente, ¿por qué necesitamos otro oblicuo?" caso afín?. La respuesta es simple: ¡las matemáticas se esfuerzan por abarcar todo y a todos! Además, en una situación determinada, la conveniencia es importante; como puede ver, es mucho más rentable trabajar con un círculo en coordenadas polares debido a la extrema simplicidad de la ecuación.
Y aveces modelo matemático anticipa descubrimientos cientificos. Entonces, en un momento el rector de la Universidad de Kazán, N.I. lobachevski estrictamente probado, a través de punto arbitrario se pueden dibujar aviones infinitas lineas rectas, paralelo a este. Como resultado, fue difamado por todo. mundo científico, pero... refutar este hecho nadie pudo. Sólo un buen siglo después, los astrónomos descubrieron que la luz en el espacio viaja a lo largo de trayectorias curvas, donde la geometría no euclidiana de Lobachevsky, desarrollada formalmente por él mucho antes de este descubrimiento, comienza a funcionar. Se supone que esta es una propiedad del espacio mismo, cuya curvatura es invisible para nosotros debido a distancias pequeñas (según estándares astronómicos).
Consideremos tareas de construcción más significativas:
Ejemplo 2
construir una línea
Solución: primero que nada busquemos dominio. Como el radio polar no es negativo, la desigualdad debe cumplirse. Puedes recordar las reglas escolares para resolver desigualdades trigonométricas, pero en casos simples como este, recomiendo más rápido y método visual soluciones:
Imagina una gráfica de coseno. Si aún no se ha registrado en su memoria, búsquelo en la página Gráficas de funciones elementales.. ¿Qué nos dice la desigualdad? Nos dice que la gráfica del coseno debe ubicarse no menos eje de abscisas. Y esto sucede en el segmento. Y, en consecuencia, el intervalo no es adecuado.
Por tanto, el dominio de definición de nuestra función es: , es decir, la gráfica está ubicada a la derecha del polo (en la terminología del sistema cartesiano, en el semiplano derecho).
En las coordenadas polares, a menudo hay una idea vaga de qué línea recta define una ecuación particular, por lo que para construirla es necesario encontrar los puntos que le pertenecen, y cuantos más, mejor. Por lo general, se limitan a una docena o dos (o incluso menos). La forma más fácil, por supuesto, es tomar valores de ángulo de la tabla. Para mayor claridad, valores negativos Voy a "joder" una vuelta: 
Debido a la paridad del coseno 
importante valores positivos no tienes que volver a contar: 
Representaremos el sistema de coordenadas polares y trazaremos los puntos encontrados, mientras mismos valores Es conveniente posponer el "er" a la vez haciendo muescas emparejadas con una brújula utilizando la tecnología comentada anteriormente: 
En principio, la línea está claramente trazada, pero para confirmar completamente la suposición, encontremos su ecuación en el sistema de coordenadas cartesiano. Puede aplicar las fórmulas derivadas recientemente. 
, pero te contaré un truco más astuto. Multiplicamos artificialmente ambos lados de la ecuación por "er": y utilizamos fórmulas de transición más compactas:
Destacando cuadrado perfecto, llevamos la ecuación de la recta a una forma reconocible: 
– ecuación de un círculo con centro en el punto , radio 2.
Dado que según la condición simplemente era necesario realizar la construcción y listo, conectamos suavemente los puntos encontrados con una línea: 
Listo. Está bien si queda un poco desigual, no tenías por qué saber que era un círculo ;-)
¿Por qué no consideramos los valores de los ángulos fuera del intervalo? La respuesta es sencilla: no tiene sentido. Debido a la periodicidad de la función, nos enfrentamos a una carrera interminable a lo largo del círculo construido.
Es fácil realizar un análisis simple y llegar a la conclusión de que una ecuación de la forma especifica un círculo de diámetro con centro en el punto . En sentido figurado, todos esos círculos "se asientan" en el eje polar y necesariamente pasan por el polo. Si entonces compañía divertida migrará hacia la izquierda, hacia la continuación del eje polar (piense por qué).
tarea similar para decisión independiente:
Ejemplo 3
Construye una recta y encuentra su ecuación en un sistema de coordenadas rectangular.
Sistematicemos el procedimiento para resolver el problema:
En primer lugar encontramos el dominio de definición de la función, para ello conviene fijarse; sinusoide para comprender inmediatamente dónde el seno no es negativo.
En el segundo paso, calculamos las coordenadas polares de los puntos usando valores de ángulo de la tabla; ¿Analizar si es posible reducir el número de cálculos?
En el tercer paso, trazamos los puntos en el sistema de coordenadas polares y los conectamos cuidadosamente con una línea.
Y finalmente encontramos la ecuación de la recta en el sistema de coordenadas cartesiano.
muestra aproximada soluciones al final de la lección.
Algoritmo general y detallamos la técnica de construcción en coordenadas polares.
y acelerar significativamente en la segunda parte de la conferencia, pero antes nos familiarizaremos con otra línea común:
Rosa polar
Así es, estamos hablando de una flor con pétalos:
Ejemplo 4
Construir rectas dadas por ecuaciones en coordenadas polares.
Hay dos métodos para construir una rosa polar. Primero, sigamos la pista moleteada, suponiendo que el radio polar no puede ser negativo:
Solución:
a) Encontremos el dominio de definición de la función: 
Este desigualdad trigonométrica Tampoco es difícil resolverlo gráficamente: a partir de los materiales del artículo. Transformaciones geométricas de gráficos. Se sabe que si se duplica el argumento de una función, su gráfica se reducirá al eje de ordenadas 2 veces. Encuentre la gráfica de la función en el primer ejemplo. la lección especificada. ¿Dónde está ubicada esta sinusoide sobre el eje x? A intervalos 
. En consecuencia, la desigualdad es satisfecha por los segmentos correspondientes, y dominio nuestra función: 
.
En términos generales, la solución a las desigualdades consideradas es la unión número infinito segmentos, pero, nuevamente, nos interesa solo un período.
Quizás a algunos lectores les resulte más fácil método analítico Al encontrar el dominio de la definición, lo llamaré condicionalmente "rebanar un pastel redondo". vamos a cortar en partes iguales y, antes que nada, encontrar los límites de la primera pieza. Razonamos de la siguiente manera: el seno no es negativo, Cuando su argumento varía de 0 a rad. inclusivo. En nuestro ejemplo: . Dividiendo todas las partes de la doble desigualdad por 2, obtenemos el intervalo requerido:
Ahora comenzamos a "cortar piezas iguales de 90 grados" secuencialmente en sentido antihorario:
– el segmento encontrado está, por supuesto, incluido en el dominio de definición;
– siguiente intervalo – no incluido;
– siguiente segmento – incluido;
– y finalmente, el intervalo – no está incluido.
Como una margarita - “ama, no ama, ama, no ama” =) Con la diferencia de que aquí no hay adivinación. Sí, es sólo una especie de amor en chino….
Entonces, 
y la línea representa una rosa con dos pétalos idénticos. Es muy posible dibujar el dibujo de forma esquemática, pero es muy recomendable buscarlo y marcarlo correctamente. cimas de pétalos. Los vértices corresponden a puntos medios de segmentos del dominio de definición, En cual en este ejemplo tener coordenadas angulares obvias 
. Donde longitudes de pétalos son: 
Aquí está el resultado natural de un jardinero cariñoso: 
Cabe señalar que la longitud del pétalo se puede ver fácilmente en la ecuación; dado que el seno es limitado: , entonces valor máximo“er” ciertamente no excederá de dos.
b) Construyamos una línea, dado por la ecuación. Evidentemente, la longitud del pétalo de esta rosa también es dos, pero, ante todo, nos interesa el dominio de la definición. Aplicable método analítico"cortes": el seno es no negativo cuando su argumento está en el rango de cero a “pi” inclusive, en en este caso: . Dividimos todas las partes de la desigualdad entre 3 y obtenemos el primer intervalo:
A continuación, comenzamos a “cortar el pastel en pedazos” por rad. (60 grados):
– el segmento entrará en el dominio de definición;
– intervalo – no se incluirá;
– segmento – encajará;
– intervalo – no se incluirá;
– segmento – encajará;
– intervalo – no se incluirá.
El proceso se completa con éxito en 360 grados.
Por tanto, el alcance de la definición es: 
.
Las acciones realizadas total o parcialmente son fáciles de realizar mentalmente.
Construcción. Si en el párrafo anterior todo salió bien con ángulos rectos y ángulos de 45 grados, entonces aquí tendrás que retocar un poco. Encontremos cimas de pétalos. Su longitud fue visible desde el comienzo de la tarea; solo queda calcular las coordenadas angulares, que son iguales a los puntos medios de los segmentos del dominio de definición: 
Tenga en cuenta que debe haber espacios iguales entre las partes superiores de los pétalos, en este caso 120 grados.
Es recomendable marcar el dibujo en sectores de 60 grados (delimitados lineas verdes) y dibuja las direcciones de los vértices de los pétalos (líneas grises). Es conveniente marcar los vértices con una brújula: mida una distancia de 2 unidades una vez y haga tres muescas en las direcciones dibujadas de 30, 150 y 270 grados: 
Listo. Entiendo que esta es una tarea problemática, pero si quieres organizar todo sabiamente, tendrás que dedicar tiempo.
formulemos formula general : una ecuación de la forma , es un número natural), define una rosa de pétalos polares, cuya longitud de pétalo es igual a .
Por ejemplo, la ecuación especifica un cuatrifolio con una longitud de pétalo de 5 unidades, la ecuación especifica una rosa de 5 pétalos con una longitud de pétalo de 3 unidades. etc.
