Unité imaginaire- un nombre complexe dont le carré est égal à moins un.
En mathématiques et en physique, l'unité imaginaire est désignée par le latin je ou j. Il permet d'étendre le domaine des nombres réels au domaine des nombres complexes. Définition précise dépend de la méthode de cette extension.
La principale raison de l’introduction de l’unité imaginaire est que tous les équation polynomiale F(X) = 0 avec des coefficients réels a des solutions dans le domaine des nombres réels. Par exemple, l'équation X 2 + 1 = 0 n’a pas de vraies racines. Cependant, si nous supposons que les racines sont des nombres complexes, alors cette équation, comme n'importe lequel une autre équation polynomiale a une solution.
L’affirmation selon laquelle l’unité imaginaire est la « racine carrée de −1 » n’est pas entièrement correcte, car −1 a deux valeurs arithmétiques racines carrées, dont l'un peut être désigné comme je, et l'autre comme - je.
Définition
Une unité imaginaire est un nombre dont le carré est égal à −1. Ainsi je est la solution de l'équation
ou
Si l'on définit je Ainsi, nous la considérerons comme une variable inconnue (« imaginaire », « imaginaire »), alors la deuxième solution de l'équation sera - je, qui peut être vérifié par substitution.
Qui l'a ouvert et quand : Le mathématicien italien Gerolamo Cardano, ami de Léonard de Vinci, en 1545.
Le nombre i ne peut pas être appelé une constante ni même un nombre réel. Les manuels le décrivent comme une quantité qui, une fois mise au carré, donne moins un. En d’autres termes, c’est le côté du carré d’aire négative. En réalité, cela n’arrive pas. Mais parfois, on peut aussi profiter de l’irréel.
L'histoire de la découverte de cette constante est la suivante. Le mathématicien Gerolamo Cardano, en résolvant des équations avec des cubes, a introduit l'unité imaginaire. Ce n'était qu'une astuce auxiliaire : il n'y avait pas de i dans les réponses finales : les résultats qui le contenaient étaient rejetés. Mais plus tard, après avoir examiné de plus près leurs « déchets », les mathématiciens ont essayé de les mettre à profit : multiplier et diviser nombres ordinaires par unité imaginaire, additionnez les résultats les uns aux autres et remplacez-les dans de nouvelles formules. C’est ainsi qu’est née la théorie des nombres complexes.
L’inconvénient est que le « réel » ne peut pas être comparé à « l’irréel » : cela ne fonctionnera pas de dire que le plus grand est une unité imaginaire ou 1. D’un autre côté, il ne reste pratiquement plus d’équations insolubles si vous utilisez des nombres complexes. Par conséquent, avec des calculs complexes, il est plus pratique de travailler avec eux et de « nettoyer » les réponses uniquement à la toute fin. Par exemple, pour déchiffrer une tomographie cérébrale, on ne peut pas se passer de i.
C’est exactement ainsi que les physiciens traitent les champs et les ondes. On peut même considérer qu’ils existent tous dans un espace complexe, et que ce que l’on voit n’est que l’ombre des processus « réels ». Mécanique quantique, où l’atome et la personne sont des ondes, rend cette interprétation encore plus convaincante.
Le nombre i permet de résumer les principales constantes et actions mathématiques en une seule formule. La formule ressemble à ceci : eπi+1 = 0, et certains disent qu'un tel ensemble condensé de règles mathématiques peut être envoyé aux extraterrestres pour les convaincre de notre intelligence.
Les expressions de la forme qui apparaissent lors de la résolution d'équations quadratiques et cubiques ont commencé à être appelées « imaginaires » dans XVIe-XVIIe siècles Cependant, même pour de nombreux scientifiques éminents du XVIIe siècle, l'essence algébrique et géométrique des quantités imaginaires semblait floue. Leibniz écrit par exemple : « L’Esprit de Dieu a trouvé l’exutoire le plus subtil dans ce miracle de l’analyse, monstre du monde des idées, essence double située entre l’être et le non-être, que nous appelons la racine imaginaire du négatif. unité."
Pendant longtemps, on ne savait pas si toutes les opérations sur des nombres complexes conduisaient à des résultats complexes ou si, par exemple, l'extraction d'une racine pouvait conduire à la découverte d'un nouveau type de nombres. Le problème de l'expression des racines des diplômes n depuis numéro donné a été résolu dans les travaux de Moivre (1707) et Cotes (1722).
Le symbole a été proposé par Euler (1777, publié en 1794), qui a pris pour cela la première lettre du mot latin. imaginaire. Il a tout répandu caractéristiques standards, y compris le logarithme, sur le domaine complexe. Euler a également exprimé l'idée en 1751 que le domaine des nombres complexes est algébriquement fermé. D'Alembert (1747) arrivait à la même conclusion, mais le premier preuve stricte Ce fait appartient à Gauss (1799). Gauss a introduit le terme « nombre complexe » dans un usage généralisé en 1831, bien que le terme ait déjà été utilisé dans le même sens. mathématicien français Lazare Carnot en 1803.
L'interprétation géométrique des nombres complexes et des opérations sur ceux-ci est apparue pour la première fois dans les travaux de Wessel (1799). Les premiers pas dans cette direction furent faits par Wallis (Angleterre) en 1685. Moderne représentation géométrique, parfois appelé « diagramme d’Argand », est devenu utilisé après la publication en 1806 et 1814 des travaux de J. R. Argand, qui répétait indépendamment les conclusions de Wessel.
Modèle arithmétique de nombres complexes par paires nombres réels a été construit par Hamilton (1837); cela prouvait la cohérence de leurs propriétés. Hamilton a également proposé une généralisation des nombres complexes - les quaternions, dont l'algèbre est non commutative.
Considérons l'équation quadratique incomplète :
X 2 = un,
Où UN est une quantité connue. La solution de cette équation peut s’écrire :
Il y a trois cas possibles ici :
| 1). | Si une = 0, alors X = 0. |
| 2). | Si UN – nombre positif, alors sa racine carrée a deux valeurs : l'une positive, l'autre négative ; par exemple l'équation X 2 = 25 a deux racines : 5 et – 5. Ceci s'écrit souvent sous forme de racine avec un double signe : |
| 3). | Si UN est un nombre négatif, alors cette équation n'a pas de solution parmi les nombres positifs et négatifs que nous connaissons, car la puissance seconde de tout nombre est le nombre non négatif. Mais si l'on veut obtenir des solutions à l'équation X 2 = un aussi pour valeurs négatives UN, nous sommes obligés d'introduire des nombres d'un nouveau type - nombres imaginaires . Ainsi, imaginaire le numéro est appelé dont la puissance seconde est un nombre négatif. Selon cette définition des nombres imaginaires, nous pouvons définir et imaginaire unité: |
Alors pour l'équation X 2 = – 25 on en obtient deux imaginaire racine:
En substituant ces deux racines dans notre équation, nous obtenons l'identité. Contrairement aux nombres imaginaires, tous les autres nombres (positifs et négatifs, entiers et fractions, rationnels et irrationnels) sont appelés valide ou nombres réels . La somme d'un nombre réel et d'un nombre imaginaire s'appelle nombre complexe et est désigné :
une + b je ,
Où un B- nombres réels, je– unité imaginaire.
Pour plus d'informations sur les nombres complexes, consultez la section sur les nombres complexes.
Exemples de nombres complexes : 3 + 4 je, 7 – 13.6 je , 0 + 25 je = 25 je , 2 + je.
Pouvoirs d'une unité imaginaire
Degrés je répété en boucle :
Qui peut s’écrire pour n’importe quel diplôme sous la forme :
Où n- n'importe quel entier.
D'ici:
Où module 4 représente le reste lorsqu'il est divisé par 4.
La raison pour laquelle on introduit une unité imaginaire est que toutes les équations polynomiales ne avec des coefficients réels a des solutions dans le domaine des nombres réels. Donc l'équation n'a pas de véritables racines. Cependant, il s’avère que toute équation polynomiale à coefficients complexes a solution globale- "Théorème fondamental de l'algèbre."
Historiquement, l'unité imaginaire a été introduite pour la première fois pour résoudre l'équation cubique réelle : souvent, s'il y avait trois racines réelles, pour en obtenir deux, la formule de Cardano nécessitait de prendre la racine cubique des nombres complexes.
L’affirmation selon laquelle l’unité imaginaire est la « racine carrée de −1 » n’est pas précise : après tout, « −1 » a deux racines carrées, dont l’une peut être désignée par « i » et l’autre par « -i ». Peu importe quelle racine est prise comme unité imaginaire : toutes les égalités resteront valables si tous les « i » sont simultanément remplacés par « -i » et « -i » par « i ». Cependant, en raison de cette ambiguïté, afin d'éviter des calculs erronés, il ne faut pas utiliser la notation pour à travers le radical (comme ).
Définition
Une unité imaginaire est un nombre dont le carré vaut −1. Ceux. est l'une des solutions de l'équation
ou
Et puis sa deuxième solution à l’équation sera , ce qui est vérifié par substitution.
Pouvoirs d'une unité imaginaire
Degrés répété en boucle :
Qui peut s’écrire pour n’importe quel diplôme sous la forme :
Où n- n'importe quel entier.
D'ici: Où module 4 est le reste lorsqu'il est divisé par 4.
Nombre est vrai:
Factorielle
Factorielle d'unité imaginaire je peut être défini comme la valeur de la fonction gamma à partir de l'argument 1 + je :
Racines de l'unité imaginaire
Dans le domaine des nombres complexes, la racine n a n les décisions. Sur plan complexe les racines de l'unité imaginaire sont aux sommets d'un n-gone régulier inscrit dans un cercle de rayon unité.
Cela découle de la formule de Moivre et du fait que l'unité imaginaire peut être représentée dans forme trigonométrique:
En particulier, Et
De plus, les racines d'une unité imaginaire peuvent être représentées sous forme exponentielle :
Autres unités imaginaires
Dans la construction de Cayley-Dixon (ou dans les algèbres de Clifford), il peut y avoir plusieurs « unités d'expansion imaginaires », et/ou leur carré peut être ="+1" ou même ="0". Mais dans ce cas, des diviseurs nuls peuvent apparaître, et il existe d'autres propriétés qui diffèrent des propriétés du complexe « i ». Par exemple, il y a trois unités imaginaires anticommutatives dans le corps du quaternion, et il existe également une infinité de solutions à l'équation " ».
Sur la question de l'interprétation et du nom
| Gauss a également fait valoir que si les quantités 1, −1 et √−1 étaient appelées respectivement non pas des unités positives, négatives et imaginaires, mais directes, inverses et secondaires, alors les gens n'auraient pas l'impression qu'il existe une sorte de lien avec ces chiffres. secret sombre. Selon Gauss, la représentation géométrique donne sous un jour nouveau la véritable métaphysique des nombres imaginaires. C’est Gauss qui a introduit le terme « nombres complexes » (par opposition aux « nombres imaginaires » de Descartes) et a utilisé le symbole i pour désigner √−1. Maurice Kline, Mathématiques. Perte de certitude." Chapitre VII. Développement illogique : difficultés sérieuses au seuil du XIXe siècle. |
Désignations
Désignation commune , mais en ingénierie radio, l'unité imaginaire est généralement notée pour ne pas être confondu avec la désignation de courant instantané : .
Voir également
- Numéros doubles et numéros doubles
Donnez votre avis sur l'article "Unité imaginaire"
Remarques
Liens
- Unité imaginaire // Grande Encyclopédie Soviétique : [en 30 volumes] / ch. éd. A.M. Prokhorov. - 3e éd. -M. : Encyclopédie soviétique, 1969-1978.
|
||||||||||||||||||||||||||
Extrait caractérisant l'Unité Imaginaire
Plusieurs marchands se pressaient autour de l'officier.- Euh ! c'est une perte de temps de mentir ! - dit l'un d'eux, mince, au visage sévère. "Quand tu t'enlèves la tête, tu ne pleures pas sur tes cheveux." Prenez ce que vous voulez ! « Et il a agité la main d’un geste énergique et s’est tourné de côté vers l’officier.
"C'est bien pour toi, Ivan Sidorich, de parler", dit avec colère le premier marchand. - De rien, votre honneur.
- Qu'est-ce que je devrais dire! – cria l’homme maigre. "J'ai cent mille marchandises dans trois magasins ici." Pourrez-vous le sauver lorsque l’armée sera partie ? Eh, les gens, La puissance de Dieu ne le pliez pas avec vos mains !
"S'il vous plaît, votre honneur", dit le premier marchand en s'inclinant. L'officier était perplexe et l'indécision était visible sur son visage.
- De quoi me soucier! - il a soudainement crié et a marché à pas rapides le long de la rangée. Dans un magasin ouvert, des coups et des injures ont été entendus, et tandis que l'officier s'en approchait, un homme en pardessus gris et au crâne rasé a sauté par la porte.
Cet homme, penché, se précipita devant les marchands et l'officier. L'officier a attaqué les soldats qui se trouvaient dans le magasin. Mais à ce moment-là, des cris terribles d'une foule immense se sont fait entendre sur le pont Moskvoretsky et l'officier a couru sur la place.
- Ce qui s'est passé? Ce qui s'est passé? - demanda-t-il, mais son camarade galopait déjà vers les cris, devant Saint-Basile le Bienheureux. L'officier monta à cheval et le suivit. Lorsqu'il s'approcha du pont, il vit deux canons retirés des ailes, de l'infanterie marchant le long du pont, plusieurs charrettes tombées, plusieurs visages effrayés et les visages rieurs des soldats. Près des canons se trouvait une charrette tirée par deux. Derrière la charrette, quatre lévriers en collier se blottissaient derrière les roues. Il y avait une montagne de choses sur le chariot, et tout en haut, à côté de la chaise pour enfants, une femme était assise, les jambes renversées, criant de façon stridente et désespérée. Les camarades ont déclaré à l'officier que les cris de la foule et les cris de la femme étaient dus au fait que le général Ermolov, qui s'était précipité dans cette foule, ayant appris que les soldats se dispersaient parmi les magasins et que des foules d'habitants bloquaient le pont, avait ordonné de tirer. être retiré des ailes et un exemple a été donné selon lequel il tirerait sur le pont. La foule, renversant les charrettes, s'écrasant les unes les autres, criant désespérément, se pressant, dégagea le pont et les troupes avancèrent.
Pendant ce temps, la ville elle-même était vide. Il n'y avait presque personne dans les rues. Les portes et les magasins étaient tous fermés à clé ; çà et là, près des tavernes, des cris solitaires ou des chants ivres se faisaient entendre. Personne ne circulait dans les rues et les pas des piétons étaient rarement entendus. Sur Povarskaya, c'était complètement calme et désert. Dans l'immense cour de la maison des Rostov, il y avait des restes de foin et des crottes d'un train de transport, et personne n'était visible. Dans la maison de Rostov, laissée avec toutes ses bonnes choses, deux personnes se trouvaient dans le grand salon. Il s’agissait du concierge Ignat et du cosaque Mishka, petit-fils de Vasilitch, resté à Moscou avec son grand-père. Mishka ouvrit le clavicorde et en joua avec un doigt. Le concierge, les bras sur les hanches et souriant joyeusement, se tenait devant un grand miroir.
- C'est malin! UN? Oncle Ignat ! - dit le garçon en commençant soudain à taper sur les clés avec les deux mains.
- Regarder! - répondit Ignat, émerveillé par la façon dont son visage souriait de plus en plus dans le miroir.
- Sans vergogne ! Vraiment, sans vergogne ! – la voix de Mavra Kuzminishna, qui est entrée tranquillement, a parlé derrière eux. - Eka, aux cornes épaisses, il montre les dents. Allez-y! Tout là-bas n'est pas bien rangé, Vasilich est renversé. Lui donner le temps!
Ignat, ajustant sa ceinture, cessa de sourire et baissa docilement les yeux, sortit de la pièce.
«Tante, je vais y aller doucement», dit le garçon.
- Je vais t'en donner un léger. Petit tireur ! – a crié Mavra Kuzminishna en levant la main vers lui. - Allez installer un samovar pour grand-père.
Mavra Kuzminishna, époussetant la poussière, ferma le clavicorde et, soupirant lourdement, quitta le salon et verrouilla la porte d'entrée.
En sortant dans la cour, Mavra Kuzminishna réfléchit à l'endroit où elle devrait aller maintenant : devrait-elle boire du thé dans la dépendance de Vasilich ou ranger ce qui n'avait pas encore été rangé dans le garde-manger ?
Des pas rapides se firent entendre dans la rue calme. Les pas s'arrêtèrent à la porte ; le loquet commença à cogner sous la main qui essayait de l'ouvrir.
Mavra Kuzminishna s'est approchée de la porte.
- Qui avez-vous besoin?
- Comte, comte Ilya Andreich Rostov.
- Qui es-tu?
- Je suis officier. "J'aimerais voir", dit la voix russe agréable et seigneuriale.
Mavra Kuzminishna a déverrouillé la porte. Et un officier au visage rond, âgé d'environ dix-huit ans, avec un visage semblable à celui des Rostov, entra dans la cour.
- Nous sommes partis, père. "Nous avons daigné partir hier aux vêpres", dit affectueusement Mavra Kuzmipishna.
Le jeune officier, debout à la porte, comme s'il hésitait à entrer ou à ne pas entrer, claqua la langue.
"Oh, quel dommage !..." dit-il. - J'aurais aimé l'avoir hier... Oh, quel dommage !..
Mavra Kuzminishna, quant à elle, a examiné avec soin et sympathie les traits familiers de la race Rostov sur le visage. un jeune homme, et le pardessus en lambeaux, et les bottes usées qu'il portait.
- Pourquoi aviez-vous besoin d'un décompte ? - elle a demandé.
- Ouais... que faire ! - dit l'officier avec agacement et attrapa le portail, comme s'il avait l'intention de partir. Il s'arrêta encore, indécis.
- Est-ce que tu vois? - dit-il soudain. "Je suis un parent du comte, et il a toujours été très gentil avec moi." Alors, voyez-vous (il regardait son manteau et ses bottes avec un sourire gentil et joyeux), et il était épuisé, et il n'y avait pas d'argent ; alors je voulais demander au Comte...
Mavra Kuzminishna ne l'a pas laissé finir.
Unité imaginaire- généralement un nombre complexe dont le carré est égal à −1 (moins un). Cependant, d'autres options sont également possibles : dans la construction du doublement selon Cayley-Dixon ou dans le cadre de l'algèbre selon Clifford.
Pour les nombres complexes
En mathématiques et en physique, l'unité imaginaire est désignée par le latin texvc ou Impossible d'analyser l'expression (fichier exécutable texvc . Il permet d'étendre le domaine des nombres réels au domaine des nombres complexes. La définition exacte dépend de la méthode d'extension.
La raison pour laquelle on introduit une unité imaginaire est que toutes les équations polynomiales ne Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour obtenir de l'aide sur la configuration.) : f(x)=0 avec des coefficients réels a des solutions dans le domaine des nombres réels. Donc l'équation Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour l'aide à la configuration.) : x^2 + 1 = 0 n'a pas de véritables racines. Cependant, il s'avère que toute équation polynomiale avec des coefficients complexes a une solution complexe - le « Théorème fondamental de l'algèbre ».
Historiquement, l'unité imaginaire a été introduite pour la première fois pour résoudre l'équation cubique réelle : souvent, s'il y avait trois racines réelles, pour en obtenir deux, la formule de Cardano nécessitait de prendre la racine cubique des nombres complexes.
L’affirmation selon laquelle l’unité imaginaire est la « racine carrée de −1 » n’est pas précise : après tout, « −1 » a deux racines carrées, dont l’une peut être désignée par « i » et l’autre par « -i ». Peu importe quelle racine est prise comme unité imaginaire : toutes les égalités resteront valables si tous les « i » sont simultanément remplacés par « -i » et « -i » par « i ». Cependant, en raison de cette ambiguïté, afin d'éviter des calculs erronés, il ne faut pas utiliser la notation pour Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour l'aide à la configuration.) : ià travers le radical (comme Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour l'aide à la configuration.) : \sqrt(-1)).
Définition
Une unité imaginaire est un nombre dont le carré vaut −1. Ceux. Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour l'aide à la configuration.) : i est l'une des solutions de l'équation
texvc pas trouvé; Voir math/README - aide à la configuration.) : x^2 + 1 = 0, ou Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour obtenir de l'aide sur la configuration.) : x^2 = -1.
Et puis sa deuxième solution à l’équation sera Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour l'aide à la configuration.) : -i, ce qui est vérifié par substitution.
Pouvoirs d'une unité imaginaire
Degrés Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour l'aide à la configuration.) : i répété en boucle :
texvc
Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour obtenir de l'aide sur la configuration.) : i^(-3) = i
Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour obtenir de l'aide sur la configuration.) : i^(-2) = -1
Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour l'aide à la configuration.) : i^(-1) = -i
Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README - aide à la configuration.) : i^0 = 1
Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour l'aide à la configuration.) : i^1 = i
Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README - aide à la configuration.) : i^2 = -1
Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour obtenir de l'aide sur la configuration.) : i^3 = -i
Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour obtenir de l'aide sur la configuration.) : i^4 = 1
Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour l'aide à la configuration.) : \ldots
Qui peut s’écrire pour n’importe quel diplôme sous la forme :
Impossible d'analyser l'expression (fichier exécutabletexvc pas trouvé; Voir math/README pour l'aide à la configuration.) : i^(4n) = 1
Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour obtenir de l'aide sur la configuration.) : i^(4n+1) = i
Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour obtenir de l'aide sur la configuration.) : i^(4n+2) = -1
Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour obtenir de l'aide sur la configuration.) : i^(4n+3) = -i.
Où n- n'importe quel entier.
D'ici: Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour l'aide à la configuration.) : i^n = i^(n \bmod 4) Où module 4 est le reste lorsqu'il est divisé par 4.
Nombre Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README - aide à la configuration.) : i^i est vrai:
texvc pas trouvé; Voir math/README - aide à la configuration.) : i^i=(e^((i\pi/2)i))=e^(i^2\pi/2)=e^(-\pi/ 2 )=0(,)20787957635\ldots
Factorielle
Factorielle d'unité imaginaire je peut être défini comme la valeur de la fonction gamma à partir de l'argument 1 + je :
Impossible d'analyser l'expression (fichier exécutabletexvc pas trouvé; Voir math/README pour l'aide à la configuration.) : i! = \Gamma(1+i) \environ 0,4980 - 0,1549i.
Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour l'aide à la configuration.) : |i!| = \sqrt(\pi \over \sinh(\pi)) \environ 0,521564... .
Racines de l'unité imaginaire
Dans le domaine des nombres complexes, la racine n a n les décisions. Dans le plan complexe, les racines de l'unité imaginaire sont situées aux sommets d'un n-gone régulier inscrit dans un cercle de rayon unité.
Impossible d'analyser l'expression (fichier exécutabletexvc pas trouvé; Voir math/README pour obtenir de l'aide sur la configuration.) : u_k=\cos (\frac((\frac(\pi)(2)) + 2\pi k)(n)) +i\ \sin (\frac( (\frac(\pi)(2)) + 2\pi k)(n)), \quad k=0,1,...,n-1
Cela découle de la formule de Moivre et du fait que l'unité imaginaire peut être représentée sous forme trigonométrique :
Impossible d'analyser l'expression (fichier exécutabletexvc pas trouvé; Voir math/README - aide à la configuration.) : i=\cos\ (\frac(\pi)(2)) + i\ \sin\ (\frac(\pi)(2))
En particulier, Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour obtenir de l'aide sur la configuration.) : \sqrt(i ) = \left\(\frac(1 + i)(\sqrt(2));\ \frac(-1 - i)(\sqrt( 2 )) \droite\) Et Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour l'aide à la configuration.) : \sqrt(i ) = \left\(-i;\ \frac(i + (\sqrt(3)))(2);\ \frac(i - ( \sqrt (3)))(2) \droite\)
De plus, les racines d'une unité imaginaire peuvent être représentées sous forme exponentielle :
Impossible d'analyser l'expression (fichier exécutabletexvc pas trouvé; Voir math/README - aide à la configuration.) : u_k=e^(\frac((\frac(\pi)(2) + 2\pi k) i)(n) ), \quad k=0,1 , ...,n-1
Autres unités imaginaires
Dans la construction de Cayley-Dixon (ou dans les algèbres de Clifford), il peut y avoir plusieurs « unités d'expansion imaginaires », et/ou leur carré peut être ="+1" ou même ="0". Mais dans ce cas, des diviseurs nuls peuvent apparaître, et il existe d'autres propriétés qui diffèrent des propriétés du complexe « i ». Par exemple, il y a trois unités imaginaires anticommutatives dans le corps du quaternion, et il existe également une infinité de solutions à l'équation " Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour l'aide à la configuration.) : x^2 = -1
».
Sur la question de l'interprétation et du nom
| Gauss a également fait valoir que si les quantités 1, −1 et √−1 étaient appelées respectivement non pas des unités positives, négatives et imaginaires, mais directes, inverses et secondaires, alors les gens n'auraient pas l'impression qu'une sorte de chose sombre est associée avec ces chiffres secrets. Selon Gauss, la représentation géométrique donne sous un jour nouveau la véritable métaphysique des nombres imaginaires. C’est Gauss qui a introduit le terme « nombres complexes » (par opposition aux « nombres imaginaires » de Descartes) et a utilisé le symbole i pour désigner √−1. Maurice Kline, Mathématiques. Perte de certitude." Chapitre VII. Développement illogique : difficultés sérieuses au seuil du XIXe siècle. |
Désignations
Désignation commune Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour l'aide à la configuration.) : i, mais en ingénierie radio, l'unité imaginaire est généralement notée Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour l'aide à la configuration.) : j pour ne pas être confondu avec la désignation de courant instantané : Impossible d'analyser l'expression (fichier exécutable texvc pas trouvé; Voir math/README pour l'aide à la configuration.) : i = i (t)
.
Voir également
- Numéros doubles et numéros doubles
Donnez votre avis sur l'article "Unité imaginaire"
Remarques
Liens
- Unité imaginaire // Grande Encyclopédie Soviétique : [en 30 volumes] / ch. éd. A.M. Prokhorov. - 3e éd. -M. : Encyclopédie soviétique, 1969-1978.
|
||||||||||||||||||||||||||
Extrait caractérisant l'Unité Imaginaire
– Cela ne s’enseigne pas, Isidora. Les gens doivent avoir un besoin de Lumière, un besoin de Bien. Eux-mêmes doivent vouloir le changement. Pour ce qui est donné par la force, une personne essaie instinctivement de le rejeter rapidement, sans même essayer de comprendre quoi que ce soit. Mais nous nous éloignons du sujet, Isidora. Voulez-vous que je continue l'histoire de Radomir et Magdalena ?J'ai hoché la tête affirmativement, regrettant profondément dans mon cœur de ne pas pouvoir avoir une conversation avec lui aussi simplement et calmement, sans me soucier de ce que le destin m'avait donné. dernières minutes ma vie infirme et sans penser avec horreur au malheur qui pèse sur Anna...
– La Bible écrit beaucoup sur Jean-Baptiste. Était-il vraiment avec Radomir et les Chevaliers du Temple ? Son image est si étonnamment belle qu'elle fait parfois douter que John soit le vrai personnage ? Pouvez-vous répondre, Nord ?
North sourit chaleureusement, se souvenant apparemment de quelque chose de très agréable et cher pour lui...
– John était sage et gentil, comme un grand soleil chaud... Il était le père de tous ceux qui marchaient avec lui, leur professeur et ami... Il était valorisé, obéi et aimé. Mais il n’a jamais été le jeune et incroyablement beau jeune homme sous lequel les artistes le peignaient habituellement. John à cette époque était déjà un sorcier âgé, mais toujours très fort et persistant. Aux cheveux gris et grand, il ressemblait plus à un puissant guerrier épique qu'à un jeune homme incroyablement beau et doux. Il portait très cheveux longs, ainsi que tous ceux qui sont avec Radomir.
C'était Radan, il était vraiment extraordinairement beau. Comme Radomir, il a vécu aux Météores dès son plus jeune âge, aux côtés de sa mère, la sorcière Maria. Rappelez-vous, Isidora, combien de tableaux il y a dans lesquels Marie est peinte avec deux bébés, presque du même âge. Pour une raison quelconque, tous les artistes célèbres les ont peints, peut-être même sans comprendre QUI leur pinceau représentait réellement... Et ce qui est le plus intéressant, c'est que c'est Radan que Maria regarde dans toutes ces peintures. Apparemment, même alors, alors qu'il était encore bébé, Radan était déjà aussi joyeux et attirant qu'il l'est resté tout au long de sa courte vie...
Et pourtant... même si les artistes représentaient Jean dans ces tableaux, comment ce même Jean aurait-il pu vieillir si monstrueusement au moment de son exécution, réalisée à la demande de la capricieuse Salomé ?.. Après tout, selon le Bible, cela s'est produit avant même la crucifixion du Christ, ce qui signifie que Jean n'aurait pas dû avoir plus de trente ans à cette époque quatre années! Comment est-il passé d’un beau jeune homme aux cheveux dorés à un vieux juif complètement peu attrayant ?!
- Alors le Mage John n'est pas mort, Sever ? – ai-je demandé avec joie. – Ou est-il mort d’une autre manière ?..
«Malheureusement, le vrai John a vraiment eu la tête coupée, Isidora, mais cela ne s'est pas produit à cause de la mauvaise volonté d'une femme gâtée capricieuse. La cause de sa mort était la trahison d'un « ami » juif en qui il avait confiance et dans la maison duquel il a vécu plusieurs années...
- Mais comment se fait-il qu'il ne l'ait pas ressenti ? Comment n’avez-vous pas vu quel genre d’« ami » il s’agissait ?! – J'étais indigné.
– Il est probablement impossible de soupçonner tout le monde, Isidora... Je pense que c'était déjà assez difficile pour eux de faire confiance à quelqu'un, car ils ont tous dû d'une manière ou d'une autre s'adapter et vivre dans ce pays étranger et inconnu, ne l'oubliez pas. Parce que, du grand et moindre mal ils ont apparemment essayé de choisir moins. Mais il est impossible de tout prévoir, tu le sais très bien, Isidora... La mort du Mage Jean est survenue après la crucifixion de Radomir. Il a été empoisonné par un Juif, dans la maison duquel Jean vivait à cette époque avec la famille de Jésus décédé. Un soir, alors que toute la maison dormait déjà, le propriétaire, discutant avec John, lui présenta son thé préféré mélangé à un puissant poison végétal... Le lendemain matin, personne n'était même capable de comprendre ce qui s'était passé. Selon le propriétaire, John s'est simplement endormi instantanément et ne s'est plus jamais réveillé... Son corps a été retrouvé le matin dans son lit ensanglanté avec... une tête coupée... Selon le même propriétaire, les Juifs étaient très Ils avaient peur de John, car ils le considéraient comme un magicien inégalé. Et pour être sûr qu'il ne se relèverait plus, ils le décapitèrent. La tête de Jean leur fut ensuite achetée (!!!) et emportée avec eux par les Chevaliers du Temple, parvenant à la conserver et à l'amener à la Vallée des Mages, afin de donner ainsi à Jean au moins un si petit, mais respect digne et mérité, sans permettre aux Juifs de simplement se moquer de lui, en faisant rituels magiques. À partir de ce moment-là, la tête de John était toujours avec eux, où qu'ils soient. Et pour ce même chef, deux cents ans plus tard, les Chevaliers du Temple furent accusés de culte criminel du Diable... Tu te souviens du dernier « cas des Templiers » (Chevaliers du Temple), n'est-ce pas, Isidora ? C'est là qu'ils furent accusés d'adorer une « tête parlante », ce qui exaspéra tout le clergé de l'église.
- Pardonnez-moi, Sever, mais pourquoi les Chevaliers du Temple n'ont-ils pas apporté la tête de Jean ici aux Météores ? Parce que, d'après ce que j'ai compris, vous l'aimiez tous beaucoup ! Et comment connaissez-vous tous ces détails ? Vous n'étiez pas avec eux, n'est-ce pas ? Qui t'a dit tout ça ?
- Nous a dit tout ça histoire triste Sorcière Maria, mère de Radan et Radomir...
– Marie est-elle revenue vers vous après l'exécution de Jésus ?!.. Après tout, autant que je sache, elle était avec son fils lors de la crucifixion. Quand est-elle revenue vers vous ? Est-il possible qu'elle soit encore en vie ?.. – ai-je demandé en retenant mon souffle.
Sujet: Unité imaginaire , son degrés. Complexe Nombres.
Algébrique formulaire complet Nombres.
Objectifs:élargir la notion de nombre, introduire la notion d'unité imaginaire et ses pouvoirs, la notion nombre complexe; considérons la forme algébrique d'un nombre complexe ; développer la capacité de généraliser les connaissances acquises, favoriser le développement;
pensée logique éduquer les étudiants attitude consciente
au processus d’apprentissage. ( Plan )
questions à l'étude
Définition d'un nombre complexe.
Forme algébrique nombre complexe.
1.Nombres imaginaires
Définition. Un nombre dont le carré est -1 est appelé unité imaginaire et
désigné par і ; і 2 = -1
Définition. Nombres qui ont la forme b і , où b est un nombre réel, sont appelés
nombres imaginaires.
Par exemple:
On sait que les nombres réels sont représentés par des points sur l'axe OX. Les nombres imaginaires sont représentés par des points sur l'axe OU, et donc l'axe OX est appelé axe réel, et l'axe OU est l'axe imaginaire. L’ensemble des nombres imaginaires est en correspondance bijective avec l’ensemble des nombres réels.
Définition. Deux nombres imaginaires b 1 je Et b 2 je sont dits égaux si b 1 = b 2
Définition. Nombre imaginaire (- bi ) appelé le contraire d'un nombre imaginaire b і .
Par exemple:
 Et
Et

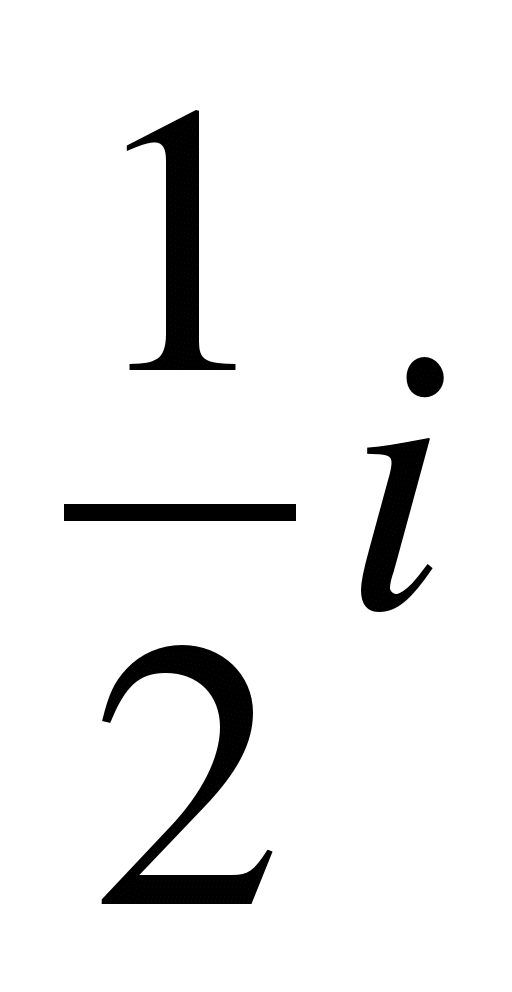 Et
Et  .
.
Théorème. Toute puissance naturelle d'un nombre і peut être converti en
un des quatre types 1; і ; -1; -і.
Preuve .
Considérons l'expression і m , où m - entier naturel. Il est clair que quatre cas sont possibles :
1) m = 4 k , k =1,2, ...
2) m=4k +1, k =0, 1,2,...
3) m 4k +2, k = 0,1,2,...
4) m = 4k +3, k =0,1,2, ....
Laisser m = 4 k , Alors і m =і Ak =(і UN ) À =1 À =1
Laisserm =4 k +1, Alors і m = і Ak+1 = і Ak je = 1 je = je
Laisser m = 4 k +2, Alorsі m =і Ak+2 = і Ak і 2 = 1(-1)=-1
Laisserm =4 k +3, Alors і m
Exemple. Calculer la valeur d'une expression
Solution:
Commentaire. Afin de calculer la puissance d'une unité imaginaire, il convient d'utiliser la règle suivante :
1) diviser l'exposant par 4 ;
2) remplacer je m sur moi R. , où p est le reste obtenu en divisant t par 4, c'est-à-dire que le nombre p est trouvé à partir de l'égalité t = 4k + p.
2. Nombres complexes
Définition. Un nombre complexe est un nombre qui a la formea+bi , où une, b –
nombres réels, i est l'unité imaginaire. Dans ce cas, le nombre « a » est appelé
partie réelle d'un nombre complexe, "b" - partie imaginaire
nombre complexe.
Symboliquement, les parties réelle et imaginaire d'un nombre complexe sont notées comme suit :(réinitialiser), (ils ne le font pas).
Ces désignations sont basées sur les premières lettres Mots latins, qui signifie « réel » et « Imaginaires », qui signifie « imaginaire ».
Commentaire. Parfois la partie imaginaire d'un nombre complexez = UN + b і appelé bi.
Définition. Deux nombres complexesZ 1 = un 1 + b 1 je Etz 2 = UN 2 + b 1 je sont dits égaux si
Concernantz 1 =Réz 2 , Je suisz 1 = Je suisz 2 .
Pour les nombres complexes, il n’existe pas de concepts de plus ou moins, c’est-à-dire que les nombres complexes ne sont pas comparables.
Définition. Nombre complexe(-UN- bi ) appelé l'opposé d'un nombre complexe
a + b.
Définition. Deux nombres complexes dont les parties réelles sont égales et dont les parties imaginaires sont égales
les piècesles opposés sont appelés nombres conjugués complexes et
sont désignés en conséquence Et.
3. Forme algébrique d'un nombre complexe. Actions sur des nombres complexes données sous forme algébrique.
Nombre complexe représenté par  appelé un nombre complexe dansforme algébrique
.
appelé un nombre complexe dansforme algébrique
.
Ajout de nombres complexes
Définition.
La somme de deux nombres complexes  Et
Et  appelé
appelé
nombre complexe .
Số 1)
Ainsi, pour additionner deux nombres complexes, il faut additionner leurs parties réelles, ce qui donne la partie réelle de la somme, et additionner les parties imaginaires, ce qui donne la partie imaginaire de la somme.
La somme des nombres conjugués est toujours réelle le numéro
c'est,  . (2)
. (2)
Soustraire des nombres complexes
Définition.
La différence de deux nombres complexes  Et
Et  c'est appelé
c'est appelé
nombre complexe  , ce qui donne le nombre
, ce qui donne le nombre  donne un numéro
donne un numéro  .
.
Soustraire des nombres complexes est toujours possible.
Théorème.
Pour tout nombre complexe  Et
Et  il y a toujours une différence
il y a toujours une différence  , qui est déterminé de manière unique.
, qui est déterminé de manière unique.
Ainsi, pour soustraire des nombres complexes, il suffit de soustraire leurs parties réelles et de prendre leur différence comme partie réelle de la différence, et également de soustraire la partie imaginaire de la différence
Il s'avère que (3)
La différence entre deux nombres conjugués est toujours un nombre imaginaire. ,
c'est,  (4)
(4)
Multiplier des nombres complexes
Définition.
Produit de deux nombres complexes
 et un tel nombre complexe est appelé, qui est déterminé par la formule : (5)
et un tel nombre complexe est appelé, qui est déterminé par la formule : (5)
Pour multiplier des nombres complexes, vous devez les multiplier selon la règle de multiplication des polynômes, en remplaçant  par -1 et amène des termes similaires.
par -1 et amène des termes similaires.
Lors de la multiplication de nombres complexes, il est préférable d'effectuer une multiplication directe. Le produit de nombres conjugués est toujours nombre réel Répondre.
1.Donnez la définition d’un nombre complexe.
2.Formuler la définition d'une unité imaginaire.
3. Comment trouver le degré d'une unité imaginaire.
4.Quels nombres complexes sont appelés égaux et conjugués ?
5.Écrivez une formule pour trouver une puissance arbitraire d’une unité imaginaire.
6. Donnez des exemples de nombres purement imaginaires.
7. Définir la somme, le produit et le quotient de deux nombres complexes.
Littérature
Écrit, D. T. Notes de cours sur mathématiques supérieures: cours complet D.T. Écrit. – 9e éd. – M. : Iris-presse, 2009. 608 p. : ill. - (L'enseignement supérieur).
Lungu, K. N. Collection de problèmes en mathématiques supérieures. 1ère année / K. N. Lungu, D. T. Pismenny, S. N. Fedin, Yu. – 7e éd. – M. : Iris-press, 2008. 576 pp. : – (Enseignement supérieur).
Grigoriev V.P. Éléments de mathématiques supérieures : un manuel pour les étudiants. établissements prof. éducation / V.P. Grigoriev, Yu. A. Dubinsky. – 10e éd., effacée. – M. Centre d'édition « Académie », 2014. – 320 p.








