Įsivaizduojamas vienetas- kompleksinis skaičius, kurio kvadratas lygus neigiamam.
Matematikoje ir fizikoje įsivaizduojamas vienetas žymimas lotynų kalba i arba j. Tai leidžia išplėsti realiųjų skaičių lauką iki kompleksinių skaičių. Tikslus apibrėžimas priklauso nuo šio išplėtimo metodo.
Pagrindinė įsivaizduojamo vieneto įvedimo priežastis yra ta, kad ne kiekvienas daugianario lygtis f(x) = 0 su realiaisiais koeficientais turi sprendinius realiųjų skaičių srityje. Pavyzdžiui, lygtis x 2 + 1 = 0 neturi tikrų šaknų. Tačiau jei darysime prielaidą, kad šaknys yra kompleksiniai skaičiai, tada ši lygtis, pvz bet koks kita daugianario lygtis turi sprendimą.
Teiginys, kad įsivaizduojamas vienetas yra „–1 kvadratinė šaknis“, nėra visiškai teisingas, nes −1 turi dvi aritmetikas kvadratinės šaknys, iš kurių vienas gali būti nurodytas kaip i, o kitas kaip − i.
Apibrėžimas
Įsivaizduojamasis vienetas yra skaičius, kurio kvadratas lygus −1. Taigi i yra lygties sprendimas
arba
Jei apibrėžtume i Taigi, laikysime jį nežinomu („įsivaizduojamu“, „įsivaizduotu“) kintamuoju, tada antrasis lygties sprendimas bus − i, kurį galima patikrinti pakeičiant.
Kas atidarė ir kada: Italų matematikas Gerolamo Cardano, Leonardo da Vinci draugas, 1545 m.
Skaičius i negali būti vadinamas pastoviu ar net tikruoju skaičiumi. Vadovėliuose jis apibūdinamas kaip dydis, kurį paskaičiavus kvadratu, gaunamas minus vienas. Kitaip tariant, tai yra kvadrato pusė su neigiamu plotu. Realybėje taip nebūna. Tačiau kartais galite gauti naudos iš nerealaus.
Šios konstantos atradimo istorija yra tokia. Matematikas Gerolamo Cardano, spręsdamas lygtis kubeliais, pristatė įsivaizduojamą vienetą. Tai buvo tik pagalbinis triukas – galutiniuose atsakymuose nebuvo i: rezultatai, kuriuose jis buvo, buvo atmesti. Tačiau vėliau, atidžiau pažvelgę į jų „šiukšles“, matematikai bandė tai pritaikyti: dauginti ir dalyti. įprasti skaičiai vienam įsivaizduojamam vienetui, pridėkite rezultatus vienas prie kito ir pakeiskite juos naujomis formulėmis. Taip gimė kompleksinių skaičių teorija.
Neigiama yra tai, kad „tikrasis“ negali būti lyginamas su „nerealu“: negalima sakyti, kad didesnis yra įsivaizduojamas vienetas arba 1. Kita vertus, naudojant kompleksinius skaičius praktiškai nebelieka neišsprendžiamų lygčių. Todėl su sudėtingais skaičiavimais patogiau dirbti su jais ir tik pačioje pabaigoje „išvalyti“ atsakymus. Pavyzdžiui, norint iššifruoti smegenų tomogramą, neapsieisite be i.
Būtent taip fizikai traktuoja laukus ir bangas. Galime net manyti, kad jie visi egzistuoja sudėtingoje erdvėje, o tai, ką matome, yra tik „tikrųjų“ procesų šešėlis. Kvantinė mechanika, kur ir atomas, ir žmogus yra bangos, šis aiškinimas tampa dar įtikinamesnis.
Skaičius i leidžia apibendrinti pagrindines matematines konstantas ir veiksmus vienoje formulėje. Formulė atrodo taip: eπi+1 = 0, o kai kurie sako, kad toks sutrumpintas matematikos taisyklių rinkinys gali būti išsiųstas ateiviams, kad jie įtikintų mūsų intelektu.
Formos išraiškos, atsirandančios sprendžiant kvadratines ir kubines lygtis, pradėtos vadinti „įsivaizduojamomis“ m. XVI-XVII a, tačiau net daugeliui žymių XVII amžiaus mokslininkų įsivaizduojamų dydžių algebrinė ir geometrinė esmė atrodė neaiški. Pavyzdžiui, Leibnicas rašė: „Dievo Dvasia šiame analizės stebukle rado subtiliausią išeitį, pabaisą iš idėjų pasaulio, dvigubą esmę, esančią tarp būties ir nebūties, kurią vadiname įsivaizduojama negatyvo šaknimi. vienybė."
Ilgą laiką buvo neaišku, ar visos operacijos su kompleksiniais skaičiais veda prie sudėtingų rezultatų, ar, pavyzdžiui, ištraukus šaknį galima atrasti kažkokį naują skaičių tipą. Laipsnių šaknų išreiškimo problema n iš duotas numeris buvo išspręsta Moivre (1707) ir Cotes (1722) darbuose.
Simbolį pasiūlė Euleris (1777 m., paskelbtas 1794 m.), kuris tam paėmė pirmą lotyniško žodžio raidę. įsivaizduojamas. Jis išplatino viską standartinės funkcijos, įskaitant logaritmą, į sudėtingą sritį. Euleris taip pat išreiškė mintį 1751 m., kad kompleksinių skaičių laukas algebriškai uždaras. D'Alembertas (1747 m.) padarė tą pačią išvadą, bet pirmąją griežtas įrodymasŠis faktas priklauso Gausui (1799). Gaussas terminą „sudėtinis skaičius“ plačiai pradėjo vartoti 1831 m., nors anksčiau šis terminas buvo vartojamas ta pačia prasme. prancūzų matematikas Lazare Carnot 1803 m.
Geometrinė kompleksinių skaičių interpretacija ir operacijos su jais pirmą kartą pasirodė Wesselio darbe (1799). Pirmuosius žingsnius šia kryptimi žengė Wallis (Anglija) 1685 m. Modernus geometrinis vaizdas, kartais vadinamas „Argando diagrama“, pradėtas naudoti po to, kai 1806 ir 1814 m. buvo paskelbtas J. R. Argando darbas, kuris nepriklausomai pakartojo Wesselio išvadas.
Kompleksinių skaičių kaip porų aritmetinis modelis realūs skaičiai pastatė Hamiltonas (1837 m.); tai įrodė jų savybių nuoseklumą. Hamiltonas taip pat pasiūlė kompleksinių skaičių apibendrinimą – ketvirčius, kurių algebra yra nekomutacinė.
Apsvarstykite nepilną kvadratinę lygtį:
x 2 = a,
Kur A yra žinomas kiekis. Šios lygties sprendimas gali būti parašytas taip:
Čia yra trys galimi atvejai:
| 1). | Jeigu a = 0, tada x = 0. |
| 2). | Jeigu A – teigiamas skaičius, tada jo kvadratinė šaknis turi dvi reikšmes: vieną teigiamą, kitą neigiamą; pavyzdžiui, lygtis x 2 = 25 turi dvi šaknis: 5 ir – 5. Tai dažnai rašoma kaip šaknis su dvigubu ženklu: |
| 3). | Jeigu A yra neigiamas skaičius, tada ši lygtis neturi mums žinomų teigiamų ir neigiamų skaičių sprendinių, nes bet kurio skaičiaus antroji laipsnis yra skaičius ne neigiamas. Bet jei norime gauti lygties sprendinius x 2 = a taip pat už neigiamos reikšmės A, esame priversti įvesti naujo tipo numerius - menami skaičiai . Taigi, įsivaizduojamas paskambino numeriu kurio antrasis laipsnis yra neigiamas skaičius. Pagal šį įsivaizduojamų skaičių apibrėžimą galime apibrėžti ir įsivaizduojamas vienetas: |
Tada už lygtį x 2 = – 25 gauname du įsivaizduojamasšaknis:
Pakeitę abi šias šaknis į mūsų lygtį, gauname tapatybę. Skirtingai nuo įsivaizduojamų skaičių, visi kiti skaičiai (teigiami ir neigiami, sveikieji skaičiai ir trupmenos, racionalieji ir neracionalieji) vadinami galioja arba realūs skaičiai . Vadinama tikrojo ir menamo skaičiaus suma kompleksinis skaičius ir yra nurodyta:
a + b i,
Kur a, b– realūs skaičiai, i– įsivaizduojamas vienetas.
Daugiau informacijos apie kompleksinius skaičius rasite skyriuje „Sudėtiniai skaičiai“.
Kompleksinių skaičių pavyzdžiai: 3 + 4 i, 7 – 13.6 i , 0 + 25 i = 25 i , 2 + i.
Menamo vieneto galios
Laipsniai i kartojama cikle:
Kuris gali būti parašytas bet kokiam laipsniui tokia forma:
Kur n- bet koks sveikasis skaičius.
Iš čia:
Kur 4 modas reiškia likutį, padalijus iš 4.
Įsivaizduojamo vieneto įvedimo priežastis yra ta, kad ne kiekviena daugianario lygtis su realiaisiais koeficientais turi sprendinius realiųjų skaičių srityje. Taigi, lygtis neturi tikrų šaknų. Tačiau paaiškėja, kad bet kuri daugianario lygtis su sudėtingais koeficientais turi kompleksinis sprendimas- „Pagrindinė algebros teorema“.
Istoriškai įsivaizduojamas vienetas pirmą kartą buvo įvestas sprendžiant tikrąją kubinę lygtį: dažnai, jei buvo trys tikrosios šaknys, norint gauti dvi iš jų, pagal Cardano formulę reikėjo paimti kompleksinių skaičių kubo šaknį.
Teiginys, kad įsivaizduojamas vienetas yra „–1 kvadratinė šaknis“, nėra tikslus: juk „-1“ turi dvi kvadratines šaknis, iš kurių viena gali būti pažymėta „i“, o kita „-i“. Nesvarbu, kuri šaknis laikoma įsivaizduojamu vienetu: visos lygybės galios, jei visi „i“ vienu metu bus pakeisti „-i“, o „-i“ – „i“. Tačiau dėl šio neaiškumo, siekiant išvengti klaidingų skaičiavimų, nereikėtų naudoti žymėjimo per radikalą (kaip ).
Apibrėžimas
Įsivaizduojamasis vienetas yra skaičius, kurio kvadratas yra −1. Tie. yra vienas iš lygties sprendinių
arba
Ir tada jo antrasis lygties sprendimas bus , kuris patikrinamas pakeitimu.
Menamo vieneto galios
Laipsniai kartojama cikle:
Kuris gali būti parašytas bet kokiam laipsniui tokia forma:
Kur n- bet koks sveikasis skaičius.
Iš čia: Kur 4 modas yra dalybos iš 4 liekana.
Skaičius yra tikras:
Faktorinis
Įsivaizduojamasis vienetas faktorialas i gali būti apibrėžta kaip gama funkcijos reikšmė iš argumento 1 + i :
Įsivaizduojamo vieneto šaknys
Kompleksinių skaičių srityje šaknis n- turi laipsnį n sprendimus. Įjungta sudėtinga plokštumaįsivaizduojamo vieneto šaknys yra taisyklingo n kampo, įbrėžto į vienetinio spindulio apskritimą, viršūnėse.
Tai išplaukia iš Moivre formulės ir fakto, kad įsivaizduojamas vienetas gali būti pavaizduotas trigonometrinė forma:
Visų pirma, Ir
Be to, įsivaizduojamo vieneto šaknys gali būti pavaizduotos eksponentine forma:
Kiti įsivaizduojami vienetai
Cayley-Dixon konstrukcijoje (arba Clifford algebrose) gali būti keli „įsivaizduojami išplėtimo vienetai“ ir (arba) jų kvadratas gali būti ="+1" arba net ="0". Tačiau šiuo atveju gali atsirasti nulinių daliklių ir yra kitų savybių, kurios skiriasi nuo komplekso „i“ savybių. Pavyzdžiui, ketvirčio kūne yra trys antikomutaciniai įsivaizduojami vienetai, taip pat yra be galo daug lygties „ ».
Dėl aiškinimo ir pavadinimo klausimo
| Gaussas taip pat teigė, kad jei dydžiai 1, −1 ir √−1 būtų vadinami atitinkamai ne teigiamais, neigiamais ir įsivaizduojamais vienetais, o tiesioginiais, atvirkštiniais ir antriniais, žmonėms nesusidarytų įspūdis, kad yra koks nors ryšys su šiuos skaičius. tamsi paslaptis. Anot Gauso, geometrinis vaizdavimas tikroji įsivaizduojamų skaičių metafizika pateikia naujoje šviesoje. Būtent Gaussas įvedė terminą „sudėtiniai skaičiai“ (priešingai nei Dekarto „įsivaizduojami skaičiai“) ir panaudojo simbolį i √−1 žymėti. Maurice'as Kline'as, „Matematika. Tikrumo praradimas“. VII skyrius. Nelogiška raida: rimti sunkumai ant XIX amžiaus slenksčio. |
Pavadinimai
Bendras žymėjimas , tačiau radijo inžinerijoje dažniausiai žymimas menamasis vienetas kad nebūtų painiojama su momentinės srovės žymėjimu: .
Taip pat žr
- Dvigubi skaičiai ir dvigubi skaičiai
Parašykite apžvalgą apie straipsnį "Įsivaizduojamas vienetas"
Pastabos
Nuorodos
- Įsivaizduojamas vienetas // Didžioji tarybinė enciklopedija: [30 tomų] / sk. red. A. M. Prokhorovas. - 3 leidimas. – M. : Sovietinė enciklopedija, 1969-1978.
|
||||||||||||||||||||||||||
Ištrauka, apibūdinanti įsivaizduojamą vienetą
Prie pareigūno būriavosi keli prekeiviai.- Ech! tai laiko švaistymas meluoti! - pasakė vienas iš jų, lieknas, griežtu veidu. „Kai nusiimi galvą, neverki dėl plaukų“. Imk viską, kas tau patinka! „Ir jis energingu mostu mostelėjo ranka ir pasuko į pareigūną šonu.
„Gerai tau, Ivanai Sidorichai, kalbėti“, – piktai kalbėjo pirmasis pirklys. - Sveiki, jūsų garbė.
- Ką aš turėčiau pasakyti! – sušuko lieknas vyras. „Turiu šimtą tūkstančių prekių trijose čia esančiose parduotuvėse. Ar galite jį išsaugoti, kai nebebus kariuomenės? Ech, žmonės Dievo galia nelankstykite jo rankomis!
- Prašau, jūsų garbė, - nusilenkė pirmasis pirklys. Pareigūnas stovėjo sutrikęs, o jo veide matėsi neryžtingumas.
- Kas man rūpi! - staiga sušuko jis ir greitais žingsniais žengė į priekį palei eilę. Vienoje atviroje parduotuvėje pasigirdo smūgiai ir keiksmai, o pareigūnui artėjant prie jos pro duris iššoko pilku paltu apsirengęs ir skusta galva vyras.
Šis vyras, pasilenkęs, puolė pro prekeivius ir pareigūną. Pareigūnas užpuolė parduotuvėje buvusius karius. Tačiau tuo metu ant Moskvoreckio tilto pasigirdo baisūs didžiulės minios riksmai, o pareigūnas išbėgo į aikštę.
- Kas nutiko? Kas nutiko? - paklausė jis, bet jo bendražygis jau šuoliavo link riksmų, pro šv. Bazilijų palaimintąjį. Pareigūnas atsisėdo ir nuvažiavo paskui jį. Priėjęs prie tilto, pamatė dvi patrankas, išimtas iš slankiųjų, tiltu einančius pėstininkus, kelis nukritusius vežimus, kelis išsigandę veidai ir besijuokiantys kareivių veidai. Prie patrankų stovėjo vienas vežimas, kurį tempė pora. Už vežimo už ratų glaudėsi keturi kurtai antkakliais. Ant vežimėlio stovėjo kalnas daiktų, o pačiame viršuje, šalia vaikiškos kėdutės, sėdėjo aukštyn kojom moteris, šiurkščiai ir beviltiškai rėkė. Bendražygiai pareigūnui pasakojo, kad minios riksmas ir moters riksmas kilo dėl to, kad į šią minią įvažiavęs generolas Ermolovas, sužinojęs, kad kareiviai blaškosi tarp parduotuvių ir minios gyventojų blokuoja tiltą, įsakė ginklus. nuimti iš limberių ir buvo padarytas pavyzdys , kad jis šaudys į tiltą . Minia, nuvertusi vežimus, traiškydama viena kitą, beviltiškai rėkė, susigrūdo, nuvalė tiltą, o kariuomenė pajudėjo į priekį.
Tuo tarpu pats miestas buvo tuščias. Gatvėse beveik niekas nebuvo. Visi vartai ir parduotuvės buvo užrakinti; šen bei ten prie smuklių pasigirsdavo vieniši riksmai ar girtas dainavimas. Gatvėmis niekas nevažiavo, o pėsčiųjų žingsnius girdėjosi retai. Povarskajoje buvo visiškai tylu ir apleista. Didžiuliame Rostovų namo kieme buvo šieno likučiai ir transporto traukinio išmatos, nesimatė nei vieno žmogaus. Rostovo name, kuris buvo paliktas su visais gerais daiktais, didelėje svetainėje buvo du žmonės. Tai buvo sargas Ignatas ir kazokas Miška, Vasiličiaus anūkas, likęs Maskvoje su seneliu. Miška atidarė klavikordą ir grojo vienu pirštu. Prižiūrėtojas, išskėstomis rankomis ir džiaugsmingai šypsodamasis, stovėjo priešais didelį veidrodį.
- Tai protinga! A? Dėdė Ignatas! - pasakė berniukas, staiga pradėjęs abiem rankomis plakti klavišus.
- Žiūrėk! - atsakė Ignatas, stebėdamasis, kaip jo veidas vis labiau šypsosi veidrodyje.
- Begėdiškas! Tikrai, begėdiškas! – iš už nugaros pasigirdo tyliai įėjusios Mavros Kuzminishnos balsas. - Eka, storaragis, atkiša dantis. Priimk tave į tai! Ten viskas nesutvarkyta, Vasiličius numuštas nuo kojų. Duok tam laiko!
Ignatas, pasitaisęs diržą, nustojo šypsotis ir paklusniai nuleido akis, išėjo iš kambario.
- Teta, aš eisiu ramiai, - pasakė berniukas.
- Aš tau duosiu lengvą. Mažasis šaulys! – sušuko Mavra Kuzminishna, pakėlęs į jį ranką. - Eik ir pastatyk seneliui samovarą.
Mavra Kuzminishna, nuvalydamas dulkes, uždarė klavikordą ir sunkiai atsidusęs išėjo iš svetainės ir užrakino lauko duris.
Išeidama į kiemą Mavra Kuzminišna galvojo, kur dabar eiti: ar gerti arbatą Vasiličiaus ūkiniame pastate, ar sutvarkyti tai, kas dar nebuvo sutvarkyta sandėliuke?
Ramioje gatvėje pasigirdo greiti žingsniai. Žingsniai sustojo prie vartų; fiksatorius pradėjo belstis po ranka, kuri bandė ją atrakinti.
Mavra Kuzminishna priėjo prie vartų.
- Kam tau reikia?
- Grafas, grafas Ilja Andreichas Rostovas.
- Kas tu esi?
– Aš pareigūnas. „Norėčiau pamatyti“, – ištarė malonus ir valdingas rusų balsas.
Mavra Kuzminishna atrakino vartus. O į kiemą įžengė maždaug aštuoniolikos metų apvaliaveidis karininkas, kurio veidas panašus į rostovų.
- Išėjome, tėve. „Vakar nusiteikėme išvykti vakarienės metu“, – meiliai pasakė Mavra Kuzmipishna.
Jaunas pareigūnas, stovėdamas prie vartų, tarsi dvejodamas, ar įeiti, ar neįeiti, spragtelėjo liežuviu.
„Oi, kokia gėda!...“ – pasakė jis. - Norėčiau, kad vakar... Oi, kaip gaila!..
Tuo tarpu Mavra Kuzminishna atidžiai ir su užuojauta ištyrė pažįstamus Rostovo veislės veido bruožus. jaunas vyras, ir nuplyšusį paltą, ir dėvėtus batus, kuriuos jis avėjo.
- Kam tau reikėjo grafo? - ji paklausė.
- Taip... ką daryti! - susierzinęs tarė pareigūnas ir, lyg ketindamas išeiti, čiupo vartus. Jis vėl sustojo, neapsisprendęs.
- Matote? - staiga pasakė jis. „Esu grafo giminaitis ir jis visada man buvo labai malonus“. Taigi, matote (jis pažvelgė į savo apsiaustą ir batus maloniai ir linksmai šypsodamasis), buvo nuvalkiotas, o pinigų nebuvo; todėl norėjau paklausti grafo...
Mavra Kuzminishna neleido jam baigti.
Įsivaizduojamas vienetas- paprastai kompleksinis skaičius, kurio kvadratas lygus −1 (atėmus vieną). Tačiau galimi ir kiti variantai: konstruojant dvigubinimą pagal Cayley-Dixoną arba pagal algebrą pagal Cliffordą.
Dėl kompleksinių skaičių
Matematikoje ir fizikoje įsivaizduojamas vienetas žymimas lotynų kalba texvc arba Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc . Tai leidžia išplėsti realiųjų skaičių lauką iki kompleksinių skaičių. Tikslus apibrėžimas priklauso nuo išplėtimo metodo.
Įsivaizduojamo vieneto įvedimo priežastis yra ta, kad ne kiekviena daugianario lygtis Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematikos / README sąrankos pagalbą.): f(x)=0 su realiaisiais koeficientais turi sprendinius realiųjų skaičių srityje. Taigi, lygtis Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Norėdami gauti pagalbos dėl sąrankos, žr. matematikos / README.): x^2 + 1 = 0 neturi tikrų šaknų. Tačiau paaiškėja, kad bet kuri daugianario lygtis su sudėtingais koeficientais turi sudėtingą sprendimą – „pagrindinę algebros teoremą“.
Istoriškai įsivaizduojamas vienetas pirmą kartą buvo įvestas sprendžiant tikrąją kubinę lygtį: dažnai, jei buvo trys tikrosios šaknys, norint gauti dvi iš jų, pagal Cardano formulę reikėjo paimti kompleksinių skaičių kubo šaknį.
Teiginys, kad įsivaizduojamas vienetas yra „–1 kvadratinė šaknis“, nėra tikslus: juk „-1“ turi dvi kvadratines šaknis, iš kurių viena gali būti pažymėta „i“, o kita „-i“. Nesvarbu, kuri šaknis laikoma įsivaizduojamu vienetu: visos lygybės galios, jei visi „i“ vienu metu bus pakeisti „-i“, o „-i“ – „i“. Tačiau dėl šio neaiškumo, siekiant išvengti klaidingų skaičiavimų, nereikėtų naudoti žymėjimo Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematikos / README sąrankos pagalbos.): i per radikalą (kaip Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematikos / README sąrankos pagalbos.): \sqrt(-1)).
Apibrėžimas
Įsivaizduojamasis vienetas yra skaičius, kurio kvadratas yra −1. Tie. Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematikos / README sąrankos pagalbos.): i yra vienas iš lygties sprendinių
texvc nerastas; Žr. matematiką / README – pagalba nustatant.): x^2 + 1 = 0, arba Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Jei reikia pagalbos dėl sąrankos, žr. matematiką / README.): x^2 = -1.
Ir tada jo antrasis lygties sprendimas bus Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematikos / README sąrankos pagalbą.): -i, kuris patikrinamas pakeitimu.
Menamo vieneto galios
Laipsniai Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematikos / README sąrankos pagalbos.): i kartojama cikle:
texvc
Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Jei reikia pagalbos dėl sąrankos, žr. matematikos / README.): i^(-3) = i
Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Jei reikia pagalbos dėl sąrankos, žr. matematikos / README.): i^(-2) = -1
Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematikos / README sąrankos pagalbą.): i^(-1) = -i
Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematiką / README – pagalba nustatant.): i^0 = 1
Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Norėdami gauti pagalbos dėl sąrankos, žr. matematikos / README.): i^1 = i
Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematiką / README – pagalba nustatant.): i^2 = -1
Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematikos / README sąrankos pagalbos.): i^3 = -i
Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematiką / README – pagalba nustatant.): i^4 = 1
Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematikos / README sąrankos pagalbos.): \ldots
Kuris gali būti parašytas bet kokiam laipsniui tokia forma:
Nepavyko išanalizuoti išraiškos (vykdomasis failastexvc nerastas; Norėdami gauti pagalbos dėl sąrankos, žr. matematikos / README.): i^(4n) = 1
Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Jei reikia pagalbos dėl sąrankos, žr. matematikos / README.): i^(4n+1) = i
Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Jei reikia pagalbos dėl sąrankos, žr. matematikos / README.): i^(4n+2) = -1
Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematikos / README, jei reikia pagalbos nustatant.): i^(4n+3) = -i.
Kur n- bet koks sveikasis skaičius.
Iš čia: Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Norėdami gauti pagalbos dėl sąrankos, žr. matematikos / README.): i^n = i^(n \bmod 4) Kur 4 modas yra dalybos iš 4 liekana.
Skaičius Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematiką / README – pagalba nustatant.): i^i yra tikras:
texvc nerastas; Žr. matematiką / README – pagalba nustatant.): i^i=(e^((i\pi/2)i))=e^(i^2\pi/2)=e^(-\pi/ 2 )=0(,)20787957635\ltaškai
Faktorinis
Įsivaizduojamasis vienetas faktorialas i gali būti apibrėžta kaip gama funkcijos reikšmė iš argumento 1 + i :
Nepavyko išanalizuoti išraiškos (vykdomasis failastexvc nerastas; Žr. matematikos / README sąrankos pagalbos.): i! = \Gama(1+i) \apytiksliai 0,4980–0,1549i.
Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematikos / README sąrankos pagalbą.): |i!| = \sqrt(\pi \over \sinh(\pi)) \apytiksliai 0,521564... .
Įsivaizduojamo vieneto šaknys
Kompleksinių skaičių srityje šaknis n- turi laipsnį n sprendimus. Kompleksinėje plokštumoje įsivaizduojamo vieneto šaknys yra taisyklingo n kampo, įbrėžto į vienetinio spindulio apskritimą, viršūnėse.
Nepavyko išanalizuoti išraiškos (vykdomasis failastexvc nerastas; Jei reikia pagalbos dėl nustatymo, žr. math/README.): u_k=\cos (\frac((\frac(\pi)(2)) + 2\pi k)(n)) +i\ \sin (\frac( (\frac(\pi)(2)) + 2\pi k)(n)), \quad k=0,1,...,n-1
Tai išplaukia iš Moivre formulės ir fakto, kad įsivaizduojamas vienetas gali būti pavaizduotas trigonometrine forma:
Nepavyko išanalizuoti išraiškos (vykdomasis failastexvc nerastas; Žr. math/README – pagalba nustatant.): i=\cos\ (\frac(\pi)(2)) + i\ \sin\ (\frac(\pi)(2))
Visų pirma, Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Jei reikia pagalbos dėl sąrankos, žr. math/README.): \sqrt(i ) = \left\(\frac(1 + i)(\sqrt(2));\ \frac(-1 - i)(\sqrt( 2) )) \teisingai\) Ir Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematikos/README sąrankos pagalbą.): \sqrt(i ) = \left\(-i;\ \frac(i + (\sqrt(3)))(2);\ \frac(i - ( \sqrt) (3))) (2) \dešinė\)
Be to, įsivaizduojamo vieneto šaknys gali būti pavaizduotos eksponentine forma:
Nepavyko išanalizuoti išraiškos (vykdomasis failastexvc nerastas; Žr. matematiką / README – pagalba nustatant.): u_k=e^(\frac((\frac(\pi)(2) + 2\pi k) i)(n) ), \quad k=0,1, ...,n-1
Kiti įsivaizduojami vienetai
Cayley-Dixon konstrukcijoje (arba Clifford algebrose) gali būti keli „įsivaizduojami išplėtimo vienetai“ ir (arba) jų kvadratas gali būti ="+1" arba net ="0". Tačiau šiuo atveju gali atsirasti nulinių daliklių ir yra kitų savybių, kurios skiriasi nuo komplekso „i“ savybių. Pavyzdžiui, ketvirčio kūne yra trys antikomutaciniai įsivaizduojami vienetai, taip pat yra be galo daug lygties „ Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematikos / README sąrankos pagalbos.): x^2 = -1
».
Dėl aiškinimo ir pavadinimo klausimo
| Gaussas taip pat teigė, kad jei dydžiai 1, −1 ir √−1 būtų vadinami atitinkamai ne teigiamais, neigiamais ir įsivaizduojamais vienetais, o tiesioginiais, atvirkštiniais ir atsitiktiniais, žmonėms nesusidarytų įspūdis, kad yra kažkoks niūrus ryšys. su šiais skaičiais. Anot Gauso, geometrinis vaizdavimas tikroji įsivaizduojamų skaičių metafizika pateikia naujoje šviesoje. Būtent Gaussas įvedė terminą „sudėtiniai skaičiai“ (priešingai nei Dekarto „įsivaizduojami skaičiai“) ir panaudojo simbolį i √−1 žymėti. Maurice'as Kline'as, „Matematika. Tikrumo praradimas“. VII skyrius. Nelogiška raida: rimti sunkumai ant XIX amžiaus slenksčio. |
Pavadinimai
Bendras žymėjimas Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematikos / README sąrankos pagalbos.): i, tačiau radijo inžinerijoje dažniausiai žymimas menamasis vienetas Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Žr. matematikos / README sąrankos pagalbos.): j kad nebūtų painiojama su momentinės srovės žymėjimu: Nepavyko išanalizuoti išraiškos (vykdomasis failas texvc nerastas; Norėdami gauti pagalbos dėl sąrankos, žr. matematikos / README.): i = i (t)
.
Taip pat žr
- Dvigubi skaičiai ir dvigubi skaičiai
Parašykite apžvalgą apie straipsnį "Įsivaizduojamas vienetas"
Pastabos
Nuorodos
- Įsivaizduojamas vienetas // Didžioji tarybinė enciklopedija: [30 tomų] / sk. red. A. M. Prokhorovas. - 3 leidimas. – M. : sovietinė enciklopedija, 1969-1978.
|
||||||||||||||||||||||||||
Ištrauka, apibūdinanti įsivaizduojamą vienetą
– To negalima išmokyti, Izidora. Žmonės turi turėti šviesos poreikį, gėrio poreikį. Jie patys turi norėti pokyčių. Už tai, kas duota jėga, žmogus instinktyviai stengiasi greitai atmesti, net nebandydamas nieko suprasti. Bet mes nukrypstame, Izidora. Ar nori, kad tęsčiau Radomiro ir Magdalenos istoriją?Teigiamai linktelėjau, giliai širdyje apgailestaudama, kad negaliu su juo taip paprastai ir ramiai pasikalbėti, nesijaudindama, ką man davė likimas paskutinės minutės mano suluošintas gyvenimas ir su siaubu negalvoju apie nelaimę, pakibusią virš Anos...
– Biblijoje daug rašoma apie Joną Krikštytoją. Ar jis tikrai buvo su Radomiru ir Šventyklos riteriais? Jo įvaizdis toks stulbinamai geras, kad kartais suabejoti, ar Jonas yra tikroji figūra? Ar gali atsakyti, Šiaurės?
Šiaurė šiltai nusišypsojo, matyt, prisimindama kažką labai malonaus ir brangaus jam...
– Jonas buvo išmintingas ir malonus, kaip didis šilta saulė... Jis buvo tėvas visiems su juo vaikščiojantiems, jų mokytojas ir draugas... Jis buvo vertinamas, paklusnus ir mylimas. Tačiau jis niekada nebuvo tas jaunas ir nuostabiai gražus jaunuolis, kokį jį dažniausiai piešė menininkai. Jonas tuo metu jau buvo pagyvenęs burtininkas, bet vis dar labai stiprus ir atkaklus. Žilaplaukis ir aukštas jis labiau atrodė kaip galingas epinis karys, nei į nuostabiai gražų ir švelnų jaunuolį. Jis nešiojo labai ilgi plaukai, taip pat visi kiti, kurie yra su Radomiru.
Tai buvo Radanas, jis buvo tikrai nepaprastai gražus. Jis, kaip ir Radomiras, nuo mažens gyveno Meteorose, šalia savo mamos burtininkės Marijos. Prisimink, Izidora, kiek yra paveikslų, kuriuose Marija nutapyta su dviem, beveik tokio paties amžiaus kūdikiais. Juos kažkodėl piešė visi žinomi menininkai, galbūt net nesuprasdami, KAS iš tikrųjų pavaizdavo jų teptuką... O įdomiausia tai, kad Marija visuose šiuose paveiksluose žvelgia į Radaną. Matyt, net tada, dar būdamas kūdikis, Radanas jau buvo toks linksmas ir patrauklus, koks išliko visą savo trumpą gyvenimą...
Ir vis dėlto... net jei menininkai šiuose paveiksluose nutapė Joną, tai kaip tas pats Jonas galėjo taip siaubingai pasenti iki jo egzekucijos, įvykdytos kaprizingosios Salomėjos prašymu?.. Juk anot Biblija, tai atsitiko dar prieš Kristaus nukryžiavimą, o tai reiškia, kad Jonui tuo metu turėjo būti ne daugiau kaip trisdešimt keturi metai! Kaip jis iš mergaitiškai gražaus, auksaplaukio jaunuolio virto senu ir visai nepatraukliu žydu?!
- Vadinasi, Magas Džonas nemirė, Severai? – džiaugsmingai paklausiau. – O gal jis mirė kitaip?..
„Deja, tikram Jonui tikrai buvo nukirsta galva, Izidora, bet tai neįvyko dėl piktos kaprizingos išlepintos moters valios. Jo mirties priežastis buvo žydo „draugo“, kuriuo jis pasitikėjo ir kurio namuose gyveno kelerius metus, išdavystė...
- Bet kaip jis to nepajuto? Kaip jūs nematei, koks tai „draugas“?! – pasipiktinau.
– Turbūt neįmanoma įtarti kiekvieno žmogaus, Izidora... Manau, jiems jau buvo pakankamai sunku kuo nors pasitikėti, nes visi turėjo kažkaip prisitaikyti ir gyventi toje svetimoje, nepažįstamoje šalyje, nepamirškite to. Kadangi, iš didžiųjų ir mažesnis blogis jie, matyt, stengėsi rinktis mažiau. Bet visko nuspėti neįmanoma, tu tai puikiai žinai, Izidora... Mago Jono mirtis įvyko po Radomiro nukryžiavimo. Jį nunuodijo žydas, kurio namuose tuo metu gyveno Jonas kartu su mirusio Jėzaus šeima. Vieną vakarą, kai visi namai jau miegojo, šeimininkas, kalbėdamas su Jonu, padovanojo jam mėgstamos arbatos, sumaišytos su stipriais žolelių nuodais... Kitą rytą niekas net negalėjo suprasti, kas atsitiko. Pasak šeimininko, Jonas tiesiog akimirksniu užmigo, ir daugiau nebepabudo... Jo kūnas ryte buvo rastas kruvinoje lovoje su... nupjauta galva... Anot to paties šeimininko, žydai buvo labai bijojo Jono, nes laikė jį nepralenkiamu burtininku. Ir norėdami įsitikinti, kad jis niekada nebeprisikels, jam nukirto galvą. Jono galvą vėliau iš jų nupirko (!!!) ir pasiėmė su savimi Šventyklos riteriai, sugebėję ją išsaugoti ir atgabenti į Magų slėnį, kad taip Jonui būtų suteiktas bent toks mažas, bet vertas ir nusipelnytos pagarbos, neleisdamas žydams tiesiog tyčiotis iš jo, darydamas kai ką savo magiški ritualai. Nuo tada Jono galva visada buvo su jais, kad ir kur jie būtų. Ir dėl tos pačios galvos po dviejų šimtų metų Šventyklos riteriai buvo apkaltinti nusikalstamu velnio garbinimu... Prisimeni paskutinę „tamplierių bylą“ (Šventyklos riteriai), ar ne, Izidora ? Būtent ten jie buvo apkaltinti „kalbančios galvos“ garbinimu, o tai supykdė visą bažnyčios dvasininkiją.
- Atleisk, Severi, bet kodėl Šventyklos riteriai neatnešė Jono galvos čia į Meteorą? Nes, kiek suprantu, jūs visi jį labai mylėjote! Ir kaip tu žinai visas šias detales? Tu nebuvai su jais, ar ne? Kas tau visa tai pasakė?
- Visa tai mums papasakojo liūdna istorija Ragana Marija, Radano ir Radomiro motina...
– Ar Marija grįžo pas jus po Jėzaus egzekucijos?!.. Juk, kiek žinau, per nukryžiavimą ji buvo su sūnumi. Kada ji pas tave grįžo? Ar gali būti, kad ji dar gyva?.. – sulaikęs kvapą paklausiau.
Tema: Įsivaizduojamas vienetas , ją laipsnių. Sudėtingas numeriai.
Algebrinė forma visapusiškas numeriai.
Tikslai: išplėsti skaičiaus sampratą, supažindinti su menamo vieneto sąvoka ir jo galiomis, sąvoka kompleksinis skaičius; apsvarstykite kompleksinio skaičiaus algebrinę formą; ugdyti gebėjimą apibendrinti įgytas žinias, skatinti tobulėjimą loginis mąstymas;
ugdyti studentus sąmoningas požiūrisį mokymosi procesą.
Planuoti ( tiriami klausimai )
Įsivaizduojami skaičiai. Menamo vieneto apibrėžimas. Menamo vieneto galios.
Kompleksinio skaičiaus apibrėžimas.
Algebrinė forma kompleksinis skaičius.
1.Įsivaizduojami skaičiai
Apibrėžimas. Skaičius, kurio kvadratas yra -1, vadinamas įsivaizduojamu vienetu ir
žymimas і ; і 2 = -1
Apibrėžimas. Skaičiai, turintys formą b і , kur b yra tikrasis skaičius, vadinami
menami skaičiai.
Pavyzdžiui:
Yra žinoma, kad tikrieji skaičiai vaizduojami taškais OX ašyje. Įsivaizduojami skaičiai vaizduojami taškais OU ašyje, todėl vadinama OX ašimi tikroji ašis, o ašis OU yra įsivaizduojama ašis. Įsivaizduojamų skaičių aibė vienas su vienu atitinka realiųjų skaičių aibę.
Apibrėžimas. Du įsivaizduojami skaičiai b 1 i Ir b 2 i vadinamos lygiomis, jei b 1 = b 2
Apibrėžimas. Įsivaizduojamas skaičius (- bi ) vadinama įsivaizduojamo skaičiaus priešingybe b і .
Pavyzdžiui:
 Ir
Ir

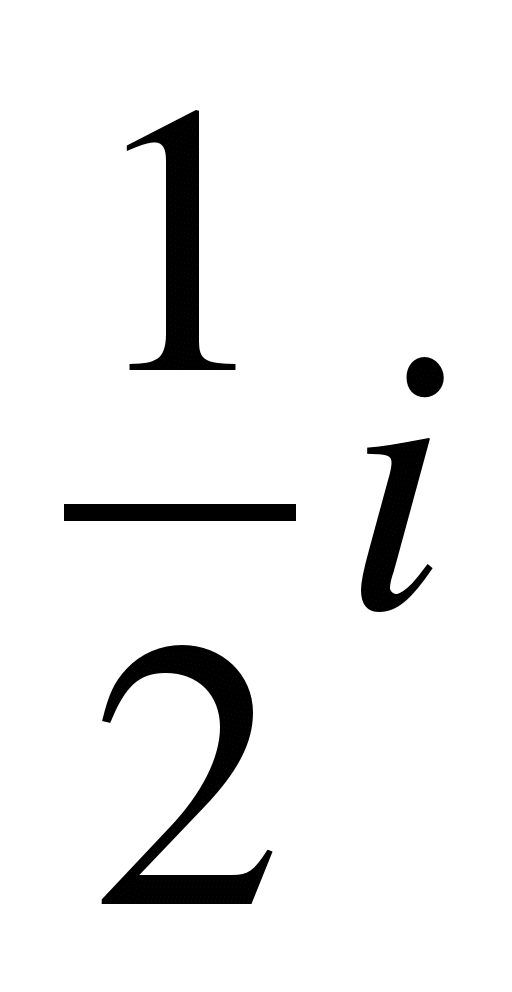 Ir
Ir  .
.
Teorema. Bet kokia natūrali skaičiaus galia і galima konvertuoti į
vienas iš keturių tipų 1; і ; -1; -і.
Įrodymas .
Apsvarstykite išraišką і m , kur m - natūralusis skaičius. Akivaizdu, kad galimi keturi atvejai:
1) m = 4 k , k =1,2, ...
2) m = 4k +1, k =0, 1,2,...
3) m 4k +2, k = 0,1,2,...
4) m = 4k +3, k =0,1,2, ....
Leisti m = 4 k , Tada і m =і Ak =(і A ) Į =1 Į =1
Leistim =4 k +1, Tada і m = і Ak+1 = і Ak i=1i=i
Leisti m = 4 k +2, Tadaі m =і Ak+2 = і Ak і 2 = 1(-1)=-1
Leistim =4 k +3, Tada і m
Pavyzdys. Apskaičiuokite išraiškos reikšmę
Sprendimas:
komentuoti. Norint apskaičiuoti įsivaizduojamo vieneto galią, patogu naudoti šią taisyklę:
1) padalykite rodiklį iš 4;
2) pakeisti i m ant i R , kur p yra liekana, gauta padalijus t iš 4, tai yra, skaičius p randamas iš lygybės t = 4k + p.
2. Sudėtiniai skaičiai
Apibrėžimas. Kompleksinis skaičius yra skaičius, turintis formąa+bi , kur a, b –
realieji skaičiai, i yra įsivaizduojamas vienetas. Tokiu atveju vadinamas skaičius „a“.
tikroji kompleksinio skaičiaus dalis, „b“ – menamoji dalis
kompleksinis skaičius.
Simboliškai tikroji ir įsivaizduojama kompleksinio skaičiaus dalys žymimos taip:(nustatyti iš naujo), (jie to nedaro).
Šie pavadinimai pagrįsti pirmosiomis raidėmis Lotynų kalbos žodžiai, o tai reiškia „tikroji“ ir „įsivaizduojama“, o tai reiškia „įsivaizduojama“.
komentuoti. Kartais įsivaizduojama kompleksinio skaičiaus dalisz = A + b і vadinamas bi.
Apibrėžimas. Du kompleksiniai skaičiaiZ 1 = a 1 + b 1 i Irz 2 = A 2 + b 1 i vadinamos lygiomis, jei
Rez 1 = Rez 2 , Ašz 1 = Ašz 2 .
Kompleksiniams skaičiams nėra didesnio ir mažesnio sąvokų, tai yra, kompleksiniai skaičiai nėra palyginami.
Apibrėžimas. Sudėtingas skaičius(-A- bi ) vadinamas kompleksinio skaičiaus priešingybe
a + b.
Apibrėžimas. Du kompleksiniai skaičiai, kurių tikrosios dalys yra lygios, o menamos dalys yra lygios
dalyspriešingybės vadinamos kompleksiniais konjuguotais skaičiais ir
yra atitinkamai paskirti Ir.
3. Algebrinė kompleksinio skaičiaus forma. Veiksmai su kompleksiniais skaičiais, pateiktais algebrine forma.
Kompleksinis skaičius vaizduojamas kaip  vadinamas kompleksiniu skaičiumialgebrinė forma
.
vadinamas kompleksiniu skaičiumialgebrinė forma
.
Kompleksinių skaičių sudėjimas
Apibrėžimas.
Dviejų kompleksinių skaičių suma  Ir
Ir  paskambino
paskambino
kompleksinis skaičius.
Taigi, (1)
Taigi, norint sudėti du kompleksinius skaičius, reikia sudėti jų tikrąsias dalis ir taip gaunama tikroji sumos dalis, o sudėti menamas dalis – taip gaunama įsivaizduojama sumos dalis.
Konjuguotų skaičių suma visada yra reali skaičius
tai yra,  . (2)
. (2)
Kompleksinių skaičių atėmimas
Apibrėžimas.
Dviejų kompleksinių skaičių skirtumas  Ir
Ir  tai vadinama
tai vadinama
kompleksinis skaičius  , kuris pridedamas prie skaičiaus
, kuris pridedamas prie skaičiaus  suteikia skaičių
suteikia skaičių  .
.
Visada galima atimti kompleksinius skaičius.
Teorema.
Bet kokiems kompleksiniams skaičiams  Ir
Ir  visada yra skirtumas
visada yra skirtumas  , kuri yra vienareikšmiškai nustatyta.
, kuri yra vienareikšmiškai nustatyta.
Taigi, norint atimti kompleksinius skaičius, pakanka atimti jų realiąsias dalis ir jų skirtumą laikyti tikrąja skirtumo dalimi, taip pat atimti įsivaizduojamą skirtumo dalį
Pasirodo, (3)
Dviejų konjuguotų skaičių skirtumas visada yra įsivaizduojamas skaičius. ,
tai yra,  (4)
(4)
Kompleksinių skaičių dauginimas
Apibrėžimas.
Dviejų kompleksinių skaičių sandauga
 ir vadinamas toks kompleksinis skaičius, kuris nustatomas pagal formulę: (5)
ir vadinamas toks kompleksinis skaičius, kuris nustatomas pagal formulę: (5)
Norėdami padauginti kompleksinius skaičius, turėtumėte juos padauginti pagal polinomų dauginimo taisyklę, pakeičiant  iki -1 ir pateikti panašias sąlygas.
iki -1 ir pateikti panašias sąlygas.
Dauginant kompleksinius skaičius, geriau atlikti tiesioginį dauginimą. Konjuguotų skaičių sandauga visada yra tikras numeris Atsakymas.
1. Pateikite kompleksinio skaičiaus apibrėžimą.
2.Suformuluokite įsivaizduojamo vieneto apibrėžimą.
3. Kaip rasti įsivaizduojamo vieneto laipsnį.
4.Kokie kompleksiniai skaičiai vadinami lygiais ir konjuguotais?
5.Parašykite formulę įsivaizduojamo vieneto savavališko laipsnio radimui.
6. Pateikite grynai įsivaizduojamų skaičių pavyzdžių.
7. Apibrėžkite dviejų kompleksinių skaičių sumą, sandaugą ir dalinį.
Literatūra
Rašyta, D. T. Paskaitų konspektai apie aukštoji matematika: pilnas kursas D.T. Parašyta. – 9-asis leidimas. – M.: Iris-press, 2009. 608 p.: iliustr. - (Aukštasis išsilavinimas).
Lungu, K. N. Aukštosios matematikos uždavinių rinkinys. 1 metai / K. N. Lungu, D. T. Pismenny, S. N. Fedinas, Yu A. Shevchenko. – 7-asis leidimas. – M.: Iris-press, 2008. 576 p.: – (Aukštasis mokslas).
Grigorjevas V.P. Aukštosios matematikos elementai: vadovėlis studentams. aplinkosaugos institucijos prof. išsilavinimas / V. P. Grigorjevas, Yu A. Dubinskis. – 10 leid., ištrintas. – M. Leidybos centras „Akademija“, 2014. – 320 p.








