Bir fonksiyonun bükülme noktaları nasıl bulunur? Fonksiyon grafiğinin dışbükey yönü

Çevrimiçi bir hesap makinesi ile bulabilirsiniz bir fonksiyon grafiğinin bükülme noktaları ve dışbükeylik aralıkları Word'de çözümün tasarımı ile. İki değişkenli f(x1,x2) fonksiyonunun dışbükey olup olmadığına Hessian matrisi kullanılarak karar verilir.

İşlev giriş kuralları:

Fonksiyon grafiğinin dışbükey yönü. Eğilme noktaları

Tanım: y=f(x) eğrisi (a; b) aralığında, bu aralığın herhangi bir noktasında teğetin altında bulunuyorsa yukarı doğru dışbükey olarak adlandırılır.

Tanım: Fonksiyonun grafiğinin dışbükey yukarı veya aşağı olduğu aralıklara, fonksiyonun grafiğinin dışbükey aralıkları denir.

y=f(x) fonksiyonunun grafiği olan eğrinin aşağı veya yukarı konveksliği, ikinci türevinin işareti ile karakterize edilir: f''(x) > 0 aralığında ise, eğri dışbükeydir bu aralıkta aşağı doğru; f''(x) ise< 0, то кривая выпукла вверх на этом промежутке.

Tanım: y=f(x) fonksiyonunun grafiğinin dışbükey boşluklarını ayıran noktası zıt yönler bu grafiğe bükülme noktası denir.

Bükülme noktaları yalnızca kritik noktalar II tür, yani f''(x)'in ikinci türevinin kaybolduğu veya kırıldığı y = f(x) fonksiyonunun etki alanına ait noktalar.

y = f(x) fonksiyon grafiğinin bükülme noktalarını bulma kuralı

1. f''(x)'in ikinci türevini bulun.
2. y=f(x) fonksiyonunun ikinci türünün kritik noktalarını bulun, yani f''(x)'in kaybolduğu veya kırıldığı nokta.
3. İkinci türev f''(x)'in işaretini, bulunan kritik noktaların f(x) fonksiyonunun tanım kümesini böldüğü aralıklarda araştırın. Bu durumda x 0 kritik noktası zıt yönlerdeki dışbükeylik aralıklarını ayırırsa, o zaman x 0 fonksiyon grafiğinin bükülme noktasının apsisidir.
4. Bükülme noktalarındaki fonksiyon değerlerini hesaplayın.

Örnek 1 . Aşağıdaki eğrinin dışbükey boşluklarını ve bükülme noktalarını bulun: f(x) = 6x 2 –x 3 .
Çözüm: f '(x) = 12x - 3x 2 , f ''(x) = 12 - 6x'i bulun.
12-6x=0 denklemini çözerek ikinci türevin kritik noktalarını bulalım. x=2


f(2) = 6*2 2 - 2 3 = 16
Yanıt: x∈(2; +∞) ; için fonksiyon yukarı doğru dışbükeydir; x∈(-∞; 2) için fonksiyon aşağı doğru dışbükeydir; bükülme noktası (2;16) .

Örnek 2 . Fonksiyonun bükülme noktaları var mı: f(x)=x 3 -6x 2 +2x-1

Örnek 3 . Fonksiyon grafiğinin dışbükey ve dışbükey olduğu aralıkları bulun: f(x)=x 3 -6x 2 +12x+4

-de bir fonksiyonu incelemek ve grafiğini çizmek aşamalardan birinde bükülme noktalarını ve dışbükeylik aralıklarını belirliyoruz. Bu verilerle birlikte artış ve azalma aralıkları incelenen fonksiyonun grafiğini şematik olarak göstermenizi sağlar.

Aşağıdakiler, belirli bir düzene ve farklı türlere kadar bildiğinizi varsayar.

ile öğrenmeye başlayalım gerekli tanımlar ve kavramlar. Daha sonra, bir fonksiyonun belirli bir aralıktaki ikinci türevinin değeri ile dışbükey yönü arasındaki ilişkiyi dile getiriyoruz. Bundan sonra fonksiyon grafiğinin bükülme noktalarını belirlememizi sağlayan koşullara geçelim. Vereceğimiz metne göre karakteristik örnekler detaylı çözümler ile.

Sayfa gezintisi.

Dışbükeylik, bir fonksiyonun içbükeyliği, bükülme noktası.

Tanım.

aşağı dışbükey grafiği, X aralığının herhangi bir noktasında kendisine teğetten daha düşük değilse, X aralığında.

Tanım.

türevlenebilir fonksiyon denir yukarı dışbükey X aralığında, grafiği X aralığının herhangi bir noktasında kendisine teğetten daha yüksek değilse.

Genellikle yukarı doğru bir dışbükey fonksiyon denir dışbükey ve aşağı dışbükey - içbükey.

Bu tanımları gösteren çizime bakın.

Tanım.

nokta denir fonksiyonun grafiğinin bükülme noktası y \u003d f (x) belirli bir noktada fonksiyon grafiğine bir teğet varsa (Oy eksenine paralel olabilir) ve noktanın böyle bir mahallesi varsa , içinde fonksiyon grafiğinin farklı yönlere sahip olduğu M noktasının soluna ve sağına dışbükeylik.

Başka bir deyişle, M noktası, bu noktada bir teğet varsa ve fonksiyonun grafiği dışbükeyliğin yönünü değiştirip içinden geçerek değiştiriyorsa, M noktasına fonksiyonun grafiğinin bükülme noktası denir.

Gerekirse, dikey olmayan ve dikey bir teğetin var olma koşullarını hatırlamak için bölüme bakın.

Aşağıdaki şekil, birkaç bükülme noktası örneğini göstermektedir (kırmızı noktalarla işaretlenmiştir). Bazı fonksiyonların bükülme noktaları olmayabilirken diğerlerinin bir, birkaç veya sonsuz sayıda bükülme noktası olabileceğini unutmayın.

Bir fonksiyonun konveksite aralıklarını bulma.

Bir fonksiyonun dışbükeylik aralıklarını belirlememizi sağlayan bir teorem formüle ediyoruz.

teorem.

y=f(x) fonksiyonunun X aralığında sonlu bir ikinci türevi varsa ve eşitsizlik (), o zaman fonksiyonun grafiği X üzerinde aşağı (yukarı) yönlendirilmiş bir dışbükeyliğe sahiptir.

Bu teorem, bir fonksiyonun içbükeylik ve dışbükeylik aralıklarını bulmanızı sağlar, yalnızca eşitsizlikleri çözmeniz gerekir ve sırasıyla, orijinal fonksiyonun tanım alanında.

y=f(x) fonksiyonunun tanımlı olduğu ve ikinci türevinin olmadığı noktaların içbükeylik ve dışbükeylik aralıklarına dahil edileceğine dikkat edilmelidir.

Bunu bir örnekle ele alalım.

Örnek.

Fonksiyonun grafiğinin hangi aralıklarda olduğunu bulun yukarı doğru bir dışbükeyliğe ve aşağı doğru bir dışbükeyliğe sahiptir.

Çözüm.

işlev kapsamı- her şey hazır gerçek sayılar.

İkinci türevi bulalım.

İkinci türevin tanım alanı, orijinal fonksiyonun tanım alanı ile çakışmaktadır, bu nedenle içbükeylik ve dışbükeylik aralıklarını bulmak için sırasıyla ve çözmek yeterlidir.

Bu nedenle, fonksiyon aralıkta aşağı doğru dışbükey ve aralıkta yukarı doğru dışbükeydir.

Grafik illüstrasyon.

Dışbükey aralıktaki fonksiyonun grafiğinin bir kısmı mavi, içbükey aralıkta - kırmızı olarak gösterilir.

Şimdi, ikinci türevin tanım kümesinin, fonksiyonun tanım kümesiyle çakışmadığı bir örneği ele alalım. Bu durumda, daha önce belirttiğimiz gibi, sonlu ikinci türevin olmadığı tanım bölgesinin noktaları, dışbükeylik ve (veya) içbükeylik aralıklarına dahil edilmelidir.

Örnek.

Fonksiyon grafiğinin dışbükeylik ve içbükeylik aralıklarını bulun.

Çözüm.

Fonksiyonun kapsamı ile başlayalım:

İkinci türevi bulalım:

İkinci türevin alanı kümedir . Gördüğünüz gibi, x=0 orijinal fonksiyonun tanım alanındadır, ancak ikinci türevin tanım alanında değildir. Bu noktayı unutmayın, dışbükey ve (veya) içbükey aralığına dahil edilmesi gerekecektir.

Şimdi eşitsizlikleri ve orijinal fonksiyonun etki alanında çözüyoruz. uygulanabilir İfade payı sıfıra gider veya , payda - en x = 0 veya x = 1 . Bu noktaları sayı doğrusunda şematik olarak çizeriz ve orijinal fonksiyonun tanım alanında yer alan aralıkların her birinde ifadenin işaretini buluruz (alt sayı satırında gölgeli alanla gösterilir). Pozitif bir değer artı işaretidir, negatif bir değer eksi işaretidir.

Böylece,

Ve

Bu nedenle, x=0 noktasını dahil ederek cevabı elde ederiz.

-de fonksiyonun grafiği, aşağı doğru yönlendirilmiş bir dışbükeyliğe sahiptir; - çıkıntı yukarı doğru yönlendirildi.

Grafik illüstrasyon.

Dışbükey aralıktaki fonksiyonun grafiğinin bir kısmı mavi, içbükey aralıklarda gösterilir - kırmızı, siyah noktalı çizgi dikey asimptot.

Bir çekim için gerekli ve yeterli koşullar.

Bir çekim için gerekli koşul.

formüle edelim çekim için gerekli koşul fonksiyon grafiği.

y=f(x) fonksiyonunun grafiğinin bir noktada bükülmesi ve için sürekli bir ikinci türevi olsun, o zaman eşitlik doğrudur.

Bu koşuldan, bükülme noktalarının apsislerinin, fonksiyonun ikinci türevinin kaybolduğu noktalar arasında aranması gerektiği sonucu çıkar. ANCAK, bu koşul yeterli değildir, yani ikinci türevin sıfıra eşit olduğu tüm değerler, bükülme noktalarının apsisleri değildir.

Ayrıca, bükülme noktasının tanımı gereği bir teğet çizginin varlığının gerekli olduğu, dikey de olabileceği belirtilmelidir. Bu ne anlama gelir? Ve bu şu anlama gelir: bükülme noktalarının apsisleri, fonksiyonun etki alanından her şey olabilir; Ve . Genellikle bunlar, birinci türevin paydasının kaybolduğu noktalardır.

Bir çekim için ilk yeterli koşul.

Bükülme noktalarının apsisi olabilecek her şey bulunduktan sonra, kullanmalısınız çekim için ilk yeterli koşul fonksiyon grafiği.

y=f(x) fonksiyonunun noktasında sürekli olsun, teğeti olsun (muhtemelen dikey) ve bu fonksiyonun noktanın bir komşuluğunda ikinci bir türevi olsun. Daha sonra, eğer bu komşuluk içinde nin solunda ve sağında ise, ikinci türev farklı işaretler, o zaman fonksiyonun grafiğinin bükülme noktasıdır.

Görüldüğü gibi, birinci yeterli koşul, ikinci türevin noktanın kendisinde olmasını değil, noktanın çevresinde bulunmasını gerektirir.

Şimdi tüm bilgileri bir algoritma şeklinde özetliyoruz.

Bir fonksiyonun bükülme noktalarını bulmak için algoritma.

Fonksiyon grafiğinin olası bükülme noktalarının tüm apsislerini buluyoruz (veya Ve ) ve hangi ikinci türevin işaret değiştirdiğini geçerek öğrenin. Bu tür değerler, bükülme noktalarının apsisleri olacak ve bunlara karşılık gelen noktalar, fonksiyon grafiğinin bükülme noktaları olacaktır.

Açıklama için bükülme noktaları bulmanın iki örneğini ele alalım.

Örnek.

Bir fonksiyon grafiğinin bükülme noktalarını ve dışbükeylik ve içbükeylik aralıklarını bulun .

Çözüm.

Fonksiyonun alanı tüm gerçek sayılar kümesidir.

Birinci türevi bulalım:

Birinci türevin alanı aynı zamanda tüm gerçek sayılar kümesidir, bu nedenle eşitlikler Ve herhangi biri için yürütülmez.

İkinci türevi bulalım:

İkinci türevin x argümanının hangi değerlerinde kaybolduğunu bulalım:

Dolayısıyla, olası bükülme noktalarının apsisleri x=-2 ve x=3'tür.

Şimdi geriye, yeterli bir bükülme kriteri ile, bu noktalardan hangisinde ikinci türevin işaret değiştirdiğini kontrol etmek kalıyor. Bunu yapmak için x=-2 ve x=3 noktalarını yerleştirin. sayısal eksen ve, olduğu gibi genelleştirilmiş aralık yöntemi, ikinci türevin işaretlerini her aralığa yerleştiririz. Her aralığın altında, fonksiyonun grafiğinin dışbükey yönü yaylarla şematik olarak gösterilmiştir.

İkinci türev, soldan sağa x=-2 noktasından geçerek işareti artıdan eksiye ve x=3 noktasından geçerek işareti eksiden artıya değiştirir. Bu nedenle, hem x=-2 hem de x=3 fonksiyon grafiğinin bükülme noktalarının apsisidir. Grafik noktalarına karşılık gelirler ve .

Gerçel eksene ve aralıklarındaki ikinci türevin işaretlerine tekrar baktığımızda, dışbükeylik ve içbükeylik aralıkları hakkında sonuca varabiliriz. Fonksiyonun grafiği, aralıkta dışbükey ve ve aralıklarında içbükeydir.

Grafik illüstrasyon.

Dışbükey aralıktaki fonksiyonun grafiğinin bir kısmı mavi, içbükey aralıklarda - kırmızı, bükülme noktaları siyah noktalar olarak gösterilir.

Örnek.

Bir fonksiyon grafiğinin tüm bükülme noktalarının apsislerini bulun .

Çözüm.

Bu fonksiyonun etki alanı, gerçek sayılar kümesinin tamamıdır.

Türevini bulalım.

Birinci türev, orijinal fonksiyondan farklı olarak x=3'te tanımlı değildir. Ancak Ve . Bu nedenle, apsisin x=3 olduğu noktada, orijinal fonksiyonun grafiğine dikey bir teğet vardır. Yani x=3, fonksiyon grafiğinin bükülme noktasının apsisi olabilir.

İkinci türevi, tanım alanını ve kaybolduğu noktaları buluyoruz:

Bükülme noktalarının iki olası apsisine daha sahibiz. Üç noktayı da sayı doğrusu üzerinde işaretliyoruz ve elde edilen aralıkların her birinde ikinci türevin işaretini belirliyoruz.

İkinci türev, noktaların her birinden geçerek işaret değiştirir, bu nedenle, hepsi bükülme noktalarının apsisidir.

Fonksiyon Grafiği y=f(x) isminde dışbükey aralıkta (a;b), bu aralıkta teğetlerinden herhangi birinin altında bulunuyorsa.

Fonksiyon Grafiği y=f(x) isminde içbükey aralıkta (a;b), bu aralıkta teğetlerinden herhangi birinin üzerinde yer alıyorsa.

Şekilde dışbükey bir eğri gösterilmektedir (a;b) ve içbükey (M.Ö).

Örnekler.

Belirli bir aralıktaki bir fonksiyonun grafiğinin dışbükey mi yoksa içbükey mi olacağını belirlemenizi sağlayan yeterli bir işaret düşünün.

teorem. İzin vermek y=f(x) ile ayırt edilebilir (a;b). Aralığın tüm noktalarında ise (a;b) fonksiyonun ikinci türevi y = f(x) negatif, yani F ""(X) < 0, то график функции на этом интервале выпуклый, если же F""(X) > 0 içbükeydir.

Kanıt. Kesinlik için varsayalım ki F""(X) < 0 и докажем, что график функции будет выпуклым.

Fonksiyon grafiğini ele alın y = f(x) keyfi nokta M0 apsisli x0 Î ( A; B) ve noktadan çizin M0 teğet. Onun denklemi. fonksiyonunun grafiğini göstermeliyiz. (a;b) bu teğetin altında yer alır, yani aynı değere sahip X eğri ordinatı y = f(x) teğetin ordinatından küçük olacaktır.

Yani eğrinin denklemi y = f(x). Apseye karşılık gelen teğet ordinatı gösterelim X. Daha sonra . Bu nedenle, eğrinin ordinatları ile teğet arasındaki fark aynı değerdedir. X irade .

Fark f(x) – f(x0) Lagrange teoremine göre dönüşüm, burada C arasında X Ve x0.

Böylece,

Lagrange teoremini yine köşeli parantez içindeki ifadeye uyguluyoruz: , burada c 1 arasında c 0 Ve x0. teoreme göre F ""(X) < 0. Определим знак произведения второго и третьего сомножителей.

Böylece, eğrinin herhangi bir noktası, tüm değerler için eğrinin teğetinin altında yer alır. X Ve x0 Î ( A; B), yani eğri dışbükeydir. Teoremin ikinci kısmı da benzer şekilde ispatlanmıştır.

örnekler.

grafik noktası sürekli fonksiyon Dışbükey kısmını içbükey olandan ayıran , denir dönüm noktası.

Açıkçası, bükülme noktasında, teğet, eğer varsa, eğriyi keser, çünkü bu noktanın bir tarafında eğri teğetin altında, diğer tarafında ise üstünde yer alır.

olması için yeterli koşulları tanımlayalım. verilen nokta eğri bir bükülme noktasıdır.

teorem. Eğrinin denklemle tanımlanmasına izin verin y = f(x). Eğer F ""(X 0) = 0 veya F ""(X 0) yok ve değeri geçerken X = x0 türev F ""(X) işareti değiştirir, ardından apsisli fonksiyonun grafiğinin noktası X = x0 bir dönüm noktası vardır.

Kanıt. İzin vermek F ""(X) < 0 при X < x0 Ve F ""(X) > 0 de X > x0. sonra X < x0 eğri dışbükeydir ve X > x0- içbükey. bu yüzden nokta A, eğri üzerinde uzanan, apsisli x0 bir dönüm noktası vardır. Benzer şekilde ikinci durumu da ele alabiliriz. F ""(X) > 0 de X < x0 Ve F ""(X) < 0 при X > x0.

Bu nedenle, bükülme noktaları yalnızca ikinci türevin sıfır olduğu veya bulunmadığı noktalar arasında aranmalıdır.

Örnekler. Bükülme noktalarını bulun ve eğrilerin dışbükeylik ve içbükeylik aralıklarını belirleyin.

BİR FONKSİYONUN GRAFİĞİNİN ASİMPTOTLARI

Bir fonksiyonu araştırırken, grafiğin şeklini, grafik noktasının orijinden sınırsız olarak çıkarılmasıyla oluşturmak önemlidir.

Fonksiyonun grafiği çıkarıldığında özellikle ilgi çekici olan durumdur. değişken nokta sonsuza kadar bir düz çizgiye süresiz olarak yaklaşır.

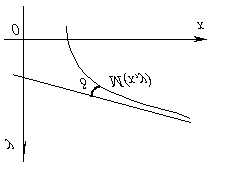
Doğrudan arandı asimptot fonksiyon grafiği y = f(x) değişken noktadan uzaklık ise M nokta kaldırıldığında bu çizgiye grafik M sonsuza sıfıra eğilimlidir, yani fonksiyonun grafiğinin noktası, sonsuza meylettiği için, asimptota süresiz olarak yaklaşmalıdır.

Eğri, asimptota yaklaşabilir, bir tarafında kalabilir veya farklı taraflar, sonsuz küme asimptotu bir kez geçmek ve onun bir tarafından diğer tarafına geçmek.

Noktadan uzaklığı d ile gösterirsek M asimptot eğrisi, nokta kaldırıldıkça d'nin sıfıra eğilimli olduğu açıktır. M sonsuzluğa.

Dikey ve eğik asimptotlar arasında daha fazla ayrım yapacağız.

DİKEY ASYMPTOTLAR

izin ver X→ x0 fonksiyonun her iki tarafı y = f(x) mutlak değerde süresiz olarak artar, yani yada yada . Ardından, asimptotun tanımından, çizginin X = x0 bir asimptottur. Satır varsa sohbet de açıktır X = x0 bir asimptottur, yani .

Böylece, fonksiyonun grafiğinin dikey asimptotu y = f(x) eğer çizgi denir f(x)→ ∞ koşullardan en az biri altında X→ x0– 0 veya X → x0 + 0, X = x0

Bu nedenle, fonksiyonun grafiğinin dikey asimptotlarını bulmak için y = f(x) bu değerleri bulman lazım X = x0, burada fonksiyon sonsuza gider (sonsuz bir süreksizliğe maruz kalır). O zaman dikey asimptot denkleme sahiptir X = x0.

Örnekler.

EĞİMLİ ASYMPTOTLAR

Asimptot düz bir çizgi olduğundan, eğer eğri y = f(x) eğik bir asimptota sahipse denklemi şu şekilde olacaktır: y = kx + B. Görevimiz katsayıları bulmaktır. k Ve B.

teorem. Dümdüz y = kx + B eğik bir asimptot olarak hizmet eder X→ +∞ fonksiyonun grafiği için y = f(x) ancak ve ancak . için de benzer bir ifade doğrudur. X → –∞.

Kanıt. İzin vermek Milletvekili- segmentin uzunluğu, mesafeye eşit noktadan M asimptota. Koşula göre. Asimptotun eksene eğim açısını φ ile belirtin Öküz. Sonra ΔMNP bunu takip eder. φ sabit bir açı olduğundan (φ ≠ π/2), o zaman , fakat

Talimat

puan bükülme fonksiyonlarönce bulunması gereken tanımının kapsamına ait olmalıdır. Takvim fonksiyonlar- Bu, sürekli veya kesintili olabilen, monoton azalan veya artan, minimum veya maksimum olan bir çizgidir. puan(asimptotlar), dışbükey veya içbükey olun. İki kişilik ani değişiklik son durumlar ve kink denir.

Gerekli kondisyon varoluş bükülme fonksiyonlar saniyenin sıfıra eşitliğinden oluşur. Böylece, fonksiyonun iki kez türevini alarak ve ortaya çıkan ifadeyi sıfıra eşitleyerek, olası noktaların apsisini bulabiliriz. bükülme.

Bu koşul, grafiğin dışbükeylik ve içbükeylik özelliklerinin tanımından kaynaklanır. fonksiyonlar, yani negatif ve pozitif değer ikinci türev. Noktada bükülme ani değişiklik bu özellikler, daha sonra türev sıfıra gider. Bununla birlikte, sıfıra eşitlik, bir bükülme noktasını belirtmek için hala yeterli değildir.

Bir önceki aşamada bulunan apsisin o noktaya ait olması için iki yeterli koşul vardır. bükülme:Bu noktadan bir teğet çizebilirsiniz. fonksiyonlar. İkinci türev, beklenen değerin sağında ve solunda farklı işaretlere sahiptir. puan bükülme. Bu nedenle, noktanın kendisinde bulunması gerekli değildir, o noktada işaret değiştirdiğini belirlemek yeterlidir. fonksiyonlar sıfırdır ve üçüncü değildir.

Çözüm: bulun. İÇİNDE bu durum herhangi bir kısıtlama yoktur, bu nedenle, gerçek sayıların tüm uzayıdır. Birinci türevi hesaplayın: y' = 3 ∛ (x - 5) + (3 x + 3) / ∛ (x - 5)².

Dikkat et . Bundan, türevin tanım alanının sınırlı olduğu sonucu çıkar. x = 5 noktası delinmiştir, bu da içinden bir teğetin geçebileceği anlamına gelir, bu da kısmen ilk yeterlilik işaretine karşılık gelir bükülme.

Ortaya çıkan ifadeyi x → 5 - 0 ve x → 5 + 0'da belirleyin. Bunlar -∞ ve +∞'ye eşittir. x=5 noktasından dikey bir teğetin geçtiğini ispatladınız. Bu nokta bir nokta olabilir. bükülme, ancak önce ikinci türevi hesaplayın: (2 x - 22)/∛(x - 5)^5.

Paydayı atlayın, çünkü zaten x = 5 noktasını hesaba kattınız. 2 x - 22 \u003d 0 denklemini çözün. Tek bir x \u003d 11 kökü vardır. Son adım, bunu doğrulamaktır. puan x=5 ve x=11 puandır bükülme. Çevrelerindeki ikinci türevin davranışını analiz edin. Açıkçası, x = 5 noktasında işareti "+" dan "-" ye ve x = 11 noktasında, tersi değişir. Sonuç: ikisi de puan noktalar bükülme. Birinci yeterli koşul sağlanır.