Tanım . Bir fonksiyonun grafiğinin asimptotu, bir fonksiyonun grafiğindeki bir noktadan bu düz çizgiye olan mesafenin, grafik noktası orijinden süresiz olarak hareket ettikçe sıfıra yönelme özelliğine sahip düz bir çizgidir..

Bunları bulma yöntemlerine göre üç tür asimptot ayırt edilir: dikey, yatay, eğik.

Açıkçası, yatay olanlar eğimli olanların ('da) özel durumlarıdır.

Bir fonksiyonun grafiğinin asimptotlarının bulunması aşağıdaki ifadelere dayanmaktadır.

Teorem 1 . Fonksiyonun en azından bir noktanın yarı komşuluğunda tanımlı olduğunu ve bu noktadaki tek taraflı limitlerinden en az birinin sonsuz olduğunu varsayalım; eşitlendi. O halde düz çizgi, fonksiyonun grafiğinin dikey asimptotudur..

Bu nedenle, bir fonksiyonun grafiğinin dikey asimptotları, fonksiyonun süreksizlik noktalarında veya tanım kümesinin uçlarında (eğer bunlar sonlu sayılar ise) aranmalıdır.

Teorem 2 . Fonksiyonun mutlak değeri yeterince büyük argüman değerleri için tanımlansın ve fonksiyonun sonlu bir limiti olsun . O halde düz çizgi, fonksiyonun grafiğinin yatay asimptotudur.

öyle olabilir , A ve ve sonlu sayılar ise, grafiğin iki farklı değeri vardır. yatay asimptotlar: sol el ve sağ el. Eğer sonlu limitlerden yalnızca biri mevcutsa, o zaman grafiğin ya bir sol yönlü ya da bir sağ yönlü yatay asimptotu vardır.

Teorem 3 . Mutlak değerde yeterince büyük argüman değerleri için fonksiyon tanımlansın ve var olsun sonlu sınırlarVe . O halde düz çizgi, fonksiyonun grafiğinin eğik asimptotudur..

Bu sınırlardan en az birinin sonsuz olması halinde eğik asimptot olmayacağını unutmayın.

Yatay asimptot gibi eğik bir asimptot da tek taraflı olabilir.

Örnek. Fonksiyonun grafiğinin tüm asimptotlarını bulun.

Çözüm.

Fonksiyon adresinde tanımlanır. Noktalardaki tek taraflı limitlerini bulalım.

Çünkü Ve (diğer iki tek taraflı limit artık bulunamayabilir), bu durumda düz çizgiler fonksiyonun grafiğinin dikey asimptotlarıdır.

Haydi hesaplayalım

(L'Hopital kuralını uygulayın) = .

Bu, düz çizginin yatay bir asimptot olduğu anlamına gelir.

Yatay asimptot mevcut olduğundan, artık eğimli olanları aramıyoruz (onlar mevcut değil).

Cevap: Grafiğin iki dikey asimptotu ve bir yatay asimptotu vardır.

Genel araştırma fonksiyonlarısen = F (X ).

Fonksiyonun kapsamı. Tanım alanını bulun D(F). Çok zor değilse aralığını da bulmakta fayda var e(F). (Ancak çoğu durumda bulma sorunu e(F) fonksiyonun ekstremum değerleri bulunana kadar ertelenir.)

Fonksiyonun özel özellikleri. Açığa çıkarmak Genel Özellikler işlevler: çift, tek, periyodiklik vb. Her fonksiyonun çift veya tek gibi özellikleri yoktur. Bir fonksiyonun tanım bölgesi eksen üzerindeki 0 noktasına göre asimetrikse, bu fonksiyon açıkça ne çift ne de tektir. Öküz. Aynı şekilde, herhangi bir periyodik fonksiyon için tanım alanı ya tüm gerçek eksenden ya da periyodik olarak tekrarlanan aralık sistemlerinin birleşiminden oluşur.

Dikey asimtotlar. Argüman tanım kümesinin sınır noktalarına yaklaştığında fonksiyonun nasıl davrandığını öğrenin D(F), eğer bu tür sınır noktaları mevcutsa. Bu durumda dikey asimptotlar ortaya çıkabilir. Bir fonksiyonun tanımlanmamış süreksizlik noktaları varsa, bu noktalarda fonksiyonun düşey asimptotlarının varlığı da kontrol edilmelidir.

Eğik ve yatay asimptotlar. Tanım alanı ise D(F) (a;+) veya (−;b) formundaki ışınları içeriyorsa, sırasıyla x+ veya x− için eğik asimptotları (veya yatay asimptotları) bulmayı deneyebilirsiniz, yani limxf(x)'i bulun. Eğik asimptotlar : sen = kx + B, burada k=limx+xf(x) ve b=limx+(f(x)−x). Asimptotlar yataydır : sen = B, burada limxf(x)=b.

Grafiğin eksenlerle kesişme noktalarını bulma. Grafiğin eksenle kesişme noktasını bulma Oy. Bunu yapmak için değeri hesaplamanız gerekir. F(0). Grafiğin eksenle kesişme noktalarını da bulun Öküz, neden denklemin köklerini buluyoruz? F(X) = 0 (veya kök olmadığından emin olun). Denklem genellikle yalnızca yaklaşık olarak çözülebilir, ancak kökleri ayırmak grafiğin yapısının daha iyi anlaşılmasına yardımcı olur. Daha sonra, kökler ve kesme noktaları arasındaki aralıklarda fonksiyonun işaretini belirlemeniz gerekir.

Grafiğin asimptotla kesişme noktalarını bulma. Bazı durumlarda bulmak gerekli olabilir karakteristik noktalarönceki paragraflarda bahsedilmeyen grafikler. Örneğin, bir fonksiyonun eğik bir asimptotu varsa grafiğin bu asimptotla kesişim noktaları olup olmadığını bulmaya çalışabilirsiniz.

Dışbükeylik ve içbükeylik aralıklarını bulma. Bu, ikinci türev f(x)'in işareti incelenerek yapılır. Dışbükey ve içbükey aralıkların birleşim noktalarındaki bükülme noktalarını bulun. Fonksiyonun büküm noktalarındaki değerini hesaplayın. Bir fonksiyonun başka süreklilik noktaları varsa (hariç) Eğilme noktaları), ikinci türevin 0'a eşit olduğu veya mevcut olmadığı durumlarda, bu noktalarda fonksiyonun değerini hesaplamak da faydalıdır. f(x)'i bulduktan sonra f(x)0 eşitsizliğini çözüyoruz. Çözüm aralıklarının her birinde fonksiyon aşağı doğru dışbükey olacaktır. Ters f(x)0 eşitsizliğini çözerek, fonksiyonun yukarı doğru dışbükey (yani içbükey) olduğu aralıkları buluruz. Bükülme noktalarını, fonksiyonun dışbükeylik yönünü değiştirdiği (ve sürekli olduğu) noktalar olarak tanımlarız.

Bir fonksiyonun grafiğinin asimptotları

Bir fonksiyonun grafiğinin asimptotu y = f(x), grafik noktası başlangıç ​​noktasından süresiz olarak hareket ettikçe (x, f(x)) noktasından bu düz çizgiye olan mesafenin sıfıra yaklaşması özelliğine sahip bir düz çizgidir.

Şekil 3.10'da. verildi grafik örnekleri dikey, yatay Ve eğimli asimptot.

Grafiğin asimptotlarının bulunması aşağıdaki üç teoreme dayanmaktadır.

Dikey asimptot teoremi. y = f(x) fonksiyonunun x 0 noktasının belirli bir komşuluğunda tanımlandığını varsayalım (muhtemelen bu noktanın kendisi hariç) ve fonksiyonun tek taraflı limitlerinden en az biri sonsuza eşit olsun, yani. O halde x = x 0 düz çizgisi, y = f(x) fonksiyonunun grafiğinin dikey asimptotudur.

Açıkçası, eğer fonksiyon x 0 noktasında sürekli ise, x = x 0 düz çizgisi dikey bir asimptot olamaz, çünkü bu durumda . Sonuç olarak, fonksiyonun süreksizlik noktalarında veya tanım kümesinin uçlarında dikey asimptotlar aranmalıdır.

Yatay asimptot teoremi. Yeterince büyük x için y = f(x) fonksiyonu tanımlansın ve fonksiyonun sonlu bir limiti vardır. O halde y = b doğrusu, fonksiyonun grafiğinin yatay asimptotudur.

Yorum. Limitlerden sadece biri sonlu ise, o zaman fonksiyon buna göre, Solak veya sağ taraflı Yatay asimptot.

Bu durumda fonksiyonun eğik bir asimptotu olabilir.

Eğik asimptot teoremi. Yeterince büyük x için y = f(x) fonksiyonu tanımlansın ve sonlu limitler olsun . O halde y = kx + b düz çizgisi, fonksiyonun grafiğinin eğik asimptotudur.

Kanıt yok.

Eğik bir asimptot, tıpkı yatay bir asimptot gibi, karşılık gelen limitlerin tabanı belirli bir işaretin sonsuzluğu içeriyorsa sağ veya sol yönlü olabilir.

Fonksiyonları incelemek ve grafiklerini oluşturmak genellikle aşağıdaki adımları içerir:

1. Fonksiyonun tanım tanım kümesini bulun.

2. Çift-tek eşlik fonksiyonunu inceleyin.

3. Süreksizlik noktalarını ve fonksiyonun, eğer sonluysa, tanım bölgesinin sınırlarındaki davranışını inceleyerek düşey asimptotları bulun.

4. Fonksiyonun sonsuzdaki davranışını inceleyerek yatay veya eğik asimptotları bulun.

Bir fonksiyonun grafiğinin asimptotları

Asimptotun hayaleti, sonunda ayrı bir makalede ortaya çıkmak ve kafası karışan okuyuculara özel bir keyif vermek için uzun süredir sitede dolaşıyor. fonksiyonun tam çalışması. Bir grafiğin asimptotlarını bulmak bu görevin bu bölümde ele alınan birkaç bölümünden biridir. okul kursu olaylar hesaplama etrafında döndüğü için yalnızca genel bakışta fonksiyon sınırları, ama yine de ilgililer yüksek Matematik. Matematiksel analiz konusunda çok az bilgisi olan ziyaretçiler için ipucunun açık olduğunu düşünüyorum ;-) ...dur, dur, nereye gidiyorsun? Sınırlar- bu kolay!

Asimptot örneklerine ilk dersimizde hemen karşılaşıldı. temel fonksiyonların grafikleri ve konu şu anda ayrıntılı olarak ele alınmaktadır.

Peki asimptot nedir?

Hayal etmek değişken nokta, fonksiyonun grafiği boyunca "seyahat eden". Asimptot: dümdüz, neye süresiz olarak yakın bir fonksiyonun grafiği onu kaldırdığınızda ona yaklaşır değişken nokta sonsuzluğa.

Not : Gösterimde formülasyona ihtiyacınız varsa tanım anlamlıdır matematiksel analiz, lütfen öğreticiye bakın.

Düzlemde asimptotlar doğal konumlarına göre sınıflandırılır:

1) Dikey asimtotlar"alfa"nın olduğu formdaki bir denklemle verilir gerçek Numara. Popüler bir temsilci ordinat eksenini kendisi tanımlar,
hafif bir mide bulantısıyla abartıyı hatırlıyoruz.

2) Eğik asimptotlar geleneksel olarak yazılmış düz bir çizginin denklemiİle eğim. Bazen ayrı grup tahsis etmek özel durum – yatay asimptotlar. Örneğin asimptotlu aynı hiperbol.

Çabuk gidelim, kısa bir makineli tüfek ateşiyle konuya girelim:

Bir fonksiyonun grafiğinde kaç asimptot olabilir?

Bir, bir, iki, üç ya da sonsuz sayıda değil. Örnekler için fazla uzağa gitmeyeceğiz, hatırlayalım temel işlevler. Bir parabol, kübik parabol ve sinüs dalgasının asimptotu yoktur. üstel grafik, logaritmik fonksiyon benzersiz bir asimptotu vardır. Arktanjant ve arkkotanjant bunlardan iki taneye sahiptir ve teğet ve kotanjant sonsuz sayıdadır. Bir grafiğin hem yatay hem de dikey asimptotlara sahip olması alışılmadık bir durum değildir. Abartı, seni her zaman sevecek.

Ne demek ?

Bir fonksiyonun grafiğinin dikey asimptotları

Grafiğin dikey asimptotu genellikle bulunur sonsuz süreksizliğin noktasında işlevler. Çok basit: Eğer bir fonksiyonun bir noktada sonsuz süreksizliği varsa o zaman düz çizgi denklem tarafından verilen grafiğin dikey asimptotudur.

Not : Gösterimin tamamen ikiye atıfta bulunmak için kullanıldığını lütfen unutmayın. farklı kavramlar. Bir noktanın mı yoksa bir doğrunun denkleminin mi ima edildiği bağlama bağlıdır.

Bu nedenle, bir noktada dikey bir asimptotun varlığını belirlemek için şunu göstermek yeterlidir: en az bir tek taraflı sınırlardan sonsuz. Çoğu zaman bu, fonksiyonun paydasının olduğu noktadır. sıfıra eşit. Esasen, halihazırda dikey asimptotları bulduk. son örnekler ders Bir fonksiyonun sürekliliği hakkında. Ancak bazı durumlarda yalnızca tek taraflı bir sınır vardır ve eğer sonsuzsa, o zaman yine dikey asimptotu sevin ve tercih edin. En basit örnek: ve ordinat ekseni (bkz. Temel fonksiyonların grafikleri ve özellikleri).

Yukarıdakilerden şu da çıkıyor apaçık gerçek: eğer fonksiyon sürekli açıksa, o zaman dikey asimptot yoktur. Nedense aklıma bir parabol geldi. Gerçekten, buraya düz bir çizgiyi nereye "yapıştırabilirsiniz"? ...evet... anlıyorum... Freud Amca'nın takipçileri histerik hale geldi =)

Bunun tersi ifade genellikle yanlıştır: örneğin, fonksiyon sayı doğrusunda tanımlanmamıştır ancak asimptotlardan tamamen yoksundur.

Bir fonksiyonun grafiğinin eğimli asimptotları

Fonksiyonun argümanı "artı sonsuz" veya "eksi sonsuz" eğilimindeyse eğik (özel bir durum olarak - yatay) asimptotlar çizilebilir. Bu yüzden Bir fonksiyonun grafiğinde ikiden fazla eğik asimptot bulunamaz. Örneğin, bir üstel fonksiyonun grafiğinde tek bir yatay asimptot vardır ve arktanjantın grafiğinde bu tür iki asimptot vardır ve bu asimptotlarda farklıdır.

Her iki yerdeki grafik tek bir eğik asimptot'a yaklaştığında, "sonsuzluklar" genellikle şu şekilde birleştirilir: tek giriş. Örneğin, ...doğru tahmin ettiniz: .

Genel temel kural :

Eğer iki tane varsa son sınır , o zaman düz çizgi, fonksiyonun grafiğinin eğik asimptotudur. Eğer en az bir Listelenen sınırların sonsuz olması durumunda eğik asimptot yoktur.

Not : "x" yalnızca "artı sonsuza" veya yalnızca "eksi sonsuza" yöneliyorsa formüller geçerli kalır.

Parabolün eğik asimptotu olmadığını gösterelim:

Limit sonsuzdur, yani eğik asimptot yoktur. Limiti bulurken şunu unutmayın Cevap zaten alındığı için ihtiyaç ortadan kalktı.

Not : Artı-eksi, eksi-artı işaretlerini anlamakta zorlanıyorsanız (ya da yaşayacaksanız), lütfen dersin başındaki yardıma bakın.
sonsuz küçük fonksiyonlar üzerinde, size bu işaretleri nasıl doğru şekilde yorumlayacağınızı anlattım.

Açıkçası, herhangi bir ikinci dereceden ifade için, kübik fonksiyon, polinom 4'üncü ve daha yüksek dereceler ayrıca eğik asimptotlar da yoktur.

Şimdi grafiğin eğik asimptotu olmadığından da emin olalım. Belirsizliği ortaya çıkarmak için kullandığımız L'Hopital'in kuralı:
, kontrol edilmesi gereken şey buydu.

Ancak fonksiyon sonsuza kadar büyüdüğünde grafiğinin yaklaşacağı düz bir çizgi yoktur. sonsuz yakın.

Dersin pratik kısmına geçelim:

Bir fonksiyonun grafiğinin asimptotları nasıl bulunur?

Tam olarak bu şekilde formüle edilmiştir tipik görev ve grafiğin TÜM asimptotlarının (dikey, eğimli/yatay) bulunmasını içerir. Her ne kadar soruyu sorarken daha kesin olmak gerekirse, asimptotların varlığına yönelik araştırmalardan bahsediyoruz (sonuçta hiç olmayabilir). Basit bir şeyle başlayalım:

örnek 1

Bir fonksiyonun grafiğinin asimptotlarını bulun

Çözüm Bunu iki noktaya ayırmak uygun olur:

1) Öncelikle dikey asimptotların olup olmadığını kontrol ederiz. Payda sıfıra gider ve bu noktada fonksiyonun sorun yaşadığı hemen anlaşılır. sonsuz boşluk ve denklem tarafından verilen düz çizgi, fonksiyonun grafiğinin dikey asimptotudur. Ancak böyle bir sonuca varmadan önce tek taraflı sınırları bulmak gerekir:

Yazıda benzer şekilde üzerinde durduğum hesaplama tekniğini size hatırlatıyorum. Fonksiyonun sürekliliği. Kırılma noktaları. Limit işaretinin altındaki ifadede yerine koyarız. Payda ilginç bir şey yok:
.

Ancak paydada ortaya çıkıyor sonsuz küçük negatif bir sayı :
sınırın kaderini belirler.

Soldaki limit sonsuzdur ve prensip olarak dikey bir asimptotun varlığına dair bir karara varmak zaten mümkündür. Ancak tek taraflı sınırlara sadece bunun için ihtiyaç duyulmuyor, aynı zamanda ANLAŞILMASINA YARDIMCI OLUYORLAR NASIL Fonksiyonun grafiğini bulun ve oluşturun DOĞRU ŞEKİLDE. Bu nedenle sağ el limitini de hesaplamamız gerekir:

Çözüm: Tek taraflı limitler sonsuzdur, bu da düz çizginin fonksiyonun grafiğinin dikey asimptotu olduğu anlamına gelir.

İlk sınır sonlu, bu da "konuşmaya devam etmenin" ve ikinci sınırı bulmanın gerekli olduğu anlamına gelir:

İkinci sınır da sonlu.

Böylece asimptotumuz:

Çözüm: Denklem tarafından verilen düz çizgi, fonksiyonun grafiğinin yatay asimptotudur.

Yatay asimptotu bulmak için
basitleştirilmiş bir formül kullanabilirsiniz:

Varsa sonlu limit ise, bu durumda düz çizgi fonksiyonun grafiğinin yatay asimptotudur.

Fonksiyonun pay ve paydasının olduğunu görmek kolaydır. aynı büyüme sırası Bu, aranan sınırın sonlu olacağı anlamına gelir: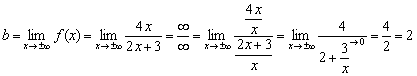

Cevap:

Duruma göre çizimi tamamlamanıza gerek yok, ancak tüm hızıyla devam ederse fonksiyon çalışması, sonra taslakta hemen bir eskiz yaparız:

Bulunan üç limite dayanarak, fonksiyonun grafiğinin nasıl konumlandırılabileceğini kendiniz bulmaya çalışın. Hiç zor mu? 5-6-7-8 noktayı bulun ve çizim üzerinde işaretleyin. Ancak bu fonksiyonun grafiği kullanılarak oluşturulur. bir temel fonksiyonun grafiğinin dönüşümleri Yukarıdaki makaledeki Örnek 21'i dikkatle inceleyen okuyucular bunun nasıl bir eğri olduğunu rahatlıkla tahmin edebilirler.

Örnek 2

Bir fonksiyonun grafiğinin asimptotlarını bulun

Bu bir örnektir bağımsız karar. Sürecin rahatlıkla iki noktaya bölündüğünü hatırlatmama izin verin: dikey asimptotlar ve eğik asimptotlar. Örnek çözümde yatay asimptot basitleştirilmiş bir şema kullanılarak bulunur.

Pratikte kesirli-rasyonel fonksiyonlarla en sık karşılaşılır ve hiperboller üzerinde eğitim aldıktan sonra görevi karmaşıklaştıracağız:

Örnek 3

Bir fonksiyonun grafiğinin asimptotlarını bulun

Çözüm: Bir, iki ve bitti:

1) Dikey asimptotlar bulunur sonsuz süreksizlik noktalarında, bu nedenle paydanın sıfıra gidip gitmediğini kontrol etmeniz gerekir. Haydi karar verelim ikinci dereceden denklem:

Diskriminant pozitif olduğundan denklemin iki gerçek kökü vardır ve iş önemli ölçüde artar =)

Tek taraflı limitleri daha da bulmak için ikinci dereceden üç terimliçarpanlara ayırmanın uygun olduğu:
(Kısa gösterim için “eksi” ilk parantez içine dahil edilmiştir). Güvenli tarafta olmak için parantezleri zihinsel olarak veya taslak üzerinde açarak kontrol edelim.

Fonksiyonu formda yeniden yazalım.

Bu noktada tek taraflı limitleri bulalım:

Ve bu noktada:

Dolayısıyla düz çizgiler, söz konusu fonksiyonun grafiğinin dikey asimptotlarıdır.

2) Eğer fonksiyona bakarsanız O zaman limitin sonlu olacağı ve yatay bir asimptotumuz olacağı oldukça açıktır. Kısaca varlığını gösterelim:

Dolayısıyla düz çizgi (apsis ekseni) bu fonksiyonun grafiğinin yatay asimptotudur.

Cevap:

Bulunan limitler ve asimptotlar fonksiyonun grafiği hakkında birçok bilgi sağlar. Aşağıdaki gerçekleri dikkate alarak çizimi zihinsel olarak hayal etmeye çalışın:

Grafiğin kendi versiyonunu taslağınıza çizin.

Elbette bulunan sınırlar grafiğin görünümünü net bir şekilde belirlemez ve hata yapabilirsiniz, ancak alıştırmanın kendisi sırasında çok değerli bir yardım sağlayacaktır. tam fonksiyon çalışması. Doğru resim dersin sonundadır.

Örnek 4

Bir fonksiyonun grafiğinin asimptotlarını bulun

Örnek 5

Bir fonksiyonun grafiğinin asimptotlarını bulun

Bunlar bağımsız çözüme yönelik görevlerdir. Her iki grafik de yine yatay asimptotlara sahiptir ve bunlar hemen şu şekilde tespit edilir: aşağıdaki işaretler: Örnek 4'te büyüme sırası payda Daha, payın büyüme sırasına göre ve Örnek 5'te pay ve payda aynı büyüme sırası. Örnek çözümde, ilk fonksiyon tam olarak eğik asimptotların varlığı açısından, ikincisi ise limit boyunca incelenir.

Benim öznel izlenimime göre yatay asimptotlar, "gerçekten eğik" olanlardan belirgin şekilde daha yaygındır. Uzun zamandır beklenen Genel dava:

Örnek 6

Bir fonksiyonun grafiğinin asimptotlarını bulun

Çözüm: türün klasikleri:

1) Payda pozitif olduğundan fonksiyon sürekli tüm sayı doğrusu boyunca ve dikey asimptotlar yoktur. …İyi mi? Kelime bu değil - harika! 1 No'lu nokta kapalı.

2) Eğik asimptotların varlığını kontrol edelim:

İlk sınır sonlu, o halde devam edelim. Ortadan kaldırmak için ikinci limitin hesaplanması sırasında belirsizlik "sonsuz eksi sonsuzluk" ifadeyi şuna indirgeriz: ortak payda:

İkinci sınır da sonlu Dolayısıyla söz konusu fonksiyonun grafiğinin eğik bir asimptotu vardır:

Çözüm:

Böylece, fonksiyonun grafiği sonsuz yakın düz bir çizgiye yaklaşır:

Orijinde eğik asimptotuyla kesiştiğine ve bu tür kesişme noktalarının oldukça kabul edilebilir olduğuna dikkat edin - sonsuzda "her şeyin normal olması" önemlidir (aslında asimptotlardan bahsettiğimiz yer burasıdır).

Örnek 7

Bir fonksiyonun grafiğinin asimptotlarını bulun

Çözüm: Yorum yapacak özel bir şey yok o yüzden resmileştireceğim yaklaşık örnek son çözüm:

1) Dikey asimptotlar. Gelin noktayı keşfedelim.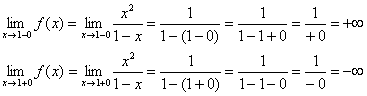

Düz çizgi, grafiğin dikey asimptotudur.

2) Eğik asimptotlar:

Düz çizgi, grafiğin eğik asimptotudur.

Cevap:

Bulunan tek taraflı limitler ve asimptotlar, bu fonksiyonun grafiğinin neye benzeyeceğini yüksek bir güvenle tahmin etmemizi sağlar. Dersin sonunda doğru çizim.

Örnek 8

Bir fonksiyonun grafiğinin asimptotlarını bulun

Bu bağımsız çözüme bir örnektir; bazı limitlerin hesaplanmasında kolaylık sağlamak için payı paydaya, terime bölebilirsiniz. Yine sonuçlarınızı analiz ederken bu fonksiyonun grafiğini çizmeye çalışın.

Açıkçası, "gerçek" eğik asimptotların sahipleri bunların grafikleridir. kesirli rasyonel fonksiyonlar, payın derecesi daha yüksek olan bir tane daha paydanın en yüksek derecesi. Daha fazlaysa eğik asimptot olmayacaktır (örneğin, ).

Ancak hayatta başka mucizeler de olur:

Örnek 9

Örnek 11

Bir fonksiyonun grafiğini asimptotların varlığı açısından inceleyin

Çözüm: belli ki bu nedenle yalnızca fonksiyonun grafiğinin bulunduğu sağ yarı düzlemi dikkate alıyoruz.

Dolayısıyla, düz çizgi (koordinat ekseni), fonksiyonun grafiğinin .'deki dikey asimptotudur.

2) Eğik asimptot üzerine çalışma şu şekilde yapılabilir: tam şema, ancak makalede L'Hopital'in kuralları bunu öğrendik doğrusal fonksiyon Daha yüksek sipariş logaritmik büyümeden daha fazla, bu nedenle: (Aynı dersteki Örnek 1'e bakın).

Sonuç: x ekseni, fonksiyonun grafiğinin yatay asimptotudur.

Cevap:
, Eğer ;
, Eğer .

Netlik sağlamak için çizim:

Görünüşte benzer bir fonksiyonun hiç asimptotu olmaması ilginçtir (dileyenler bunu kontrol edebilir).

İki son örneklerİçin bireysel çalışma:

Örnek 12

Bir fonksiyonun grafiğini asimptotların varlığı açısından inceleyin

Çoğu durumda, ilk önce eğrinin asimptotlarını oluşturursanız bir fonksiyonun grafiğini oluşturmak daha kolaydır.

Tanım 1. Asimptotlar, değişken artı sonsuza veya eksi sonsuzluğa eğilim gösterdiğinde, bir fonksiyonun grafiğinin keyfi olarak yakından yaklaştığı düz çizgilerdir.

Tanım 2. Değişken noktadan uzaklığı varsa, bir fonksiyonun grafiğinin asimptotu düz bir çizgiye denir. M fonksiyonun bu doğruya kadar olan grafiği, nokta sonsuza kadar uzaklaştıkça sıfıra yönelir M orijinden itibaren fonksiyon grafiğinin herhangi bir dalı boyunca.

Üç tür asimptot vardır: dikey, yatay ve eğik.

Dikey asimtotlar

Tanım. Dümdüz X = A dır-dir fonksiyonun grafiğinin dikey asimptotu , eğer nokta X = A dır-dir ikinci türün süreksizlik noktası bu işlev için.

Tanımdan şu sonuç çıkıyor: düz çizgi X = A fonksiyonun grafiğinin dikey asimptotudur F(X) koşullardan en az birinin karşılanması durumunda:

Bu durumda fonksiyon F(X) sırasıyla hiç tanımlanamayabilir, X ≥ A Ve X ≤ A .

Yorum:

Örnek 1. Bir fonksiyonun grafiği sen=n X dikey bir asimptotu var X= 0 (yani eksenle çakışıyor) Oy) tanım alanının sınırında, çünkü x sağdan sıfıra doğru yönelirken fonksiyonun limiti eksi sonsuza eşittir:

(yukarıdaki resim).

kendiniz ve ardından çözümleri görün

Örnek 2. Fonksiyonun grafiğinin asimptotlarını bulun.

Örnek 3. Bir fonksiyonun grafiğinin asimptotlarını bulun

Yatay asimptotlar

If (argüman olarak bir fonksiyonun limiti artı veya eksi sonsuza doğru belirli bir değere eşitse) B), O sen = B – Yatay asimptot çarpık sen = F(X ) (X artı sonsuza doğru eğilim gösterdiğinde sağ, X eksi sonsuza doğru eğilim gösterdiğinde sol ve X artı veya eksi sonsuza doğru eğilim gösterdiğinde sınırlar eşitse iki taraflı).

Örnek 5. Bir fonksiyonun grafiği

en A> 1 yatay asimpototu bıraktı sen= 0 (yani eksenle çakışıyor) Öküz), çünkü “x” eksi sonsuza doğru gittiği için fonksiyonun limiti sıfırdır:

"x" artı sonsuza eğilim gösterdiğinden fonksiyonun limiti sonsuza eşit olduğundan eğrinin sağ yatay asimptotu yoktur:

Eğik asimptotlar

Yukarıda incelediğimiz dikey ve yatay asimptotlar koordinat eksenlerine paralel olduğundan bunları oluşturmak için yalnızca ihtiyacımız vardı. belli bir sayı- Asimptotun içinden geçtiği apsis veya ordinat ekseni üzerindeki bir nokta. Eğik bir asimptot için daha büyük bir eğime ihtiyaç vardır k düz çizginin eğim açısını gösteren ve Ücretsiz Üye Bçizginin orijinin ne kadar üstünde veya altında olduğunu gösterir. Analitik geometriyi ve ondan düz çizgi denklemlerini unutmayanlar, eğik asimptot için buldukları şeyin farkına varacaklardır. eğimi olan bir doğrunun denklemi. Eğik bir asimptotun varlığı, az önce bahsedilen katsayıların bulunduğu aşağıdaki teorem ile belirlenir.

Teorem. Eğriyi yapmak için sen = F(X) bir asimptotu vardı sen = kx + B sonlu sınırların olması gerekli ve yeterlidir k Ve B Değişken eğiliminde olduğundan söz konusu fonksiyonun X artı sonsuza ve eksi sonsuza:

(1)

(2)

Bu şekilde bulunan sayılar k Ve B ve eğik asimptot katsayılarıdır.

İlk durumda (x artı sonsuza doğru eğilim gösterdiği için) sağa eğimli bir asimptot elde edilir, ikinci durumda (x eksi sonsuza doğru eğilim gösterdiği için) bir sola eğik asimptot elde edilir. Sağ eğik asimptot Şekil 2'de gösterilmektedir. altında.

Eğik bir asimptot için denklemi bulurken, X'in hem artı sonsuza hem de eksi sonsuza olan eğilimini hesaba katmak gerekir. Bazı fonksiyonlar için, örneğin kesirli rasyonel olanlar için, bu sınırlar çakışır, ancak birçok fonksiyon için bu sınırlar farklıdır ve bunlardan yalnızca biri mevcut olabilir.

Limitler çakışıyorsa ve x artı sonsuza ve eksi sonsuzluğa yöneliyorsa, düz çizgi sen = kx + B eğrinin iki taraflı asimptotudur.

Asimptotu tanımlayan limitlerden en az biri ise sen = kx + B , mevcut değilse, fonksiyonun grafiğinin eğik bir asimptotu yoktur (ancak dikey bir asimptotu olabilir).

Yatay asimptotun olduğunu görmek kolaydır. sen = B eğikliğin özel bir durumudur sen = kx + B en k = 0 .

Bu nedenle, herhangi bir yönde bir eğrinin yatay bir asimptotu varsa, o zaman bu yönde eğimli bir asimptot yoktur ve bunun tersi de geçerlidir.

Örnek 6. Bir fonksiyonun grafiğinin asimptotlarını bulun

Çözüm. Fonksiyon sayı doğrusu dışında tüm sayı doğrusunda tanımlanmıştır. X= 0, yani

Bu nedenle kırılma noktasında X= 0 eğrinin dikey bir asimptotu olabilir. Aslında, x soldan sıfıra doğru giderken fonksiyonun limiti artı sonsuza eşittir:

Buradan, X = 0 – dikey asimptot Bu fonksiyonun grafiği.

Bu fonksiyonun grafiğinin yatay bir asimptotu yoktur, çünkü x artı sonsuza doğru fonksiyonun limiti artı sonsuza eşittir:

Eğik bir asimptotun varlığını bulalım:

Sonlu sınırları var k= 2 ve B= 0. Dümdüz sen = 2X bu fonksiyonun grafiğinin iki yönlü eğik asimptotudur (örnek içindeki şekil).

Örnek 7. Bir fonksiyonun grafiğinin asimptotlarını bulun

Çözüm. Fonksiyonun bir kırılma noktası vardır X= −1 . Tek taraflı limitleri hesaplayalım ve süreksizliğin tipini belirleyelim:

Çözüm: X= −1 ikinci türden bir süreksizlik noktasıdır, dolayısıyla düz çizgi X= −1 bu fonksiyonun grafiğinin dikey asimptotudur.

Eğik asimptotları arıyoruz. Çünkü bu fonksiyon- kesirli-rasyonel, ve noktasındaki sınırlar çakışacaktır. Böylece, düz çizgi - eğik asimptotu denklemde değiştirmek için katsayıları buluyoruz:

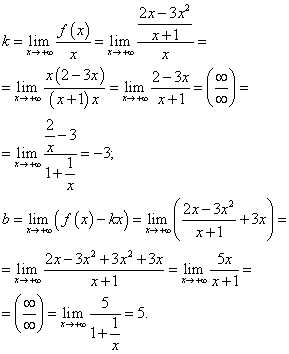
Bulunan katsayıları düz çizgi denkleminde eğim katsayısıyla değiştirerek eğik asimptot denklemini elde ederiz:

sen = −3X + 5 .

Şekilde fonksiyonun grafiği bordo renkle, asimptotlar ise siyah renkle gösterilmiştir.

Örnek 8. Bir fonksiyonun grafiğinin asimptotlarını bulun

Çözüm. Bu fonksiyon sürekli olduğundan grafiğinin dikey asimptotu yoktur. Eğik asimptotları arıyoruz:

.

Dolayısıyla bu fonksiyonun grafiğinin asimptotu vardır. sen= 0'dır ve 'de asiptodu yoktur.

Örnek 9. Bir fonksiyonun grafiğinin asimptotlarını bulun

Çözüm. İlk önce dikey asimptotları ararız. Bunu yapmak için fonksiyonun tanım tanım kümesini buluyoruz. Eşitsizlik ve olduğunda bir fonksiyon tanımlanır. Değişkenin işareti X işaretiyle eşleşir. Bu nedenle eşdeğer eşitsizliği düşünün. Bundan fonksiyonun tanım alanını elde ederiz: . Dikey bir asimptot yalnızca fonksiyonun tanım bölgesinin sınırında olabilir. Ancak X= 0 dikey bir asimptot olamaz çünkü fonksiyon şurada tanımlıdır: X = 0 .

Sağdan limiti göz önünde bulundurun (soldan limit yoktur):

.

Nokta X= 2 ikinci türden bir süreksizlik noktasıdır, yani düz çizgi X= 2 - bu fonksiyonun grafiğinin dikey asimptotu.

Eğik asimptotları arıyoruz:

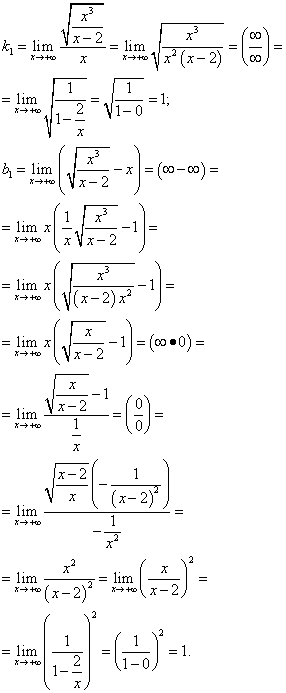
Bu yüzden, sen = X+ 1 - bu fonksiyonun grafiğinin eğik asimptotu. Eğik bir asimptot arıyoruz:

Bu yüzden, sen = −X − 1 - eğik asimptot .

Örnek 10. Bir fonksiyonun grafiğinin asimptotlarını bulun

Çözüm. Bir fonksiyonun bir tanım alanı vardır . Bu fonksiyonun grafiğinin dikey asimptotu yalnızca tanım kümesinin sınırında olabileceğinden, fonksiyonun tek taraflı limitlerini .