Fonksiyonun ekstremumunu bulun. Bir fonksiyonun artan, azalan ve ekstremum değerleri

Bir fonksiyonun ekstremumu nedir ve bir ekstremum için gerekli koşul nedir?

Bir fonksiyonun ekstremumu, fonksiyonun maksimum ve minimumudur.

Önkoşul Bir fonksiyonun maksimum ve minimum (ekstrem) değerleri şu şekildedir: f(x) fonksiyonunun x = a noktasında bir ekstremumu varsa, o zaman bu noktada türev ya sıfırdır ya da sonsuzdur ya da yoktur.

Bu koşul gereklidir ancak yeterli değildir. X = a noktasındaki türev sıfıra, sonsuza gidebilir veya fonksiyon bu noktada bir ekstremuma sahip olmadan var olmayabilir.

Nasıl bir şey yeterli koşul Fonksiyonun ekstremumu (maksimum veya minimum)?

İlk koşul:

Eğer x = a noktasına yeterli yakınlıkta f?(x) türevi a'nın solunda pozitif ve sağında negatif ise, o zaman x = a noktasında f(x) fonksiyonu şuna sahiptir: maksimum

Eğer x = a noktasına yeterli yakınlıkta f?(x) türevi a'nın solunda negatif ve sağında pozitif ise, o zaman x = a noktasında f(x) fonksiyonu şuna sahiptir: minimum f(x) fonksiyonunun burada sürekli olması şartıyla.

Bunun yerine, bir fonksiyonun ekstremumu için ikinci yeterli koşulu kullanabilirsiniz:

x = a noktasında birinci türev f?(x) sıfır olsun; f??(a) ikinci türevi negatifse, f(x) fonksiyonunun x = a noktasında maksimumu vardır, pozitifse minimumu vardır.

Bir fonksiyonun kritik noktası nedir ve nasıl bulunur?

Bu, fonksiyonun bir uç noktaya (yani maksimum veya minimum) sahip olduğu fonksiyon argümanının değeridir. Onu bulmak için ihtiyacın var türevi bul f?(x) fonksiyonu ve bunu sıfıra eşitleyerek, denklemi çöz f?(x) = 0. Bu denklemin kökleri ve bu fonksiyonun türevinin mevcut olmadığı noktalar kritik noktalardır, yani bir ekstremum olabilecek argümanın değerleridir. Bakılarak kolaylıkla tespit edilebilirler. türev grafiği: fonksiyonun grafiğinin apsis ekseniyle (Ox ekseni) kesiştiği ve grafiğin süreksizliklere maruz kaldığı argümanın değerleriyle ilgileniyoruz.

Örneğin, bulalım bir parabolün ekstremumu.

Fonksiyon y(x) = 3x2 + 2x - 50.

Fonksiyonun türevi: y?(x) = 6x + 2

Denklemi çözün: y?(x) = 0

6x + 2 = 0, 6x = -2, x = -2/6 = -1/3

İÇİNDE bu durumda kritik nokta x0=-1/3'tür. Fonksiyonun sahip olduğu bu argüman değeridir. ekstremum. Ona bulmak, "x" yerine fonksiyon yerine ifadede bulunan sayıyı yazın:

y0 = 3*(-1/3)2 + 2*(-1/3) - 50 = 3*1/9 - 2/3 - 50 = 1/3 - 2/3 - 50 = -1/3 - 50 = -50,333.

Bir fonksiyonun maksimum ve minimumu nasıl belirlenir? en büyük ve en küçük değerleri?

Türevin işareti geçerken kritik nokta x0 “artı”dan “eksi”ye değişir, sonra x0 olur maksimum nokta; türevin işareti eksiden artıya değişirse x0 minimum puan; işaret değişmezse, x0 noktasında ne maksimum ne de minimum vardır.

Ele alınan örnek için:

Kritik noktanın solundaki argümanın keyfi bir değerini alıyoruz: x = -1

x = -1'de türevin değeri y?(-1) = 6*(-1) + 2 = -6 + 2 = -4 olacaktır (yani işareti “eksi”).

Şimdi kritik noktanın sağındaki argümanın keyfi bir değerini alıyoruz: x = 1

x = 1'de türevin değeri y(1) = 6*1 + 2 = 6 + 2 = 8 olacaktır (yani işareti “artı”dır).

Gördüğünüz gibi kritik noktadan geçerken türevin işareti eksiden artıya değişti. Bu, x0 kritik değerinde minimum bir noktaya sahip olduğumuz anlamına gelir.

En büyük ve en küçük değer işlevler aralıkta(bir segment üzerinde) aynı prosedür kullanılarak bulunur, ancak belki de tüm kritik noktaların belirtilen aralıkta olmayacağı gerçeği dikkate alınır. Aralığın dışındaki kritik noktalar değerlendirme dışı bırakılmalıdır. Aralık içinde yalnızca bir kritik nokta varsa, bu noktanın ya maksimumu ya da minimumu olacaktır. Bu durumda fonksiyonun en büyük ve en küçük değerlerini belirlemek için fonksiyonun aralığın uçlarındaki değerlerini de dikkate alıyoruz.

Örneğin fonksiyonun en büyük ve en küçük değerlerini bulalım

y(x) = 3sin(x) - 0,5x

aralıklarla:

Yani fonksiyonun türevi

y?(x) = 3cos(x) - 0,5

3cos(x) - 0,5 = 0 denklemini çözüyoruz

cos(x) = 0,5/3 = 0,16667

x = ±arccos(0,16667) + 2πk.

[-9; 9]:

x = arccos(0,16667) - 2π*2 = -11,163 (aralığa dahil değildir)

x = -arccos(0,16667) – 2π*1 = -7,687

x = arccos(0,16667) - 2π*1 = -4,88

x = -arccos(0,16667) + 2π*0 = -1,403

x = arccos(0,16667) + 2π*0 = 1,403

x = -arccos(0,16667) + 2π*1 = 4,88

x = arccos(0,16667) + 2π*1 = 7,687

x = -arccos(0,16667) + 2π*2 = 11,163 (aralığa dahil değildir)

Fonksiyonun değerlerini şurada buluyoruz: kritik değerler argüman:

y(-7,687) = 3cos(-7,687) - 0,5 = 0,885

y(-4,88) = 3cos(-4,88) - 0,5 = 5,398

y(-1,403) = 3cos(-1,403) - 0,5 = -2,256

y(1,403) = 3cos(1,403) - 0,5 = 2,256

y(4,88) = 3cos(4,88) - 0,5 = -5,398

y(7,687) = 3cos(7,687) - 0,5 = -0,885

[-9; 9] en yüksek değer fonksiyon x = -4,88'dedir:

x = -4,88, y = 5,398,

ve en küçüğü - x = 4,88'de:

x = 4,88, y = -5,398.

[-6; -3] tek bir kritik noktamız var: x = -4,88. Fonksiyonun x = -4,88'deki değeri y = 5,398'e eşittir.

Aralığın sonunda fonksiyonun değerini bulun:

y(-6) = 3cos(-6) - 0,5 = 3,838

y(-3) = 3cos(-3) - 0,5 = 1,077

[-6; -3] fonksiyonun en büyük değerine sahibiz

y = 5,398, x = -4,88'de

en küçük değer -

x = -3'te y = 1,077

Bir fonksiyon grafiğinin bükülme noktaları nasıl bulunur ve dışbükey ve içbükey taraflar nasıl belirlenir?

Y = f(x) doğrusundaki tüm bükülme noktalarını bulmak için, ikinci türevi bulmanız, onu sıfıra eşitlemeniz (denklemi çözmeniz) ve ikinci türevin sıfır olduğu tüm x değerlerini test etmeniz gerekir, sonsuzdur veya yoktur. Bu değerlerden birinden geçerken ikinci türev işaret değiştirirse, fonksiyonun grafiği bu noktada bir bükülmeye sahiptir. Eğer değişmezse bükülme olmaz.

f denkleminin kökleri? (x) = 0, fonksiyonun ve ikinci türevinin olası süreksizlik noktalarının yanı sıra, fonksiyonun tanım bölgesini bir dizi aralığa böler. Aralıklarının her birindeki dışbükeylik, ikinci türevin işaretiyle belirlenir. İncelenen aralıktaki bir noktadaki ikinci türev pozitifse, o zaman y = f(x) doğrusu yukarıya doğru içbükeydir, negatifse aşağıya doğru içbükeydir.

İki değişkenli bir fonksiyonun ekstremumunu nasıl bulabilirim?

Spesifikasyon tanım kümesinde türevlenebilir f(x,y) fonksiyonunun ekstremumunu bulmak için şunlara ihtiyacınız vardır:

1) kritik noktaları bulun ve bunun için denklem sistemini çözün

fх? (x,y) = 0, yani? (x,y) = 0

2) her kritik nokta P0(a;b) için farkın işaretinin değişmeden kalıp kalmadığını araştırın

tüm (x;y) noktaları için P0'a yeterince yakın. Fark devam ederse olumlu işaret, o zaman P0 noktasında bir minimumumuz var, eğer negatifse o zaman bir maksimumumuz var. Eğer fark işaretini korumuyorsa P0 noktasında ekstremum yoktur.

Fonksiyonun ekstremumları benzer şekilde belirlenir. Daha argümanlar.

Bryansk Bölgesi Devlet Çalışma Müfettişliği'nin resmi web sitesini internette nerede bulabilirim?
www.rostrud.ru - Rostrud'un resmi web sitesi - Federal hizmet işgücü ve istihdam hakkında Rostrud referansı - 8-800-707-88-41 Rostrud'a elektronik bir itiraz gönderin (e-posta adresi: [e-posta korumalı]) git77.rostrud.ru &mda

İspanyol futbolu hakkında bilgiyi nerede bulabilirsiniz?
Primera Division (İspanyolca: Primera División), İspanya'da (İspanyolca: Liga de Fútbol Profesional, LFP) profesyonel bir futbol ligi olup, aynı zamanda Primera veya La Liga (İspanyolca: La Liga) olarak da bilinir, profesyonel bir futbol turnuvasıdır.

Rusya'nın resmi para birimi nedir
Ülke adı Adı - para/para değişimi Avustralya Avustralya doları/cent Avusturya Avusturya şilini/grosz - euro Azerbaycan Manat Arnavutluk Lek/kidarka Cezayir Cezayir dinarı/centimo Arjantin Arjantin austral/centavo Afganistan Afgan/pul Bangladeş Taka/pais Belçika Belçika frangı/centimo - Euro Bulgaristan Leva/stotinka

2 Kasım'da hangi ünlüler öldü?
2 Kasım yılın 306. günüdür (307. artık yıllar)V Gregoryen takvimi. Yıl sonuna 59 gün kaldı Tatiller 2 Kasım Ulusal: Virgin Adaları (ABD) - Özgürlük Günü; Belarus - Büyükbabalar (Anma Günü); Liberya - Şükran Günü; Meksika, Polonya, Po

Sıfır biçimlendirici son ekler nelerdir?
Sıfır eki nedir? Sıfır, konuşmadaki seslerle veya yazılı harflerle ifade edilmeyen, yardımıyla yeni kelimelerin oluşturulduğu bir ektir. Sıfır ek kullanarak kelime oluşturma yöntemine bazı kılavuzlarda eksiz, bazılarında ise sıfır ek denir. Sıfır son eki grafiksel olarak &Osla ile gösterilir

Ana kiracı kimdir?
Sabit kiracı - ana kiracı alışveriş merkezi, alıcıları ona çekiyor. Bir tanesi en önemli işaretler"Çapalar", müşteriler arasındaki tanınırlığını göz önünde bulundurur; bu, markanın ayrı bir mağaza biçiminde tanıtımını ve varlığını ima eder - örneğin Zara, M-video gibi sokak perakendeciliği

Rusya Ekonomi Akademisi'nin adını taşıyan resmi web sitesi nedir? G.V. Plehanov (REA)
Aşağıda ana şirketlerin resmi web siteleri bulunmaktadır. devlet üniversiteleri Moskova: Moskovski devlet üniversitesi M.V.'nin adını almıştır. Başsavcılık Lomonosov Akademisi Rusya Federasyonu Devlet Akademisi itfaiye servisi Rusya Akademisi EMERCOM ulusal ekonomi Rusya Federasyonu Hükümeti (ANH) Çalışma Akademisi ve sosyal ilişkiler(ATISO) Akademisyen

16 Mayıs'ta hangi tatiller kutlanıyor?
16 Mayıs, Gregoryen takvimine göre yılın 136. (artık yıllarda 137.) günüdür. Yıl sonuna 229 gün kaldı. 16 Mayıs'ta kutlanan etkinlikler ve bayramlar: Dünya AIDS'ten Ölenleri Anma Günü; Biyografi Yazarları Günü; Hindistan'da Apara Ekadashi. Dini olaylar Ortodoksluk: Pechersk Aziz Theodosius Günü; İtibaren

Yabani otun dağılım coğrafyası nedir?
Ambrosia pelin yıllık, ilkbahar sonu. Biyoloji ve morfoloji Gövde 20-200 cm boyunda, düz, panikulat dallı, üstte köşeli, zayıf veya oldukça kuvvetli, bastırılmış kıllı tüylere sahiptir. Kök kazık köktür, toprağa 4 m derinliğe kadar nüfuz eder. Yapraklar 4-15 cm uzunluğunda, üst kısmı koyu yeşil, neredeyse tüysüz, alt kısmı gri-yeşil, yoğun kıllı-tüylü; üst

Poikilotermik hayvanlar nelerdir?
Poikilothermic hayvanlar soğukkanlı hayvanlardır, sıcaklığa bağlı olarak değişen dengesiz iç vücut sıcaklığına sahip hayvanlardır. dış çevre. Poikilothermic hayvanlar tüm omurgasızları içerir ve omurgalılar arasında balıklar, amfibiler ve sürüngenler bulunur. Poikilotermik hayvanların vücut sıcaklığı genellikle ortam sıcaklığından yalnızca 1-20C daha yüksektir.

Pull-up'lar doğru şekilde nasıl yapılır
Pull-up'lar - temel egzersiz kol, sırt ve göğüs kasları için. Yukarı çekmek anahtar egzersiz, güç geliştiriyor. Pull-up'lar her zaman ve neredeyse her yerde yapılabilir; herhangi bir özel ekipman gerektirmez veya spor salonuna gitmeyi gerektirmez ki bu çok önemlidir. Bardaki pull-up'lar en çok etkili egzersiz Açık

Gördüğünüz gibi, bir fonksiyonun ekstremumunun bu işareti, o noktada en azından ikinci dereceden bir türevin varlığını gerektirir.

Örnek.

Fonksiyonun ekstremumunu bulun.

Çözüm.

Tanım alanıyla başlayalım:

Orijinal fonksiyonun türevini alalım:

x=1 yani bu olası bir ekstremum noktasıdır. Fonksiyonun ikinci türevini bulup değerini hesaplıyoruz.:

x = 1 x=1 Bu nedenle, bir ekstremum için ikinci yeterli koşula göre, - maksimum nokta. Daha sonra

- maksimum işlev.

Grafik illüstrasyon.

Cevap:

Bir fonksiyonun ekstremumu için üçüncü yeterli koşul. Fonksiyona izin ver y=f(x) kadar türevleri vardır N Noktanın -komşuluğundaki -inci mertebeden ve türevlere kadar n+1

Örnek.

-th'inci sıra noktanın kendisinde. Bırak olsun. .

Çözüm.

Fonksiyonun ekstremum noktalarını bulun

Orijinal fonksiyon rasyonel bir tam fonksiyondur; tanım alanı, gerçek sayılar kümesinin tamamıdır.

Fonksiyonun türevini alalım: Türev sıfıra gider

dolayısıyla bunlar olası ekstremum noktalarıdır. Bir ekstremum için üçüncü yeterli koşulu kullanalım.

İkinci türevi buluyoruz ve değerini olası ekstrem noktalarda hesaplıyoruz (ara hesaplamaları atlayacağız): Sonuç olarak maksimum nokta (elde ettiğimiz üçüncü yeterli ekstremum işareti için) n=1

Ve ). Noktaların doğasını öğrenmek için

üçüncü türevi buluyoruz ve değerini şu noktalarda hesaplıyoruz: Bu nedenle, fonksiyonun dönüm noktasıdır ( n=1

Geriye bu konuyla ilgilenmek kalıyor. Bu noktada dördüncü türevi bulup değerini hesaplıyoruz:

Bu nedenle fonksiyonun minimum noktasıdır.

- maksimum işlev.

Grafik illüstrasyon.

Maksimum nokta fonksiyonun minimum noktasıdır.

10. Bir fonksiyonun ekstremumu Bir ekstremun tanımı

y = f(x) fonksiyonu çağrılır artan (azalan) belirli bir aralıkta, eğer x 1 için< x 2 выполняется неравенство (f(x 1) < f (x 2) (f(x 1) >f(x2)).

Türevlenebilir fonksiyon y = f(x) bir aralıkta artarsa ​​(azalırsa), bu aralıktaki türevi f " (x)  0

(f" (x) = 0).

Nokta X O isminde yerel maksimum nokta (minimum) f(x) fonksiyonu, eğer noktanın bir komşuluğu varsa X O f(x) ≤ f(x о) (f(x) ≥ f(x о)) eşitsizliğinin doğru olduğu tüm noktalar için.

Maksimum ve minimum noktalara denir ekstrem noktalar ve fonksiyonun bu noktalardaki değerleri onun aşırılıklar.

Ekstrem noktalar

Bir ekstremum için gerekli koşullar. Eğer nokta X O f(x) fonksiyonunun bir uç noktası ise, bu durumda ya f " (x o) = 0 olur ya da f (x o) mevcut olmaz. Bu tür noktalara denir kritik, ve fonksiyonun kendisi kritik noktada tanımlanır. Bir fonksiyonun ekstremum değerleri kritik noktaları arasında aranmalıdır.

İlk yeterli koşul.İzin vermek X O- kritik nokta. Eğer f "(x) bir noktadan geçerken X O artı işaretini eksi olarak değiştirir, ardından bu noktada X O fonksiyonun bir maksimumu vardır, aksi takdirde bir minimumu vardır. Kritik noktadan geçerken türev işaret değiştirmiyorsa, o noktada X O aşırı bir durum yok.

İkinci yeterli koşul. f(x) fonksiyonunun noktanın yakınında bir f " (x) türevi olsun X O ve noktanın kendisindeki ikinci türev X O. Eğer f "(x o) = 0, >0 (<0), то точка X O f(x) fonksiyonunun yerel minimum (maksimum) noktasıdır. =0 ise ya ilk yeterli koşulu kullanmanız ya da daha yüksek türevleri kullanmanız gerekir.

Bir parça üzerinde y = f(x) fonksiyonu minimum veya maksimum değerine kritik noktalarda veya parçanın uçlarında ulaşabilir.

Örnek 3.22. f(x) = 2x 3 - 15x 2 + 36x - 14 fonksiyonunun ekstremumunu bulun.

Çözüm. F "(x) = 6x 2 - 30x +36 = 6(x ​​-2)(x - 3) olduğundan, x 1 = 2 ve x 2 = 3 fonksiyonunun kritik noktaları. Ekstrem yalnızca şu şekilde olabilir: x 1 = 2 noktasından geçerken türevin işareti artıdan eksiye değiştiği için, bu noktada fonksiyon bir maksimuma sahiptir. x 2 = 3 noktasından geçerken türevin işareti eksiden değişir. artıya, dolayısıyla x 2 = 3 noktasında fonksiyonun minimum değeri vardır. Fonksiyonun x 1 = 2 ve x 2 = 3 noktalarındaki değerlerini hesapladıktan sonra fonksiyonun ekstremumunu buluruz: maksimum f( 2) = 14 ve minimum f(3) = 13.

Sürekli bir fonksiyonun grafiğini düşünün Fonksiyona izin verşekilde gösterilmiştir.

Bir noktada fonksiyon değeri X 1, hem solundaki hem de sağındaki tüm komşu noktalardaki fonksiyon değerlerinden büyük olacaktır X 1. Bu durumda fonksiyonun şu noktada olduğunu söylüyoruz. X Maksimum 1. bu noktada X Fonksiyon 3'ün de bir maksimumu olduğu açıktır. konuyu ele alırsak X 2 ise, içindeki fonksiyon değeri tüm komşu değerlerden küçüktür. Bu durumda fonksiyonun şu noktada olduğunu söylüyoruz. X 2 minimum. Aynı şekilde nokta için X 4 .

İşlev Fonksiyona izin ver bu noktada X 0 var maksimum, eğer fonksiyonun bu noktadaki değeri, o noktayı içeren bir aralığın tüm noktalarındaki değerlerinden büyükse X 0, yani eğer bir noktanın böyle bir komşuluğu varsa X 0, herkes içindir X≠X 0 , bu mahalleye ait eşitsizlik devam ediyor f(x)<f(x 0 ) .

İşlev Fonksiyona izin ver sahip olmak minimum bu noktada X 0 , eğer bir noktanın böyle bir komşuluğu varsa X 0 , bu herkes için X≠X 0 bu mahalleye ait, eşitsizlik geçerli f(x)>f(x 0.

Fonksiyonun maksimum ve minimum değerine ulaştığı noktalara ekstrem noktalar, fonksiyonun bu noktalardaki değerlerine ise fonksiyonun ekstremum değerleri denir.

Bir parça üzerinde tanımlanan bir fonksiyonun maksimum ve minimum değerlerine ancak söz konusu parçanın içerdiği noktalarda ulaşabileceğine dikkat edelim.

Bir fonksiyonun bir noktada maksimuma sahip olması, o noktada fonksiyonun tüm tanım alanında en büyük değere sahip olduğu anlamına gelmediğini unutmayın. Yukarıda tartışılan şekilde, noktadaki fonksiyon X 1'in bir maksimumu vardır, ancak fonksiyon değerlerinin noktadan daha büyük olduğu noktalar olmasına rağmen X 1 . özellikle, F(X 1) < F(X 4) yani Fonksiyonun minimumu maksimumundan büyüktür. Maksimumun tanımından yalnızca bunun, fonksiyonun maksimum noktasına yeterince yakın noktalardaki en büyük değeri olduğu sonucu çıkar.

Teorem 1. (Bir ekstremun varlığı için gerekli koşul.) Türevlenebilir fonksiyon ise Fonksiyona izin verşu noktada var x=x ekstremum 0 ise bu noktadaki türevi sıfır olur.

Kanıt. Kesinlik açısından şu noktada X 0 fonksiyonunun maksimumu vardır. Daha sonra, yeterince küçük artışlar için Δ X sahibiz f(x 0 + Δ X) 0 ) yani Ama sonra

Bu eşitsizlikleri Δ'daki limite geçirmek X→ 0 ve türev dikkate alındığında F "(X 0) vardır ve bu nedenle soldaki limit Δ'nın nasıl olduğuna bağlı değildir. X→ 0, şunu elde ederiz: Δ'da X → 0 – 0 F"(X 0) ≥ 0 a'da Δ X → 0 + 0 F"(X 0) ≤ 0. Çünkü F"(X 0) bir sayıyı tanımlıyorsa bu iki eşitsizlik ancak şu durumlarda uyumludur: F"(X 0) = 0.

Kanıtlanmış teorem, maksimum ve minimum noktaların yalnızca türevin sıfır olduğu argümanın değerleri arasında olabileceğini belirtir.

Bir fonksiyonun belirli bir parçanın tüm noktalarında türevinin olduğu durumu düşündük. Türevin bulunmadığı durumlarda durum nedir? Örneklere bakalım.

Örnekler.

1. sen=|X|.

   Fonksiyonun bu noktada türevi yoktur X=0 (bu noktada fonksiyonun grafiğinin tanımlanmış bir teğeti yoktur), ancak bu noktada fonksiyonun bir minimumu vardır, çünkü sen(0)=0 ve tümü için X≠ 0sen > 0.



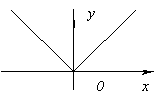
Fonksiyonun türevi yoktur X=0, sonsuza gittiği için X=0. Ancak bu noktada fonksiyonun maksimumu vardır.



Fonksiyonun türevi yoktur X=0, çünkü en X→0. Bu noktada fonksiyonun ne maksimumu ne de minimumu vardır. Gerçekten mi, f(x)=0 ve X<0f(x)<0, а при X>0f(x)>0.



Dolayısıyla verilen örneklerden ve formüle edilen teoremden, bir fonksiyonun yalnızca iki durumda bir ekstrema sahip olabileceği açıktır: 1) türevin mevcut olduğu ve sıfıra eşit olduğu noktalarda; 2) Türevin bulunmadığı noktada.

Ancak eğer bir noktada X 0 bunu biliyoruz f "(x 0 ) =0 ise bundan şu noktada sonuç çıkarılamaz: X 0 fonksiyonun bir ekstremumu vardır.

Örneğin. .



Ama dönem X=0 bir ekstrem nokta değildir, çünkü bu noktanın solunda fonksiyon değerleri eksenin altında yer alır Öküz ve sağ üstte.

Fonksiyonun türevinin sıfır olduğu veya mevcut olmadığı bir fonksiyonun tanım kümesindeki bir argümanın değerlerine denir kritik noktalar.




Yukarıdakilerin hepsinden, fonksiyonun uç noktalarının kritik noktalar arasında olduğu sonucu çıkar, ancak her kritik nokta bir uç nokta değildir. Bu nedenle, bir fonksiyonun ekstremumunu bulmak için, fonksiyonun tüm kritik noktalarını bulmanız ve ardından bu noktaların her birini maksimum ve minimum için ayrı ayrı incelemeniz gerekir. Aşağıdaki teorem bu amaca hizmet eder.

Teorem 2. (Bir ekstremumun varlığı için yeterli koşul.) Fonksiyonun kritik noktayı içeren bir aralıkta sürekli olmasına izin verin X 0'dır ve bu aralığın tüm noktalarında türevlenebilirdir (belki de noktanın kendisi hariç) X 0). Bu noktadan soldan sağa doğru hareket ederken türevin işareti artıdan eksiye değişirse, o zaman bu noktada X = X 0 fonksiyonunun maksimumu vardır. Eğer geçerken X Soldan sağa 0, türevin işareti eksiden artıya değişir, o zaman fonksiyonun bu noktada minimumu vardır.

Böylece eğer

Kanıt. Öncelikle şunu varsayalım ki geçerken X 0 türevin işareti artıdan eksiye değişir, yani. herkesin önünde X, noktaya yakın X 0 f "(x)> 0 için X< x 0 , f "(x)< 0 için x>x 0. Lagrange teoremini farka uygulayalım f(x) - f(x) 0 ) = f "(c)(x- x 0), nerede C arasında yatıyor X Ve X 0 .

1. İzin vermek X< x 0. Daha sonra C< x 0 ve f "(c)> 0. Bu yüzden f "(c)(x- x 0)< 0 ve dolayısıyla

   f(x) - f(x) 0 )< 0, yani f(x)< f(x 0 ).

2. İzin vermek x > x 0. Daha sonra c>x 0 ve f "(c)< 0. Araç f "(c)(x- x 0)< 0. Bu yüzden f(x) - f(x) 0 ) <0,т.е.f(x)< f(x 0 ) .

Böylece tüm değerler için X yeterince yakın X 0 f(x)< f(x 0 ) . Ve bu şu anlama geliyor: o noktada X 0 fonksiyonunun maksimumu vardır.

Minimum teoremin ikinci kısmı da benzer şekilde kanıtlanır.



Bu teoremin anlamını şekilde açıklayalım. İzin vermek f "(x 1 ) =0 ve herhangi biri için X, yeterince yakın X 1, eşitsizlikler sağlandı

f "(x)< 0 saat X< x 1 , f "(x)> 0 saat x>x 1 .

Daha sonra noktanın solunda X 1 fonksiyon sağda artar ve azalır, bu nedenle X = X 1 fonksiyon artandan azalana doğru gider, yani maksimumu vardır.

Benzer şekilde noktaları da dikkate alabiliriz. X 2 ve X 3 .


Yukarıdakilerin tümü resimde şematik olarak gösterilebilir:

Ekstremum için y=f(x) fonksiyonunu inceleme kuralı

1. Bir fonksiyonun tanım kümesini bulun f(x).
2. Bir fonksiyonun ilk türevini bulun f "(x).
3. Bunun için kritik noktaları belirleyin:
   1. Denklemin gerçek köklerini bulun f "(x)=0;
   2. tüm değerleri bul X bunun için türev f "(x) mevcut değil.
4. Kritik noktanın solunda ve sağında türevin işaretini belirleyin. Türevin işareti iki kritik nokta arasında sabit kaldığından, türevin işaretini kritik noktanın bir noktasında solunda ve bir noktasında sağında belirlemek yeterlidir.
5. Fonksiyonun ekstrem noktalardaki değerini hesaplayın.

Örnekler. Minimum ve maksimum işlevleri keşfedin.




BİR FONKSİYONUN BİR BÖLÜM ÜZERİNDEKİ MAKSİMUM VE EN KÜÇÜK DEĞERLERİ

En büyüğü Bir fonksiyonun bir aralıktaki değeri, bu aralıktaki tüm değerlerinin en büyüğüdür ve en küçük– tüm değerlerinin en küçüğü.

İşlevi düşünün Fonksiyona izin ver segmentte sürekli [ a, b] Bilindiği gibi böyle bir fonksiyon maksimum ve minimum değerlerine parçanın sınırında veya içinde ulaşır. Bir fonksiyonun en büyük veya en küçük değerine parçanın iç noktasında ulaşılıyorsa bu değer, fonksiyonun maksimum veya minimum değeridir, yani kritik noktalarda elde edilir.

Böylece aşağıdakileri elde ederiz bir segmentteki bir fonksiyonun en büyük ve en küçük değerlerini bulma kuralı[ a, b] :

1. Fonksiyonun aralıktaki tüm kritik noktalarını bulun ( a, b) ve bu noktalardaki fonksiyon değerlerini hesaplayın.
2. Segmentin uçlarındaki fonksiyonun değerlerini hesaplayın. x = a, x = b.
3. Elde edilen tüm değerlerden en büyüğünü ve en küçüğünü seçin.

giriiş

Bilimin birçok alanında ve pratik faaliyetlerde, çoğu zaman bir fonksiyonun ekstremumunu bulma problemi ile uğraşmak gerekir. Gerçek şu ki, birçok teknik, ekonomik vb. süreçler, değişkenlere (modellenen olgunun durumunu etkileyen faktörler) bağlı olan bir işlev veya birkaç işlev tarafından modellenir. Optimum (rasyonel) durumu ve süreç kontrolünü belirlemek için bu tür fonksiyonların ekstremumlarını bulmak gerekir. Yani ekonomide, maliyetleri en aza indirme veya karı en üst düzeye çıkarma sorunları genellikle çözülür - şirketin mikroekonomik sorunu. Bu çalışmada, modelleme konularını dikkate almayız, ancak değişkenlere hiçbir kısıtlama getirilmediğinde (koşulsuz optimizasyon) ve ekstremumun yalnızca bir amaç fonksiyonu için arandığı en basit versiyonda, yalnızca ekstremumları aramaya yönelik algoritmaları ele alırız.

FONKSİYONUN EKstreMASI

Sürekli bir fonksiyonun grafiğini düşünün Fonksiyona izin verşekilde gösterilmiştir. Bir noktada fonksiyon değeri X 1, hem solundaki hem de sağındaki tüm komşu noktalardaki fonksiyon değerlerinden büyük olacaktır X 1. Bu durumda fonksiyonun şu noktada olduğunu söylüyoruz. X Maksimum 1. bu noktada X Fonksiyon 3'ün de bir maksimumu olduğu açıktır. konuyu ele alırsak X 2 ise, içindeki fonksiyon değeri tüm komşu değerlerden küçüktür. Bu durumda fonksiyonun şu noktada olduğunu söylüyoruz. X 2 minimum. Aynı şekilde nokta için X 4 .

İşlev Fonksiyona izin ver bu noktada X 0 var maksimum, eğer fonksiyonun bu noktadaki değeri, o noktayı içeren bir aralığın tüm noktalarındaki değerlerinden büyükse X 0, yani eğer bir noktanın böyle bir komşuluğu varsa X 0, herkes içindir X ≠X 0 , bu mahalleye ait eşitsizlik devam ediyor f(x) <f(x 0 ) .

İşlev Fonksiyona izin ver sahip olmak minimum bu noktada X 0 , eğer bir noktanın böyle bir komşuluğu varsa X 0 , bu herkes için X ≠X 0 bu mahalleye ait, eşitsizlik geçerli f(x) >f(x 0 .

Fonksiyonun maksimum ve minimum değerine ulaştığı noktalara ekstrem noktalar, fonksiyonun bu noktalardaki değerlerine ise fonksiyonun ekstremum değerleri denir.

Bir parça üzerinde tanımlanan bir fonksiyonun maksimum ve minimum değerlerine ancak söz konusu parçanın içerdiği noktalarda ulaşabileceğine dikkat edelim.

Bir fonksiyonun bir noktada maksimuma sahip olması, o noktada fonksiyonun tüm tanım alanında en büyük değere sahip olduğu anlamına gelmediğini unutmayın. Yukarıda tartışılan şekilde, noktadaki fonksiyon X 1'in maksimum değeri vardır, ancak fonksiyon değerlerinin noktadan daha büyük olduğu noktalar vardır X 1 . özellikle, F (X 1) < F (X 4) yani Fonksiyonun minimumu maksimumundan büyüktür. Maksimumun tanımından yalnızca bunun, fonksiyonun maksimum noktasına yeterince yakın noktalardaki en büyük değeri olduğu sonucu çıkar.

Teorem 1. (Bir ekstremun varlığı için gerekli bir koşul.) Türevlenebilir fonksiyon ise Fonksiyona izin verşu noktada var x=x ekstremum 0 ise bu noktadaki türevi sıfır olur.

Kanıt. Kesinlik açısından şu noktada X 0 fonksiyonunun maksimumu vardır. Daha sonra, yeterince küçük artışlar için Δ X sahibiz f(x 0 + Δ X) 0 ) yani

Ama sonra

Bu eşitsizlikleri Δ'daki limite geçirmek X→ 0 ve türev dikkate alındığında F "(X 0) vardır ve bu nedenle soldaki limit Δ'nın nasıl olduğuna bağlı değildir. X→ 0, şunu elde ederiz: Δ'da X → 0 – 0 F" (X 0) ≥ 0 a'da Δ X → 0 + 0 F" (X 0) ≤ 0. Çünkü F" (X 0) bir sayıyı tanımlıyorsa bu iki eşitsizlik ancak şu durumlarda uyumludur: F" (X 0) = 0.

Kanıtlanmış teorem, maksimum ve minimum noktaların yalnızca türevin sıfır olduğu argümanın değerleri arasında olabileceğini belirtir.

Bir fonksiyonun belirli bir parçanın tüm noktalarında türevinin olduğu durumu düşündük. Türevin bulunmadığı durumlarda durum nedir? Örneklere bakalım.

sen =|X |.

Fonksiyonun bu noktada türevi yoktur X=0 (bu noktada fonksiyonun grafiğinin tanımlanmış bir teğeti yoktur), ancak bu noktada fonksiyonun bir minimumu vardır, çünkü sen(0)=0 ve tümü için X ≠ 0sen > 0.

türevi yoktur X=0, sonsuza gittiği için X=0. Ancak bu noktada fonksiyonun maksimumu vardır. türevi yoktur X=0, çünkü en X→0. Bu noktada fonksiyonun ne maksimumu ne de minimumu vardır. Gerçekten mi, f(x)=0 ve X <0f(x) <0, а при X >0f(x) >0.

Dolayısıyla verilen örneklerden ve formüle edilen teoremden, bir fonksiyonun yalnızca iki durumda bir ekstrema sahip olabileceği açıktır: 1) türevin mevcut olduğu ve sıfıra eşit olduğu noktalarda; 2) Türevin bulunmadığı noktada.

Ancak eğer bir noktada X 0 bunu biliyoruz f "(x 0 ) =0 ise bundan şu noktada sonuç çıkarılamaz: X 0 fonksiyonun bir ekstremumu vardır.

Örneğin.

.

Ama dönem X=0 bir ekstrem nokta değildir, çünkü bu noktanın solunda fonksiyon değerleri eksenin altında yer alır Öküz ve sağ üstte.

Fonksiyonun türevinin sıfır olduğu veya mevcut olmadığı bir fonksiyonun tanım kümesindeki bir argümanın değerlerine denir kritik noktalar .

Yukarıdakilerin hepsinden, fonksiyonun uç noktalarının kritik noktalar arasında olduğu sonucu çıkar, ancak her kritik nokta bir uç nokta değildir. Bu nedenle, bir fonksiyonun ekstremumunu bulmak için, fonksiyonun tüm kritik noktalarını bulmanız ve ardından bu noktaların her birini maksimum ve minimum için ayrı ayrı incelemeniz gerekir. Aşağıdaki teorem bu amaca hizmet eder.

Teorem 2. (Bir ekstremun varlığı için yeterli koşul.) Fonksiyonun kritik noktayı içeren bir aralıkta sürekli olmasına izin verin. X 0'dır ve bu aralığın tüm noktalarında türevlenebilirdir (belki de noktanın kendisi hariç) X 0). Bu noktadan soldan sağa doğru hareket ederken türevin işareti artıdan eksiye değişirse, o zaman bu noktada X = X 0 fonksiyonunun maksimumu vardır. Eğer geçerken X Soldan sağa 0, türevin işareti eksiden artıya değişir, o zaman fonksiyonun bu noktada minimumu vardır.

Böylece eğer

f "(x)>0 saat X <X 0 ve f "(x)< 0 saat x>x 0, o zaman X 0 – maksimum nokta;

en X <X 0 ve f "(x)> 0 saat x>x 0, o zaman X 0 – minimum puan.

Kanıt. Öncelikle şunu varsayalım ki geçerken X 0 türevin işareti artıdan eksiye değişir, yani. herkesin önünde X, noktaya yakın X 0 f "(x)> 0 için X< x 0 , f "(x)< 0 için x>x 0. Lagrange teoremini farka uygulayalım f(x) - f(x) 0 ) = f "(c)(x- x 0), nerede C arasında yatıyor X Ve X 0 .

İzin vermek X< x 0. Daha sonra C< x 0 ve f "(c)> 0. Bu yüzden f "(c)(x- x 0)< 0 ve dolayısıyla

f(x) - f(x) 0 )< 0, yani f(x)< f(x 0 ).

İzin vermek x > x 0. Daha sonra c>x 0 ve f "(c)< 0. Araç f "(c)(x- x 0)< 0. Bu yüzden f(x) - f(x) 0 ) <0,т.е.f(x) < f(x 0 ) .

Böylece tüm değerler için X yeterince yakın X 0 f(x) < f(x 0 ) . Ve bu şu anlama geliyor: o noktada X 0 fonksiyonunun maksimumu vardır.

Minimum teoremin ikinci kısmı da benzer şekilde kanıtlanır.

Bu teoremin anlamını şekilde açıklayalım. İzin vermek f "(x 1 ) =0 ve herhangi biri için X, yeterince yakın X 1, eşitsizlikler sağlandı

f "(x)< 0 saat X< x 1 , f "(x)> 0 saat x>x 1 .

Daha sonra noktanın solunda X 1 fonksiyon sağda artar ve azalır, bu nedenle X = X 1 fonksiyon artandan azalana doğru gider, yani maksimumu vardır.

Benzer şekilde noktaları da dikkate alabiliriz. X 2 ve X 3 .

Yukarıdakilerin tümü resimde şematik olarak gösterilebilir:

Ekstremum için y=f(x) fonksiyonunu inceleme kuralı

Bir fonksiyonun tanım kümesini bulun f(x).

Bir fonksiyonun ilk türevini bulun f "(x) .

Bunun için kritik noktaları belirleyin:

Denklemin gerçek köklerini bulun f "(x) =0;

tüm değerleri bul X bunun için türev f "(x) mevcut değil.

Kritik noktanın solunda ve sağında türevin işaretini belirleyin. Türevin işareti iki kritik nokta arasında sabit kaldığından, türevin işaretini kritik noktanın bir noktasında solunda ve bir noktasında sağında belirlemek yeterlidir.

Fonksiyonun ekstrem noktalardaki değerini hesaplayın.

Bu, kesinlikle tüm mezunların ve öğrencilerin karşılaştığı oldukça ilginç bir matematik bölümüdür. Ancak herkes matan'ı sevmez. Bazıları görünüşte standart bir fonksiyon çalışması gibi temel şeyleri bile anlayamıyor. Bu makale böyle bir yanlış anlaşılmayı düzeltmeyi amaçlamaktadır. Fonksiyon analizi hakkında daha fazla bilgi edinmek ister misiniz? Ekstrem noktaların ne olduğunu ve bunları nasıl bulacağınızı bilmek ister misiniz? O halde bu yazı tam size göre.

Bir fonksiyonun grafiğini incelemek

Öncelikle grafiği neden analiz etmeniz gerektiğini anlamakta fayda var. Çizilmesi zor olmayan basit işlevler vardır. Böyle bir fonksiyonun çarpıcı bir örneği paraboldür. Grafik çizmek zor olmayacak. İhtiyacınız olan tek şey, basit bir dönüşüm kullanarak fonksiyonun 0 değerini aldığı sayıları bulmaktır. Prensip olarak bir parabol grafiği çizmek için bilmeniz gereken tek şey budur.

Peki ya grafiğini çizmemiz gereken fonksiyon çok daha karmaşıksa? Karmaşık fonksiyonların özellikleri çok açık olmadığından bütünsel bir analiz yapılması gerekmektedir. Ancak bundan sonra fonksiyon grafiksel olarak gösterilebilir. Bu nasıl yapılır? Bu sorunun cevabını bu yazıda bulabilirsiniz.

Fonksiyon Analiz Planı

Yapmamız gereken ilk şey, fonksiyonun yüzeysel bir incelemesini yapmaktır, bu sırada tanım alanını buluruz. O halde sırayla başlayalım. Tanım alanı, fonksiyonun tanımlandığı değerler kümesidir. Basitçe söylemek gerekirse bunlar bir fonksiyonda x yerine kullanılabilecek sayılardır. Kapsamı belirlemek için kayda bakmanız yeterlidir. Örneğin, y (x) = x 3 + x 2 - x + 43 fonksiyonunun gerçek sayılar kümesi olan bir tanım alanına sahip olduğu açıktır. (x 2 - 2x)/x gibi bir fonksiyonda her şey biraz farklıdır. Paydadaki sayının 0'a eşit olmaması gerektiğinden, bu fonksiyonun tanım kümesi sıfır dışındaki tüm gerçek sayılar olacaktır.

Daha sonra, fonksiyonun sözde sıfırlarını bulmanız gerekir. Bunlar, fonksiyonun tamamının sıfır değerini aldığı argüman değerleridir. Bunun için fonksiyonu sıfıra eşitlemek, detaylı düşünmek ve bazı dönüşümler yapmak gerekiyor. Zaten tanıdık olan y(x) = (x 2 - 2x)/x fonksiyonunu ele alalım. Okul derslerinden, pay sıfıra eşit olduğunda kesrin 0'a eşit olduğunu biliyoruz. Bu nedenle paydayı atıyoruz ve payla çalışmaya başlayarak onu sıfıra eşitliyoruz. x 2 - 2x = 0 elde ederiz ve x'i parantezlerin dışına çıkarırız. Dolayısıyla x (x - 2) = 0. Sonuç olarak, x 0 veya 2'ye eşit olduğunda fonksiyonumuzun sıfıra eşit olduğunu buluyoruz.

Bir fonksiyonun grafiğini incelerken birçok kişi ekstrem noktalar şeklinde problemlerle karşılaşır. Ve bu garip. Sonuçta aşırılıklar oldukça basit bir konudur. Bana inanmıyor musun? Makalenin minimum ve maksimum puanlardan bahsedeceğimiz bu bölümünü okuyarak kendiniz görün.

İlk olarak, ekstremun ne olduğunu anlamaya değer. Ekstrem, bir fonksiyonun grafik üzerinde ulaştığı sınır değerdir. Maksimum ve minimum olmak üzere iki aşırı değer olduğu ortaya çıktı. Netlik sağlamak için yukarıdaki resme bakabilirsiniz. İncelenen alanda -1 noktası y (x) = x 5 - 5x fonksiyonunun maksimumu ve buna göre 1 noktası minimumudur.

Ayrıca kavramları karıştırmayın. Bir fonksiyonun ekstrem noktaları, belirli bir fonksiyonun ekstrem değerler elde ettiği argümanlardır. Buna karşılık ekstremum, bir fonksiyonun minimum ve maksimumlarının değeridir. Örneğin yukarıdaki şekli tekrar düşünün. -1 ve 1 fonksiyonun ekstremum noktalarıdır, 4 ve -4 ise ekstremumların kendisidir.

Ekstrem noktaları bulma

Peki yine de bir fonksiyonun ekstremum noktalarını nasıl bulacaksınız? Her şey oldukça basit. Yapılacak ilk şey denklemin türevini bulmaktır. Diyelim ki şu görevi aldık: “Y (x) fonksiyonunun uç noktalarını bulun, x argümandır. Açıklık sağlamak için y (x) = x 3 + 2x 2 + x + 54 fonksiyonunu alalım. şu denklemi elde edin: 3x 2 + 4x + 1. Sonuç olarak elimizde standart bir ikinci dereceden denklem var. Bundan sonra yapılması gereken tek şey onu sıfıra eşitlemek ve diskriminant sıfırdan büyük olduğundan kökleri bulmak. = 16 - 12 = 4), bu denklem iki kök tarafından belirlenir ve iki değer elde ederiz: 1/3 ve -1. Ancak fonksiyonun uç noktaları olacak. Hangi nokta maksimum, hangisi minimum? Bunu yapmak için komşu noktayı alıp değerini bulmanız, -'den koordinat çizgisinin solunda bulunan -2 sayısını almanız gerekir. 1. Bu değeri y(-2) = 12 - 8 + 1 = 5 denklemimizde yerine koyun. Sonuç olarak pozitif bir sayı elde ederiz. Bu, 1/3 ile -1 aralığında fonksiyonun arttığı anlamına gelir. Bu da eksi sonsuzdan 1/3'e ve -1'den artı sonsuza kadar olan aralıklarda fonksiyonun azaldığı anlamına gelir. Böylece, 1/3 sayısının çalışılan aralıktaki fonksiyonun minimum noktası, -1 sayısının maksimum noktası olduğu sonucuna varabiliriz.

Ayrıca, Birleşik Devlet Sınavının yalnızca uç noktaları bulmayı değil, aynı zamanda onlarla bir tür işlem (toplama, çarpma vb.) Gerçekleştirmeyi de gerektirdiğini belirtmekte fayda var. Bu nedenle sorunun koşullarına özellikle dikkat etmek önemlidir. Sonuçta dikkatsizlik nedeniyle puan kaybedebilirsiniz.