Skrivnostna motnja: zgodovina fraktalov in njihova področja uporabe. Fraktali v praštevilih

Uvod

Koncept fraktala..................................................... ......................................................4

Zgodovina pojava fraktalov……………………………………………………………………………………………………………………………………………………….

Algebraični fraktali………………..…………………………….8

1. Maldebrod set……………………………………………...9

   Komplet Julia……………………………………………………11

   Newtonovi bazeni (fraktali)………………………………………………………13

   Fraktal (mehurčki) Halley……………………………………………..14

Praktična uporaba fraktali…………………………………...15

Zaključek………………………………………………………………………………….19

Seznam referenc………………………………………………………………...20

Uvod

Jezik znanosti se hitro spreminja sodobni svet. Zgodovina razvoja fizike sega več kot stoletje. V tem času je bilo raziskanih ogromno različnih naravnih pojavov, odkriti so bili temeljni zakoni fizike, ki pojasnjujejo različna eksperimentalna dejstva.

Večina sistemov v naravi združuje dve lastnosti: prvič, so zelo veliki, pogosto večplastni, raznoliki in zapleteni ter Drugič nastanejo pod vplivom zelo ne velika količina preprostih vzorcev in se naprej razvijati, pri tem pa upoštevati te preproste vzorce. Teh je največ različne sisteme, začenši s kristali in preprosto grozdi (različne vrste kopičenja, kot so oblaki, reke, gore, celine, zvezde), konča z ekosistemi in bioloških predmetov(od praprotnega lista do človeški možgani). Fraktali so prav takšni objekti: po eni strani kompleksni (vsebujejo neskončno veliko elementov), ​​po drugi strani pa zgrajeni po zelo preprosti zakoni. Zahvaljujoč tej lastnosti imajo fraktali veliko skupnega z mnogimi naravnimi predmeti. Toda fraktal je v primerjavi z naravni objekt dejstvo, da ima fraktal strogo matematično definicijo in je primeren za strog opis in analizo. Zato teorija fraktalov omogoča napovedovanje stopnje rasti koreninskega sistema rastlin, stroškov dela za izsuševanje močvirij, odvisnosti mase slame od višine poganjkov in še veliko več. To je nova smer v matematiki, ki je naredila znanstvena paradigma revolucija, ki je po pomenu primerljiva s teorijo relativnosti in kvantna mehanika. Objekti fraktalne geometrije na svoj način videz močno razlikuje od "pravilnih" geometrijskih oblik, ki smo jih vajeni. Pravzaprav je to preboj v matematični opis sistemov, ki dolgo časa niso bili primerni za tak opis.

Fraktalna geometrija ni "čista" geometrijska teorija. To je bolj koncept Nov videz na dobro znanih stvareh, prestrukturiranje percepcije, ki raziskovalca prisili, da vidi svet na nov način.

Namen mojega dela je, da se seznanimo s pojmom fraktal in njegovo različico algebraični fraktal.

Fraktalni koncept

Relativno nedavno se je v matematiki pojavila podoba predmeta, bolj obsežna, a kljub temu podobna črti. Nekateri znanstveniki so se težko sprijaznili s konceptom črte brez širine, zato so postopoma začeli preučevati geometrijske oblike in strukture z delno prostorsko dimenzijo. Zvezne krivulje, ki imajo vse svoje izpeljanke, so zamenjale lomljene ali zelo nazobčane krivulje. Osupljiv primer takšne krivulje je tirnica Brownovega delca. Tako se je v znanosti pojavil koncept fraktala.

Fraktal(lat. fractus - zdrobljen, zlomljen, zlomljen) - kompleksen geometrijski lik, ki ima lastnost samopodobnosti, to je sestavljen iz več delov, od katerih je vsak podoben celotni figuri (slika 1). V več v širšem smislu Fraktale razumemo kot množice točk v evklidskem prostoru, ki imajo delno metrično dimenzijo (v smislu Minkowskega ali Hausdorffa) ali metrično dimenzijo.

riž. 1
Treba je opozoriti, da beseda "fraktal" ni matematični izraz in nima splošno sprejetega strogega matematična definicija. Uporablja se lahko, če ima zadevna figura katero koli od naslednjih lastnosti:

Ima netrivialno strukturo na vseh lestvicah. To je v nasprotju z običajnimi figurami (kot so krog, elipsa, graf gladko delovanje): Če pogledamo majhen delček pravilne figure v zelo velikem merilu, bo videti kot delček ravne črte. Pri fraktalu povečanje obsega ne vodi do poenostavitve strukture; na vseh merilih bomo videli enako kompleksno sliko.

Je sebi podoben ali približno sam sebi podoben.

Ima delno metrično dimenzijo.

Mnogi predmeti v naravi imajo fraktalne lastnosti, na primer obale, oblaki, krošnje dreves, cirkulacijski sistem in alveolarni sistem pri ljudeh ali živalih.
Fraktali, zlasti na ravnini, so priljubljeni zaradi kombinacije lepote in enostavnosti gradnje z uporabo računalnika.

Zgodovina fraktalov

Preučevanje fraktalov na prehodu iz 19. v 20. stoletje je bilo bolj epizodično kot sistematično, saj so prej matematiki preučevali predvsem »dobre« objekte, ki jih je bilo mogoče preučevati z običajne metode in teorije. Leta 1872 je nemški matematik Karl Weierstrass sestavil primer neprekinjena funkcija, ki ni nikjer diferencibilna, to pomeni, da nima tangente v nobeni od svojih točk. Vendar je bila njegova konstrukcija povsem abstraktna in težko razumljiva. Zato je leta 1904 Šved Helge von Koch prišel do zvezne krivulje, ki nima nikjer tangente in jo je precej enostavno narisati. Izkazalo se je, da ima lastnosti fraktala. Ena različica te krivulje se imenuje "Kochova snežinka".
Zamisel o samopodobnosti figur je prevzel Francoz Paul Pierre Levy, bodoči mentor Benoit Mandelbrot. Leta 1938 je bil objavljen njegov članek "Ravne in prostorske krivulje ter površine, sestavljene iz delov, podobnih celoti", ki je opisal še en fraktal - Levyjevo C-krivuljo. Vse zgoraj naštete fraktale lahko pogojno uvrstimo v en razred konstruktivnih (geometričnih) fraktalov.
Drugi razred so dinamični (algebraični) fraktali, ki vključujejo Mandelbrotovo množico. Prve raziskave v tej smeri so se začele v začetku 20. stoletja in so povezane z imeni francoski matematiki Gaston Julia in Pierre Fatu. Leta 1918 je bilo objavljeno Julijino delo o ponovitvah kompleksa racionalne funkcije, ki opisuje Julijeve množice, celotno družino fraktalov, tesno povezanih z Mandelbrotovo množico. To delo je bilo nagrajeno Francoska akademija, vendar ni vseboval niti ene ilustracije, zato je bilo nemogoče ceniti lepoto odprtih predmetov

Prve ideje o fraktalni geometriji so se pojavile v 19. stoletju. Cantor je s preprostim rekurzivnim (ponavljajočim) postopkom premico spremenil v zbirko nepovezanih točk (t.i. Cantorjev prah). Vzel bi črto in odstranil osrednjo tretjino ter nato isto ponovil s preostalimi deli. (slika 2)

riž. 2

Peano je remiziral posebna vrstačrte. (slika 3)

riž. 3

Za risanje je Peano uporabil naslednji algoritem.

V prvem koraku je vzel ravno črto in jo nadomestil z 9 segmenti, ki so bili 3-krat krajši od dolžine prvotne črte (1. in 2. del slike). Nato je naredil enako z vsakim segmentom nastale črte. In tako naprej v nedogled. Edinstvenost črte je v tem, da zapolni celotno ravnino. Dokazano je, da je za vsako točko na ravnini mogoče najti točko ki pripada črti Peano.

Peanova krivulja in Cantorjev prah sta presegla običajne geometrijske predmete. Niso imeli jasne razsežnosti. Zdelo se je, da je Cantorjev prah zgrajen na podlagi enodimenzionalne ravne črte, vendar je sestavljen iz točk (dimenzija 0). In Peanova krivulja je bila zgrajena na podlagi enodimenzionalne črte, rezultat pa je bila ravnina. Na mnogih drugih področjih znanosti so se pojavili problemi, katerih reševanje je vodilo do čudnih rezultatov, podobnih zgoraj opisanim ( Brownovo gibanje, borzne cene).

Do 20. stoletja podatki o takih čudni predmeti, ne da bi jih poskušali sistematizirati. To je bilo, dokler jih ni prevzel Benoit Mandelbrot, oče moderne fraktalne geometrije in besede fraktal. S postopnim primerjanjem dejstev je prišel do odkritja nove smeri v matematiki - fraktalne geometrije.

Da bi si bolj jasno predstavljali fraktal, si oglejmo primer iz knjige B. Mandelbrota "Fraktalna geometrija narave", ki je postala klasika - "Kakšna je dolžina obale Britanije?" Odgovor na to vprašanje ni tako preprost, kot se zdi. Vse je odvisno od dolžine uporabljenega orodja. Z merjenjem obale s kilometrskim ravnilom dobijo nekaj dolžine. Vendar pa so zgrešeni številni majhni zalivi in ​​polotoki, ki so po velikosti veliko manjši od izmerjenega ravnila. Z zmanjšanjem velikosti ravnila na 1 meter se izkaže, da bo dolžina obale postala daljša. Pri merjenju dolžine brežine z milimetrskim ravnilom bo dolžina ob upoštevanju delov, večjih od milimetra, še večja. Posledično lahko odgovor na tako na videz preprosto vprašanje zmede vsakogar - dolžina britanske obale je neskončna.

Algebraični fraktali

Algebrski fraktali so dobili ime, ker so zgrajeni na podlagi algebraične formule. Obstaja več metod za pridobivanje algebraičnih fraktalov. Eden od načinov je večkratno izračunavanje funkcije, kjerz - kompleksno število in f je določena funkcija. Izračun te funkcije se nadaljuje, dokler ni izpolnjen določen pogoj. In ko je ta pogoj izpolnjen, se na zaslonu prikaže pika. V tem primeru so vrednosti funkcije za različne točke kompleksna ravnina lahko drugačno vedenje:

teži v neskončnost skozi čas;

teži k 0;
ima več fiksnih vrednosti in jih ne presega;
vedenje je kaotično, brez trendov.

3.1 Mandelbrotov niz

Mandelbrotov niz (enega najbolj znanih fraktalnih objektov) je prvi (vizualno z uporabo računalnika) sestavil Benoit Mandelbrot spomladi 1980 leta raziskovalno središče Podjetje IBM, imenovano po. Thomas J. Watson. In čeprav so se raziskave takšnih predmetov začele v prejšnjem stoletju, je bilo odkritje tega sklopa in izboljšanje strojne opreme računalniška grafika V odločilna stopnja vplival na razvoj fraktalne geometrije in teorije kaosa. Torej, kaj je Mandelbrotov niz?

Razmislite o funkciji kompleksne spremenljivke. Postavimoin razmislite o zaporedju, kjer za katero. Tako zaporedje je lahko omejeno (tj. lahko obstaja r, tako da za katero koli) ali "pobegniti v neskončnost" (tj. za vsak r > 0 obstaja). Mandelbrotovo množico lahko definiramo kot množico kompleksnih števil c, za katere je podano zaporedje omejeno. Na žalost ni znano analitično izražanje, ki bi danemu c omogočil določitev, ali pripada Mandelbrotovi množici ali ne. Zato se za konstrukcijo množice uporabi računalniški eksperiment: skozi množico točk na kompleksni ravnini pogledajo z določenim korakom in za vsako točko izvedejo določeno število iteracije (poiščite določeno število členov zaporedja) in opazujte njegovo »obnašanje«. (slika 4).

Dokazano je, da se Mandelbrotova množica nahaja v krogu s polmerom r=2 s središčem v izhodišču. Če torej na nekem koraku modul naslednjega člena zaporedja preseže 2, lahko takoj sklepamo, da točka, ki ustreza c, ki določa to zaporedje, ne pripada Mandelbrotovi množici.

Z zmanjšanjem koraka skeniranja kompleksnih števil in povečanjem števila iteracij lahko dobimo poljubno podrobne, a vedno le približne slike množice.

Naj imamo na voljo N barv, oštevilčenih za določnost od 0 do N-1. Ponovno zaradi določnosti bomo predpostavili, da ima črna barva številko 0. Če za dani c po N-1 ponovitvah točka ne preseže kroga s polmerom 2, bomo predpostavili, da c pripada Mandelbrotovi množici, in to pobarvali točka c črna. V nasprotnem primeru, če je na nekem koraku k (k Є ) naslednja točka šla izven kroga polmera 2 (tj. na k-tem koraku smo ugotovili, da »beži«), jo pobarvaj z barvo k.

Čudovite slike nastanejo, ko dobra izbira palete in soseščine množice (izven množice namreč dobimo »barvne pike«) (sl. 5, 6).

riž. 4

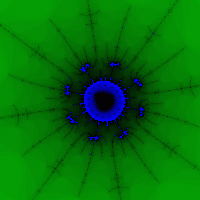
riž. 5 sl. 6

3.2 Julia set

Julijine množice, tesno povezane z Mandelbrotovo množico, sta v začetku 20. stoletja proučevala matematika Gaston Julia in Pierre Fatou (glej). V letih 1917-1919 Dobili so temeljne rezultate v zvezi s ponavljanjem funkcij kompleksne spremenljivke. Na splošno si to dejstvo zasluži ločeno razpravo in je impresiven primer matematične raziskave, mnogo desetletij pred svojim časom (znanstveniki so si lahko le približno predstavljali, kako izgledajo predmeti, ki so jih preučevali!), vendar bomo opisali le metodo za konstruiranje Juliinih množic za funkcijo kompleksne spremenljivke. Natančneje, gradili bomo t.i. "polnjenje kompletov Julia".

Razmislite o pravokotniku (x 1 ;y 1 )-(x 2 ;y 2 ). Popravimo konstanto c in začnemo z določenim korakom ogledovati točke izbranega pravokotnika. Za vsako točko, kot pri konstruiranju Mandelbrotove množice, bomo izvedli serijo iteracij (kot večje število ponovitve, bolj natančen bo nabor pridobljen). Če po nizu iteracij točka ne »pobegne« čez mejo kroga polmera 2, jo pobarvamo s črno barvo, sicer pa z barvo iz palete. (Slike 7, 8, 9, 10).

riž. 7

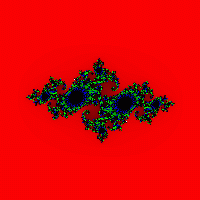
Sl.8 Sl. 9

riž. 10

3.3 Newtonovi bazeni (fraktali)

Druga vrsta dinamičnih fraktalov so Newtonovi fraktali (tako imenovani bazeni). (Slika 11). Formule za njihovo konstrukcijo temeljijo na metodi rešitve nelinearne enačbe, ki ga je izumil veliki matematik že v 17. stoletju. Prijavljanje splošna formula Newtonova metoda zn+1 = zn - f (zn)/f"(zn), n=0, 1, 2… za rešitev enačbe f (x)=0 na polinom zk-a, dobimo zaporedje točk : zn+1 = (k-1)znk/kznk-1, n=0, 1, 2... Če izberemo različna kompleksna števila z0 kot začetne približke, bomo dobili zaporedja, ki konvergirajo h koreninam tega polinoma ima točno k korenin, potem je celotna ravnina razdeljena na k delov - meje teh delov imajo fraktalno strukturo.

riž. enajst

3.4 Fraktal (mehurčki) Halley

Takšne fraktale dobimo, če praviloma za konstrukcijo dinamičnega fraktala uporabimo Halleyjevo formulo za iskanje približnih vrednosti korenin funkcije. (Slika 12).

Metoda je sestavljena iz zaporedja ponovitev:

Ideja metode je skoraj enaka tisti, ki se uporablja za risanje dinamičnih fraktalov: vzamemo nekaj začetna vrednost(kot ponavadi govorimo o vrednosti spremenljivk in funkcij) in večkrat uporabite formulo, tako da dobite zaporedje številk. Skoraj vedno konvergira k eni od ničel funkcije (to je vrednost spremenljivke, pri kateri funkcija prevzame vrednost 0). Halleyeva metoda kljub okorni formuli deluje učinkovitejši od metode : Zaporedje hitreje konvergira k ničelnim funkcijam.

riž. 12

Praktična uporaba fraktalov

Fraktali najdejo vse večjo uporabo v znanosti. Glavni razlog za to je, da opisujejo resnični svet včasih celo boljši od tradicionalne fizike ali matematike. Tukaj je nekaj primerov.

Računalniški sistemi

Od vseh slik, ki jih lahko ustvari računalnik, se le redke lahko kosajo s fraktalnimi slikami govorimo o o pravi lepoti.

večina koristno uporabo Fraktali v računalništvu so fraktalno stiskanje podatkov. Ta vrsta stiskanja temelji na dejstvu, da je realni svet dobro opisan s fraktalno geometrijo. Hkrati so slike stisnjene veliko bolje kot z običajnimi metodami (kot sta jpeg ali gif). Druga prednost fraktalne kompresije je, da ko je slika povečana, ni učinka pikselizacije (povečanje velikosti pik na velikosti, ki popačijo sliko). Pri fraktalni kompresiji je slika po povečavi pogosto videti še boljša kot prej.

Mehanika tekočin

Preučevanje turbulenc v tokovih je zelo dobro prilagojeno

fraktali. Turbulentni tokovi so kaotični in jih je zato težko natančno modelirati. In tu pomaga prehod na fraktalno predstavitev, ki močno olajša delo inženirjev in fizikov, kar jim omogoča boljše razumevanje dinamike kompleksnih tokov.

Z uporabo fraktalov lahko simulirate tudi plamen.

Porozni materiali so dobro predstavljeni v fraktalni obliki zaradi dejstva, da imajo zelo kompleksno geometrijo. Uporablja se v naftni znanosti.

Telekomunikacije

Za prenos podatkov na daljavo, antene z

fraktalne oblike, kar močno zmanjša njihovo velikost in težo. Fraktali se uporabljajo za opisovanje ukrivljenosti površin. Za neravno površino je značilna kombinacija dveh različnih fraktalov.
Zdravilo

Biosenzorične interakcije. Srčni utrip.
Biologija

Modeliranje kaotičnih procesov, zlasti pri opisovanju populacijskih modelov.
Nanotehnologija

V primeru nanotehnologije imajo fraktali prav tako vlogo pomembno vlogo, saj imajo številni nanosistemi zaradi svoje hierarhične samoorganizacije neceloštevilsko dimenzijo, torej so fraktali po svoji geometrijski, fizikalno-kemijski ali funkcionalni naravi. na primer svetel primer kemijski fraktalni sistemi so molekule "dendrimerji » . (slika 13)

riž. 13

Literatura

Med literarna dela poiščite tiste, ki imajo besedilno, strukturno ali semantično fraktalno naravo. V besedilnih fraktalih se elementi besedila potencialno neskončno ponavljajo (»Duhovnik je imel psa ...«, »Prispodoba o filozofu, ki sanja, da je on metulj, ki sanja, da je ona filozof, ki sanja ...« in besedila z razširitvami ("Hiša, ki jo je zgradil Jack")

Pri strukturnih fraktalih je besedilna shema potencialno fraktalna: venec sonetov (15 pesmi), venec vencev sonetov (211 pesmi), venec vencev sonetov (2455 pesmi).

Zaključek

Fraktal je objekt neskončne kompleksnosti, ki vam omogoča, da vidite toliko njegovih podrobnosti od blizu kot od daleč. Zemlja - klasičen primer fraktalni objekt. Iz vesolja je videti kot žoga. Če se mu približamo, bomo našli oceane, celine, obale in gorovja. Poglejmo gore pobližje - vidne bodo še bolj drobne podrobnosti: kos zemlje na površju gore je v svojem obsegu tako zapleten in neenakomeren kot gora sama. In še večja povečava bo razkrila drobne delce zemlje, od katerih je vsak sam fraktalni objekt.

Na koncu bi rad povedal, da je po odkritju fraktalov mnogim znanstvenikom postalo očitno, da so dobre stare oblike evklidske geometrije veliko slabše od večine naravnih predmetov zaradi pomanjkanja nekaterih nepravilnosti, nereda in nepredvidljivosti v njih. Možno je, da bodo nove ideje v fraktalni geometriji pomagale preučiti mnoge skrivnostni pojavi okoliško naravo. Trenutno fraktali hitro vdirajo v številna področja fizike, biologije, medicine, sociologije in ekonomije. Metode obdelave slik in prepoznavanja vzorcev, ki uporabljajo nove koncepte, omogočajo raziskovalcem uporabo tega matematičnega aparata za kvantitativni opis velika količina naravni objekti in strukture.

Bibliografija

1. Uvod v fraktale,

2. Zhikov V.V. Na Julijskih nizih. // Sodobno naravoslovje: Enciklopedija: V 10 zvezkih T.1: Matematika. Mehanika. M., 2000.

3. Zhikov V.V. Fraktali. // Sodobno naravoslovje: Enciklopedija: V 10 zvezkih T.1: Matematika. Mehanika. M., 2000.

4. Mandelbrot B. Fraktalna geometrija narave. – M: Inštitut za računalniške raziskave, 2002.

5. Morozov A.D. Uvod v teorijo fraktalov, Moskva-Iževsk: Inštitut za računalniške raziskave, 2002, 160 strani.

6. Dinamični (algebraični) fraktali // Elementi.. URL:http:// elementy. ru/ plakati/ fraktali/ dinamično

7. Dinamični (algebraični) fraktali // Elementi.. URL:http:// elementy.ru/posters/fractals/Mandelbrot#nop

8. Algebraični fraktali // Fraktali.. URL:http://rusproject.narod.ru/article/fractals.htm

Metulji seveda ne vedo ničesar o kačah. Toda ptice, ki lovijo metulje, vedo zanje. Ptice, ki kač ne prepoznajo dobro, pogosteje ...

(Dinamični) fraktali

Fraktali te vrste nastanejo pri preučevanju nelinearnih dinamičnih sistemov (od tod tudi ime). Obnašanje takega sistema je mogoče opisati s kompleksom nelinearna funkcija(polinom) f(z). Vzemimo neko začetno točko z0 na kompleksni ravnini. Zdaj razmislimo o neskončnem zaporedju števil na kompleksni ravnini, od katerih je vsako dobljeno iz prejšnjega: z0, z1 = f(z0), z2 = f(z1), ... zn+1 = f(zn). Odvisno od Izhodišče z0 se takšno zaporedje lahko obnaša drugače: teži v neskončnost pri n → ∞; približati nekaterim končna točka; ciklično zavzema niz fiksnih vrednosti; Možne so tudi bolj zapletene možnosti.

Tako ima vsaka točka z kompleksne ravnine svoje lastno obnašanje med iteracijami funkcije f(z), celotna ravnina pa je razdeljena na dele. Poleg tega imajo točke, ki ležijo na mejah teh delov, naslednjo lastnost: s poljubno majhnim premikom se narava njihovega obnašanja močno spremeni (takšne točke imenujemo bifurkacijske točke). Torej se izkaže, da imajo množice točk, ki imajo eno specifično vrsto obnašanja, kot tudi množice bifurkacijskih točk, pogosto fraktalne lastnosti. To so Julijeve množice za funkcijo f(z).

Mandelbrotova množica je zgrajena nekoliko drugače. Razmislite o funkciji fc(z) = z2 + c, kjer je c kompleksno število. Konstruirajmo zaporedje te funkcije z z0 = 0; odvisno od parametra c lahko divergira v neskončnost ali ostane omejena. Poleg tega vse vrednosti c, za katere je to zaporedje omejeno, tvorijo Mandelbrotov niz. Podrobno so jo preučevali sam Mandelbrot in drugi matematiki, ki so odkrili mnoge zanimive lastnosti te množice.

Vidimo, da sta si definiciji Julijine in Mandelbrotove množice podobni. Pravzaprav sta ta dva niza tesno povezana. Mandelbrotova množica je namreč vse vrednosti kompleksnega parametra c, za katere je Julijeva množica fc(z) povezana (množica se imenuje povezana, če je ni mogoče razdeliti na dva nepovezana dela, z nekaterimi dodatnimi pogoji).

To je največ velika skupina fraktali. Pridobljeni so z uporabo nelinearnih procesov v n-dimenzionalni prostori. Najbolj raziskani so dvodimenzionalni procesi. Pri razlagi nelinearnega iterativnega procesa kot diskretnega dinamičnega sistema lahko uporabimo terminologijo teorije teh sistemov: fazni portret, stacionarni proces, atraktor itd.

Znano je, da imajo nelinearni dinamični sistemi več stabilnih stanj. Stanje, v katerem se dinamični sistem znajde po določenem številu iteracij, je odvisno od njegovega začetnega stanja. Zato ima vsako stabilno stanje (ali, kot pravijo, atraktor) določeno območje začetnih stanj, iz katerih bo sistem nujno padel v obravnavana končna stanja. torej fazni prostor sistem je razdeljen na področja privlačnosti atraktorjev. Če je fazni prostor dvodimenzionalen, potem obarvanje območij privlačnosti različne barve, lahko dobite barvni fazni portret tega sistema (iterativni postopek). Če spremenite algoritem za izbiro barv, lahko dobite zapletene fraktalne vzorce z bizarnimi večbarvnimi vzorci. Presenečenje za matematike je bila zmožnost ustvarjanja zelo zapletenih netrivialnih struktur z uporabo primitivnih algoritmov.

Kot primer razmislite o Mandelbrotovem nizu (glej sliki 3 in sliki 4). Algoritem za njegovo konstrukcijo je precej preprost in temelji na preprostem iterativnem izrazu:

Z = Z[i] * Z[i] + C,

kjer sta Zi in C kompleksni spremenljivki. Ponovitve se izvedejo za vsako začetno točko C pravokotnega ali kvadratnega območja - podmnožice kompleksne ravnine. Iterativni proces se nadaljuje, dokler Z[i] ne preseže kroga polmera 2, katerega središče leži v točki (0,0), (to pomeni, da je atraktor dinamični sistem je v neskončnosti) ali po dovolj veliko število ponovitev (na primer 200-500) Z[i] konvergira v neko točko na krogu. Glede na število iteracij, med katerimi je Z[i] ostal znotraj kroga, lahko nastavite barvo točke C (če Z[i] ostane znotraj kroga dovolj veliko število iteracij, se postopek iteracije ustavi in ​​ta raster točka je pobarvana črno).

Zgornji algoritem daje približek tako imenovani Mandelbrotovi množici. Mandelbrotova množica vsebuje točke, ki med neskončno število iteracije ne gredo v neskončnost (točke so črne). Točke, ki pripadajo meji množice (tu je kompleksne strukture) pojdite v neskončnost za končna številka iteracije, točke, ki ležijo izven množice, pa gredo po več iteracijah v neskončnost (belo ozadje).

Primeri algebraičnih fraktalov:

• Mandelbrotov komplet
• Julia kompleti
• Halleyev fraktal
• Newtonov fraktal

Ta fraktal sem odkril, ko sem opazoval interferenco valov na gladini reke. Val se pomika proti obali, se odbija in prekriva vase. Ali obstaja red v vzorcih, ki jih ustvarjajo valovi? Poskusimo ga najti. Ne upoštevajmo celotnega vala, ampak le vektor njegovega gibanja. Naredimo "obrege" gladke, da poenostavimo poskus.

Poskus lahko izvedemo na navadnem listu papirja iz šolskega zvezka.

Ali z uporabo JavaScript implementacije algoritma.

Vzemite pravokotnik s stranicama q in p. Pošljimo žarek (vektor) od kota do kota. Žarek se premakne na eno stran pravokotnika, se odbije in nadaljuje s premikanjem na naslednjo stran. To se nadaljuje, dokler žarek ne zadene enega od preostalih vogalov. Če sta velikosti stranice q in p soprosti števili, dobimo vzorec (kot bomo videli kasneje, fraktal).

Na sliki lahko jasno vidimo, kako ta algoritem deluje.

Gif animacija:

Najbolj neverjetno je to, da z različne strani pravokotnik - dobimo različne vzorce.

Zakaj te vzorce imenujem fraktali? Kot veste, je "fraktal" geometrijska figura, ki ima lastnosti samopodobnosti. Del slike ponavlja celotno sliko. Če znatno povečate dimenzije strani Q in P, je jasno, da imajo ti vzorci lastnosti samopodobnosti.

Poskusimo ga povečati. Povečali ga bomo na zvit način. Vzemimo za primer vzorec 17x29. Naslednji vzorci bodo: 29x(17+29=46), 46x(29+46=75)…
Ena stran: F(n);
Druga stran: F(n+1)=F(n)+F(n-1);
17, 29, 46, 75, 121, 196, 317, 513, 830, 1343
Kot Fibonaccijeva števila, le z različnima prvim in drugim členom zaporedja: F(0)=17, F(1)=29.

če velika stran celo je rezultat naslednji vzorec:

Če je krajša stranica soda:

Če sta obe strani lihi, dobimo simetričen vzorec:

Odvisno od tega, kako se žarek začne:

oz

Poskušal bom razložiti, kaj se dogaja v teh pravokotnikih.

Ločimo kvadrat od pravokotnika in poglejmo, kaj se zgodi na meji.

Žarek izstopa na isti točki, iz katere je vstopil.

Hkrati je število kvadratov, skozi katere gre žarek, vedno sodo število.

Torej, če odrežete kvadrat od pravokotnika, bo ostal nespremenjen del fraktala.

Če čim večkrat ločite kvadrate od fraktala, lahko pridete do »začetka« fraktala.

Je videti kot Fibonaccijeva spirala?

Fraktale lahko dobimo tudi iz Fibonaccijevih števil.

V matematiki so Fibonaccijeva števila (Fibonaccijeva vrsta, Fibonaccijevo zaporedje) števila:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…
Po definiciji sta prvi dve števili v Fibonaccijevem zaporedju 0 in 1, vsako naslednje število pa je enako vsoti prejšnjih dveh.
F(n)=F(n-1)+F(n-2)
F(0)=0, F(1)=1

Pojdi:

Kot lahko vidimo, bolj ko se razmerje stranic približuje zlatemu rezu, večja je podrobnost fraktala.

V tem primeru fraktal ponavlja del fraktala, povečan za .

Namesto Fibonaccijevih števil lahko uporabite iracionalne velikosti strani:

Dobimo isti fraktal.

Enake fraktale lahko dobite v kvadratu, če streljate žarek pod drugačnim kotom:

Kaj lahko rečete za zaključek?
Kaos je tudi red. S svojimi zakoni. Ta red ni bil raziskan, vendar ga je mogoče preučiti. In vsa želja znanosti je odkriti te vzorce. In na koncu povežite koščke sestavljanke, da vidite veliko sliko.
Poglejmo gladino reke. Če vanj vržeš kamen, bodo prišli valovi. Krogi, ki so precej primerni za študij. Hitrost, perioda, valovna dolžina - vse to je mogoče izračunati. Toda dokler val ne doseže obale, se ne odbije in se začne prekrivati. Dobimo kaos (interferenco), ki ga je že težko preučevati.
Kaj pa če gremo iz nasprotne smeri? Čim bolj poenostavite obnašanje vala. Poenostavite, poiščite vzorec in ga poskusite opisati polna slika kaj se dogaja.
Kaj je mogoče poenostaviti? Seveda naj bo odsevna površina ravna, brez pregibov. Nato namesto samega vala uporabite samo vektor valovnega gibanja. Načeloma je to dovolj za izdelavo preprostega algoritma in simulacijo procesa na računalniku. In to je celo povsem dovolj, da naredite "model" obnašanja valov na navadnem karirastem listu papirja.
Kaj imamo kot rezultat? Posledično to vidimo v valovni procesi(enako valovanje na gladini reke) nimamo kaosa, ampak prekrivanje fraktalov (samo podobnih struktur) enega na drugega.

Razmislimo o drugi vrsti valov. Kot je znano, elektromagnetno valovanje sestoji iz treh vektorjev - valovnega ter električnega in napetostnega vektorja magnetno polje. Kot lahko vidimo, če "ujamete" tak val zaprto območje– kjer se ti vektorji križajo, dobimo precej jasne zaprte strukture. morda, elementarni delci– so to isti fraktali?

Vsi fraktali v pravokotnikih od 1 do 80 (6723x6723 px):

Zaprta območja v fraktalih (6723x6723 px):

Samo lep fraktal (4078x2518 px):