Preparación en línea para el examen. Simulador del examen estatal unificado en inglés

Instrucciones

Según la propiedad de un trapezoide isósceles, el segmento n es igual a la mitad de la diferencia de las bases xey. Por lo tanto, la base más pequeña del trapezoide y se puede representar como la diferencia entre la base más grande y el segmento n multiplicada por dos: y = x - 2*n.

Encuentra el segmento más pequeño desconocido n. Para hacer esto, calcule uno de los lados del resultado. triángulo rectángulo. Un triángulo está formado por una altura - h (cateto), un lado - a (hipotenusa) y un segmento - n (cateto). Según el teorema de Pitágoras, el cateto desconocido n² = a² - h². Sustituto valores numéricos y calcular el cuadrado del cateto n. Tome la raíz cuadrada del valor resultante; esta será la longitud del segmento n.

Sustituye este valor en la primera ecuación para calcular y. El área del trapezoide se calcula mediante la fórmula S = ((x + y)*h)/2. Expresa la variable desconocida: y = 2*S/h – x.

Fuentes:

• altura de un trapezoide isósceles

Para definir un cuadrilátero como un trapecio, se deben definir al menos tres de sus lados. Por tanto, por ejemplo, podemos considerar un problema en el que las longitudes de las diagonales están dadas trapecios, así como uno de los vectores laterales.

Instrucciones

La figura de las condiciones del problema se presenta en 1.B. en este caso se debe suponer que el que estamos considerando es ABCD, en el que se dan las longitudes de las diagonales AC y BD, así como lado AB, representado por el vector a(ax,ay). Los datos iniciales aceptados nos permiten encontrar ambos. jardines trapecios(tanto arriba como abajo). EN ejemplo específico el AD de base inferior se encontrará primero.

Considere el triángulo ABD. La longitud de su lado AB es igual al valor absoluto del vector a. Sea |a|=sqrt((ax)^2+(ay)^2)=a, entonces cosф =ax/sqrt(((ax)^2+(ay)^2), como el coseno director de a. Sea la diagonal dada BD longitud p, y el AD deseado longitud X. Entonces, según el teorema del coseno, P^2=a^2+ x^2-2axcosф. O x^2-2axcosф+(a^2-p^2)=0.

Para encontrar la cima jardines BC (su longitud también se denota por x en la búsqueda), se utiliza el módulo |a|=a, así como la segunda diagonal BD=q y el coseno del ángulo ABC, que obviamente es igual a (n-ph) .

A continuación consideramos triangulo abc, a lo que, como antes, surge el teorema del coseno, y lo siguiente. Considerando que cos(п-ф)=-cosф, basándonos en la solución para AD, podemos usar la siguiente fórmula, reemplazando p por q:ВС=- a*ax|sqrt(((ax)^2+(ay) ^2) +sqrt((((a)^2)(ax^2))/(ax^2+ay^2))-a^2+q^2).

Es un cuadrado y, en consecuencia, tiene dos raíces. Así, en este caso queda por elegir solo aquellas raíces que tienen valor positivo, ya que la longitud no puede ser negativa.

Ejemplo Dejar entrar trapecios El lado ABCD AB está dado por el vector a(1, sqrt3), p=4, q=6. Encontrar jardines trapecios.Solución. Usando los algoritmos obtenidos anteriormente, podemos escribir: |a|=a=2, cosф=1/2. AD=1/2+sqrt(4/4 -4+16)=1/2 +sqrt(13)=(sqrt(13)+1)/2.BC=-1/2+sqrt(-3+36 )=(sqrt(33)-1)/2.

Vídeo sobre el tema.

Un trapezoide es un cuadrilátero en el que dos lados son paralelos y los otros dos no. La altura de un trapezoide es un segmento trazado perpendicularmente entre dos rectas paralelas. Dependiendo de los datos de origen, se pueden calcular de diferentes maneras.

Necesitará

• Conocimiento de los lados, terrenos, línea media trapezoide, así como, opcionalmente, su área y/o perímetro.

Instrucciones

Digamos que hay un trapecio con los mismos datos que en la Figura 1. Dibujemos 2 alturas, obtenemos , que tiene 2 lados más pequeños por los catetos de triángulos rectángulos. Denotaremos el rollo más pequeño como x. Se localiza dividiendo la diferencia de longitud entre las bases más grandes y más pequeñas. Entonces, según el teorema de Pitágoras, el cuadrado de la altura igual a la suma cuadrados de la hipotenusa d y el cateto x. Extraemos de esta suma y obtenemos la altura h. (Figura 2)

Vídeo sobre el tema.

Fuentes:

• cómo calcular la altura de un trapezoide

figura matematica con cuatro vértices se llama trapecio si un par de sus lados opuestos son paralelos y el otro par no lo es. Los lados paralelos se llaman razones trapecios, los otros dos son laterales. en un rectangular trapecios uno de los ángulos laterales es recto.

Instrucciones

Tarea 1. Encuentra las bases BC y AD. trapecios, si se conoce la longitud AC = f; longitud del lado CD = c y ángulo ADC = α Solución: Considere un CED rectangular. Se conocen la hipotenusa c y el ángulo entre la hipotenusa y el cateto EDC. Encuentre las longitudes CE y ED: usando la fórmula del ángulo CE = CD*sin(ADC); ED = CD*cos(ADC). Entonces: CE = c*senα; ED=c*cosα.

Considere el triángulo rectángulo ACE. Conoces la hipotenusa AC y CE, encuentra el lado AE usando la regla: la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. Entonces: AE(2) = AC(2) - CE(2) = f(2) - c*sinα. Calcular Raíz cuadrada desde el lado derecho de la igualdad. Encontraste el rectangular superior. trapecios.

La longitud de la base AD es la suma de las longitudes de dos segmentos AE y ED. AE = raíz cuadrada(f(2) - c*sinα); ED = c*cosα). Entonces: AD = raíz cuadrada (f(2) - c*sinα) + c*cosα. Has encontrado la base inferior del rectángulo. trapecios.

Tarea 2. Encuentra las bases BC y AD del rectangular. trapecios, si se conoce la longitud de la diagonal BD = f; longitud del lado CD = c y ángulo ADC = α Solución: Considere el triángulo rectángulo CED. Encuentre las longitudes de los lados CE y ED: CE = CD*sin(ADC) = c*sinα; ED = CD*cos(ADC) = c*cosα.

Considere el rectángulo ABCE. Por la propiedad AB = CE = c*sinα Considere el triángulo rectángulo ABD. Según la propiedad de un triángulo rectángulo, el cuadrado de la hipotenusa es la suma de los cuadrados de los catetos. Por lo tanto AD(2) = BD(2) - AB(2) = f(2) - c*sinα Has encontrado la base inferior del rectángulo. trapecios AD = raíz cuadrada(f(2) - c*senα).

Según la regla del rectángulo, BC = AE = AD - ED = raíz cuadrada (f(2) - c*sinα) - c*cosα. Has encontrado la base superior del rectángulo. trapecios.

La base más pequeña de un trapezoide es uno de sus lados paralelos, que tiene una longitud mínima. Este valor se puede calcular de varias formas utilizando determinados datos.

Necesitará

• - calculadora.

Instrucciones

Si se conocen dos longitudes (la base y la línea media), utilice la propiedad del trapezoide para calcular la base más pequeña. Según él, la línea media de un trapezoide es idéntica a la mitad de la suma de las bases. En este caso, la base más pequeña será igual a la diferencia entre el doble de la longitud de la línea media y la longitud de la base grande de esta figura.

Si se conocen parámetros del trapezoide como , altura, longitud de la base grande, entonces calcule la base más pequeña de esta base basándose en el trapezoide. En este caso resultado final Se obtiene restando de la diferencia entre el cociente del doble del área y la altura un parámetro como la longitud de la base grande del trapezoide.

Calcula la longitud del lado del otro.

En los materiales de diversas pruebas y exámenes, se encuentran muy a menudo. problemas trapezoidales, cuya solución requiere el conocimiento de sus propiedades.

Averigüemos qué propiedades interesantes y útiles tiene un trapezoide para resolver problemas.

Después de estudiar las propiedades de la línea media de un trapezoide, se puede formular y demostrar propiedad de un segmento que conecta los puntos medios de las diagonales de un trapezoide. El segmento que une los puntos medios de las diagonales de un trapezoide es igual a la mitad de la diferencia de las bases.

MO – línea media triangulo abc e igual a 1/2ВС (Figura 1).

MQ es la línea media del triángulo ABD y es igual a 1/2AD.

Entonces OQ = MQ – MO, por lo tanto OQ = 1/2AD – 1/2BC = 1/2(AD – BC).

A la hora de resolver muchos problemas sobre un trapezoide, una de las principales técnicas es dibujar en él dos alturas.

Considera lo siguiente tarea.

Sea BT la altura de un trapezoide isósceles ABCD con bases BC y AD, con BC = a, AD = b. Encuentre las longitudes de los segmentos AT y TD.

Solución.

Resolver el problema no es difícil. (Figura 2), pero te permite obtener propiedad de la altura de un trapecio isósceles extraído del vértice ángulo obtuso : la altura de un trapecio isósceles dibujado desde el vértice de un ángulo obtuso se divide base más grande en dos segmentos, el menor de los cuales es igual a la mitad de la diferencia de las bases, y el mayor es igual a la mitad de la suma de las bases.

Al estudiar las propiedades de un trapezoide, es necesario prestar atención a una propiedad como la similitud. Entonces, por ejemplo, las diagonales de un trapezoide lo dividen en cuatro triángulos, y los triángulos adyacentes a las bases son similares y los triángulos adyacentes a los lados tienen el mismo tamaño. Esta afirmación se puede llamar Propiedad de los triángulos en la que se divide un trapezoide por sus diagonales.. Además, la primera parte de la afirmación se puede demostrar muy fácilmente mediante el signo de semejanza de triángulos en dos ángulos. vamos a demostrar Segunda parte del comunicado.

Los triángulos BOC y COD tienen una altura común. (Fig. 3), si tomamos como bases los segmentos BO y OD. Entonces S BOC /S COD = BO/OD = k. Por lo tanto, S COD = 1/k · S BOC.

De manera similar, los triángulos BOC y AOB tienen una altura común si tomamos como bases los segmentos CO y OA. Entonces S BOC /S AOB = CO/OA = k y S A O B = 1/k · S BOC .

De estas dos frases se deduce que S COD = S A O B.

No nos detengamos en la declaración formulada, sino que encontremos la relación entre las áreas de los triángulos en los que se divide el trapezoide por sus diagonales. Para ello, resolvamos el siguiente problema.

Sea el punto O el punto de intersección de las diagonales del trapezoide ABCD con las bases BC y AD. Se sabe que las áreas de los triángulos BOC y AOD son iguales a S 1 y S 2, respectivamente. Encuentra el área del trapezoide.

Dado que S COD = S A O B, entonces S ABC D = S 1 + S 2 + 2S COD.

De la similitud de los triángulos BOC y AOD se deduce que BO/OD = √(S₁/S 2).

Por lo tanto, S₁/S COD = BO/OD = √(S₁/S 2), lo que significa S COD = √(S 1 · S 2).

Entonces S ABC D = S 1 + S 2 + 2√(S 1 · S 2) = (√S 1 + √S 2) 2.

Utilizando la semejanza se demuestra que propiedad de un segmento que pasa por el punto de intersección de las diagonales de un trapecio paralelo a las bases.

Consideremos tarea:

Sea el punto O el punto de intersección de las diagonales del trapezoide ABCD con las bases BC y AD. antes de Cristo = a, ANUNCIO = b. Encuentre la longitud del segmento PK que pasa por el punto de intersección de las diagonales del trapecio paralelo a las bases. ¿En qué segmentos se divide PK por el punto O (Fig. 4)?

De la semejanza de los triángulos AOD y BOC se deduce que AO/OC = AD/BC = b/a.

De la semejanza de los triángulos AOP y ACB se deduce que AO/AC = PO/BC = b/(a + b).

Por tanto PO = BC b / (a ​​​​+ b) = ab/(a + b).

De manera similar, de la similitud de los triángulos DOK y DBC, se deduce que OK = ab/(a + b).

Por tanto PO = OK y PK = 2ab/(a + b).

Entonces, la propiedad probada se puede formular de la siguiente manera: el segmento, paralelo a las bases un trapezoide que pasa por el punto de intersección de las diagonales y conecta dos puntos de los lados es bisecado por el punto de intersección de las diagonales. Su longitud es la media armónica de las bases del trapezoide.

Siguiente propiedad de cuatro puntos: en un trapezoide, el punto de intersección de las diagonales, el punto de intersección de la continuación de los lados, los puntos medios de las bases del trapecio se encuentran en la misma recta.

Los triángulos BSC y ASD son similares (Figura 5) y en cada una de ellas las medianas ST y SG dividen el ángulo del vértice S en partes iguales. Por tanto, los puntos S, T y G se encuentran en la misma recta.

De la misma manera, los puntos T, O y G están ubicados en la misma línea. Esto se desprende de la similitud de los triángulos BOC y AOD.

Esto significa que los cuatro puntos S, T, O y G se encuentran en la misma recta.

También puedes encontrar la longitud del segmento que divide el trapecio en dos similares.

Si los trapecios ALFD y LBCF son similares (Figura 6), entonces a/LF = LF/b.

Por tanto, LF = √(ab).

Por tanto, un segmento que divide un trapezoide en dos trapecios similares tiene una longitud igual a la media geométrica de las longitudes de las bases.

vamos a demostrar propiedad de un segmento que divide un trapezoide en dos áreas iguales.

Sea el área del trapecio S (Figura 7). h 1 y h 2 son partes de la altura y x es la longitud del segmento deseado.

Entonces S/2 = h 1 (a + x)/2 = h 2 (b + x)/2 y

S = (h 1 + h 2) · (a + b)/2.

Creemos un sistema

(h 1 (a + x) = h 2 (b + x)
(h 1 · (a + x) = (h 1 + h 2) · (a + b)/2.

decidir este sistema, obtenemos x = √(1/2(a 2 + b 2)).

De este modo, la longitud del segmento que divide el trapezoide en dos iguales es igual a √((a 2 + b 2)/2)(medio cuadrado de las longitudes de las bases).

Entonces, para el trapezoide ABCD con bases AD y BC (BC = a, AD = b) demostramos que el segmento:

1) MN, que conecta los puntos medios de los lados laterales del trapezoide, es paralelo a las bases e igual a su media suma (promedio números aritméticos a y B);

2) PK que pasa por el punto de intersección de las diagonales del trapecio paralelo a las bases es igual a
2ab/(a + b) (media armónica de los números a y b);

3) LF, que divide un trapezoide en dos trapecios similares, tiene una longitud igual a la media números geométricos a y b, √(ab);

4) EH, al dividir un trapecio en dos iguales, tiene longitud √((a 2 + b 2)/2) (la raíz cuadrática media de los números a y b).

Signo y propiedad de un trapecio inscrito y circunscrito.

Propiedad de un trapecio inscrito: Un trapezoide puede inscribirse en una circunferencia si y sólo si es isósceles.

Propiedades del trapezoide descrito. Un trapecio se puede describir alrededor de un círculo si y sólo si la suma de las longitudes de las bases es igual a la suma de las longitudes de los lados.

Consecuencias útiles del hecho de que un círculo esté inscrito en un trapezoide:

1. La altura del trapecio circunscrito es igual a dos radios del círculo inscrito.

2. El lado del trapezoide descrito es visible desde el centro del círculo inscrito en ángulo recto.

La primera es obvia. Para demostrar el segundo corolario, es necesario establecer que el ángulo COD es recto, lo cual tampoco es difícil. Pero conocer este corolario te permite utilizar un triángulo rectángulo al resolver problemas.

especifiquemos Corolarios de un trapecio circunscrito isósceles:

La altura de un trapecio circunscrito isósceles es el promedio bases geométricas trapecios
h = 2r = √(ab).

Las propiedades consideradas le permitirán comprender más profundamente el trapezoide y garantizar el éxito en la resolución de problemas utilizando sus propiedades.

¿Aún tienes preguntas? ¿No sabes cómo resolver problemas de trapecio?
Para obtener ayuda de un tutor -.
¡La primera lección es gratis!

blog.site, al copiar material total o parcialmente, se requiere un enlace a la fuente original.

Círculo circunscrito y trapezoide. ¡Hola! Hay una publicación más para usted, en la que veremos los problemas con los trapecios. Las tareas son parte del examen de matemáticas. Aquí se combinan en un grupo; no se da solo un trapezoide, sino una combinación de cuerpos: un trapezoide y un círculo. La mayoría de estos problemas se resuelven oralmente. Pero también hay algunos que es necesario abordar. Atención especial, por ejemplo, tarea 27926.

¿Qué teoría necesitas recordar? Este:

Se pueden ver los problemas con trapecios que están disponibles en el blog. Aquí.

27924. Se describe un círculo alrededor de un trapezoide. El perímetro del trapezoide es 22, la línea media es 5. Encuentra el lado del trapezoide.

Tenga en cuenta que un círculo sólo se puede describir alrededor de un trapezoide isósceles. Se nos da la línea media, lo que significa que podemos determinar la suma de las bases, es decir:

Esto significa que la suma de los lados será igual a 22–10=12 (perímetro menos la base). Como los lados de un trapecio isósceles son iguales, un lado será igual a seis.

27925. El lado lateral de un trapezoide isósceles es igual a su base más pequeña, el ángulo en la base es 60 0, la base más grande es 12. Encuentra el radio del círculo circunscrito de este trapezoide.

Si resolviste problemas con un círculo y un hexágono inscrito en él, inmediatamente dirás la respuesta: el radio es 6. ¿Por qué?

Mira: un trapezoide isósceles con un ángulo base igual a 60 0 y lados iguales AD, DC y CB, representa la mitad de un hexágono regular:

En tal hexágono, el segmento que conecta vértices opuestos pasa por el centro del círculo. *El centro del hexágono y el centro del círculo coinciden, más detalles

Es decir, la base mayor de este trapezoide coincide con el diámetro del círculo circunscrito. Entonces el radio es seis.

*Por supuesto, podemos considerar la igualdad de los triángulos ADO, DOC y OCB. Demuestre que son equiláteros. A continuación, concluimos que el ángulo AOB es igual a 180 0 y el punto O equidista de los vértices A, D, C y B, y por tanto AO=OB=12/2=6.

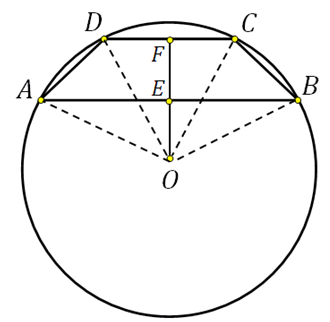
27926. Las bases de un trapecio isósceles son 8 y 6. El radio del círculo circunscrito es 5. Calcula la altura del trapezoide.

Tenga en cuenta que el centro del círculo circunscrito se encuentra en el eje de simetría, y si construimos la altura del trapecio que pasa por este centro, cuando se cruza con las bases las dividirá por la mitad. Mostremos esto en el boceto y también conectemos el centro con los vértices:

El segmento EF es la altura del trapezoide, necesitamos encontrarlo.

En el triángulo rectángulo OFC conocemos la hipotenusa (este es el radio del círculo), FC=3 (ya que DF=FC). Usando el teorema de Pitágoras podemos calcular OF:

En el triángulo rectángulo OEB, conocemos la hipotenusa (este es el radio del círculo), EB=4 (ya que AE=EB). Usando el teorema de Pitágoras podemos calcular OE:

Así EF=FO+OE=4+3=7.

¡Ahora un matiz importante!

En este problema, la figura muestra claramente que las bases se encuentran a lo largo lados diferentes desde el centro del círculo, por lo que el problema se resuelve de esta manera.

¿Y si las condiciones no incluyeran un boceto?

Entonces el problema tendría dos respuestas. ¿Por qué? Mire con atención: en cualquier círculo se pueden inscribir dos trapecios con bases determinadas:

*Es decir, dadas las bases del trapezoide y el radio del círculo, existen dos trapecios.

Y la solución a la “segunda opción” será la siguiente.

Usando el teorema de Pitágoras calculamos OF:

Calculemos también OE:

Por tanto, EF=FO–OE=4–3=1.

Por supuesto, en un problema con una respuesta corta en el Examen Estatal Unificado no puede haber dos respuestas, y no se planteará un problema similar sin un boceto. Por eso, ¡presta especial atención al boceto! A saber: cómo se ubican las bases del trapezoide. Pero en las tareas con respuesta detallada, esto estuvo presente en años anteriores (con una condición un poco más complicada). Quien considerara sólo una opción para la ubicación del trapezoide perdería un punto en esta tarea.

27937. Un trapecio está circunscrito a un círculo cuyo perímetro es 40. Halla su línea media.

Aquí conviene recordar inmediatamente la propiedad de un cuadrilátero circunscrito a un círculo:

Cantidades lados opuestos cualquier cuadrilátero circunscrito a un círculo son iguales.

Para sentirse seguro y resolver con éxito problemas en las lecciones de geometría, no basta con aprender las fórmulas. Primero hay que entenderlos. Tener miedo, y más aún odiar las fórmulas, es improductivo. En este articulo lenguaje accesible será analizado varias maneras Encontrar el área de un trapezoide. Para comprender mejor las reglas y teoremas correspondientes, prestaremos atención a sus propiedades. Esto le ayudará a comprender cómo funcionan las reglas y en qué casos se deben aplicar determinadas fórmulas.

Definiendo un trapezoide

¿Qué tipo de cifra es esta en general? Un trapezoide es un polígono con cuatro vértices y dos lados paralelos. Los otros dos lados del trapecio pueden estar inclinados en diferentes ángulos. Su lados paralelos se llaman bases, y para los lados no paralelos se usa el nombre “lados” o “caderas”. Estas cifras son bastante comunes en la vida cotidiana. Los contornos del trapezoide se pueden ver en las siluetas de ropa, elementos de interior, muebles, platos y muchos otros. trapecio sucede diferentes tipos: escaleno, equilátero y rectangular. Examinaremos sus tipos y propiedades con más detalle más adelante en el artículo.

Propiedades de un trapecio

Detengámonos brevemente en las propiedades de esta figura. La suma de los ángulos adyacentes a cualquier lado es siempre 180°. Cabe señalar que todos los ángulos de un trapezoide suman 360°. El trapezoide tiene el concepto de línea media. Si conectas los puntos medios de los lados con un segmento, esta será la línea media. Se designa m. La línea media tiene propiedades importantes: siempre es paralela a las bases (recordamos que las bases también son paralelas entre sí) e igual a su media suma:

Esta definición debe aprenderse y comprenderse, ¡porque es la clave para resolver muchos problemas!

Con un trapezoide siempre puedes bajar la altura hasta la base. Una altitud es una perpendicular, a menudo denotada con el símbolo h, que se traza desde cualquier punto de una base a otra base o su extensión. La línea media y la altura te ayudarán a encontrar el área del trapezoide. Tareas similares son los más comunes en curso escolar geometría y aparecen regularmente entre las pruebas y exámenes.

Las fórmulas más simples para el área de un trapezoide.

Veamos los dos más populares y fórmulas simples, con cuya ayuda se encuentra el área de un trapezoide. Basta con multiplicar la altura por la mitad de la suma de las bases para encontrar fácilmente lo que buscas:

S = h*(a + b)/2.

En esta fórmula, a, b denotan las bases del trapezoide, h - la altura. Para facilitar la percepción, en este artículo, los signos de multiplicación están marcados con un símbolo (*) en las fórmulas, aunque en los libros de referencia oficiales el signo de multiplicación generalmente se omite.

Veamos un ejemplo.

Dado: un trapecio con dos bases iguales a 10 y 14 cm, la altura es 7 cm ¿Cuál es el área del trapezoide?

Veamos la solución a este problema. Usando esta fórmula, primero necesitas encontrar la mitad de la suma de las bases: (10+14)/2 = 12. Entonces, la mitad de la suma es igual a 12 cm. Ahora multiplicamos la mitad de la suma por la altura: 12*7 = 84. Lo que buscamos se encuentra. Respuesta: El área del trapezoide es 84 metros cuadrados. cm.

Segundo formula famosa dice: el área de un trapezoide es igual al producto de la línea media por la altura del trapezoide. Es decir, en realidad se sigue del concepto anterior de línea media: S=m*h.

Usar diagonales para cálculos.

Otra forma de encontrar el área de un trapecio en realidad no es tan complicada. Está conectado a sus diagonales. Usando esta fórmula, para encontrar el área, debes multiplicar el medio producto de sus diagonales (d 1 d 2) por el seno del ángulo entre ellas:

S = ½ d 1 d 2 pecado a.

Consideremos un problema que muestra la aplicación de este método. Dado: un trapecio cuya longitud de las diagonales es igual a 8 y 13 cm, respectivamente. El ángulo a entre las diagonales es de 30°. Encuentra el área del trapezoide.

Solución. Usando la fórmula anterior, es fácil calcular lo que se requiere. Como sabes, sen 30° es 0,5. Por lo tanto, S = 8*13*0,5=52. Respuesta: el área es de 52 metros cuadrados. cm.

Encontrar el área de un trapezoide isósceles

Un trapezoide puede ser isósceles (isosceles). Sus lados son iguales y los ángulos en las bases son iguales, lo cual queda bien ilustrado en la figura. Trapecio isósceles Tiene las mismas propiedades que el normal, más una serie de especiales. Se puede circunscribir un círculo alrededor de un trapezoide isósceles y se puede inscribir un círculo dentro de él.

¿Qué métodos existen para calcular el área de dicha figura? El siguiente método requerirá muchos cálculos. Para utilizarlo es necesario conocer los valores del seno (sin) y el coseno (cos) del ángulo en la base del trapezoide. Sus cálculos requieren tablas Bradis o calculadora de ingenieria. Aquí está la fórmula:

S= C*pecado a*(a - C*porque a),

Dónde Con- muslo lateral, a- ángulo en la base inferior.

Un trapezoide equilátero tiene diagonales de igual longitud. Lo contrario también es cierto: si un trapezoide tiene diagonales iguales, entonces es isósceles. De aquí siguiente fórmula, que ayuda a encontrar el área de un trapecio: la mitad del producto del cuadrado de las diagonales y el seno del ángulo entre ellas: S = ½ d 2 sin a.

Encontrar el área de un trapezoide rectangular

Famoso caso especial trapezoide rectangular. Este es un trapezoide, en el que un lado (su muslo) linda con las bases en ángulo recto. Tiene las propiedades de un trapezoide regular. Además, ella tiene muy característica interesante. La diferencia de los cuadrados de las diagonales de dicho trapezoide es igual a la diferencia de los cuadrados de sus bases. Para ello se utilizan todos los métodos descritos anteriormente para calcular el área.

Usamos el ingenio

Hay un truco que puede ayudarte si olvidas fórmulas específicas. Echemos un vistazo más de cerca a qué es un trapezoide. Si lo dividimos mentalmente en partes, obtendremos formas geométricas familiares y comprensibles: un cuadrado o rectángulo y un triángulo (uno o dos). Si se conocen la altura y los lados del trapecio, puedes usar las fórmulas para el área de un triángulo y un rectángulo y luego sumar todos los valores resultantes.

Ilustremos esto siguiente ejemplo. Dana trapezoide rectangular. El ángulo C = 45°, los ángulos A, D miden 90°. La base superior del trapecio mide 20 cm, la altura es 16 cm. Necesitas calcular el área de la figura.

Esta figura obviamente consta de un rectángulo (si dos ángulos miden 90°) y un triángulo. Como el trapezoide es rectangular, por tanto, su altura es igual a su lado, es decir, 16 cm. Tenemos un rectángulo con lados de 20 y 16 cm, respectivamente. Consideremos ahora un triángulo cuyo ángulo mide 45°. Sabemos que un lado mide 16 cm, ya que este lado también es la altura del trapezoide (y sabemos que la altura desciende hasta la base en ángulo recto), por lo tanto, el segundo ángulo del triángulo es de 90°. Por tanto, el ángulo restante del triángulo es de 45°. Como consecuencia de esto obtenemos un rectángulo. triángulo isósceles, cuyos dos lados son iguales. Esto significa que el otro lado del triángulo es igual a la altura, es decir, 16 cm. Resta calcular el área del triángulo y el rectángulo y sumar los valores resultantes.

El área de un triángulo rectángulo es igual a la mitad del producto de sus catetos: S = (16*16)/2 = 128. El área de un rectángulo es igual al producto de su ancho por su largo: S = 20*16 = 320. Encontramos el área requerida del trapezoide S = 128 + 320 = 448 m2. Puedes comprobarlo tú mismo fácilmente utilizando las fórmulas anteriores, la respuesta será idéntica.

Usamos la fórmula Pick

S = M/2 + N - 1,

en esta fórmula M es el número de nodos, es decir intersecciones de las líneas de la figura con las líneas de la celda en los límites del trapecio (puntos naranjas en la figura), N es el número de nodos dentro de la figura (puntos azules). Es más conveniente usarlo al encontrar el área. polígono irregular. Sin embargo, cuanto mayor sea el arsenal de técnicas utilizadas, menos errores y mejores serán los resultados.

Por supuesto, la información proporcionada no agota los tipos y propiedades de un trapezoide, ni tampoco los métodos para encontrar su área. Este artículo proporciona una descripción general de sus características más importantes. Al resolver problemas geométricos, es importante actuar gradualmente, comenzar con fórmulas y problemas sencillos, consolidar constantemente su comprensión y pasar a otro nivel de complejidad.

Reunidas, las fórmulas más comunes ayudarán a los estudiantes a navegar por las diversas formas de calcular el área de un trapezoide y prepararse mejor para los exámenes y pruebas sobre este tema.