Pour résoudre avec succès équations trigonométriques pratique à utiliser méthode de réductionà des problèmes déjà résolus. Voyons quelle est l'essence de cette méthode ?
Dans toute tâche proposée, vous devez voir un problème précédemment résolu, puis, en utilisant des transformations équivalentes essayez de réduire la tâche qui vous est confiée à une tâche plus simple.
Alors, au moment de décider équations trigonométriques s'élève généralement à quelques séquence finieéquations équivalentes dont le dernier maillon est une équation à solution évidente. Il est seulement important de se rappeler que si les compétences nécessaires pour résoudre les équations trigonométriques les plus simples ne sont pas formées, la solution est alors plus équations complexes sera difficile et inefficace.
De plus, lors de la résolution d’équations trigonométriques, il ne faut jamais oublier qu’il existe plusieurs méthodes de résolution possibles.
Exemple 1. Trouver le nombre de racines équations du cos x = -1/2 sur l'intervalle .
Solution:
Méthode I Traçons les fonctions y = cos x et y = -1/2 et trouvons le nombre de leurs points communs sur l'intervalle (Fig. 1).
Puisque les graphes de fonctions ont deux des points communs sur l'intervalle, alors l'équation contient deux racines sur cet intervalle.
IIème méthode. A l'aide d'un cercle trigonométrique (Fig. 2) on connaît le nombre de points appartenant à l'intervalle, dans lequel cos x = -1/2. La figure montre que l'équation a deux racines. 
Méthode III. En utilisant la formule des racines de l'équation trigonométrique, nous résolvons l'équation cos x = -1/2.
x = ± arccos (-1/2) + 2πk, k – entier (k € Z) ;
x = ± (π – arccos 1/2) + 2πk, k – entier (k € Z) ;
x = ± (π – π/3) + 2πk, k – entier (k € Z) ;
x = ± 2π/3 + 2πk, k – entier (k € Z).
L'intervalle contient les racines 2π/3 et -2π/3 + 2π, k est un entier. Ainsi, l’équation a deux racines sur un intervalle donné.
Réponse : 2.
À l'avenir, les équations trigonométriques seront résolues à l'aide de l'une des méthodes proposées, ce qui, dans de nombreux cas, n'exclut pas l'utilisation d'autres méthodes.
Exemple 2. Trouver le nombre de solutions de l'équation tg (x + π/4) = 1 sur l'intervalle [-2π ; 2π].
Solution:
En utilisant la formule des racines d'une équation trigonométrique, on obtient :
x + π/4 = arctan 1 + πk, k – entier (k € Z) ;
x + π/4 = π/4 + πk, k – entier (k € Z) ;
x = πk, k – entier (k € Z) ;
L'intervalle [-2π; 2π] appartiennent aux nombres -2π ; -π; 0 ; π ; 2π. L’équation a donc cinq racines sur un intervalle donné.
Réponse : 5.
Exemple 3. Trouver le nombre de racines de l'équation cos 2 x + sin x · cos x = 1 sur l'intervalle [-π ; π].
Solution:
Puisque 1 = sin 2 x + cos 2 x (de base identité trigonométrique), alors l'équation originale prend la forme :
cos 2 x + péché x · cos x = péché 2 x + cos 2 x ;
péché 2 x – péché x cos x = 0 ;
sin x(sin x – cos x) = 0. Le produit est égal à zéro, ce qui signifie qu'au moins un des facteurs doit être égal à zéro, C'est pourquoi:
péché x = 0 ou péché x – cos x = 0.
Puisque les valeurs de la variable pour laquelle cos x = 0 ne sont pas les racines de la deuxième équation (le sinus et le cosinus du même nombre ne peuvent pas être égaux à zéro en même temps), on divise les deux côtés de la deuxième équation par cos x :
sin x = 0 ou sin x / cos x - 1 = 0.
Dans la deuxième équation on utilise le fait que tg x = sin x / cos x, alors :
sin x = 0 ou tan x = 1. En utilisant des formules nous avons :
x = πk ou x = π/4 + πk, k – entier (k € Z).
De la première série de racines à l'intervalle [-π; π] appartiennent aux nombres -π ; 0 ; π. De la deuxième série : (π/4 – π) et π/4.
Il y a donc cinq racines équation originale appartiennent à l'intervalle [-π; π].
Réponse : 5.
Exemple 4. Trouver la somme des racines de l'équation tg 2 x + сtg 2 x + 3tg x + 3сtgx + 4 = 0 sur l'intervalle [-π ; 1.1π].
Solution:
Réécrivons l'équation comme suit :
tg 2 x + сtg 2 x + 3(tg x + сtgx) + 4 = 0 et effectuez un remplacement.
Soit tg x + сtgx = a. Mettons au carré les deux côtés de l'équation :
(tg x + сtg x) 2 = une 2. Développons les parenthèses :
tg 2 x + 2tg x · сtgx + сtg 2 x = a 2.
Puisque tg x · сtgx = 1, alors tg 2 x + 2 + сtg 2 x = a 2, ce qui signifie
tg 2 x + сtg 2 x = a 2 – 2.
Maintenant, l'équation originale ressemble à :
une 2 – 2 + 3une + 4 = 0 ;
a 2 + 3a + 2 = 0. En utilisant le théorème de Vieta, nous trouvons que a = -1 ou a = -2.
Faisons la substitution inverse, nous avons :
tg x + сtgx = -1 ou tg x + сtgx = -2. Résolvons les équations résultantes.
tg x + 1/tgx = -1 ou tg x + 1/tgx = -2.
Selon la propriété des deux, ils sont mutuellement nombres réciproques nous déterminons que la première équation n'a pas de racines, et à partir de la deuxième équation nous avons :
tg x = -1, c'est-à-dire x = -π/4 + πk, k – entier (k € Z).
L'intervalle [-π; 1,1π] appartiennent aux racines : -π/4 ; -π/4 + π. Leur somme :
-π/4 + (-π/4 + π) = -π/2 + π = π/2.
Réponse : π/2.
Exemple 5. Trouver la moyenne racines arithmétiques équations du péché 3x + sin x = sin 2x sur l'intervalle [-π; 0,5π].
Solution:
Profitons formule péchéα + sin β = 2sin ((α + β)/2) cos ((α – β)/2), alors
sin 3x + sin x = 2sin ((3x + x)/2) cos ((3x – x)/2) = 2sin 2x cos x et l'équation devient
2 péché 2x cos x = péché 2x ;
2sin 2x · cos x – sin 2x = 0. Sortons multiplicateur commun péché 2x hors parenthèses
sin 2x(2cos x – 1) = 0. Résolvez l’équation résultante :
sin 2x = 0 ou 2cos x – 1 = 0 ; 
péché 2x = 0 ou cos x = 1/2 ;
2x = πk ou x = ±π/3 + 2πk, k – entier (k € Z).
Nous avons donc des racines
x = πk/2, x = π/3 + 2πk, x = -π/3 + 2πk, k – entier (k € Z).
L'intervalle [-π; 0,5π] appartiennent aux racines -π ; -π/2; 0 ; π/2 (de la première série de racines) ; π/3 (de la deuxième série) ; -π/3 (de la troisième série). Leur moyenne arithmétique est :
(-π – π/2 + 0 + π/2 + π/3 – π/3)/6 = -π/6.
Réponse : -π/6.
Exemple 6. Trouver le nombre de racines de l'équation sin x + cos x = 0 sur l'intervalle [-1,25π ; 2π].
Solution:
Cette équation est une équation homogène du premier degré. Divisons ses deux parties par cosx (la valeur de la variable pour laquelle cos x = 0 ne sont pas des racines équation donnée, puisque le sinus et le cosinus d'un même nombre ne peuvent pas être égaux à zéro en même temps). L'équation originale est :
x = -π/4 + πk, k – entier (k € Z).
L'intervalle [-1,25π; 2π] appartiennent aux racines -π/4 ; (-π/4 + π); et (-π/4 + 2π).
Ainsi, l'intervalle donné contient trois racines de l'équation.
Réponse : 3.
Apprenez à faire la chose la plus importante : imaginez clairement un plan pour résoudre un problème, et n'importe quelle équation trigonométrique sera alors à votre portée.
Vous avez encore des questions ? Vous ne savez pas comment résoudre des équations trigonométriques ?
Pour obtenir l'aide d'un tuteur, inscrivez-vous.
site Web, lors de la copie du matériel en totalité ou en partie, un lien vers la source est requis.
Vous pouvez commander solution détaillée ta tâche!!!
L'égalité contenant l'inconnu sous le signe fonction trigonométrique(`sin x, cos x, tan x` ou `ctg x`) est appelé une équation trigonométrique, et ce sont leurs formules que nous examinerons plus en détail.
Les équations les plus simples sont appelées « sin x=a, cos x=a, tg x=a, ctg x=a », où « x » est l'angle à trouver, « a » est n'importe quel nombre. Écrivons les formules racines de chacun d'eux.
1. Équation `sin x=a`.
Pour `|a|>1`, il n'a pas de solutions.
Quand `|a| \leq 1` a nombre infini les décisions.
Formule racine : `x=(-1)^n arcsin a + \pi n, n \in Z`
2. Équation `cos x=a`
Pour `|a|>1` - comme dans le cas du sinus, les solutions parmi nombres réels n'a pas.
Quand `|a| \leq 1` a ensemble infini les décisions.
Formule racine : `x=\pm arccos a + 2\pi n, n \in Z`

Cas particuliers du sinus et du cosinus dans les graphiques. 
3. Équation `tg x=a`
Possède un nombre infini de solutions pour toutes les valeurs de « a ».
Formule racine : `x=arctg a + \pi n, n \in Z`

4. Équation `ctg x=a`
Possède également un nombre infini de solutions pour toutes les valeurs de « a ».
Formule racine : `x=arcctg a + \pi n, n \in Z`

Formules pour les racines des équations trigonométriques dans le tableau
Pour le sinus :  Pour le cosinus :
Pour le cosinus :  Pour la tangente et la cotangente :
Pour la tangente et la cotangente :  Formules pour résoudre des équations contenant des fonctions trigonométriques inverses :
Formules pour résoudre des équations contenant des fonctions trigonométriques inverses :

Méthodes de résolution d'équations trigonométriques
La résolution de toute équation trigonométrique comprend deux étapes :
- avec l'aide de le transformer au plus simple ;
- résolvez l'équation la plus simple obtenue en utilisant les formules de racine et les tableaux écrits ci-dessus.
Examinons les principales méthodes de solution à l'aide d'exemples.
Méthode algébrique.
Cette méthode consiste à remplacer une variable et à la substituer par une égalité.
Exemple. Résolvez l'équation : `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`
`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,
faites un remplacement : `cos(x+\frac \pi 6)=y`, puis `2y^2-3y+1=0`,
on retrouve les racines : `y_1=1, y_2=1/2`, d'où découlent deux cas :
1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.
2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.
Réponse : `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Factorisation.
Exemple. Résolvez l'équation : `sin x+cos x=1`.
Solution. Déplaçons tous les termes de l'égalité vers la gauche : `sin x+cos x-1=0`. En utilisant , nous transformons et factorisons le membre de gauche :
`sin x — 2sin^2 x/2=0`,
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sin x/2 (cos x/2-sin x/2)=0`,
- `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n` , `x_2=\pi/2+ 2\pi n`.
Réponse : `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.
Réduction à une équation homogène
Tout d’abord, vous devez réduire cette équation trigonométrique à l’une des deux formes suivantes :
`un péché x+b cos x=0` ( équation homogène premier degré) ou `a sin^2 x + b sin x cos x +c cos^2 x=0` (équation homogène du deuxième degré).
Divisez ensuite les deux parties par `cos x \ne 0` - pour le premier cas, et par `cos^2 x \ne 0` - pour le second. Nous obtenons des équations pour `tg x` : `a tg x+b=0` et `a tg^2 x + b tg x +c =0`, qui doivent être résolues à l'aide de méthodes connues.
Exemple. Résolvez l'équation : `2 sin^2 x+sin x cos x - cos^2 x=1`.
Solution. Écrivons-le côté droit comme `1=sin^2 x+cos^2 x` :
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`
`sin^2 x+sin x cos x — 2 cos^2 x=0`.
Il s'agit d'une équation trigonométrique homogène du deuxième degré, on divise ses côtés gauche et droit par `cos^2 x \ne 0`, on obtient :
`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) — \frac(2 cos^2 x)(cos^2 x)=0`
`tg^2x+tgx — 2=0`. Introduisons le remplacement `tg x=t`, résultant en `t^2 + t - 2=0`. Les racines de cette équation sont « t_1=-2 » et « t_2=1 ». Alors:
- `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
- `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, `n \in Z`.
Répondre. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.
Allez au demi-coin
Exemple. Résolvez l'équation : « 11 sin x - 2 cos x = 10 ».
Solution. Appliquons les formules double angle, ce qui donne : `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^ 2x/2`
`4 tg^2 x/2 — 11 tg x/2 +6=0`
Appliquer ce qui précède méthode algébrique, on a:
- `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Répondre. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Introduction de l'angle auxiliaire
Dans l'équation trigonométrique « a sin x + b cos x = c », où a,b,c sont des coefficients et x est une variable, divisez les deux côtés par « sqrt (a^2+b^2) » :
`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2) ) +b^2))`.
Les coefficients du côté gauche ont les propriétés du sinus et du cosinus, à savoir que la somme de leurs carrés est égale à 1 et que leurs modules ne sont pas supérieurs à 1. Notons-les ainsi : `\frac a(sqrt (a^2 +b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2)) =C`, alors :
`cos \varphi sin x + sin \varphi cos x =C`.
Regardons de plus près l'exemple suivant :
Exemple. Résolvez l'équation : `3 sin x+4 cos x=2`.
Solution. Divisez les deux côtés de l'égalité par `sqrt (3^2+4^2)`, nous obtenons :
`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))`
`3/5 péché x+4/5 cos x=2/5`.
Notons `3/5 = cos \varphi` , `4/5=sin \varphi`. Puisque `sin \varphi>0`, `cos \varphi>0`, alors comme angle auxiliaire prenons `\varphi=arcsin 4/5`. Ensuite nous écrivons notre égalité sous la forme :
`cos \varphi sin x+sin \varphi cos x=2/5`
En appliquant la formule de la somme des angles pour le sinus, on écrit notre égalité sous la forme suivante :
`sin (x+\varphi)=2/5`,
`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Répondre. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Équations trigonométriques rationnelles fractionnaires
Ce sont des égalités avec des fractions dont les numérateurs et dénominateurs contiennent des fonctions trigonométriques.
Exemple. Résous l'équation. `\frac (sin x)(1+cos x)=1-cos x`.
Solution. Multipliez et divisez le côté droit de l'égalité par « (1+cos x) ». En conséquence nous obtenons :
`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)`
`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`
`\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`
`\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0`
`\frac (sin x-sin^2 x)(1+cos x)=0`
Considérant que le dénominateur ne peut pas être égal à zéro, on obtient `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.
Assumons le numérateur de la fraction à zéro : `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Alors `sin x=0` ou `1-sin x=0`.
- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Étant donné que ` x \ne \pi+2\pi n, n \in Z`, les solutions sont `x=2\pi n, n \in Z` et `x=\pi /2+2\pi n` , `n \in Z`.
Répondre. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
La trigonométrie, et les équations trigonométriques en particulier, sont utilisées dans presque tous les domaines de la géométrie, de la physique et de l'ingénierie. Les études commencent en 10e année, il y a toujours des tâches pour l'examen d'État unifié, alors essayez de vous souvenir de toutes les formules des équations trigonométriques - elles vous seront certainement utiles !
Cependant, vous n'avez même pas besoin de les mémoriser, l'essentiel est d'en comprendre l'essence et de pouvoir la dériver. Ce n'est pas aussi difficile qu'il y paraît. Voyez par vous-même en regardant la vidéo.
Résoudre des équations trigonométriques simples.
Résoudre des équations trigonométriques de tout niveau de complexité revient en fin de compte à résoudre les équations trigonométriques les plus simples. Et dans ce meilleure aide encore une fois, il s'agit d'un cercle trigonométrique.
Rappelons les définitions du cosinus et du sinus.
Le cosinus d'un angle est l'abscisse (c'est-à-dire la coordonnée le long de l'axe) d'un point sur cercle unitaire, correspondant à une rotation d'un angle donné.
Le sinus d'un angle est l'ordonnée (c'est-à-dire la coordonnée le long de l'axe) d'un point du cercle unité correspondant à une rotation d'un angle donné.
Direction positive du mouvement le long cercle trigonométrique Un mouvement dans le sens antihoraire est pris en compte. Une rotation de 0 degré (ou 0 radian) correspond à un point de coordonnées (1;0)
Nous utilisons ces définitions pour résoudre des équations trigonométriques simples.
1. Résolvez l'équation
Cette équation est satisfaite par toutes les valeurs de l'angle de rotation qui correspondent aux points du cercle dont l'ordonnée est égale à .
Marquons un point d'ordonnée sur l'axe des ordonnées :

Réalisons ligne horizontale parallèle à l'axe des x jusqu'à ce qu'il croise le cercle. On obtient deux points situés sur le cercle et ayant une ordonnée. Ces points correspondent aux angles de rotation en et en radians :

Si on, en quittant le point correspondant à l'angle de rotation en radians, faire le tour cercle complet, on arrivera alors à un point correspondant à l'angle de rotation par radian et ayant la même ordonnée. Autrement dit, cet angle de rotation satisfait également notre équation. Nous pouvons faire autant de révolutions « à vide » que nous le souhaitons, en revenant au même point, et toutes ces valeurs d'angle satisferont notre équation. Le nombre de tours « au ralenti » sera désigné par la lettre (ou). Puisque nous pouvons faire ces révolutions à la fois en positif et en sens négatif, (ou ) peut prendre n’importe quelle valeur entière.
Autrement dit, la première série de solutions à l’équation originale a la forme :
![]() , , - ensemble d'entiers (1)
, , - ensemble d'entiers (1)
De même, la deuxième série de solutions a la forme :
![]() , Où , . (2)
, Où , . (2)
Comme vous l'avez peut-être deviné, cette série de solutions est basée sur le point du cercle correspondant à l'angle de rotation de .
Ces deux séries de solutions peuvent être combinées en une seule entrée :
Si nous prenons (c'est-à-dire pair) cette entrée, nous obtiendrons alors la première série de solutions.
Si nous prenons (c'est-à-dire impair) cette entrée, alors nous obtenons la deuxième série de solutions.
2. Résolvons maintenant l'équation
Puisqu'il s'agit de l'abscisse d'un point sur le cercle unité obtenu en tournant d'un angle, on marque le point en abscisse sur l'axe :

Réalisons ligne verticale parallèle à l'axe jusqu'à ce qu'il coupe le cercle. Nous obtiendrons deux points situés sur le cercle et ayant une abscisse. Ces points correspondent aux angles de rotation en et en radians. Rappelons qu'en se déplaçant dans le sens des aiguilles d'une montre, nous obtenons angle négatif rotation:

Écrivons deux séries de solutions :
![]() ,
,
![]() ,
,
(On arrive au point souhaité en partant du cercle complet principal, bien sûr.
Combinons ces deux séries en une seule entrée :
![]()
3. Résolvez l'équation
La tangente passe par le point de coordonnées (1,0) du cercle unité parallèle à l'axe OY
Marquons dessus un point avec une ordonnée égale à 1 (on recherche la tangente dont les angles sont égaux à 1) :

Relions ce point à l'origine des coordonnées par une ligne droite et marquons les points d'intersection de la ligne avec le cercle unité. Les points d'intersection de la droite et du cercle correspondent aux angles de rotation sur et :

Puisque les points correspondant aux angles de rotation qui satisfont notre équation se trouvent à une distance de radians les uns des autres, nous pouvons écrire la solution de cette façon :
4. Résolvez l'équation
La ligne des cotangentes passe par le point dont les coordonnées du cercle unité sont parallèles à l'axe.
Marquons un point d'abscisse -1 sur la ligne des cotangentes :

Relions ce point à l'origine de la ligne droite et continuons-le jusqu'à ce qu'il coupe le cercle. Cette droite coupera le cercle en des points correspondant aux angles de rotation en et en radians :

Puisque ces points sont séparés les uns des autres par une distance égale à , alors décision commune On peut écrire cette équation comme ceci :
![]()
Dans les exemples donnés illustrant la solution des équations trigonométriques les plus simples, des valeurs tabulaires de fonctions trigonométriques ont été utilisées.
Cependant, si du côté droit de l’équation il n’y a pas valeur du tableau, puis nous substituons la valeur dans la solution générale de l'équation :




SOLUTIONS SPÉCIALES :
Marquons les points sur le cercle dont l'ordonnée est 0 :

Marquons un seul point sur le cercle dont l'ordonnée est 1 :

Marquons un seul point sur le cercle dont l'ordonnée est égale à -1 :

Puisqu'il est d'usage d'indiquer les valeurs les plus proches de zéro, on écrit la solution comme suit :
Marquons les points sur le cercle dont l'abscisse est égale à 0 :

5.
Marquons un seul point sur le cercle dont l'abscisse est égale à 1 :

Marquons un seul point sur le cercle dont l'abscisse est égale à -1 :

Et des exemples un peu plus complexes :
1.
Sinus égal à un, si l'argument est égal
L'argument de notre sinus est égal, nous obtenons donc :
Divisons les deux côtés de l'égalité par 3 :
Répondre:
2.
Le cosinus est nul si l'argument du cosinus est
L'argument de notre cosinus est égal à , on obtient donc :
Exprimons , pour ce faire on se déplace d'abord vers la droite avec le signe opposé :
Simplifions le côté droit :
Divisez les deux côtés par -2 :
Notez que le signe devant le terme ne change pas, puisque k peut prendre n'importe quelle valeur entière.
Répondre:
Et enfin, regardez le didacticiel vidéo « Sélection de racines dans une équation trigonométrique à l'aide de cercle trigonométrique"
Ceci conclut notre conversation sur la résolution d’équations trigonométriques simples. La prochaine fois, nous parlerons de la façon de décider.
Équations trigonométriques. Dans le cadre de l'examen de mathématiques de la première partie, il y a une tâche liée à la résolution d'une équation - celle-ci équations simples qui sont résolus en quelques minutes, de nombreux types peuvent être résolus oralement. Comprend : les équations linéaires, quadratiques, rationnelles, irrationnelles, exponentielles, logarithmiques et trigonométriques.
Dans cet article, nous examinerons les équations trigonométriques. Leur solution diffère tant par le volume des calculs que par la complexité des autres problèmes de cette partie. Ne vous inquiétez pas, le mot « difficulté » fait référence à leur difficulté relative par rapport à d’autres tâches.
En plus de trouver les racines de l'équation elles-mêmes, il est nécessaire de déterminer le plus grand négatif ou le plus petit racine positive. La probabilité que vous obteniez une équation trigonométrique à l’examen est bien entendu faible.
Ils sont moins de 7 % dans cette partie de l'examen d'État unifié. Mais cela ne veut pas dire qu’il faut les ignorer. Dans la partie C, vous devez également résoudre une équation trigonométrique, une bonne compréhension de la technique de résolution et une bonne compréhension de la théorie sont donc simplement nécessaires.
Comprendre la section trigonométrie des mathématiques déterminera grandement votre réussite dans la résolution de nombreux problèmes. Je vous rappelle que la réponse est un entier ou un nombre fini décimal. Après avoir obtenu les racines de l’équation, ASSUREZ-VOUS de vérifier. Cela ne prendra pas beaucoup de temps et vous évitera de commettre des erreurs.
Nous examinerons également d’autres équations à l’avenir, ne les manquez pas ! Rappelons les formules des racines des équations trigonométriques, il faut les connaître :

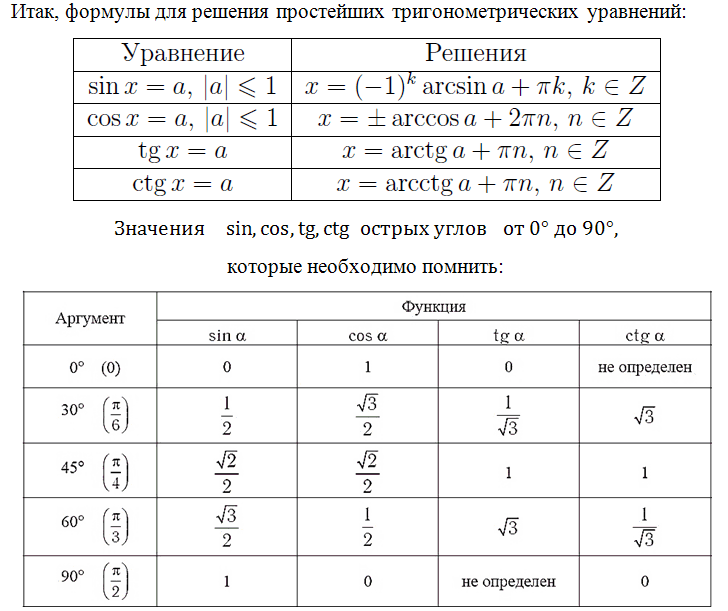
La connaissance de ces valeurs est nécessaire ; c'est « l'alphabet », sans lequel il sera impossible de faire face à de nombreuses tâches. Génial, si votre mémoire est bonne, vous avez facilement appris et mémorisé ces valeurs. Que faire si vous ne pouvez pas faire cela, s'il y a de la confusion dans votre tête, mais que vous êtes simplement confus en passant l'examen. Ce serait dommage de perdre un point parce que vous avez noté une mauvaise valeur dans vos calculs.
Ces valeurs sont simples, elles sont également données dans la théorie que vous avez reçue dans la deuxième lettre après votre inscription à la newsletter. Si vous n'êtes pas encore abonné, faites-le ! À l’avenir, nous verrons également comment ces valeurs peuvent être déterminées à partir d’un cercle trigonométrique. Ce n’est pas pour rien qu’on l’appelle le « Cœur d’Or de la Trigonométrie ».
Permettez-moi d'expliquer immédiatement, afin d'éviter toute confusion, que dans les équations considérées ci-dessous, les définitions de l'arc sinus, arc cosinus, arc tangente utilisant l'angle sont données X pour les équations correspondantes : cosx=a, sinx=a, tgx=a, où X peut aussi être une expression. Dans les exemples ci-dessous, notre argument est spécifié précisément par une expression.
Considérons donc les tâches suivantes :
Trouvez la racine de l'équation :

Notez la plus grande racine négative de votre réponse.
La solution de l'équation cos x = a est constituée de deux racines :

Définition : Que le nombre a en module ne dépasse pas un. L'arc cosinus d'un nombre est l'angle x compris entre 0 et Pi dont le cosinus est égal à a.

Moyens

Exprimons X:

Trouvons la plus grande racine négative. Comment faire? Remplaçons différentes significations n dans les racines résultantes, calculez et sélectionnez la plus grande négative.
On calcule :
Avec n = – 2 x 1 = 3 (– 2) – 4,5 = – 10,5 x 2 = 3 (– 2) – 5,5 = – 11,5
Avec n = – 1 x 1 = 3 (– 1) – 4,5 = – 7,5 x 2 = 3 (– 1) – 5,5 = – 8,5
Avec n = 0 x 1 = 3∙0 – 4,5 = – 4,5 x 2 = 3∙0 – 5,5 = – 5,5
Avec n = 1 x 1 = 3∙1 – 4,5 = – 1,5 x 2 = 3∙1 – 5,5 = – 2,5
Avec n = 2 x 1 = 3∙2 – 4,5 = 1,5 x 2 = 3∙2 – 5,5 = 0,5
Nous avons constaté que la plus grande racine négative est –1,5
Réponse : –1,5
Décider vous-même:

Résous l'équation:

La solution de l'équation sin x = a est constituée de deux racines :

Soit (il combine les deux ci-dessus) :

Définition : Que le nombre a en module ne dépasse pas un. L'arc sinus d'un nombre est l'angle x compris entre – 90° et 90°, dont le sinus est égal à a.

Moyens

Exprimez x (multipliez les deux côtés de l’équation par 4 et divisez par Pi) :

Trouvons la plus petite racine positive. Ici, il est immédiatement clair que lors du remplacement valeurs négatives n nous obtiendrons racines négatives. Par conséquent, nous remplacerons n = 0,1,2...
Lorsque n = 0 x = (– 1) 0 + 4∙0 + 3 = 4
Quand n = 1 x = (– 1) 1 + 4∙1 + 3 = 6
Quand n = 2 x = (– 1) 2 + 4∙2 + 3 = 12
Vérifions avec n = –1 x = (–1) –1 + 4∙(–1) + 3 = –2
La plus petite racine positive est donc 4.
Réponse : 4
Décider vous-même:

Résous l'équation:

Écrivez la plus petite racine positive dans votre réponse.








