ત્રિકોણમિતિ સમીકરણોના મૂળ નક્કી કરવા. ત્રિકોણમિતિ સમીકરણો

સફળતાપૂર્વક ઉકેલવા માટે ત્રિકોણમિતિ સમીકરણોવાપરવા માટે અનુકૂળ ઘટાડવાની પદ્ધતિઅગાઉ ઉકેલાયેલી સમસ્યાઓ માટે. ચાલો જાણીએ કે આ પદ્ધતિનો સાર શું છે?

કોઈપણ સૂચિત સમસ્યામાં, તમારે અગાઉ ઉકેલાયેલી સમસ્યા જોવાની જરૂર છે, અને પછી, ક્રમિક ઉપયોગ કરીને સમકક્ષ પરિવર્તનોતમને આપવામાં આવેલ કાર્યને સરળ કરવા માટે ઘટાડવાનો પ્રયાસ કરો.

તેથી, જ્યારે નક્કી કરો ત્રિકોણમિતિ સમીકરણોસામાન્ય રીતે અમુક રકમ મર્યાદિત ક્રમસમકક્ષ સમીકરણો, જેની છેલ્લી કડી સ્પષ્ટ ઉકેલ સાથેનું સમીકરણ છે. એટલું જ યાદ રાખવું અગત્યનું છે કે જો સૌથી સરળ ત્રિકોણમિતિ સમીકરણો ઉકેલવા માટેની કુશળતા રચાતી નથી, તો ઉકેલ વધુ છે. જટિલ સમીકરણોમુશ્કેલ અને બિનઅસરકારક રહેશે.

વધુમાં, ત્રિકોણમિતિ સમીકરણો ઉકેલતી વખતે, તમારે ક્યારેય ભૂલવું જોઈએ નહીં કે ઉકેલની ઘણી સંભવિત પદ્ધતિઓ છે.

ઉદાહરણ 1. મૂળની સંખ્યા શોધો cos સમીકરણો x = -1/2 અંતરાલ પર .

ઉકેલ:

પદ્ધતિ Iચાલો ફંક્શન્સ y = cos x અને y = -1/2નું પ્લોટ કરીએ અને અંતરાલ પર તેમના સામાન્ય બિંદુઓની સંખ્યા શોધીએ (ફિગ. 1).

ફંક્શન ગ્રાફમાં બે હોવાથી સામાન્ય બિંદુઓઅંતરાલ પર , પછી સમીકરણ આ અંતરાલ પર બે મૂળ ધરાવે છે.

II પદ્ધતિ.ત્રિકોણમિતિ વર્તુળ (ફિગ. 2) નો ઉપયોગ કરીને આપણે બિંદુઓની સંખ્યા શોધીએ છીએ અંતરાલ સાથે સંબંધિત, જેમાં cos x = -1/2. આકૃતિ બતાવે છે કે સમીકરણના બે મૂળ છે.

III પદ્ધતિ.ત્રિકોણમિતિ સમીકરણના મૂળ માટેના સૂત્રનો ઉપયોગ કરીને, આપણે સમીકરણ cos x = -1/2 ઉકેલીએ છીએ.

x = ± આર્કોસ (-1/2) + 2πk, k – પૂર્ણાંક (k € Z);

x = ± (π – arccos 1/2) + 2πk, k – પૂર્ણાંક (k € Z);

x = ± (π – π/3) + 2πk, k – પૂર્ણાંક (k € Z);

x = ± 2π/3 + 2πk, k – પૂર્ણાંક (k€ Z).

અંતરાલમાં મૂળ 2π/3 અને -2π/3 + 2π હોય છે, k એ પૂર્ણાંક છે. આમ, આપેલ અંતરાલ પર સમીકરણ બે મૂળ ધરાવે છે.

જવાબ: 2.

ભવિષ્યમાં, ત્રિકોણમિતિ સમીકરણો સૂચિત પદ્ધતિઓમાંથી એકનો ઉપયોગ કરીને ઉકેલવામાં આવશે, જે ઘણા કિસ્સાઓમાં અન્ય પદ્ધતિઓના ઉપયોગને બાકાત રાખતી નથી.

ઉદાહરણ 2. અંતરાલ [-2π પર tg (x + π/4) = 1 સમીકરણના ઉકેલોની સંખ્યા શોધો; 2π].

ઉકેલ:

ત્રિકોણમિતિ સમીકરણના મૂળ માટેના સૂત્રનો ઉપયોગ કરીને, આપણે મેળવીએ છીએ:

x + π/4 = આર્ક્ટન 1 + πk, k – પૂર્ણાંક (k € Z);

x + π/4 = π/4 + πk, k – પૂર્ણાંક (k € Z);

x = πk, k – પૂર્ણાંક (k € Z);

અંતરાલ [-2π; 2π] નંબરો -2π સાથે સંબંધિત છે; -π; 0; π; 2π. તેથી, આપેલ અંતરાલ પર સમીકરણ પાંચ મૂળ ધરાવે છે.

જવાબ: 5.

ઉદાહરણ 3. અંતરાલ પર cos 2 x + sin x · cos x = 1 સમીકરણના મૂળની સંખ્યા શોધો [-π; π].

ઉકેલ:

ત્યારથી 1 = sin 2 x + cos 2 x (મૂળભૂત ત્રિકોણમિતિ ઓળખ), પછી મૂળ સમીકરણ ફોર્મ લે છે:

cos 2 x + sin x · cos x = sin 2 x + cos 2 x;

sin 2 x – sin x cos x = 0;

sin x(sin x – cos x) = 0. ઉત્પાદન શૂન્યની બરાબર છે, જેનો અર્થ છે કે ઓછામાં ઓછું એક પરિબળ હોવું જોઈએ શૂન્ય બરાબર, તેથી જ:

sin x = 0 અથવા sin x – cos x = 0.

ચલના મૂલ્યો કે જેના પર cos x = 0 એ બીજા સમીકરણના મૂળ નથી (સમાન સંખ્યાની સાઈન અને કોસાઈન એક જ સમયે શૂન્યની બરાબર ન હોઈ શકે), આપણે બીજા સમીકરણની બંને બાજુઓને વિભાજીત કરીએ છીએ. cos x દ્વારા:

sin x = 0 અથવા sin x / cos x - 1 = 0.

બીજા સમીકરણમાં આપણે એ હકીકતનો ઉપયોગ કરીએ છીએ કે tg x = sin x / cos x, પછી:

sin x = 0 અથવા tan x = 1. ફોર્મ્યુલાનો ઉપયોગ કરીને અમારી પાસે છે:

x = πk અથવા x = π/4 + πk, k – પૂર્ણાંક (k € Z).

મૂળની પ્રથમ શ્રેણીથી અંતરાલ [-π; π] સંખ્યાઓથી સંબંધિત છે -π; 0; π બીજી શ્રેણીમાંથી: (π/4 – π) અને π/4.

તેથી પાંચ મૂળ છે મૂળ સમીકરણઅંતરાલ [-π; π].

જવાબ: 5.

ઉદાહરણ 4. સમીકરણ tg 2 x + сtg 2 x + 3tg x + 3сtgx + 4 = 0 અંતરાલ [-π; 1.1π].

ઉકેલ:

ચાલો નીચે પ્રમાણે સમીકરણ ફરીથી લખીએ:

tg 2 x + сtg 2 x + 3(tg x + сtgx) + 4 = 0 અને રિપ્લેસમેન્ટ કરો.

ચાલો tg x + стgx = a. ચાલો સમીકરણની બંને બાજુઓને ચોરસ કરીએ:

(tg x + стg x) 2 = a 2 . ચાલો કૌંસને વિસ્તૃત કરીએ:

tg 2 x + 2tg x · сtgx + сtg 2 x = a 2.

ત્યારથી tg x · сtgx = 1, પછી tg 2 x + 2 + сtg 2 x = a 2, જેનો અર્થ થાય છે

tg 2 x + стg 2 x = a 2 – 2.

હવે મૂળ સમીકરણ આના જેવું દેખાય છે:

a 2 – 2 + 3a + 4 = 0;

a 2 + 3a + 2 = 0. Vieta ના પ્રમેયનો ઉપયોગ કરીને, આપણે શોધીએ છીએ કે a = -1 અથવા a = -2.

ચાલો વિપરીત અવેજીકરણ કરીએ, અમારી પાસે છે:

tg x + сtgx = -1 અથવા tg x + сtgx = -2. ચાલો પરિણામી સમીકરણો હલ કરીએ.

tg x + 1/tgx = -1 અથવા tg x + 1/tgx = -2.

બંનેની મિલકત પ્રમાણે તેઓ પરસ્પર છે પારસ્પરિક સંખ્યાઓઅમે નક્કી કરીએ છીએ કે પ્રથમ સમીકરણમાં કોઈ મૂળ નથી, અને બીજા સમીકરણમાંથી અમારી પાસે છે:

tg x = -1, એટલે કે. x = -π/4 + πk, k – પૂર્ણાંક (k € Z).

અંતરાલ [-π; 1,1π] મૂળથી સંબંધિત છે: -π/4; -π/4 + π. તેમનો સરવાળો:

-π/4 + (-π/4 + π) = -π/2 + π = π/2.

જવાબ: π/2.

ઉદાહરણ 5. સરેરાશ શોધો અંકગણિત મૂળ પાપ સમીકરણોઅંતરાલ પર 3x + sin x = sin 2x [-π; 0.5π].

ઉકેલ:

ચાલો લાભ લઈએ સૂત્ર પાપα + sin β = 2sin ((α + β)/2) cos ((α – β)/2), પછી

sin 3x + sin x = 2sin ((3x + x)/2) cos ((3x – x)/2) = 2sin 2x cos x અને સમીકરણ બને છે

2sin 2x cos x = sin 2x;

2sin 2x · cos x – sin 2x = 0. ચાલો બહાર કાઢીએ સામાન્ય ગુણકકૌંસમાંથી 2x sin

sin 2x(2cos x – 1) = 0. પરિણામી સમીકરણ ઉકેલો:

sin 2x = 0 અથવા 2cos x – 1 = 0;

sin 2x = 0 અથવા cos x = 1/2;

2x = πk અથવા x = ±π/3 + 2πk, k – પૂર્ણાંક (k € Z).

આમ આપણી પાસે મૂળ છે

x = πk/2, x = π/3 + 2πk, x = -π/3 + 2πk, k – પૂર્ણાંક (k€ Z).

અંતરાલ [-π; 0.5π] મૂળથી સંબંધિત છે -π; -π/2; 0; π/2 (મૂળની પ્રથમ શ્રેણીમાંથી); π/3 (બીજી શ્રેણીમાંથી); -π/3 (ત્રીજી શ્રેણીમાંથી). તેમનો અંકગણિત અર્થ છે:

(-π – π/2 + 0 + π/2 + π/3 – π/3)/6 = -π/6.

જવાબ: -π/6.

ઉદાહરણ 6. અંતરાલ [-1.25π પર sin x + cos x = 0 સમીકરણના મૂળની સંખ્યા શોધો; 2π].

ઉકેલ:

આ સમીકરણ એ પ્રથમ ડિગ્રીનું સજાતીય સમીકરણ છે. ચાલો તેના બંને ભાગોને cosx દ્વારા વિભાજીત કરીએ (ચલનું મૂલ્ય કે જેના પર cos x = 0 મૂળ નથી આપેલ સમીકરણ, કારણ કે સમાન સંખ્યાની સાઈન અને કોસાઈન એક જ સમયે શૂન્યની બરાબર ન હોઈ શકે). મૂળ સમીકરણ છે:

x = -π/4 + πk, k – પૂર્ણાંક (k € Z).

અંતરાલ [-1.25π; 2π] મૂળથી સંબંધિત છે -π/4; (-π/4 + π); અને (-π/4 + 2π).

આમ, આપેલ અંતરાલ સમીકરણના ત્રણ મૂળ ધરાવે છે.

જવાબ: 3.

સૌથી મહત્વની વસ્તુ કરવાનું શીખો - સમસ્યાને ઉકેલવા માટેની યોજનાની સ્પષ્ટ કલ્પના કરો અને પછી કોઈપણ ત્રિકોણમિતિ સમીકરણ તમારી સમજમાં આવશે.

હજુ પણ પ્રશ્નો છે? ત્રિકોણમિતિ સમીકરણો કેવી રીતે ઉકેલવા તે ખબર નથી?
શિક્ષક પાસેથી મદદ મેળવવા માટે, નોંધણી કરો.

વેબસાઇટ, જ્યારે સામગ્રીની સંપૂર્ણ અથવા આંશિક નકલ કરતી વખતે, સ્રોતની લિંક આવશ્યક છે.

તમે ઓર્ડર કરી શકો છો વિગતવાર ઉકેલતમારું કાર્ય !!!

ચિહ્ન હેઠળ અજ્ઞાત સમાયેલ સમાનતા ત્રિકોણમિતિ કાર્ય(`sin x, cos x, tan x` અથવા `ctg x`) ને ત્રિકોણમિતિ સમીકરણ કહેવામાં આવે છે, અને તે તેમના સૂત્રો છે જેનો આપણે આગળ વિચાર કરીશું.

સૌથી સરળ સમીકરણોને `sin x=a, cos x=a, tg x=a, ctg x=a` કહેવામાં આવે છે, જ્યાં `x` એ શોધવાનો ખૂણો છે, `a` કોઈપણ સંખ્યા છે. ચાલો તે દરેક માટે મૂળ સૂત્રો લખીએ.

1. સમીકરણ `sin x=a`.

`|a|>1` માટે તેનો કોઈ ઉકેલ નથી.

જ્યારે `|a| \leq 1` પાસે છે અનંત સંખ્યાનિર્ણયો

મૂળ સૂત્ર: `x=(-1)^n arcsin a + \pi n, n \in Z`

2. સમીકરણ `cos x=a`

`|a|>1` માટે - સાઈનના કિસ્સામાં, વચ્ચેના ઉકેલો વાસ્તવિક સંખ્યાઓપાસે નથી.

જ્યારે `|a| \leq 1` પાસે છે અનંત સમૂહનિર્ણયો

મૂળ સૂત્ર: `x=\pm arccos a + 2\pi n, n \in Z`

આલેખમાં સાઈન અને કોસાઈન માટે ખાસ કેસ.

3. સમીકરણ `tg x=a`

`a` ના કોઈપણ મૂલ્યો માટે અનંત સંખ્યામાં ઉકેલો ધરાવે છે.

મૂળ સૂત્ર: `x=arctg a + \pi n, n \in Z`

4. સમીકરણ `ctg x=a`

`a` ના કોઈપણ મૂલ્યો માટે અનંત સંખ્યામાં ઉકેલો પણ ધરાવે છે.

મૂળ સૂત્ર: `x=arcctg a + \pi n, n \in Z`

કોષ્ટકમાં ત્રિકોણમિતિ સમીકરણોના મૂળ માટેના સૂત્રો

સાઈન માટે:
કોસાઇન માટે:
સ્પર્શક અને કોટેન્જેન્ટ માટે:
વ્યસ્ત ત્રિકોણમિતિ કાર્યો ધરાવતા સમીકરણો ઉકેલવા માટેના સૂત્રો:

ત્રિકોણમિતિ સમીકરણો ઉકેલવા માટેની પદ્ધતિઓ

કોઈપણ ત્રિકોણમિતિ સમીકરણને ઉકેલવામાં બે તબક્કાઓનો સમાવેશ થાય છે:

• તેને સરળમાં રૂપાંતરિત કરવાની સહાયથી;
• ઉપર લખેલ મૂળ સૂત્રો અને કોષ્ટકોનો ઉપયોગ કરીને મેળવેલ સૌથી સરળ સમીકરણ ઉકેલો.

ચાલો ઉદાહરણોનો ઉપયોગ કરીને મુખ્ય ઉકેલ પદ્ધતિઓ જોઈએ.

બીજગણિત પદ્ધતિ.

આ પદ્ધતિમાં ચલને બદલવાનો અને તેને સમાનતામાં બદલવાનો સમાવેશ થાય છે.

ઉદાહરણ. સમીકરણ ઉકેલો: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`

`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,

રિપ્લેસમેન્ટ કરો: `cos(x+\frac \pi 6)=y`, પછી `2y^2-3y+1=0`,

આપણે મૂળ શોધીએ છીએ: `y_1=1, y_2=1/2`, જેમાંથી બે કેસ અનુસરે છે:

1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.

2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm આર્કોસ 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.

જવાબ: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.

ફેક્ટરાઇઝેશન.

ઉદાહરણ. સમીકરણ ઉકેલો: `sin x+cos x=1`.

ઉકેલ. ચાલો સમાનતાની બધી શરતોને ડાબી બાજુએ ખસેડીએ: `sin x+cos x-1=0`. નો ઉપયોગ કરીને , અમે ડાબી બાજુનું રૂપાંતર અને ફેક્ટરાઇઝ કરીએ છીએ:

`sin x — 2sin^2 x/2=0`,

`2sin x/2 cos x/2-2sin^2 x/2=0`,

`2sin x/2 (cos x/2-sin x/2)=0`,

1. `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
2. `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n` , `x_2=\pi/2+ 2\pi n`.

જવાબ: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.

સજાતીય સમીકરણમાં ઘટાડો

પ્રથમ, તમારે આ ત્રિકોણમિતિ સમીકરણને બેમાંથી એક સ્વરૂપમાં ઘટાડવાની જરૂર છે:

`a sin x+b cos x=0` ( સજાતીય સમીકરણપ્રથમ ડિગ્રી) અથવા `a sin^2 x + b sin x cos x +c cos^2 x=0` (બીજી ડિગ્રીનું સજાતીય સમીકરણ).

પછી બંને ભાગોને `cos x \ne 0` દ્વારા વિભાજિત કરો - પ્રથમ કેસ માટે, અને `cos^2 x \ne 0` દ્વારા - બીજા માટે. અમે `tg x`: `a tg x+b=0` અને `a tg^2 x + b tg x +c =0` માટે સમીકરણો મેળવીએ છીએ, જેને જાણીતી પદ્ધતિઓનો ઉપયોગ કરીને ઉકેલવાની જરૂર છે.

ઉદાહરણ. સમીકરણ ઉકેલો: `2 sin^2 x+sin x cos x - cos^2 x=1`.

ઉકેલ. ચાલો તેને લખીએ જમણી બાજુજેમ કે `1=sin^2 x+cos^2 x`:

`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,

`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`

`sin^2 x+sin x cos x — 2 cos^2 x=0`.

આ બીજી ડિગ્રીનું એક સમાન ત્રિકોણમિતિ સમીકરણ છે, આપણે તેની ડાબી અને જમણી બાજુઓને `cos^2 x \ne 0` વડે વિભાજીત કરીએ છીએ, આપણને મળે છે:

`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) — \frac(2 cos^2 x)(cos^2 x)=0`

`tg^2 x+tg x — 2=0`. ચાલો બદલીએ `tg x=t`, પરિણામે `t^2 + t - 2=0`. આ સમીકરણના મૂળ છે `t_1=-2` અને `t_2=1`. પછી:

1. `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
2. `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.

જવાબ આપો. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.

હાફ એંગલ પર ખસેડવું

ઉદાહરણ. સમીકરણ ઉકેલો: `11 sin x - 2 cos x = 10`.

ઉકેલ. ચાલો સૂત્રો લાગુ કરીએ ડબલ કોણ, પરિણામે: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^ 2 x/2`

`4 tg^2 x/2 — 11 tg x/2 +6=0`

ઉપરોક્ત લાગુ કરવું બીજગણિત પદ્ધતિ, અમને મળે છે:

1. `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
2. `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

જવાબ આપો. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

સહાયક કોણનો પરિચય

ત્રિકોણમિતિ સમીકરણમાં `a sin x + b cos x =c`, જ્યાં a,b,c ગુણાંક છે અને x એ ચલ છે, બંને બાજુઓને `sqrt (a^2+b^2)` વડે વિભાજીત કરો:

`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2) ) +b^2))`.

ડાબી બાજુના ગુણાંકમાં સાઈન અને કોસાઈનના ગુણધર્મો છે, એટલે કે તેમના ચોરસનો સરવાળો 1 જેટલો છે અને તેમના મોડ્યુલ 1 કરતા વધારે નથી. ચાલો તેમને નીચે પ્રમાણે દર્શાવીએ: `\frac a(sqrt (a^2) +b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2)) =C`, પછી:

`cos \varphi sin x + sin \varphi cos x =C`.

ચાલો નીચેના ઉદાહરણ પર નજીકથી નજર કરીએ:

ઉદાહરણ. સમીકરણ ઉકેલો: `3 sin x+4 cos x=2`.

ઉકેલ. સમાનતાની બંને બાજુઓને `sqrt (3^2+4^2)` ​​વડે વિભાજીત કરીએ તો આપણને મળે છે:

`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))`

`3/5 sin x+4/5 cos x=2/5`.

ચાલો `3/5 = cos \varphi` , `4/5=sin \varphi` સૂચવીએ. ત્યારથી `sin \varphi>0`, `cos \varphi>0`, પછી તરીકે સહાયક કોણચાલો `\varphi=arcsin 4/5` લઈએ. પછી અમે ફોર્મમાં અમારી સમાનતા લખીએ છીએ:

`cos \varphi sin x+sin \varphi cos x=2/5`

સાઈન માટેના ખૂણાઓના સરવાળા માટે સૂત્ર લાગુ કરીને, અમે અમારી સમાનતા નીચેના સ્વરૂપમાં લખીએ છીએ:

`sin (x+\varphi)=2/5`,

`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,

`x=(-1)^n આર્ક્સીન 2/5-` `આર્કસિન 4/5+ \pi n`, `n \in Z`.

જવાબ આપો. `x=(-1)^n આર્ક્સીન 2/5-` `આર્કસિન 4/5+ \pi n`, `n \in Z`.

અપૂર્ણાંક તર્કસંગત ત્રિકોણમિતિ સમીકરણો

આ અપૂર્ણાંકો સાથે સમાનતા છે જેના અંશ અને છેદ ત્રિકોણમિતિ કાર્યો ધરાવે છે.

ઉદાહરણ. સમીકરણ ઉકેલો. `\frac (sin x)(1+cos x)=1-cos x`.

ઉકેલ. સમાનતાની જમણી બાજુને `(1+cos x)` વડે ગુણાકાર અને ભાગાકાર કરો. પરિણામે આપણને મળે છે:

`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0`

`\frac (sin x-sin^2 x)(1+cos x)=0`

છેદ શૂન્યની બરાબર ન હોઈ શકે તે ધ્યાનમાં લેતા, આપણને `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z` મળે છે.

ચાલો અપૂર્ણાંકના અંશને શૂન્ય સાથે સરખાવીએ: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. પછી `sin x=0` અથવા `1-sin x=0`.

1. `sin x=0`, `x=\pi n`, `n \in Z`
2. `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.

આપેલ છે કે ` x \ne \pi+2\pi n, n \in Z`, ઉકેલો છે `x=2\pi n, n \in Z` અને `x=\pi /2+2\pi n` , `n \in Z`.

જવાબ આપો. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.

ત્રિકોણમિતિ અને ખાસ કરીને ત્રિકોણમિતિ સમીકરણોનો ઉપયોગ ભૂમિતિ, ભૌતિકશાસ્ત્ર અને એન્જિનિયરિંગના લગભગ તમામ ક્ષેત્રોમાં થાય છે. 10મા ધોરણમાં અભ્યાસ શરૂ થાય છે, યુનિફાઇડ સ્ટેટ પરીક્ષા માટે હંમેશા કાર્યો હોય છે, તેથી ત્રિકોણમિતિ સમીકરણોના તમામ સૂત્રો યાદ રાખવાનો પ્રયાસ કરો - તે ચોક્કસપણે તમારા માટે ઉપયોગી થશે!

જો કે, તમારે તેમને યાદ રાખવાની પણ જરૂર નથી, મુખ્ય વસ્તુ એ છે કે સારને સમજવું અને તેને પ્રાપ્ત કરવામાં સક્ષમ થવું. તે લાગે છે તેટલું મુશ્કેલ નથી. વિડીયો જોઈને જાતે જ જોઈ લો.

સરળ ત્રિકોણમિતિ સમીકરણો ઉકેલવા.

જટિલતાના કોઈપણ સ્તરના ત્રિકોણમિતિ સમીકરણો ઉકેલવાથી આખરે સરળ ત્રિકોણમિતિ સમીકરણો ઉકેલવામાં આવે છે. અને આમાં શ્રેષ્ઠ મદદગારફરીથી તે ત્રિકોણમિતિ વર્તુળ હોવાનું બહાર આવ્યું છે.

ચાલો કોસાઈન અને સાઈનની વ્યાખ્યાઓ યાદ કરીએ.

ખૂણાનો કોસાઇન એ પરના બિંદુનો એબ્સીસા (એટલે ​​​​કે, ધરી સાથે સંકલન) છે એકમ વર્તુળ, આપેલ કોણ દ્વારા પરિભ્રમણને અનુરૂપ.

ખૂણાની સાઈન એ આપેલ કોણ દ્વારા પરિભ્રમણને અનુરૂપ એકમ વર્તુળ પરના બિંદુનો ઓર્ડિનેટ (એટલે ​​​​કે ધરી સાથે સંકલન) છે.

સાથે હલનચલનની સકારાત્મક દિશા ત્રિકોણમિતિ વર્તુળકાઉન્ટરક્લોકવાઇઝ ચળવળ ગણવામાં આવે છે. 0 ડિગ્રી (અથવા 0 રેડિયન)નું પરિભ્રમણ કોઓર્ડિનેટ્સ (1;0) સાથેના બિંદુને અનુરૂપ છે

અમે આ વ્યાખ્યાઓનો ઉપયોગ સરળ ત્રિકોણમિતિ સમીકરણોને ઉકેલવા માટે કરીએ છીએ.

1. સમીકરણ ઉકેલો

આ સમીકરણ પરિભ્રમણ કોણના તમામ મૂલ્યો દ્વારા સંતુષ્ટ છે જે વર્તુળ પરના બિંદુઓને અનુરૂપ છે કે જેની ઓર્ડિનેટ બરાબર છે.

ચાલો ઓર્ડિનેટ અક્ષ પર ઓર્ડિનેટ સાથે બિંદુને ચિહ્નિત કરીએ:

ચાલો હાથ ધરીએ આડી રેખા x-અક્ષની સમાંતર જ્યાં સુધી તે વર્તુળ સાથે છેદે નહીં. આપણને વર્તુળ પર પડેલા અને ઓર્ડિનેટ ધરાવતા બે બિંદુઓ મળે છે. આ બિંદુઓ અને રેડિયનમાં પરિભ્રમણ ખૂણાને અનુરૂપ છે:

જો આપણે, રેડિયન દ્વારા પરિભ્રમણના ખૂણાને અનુરૂપ બિંદુ છોડીએ, તો આસપાસ જઈએ સંપૂર્ણ વર્તુળ, પછી આપણે રેડિયન દીઠ પરિભ્રમણ કોણને અનુરૂપ બિંદુ પર પહોંચીશું અને સમાન ઓર્ડિનેટ ધરાવીશું. એટલે કે, આ પરિભ્રમણ કોણ આપણા સમીકરણને પણ સંતોષે છે. આપણે ગમે તેટલી "નિષ્ક્રિય" ક્રાંતિ કરી શકીએ છીએ, તે જ બિંદુ પર પાછા આવીએ છીએ, અને આ બધા ખૂણા મૂલ્યો આપણા સમીકરણને સંતોષશે. "નિષ્ક્રિય" ક્રાંતિની સંખ્યા અક્ષર (અથવા) દ્વારા સૂચવવામાં આવશે. કારણ કે આપણે આ ક્રાંતિ હકારાત્મક અને નકારાત્મક બંને રીતે કરી શકીએ છીએ નકારાત્મક દિશા, (અથવા ) કોઈપણ પૂર્ણાંક મૂલ્ય લઈ શકે છે.

એટલે કે, મૂળ સમીકરણના ઉકેલોની પ્રથમ શ્રેણીનું સ્વરૂપ છે:

, , - પૂર્ણાંકોનો સમૂહ (1)

એ જ રીતે, ઉકેલોની બીજી શ્રેણીનું સ્વરૂપ છે:

, ક્યાં , . (2)

જેમ તમે અનુમાન લગાવ્યું હશે, ઉકેલોની આ શ્રેણી વર્તુળ પરના બિંદુ પર આધારિત છે જે દ્વારા પરિભ્રમણના કોણને અનુરૂપ છે.

ઉકેલોની આ બે શ્રેણીને એક એન્ટ્રીમાં જોડી શકાય છે:

જો આપણે આ એન્ટ્રીમાં (એટલે ​​કે સમ) લઈશું, તો આપણને ઉકેલોની પ્રથમ શ્રેણી મળશે.

જો આપણે આ એન્ટ્રીમાં (એટલે ​​​​કે, વિચિત્ર) લઈએ, તો આપણને ઉકેલોની બીજી શ્રેણી મળે છે.

2. હવે ચાલો સમીકરણ હલ કરીએ

કારણ કે આ એકમ વર્તુળ પરના એક બિંદુનો એબ્સીસા છે જે કોણ દ્વારા ફેરવીને મેળવે છે, અમે ધરી પરના એબ્સીસા સાથે બિંદુને ચિહ્નિત કરીએ છીએ:

ચાલો હાથ ધરીએ ઊભી રેખાજ્યાં સુધી તે વર્તુળ સાથે છેદે નહીં ત્યાં સુધી ધરીની સમાંતર. આપણને વર્તુળ પર પડેલા અને એબ્સીસા ધરાવતા બે બિંદુઓ મળશે. આ બિંદુઓ અને રેડિયનમાં પરિભ્રમણ ખૂણાને અનુરૂપ છે. યાદ કરો કે જ્યારે ઘડિયાળની દિશામાં ખસેડીએ છીએ ત્યારે આપણને મળે છે નકારાત્મક કોણપરિભ્રમણ:

ચાલો ઉકેલોની બે શ્રેણી લખીએ:

,

,

(મુખ્ય પૂર્ણ વર્તુળમાંથી જઈને આપણે ઇચ્છિત બિંદુ પર પહોંચીએ છીએ, એટલે કે.

ચાલો આ બે શ્રેણીઓને એક એન્ટ્રીમાં જોડીએ:

3. સમીકરણ ઉકેલો

સ્પર્શરેખા OY અક્ષની સમાંતર એકમ વર્તુળના કોઓર્ડિનેટ્સ (1,0) સાથે બિંદુમાંથી પસાર થાય છે

ચાલો તેના પર એક બિંદુને 1 ની બરાબર ઓર્ડિનેટ સાથે ચિહ્નિત કરીએ (આપણે તે સ્પર્શક શોધી રહ્યા છીએ જેનો કોણ 1 બરાબર છે):

ચાલો આ બિંદુને કોઓર્ડિનેટ્સના મૂળ સાથે સીધી રેખા સાથે જોડીએ અને એકમ વર્તુળ સાથે રેખાના આંતરછેદના બિંદુઓને ચિહ્નિત કરીએ. સીધી રેખા અને વર્તુળના આંતરછેદ બિંદુઓ આના પરના પરિભ્રમણના ખૂણાઓને અનુરૂપ છે અને :

આપણા સમીકરણને સંતોષતા પરિભ્રમણ ખૂણાઓને અનુરૂપ બિંદુઓ એકબીજાથી રેડિયનના અંતરે આવેલા હોવાથી, આપણે ઉકેલને આ રીતે લખી શકીએ:

4. સમીકરણ ઉકેલો

કોટેન્જેન્ટ્સની રેખા અક્ષની સમાંતર એકમ વર્તુળના કોઓર્ડિનેટ્સ સાથે બિંદુમાંથી પસાર થાય છે.

ચાલો કોટેન્જેન્ટ્સની રેખા પર abscissa -1 સાથે બિંદુને ચિહ્નિત કરીએ:

ચાલો આ બિંદુને સીધી રેખાના મૂળ સાથે જોડીએ અને જ્યાં સુધી તે વર્તુળ સાથે છેદે નહીં ત્યાં સુધી તેને ચાલુ રાખીએ. આ સીધી રેખા વર્તુળને અને રેડિયનમાં પરિભ્રમણના ખૂણાઓને અનુરૂપ બિંદુઓ પર છેદે છે:

કારણ કે આ બિંદુઓ એકબીજાથી , પછી સમાન અંતરથી અલગ પડે છે સામાન્ય ઉકેલઆપણે આ સમીકરણને આ રીતે લખી શકીએ છીએ:

સૌથી સરળ ત્રિકોણમિતિ સમીકરણોના ઉકેલને દર્શાવતા આપેલા ઉદાહરણોમાં, ત્રિકોણમિતિ કાર્યોના ટેબ્યુલર મૂલ્યોનો ઉપયોગ કરવામાં આવ્યો હતો.

જો કે, જો સમીકરણની જમણી બાજુએ ના હોય કોષ્ટક મૂલ્ય, પછી અમે સમીકરણના સામાન્ય ઉકેલમાં મૂલ્યને બદલીએ છીએ:

ખાસ ઉકેલો:

ચાલો વર્તુળ પરના બિંદુઓને ચિહ્નિત કરીએ જેનું ઓર્ડિનેટ 0 છે:

ચાલો વર્તુળ પર એક બિંદુને ચિહ્નિત કરીએ જેનું ઓર્ડિનેટ 1 છે:

ચાલો વર્તુળ પર એક બિંદુને ચિહ્નિત કરીએ જેનું ઑર્ડિનેટ -1 બરાબર છે:

શૂન્યની નજીકના મૂલ્યો સૂચવવાનો રિવાજ હોવાથી, અમે નીચે પ્રમાણે ઉકેલ લખીએ છીએ:

ચાલો વર્તુળ પરના બિંદુઓને ચિહ્નિત કરીએ કે જેના એબ્સીસા 0 ની બરાબર છે:

5.
ચાલો વર્તુળ પર એક બિંદુને ચિહ્નિત કરીએ જેનું એબ્સીસા 1 બરાબર છે:

ચાલો વર્તુળ પર એક બિંદુને ચિહ્નિત કરીએ જેનું એબ્સીસા -1 બરાબર છે:

અને થોડા વધુ જટિલ ઉદાહરણો:

1.

સાઇનસ એક સમાન, જો દલીલ સમાન હોય

આપણી સાઈનની દલીલ સમાન છે, તેથી આપણને મળે છે:

ચાલો સમાનતાની બંને બાજુઓને 3 વડે વિભાજીત કરીએ:

જવાબ:

2.

જો કોસાઇનની દલીલ હોય તો કોસાઇન શૂન્ય છે

આપણા કોસાઇનની દલીલ બરાબર છે, તેથી આપણને મળે છે:

ચાલો વ્યક્ત કરીએ, આ કરવા માટે આપણે પહેલા વિરુદ્ધ ચિહ્ન સાથે જમણી તરફ જઈએ છીએ:

ચાલો જમણી બાજુને સરળ બનાવીએ:

બંને બાજુઓને -2 વડે વિભાજીત કરો:

નોંધ કરો કે શબ્દની આગળનું ચિહ્ન બદલાતું નથી, કારણ કે k કોઈપણ પૂર્ણાંક મૂલ્ય લઈ શકે છે.

જવાબ:

અને છેલ્લે, વિડીયો ટ્યુટોરીયલ જુઓ “ત્રિકોણમિતિ સમીકરણમાં રૂટ પસંદ કરીને ત્રિકોણમિતિ વર્તુળ"

આ સરળ ત્રિકોણમિતિ સમીકરણો ઉકેલવા વિશેની અમારી વાતચીતને સમાપ્ત કરે છે. આગલી વખતે આપણે કેવી રીતે નક્કી કરવું તે વિશે વાત કરીશું.

ત્રિકોણમિતિ સમીકરણો. ગણિતની પરીક્ષાના ભાગરૂપે પ્રથમ ભાગમાં સમીકરણ ઉકેલવા સંબંધિત કાર્ય છે - આ સરળ સમીકરણોજે મિનિટોમાં ઉકેલાય છે, ઘણા પ્રકારો મૌખિક રીતે ઉકેલી શકાય છે. સમાવે છે: રેખીય, ચતુર્ભુજ, તર્કસંગત, અતાર્કિક, ઘાતાંકીય, લઘુગણક અને ત્રિકોણમિતિ સમીકરણો.

આ લેખમાં આપણે ત્રિકોણમિતિ સમીકરણો જોઈશું. તેમનો ઉકેલ ગણતરીના જથ્થામાં અને આ ભાગની અન્ય સમસ્યાઓથી જટિલતા બંનેમાં અલગ છે. ગભરાશો નહીં, "મુશ્કેલી" શબ્દ અન્ય કાર્યોની તુલનામાં તેમની સંબંધિત મુશ્કેલીનો સંદર્ભ આપે છે.

સમીકરણના મૂળ પોતાને શોધવા ઉપરાંત, સૌથી મોટી નકારાત્મક અથવા સૌથી નાની તે નક્કી કરવી જરૂરી છે. હકારાત્મક મૂળ. પરીક્ષામાં તમને ત્રિકોણમિતિ સમીકરણ મળવાની સંભાવના, અલબત્ત, ઓછી છે.

યુનિફાઇડ સ્ટેટ પરીક્ષાના આ ભાગમાં તેમાંથી 7% કરતા ઓછા છે. પરંતુ આનો અર્થ એ નથી કે તેમની અવગણના કરવી જોઈએ. ભાગ C માં, તમારે ત્રિકોણમિતિ સમીકરણને ઉકેલવાની પણ જરૂર છે, તેથી ઉકેલની તકનીકની સારી સમજ અને સિદ્ધાંતની સમજ ફક્ત જરૂરી છે.

ગણિતના ત્રિકોણમિતિ વિભાગને સમજવાથી ઘણી સમસ્યાઓ ઉકેલવામાં તમારી સફળતા મોટા પ્રમાણમાં નક્કી થશે. હું તમને યાદ કરાવું છું કે જવાબ પૂર્ણાંક અથવા મર્યાદિત સંખ્યા છે દશાંશ. તમે સમીકરણના મૂળ મેળવ્યા પછી, તપાસવાની ખાતરી કરો. તે વધુ સમય લેશે નહીં, અને તે તમને ભૂલો કરવાથી બચાવશે.

અમે ભવિષ્યમાં અન્ય સમીકરણો પણ જોઈશું, ચૂકશો નહીં! ચાલો ત્રિકોણમિતિ સમીકરણોના મૂળ માટેના સૂત્રોને યાદ કરીએ, તમારે તેમને જાણવાની જરૂર છે:

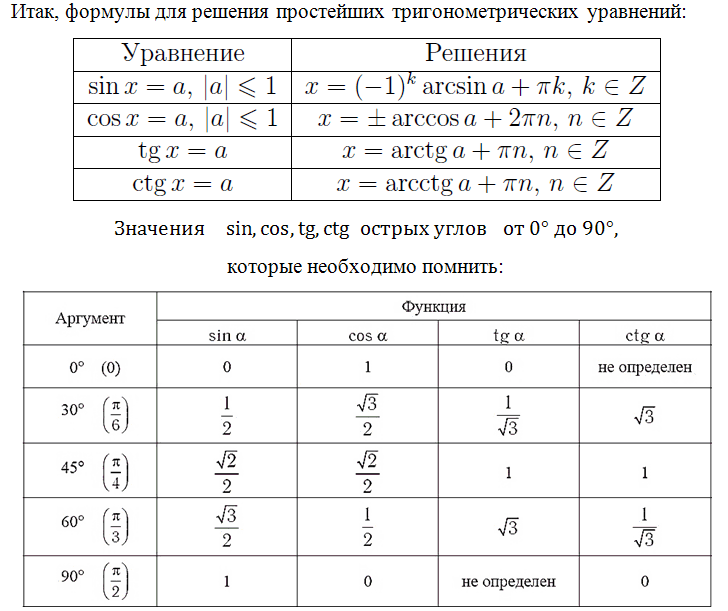
આ મૂલ્યોનું જ્ઞાન જરૂરી છે; આ "મૂળાક્ષરો" છે, જેના વિના ઘણા કાર્યોનો સામનો કરવો અશક્ય હશે. સરસ, જો તમારી યાદશક્તિ સારી છે, તો તમે સરળતાથી આ મૂલ્યો શીખ્યા અને યાદ રાખ્યા. જો તમે આ ન કરી શકો તો શું કરવું, તમારા માથામાં મૂંઝવણ છે, પરંતુ પરીક્ષા આપતી વખતે તમે મૂંઝવણમાં પડી ગયા છો. એક બિંદુ ગુમાવવું શરમજનક હશે કારણ કે તમે તમારી ગણતરીમાં ખોટું મૂલ્ય લખ્યું છે.

આ મૂલ્યો સરળ છે, તે ન્યૂઝલેટર પર સબ્સ્ક્રાઇબ કર્યા પછી તમને બીજા પત્રમાં પ્રાપ્ત થિયરીમાં પણ આપવામાં આવે છે. જો તમે હજી સુધી સબ્સ્ક્રાઇબ કર્યું નથી, તો આમ કરો! ભવિષ્યમાં આપણે ત્રિકોણમિતિ વર્તુળમાંથી આ મૂલ્યો કેવી રીતે નક્કી કરી શકાય તે પણ જોઈશું. તે કંઈપણ માટે નથી કે તેને "ત્રિકોણમિતિનું ગોલ્ડન હાર્ટ" કહેવામાં આવે છે.

મૂંઝવણ ટાળવા માટે, હું તરત જ સમજાવું કે, નીચે ધ્યાનમાં લેવાયેલા સમીકરણોમાં, કોણનો ઉપયોગ કરીને આર્કસાઇન, આર્કોસાઇન, આર્કટેન્જેન્ટની વ્યાખ્યાઓ આપવામાં આવી છે. એક્સઅનુરૂપ સમીકરણો માટે: cosx=a, sinx=a, tgx=a, જ્યાં એક્સઅભિવ્યક્તિ પણ હોઈ શકે છે. નીચેના ઉદાહરણોમાં, અમારી દલીલ અભિવ્યક્તિ દ્વારા ચોક્કસ રીતે સ્પષ્ટ થયેલ છે.

તેથી, ચાલો નીચેના કાર્યોને ધ્યાનમાં લઈએ:

સમીકરણનું મૂળ શોધો:

તમારા જવાબમાં સૌથી મોટું નકારાત્મક મૂળ લખો.

cos x = a સમીકરણનો ઉકેલ બે મૂળ છે:

વ્યાખ્યા: મોડ્યુલસમાં નંબર a ને એક કરતા વધુ ન થવા દો. સંખ્યાનો ચાપ કોસાઇન એ 0 થી Pi શ્રેણીમાં આવેલો કોણ x છે, જેનો કોસાઇન a બરાબર છે.

અર્થ

ચાલો વ્યક્ત કરીએ x:

ચાલો સૌથી મોટું નકારાત્મક મૂળ શોધીએ. આ કેવી રીતે કરવું? ચાલો અવેજી કરીએ વિવિધ અર્થો n પરિણામી મૂળમાં, ગણતરી કરો અને સૌથી મોટું નકારાત્મક પસંદ કરો.

અમે ગણતરી કરીએ છીએ:

n = – 2 x 1 = 3 (– 2) – 4.5 = – 10.5 x 2 = 3 (–2) – 5.5 = – 11.5 સાથે

n = – 1 x 1 = 3 (– 1) – 4.5 = – 7.5 x 2 = 3 (– 1) – 5.5 = – 8.5 સાથે

n = 0 x 1 = 3∙0 – 4.5 = – 4.5 x 2 = 3∙0 – 5.5 = – 5.5 સાથે

n = 1 x 1 = 3∙1 – 4.5 = – 1.5 x 2 = 3∙1 – 5.5 = – 2.5 સાથે

n = 2 x 1 = 3∙2 – 4.5 = 1.5 x 2 = 3∙2 – 5.5 = 0.5 સાથે

અમને જાણવા મળ્યું કે સૌથી મોટું નકારાત્મક મૂળ –1.5 છે

જવાબ: -1.5

તમારા માટે નક્કી કરો:

સમીકરણ ઉકેલો:

sin x = a સમીકરણનો ઉકેલ બે મૂળ છે:

ક્યાં તો (તે ઉપરના બંનેને જોડે છે):

વ્યાખ્યા: મોડ્યુલસમાં નંબર a ને એક કરતા વધુ ન થવા દો. સંખ્યાની ચાપ સાઈન એ કોણ x છે જે – 90° થી 90° ની રેન્જમાં આવેલો છે, જેની સાઈન a ની બરાબર છે.

અર્થ

એક્સપ્રેસ x (સમીકરણની બંને બાજુઓને 4 વડે ગુણાકાર કરો અને Pi વડે ભાગાકાર કરો):

ચાલો સૌથી નાનું હકારાત્મક મૂળ શોધીએ. અહીં તે તરત જ સ્પષ્ટ છે કે જ્યારે અવેજીમાં નકારાત્મક મૂલ્યો n આપણને મળશે નકારાત્મક મૂળ. તેથી, આપણે n = 0,1,2 ને બદલીશું...

જ્યારે n = 0 x = (– 1) 0 + 4∙0 + 3 = 4

જ્યારે n = 1 x = (– 1) 1 + 4∙1 + 3 = 6

n = 2 x = (– 1) 2 + 4∙2 + 3 = 12 સાથે

ચાલો n = –1 x = (–1) –1 + 4∙(–1) + 3 = –2 સાથે તપાસ કરીએ

તેથી સૌથી નાનું હકારાત્મક મૂળ 4 છે.

જવાબ: 4

તમારા માટે નક્કી કરો:

સમીકરણ ઉકેલો:

તમારા જવાબમાં સૌથી નાનું હકારાત્મક મૂળ લખો.