Le principe de moindre action en gestion. Physique et Aïkido de la plus petite action

Aïkido - l'incarnation du principe de moindre action Notre psychologie et notre technologie sont largement guidées par un concept très proche de l'idée de moindre action. Nous essayons constamment de nous faciliter la vie. Les ordinateurs d'aujourd'hui ne sont pas assez rapides ; ils devraient

Quand j'étais à l'école, notre professeur de physique, Bader, m'a appelé un jour après les cours et m'a dit : « Tu as l'air d'être terriblement fatigué de tout ; écoutez une chose intéressante. Et il m'a dit quelque chose que j'ai trouvé vraiment fascinant. Même aujourd’hui, même si beaucoup de temps s’est écoulé depuis, cela continue de me fasciner. Et chaque fois que je me souviens de ce que j’ai dit, je me remets au travail. Et cette fois, en préparant le cours, je me suis retrouvé à analyser à nouveau les mêmes choses. Et, au lieu de préparer le cours, j'ai pris la décision nouvelle tâche. Le sujet dont je parle est le principe de moindre action.

C'est ce que m'a alors dit mon professeur Bader : « Supposons, par exemple, que vous ayez une particule dans un champ gravitationnel ; cette particule, sortie de quelque part, se déplace librement ailleurs vers un autre point. Vous l'avez lancé, disons, vers le haut, et il s'est envolé puis est tombé.

Il lui a fallu un certain temps pour voyager du point de départ au point final. Essayez maintenant un autre mouvement. Qu'elle se déplace « d'ici à ici » non plus comme avant, mais comme ceci :

mais je me suis quand même retrouvé au bon endroit, au même moment qu’avant.

"Et donc", a poursuivi le professeur, "si vous calculez l'énergie cinétique à chaque instant le long du trajet de la particule, soustrayez-en l'énergie potentielle et intégrez la différence sur tout le temps où le mouvement s'est produit, vous verrez que le nombre que vous obtiendrez sera supérieur à celui du véritable mouvement de la particule.

En d'autres termes, les lois de Newton peuvent être formulées non pas sous la forme, mais comme suit : l'énergie cinétique moyenne moins l'énergie potentielle moyenne atteint sa valeur la plus basse le long de la trajectoire le long de laquelle un objet se déplace réellement d'un endroit à un autre.

Je vais essayer de vous expliquer cela un peu plus clairement.

Si nous prenons le champ gravitationnel et notons la trajectoire des particules, où est la hauteur au-dessus du sol (nous nous contenterons d'une seule dimension pour l'instant ; laissons la trajectoire se dérouler uniquement de haut en bas, et non sur les côtés), alors la cinétique l'énergie sera , et l'énergie potentielle à un moment arbitraire sera égale à .

Maintenant, pour un moment de mouvement le long de la trajectoire, je prends la différence entre les énergies cinétiques et potentielles et l'intègre sur tout le temps du début à la fin. Laissez le mouvement commencer à une certaine hauteur au moment initial et se terminer à une autre certaine hauteur.

Alors l'intégrale est égale

.

Le vrai mouvement se produit le long d’une certaine courbe (en fonction du temps, c’est une parabole) et conduit à une certaine valeur intégrale. Mais vous pouvez imaginer un autre mouvement : d’abord une forte hausse, puis des fluctuations bizarres.

Vérifions ça. Examinons d’abord ce cas : une particule libre n’a aucune énergie potentielle. Ensuite, la règle dit que lorsqu'on passe d'un point à un autre dans heure spécifiée l'intégrale de l'énergie cinétique doit être la plus petite. Cela signifie que la particule doit se déplacer uniformément. (Et c’est exact, vous et moi savons que la vitesse d’un tel mouvement est constante.) Pourquoi uniformément ? Voyons cela. S'il en était autrement, alors parfois la vitesse de la particule dépasserait la moyenne, et parfois elle serait inférieure, et la vitesse moyenne serait la même, car la particule devrait aller « d'ici à ici » en l'heure convenue. Par exemple, si vous devez vous rendre de la maison à l'école en voiture certaine heure, alors vous pouvez le faire de différentes manières : vous pouvez d'abord conduire comme un fou, puis ralentir à la fin, ou conduire à la même vitesse, ou au début vous pouvez même aller à revers, et ensuite seulement se tourner vers l'école, etc. Dans tous les cas, la vitesse moyenne, bien entendu, doit être la même - le quotient de la distance entre le domicile et l'école divisé par le temps. Mais même avec ça vitesse moyenne parfois vous alliez trop vite et parfois trop lentement. Et le carré moyen de quelque chose qui s'écarte de la moyenne, comme on le sait, est toujours plus grand que le carré de la moyenne ; Cela signifie que l'intégrale de l'énergie cinétique lors des fluctuations de la vitesse de déplacement sera toujours supérieure à celle lors d'un déplacement avec vitesse constante. Vous voyez que l'intégrale atteindra un minimum lorsque la vitesse est constante (en l'absence de forces). La bonne façon c'est comme ça.

Un objet projeté vers le haut dans un champ de gravité s’élève d’abord rapidement, puis de plus en plus lentement. Cela se produit parce qu’il possède également de l’énergie potentielle et que la différence entre les énergies cinétique et potentielle devrait atteindre sa valeur minimale. Puisque l’énergie potentielle augmente à mesure que vous montez, une différence plus petite sera obtenue si vous atteignez le plus rapidement possible les hauteurs où l’énergie potentielle est élevée. Ensuite, en soustrayant ce potentiel élevé de l'énergie cinétique, on obtient une diminution de la moyenne. Ainsi, le chemin qui monte et fournit une bonne part négative d’énergie potentielle est plus rentable.

Mais d’un autre côté, on ne peut pas aller trop vite ni aller trop haut, car cela nécessiterait trop d’énergie cinétique. Vous devez vous déplacer suffisamment vite pour monter et descendre dans le temps imparti dont vous disposez. Vous ne devriez donc pas essayer de voler trop haut, mais simplement atteindre un niveau raisonnable. En conséquence, il s'avère que la solution est une sorte d'équilibre entre le désir d'obtenir autant d'énergie potentielle que possible et le désir de réduire autant que possible la quantité d'énergie cinétique - c'est le désir d'obtenir une réduction maximale dans la différence entre les énergies cinétiques et potentielles.

C'est tout ce que mon professeur m'a dit, car il était très bon professeur et savait quand il était temps d'arrêter. Moi-même, hélas, je ne suis pas comme ça. C'est difficile pour moi de m'arrêter à temps. Et donc, au lieu de simplement susciter votre intérêt avec mon histoire, je veux vous intimider, je veux que vous en ayez marre de la complexité de la vie - je vais essayer de prouver ce dont je vous ai parlé. Le problème mathématique que nous allons résoudre est très difficile et unique. Il existe une certaine quantité appelée action. Elle est égale à l’énergie cinétique moins l’énergie potentielle intégrée dans le temps :

.

N'oubliez pas ce p.e. et k.e. - les deux fonctions du temps. Pour toute nouvelle voie envisageable, cette action prend son sens spécifique. Le problème mathématique est de déterminer quelle courbe a ce nombre inférieur aux autres.

Tu diras : "Oh, c'est facile exemple courant au maximum et au minimum. Il faut calculer l’action, la différencier et trouver le minimum.

Mais attendez. Habituellement, nous avons une fonction d'une variable et nous devons trouver la valeur de la variable à laquelle la fonction devient la plus petite ou la plus grande. Disons qu'il y a une tige chauffée au milieu. La chaleur s'y diffuse et sa propre température s'établit en chaque point de la tige. Il faut trouver le point où il est le plus élevé. Mais nous avons nous parlons de quelque chose de complètement différent - chaque chemin dans l'espace a son propre numéro, et il est censé trouver le chemin pour lequel ce nombre est minimal. Il s’agit d’un domaine mathématique complètement différent. Il ne s’agit pas d’un calcul ordinaire, mais d’un calcul variationnel (comme on l’appelle).

Ce domaine des mathématiques présente bon nombre de ses propres problèmes. Disons qu'un cercle est généralement défini comme lieu points dont les distances à un point donné sont les mêmes, mais un cercle peut être défini différemment : c'est l'une des courbes d'une longueur donnée qui limite plus grande superficie. Toute autre courbe de même périmètre délimite une aire plus petite que le cercle. Donc si vous vous fixez la tâche : trouver la courbe périmètre donné, limitant la plus grande surface, alors nous aurons un problème de calcul des variations, et non du calcul auquel vous êtes habitué.

On veut donc prendre l'intégrale sur le chemin parcouru par le corps. Faisons-le de cette façon. Le tout est d'imaginer qu'il existe un vrai chemin et que toute autre courbe que nous dessinons n'est pas le vrai chemin, de sorte que si nous calculons l'action pour cela, nous obtiendrons un nombre supérieur à celui que nous obtenons pour l'action correspondante. à la vraie manière.

La tâche est donc de trouver le vrai chemin. Où se trouve-t-il ? Une solution, bien sûr, serait de compter l'action sur des millions et des millions de chemins, puis de voir quel chemin a la plus petite action. C'est la voie dans laquelle l'action est minime et sera réelle.

Cette méthode est tout à fait possible. Cependant, cela peut être fait plus simplement. S'il existe une quantité qui a un minimum (de fonctions ordinaires, par exemple la température), alors l'une des propriétés du minimum est qu'en s'éloignant de lui d'une distance du premier ordre de petitesse, la fonction s'écarte de son minimum valeur uniquement par une valeur du second ordre. Et à tout autre endroit de la courbe, un décalage d’une petite distance modifie également la valeur de la fonction d’une valeur du premier ordre de petitesse. Mais au minimum, de légères déviations latérales n’entraînent pas de changement de fonction en première approximation.

C'est cette propriété que nous allons utiliser pour calculer le chemin réel.

Si le chemin est correct, alors une courbe légèrement différente de celui-ci ne conduira pas, en première approximation, à un changement dans l'ampleur de l'action. Tous les changements, si c'était vraiment le minimum, n'apparaîtront qu'en seconde approximation.

C’est facile à prouver. Si, avec un écart par rapport à la courbe, des changements se produisent dans le premier ordre, alors ces changements d'action sont proportionnels à l'écart. Ils sont susceptibles d’augmenter l’effet ; sinon ce ne serait pas un minimum. Mais comme les changements sont proportionnels à l’écart, changer le signe de l’écart réduira l’action. Il s'avère qu'en s'écartant dans une direction, l'effet augmente et en s'écartant dans la direction opposée, il diminue. La seule façon pour que cela soit véritablement un minimum est si, en première approximation, aucun changement ne se produit et que les changements sont proportionnels au carré de l’écart par rapport au chemin réel.

Nous suivrons donc le chemin suivant : nous désignerons (avec une ligne en dessous) le vrai chemin - celui que nous voulons trouver. Prenons un chemin d'essai , qui diffère légèrement de celui souhaité, que nous désignons .

L'idée est que si nous calculons l'action sur le chemin, alors la différence entre celle-ci et l'action que nous avons calculée pour le chemin (pour plus de simplicité, elle sera notée), ou la différence entre et, devrait être, en première approximation, zéro. Ils peuvent différer au second ordre, mais au premier la différence doit être nulle.

Et cela doit être respecté par chacun. Cependant, pas tout à fait pour tout le monde. La méthode nécessite de prendre en compte uniquement les chemins qui commencent et se terminent tous à la même paire de points, c'est-à-dire que chaque chemin doit commencer à un certain moment et se terminer à un autre moment spécifique. Ces points et moments sont enregistrés. Notre fonction (écart) doit donc être nulle aux deux extrémités : et . Dans ces conditions, notre problème mathématique devient complètement défini.

Si vous ne connaissiez pas le calcul différentiel, vous pourriez faire la même chose pour trouver le minimum d’une fonction ordinaire. Vous penseriez à ce qui se passerait si vous preniez et ajoutiez une petite valeur à , et diriez que la correction du premier ordre doit être au minimum égale à zéro. Vous remplaceriez et élargiriez au premier degré, en un mot, vous répéteriez tout ce que nous entendons faire avec.

Donc, notre idée est de remplacer dans la formule d'action

,

où l'énergie potentielle est désignée par. La dérivée est, bien sûr, la dérivée de plus la dérivée de , donc pour l'action j'obtiens cette expression :

.

Il convient maintenant de décrire cela plus en détail. Pour le terme quadratique j'obtiens

.

Mais attendez une minute ! Après tout, je n’ai pas à m’inquiéter des commandes supérieures à la première. Je peux supprimer tous les termes contenant et diplômes supérieurs, et placez-les dans une boîte appelée « deuxième et commandes plus élevées" A partir de cette expression, seul un deuxième degré y parviendra, mais à partir d'autre chose, les plus élevés peuvent également entrer. La partie liée à l’énergie cinétique est donc :

Ensuite, nous avons besoin du potentiel en certains points. Je le considère petit et je peux l'étendre dans une série Taylor. Ce sera approximativement le cas ; dans l'approximation suivante (du fait qu'il existe ici des dérivées ordinaires), la correction est égale à , multiplié par le taux de variation par rapport à, etc. :

.

Pour gagner de la place, je l'ai noté en utilisant la dérivée par rapport à . Le terme c et tout ce qui se trouve derrière entrent dans la catégorie du « second ordre et supérieur ». Et il n’y a plus lieu de s’inquiéter pour eux. Combinons tout ce qui reste :

Si nous y regardons maintenant de plus près, nous verrons que les deux premiers termes écrits ici correspondent à l'action que j'écrirais pour l'action souhaitée. vrai chemin. Je veux attirer votre attention sur le changement, c'est-à-dire sur la différence entre et ce qui se serait passé pour le vrai chemin. Nous écrirons cette différence sous la forme et l’appellerons variation. En écartant les « deuxièmes ordres et supérieurs », nous obtenons pour

.

Maintenant, la tâche ressemble à ceci. Voici devant moi une intégrale. Je ne sais pas encore ce que c’est, mais je sais fermement que, quoi que je prenne, cette intégrale doit être égal à zéro. «Eh bien», pourriez-vous penser, «la seule possibilité pour cela est que le multiplicateur at soit égal à zéro.» Mais qu'en est-il du premier terme, où est-il ? Vous direz : « S’il se transforme en néant, alors son dérivé est le même rien ; Cela signifie que le coefficient at doit également être nul. Eh bien, ce n'est pas tout à fait vrai. Ce n'est pas tout à fait vrai car il existe un lien entre l'écart et sa dérivée ; ils ne sont pas complètement indépendants, car il doit être nul à et à .

Lors de la résolution de tous les problèmes de calcul des variations, le même principe général est toujours utilisé. Vous déplacez légèrement ce que vous voulez faire varier (de la même manière que nous l'avons fait en ajoutant ), jetez un coup d'œil aux termes du premier ordre, puis organisez le tout de manière à obtenir une intégrale sous la forme : "décalez ce que vous obtenez", mais de manière à ce que il ne contenait aucun dérivé de (aucun). Il faut absolument tout transformer pour qu'il reste « quelque chose » multiplié par . Vous comprendrez maintenant pourquoi c’est si important. (Il existe des formules qui vous diront comment, dans certains cas, vous pouvez faire cela sans aucun calcul ; mais elles ne sont pas si générales qu'elles méritent d'être mémorisées ; il est préférable de faire les calculs comme nous le faisons.)

Comment refaire un pénis pour qu'il apparaisse dedans ? Je peux y parvenir en intégrant pièce par pièce. Il s'avère que dans le calcul des variations, l'astuce consiste à écrire la variation puis à l'intégrer par parties afin que leurs dérivées disparaissent. Dans tous les problèmes dans lesquels des dérivées apparaissent, la même astuce est exécutée.

Rappelons le principe général de l'intégration par parties. Si vous avez une fonction arbitraire multipliée par et intégrée, alors vous écrivez la dérivée de :

.

Dans l'intégrale qui vous intéresse, il n'y a que le dernier terme, donc

.

Dans notre formule, la fonction est considérée comme le produit de ; donc je comprends l'expression

Les limites de l'intégration doivent être substituées au premier terme. Puis sous l'intégrale je recevrai le terme d'intégration par parties et le dernier terme qui reste inchangé lors de la transformation.

Et maintenant, ce qui arrive toujours se produit : la partie intégrée disparaît. (Et s'il ne disparaît pas, il faudra alors reformuler le principe en ajoutant des conditions qui assurent une telle disparition !) Nous avons déjà dit qu'aux extrémités du chemin il devrait être égal à zéro. Après tout, quel est notre principe ? Le fait est que l'action est minime à condition que la courbe variée commence et se termine à des points sélectionnés. Cela signifie que et . Le terme intégré s’avère donc nul. Nous rassemblons le reste des membres et écrivons

.

La variation a maintenant acquis la forme que nous voulions lui donner : quelque chose est entre parenthèses (notons-le ), et tout cela est multiplié par et intégré de à .

Il s'est avéré que l'intégrale d'une expression multipliée par est toujours égale à zéro :

.

Il existe une fonction de ; Je le multiplie et l'intègre du début à la fin. Et quoi que ce soit, j'obtiens zéro. Cela signifie que la fonction est égale à zéro. En général, c'est évident, mais juste au cas où, je vais vous montrer une façon de le prouver.

Permettez-moi de choisir quelque chose qui est égal à zéro partout, pour toutes les valeurs présélectionnées sauf une. Il reste nul jusqu'à ce que j'y arrive, puis il monte un instant et retombe immédiatement. Si vous prenez l'intégrale de ceci multipliée par une fonction, alors le seul endroit où vous obtiendrez quelque chose de non nul est l'endroit où il a sauté ; et vous obtiendrez à cet endroit la valeur de l'intégrale sur le saut. L'intégrale de saut elle-même n'est pas nulle, mais lorsqu'elle est multipliée par elle, elle devrait donner zéro. Cela signifie que la fonction à l'endroit où il y a eu un saut doit s'avérer nulle. Mais le saut aurait pu être fait n’importe où ; ce qui veut dire qu'il doit être nul partout.

On voit que si notre intégrale est égale à zéro pour tout , alors le coefficient at doit devenir nul. L'intégrale d'action atteint un minimum le long du chemin qui satisfera une équation différentielle aussi complexe :

.

Ce n'est en fait pas si compliqué ; vous l'avez déjà rencontré. C'est simple. Le premier terme est la masse multipliée par l’accélération ; la seconde est la dérivée de l'énergie potentielle, c'est-à-dire la force.

Nous avons donc montré (au moins pour un système conservateur) que le principe de moindre action conduit à la bonne réponse ; il déclare que le chemin qui a l'action minimale est le chemin qui satisfait à la loi de Newton.

Une remarque supplémentaire doit être faite. Je n'ai pas prouvé que c'était le minimum. C'est peut-être le maximum. En fait, cela ne doit pas nécessairement être le minimum. Ici, tout est pareil que dans le « principe du temps le plus court », dont nous avons discuté en étudiant l'optique. Là aussi, nous avons d'abord parlé du temps « le plus court ». Cependant, il s'est avéré qu'il existe des situations dans lesquelles ce délai n'est pas nécessairement le « le plus court ». Le principe fondamental est que pour tout écart de premier ordre par rapport à chemin optique les changements au fil du temps seraient nuls ; C'est la même histoire ici. Par « minimum », nous entendons en fait que, au premier ordre de petitesse, les changements de quantité dus aux écarts par rapport au chemin devraient être nuls. Et ce n’est pas forcément le « minimum ».

Je veux maintenant passer à quelques généralisations. Tout d’abord, toute cette histoire pourrait se faire en trois dimensions. Au lieu d'une simple, j'aurais alors , à la fois comme fonctions, et l'action paraîtrait plus compliquée. En mouvement 3D, vous devez utiliser l'énergie cinétique totale : , multipliée par le carré de la vitesse totale. Autrement dit,

.

De plus, l’énergie potentielle est désormais fonction de , et . Que pouvez-vous dire du chemin ? Un chemin est une certaine courbe générale dans l’espace ; ce n'est pas si facile à dessiner, mais l'idée reste la même. Qu’en est-il de la situation ? Eh bien, il comporte trois éléments. Le chemin peut être déplacé le long de , et le long de , et le long de , ou dans les trois directions simultanément. Alors maintenant, c'est un vecteur. Cela ne crée pas de complications majeures. Puisque seules les variations du premier ordre doivent être égales à zéro, le calcul peut être effectué séquentiellement avec trois décalages. Premièrement, vous ne pouvez que changer de direction et dire que le coefficient doit tendre vers zéro. Vous obtenez une équation. Ensuite, nous avancerons dans la direction et prendrons la deuxième. Ensuite, nous le déplaçons dans la direction et nous obtenons le troisième. Vous pouvez tout faire, si vous le souhaitez, dans un ordre différent. Quoi qu’il en soit, un trio d’équations se pose. Mais la loi de Newton, c'est aussi trois équations en trois dimensions, une pour chaque composante. Il ne vous reste plus qu'à constater par vous-même que tout cela fonctionne en trois dimensions (il n'y a pas beaucoup de travail ici). À propos, vous pouvez prendre n'importe quel système de coordonnées, polaire, n'importe lequel, et obtenir immédiatement les lois de Newton par rapport à ce système, en considérant ce qui se passe lorsqu'un déplacement se produit le long du rayon ou le long de l'angle, etc.

La méthode peut être généralisée à nombre arbitraire particules. Si, disons, vous avez deux particules et qu’il y a des forces agissant entre elles et qu’il existe une énergie potentielle mutuelle, alors vous ajoutez simplement leurs énergies cinétiques et soustrayez l’énergie potentielle d’interaction de la somme. Que variez-vous ? Chemins des deux particules. Alors pour deux particules se déplaçant dans trois dimensions, six équations apparaissent. Vous pouvez faire varier la position de la particule 1 dans la direction , dans la direction et dans la direction , et faire de même avec la particule 2, il y a donc six équations. Et c'est comme ça que ça devrait être. Trois équations déterminent l'accélération de la particule 1 en raison de la force agissant sur elle, et les trois autres déterminent l'accélération de la particule 2 en raison de la force agissant sur elle. Suivez toujours les mêmes règles du jeu et vous obtiendrez la loi de Newton pour un nombre arbitraire de particules.

J'ai dit que nous obtiendrions la loi de Newton. Ce n'est pas tout à fait vrai, car la loi de Newton inclut également des forces non conservatrices, telles que la friction. Newton a soutenu qu'il est égal à chaque . Le principe de moindre action n'est valable que pour les systèmes conservateurs, ceux où toutes les forces peuvent être obtenues à partir de fonction potentielle. Mais vous savez qu’au niveau microscopique, c’est-à-dire au niveau physique le plus profond, les forces non conservatrices n’existent pas. Des forces non conservatrices (telles que la friction) apparaissent uniquement parce que nous négligeons les effets microscopiques complexes : il y a tout simplement trop de particules à analyser. Les lois fondamentales peuvent s'exprimer sous la forme du principe de moindre action.

Permettez-moi de passer à d’autres généralisations. Supposons que nous nous intéressions à ce qui se passera lorsque la particule se déplacera de manière relativiste. Jusqu’à présent, nous n’avons pas obtenu l’équation relativiste correcte du mouvement ; vrai uniquement dans les mouvements non relativistes. La question se pose : existe-t-il un principe correspondant de moindre action dans le cas relativiste ? Oui, ça existe. La formule dans le cas relativiste est :

La première partie de l’intégrale d’action est le produit de la masse au repos et de l’intégrale de la fonction vitesse. Ensuite, au lieu de soustraire l’énergie potentielle, nous avons des intégrales du potentiel scalaire et des temps de potentiel vectoriel. Bien entendu, seules les forces électromagnétiques sont prises en compte ici. Tous les champs électriques et magnétiques sont exprimés en termes de et. Cette fonction d'action donne une théorie complète du mouvement relativiste particule individuelle dans un champ électromagnétique.

Bien sûr, vous devez comprendre que partout où j'ai écrit , avant de faire des calculs, vous devez remplacer, etc. De plus, là où j'ai écrit simplement , , , vous devez imaginer les points du moment : , , . En fait, ce n'est qu'après de telles substitutions et remplacements que vous obtiendrez une formule pour l'action d'une particule relativiste. Laissez les plus expérimentés d’entre vous essayer de prouver que cette formule d’action donne réellement les équations de mouvement correctes pour la théorie de la relativité. Laissez-moi simplement vous conseiller de commencer par jeter, c'est-à-dire de vous passer des champs magnétiques pour l'instant. Ensuite, vous devrez obtenir les composantes de l’équation du mouvement, où, comme vous vous en souvenez probablement, .

Inclure en considération potentiel vectoriel beaucoup plus difficile. Les variations deviennent alors incomparablement plus complexes. Mais au final la force s'avère être égale à ce qu'elle devrait être : . Mais amusez-vous vous-même.

Je voudrais souligner que dans cas général(par exemple, dans la formule relativiste) l'intégrale en action n'inclut plus la différence entre les énergies cinétique et potentielle. Cela ne convenait que dans une approximation non relativiste. Par exemple, membre - ce n'est pas ce qu'on appelle l'énergie cinétique. La question de savoir quelle devrait être l'action à entreprendre dans un cas particulier peut être tranchée après quelques essais et erreurs. C’est le même type de problème que celui de déterminer quelles devraient être les équations du mouvement. Il vous suffit de jouer avec les équations que vous connaissez et de voir si elles peuvent être écrites comme le principe de moindre action.

Encore une remarque sur la terminologie. La fonction intégrée au fil du temps pour obtenir l’action est appelée Lagrangienne. C'est une fonction qui dépend uniquement des vitesses et des positions des particules. Ainsi le principe de moindre action s’écrit aussi sous la forme

,

où et signifie toutes les composantes des coordonnées et des vitesses. Si jamais vous entendez quelqu'un parler d'un "Lagrangien", il parle de la fonction utilisée pour obtenir . Pour un mouvement relativiste dans un champ électromagnétique

.

De plus, je dois souligner que les mesures les plus méticuleuses et des gens pédants ne s’appelle pas une action. C'est ce qu'on appelle « la première fonction principale de Hamilton ». Mais donner une conférence sur le "principe du moindre premier" fonction principale Hamilton" était au-dessus de mes forces. Je l'ai appelé "action". Et d’ailleurs, de plus en plus de gens appellent cela « l’action ». Vous voyez, historiquement, l’action a été appelée autrement, ce qui n’est pas aussi utile à la science, mais je pense qu’il est plus logique de changer la définition. Maintenant, toi aussi tu vas commencer à nommer nouvelle fonctionnalité action, et bientôt tout le monde commencera à l'appeler par ce simple nom.

Maintenant, je veux vous dire quelque chose sur notre sujet qui est similaire au raisonnement que j'ai eu sur le principe du temps le plus court. Il y a une différence dans l'essence même de la loi qui dit qu'une intégrale prise d'un point à un autre a un minimum - la loi qui nous dit quelque chose sur l'ensemble du chemin à la fois, et la loi qui dit que lorsque vous vous déplacez, alors , Cela signifie qu'il existe une force menant à l'accélération. La deuxième approche vous rend compte de chacun de vos pas, elle trace votre chemin pouce par pouce, et la première donne immédiatement une déclaration générale sur l'ensemble du chemin parcouru. En parlant de lumière, nous avons évoqué le lien entre ces deux approches. Maintenant, je veux vous expliquer pourquoi des lois différentielles devraient exister s'il existe un tel principe - le principe de moindre action. La raison est la suivante : considérons le chemin réellement parcouru dans l’espace et dans le temps. Comme précédemment, nous nous contenterons d’une seule mesure, afin de pouvoir tracer un graphique de la dépendance à l’égard de . Sur le vrai chemin, il atteint un minimum. Supposons que nous ayons ce chemin et qu'il passe par un certain point de l'espace et du temps et par un autre point voisin.

Or, si l’intégrale entière de à a atteint un minimum, il faut que l’intégrale le long d’une petite section de à soit également minimale. Il ne se peut pas que la partie de à dépasse même un peu le minimum. Sinon, vous pourriez déplacer la courbe d'avant en arrière dans cette section et réduire légèrement la valeur de l'intégrale entière.

Cela signifie que n’importe quelle partie du chemin doit également fournir un minimum. Et cela est vrai pour toutes les petites portions du chemin. Par conséquent, le principe selon lequel le chemin entier doit donner un minimum peut être formulé en disant qu'un segment infinitésimal du chemin est aussi une courbe sur laquelle l'action est minimale. Et si nous prenons un segment assez court du chemin - entre des points et très proches les uns des autres - alors peu importe comment le potentiel change d'un point à l'autre loin de cet endroit, car, en parcourant tout votre court segment, vous avez presque ne quitte jamais ta place. La seule chose que vous devez considérer est la petitesse du changement de premier ordre dans le potentiel. La réponse ne dépend peut-être que de la dérivée du potentiel, et non du potentiel ailleurs. Ainsi, une déclaration sur la propriété du chemin entier dans son ensemble devient une déclaration sur ce qui se passe sur une courte section du chemin, c'est-à-dire une déclaration différentielle. Et cette formulation différentielle inclut les dérivées du potentiel, c'est-à-dire la force en un point donné. Il s'agit d'une explication qualitative du lien entre le droit dans son ensemble et le droit différentiel.

Lorsque nous parlions de lumière, nous abordions également la question : comment une particule trouve-t-elle le bon chemin ? AVEC point différentiel C’est facile à comprendre d’un point de vue. À chaque instant, la particule subit une accélération et sait seulement ce qu’elle est censée faire à ce moment-là. Mais tous vos instincts de cause à effet se réveillent lorsque vous entendez qu’une particule « décide » du chemin à suivre, en s’efforçant d’obtenir un minimum d’action. N'est-elle pas en train de « renifler » les chemins voisins, de deviner à quoi ils mèneront - à plus ou moins d'action ? Lorsque nous avons placé un écran sur le chemin de la lumière pour que les photons ne puissent pas essayer tous les chemins, nous avons découvert qu'ils ne pouvaient pas décider quel chemin prendre, et nous avons obtenu le phénomène de diffraction.

Mais est-ce également vrai pour la mécanique ? Est-il vrai qu’une particule non seulement « va dans le bon sens », mais reconsidère toutes les autres trajectoires imaginables ? Et si, en mettant des obstacles sur son chemin, nous ne lui permettons pas de regarder vers l'avant, alors nous obtiendrons une sorte d'analogue du phénomène de diffraction ? Le plus merveilleux dans tout cela, c’est que tout se passe réellement ainsi. C’est exactement ce que disent les lois de la mécanique quantique. Notre principe de moindre action n’est donc pas pleinement formulé. Cela ne consiste pas dans le fait que la particule choisit la voie de moindre action, mais dans le fait qu'elle « sent » toutes les voies voisines et choisit celle le long de laquelle l'action est minime, et la méthode de ce choix est similaire à la manière dont la lumière est sélectionnée temps le plus court. Vous vous souvenez que la façon dont la lumière sélectionne le temps le plus court est la suivante : si la lumière suit un chemin qui nécessite un temps différent, elle arrivera avec une phase différente. Et l’amplitude totale à un moment donné est la somme des contributions d’amplitude pour tous les chemins par lesquels la lumière peut l’atteindre. Tous ces chemins dont les phases diffèrent fortement ne donnent rien après addition. Mais si vous parvenez à trouver toute la séquence de trajets dont les phases sont presque les mêmes, alors les petites contributions s'additionneront et au point d'arrivée l'amplitude totale recevra une valeur notable. De la manière la plus importante devient celui à proximité duquel se trouvent de nombreux chemins proches donnant la même phase.

Exactement la même chose se produit en mécanique quantique. La mécanique quantique complète (non relativiste et négligeant le spin de l'électron) fonctionne comme ceci : la probabilité qu'une particule, quittant le point 1 au temps , atteigne le point 2 au temps , est égale au carré de l'amplitude de probabilité. L'amplitude totale peut s'écrire comme la somme des amplitudes de tous moyens possibles- pour tout itinéraire d'arrivée. Pour tout , qui pourrait se produire pour n'importe quelle trajectoire imaginaire concevable, l'amplitude doit être calculée. Ensuite, ils doivent tous être pliés. Que prenons-nous comme amplitude de probabilité d’un certain chemin ? Notre intégrale d’action nous indique quelle devrait être l’amplitude d’un chemin individuel. L'amplitude est proportionnelle à , où est l'action le long de ce chemin. Cela signifie que si l’on représente la phase d’amplitude sous la forme nombre complexe, alors l'angle de phase sera égal à . L'action a la dimension de l'énergie dans le temps, et la constante de Planck a la même dimension. C’est la constante qui détermine quand la mécanique quantique est nécessaire.

Et c'est comme ça que tout fonctionne. Supposons que l'action soit très grande pour tous les chemins par rapport au nombre . Supposons qu'un chemin mène à une certaine valeur d'amplitude. La phase d'un chemin à proximité s'avérera complètement différente, car avec un chemin énorme, même des changements mineurs modifient fortement la phase (après tout, elle est extrêmement petite). Cela signifie que les chemins adjacents éteignent généralement leurs contributions lorsqu'ils sont ajoutés. Et ce n'est pas vrai dans un seul domaine - celui où le chemin et son voisin - tous deux, en première approximation, ont la même phase (ou, plus précisément, presque la même action, variant à l'intérieur). Seuls ces chemins sont pris en compte. Et dans le cas limite où la constante de Planck tend vers zéro, les lois correctes de la mécanique quantique peuvent se résumer en disant : « Oubliez toutes ces amplitudes de probabilité. La particule se déplace réellement manière spéciale- précisément selon lequel, en première approximation, cela ne change pas. C'est le lien entre le principe de moindre action et la mécanique quantique. Le fait que la mécanique quantique puisse être formulée de cette manière a été découvert en 1942 par un élève du même professeur, M. Bader, dont je vous ai parlé. [La mécanique quantique a été initialement formulée en utilisant équation différentielle pour l'amplitude (Schrödinger), et également en utilisant des mathématiques matricielles (Heisenberg).]

Maintenant, je veux parler d'autres principes de minimum en physique. Il existe de nombreux principes intéressants de ce type. Je ne les énumérerai pas tous, mais je n'en citerai qu'un de plus. Plus tard, lorsque nous aborderons un phénomène physique pour lequel il existe un excellent principe minimum, je vous en parlerai. Je veux maintenant montrer qu'il n'est pas nécessaire de décrire l'électrostatique en utilisant une équation différentielle pour le champ ; on peut plutôt exiger que certaines intégrales aient un maximum ou un minimum. Pour commencer, prenons le cas où la densité de charge est connue partout, mais où il faut trouver le potentiel en tout point de l'espace. Vous savez déjà que la réponse devrait être la suivante :

Une autre façon de dire la même chose est d'évaluer l'intégrale

;

c'est une intégrale de volume. Elle est prise dans tout l'espace. Avec une distribution de potentiel correcte, cette expression atteint un minimum.

Nous pouvons montrer que ces deux affirmations concernant l’électrostatique sont équivalentes. Supposons que nous ayons choisi une fonction arbitraire. Nous voulons montrer que lorsque nous prenons comme qualité la valeur correcte du potentiel plus un petit écart, alors dans le premier ordre de petitesse, la variation sera égale à zéro. Alors on écrit

voici ce que nous recherchons ; mais nous varierons pour voir ce qu'elle doit être pour que la variation soit du premier ordre de petitesse. Au premier terme, nous devons écrire

Le seul terme de premier ordre qui changera est :

Au deuxième terme, l'intégrande prend la forme

la partie changeante ici est . En ne laissant que les termes changeants, on obtient l'intégrale

.

Cela doit être intégré encore et encore. Et ici la même astuce s'impose : pour s'en débarrasser, on intègre par parties. Cela entraînera une différenciation supplémentaire par rapport à . C'est la même idée de base que nous avons utilisée pour nous débarrasser des dérivés en ce qui concerne . Nous utilisons l'égalité

.

Le terme intégré est égal à zéro, puisqu'on le considère égal à zéro à l'infini. (Cela correspond à disparaître à et . Notre principe est donc plus précisément formulé comme suit : pour le bon il est inférieur à tout autre ayant les mêmes valeurs à l'infini.) Ensuite nous ferons de même avec et avec . Notre intégrale se transforme en

.

Pour que cette variation soit égale à zéro pour tout arbitraire, le coefficient at doit être égal à zéro. Moyens,

Nous revenons à notre ancienne équation. Cela signifie que notre proposition « minimale » est correcte. Elle peut être généralisée si les calculs sont légèrement modifiés. Revenons en arrière et intégrons par parties, mais en décrivant le tout composant par composant. Commençons par écrire l'égalité suivante :

En différenciant le côté gauche, je peux montrer qu’il est exactement égal au côté droit. Cette équation convient pour effectuer une intégration par parties. Dans notre intégrale on remplace par puis intégrez-le sur le volume. Le terme à divergence après intégration sur le volume est remplacé par une intégrale sur la surface :

Et puisque nous intégrons sur tout l’espace, la surface de cette intégrale se situe à l’infini. Cela signifie , et nous obtenons le même résultat.

Ce n’est que maintenant que nous commençons à comprendre comment résoudre des problèmes dans lesquels nous ne savons pas où se situent toutes les charges. Ayons des conducteurs sur lesquels les charges sont réparties d'une manière ou d'une autre. Si les potentiels sur tous les conducteurs sont fixes, alors notre principe minimum peut toujours s'appliquer. Nous réaliserons l'intégration uniquement sur la région située en dehors de tous les conducteurs. Mais comme on ne peut pas changer sur les conducteurs, alors sur leur surface, et l'intégrale de surface

est également nul. Intégration du volume restant

doivent être effectués uniquement dans les espaces entre les conducteurs. Et bien sûr, nous obtenons à nouveau l'équation de Poisson

Nous avons donc montré que notre intégrale initiale atteint un minimum même lorsqu'elle est calculée dans l'espace entre conducteurs dont chacun est à un potentiel fixe [cela signifie que chaque fonction test doit être égale à un potentiel donné du conducteur, quand - pointe sur la surface du conducteur ].

Il y a un intéressant cas particulier, lorsque les charges sont localisées uniquement sur les conducteurs. Alors

et notre principe minimum nous dit que dans le cas où chaque conducteur a son propre potentiel prédéterminé, les potentiels dans les espaces entre eux sont ajustés pour que l'intégrale soit la plus petite possible. De quel genre d’intégrale s’agit-il ? Le membre est un champ électrique. Cela signifie que l’intégrale est l’énergie électrostatique. Le champ correct est le seul qui, parmi tous les champs obtenus sous forme de gradient de potentiel, possède l'énergie totale la plus faible.

J'aimerais utiliser ce résultat pour résoudre un problème particulier et vous montrer que toutes ces choses ont une réelle signification pratique. Supposons que je prenne deux conducteurs sous la forme d'un condensateur cylindrique.

Le potentiel du conducteur interne est, disons, , et celui du conducteur externe est nul. Soit le rayon du conducteur intérieur égal à , et celui du conducteur extérieur - . Nous pouvons maintenant supposer que la répartition des potentiels entre eux est quelconque. Mais si nous prenons la bonne valeur et calculons , alors l'énergie du système devrait être . Ainsi, en utilisant notre principe, vous pouvez également calculer la capacité. Si nous prenons une distribution de potentiel incorrecte et essayons d'estimer la capacité du condensateur en utilisant cette méthode, nous nous retrouverons avec trop de valeurs. d'une grande importance capacité à fixe. Tout potentiel estimé qui ne correspond pas exactement à sa vraie valeur entraînera une valeur incorrecte, supérieure à ce qui est nécessaire. Mais si le potentiel mal choisi est encore une approximation grossière, alors la capacité sera obtenue avec une bonne précision, car l'erreur in est une quantité du second ordre par rapport à l'erreur in.

Supposons que je ne connais pas la capacité du condensateur cylindrique. Ensuite, pour la reconnaître, je peux utiliser ce principe. Je vais simplement tester différentes fonctions potentielles jusqu'à ce que j'atteigne la valeur la plus basse. Disons par exemple que j'ai choisi un potentiel qui correspond à un champ constant. (Vous savez, bien sûr, que le champ ici n'est pas réellement constant ; il change comme .) Si le champ est constant, cela signifie que le potentiel dépend linéairement de la distance. Pour que la tension sur les conducteurs soit celle requise, la fonction doit avoir la forme

Même lorsque (et cela conduit déjà à des différences assez importantes entre les champs constant et linéaire), j'obtiens toujours une approximation assez passable. Bien sûr, comme prévu, la réponse est un peu trop élevée. Mais si un fil fin est placé à l'intérieur d'un grand cylindre, tout semble bien pire. Ensuite le champ change très fortement et le remplace champ constant ne mène à rien de bon. Quand on surestime la réponse presque deux fois. Pour les petits, la situation semble bien meilleure. Dans la limite opposée, lorsque l'écart entre les conducteurs n'est pas très grand (disons en ), un champ constant s'avère être une très bonne approximation, il donne une valeur précise au dixième de pour cent.

Je vais maintenant vous expliquer comment améliorer ce calcul. (Vous connaissez bien sûr la réponse pour un cylindre, mais la même méthode fonctionne pour d'autres formes de condensateur inhabituelles pour lesquelles vous ne connaissez peut-être pas la bonne réponse.) L'étape suivante consiste à trouver une meilleure approximation du potentiel réel que nous obtenons. je ne sais pas. Disons que vous pouvez tester une constante plus un exposant, etc. Mais comment savoir que vous avez la meilleure approximation si vous ne connaissez pas la vraie ? Réponse : Calculer ; plus il est bas, plus il est proche de la vérité. Testons cette idée. Supposons que le potentiel ne soit pas linéaire, mais, disons, quadratique dans , et que le champ électrique ne soit pas constant, mais linéaire. Le plus courant forme quadratique, qui se transforme en. J'arriverai à mon minimum. Se tourner vers l'ordinaire calcul différentiel, je m'assure que le minimum

La réponse 1.1 s’avère être 10,492065 au lieu du 10,492070 attendu. Là où on s’attendrait à une bonne réponse, elle s’avère être très, très bonne.

J'ai donné tous ces exemples, d'une part, pour démontrer la valeur théorique du principe d'action minimale et en général de tous les principes de minimum, et, d'autre part, pour vous montrer leur utilité pratique, et nullement pour calculer la capacité que nous avons déjà, nous le savons très bien. Pour toute autre forme, vous pouvez essayer un champ approximatif avec quelques paramètres inconnus (comme ) et les ajuster au minimum. Vous recevrez un excellent résultats numériques dans des problèmes qui ne peuvent être résolus autrement.

Le principe de la moindre action est le plus important au sein de la famille ; c'est l'une des dispositions clés de la physique moderne.

La première formulation du principe a été donnée (P. Maupertuis (français)) en 1744. De là, il a dérivé les lois de la réflexion et de la réfraction de la lumière.

Principe de moindre action en mécanique classique

Rappelons d'abord, en prenant l'exemple d'un système physique avec un , qu'il s'agit ici de , c'est-à-dire d'une règle qui associe un certain nombre à chaque fonction x(t). L'action ressemble à : S[x] = \int \mathcal(L)(x(t),\dot(x)(t),t) dt, Où \mathcal(L)(x(t),\dot(x)(t),t) il existe des systèmes qui dépendent de la trajectoire (c'est-à-dire des coordonnées, qui à leur tour dépendent du temps), de sa première dans le temps, et peuvent aussi dépendre explicitement de .

L’action peut être calculée pour une trajectoire complètement arbitraire, aussi « sauvage » et « contre nature » soit-elle. Cependant, parmi l’ensemble des trajectoires possibles, il n’y en a qu’une seule que le corps suivra réellement. Le principe de moindre action répond précisément à la question de savoir comment le corps va réellement bouger :

Cela signifie que si le lagrangien du système est donné, nous pouvons alors l’utiliser pour établir exactement comment le corps va bouger.

Notez que si à partir des conditions du problème il est en principe possible de trouver la loi du mouvement, alors cela signifie automatiquement qu'il est possible de construire une fonctionnelle qui prend une valeur extrême pour le mouvement vrai.

Dans nous avons brièvement examiné l'un des plus remarquables principes physiques- le principe de moindre action, et s'est arrêté sur un exemple qui semblait le contredire. Dans cet article, nous examinerons ce principe un peu plus en détail et verrons ce qui se passe dans dans cet exemple.

Cette fois, nous aurons besoin d'un peu plus de mathématiques. Cependant, j'essaierai à nouveau de présenter l'essentiel de l'article dans niveau élémentaire. Un peu plus strict et moments difficiles Je les surlignerai en couleur ; vous pouvez les ignorer sans compromettre la compréhension de base de l'article.

Conditions aux limites
Nous commencerons par l'objet le plus simple : une balle se déplaçant librement dans l'espace, sur laquelle aucune force n'agit. Comme on le sait, une telle balle se déplace de manière uniforme et rectiligne. Pour simplifier, supposons qu'il se déplace le long de l'axe

Pour décrire avec précision son mouvement, en règle générale, les conditions initiales sont spécifiées. Par exemple, il est précisé qu'à l'instant initial

le ballon était au point

avec coordonnées

et avait de la vitesse

Après avoir précisé les conditions initiales sous cette forme, on détermine de manière unique mouvement ultérieur balle - elle se déplacera à une vitesse constante et sa position à un moment donné

sera égal à la position initiale plus la vitesse multipliée par le temps écoulé :

Cette façon de régler conditions initiales très naturel et intuitif. Nous avons spécifié toutes les informations nécessaires sur le mouvement de la balle au moment initial, puis son mouvement est déterminé par les lois de Newton.

Cependant, ce n'est pas le seul moyen précisant le mouvement du ballon. Une autre manière alternative consiste à définir la position de la balle à deux moments différents.

Ceux. demande ça :
1) à l'heure actuelle

le ballon était au point

(avec coordonnées

);
2) à l'heure actuelle

le ballon était au point

(avec coordonnées

L'expression "était à un moment donné"

"ne veut pas dire que le ballon était au repos au point

À un moment donné

il pouvait voler à travers le point

Cela signifie que sa position à l'instant

coïncidait avec le point

La même chose s'applique au point

Ces deux conditions déterminent également de manière unique le mouvement de la balle. Son mouvement est facile à calculer. Pour satisfaire aux deux conditions, la vitesse de la balle doit évidemment être

La position du ballon à un moment donné

sera à nouveau égal à la position initiale plus la vitesse multipliée par le temps écoulé :

Notez que dans les conditions de la tâche, nous n'avons pas eu besoin de préciser vitesse initiale. Elle a été déterminée uniquement à partir des conditions 1) et 2).

Définir les conditions de la deuxième manière semble inhabituel. On ne sait peut-être pas pourquoi il serait nécessaire de leur demander sous cette forme. Cependant, dans le principe de moindre action, des conditions sous la forme de 1) et 2) sont utilisées, et non sous la forme d'une tâche. position initiale et la vitesse initiale.

Chemin avec le moins d'action.
Maintenant, faisons une petite pause avec la réalité libre circulation balle et considérons le problème purement mathématique suivant. Disons que nous avons une balle que nous pouvons déplacer manuellement comme bon nous semble. Dans ce cas, nous devons remplir les conditions 1) et 2). Ceux. dans le temps entre

nous devons le déplacer du point

Cela peut être fait complètement de différentes manières. Nous appellerons chacune de ces méthodes la trajectoire du mouvement de la balle et elle peut être décrite par une fonction de la position de la balle en fonction du temps.

Traçons plusieurs de ces trajectoires sur un graphique de la position de la balle en fonction du temps :

Par exemple, nous pouvons déplacer la balle avec la même vitesse égale à

(trajectoire verte). Ou nous pouvons garder le cap la moitié du temps

Et puis avancez vers le point à double vitesse

(trajectoire bleue). Vous pouvez d'abord le déplacer dans la direction opposée

côté, puis déplacez-le vers

(trajectoire marron). Vous pouvez le déplacer d'avant en arrière (chemin rouge). En général, vous pouvez le déplacer comme bon vous semble, à condition que les conditions 1) et 2) soient remplies.

À chacune de ces trajectoires, nous pouvons associer un numéro. Dans notre exemple, c'est à dire en l'absence de toute force agissant sur le ballon, ce nombre est égal à l'énergie cinétique totale accumulée pour toute la durée de son mouvement dans la période comprise entre

et s'appelle l'action.

DANS dans ce cas le mot énergie cinétique « accumulée » ne rend pas le sens très précis. En réalité, l’énergie cinétique n’est accumulée nulle part ; l’accumulation sert uniquement à calculer l’action sur la trajectoire. En mathématiques, il existe un très bon concept pour une telle accumulation : l’intégrale :

L'action est généralement indiquée par la lettre

signifie énergie cinétique. Cette intégrale signifie que l'action est égale à l'énergie cinétique accumulée de la balle sur la période de temps allant de

A titre d'exemple, prenons une balle de masse 1 kg, définissons quelques conditions aux limites et calculons l'action pour deux trajectoires différentes. Laissons le point

est à une distance de 1 mètre du point

éloigné du temps

pendant 1 seconde. Ceux. nous devons déplacer la balle qui, au moment initial, était au point

En une seconde à une distance de 1 m le long de l'axe

Dans le premier exemple (trajectoire verte), nous avons déplacé la balle uniformément, c'est-à-dire à la même vitesse, qui doit évidemment être égale à :

MS. L'énergie cinétique de la balle à chaque instant est égale à :

1/2 J. En une seconde, 1/2 J s'accumulera

avec l'énergie cinétique. Ceux. l'action pour une telle trajectoire est égale à :

Maintenant, ne déplaçons pas immédiatement le ballon du point

Et restons là pendant une demi-seconde

Et puis, dans le temps restant, nous le déplacerons uniformément jusqu'au point

Durant la première demi-seconde, la balle est au repos et son énergie cinétique est nulle. La contribution à l’action de cette partie de la trajectoire est donc également nulle. La seconde moitié d'une seconde, nous déplaçons la balle à double vitesse :

MS. L'énergie cinétique sera égale à

2 J. La contribution de cette période de temps à l'action sera égale à 2 J fois une demi-seconde, soit 1J

Avec. C'est pourquoi action générale pour une telle trajectoire, il s'avère que c'est

De même, toute autre trajectoire avec les conditions aux limites 1) et 2) données par nos soins correspond à un certain nombre égal à l'action pour cette trajectoire. Parmi toutes ces trajectoires, il existe une trajectoire qui comporte le moins d’action. On peut prouver que cette trajectoire est la trajectoire verte, c'est-à-dire mouvement uniforme du ballon. Pour toute autre trajectoire, aussi délicate soit-elle, l'action sera supérieure à 1/2.

En mathématiques, une telle cartographie pour chaque fonction un certain nombre appelé fonctionnel. Très souvent, en physique et en mathématiques, des problèmes similaires aux nôtres surviennent, c'est-à-dire trouver une fonction pour laquelle la valeur d’une certaine fonctionnelle est minimale. Par exemple, l'une des tâches qui avait une grande importance importance historique car le développement des mathématiques est une tâche concernant bachistochrone. Ceux. trouver la courbe le long de laquelle la balle roule le plus rapidement. Encore une fois, chaque courbe peut être représentée par une fonction h(x), et chaque fonction peut être associée à un nombre, en l'occurrence le temps de faire rouler la balle. Là encore, le problème revient à trouver une fonction pour laquelle la valeur de la fonctionnelle est minimale. La branche des mathématiques qui traite de tels problèmes s’appelle le calcul des variations.

Principe de moindre action.
Dans les exemples évoqués ci-dessus, nous avons deux trajectoires particulières obtenues de deux manières différentes.

La première trajectoire est obtenue à partir des lois de la physique et correspond à la trajectoire réelle d'une balle libre, sur laquelle aucune force n'agit et pour laquelle les conditions aux limites sont précisées sous la forme 1) et 2).

La deuxième trajectoire est obtenue à partir de problème mathématique trouver une trajectoire avec des conditions aux limites données 1) et 2), pour laquelle l'action est minimale.

Le principe de moindre action stipule que ces deux trajectoires doivent coïncider. En d’autres termes, si l’on sait que la balle s’est déplacée de telle manière que les conditions aux limites 1) et 2) étaient satisfaites, alors elle s’est nécessairement déplacée le long d’une trajectoire pour laquelle l’action est minime par rapport à toute autre trajectoire ayant la même limite. conditions.

On pourrait considérer cela comme une simple coïncidence. Il existe de nombreux problèmes dans lesquels apparaissent des trajectoires uniformes et des lignes droites. Cependant, le principe de moindre action s’avère être un principe très général, valable dans d’autres situations, par exemple pour le mouvement d’une balle dans un champ gravitationnel uniforme. Pour ce faire, il suffit de remplacer l’énergie cinétique par la différence entre l’énergie cinétique et potentielle. Cette différence est appelée fonction lagrangienne ou lagrangienne et l'action devient désormais égale au lagrangien total accumulé. En fait, la fonction de Lagrange contient toutes les informations nécessaires sur les propriétés dynamiques du système.

Si nous lançons une balle dans un champ de gravité uniforme de telle manière qu'elle dépasse le point

à un moment donné

et je suis arrivé au point

à un moment donné

Ensuite, selon les lois de Newton, il volera dans une parabole. C'est cette parabole qui va coïncider avec les trajectoires pour lesquelles l'action sera minime.

Ainsi, pour un corps se déplaçant dans un champ de potentiel, par exemple dans le champ gravitationnel de la Terre, la fonction de Lagrange est égale à :

Énergie cinétique

dépend de la vitesse du corps, et le potentiel dépend de sa position, c'est-à-dire coordonnées

DANS mécanique analytique l'ensemble des coordonnées qui déterminent la position du système est généralement désigné par une lettre

Pour une balle se déplaçant librement dans un champ gravitationnel,

signifie coordonnées

Pour indiquer le taux de variation d’une quantité, en physique, on met très souvent simplement un point sur cette quantité. Par exemple,

désigne le taux de changement de coordonnées

Ou, en d’autres termes, la vitesse du corps dans la direction

En utilisant ces conventions, la vitesse de notre balle en mécanique analytique est notée

désigne les composantes de vitesse

Puisque la fonction de Lagrange dépend de la vitesse et des coordonnées, et peut également dépendre explicitement du temps (explicitement dépendant du temps signifie que la valeur

à différents moments, aux mêmes vitesses et positions de la balle), alors l'action s'écrit généralement comme

Pas toujours minime
Cependant, à la fin de la partie précédente, nous avons examiné un exemple où le principe de moindre action ne fonctionne clairement pas. Pour ce faire, nous avons à nouveau pris une balle libre, sur laquelle aucune force n'agit, et avons placé un mur à ressorts à côté d'elle.

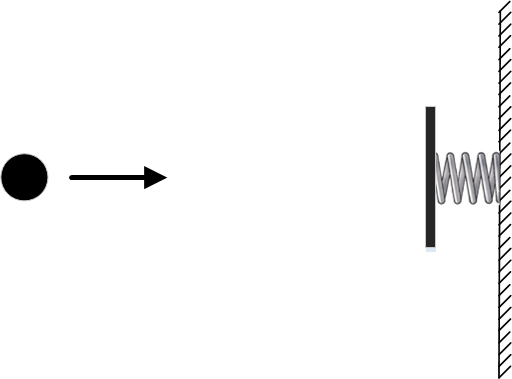
Nous fixons les conditions aux limites telles que les points

correspondre. Ceux. et en ce moment

et en ce moment

le ballon doit finir au même point

L’une des trajectoires possibles sera celle du ballon immobile. Ceux. toute la période entre

il se tiendra au point

L'énergie cinétique et potentielle dans ce cas sera égale à zéro, donc l'action pour une telle trajectoire sera également égale à zéro.

À proprement parler, l'énergie potentielle peut être considérée comme égale non pas à zéro, mais à n'importe quel nombre, puisque la différence d'énergie potentielle dans différents points espace. Cependant, la modification de la valeur de l'énergie potentielle n'affecte pas la recherche d'une trajectoire avec une action minimale. C'est juste que pour toutes les trajectoires, la valeur de l'action changera au même nombre, et la trajectoire avec l'action minimale restera la trajectoire avec l'action minimale. Pour plus de commodité, pour notre balle nous choisirons une énergie potentielle égale à zéro.

Une autre trajectoire physique possible avec les mêmes conditions aux limites serait une trajectoire dans laquelle la balle vole d'abord vers la droite, passant le point

à un moment donné

Puis il entre en collision avec un ressort, le comprime, le ressort, se redressant, repousse la balle, et elle passe à nouveau au-delà de la pointe

Vous pouvez sélectionner la vitesse de la balle pour qu'elle rebondisse sur le mur et passe le point

pile à l'heure

L'action sur une telle trajectoire sera essentiellement égale à l'énergie cinétique accumulée pendant le vol entre le point

et le mur et le dos. Il y aura une certaine période de temps pendant laquelle la balle comprimera le ressort et son énergie potentielle augmentera, et pendant cette période, l'énergie potentielle apportera une contribution négative à l'action. Mais une telle période ne sera pas très longue et ne réduira pas significativement l’effet.

La figure montre les deux trajectoires physiquement possibles du mouvement de la balle. La trajectoire verte correspond à une balle au repos, tandis que la trajectoire bleue correspond à une balle rebondissant sur un mur à ressort.

Cependant, un seul d’entre eux a un effet minime, à savoir le premier ! La deuxième trajectoire a plus d'action. Il s’avère que dans ce problème, il existe deux trajectoires physiquement possibles et une seule avec une action minimale. Ceux. Dans ce cas, le principe de moindre action ne fonctionne pas.

Points stationnaires.
Pour comprendre ce qui se passe ici, ignorons pour l'instant le principe de moindre action et passons aux fonctions ordinaires. Prenons une fonction

et tracez son graphique :

J'ai marqué sur le graphique vert quatre points particuliers. Quel est le point commun entre ces points ? Imaginons que le graphique d'une fonction soit un véritable toboggan le long duquel une balle peut rouler. Les quatre points désignés sont spéciaux dans le sens où si vous placez la balle exactement à cet endroit, elle ne roulera nulle part. À tous les autres points, par exemple au point E, il ne pourra pas rester immobile et commencera à glisser. De tels points sont appelés stationnaires. Trouver de tels points est tâche utile, puisque tout maximum ou minimum d'une fonction, s'il ne présente pas de ruptures brusques, doit nécessairement être un point stationnaire.

Si nous classons plus précisément ces points, alors le point A est le minimum absolu de la fonction, c'est-à-dire sa valeur est inférieure à toute autre valeur de fonction. Le point B n'est ni un maximum ni un minimum et est appelé point selle. Le point C est appelé maximum local, c'est-à-dire la valeur qu'il contient est supérieure à celle des points voisins de la fonction. Et le point D – minimum local, c'est-à-dire la valeur qu'il contient est inférieure à celle des points voisins de la fonction.

La recherche de tels points est effectuée par une branche des mathématiques appelée analyse mathématique. Autrement, on l’appelle parfois analyse infinitésimale, car elle peut fonctionner avec des quantités infinitésimales. Du point de vue analyse mathématique les points stationnaires ont une propriété spéciale grâce à laquelle ils sont trouvés. Pour comprendre cette propriété, nous devons comprendre à quoi ressemble la fonction à de très petites distances de ces points. Pour ce faire, nous prendrons un microscope et examinerons nos points à travers celui-ci. La figure montre à quoi ressemble la fonction à proximité de différents points à différents grossissements.

On peut voir qu'à très fort grossissement (c'est-à-dire pour de très petits écarts x), les points stationnaires se ressemblent exactement et sont très différents du point non stationnaire. Il est facile de comprendre quelle est cette différence - le graphique d'une fonction en un point stationnaire devient une ligne strictement horizontale lorsqu'il est augmenté, et en un point non stationnaire, il devient une ligne inclinée. C'est pourquoi une balle installée à un point fixe ne roulera pas.

L'horizontalité d'une fonction en un point stationnaire peut s'exprimer différemment : la fonction en un point stationnaire ne change pratiquement pas avec un très petit changement de son argument

Même comparé au changement d’argument lui-même. La fonction en un point non stationnaire avec un petit changement

change proportionnellement au changement

Et plus la pente de la fonction est grande, plus la fonction change lors du changement

En fait, à mesure que la fonction augmente, elle ressemble de plus en plus à une tangente au graphique au point en question.

Sur strict langage mathématique expression « la fonction ne change pratiquement pas au point

avec très peu de changement

" signifie que la relation entre le changement d'une fonction et le changement de son argument

tend vers 0 quand

tendant vers 0 :

$$display$$lim_(∆x à 0) frac (∆y(x_0))(∆x) = lim_(x à 0) frac (y(x_0+∆x)-y(x_0))(∆x) = 0$$affichage$$

Pour un point non stationnaire, ce rapport tend vers un nombre non nul, qui est égal à la tangente de la pente de la fonction en ce point. Ce même nombre est appelé la dérivée de la fonction en un point donné. La dérivée d'une fonction montre à quelle vitesse la fonction change autour d'un point donné lorsque petite monnaie son argument

Ainsi, les points stationnaires sont des points pour lesquels la dérivée de la fonction est égale à 0.

Trajectoires stationnaires.
Par analogie avec les points stationnaires, on peut introduire la notion de trajectoires stationnaires. Rappelons que chaque trajectoire correspond à une certaine valeur d'action, c'est-à-dire un certain nombre. Il peut alors y avoir une trajectoire telle que pour des trajectoires proches d'elle avec les mêmes conditions aux limites, les valeurs d'action correspondantes ne différeront pratiquement pas de l'action pour la trajectoire stationnaire elle-même. Une telle trajectoire est dite stationnaire. En d’autres termes, toute trajectoire proche de la stationnaire aura une valeur d’action qui diffère très peu de l’action de cette trajectoire stationnaire.

Encore une fois, en langage mathématique, « légèrement différent » signifie ce qui suit : signification exacte. Supposons que nous ayons une fonctionnalité donnée

pour les fonctions avec les conditions aux limites requises 1) et 2), c'est-à-dire

Supposons que la trajectoire

– stationnaire.

Nous pouvons prendre n'importe quelle autre fonction

De telle sorte qu'aux extrémités, il prend des valeurs nulles, c'est-à-dire

0. Prenons aussi la variable

Ce que nous ferons de moins en moins. De ces deux fonctions et une variable

on peut composer une troisième fonction

Ce qui satisfera également aux conditions aux limites

En diminuant

trajectoire, fonction correspondante

Se rapprochera de plus en plus de la trajectoire

De plus, pour les trajectoires stationnaires à petite

la valeur de la fonctionnelle pour les trajectoires

différera très peu de la valeur de la fonctionnelle pour

même par rapport à

$$display$$lim_(ε à 0) frac (S(x"(t))-S(x(t)))ε=lim_(ε à 0) frac (S(x(t)+εg(t ))-S(x(t)))ε = 0$$affichage$$

De plus, cela devrait être vrai pour toute trajectoire

Satisfaire les conditions aux limites

Un changement de fonctionnel avec un petit changement de fonction (plus précisément, la partie linéaire du changement de fonctionnel, proportionnelle au changement de fonction) est appelé une variation de fonctionnel et est noté

Le terme « calcul des variations » vient du terme « variation ».

Pour les trajectoires stationnaires, variation de la fonction

Une méthode permettant de trouver des fonctions stationnaires (non seulement pour le principe de moindre action, mais aussi pour de nombreux autres problèmes) a été trouvée par deux mathématiciens - Euler et Lagrange. Il s'avère qu'une fonction stationnaire, dont la fonctionnelle est exprimée par une intégrale similaire à l'intégrale d'action, doit satisfaire une certaine équation, désormais appelée équation d'Euler-Lagrange.

Le principe de l'action stationnaire.
La situation avec un minimum d'action pour les trajectoires est similaire à la situation avec un minimum pour les fonctions. Pour qu’une trajectoire ait le moins d’effet, il faut qu’elle soit stationnaire. Cependant, toutes les trajectoires stationnaires ne sont pas des trajectoires d’action minimale. Par exemple, une trajectoire stationnaire peut avoir un effet minime localement. Ceux. son action sera moindre que celle de toute autre trajectoire voisine. Cependant, quelque part au loin, il peut y avoir d’autres trajectoires pour lesquelles l’action sera encore moindre.

Il s’avère que les corps réels ne suivent pas nécessairement des trajectoires avec la moindre action. Ils peuvent se déplacer le long d’un ensemble plus large de trajectoires spéciales, à savoir des trajectoires stationnaires. Ceux. la trajectoire réelle du corps sera toujours stationnaire. Par conséquent, le principe de moindre action est plus correctement appelé principe d’action stationnaire. Cependant, selon la tradition établie, on l’appelle souvent le principe de moindre action, impliquant donc non seulement la minimalité, mais aussi la stationnarité des trajectoires.

Nous pouvons désormais écrire le principe de l'action stationnaire en langage mathématique, tel qu'il est habituellement écrit dans les manuels :

Ce sont des coordonnées généralisées, c'est-à-dire un ensemble de nombres qui définit de manière unique la position du système.

Taux de changement des coordonnées généralisées.

Une fonction de Lagrange qui dépend des coordonnées généralisées, de leurs vitesses et éventuellement du temps.

Une action qui dépend de la trajectoire spécifique du système (c'est-à-dire

Les trajectoires réelles du système sont stationnaires, c'est-à-dire pour eux une variation de l'action

Si l'on revient à l'exemple avec une balle et une paroi élastique, alors l'explication de cette situation devient désormais très simple. Pour donné conditions aux limites que le ballon devrait et pendant

et pendant

être au point

il y a deux trajectoires stationnaires. Et la balle peut réellement suivre n’importe laquelle de ces trajectoires. Pour sélectionner explicitement l'une des trajectoires, vous pouvez imposer au mouvement de la balle condition supplémentaire. Par exemple, disons que la balle doit rebondir sur le mur. La trajectoire sera alors déterminée sans ambiguïté.

Certaines conséquences remarquables découlent du principe de moindre action (plus précisément stationnaire), dont nous discuterons dans la partie suivante.