પરીક્ષામાં અપૂર્ણાંક સાથેની ક્રિયાઓ. બીજગણિત - OGE

વિષય પર કાર્ય નંબર 1 નું વિશ્લેષણ: "અપૂર્ણાંકો સાથેની કામગીરી: ગુણાકાર અને બાદબાકી, અયોગ્ય અપૂર્ણાંકથી સમગ્ર ભાગને અલગ કરીને, વ્યસ્ત કામગીરી"

વધારાની સામગ્રી
પ્રિય વપરાશકર્તાઓ, તમારી ટિપ્પણીઓ, સમીક્ષાઓ, શુભેચ્છાઓ આપવાનું ભૂલશો નહીં! એન્ટી-વાયરસ પ્રોગ્રામ દ્વારા તમામ સામગ્રીની તપાસ કરવામાં આવી છે.

ગ્રેડ 9 માટે ઇન્ટિગ્રલ ઑનલાઇન સ્ટોરમાં શૈક્ષણિક સહાય અને સિમ્યુલેટર
સંયોજનશાસ્ત્ર અને સંભાવના સિદ્ધાંત સમીકરણો અને અસમાનતા

મિત્રો, કાર્ય નંબર 1 એવા વિષયોને આવરી લે છે જે મુખ્યત્વે ગ્રેડ 5-6માં આવરી લેવામાં આવે છે.

માટે યોગ્ય નિર્ણય આ સોંપણીનીઆવશ્યક કુશળતા:

• સરળ અને દશાંશ અપૂર્ણાંક સાથે કામ કરો,
• સરળ અપૂર્ણાંકને દશાંશમાં કન્વર્ટ કરો અને તેનાથી વિપરીત,
• સંખ્યાઓને સંપૂર્ણ શક્તિઓ સુધી વધારવી,
• અને તર્કસંગત અને વાસ્તવિક સંખ્યાઓની વિભાવનાઓને સમજવી.

પાઠ કે જે તમને આ સોંપણી તૈયાર કરવામાં મદદ કરશે:

ચાલો તમે જે કાર્યોનો સામનો કરી શકો તેના ઉદાહરણો પર વિગતવાર જોઈએ.

ઉદાહરણ 1.
આ ઉદાહરણમાં અપૂર્ણાંકનો ગુણાકાર અને બાદબાકી કરવાની, અયોગ્ય અપૂર્ણાંકમાંથી સમગ્ર ભાગને અલગ કરવાની અને વ્યસ્ત કામગીરી કરવાની ક્ષમતાની જરૂર પડશે.
નીચેના અભિવ્યક્તિની કિંમત શોધો: $1\frac(2)(5)*2\frac(2)(3)-1\frac(2)(3)*3\frac(1)(2)$.

ઉકેલ.
મિત્રો, ચાલો નિર્ણયને ઘણી ક્રિયાઓમાં તોડીએ. પ્રથમ વસ્તુ જે આપણે જાણીએ છીએ તે એ છે કે આપણે આખા ભાગો સાથે અપૂર્ણાંકનો ગુણાકાર કેવી રીતે કરવો તે જાણતા નથી. આનો અર્થ એ છે કે આપણે દરેક અપૂર્ણાંકને અયોગ્ય અપૂર્ણાંકમાં રૂપાંતરિત કરવાની જરૂર છે.
1. ચાલો આપણે અયોગ્ય અપૂર્ણાંકમાં રૂપાંતર કરવાનો નિયમ યાદ રાખીએ: અંશ મેળવવા માટે, આખા ભાગને છેદ વડે ગુણાકાર કરવો જોઈએ અને પરિણામી સંખ્યામાં મૂળ અપૂર્ણાંકનો અંશ ઉમેરવો જોઈએ. છેદ યથાવત રહે છે; અંશ હંમેશા છેદ કરતા મોટો હોય છે:
$1\frac(2)(5)=\frac(1*5+2)(5)=\frac(7)(5)$.
ચાલો બાકીના અપૂર્ણાંકો માટે સમાન કામગીરી કરીએ:
$\frac(7)(5)*\frac(2*3+2)(3)-\frac(1*3+2)(3)*\frac(3*2+1)(2)=\ frac(7)(5)*\frac(8)(3)-\frac(5)(3)*\frac(7)(2)$.

2. દરેક વ્યક્તિ સારી રીતે યાદ રાખે છે કે સરવાળા અને બાદબાકી પહેલા ગુણાકાર કરવામાં આવે છે. આગળ, આપણે બે અપૂર્ણાંકનો ગુણાકાર કરવાનો નિયમ યાદ રાખવાની જરૂર છે, આપણે અંશને અંશ વડે, છેદને છેદ વડે ગુણાકાર કરીએ છીએ:
$\frac(7)(5)*\frac(8)(3)-\frac(5)(3)*\frac(7)(2)=\frac(56)(15)-\frac(35) )(6)$.

3. આપણે ફક્ત બે અપૂર્ણાંક બાદ કરવાના છે. યાદ કરો કે સરવાળો અને બાદબાકી કરતી વખતે, તમારે પહેલા બે અપૂર્ણાંકનો સામાન્ય છેદ શોધવાની જરૂર છે, એટલે કે, લઘુત્તમ સામાન્ય ગુણાંક. અમારી પાસે બે છેદ છે - સંખ્યાઓ 15 અને 6. આ બે સંખ્યાઓ માટે, લઘુત્તમ સામાન્ય ગુણાંક 30 નંબર છે.
જો તમે અંશ અને છેદને સમાન સંખ્યા વડે ગુણાકાર કરશો, તો અપૂર્ણાંકનું મૂલ્ય બદલાશે નહીં.
$\frac(56)(15)-\frac(35)(6)=\frac(56*2)(15*2)-\frac(35*5)(6*5)=\frac(112) (30)-\frac(175)(30)=-\frac(63)(30)$.

4. આપણે માત્ર અનુવાદ કરવાનું છે સામાન્ય અપૂર્ણાંકદશાંશ માટે, કારણ કે OGE જવાબ ફોર્મમાં, આપણે દશાંશ સ્વરૂપમાં સંખ્યાઓ લખી શકીએ છીએ.
આખો ભાગ પસંદ કરો અને પછી અપૂર્ણાંક ઓછો કરો.
$-\frac(63)(30)=-2\frac(3)(30)=-2\frac(1)(10)=-2.1$.

ચાલો ફરીથી ઉકેલ લખીએ:
$1\frac(2)(5)*2\frac(2)(3)-1\frac(2)(3)*3\frac(1)(2)=\frac(1*5+2)( 5)*\frac(2*3+2)(3)-\frac(1*3+2)(3)*\frac(3*2+1)(2)=\frac(7)(5) *\frac(8)(3)-\frac(5)(3)*\frac(7)(2)=$ $=\frac(56)(15)-\frac(35)(6)=\ frac(56*2)(15*2)-\frac(35*5)(6*5)=\frac(112)(30)-\frac(175)(30)=-\frac(63)( 30)=-2\frac(3)(30)=-2\frac(1)(10)=-2.1$.
જવાબ: $-2.1$.

ઉદાહરણ 2.
$0.007*0.00007*700$ અભિવ્યક્તિની કિંમતની ગણતરી કરો.

ઉકેલ.
આ ઉદાહરણમાં, આપણે તેને બે રીતે કરી શકીએ છીએ: 1) બધી સંખ્યાઓને "સીધી રીતે" ગુણાકાર કરો; 2) પૂર્ણાંક શક્તિ વધારવાના વિષયના જ્ઞાનનો ઉપયોગ કરો.

1. તમારે પ્રથમ વસ્તુ પર ધ્યાન આપવું જોઈએ કે દરેક નંબરમાં નંબર 7 હોય છે. આ એક કારણસર કરવામાં આવ્યું હતું. ચાલો પ્રસ્તુત અપૂર્ણાંક સંખ્યાઓને સરળ બનાવવાનો પ્રયાસ કરીએ. તમે ઉત્પાદન તરીકે 0.007 નંબરને કેવી રીતે રજૂ કરી શકો છો? $0.007=0.001*7$.

અપૂર્ણાંકોને સરળ બનાવવામાં ડરશો નહીં. જો શરૂઆતમાં અપૂર્ણાંક સંખ્યાત્યાં બધા શૂન્ય છે, અને આ અપૂર્ણાંક ચોક્કસ સંખ્યા સાથે સમાપ્ત થાય છે, પછી તે હંમેશા ઉત્પાદન તરીકે રજૂ કરી શકાય છે.
ઉદાહરણ તરીકે: $0.0256=0.0001*256$; $0.00008=0.00001*8$; $0.3562=0.0001*3562$.
મુખ્ય વસ્તુ પરિણામી અપૂર્ણાંકમાં અંકોની સંખ્યા જાળવવી છે.
$0,007*0,00007*700=0,001*7*0,00001*7*7*100$.

2. આગળ, સંખ્યાને સંપૂર્ણ શક્તિ સુધી વધારવા માટે આપણને જ્ઞાન અને ક્ષમતાની જરૂર પડશે.
જો આપણને એક અપૂર્ણાંક આપવામાં આવે જેમાં બધા શૂન્ય હોય અને તે એક સાથે સમાપ્ત થાય, તો તે હંમેશા નંબર 10 તરીકે રજૂ કરી શકાય છે. નકારાત્મક ડિગ્રી. વધુમાં, એક પહેલા શૂન્યની સંખ્યા દસની ઘાત હશે. ચાલો આપણા ઉદાહરણમાં સંખ્યાઓ પર નજીકથી નજર કરીએ. $0.001=10^(-3)$, એકની આગળ ત્રણ શૂન્ય છે, જેનો અર્થ છે કે ત્રણ દસની ઘાત હશે, માત્ર માઈનસ મૂકવાનું ભૂલશો નહીં.
$0.00001=10^(-5)$, એકની આગળ પાંચ શૂન્ય છે, જેનો અર્થ છે કે પાંચ દસની ઘાત હશે.

પરિવર્તન પછી આપણને મળે છે: $0.001*7*0.00001*7*7*100=10^(-3)*7*10^(-5)*7*7*100$.

3. આપણે માત્ર 100 નંબરને સંખ્યા તરીકે પાવરમાં કન્વર્ટ કરવાનું છે. જો કોઈ સંખ્યામાં પ્રથમ સ્થાન એક છે, અને અન્ય તમામ અંકો શૂન્ય છે, તો આવી કોઈપણ સંખ્યાને 10 ની શક્તિ તરીકે રજૂ કરી શકાય છે, અને દસની શક્તિ શૂન્યની સંખ્યા સાથે એકરુપ હશે.
ઉદાહરણ તરીકે: $10000=10^4$; $1000000=10^6$.
અમને મળે છે: $10^(-3)*7*10^(-5)*7*7*10^2=7*7*7*10^(-3)*10^(-5)*10^2 $.
આપણે પરિણામી સંખ્યાઓને કયા ક્રમમાં ગુણાકાર કરીએ છીએ તેનાથી કોઈ ફરક પડતો નથી. પૂર્ણાંક ઘાતાંક સાથે સંખ્યાઓનો ગુણાકાર કરતી વખતે અને સમાન આધાર- ડિગ્રીનો આધાર એ જ રહે છે, અને સૂચકાંકો ઉમેરવામાં આવે છે.
$7*7*7*10^{-3}*10^{-5}*10^2=243*{10}^{-3-5+2}=243*10^{-6}$.

4. પોઈન્ટ બે થી વિપરીત ઓપરેશન કરવાનું બાકી છે. દસની ઘાતમાં આપણી પાસે -6 છે, જેનો અર્થ છે કે સંખ્યા અપૂર્ણાંક હશે, કારણ કે બાદબાકી એટલે આપણી સંખ્યામાં છ શૂન્ય હશે.
$243*10^{-6}=243*0,000001=0,000243$.

ચાલો ફરીથી ઉકેલ લખીએ: $0.007*0.00007*700=0.001*7*0.00001*7*7*100=10^(-3)*7*10^(-5)*7*7*10^2 =$ $=7*7*7*10^(-3)*10^(-5)*10^2=243*10^(-3-5+2)=243*10^(-6)= 243* 0.000001=$0.000243.
જવાબ: $0.000243$.

ઉદાહરણ 3.
અભિવ્યક્તિનું મૂલ્ય શોધો: $6.3*1.8-3.6*2.1$.

ઉકેલ.
જો તમે કૉલમમાં અપૂર્ણાંક સંખ્યાઓનો ગુણાકાર કરવામાં સારા છો, તો આ ઉદાહરણનો ઉકેલ આવી શકે છે. અમે માથા પર ગણતરી કરીએ છીએ આ ઉદાહરણઅમે નહીં કરીએ, પરંતુ અમે અન્ય બે ઉકેલો આપીશું.

પદ્ધતિ 1. જો તમે કૉલમમાં અપૂર્ણાંકનો ગુણાકાર કરવામાં ખૂબ જ સારા ન હોવ, તો તમે મૂળ અભિવ્યક્તિને સો વડે ગુણાકાર કરી શકો છો, પરંતુ સૌથી અગત્યનું, પછી ફરીથી સો વડે ભાગવાનું ભૂલશો નહીં.
$\frac((6.3*1.8-3.6*2.1)*100)(100)=\frac(63*18-36*21)(100)=\frac(1134-756) (100)=\frac(378) )(100)$.
ચાલો પરિણામી સંખ્યાને 100 વડે વિભાજીત કરીએ, જે એકદમ સરળ છે, કારણ કે આપણી પાસે બે શૂન્ય છે, તો અપૂર્ણાંક સંખ્યાનો દશાંશ બિંદુ 2 અંકોથી જમણેથી ડાબે બદલાશે.
$\frac(378)(100)=$3.78.

પદ્ધતિ 2. તમે નોંધ કરી શકો છો કે મૂળ સંખ્યાઓ સમાન પરિબળો ધરાવે છે, એટલે કે, પ્રસ્તુત સંખ્યાઓમાંથી દરેક પૂર્ણાંક અને અપૂર્ણાંકના ગુણાંક તરીકે રજૂ થવી જોઈએ.
$6,3=7*0,9$.
$1,8=6*0,3$.
$3,6=6*0,6$.
$2,1=7*0,3$.
$6.3*1.8-3.6*2.1=7*0.9*6*0.3-6*0.6*7*0.3=42*0.27-42*0, 18=$ $=4*(0.27-0.18)=42*0.09=\ frac(42*9)(100)=\frac(378)(100)=$3.78.
ઉકેલની પસંદગી ફક્ત તમારી પસંદગીઓ પર આધારિત છે.

ઉદાહરણ 4.
સાચી સમાનતાઓની સંખ્યા લખો:
1) $2*\frac(1)(3)-\frac(1)(4)=\frac(1)(6)$.
2) $\frac( \frac(11)(14))(3\frac(1)(7))=0.25$.
3) $1.75-2\frac(1)(3)=-\frac(7)(12)$.
4) $\frac(1.6)(\frac(\frac(2)(3))(\frac(5)(6)))=4$.

ઉકેલ.
દરેક અભિવ્યક્તિને તપાસવા સિવાય અમારી પાસે કોઈ વિકલ્પ નથી.

1) આ ઉદાહરણમાં, આપણે યાદ રાખવું જોઈએ કે પૂર્ણાંકને અપૂર્ણાંક વડે ગુણાકાર કરવો તે અપૂર્ણાંક જેટલો પ્રકાશિત થાય છે તે સમાન નથી. આખો ભાગ. ચાલો આ ઉદાહરણ ઉકેલીએ.
$2*\frac(1)(3)-\frac(1)(4)=\frac(2)(1)*\frac(1)(3)-\frac(1)(4)=\frac( 2)(3)-\frac(1)(4)=\frac(2*4)(3*4)-\frac(1*3)(4*3)=\frac(8)(12)- \frac(3)(12)=\frac(5)(12)$.
અમને જાણવા મળ્યું કે પ્રસ્તુત સમાનતા સાચી નથી.

2) સૌ પ્રથમ, તમારે સંપૂર્ણ ભાગમાંથી છુટકારો મેળવવાની જરૂર છે, અને પછી અપૂર્ણાંકને વિભાજીત કરવા માટેના નિયમનો ઉપયોગ કરો. $\frac(\frac(11)(14))(3\frac(1)(7))=\frac(\frac(11)(14))(\frac(3*7+1)(7) )=\frac(\frac(11)(14))(\frac(22)(7))=\frac(11)(14)*\frac(7)(22)$.
હવે આપણે અપૂર્ણાંક ઘટાડવા માટે નિયમનો ઉપયોગ કરી શકીએ છીએ.
$\frac(11)(14)*\frac(7)(22)=\frac(1)(2)*\frac(1)(2)=\frac(1)(4)$.
પરિણામી અપૂર્ણાંકને દશાંશમાં રૂપાંતરિત કરવાનું બાકી છે.
$\frac(1)(4)=0.25$.
અમને સાચી સમાનતા મળી છે.

3) આ ઉદાહરણમાં, પ્રથમ, આપણે અનુવાદ કરવાની જરૂર છે દશાંશસામાન્ય સુધી. $1.75=1\frac(75)(100)=1\frac(3)(4)$.
હવે ચાલો આખા ભાગમાંથી છુટકારો મેળવીએ અને અયોગ્ય અપૂર્ણાંક મેળવીએ: $1\frac(3)(4)-2\frac(1)(3)=\frac(7)(4)-\frac(7)(3) )$.
ચાલો બે અપૂર્ણાંક બાદ કરીએ: $\frac(7)(4)-\frac(7)(3)=\frac(21)(12)-\frac(28)(12)=-\frac(7)(12) ) )$.
અમને સાચી સમાનતા મળી છે.

ચાલો ફરીથી ઉકેલ લખીએ:
$1.75-2\frac(1)(3)=1\frac(3)(4)-2\frac(1)(3)=\frac(7)(4)-\frac(7)(3 )= \frac(21)(12)-\frac(28)(12)=-\frac(7)(12)$.

4) ફરીથી, ચાલો દશાંશ અપૂર્ણાંકમાંથી સામાન્ય અપૂર્ણાંક તરફ જઈએ.
$1.6=1\frac(6)(10)=\frac(16)(10)$.
અમને સારી રીતે યાદ છે કે પ્રથમ ક્રિયા કૌંસમાં કરવામાં આવે છે.
$\frac(\frac(2)(3))(\frac(5)(6))=\frac(2)(3)*\frac(6)(5)=\frac(2)(1) *\frac(2)(5)=\frac(4)(5)$.
ચાલો કૌંસની બહાર વિભાજન કરીએ: $\frac(\frac(16)(10))(\frac(4)(5))=\frac(16)(10)*\frac(5)(4)= \frac( 4)(2)*\frac(1)(1)=2$.
અમને જાણવા મળ્યું કે મૂળ સમાનતા ખોટી છે.
જવાબ: 23.

ઉદાહરણ 5.
અભિવ્યક્તિઓનો અર્થ શોધો. તમારા જવાબમાં, મળેલ સૌથી મોટું મૂલ્ય સૂચવો.
1) $1.8-\frac(3)(5)$.
2) $\frac(1\frac(1)(3))(\frac(1)(6))$.
3) $\frac(0.8+0.3)(1.2)$.
ઉકેલ.

1) ચાલો દશાંશ અપૂર્ણાંક તરફ આગળ વધીએ.
$1.8-\frac(3)(5)=1.8-0.6=1.2$.

2) ચાલો અયોગ્ય અપૂર્ણાંક તરફ આગળ વધીએ અને અપૂર્ણાંકને વિભાજીત કરીએ. $\frac(1\frac(1)(3))(\frac(1)(6))=\frac(\frac(4)(3))(\frac(1)(6))=\frac (4)(3)*\frac(6)(1)=\frac(4)(1)*2=8$.

3) ચાલો અપૂર્ણાંકના અંશમાં ઉમેરીએ. $\frac(0.8+0.3)(1.2)=\frac(1.1)(1.2)=\frac(1.1*10)(1.2*0)=\frac (11)(12)$.
તમારે ફક્ત પસંદ કરવાનું છે સૌથી મોટો ઉકેલ, દેખીતી રીતે તે 8 હશે.
જવાબ: 8.

એલેક્ઝાંડર શબાલિન

અપૂર્ણાંક સાથેની ક્રિયાઓ. આ લેખમાં આપણે ઉદાહરણો જોઈશું, સ્પષ્ટતા સાથે બધું વિગતવાર. અમે સામાન્ય અપૂર્ણાંકોને ધ્યાનમાં લઈશું. આપણે દશાંશને પછીથી જોઈશું. હું આખી વસ્તુ જોવાની અને ક્રમિક રીતે તેનો અભ્યાસ કરવાની ભલામણ કરું છું.

1. અપૂર્ણાંકનો સરવાળો, અપૂર્ણાંકનો તફાવત.

નિયમ: સમાન છેદ સાથે અપૂર્ણાંક ઉમેરતી વખતે, પરિણામ એ અપૂર્ણાંક છે - જેનો છેદ સમાન રહે છે, અને તેનો અંશ હશે સરવાળો સમાનઅપૂર્ણાંકના અંશ.

નિયમ: સાથે અપૂર્ણાંકના તફાવતની ગણતરી કરતી વખતે સમાન છેદઆપણને અપૂર્ણાંક મળે છે - છેદ એ જ રહે છે, અને બીજાના અંશને પ્રથમ અપૂર્ણાંકના અંશમાંથી બાદ કરવામાં આવે છે.

સમાન છેદ સાથે અપૂર્ણાંકના સરવાળા અને તફાવત માટે ઔપચારિક સંકેત:

ઉદાહરણો (1):

તે સ્પષ્ટ છે કે જ્યારે સામાન્ય અપૂર્ણાંક આપવામાં આવે છે, ત્યારે બધું સરળ છે, પરંતુ જો તેઓ મિશ્રિત હોય તો શું? કંઈ જટિલ નથી...

વિકલ્પ 1- તમે તેમને સામાન્યમાં રૂપાંતરિત કરી શકો છો અને પછી તેમની ગણતરી કરી શકો છો.

વિકલ્પ 2- તમે પૂર્ણાંક અને અપૂર્ણાંક ભાગો સાથે અલગથી "કામ" કરી શકો છો.

ઉદાહરણો (2):

વધુ:

જો બે મિશ્ર અપૂર્ણાંકનો તફાવત આપવામાં આવે અને પ્રથમ અપૂર્ણાંકનો અંશ બીજાના અંશ કરતાં ઓછો હોય તો શું? તમે બે રીતે પણ કાર્ય કરી શકો છો.

ઉદાહરણો (3):

*સામાન્ય અપૂર્ણાંકમાં રૂપાંતરિત, તફાવતની ગણતરી કરી, પરિણામી અયોગ્ય અપૂર્ણાંકને મિશ્ર અપૂર્ણાંકમાં રૂપાંતરિત કર્યા.

*અમે તેને પૂર્ણાંક અને અપૂર્ણાંક ભાગોમાં તોડી નાખ્યા, ત્રણ મેળવ્યા, પછી 3 ને 2 અને 1 ના સરવાળા તરીકે રજૂ કર્યા, જેમાં એક 11/11 તરીકે રજૂ કર્યો, પછી 11/11 અને 7/11 વચ્ચેનો તફાવત શોધી કાઢ્યો અને પરિણામની ગણતરી કરી. . ઉપરોક્ત રૂપાંતરણોનો અર્થ એ છે કે એકમ લેવા (પસંદ કરો) અને તેને અપૂર્ણાંકના રૂપમાં આપણને જોઈતા છેદ સાથે રજૂ કરીએ, પછી આપણે આ અપૂર્ણાંકમાંથી બીજાને બાદ કરી શકીએ.

બીજું ઉદાહરણ:

નિષ્કર્ષ: ત્યાં એક સાર્વત્રિક અભિગમ છે - સમાન છેદ સાથે મિશ્ર અપૂર્ણાંકના સરવાળા (તફાવત) ની ગણતરી કરવા માટે, તેઓ હંમેશા અયોગ્ય રાશિઓમાં રૂપાંતરિત થઈ શકે છે, પછી પ્રદર્શન કરો જરૂરી કાર્યવાહી. આ પછી, જો પરિણામ અયોગ્ય અપૂર્ણાંક છે, તો અમે તેને મિશ્ર અપૂર્ણાંકમાં રૂપાંતરિત કરીએ છીએ.

ઉપર આપણે એવા અપૂર્ણાંકો સાથેના ઉદાહરણો જોયા કે જેમાં સમાન છેદ હોય. જો છેદ અલગ હોય તો શું? આ કિસ્સામાં, અપૂર્ણાંક સમાન છેદમાં ઘટાડવામાં આવે છે અને નીચે આપેલ સાચું છે: ઉલ્લેખિત ક્રિયા. અપૂર્ણાંકને બદલવા (રૂપાંતર) કરવા માટે, અપૂર્ણાંકના મૂળ ગુણધર્મનો ઉપયોગ થાય છે.

ચાલો સરળ ઉદાહરણો જોઈએ:

આ ઉદાહરણોમાં, આપણે તરત જ જોઈ શકીએ છીએ કે કેવી રીતે અપૂર્ણાંકોમાંથી એકને સમાન છેદ મેળવવા માટે રૂપાંતરિત કરી શકાય છે.

જો આપણે અપૂર્ણાંકને સમાન છેદમાં ઘટાડવાની રીતો નિયુક્ત કરીએ, તો આપણે તેને કહીશું પદ્ધતિ એક.

એટલે કે, જ્યારે કોઈ અપૂર્ણાંકનો "અંદાજ" કરો, ત્યારે તમારે આ અભિગમ કામ કરશે કે કેમ તે શોધવાની જરૂર છે - અમે તપાસીએ છીએ કે મોટા છેદ નાના દ્વારા વિભાજ્ય છે કે કેમ. અને જો તે વિભાજ્ય હોય, તો આપણે રૂપાંતર કરીએ છીએ - આપણે અંશ અને છેદનો ગુણાકાર કરીએ છીએ જેથી બંને અપૂર્ણાંકના છેદ સમાન બને.

હવે આ ઉદાહરણો જુઓ:

આ અભિગમ તેમને લાગુ પડતો નથી. અપૂર્ણાંકને ઘટાડવાની અન્ય રીતો છે સામાન્ય છેદ, ચાલો તેમને ધ્યાનમાં લઈએ.

પદ્ધતિ TWO.

અમે પ્રથમ અપૂર્ણાંકના અંશ અને છેદને બીજાના છેદ દ્વારા અને બીજા અપૂર્ણાંકના અંશ અને છેદને પ્રથમના છેદ દ્વારા ગુણાકાર કરીએ છીએ:

*હકીકતમાં, જ્યારે છેદ સમાન બને છે ત્યારે આપણે અપૂર્ણાંકને ઘટાડીએ છીએ. આગળ, આપણે સમાન છેદ સાથે અપૂર્ણાંક ઉમેરવા માટે નિયમનો ઉપયોગ કરીએ છીએ.

ઉદાહરણ:

*આ પદ્ધતિને સાર્વત્રિક કહી શકાય, અને તે હંમેશા કામ કરે છે. એકમાત્ર નુકસાન એ છે કે ગણતરીઓ પછી તમે અપૂર્ણાંક સાથે સમાપ્ત થઈ શકો છો જેને વધુ ઘટાડવાની જરૂર પડશે.

ચાલો એક ઉદાહરણ જોઈએ:

તે જોઈ શકાય છે કે અંશ અને છેદ 5 વડે વિભાજ્ય છે:

પદ્ધતિ ત્રણ.

તમારે છેદના ઓછામાં ઓછા સામાન્ય બહુવિધ (LCM) શોધવાની જરૂર છે. આ સામાન્ય છેદ હશે. આ કયા પ્રકારનો નંબર છે? આ સૌથી ઓછું છે કુદરતી સંખ્યા, જે દરેક સંખ્યા દ્વારા વિભાજ્ય છે.

જુઓ, અહીં બે સંખ્યાઓ છે: 3 અને 4, એવી ઘણી સંખ્યાઓ છે જે તેમના દ્વારા વિભાજ્ય છે - આ છે 12, 24, 36, ... તેમાંથી સૌથી નાની સંખ્યા 12 છે. અથવા 6 અને 15, તે 30 વડે વિભાજ્ય છે, 60, 90.... ન્યૂનતમ 30 છે. પ્રશ્ન એ છે કે - આ લઘુત્તમ સામાન્ય ગુણાંક કેવી રીતે નક્કી કરવો?

ત્યાં એક સ્પષ્ટ અલ્ગોરિધમનો છે, પરંતુ ઘણીવાર આ ગણતરીઓ વિના તરત જ કરી શકાય છે. ઉદાહરણ તરીકે, ઉપરોક્ત ઉદાહરણો અનુસાર (3 અને 4, 6 અને 15) કોઈ અલ્ગોરિધમની જરૂર નથી, અમે મોટી સંખ્યાઓ (4 અને 15) લીધી, તેમને બમણી કરી અને જોયું કે તેઓ બીજી સંખ્યા દ્વારા વિભાજ્ય છે, પરંતુ સંખ્યાઓની જોડી અન્ય બનો, ઉદાહરણ તરીકે 51 અને 119.

અલ્ગોરિધમ. અનેક સંખ્યાઓનો લઘુત્તમ સામાન્ય ગુણાંક નક્કી કરવા માટે, તમારે:

- દરેક સંખ્યાને તેમાં વિઘટન કરો સરળ પરિબળો

- તેમાંથી મોટાનું વિઘટન લખો

- તેને અન્ય સંખ્યાઓના ખૂટતા પરિબળો દ્વારા ગુણાકાર કરો

ચાલો ઉદાહરણો જોઈએ:

50 અને 60 => 50 = 2∙5∙5 60 = 2∙2∙3∙5

વિઘટન માં વધુએક પાંચ ખૂટે છે

=> LCM(50,60) = 2∙2∙3∙5∙5 = 300

48 અને 72 => 48 = 2∙2∙2∙2∙3 72 = 2∙2∙2∙3∙3

મોટી સંખ્યાના વિસ્તરણમાં બે અને ત્રણ ખૂટે છે

=> LCM(48.72) = 2∙2∙2∙2∙3∙3 = 144

* બેનો ઓછામાં ઓછો સામાન્ય ગુણાંક અવિભાજ્ય સંખ્યાઓતેમના ઉત્પાદન સમાન

પ્રશ્ન! શા માટે ઓછામાં ઓછા સામાન્ય બહુવિધ શોધવા ઉપયોગી છે, કારણ કે તમે બીજી પદ્ધતિનો ઉપયોગ કરી શકો છો અને પરિણામી અપૂર્ણાંકને ખાલી ઘટાડી શકો છો? હા, તે શક્ય છે, પરંતુ તે હંમેશા અનુકૂળ નથી. 48 અને 72 નંબરો માટે છેદ જુઓ જો તમે તેમને 48∙72 = 3456 નો ગુણાકાર કરો. તમે સંમત થશો કે નાની સંખ્યાઓ સાથે કામ કરવું વધુ સુખદ છે.

ચાલો ઉદાહરણો જોઈએ:

*51 = 3∙17 119 = 7∙17

મોટી સંખ્યાના વિસ્તરણમાં ટ્રિપલ ખૂટે છે

=> NOC(51,119) = 3∙7∙17

હવે ચાલો પ્રથમ પદ્ધતિનો ઉપયોગ કરીએ:

*ગણતરીમાં તફાવત જુઓ, પ્રથમ કિસ્સામાં તેમાં ઓછામાં ઓછા છે, પરંતુ બીજા કિસ્સામાં તમારે કાગળના ટુકડા પર અલગથી કામ કરવાની જરૂર છે, અને તમને પ્રાપ્ત થયેલ અપૂર્ણાંકને પણ ઘટાડવાની જરૂર છે. LOC શોધવાથી કામ નોંધપાત્ર રીતે સરળ બને છે.

વધુ ઉદાહરણો:

*બીજા ઉદાહરણમાં તે સ્પષ્ટ છે કે 40 અને 60 વડે ભાગી શકાય તેવી સૌથી નાની સંખ્યા 120 છે.

પરિણામ! સામાન્ય કમ્પ્યુટિંગ અલ્ગોરિધમ!

- જો પૂર્ણાંક ભાગ હોય તો અમે અપૂર્ણાંકને સામાન્યથી ઘટાડીએ છીએ.

- અમે અપૂર્ણાંકોને સામાન્ય છેદમાં લાવીએ છીએ (પહેલા આપણે જોઈએ છીએ કે એક છેદ બીજા વડે વિભાજ્ય છે કે કેમ; જો તે વિભાજ્ય હોય, તો પછી આપણે આ બીજા અપૂર્ણાંકના અંશ અને છેદનો ગુણાકાર કરીએ છીએ; જો તે વિભાજ્ય ન હોય તો, અમે અન્ય પદ્ધતિઓનો ઉપયોગ કરીને કાર્ય કરીએ છીએ. ઉપર દર્શાવેલ).

- સમાન છેદ સાથે અપૂર્ણાંક પ્રાપ્ત કર્યા પછી, અમે કામગીરી કરીએ છીએ (ઉમેર, બાદબાકી).

- જો જરૂરી હોય તો, અમે પરિણામ ઘટાડીશું.

- જો જરૂરી હોય, તો પછી આખો ભાગ પસંદ કરો.

2. અપૂર્ણાંકનું ઉત્પાદન.

નિયમ સરળ છે. અપૂર્ણાંકનો ગુણાકાર કરતી વખતે, તેમના અંશ અને છેદનો ગુણાકાર કરવામાં આવે છે:

ઉદાહરણો:

સમાન છેદ સાથે અપૂર્ણાંક ઉમેરી રહ્યા છે

અપૂર્ણાંકના ઉમેરાના બે પ્રકાર છે:

1. સમાન છેદ સાથે અપૂર્ણાંક ઉમેરી રહ્યા છે
2. વિવિધ છેદ સાથે અપૂર્ણાંક ઉમેરી રહ્યા છે

પ્રથમ, ચાલો સમાન છેદ સાથે અપૂર્ણાંકનો ઉમેરો શીખીએ. અહીં બધું સરળ છે. સમાન છેદ સાથે અપૂર્ણાંક ઉમેરવા માટે, તમારે તેમના અંશ ઉમેરવાની અને છેદને યથાવત રાખવાની જરૂર છે. ઉદાહરણ તરીકે, ચાલો અપૂર્ણાંક ઉમેરીએ અને. અંશ ઉમેરો અને છેદને યથાવત રાખો:

જો આપણે પિઝાને યાદ કરીએ, જે ચાર ભાગમાં વહેંચાયેલું છે, તો આ ઉદાહરણ સરળતાથી સમજી શકાય છે. જો તમે પિઝામાં પિઝા ઉમેરો છો, તો તમને પિઝા મળશે:

ઉદાહરણ 2.અપૂર્ણાંક ઉમેરો અને.

જવાબ અયોગ્ય અપૂર્ણાંક હોવાનું બહાર આવ્યું. જો કાર્યનો અંત આવે છે, તો પછીથી અયોગ્ય અપૂર્ણાંકતેમાંથી છુટકારો મેળવવાનો રિવાજ છે. અયોગ્ય અપૂર્ણાંકથી છુટકારો મેળવવા માટે, તમારે તેનો સંપૂર્ણ ભાગ પસંદ કરવાની જરૂર છે. અમારા કિસ્સામાં, આખો ભાગ સરળતાથી અલગ થઈ જાય છે - બે ભાગ્યા બે બરાબર એક:

જો આપણે બે ભાગમાં વહેંચાયેલ પિઝા વિશે યાદ રાખીએ તો આ ઉદાહરણ સરળતાથી સમજી શકાય છે. જો તમે પિઝામાં વધુ પિઝા ઉમેરશો, તો તમને એક આખો પિઝા મળશે:

ઉદાહરણ 3. અપૂર્ણાંક ઉમેરો અને.

ફરીથી, અમે અંશ ઉમેરીએ છીએ અને છેદને યથાવત છોડીએ છીએ:

જો આપણે પિઝાને યાદ કરીએ, જે ત્રણ ભાગમાં વહેંચાયેલું છે, તો આ ઉદાહરણ સરળતાથી સમજી શકાય છે. જો તમે પિઝામાં વધુ પિઝા ઉમેરો છો, તો તમને પિઝા મળશે:

ઉદાહરણ 4.અભિવ્યક્તિનું મૂલ્ય શોધો

આ ઉદાહરણ અગાઉના મુદ્દાઓની જેમ બરાબર એ જ રીતે હલ કરવામાં આવ્યું છે. અંશ ઉમેરવા જોઈએ અને છેદ યથાવત છોડવું જોઈએ:

ચાલો ડ્રોઇંગનો ઉપયોગ કરીને અમારા સોલ્યુશનને દર્શાવવાનો પ્રયાસ કરીએ. જો તમે પિઝામાં પિઝા ઉમેરો અને વધુ પિઝા ઉમેરો, તો તમને 1 આખો પિઝા અને વધુ પિઝા મળશે.

જેમ તમે જોઈ શકો છો, સમાન છેદ સાથે અપૂર્ણાંક ઉમેરવામાં કંઈ જટિલ નથી. નીચેના નિયમોને સમજવા માટે તે પૂરતું છે:

1. સમાન છેદ સાથે અપૂર્ણાંક ઉમેરવા માટે, તમારે તેમના અંશ ઉમેરવાની અને છેદને યથાવત રાખવાની જરૂર છે;

વિવિધ છેદ સાથે અપૂર્ણાંક ઉમેરી રહ્યા છે

હવે ચાલો શીખીએ કે વિવિધ છેદ સાથે અપૂર્ણાંક કેવી રીતે ઉમેરવા. અપૂર્ણાંક ઉમેરતી વખતે, અપૂર્ણાંકના છેદ સમાન હોવા જોઈએ. પરંતુ તેઓ હંમેશા સમાન હોતા નથી.

ઉદાહરણ તરીકે, અપૂર્ણાંક ઉમેરી શકાય છે કારણ કે તેમાં સમાન છેદ છે.

પરંતુ અપૂર્ણાંકો તરત જ ઉમેરી શકાતા નથી, કારણ કે આ અપૂર્ણાંકો છે વિવિધ છેદ. આવા કિસ્સાઓમાં, અપૂર્ણાંકને સમાન (સામાન્ય) છેદ સુધી ઘટાડવું આવશ્યક છે.

અપૂર્ણાંકને સમાન છેદમાં ઘટાડવાની ઘણી રીતો છે. આજે આપણે તેમાંથી ફક્ત એક જ જોઈશું, કારણ કે અન્ય પદ્ધતિઓ શિખાઉ માણસ માટે જટિલ લાગી શકે છે.

આ પદ્ધતિનો સાર એ છે કે પહેલા બંને અપૂર્ણાંકના છેદના LCM શોધવામાં આવે છે. LCM પછી પ્રથમ વધારાના પરિબળ મેળવવા માટે પ્રથમ અપૂર્ણાંકના છેદ દ્વારા વિભાજિત કરવામાં આવે છે. તેઓ બીજા અપૂર્ણાંક સાથે તે જ કરે છે - એલસીએમ બીજા અપૂર્ણાંકના છેદ દ્વારા વિભાજિત થાય છે અને બીજો વધારાનો પરિબળ મેળવવામાં આવે છે.

અપૂર્ણાંકના અંશ અને છેદ પછી તેમના વધારાના અવયવો દ્વારા ગુણાકાર કરવામાં આવે છે. આ ક્રિયાઓના પરિણામે, અલગ-અલગ છેદ ધરાવતા અપૂર્ણાંક સમાન છેદ ધરાવતા અપૂર્ણાંકમાં ફેરવાય છે. અને આપણે પહેલાથી જ જાણીએ છીએ કે આવા અપૂર્ણાંકને કેવી રીતે ઉમેરવું.

ઉદાહરણ 1. ચાલો અપૂર્ણાંક ઉમેરીએ અને

સૌ પ્રથમ, આપણે બંને અપૂર્ણાંકના છેદનો લઘુત્તમ સામાન્ય ગુણાંક શોધીએ છીએ. પ્રથમ અપૂર્ણાંકનો છેદ નંબર 3 છે, અને બીજા અપૂર્ણાંકનો છેદ નંબર 2 છે. આ સંખ્યાઓનો સૌથી ઓછો સામાન્ય ગુણાંક 6 છે

LCM (2 અને 3) = 6

હવે ચાલો અપૂર્ણાંક અને પર પાછા જઈએ. પ્રથમ, પ્રથમ અપૂર્ણાંકના છેદ દ્વારા LCM ને વિભાજીત કરો અને પ્રથમ વધારાનું અવયવ મેળવો. LCM એ સંખ્યા 6 છે, અને પ્રથમ અપૂર્ણાંકનો છેદ નંબર 3 છે. 6 ને 3 વડે ભાગો, આપણને 2 મળશે.

પરિણામી સંખ્યા 2 એ પ્રથમ વધારાનો ગુણક છે. અમે તેને પ્રથમ અપૂર્ણાંકમાં લખીએ છીએ. આ કરવા માટે, અપૂર્ણાંક પર એક નાની ત્રાંસી રેખા બનાવો અને તેની ઉપર મળેલ વધારાના પરિબળને લખો:

અમે બીજા અપૂર્ણાંક સાથે તે જ કરીએ છીએ. આપણે બીજા અપૂર્ણાંકના છેદ દ્વારા LCM ને વિભાજીત કરીએ છીએ અને બીજો વધારાનો અવયવ મેળવીએ છીએ. LCM એ નંબર 6 છે, અને બીજા અપૂર્ણાંકનો છેદ એ નંબર 2 છે. 6 ને 2 વડે ભાગો, આપણને 3 મળશે.

પરિણામી સંખ્યા 3 એ બીજો વધારાનો ગુણક છે. અમે તેને બીજા અપૂર્ણાંકમાં લખીએ છીએ. ફરીથી, અમે બીજા અપૂર્ણાંક પર એક નાની ત્રાંસી રેખા બનાવીએ છીએ અને તેની ઉપર મળેલ વધારાના પરિબળને લખીએ છીએ:

હવે અમારી પાસે ઉમેરવા માટે બધું તૈયાર છે. અપૂર્ણાંકના અંશ અને છેદને તેમના વધારાના પરિબળો દ્વારા ગુણાકાર કરવાનું બાકી છે:

અમે શું આવ્યા છીએ તે ધ્યાનથી જુઓ. અમે એવા નિષ્કર્ષ પર આવ્યા કે જે અપૂર્ણાંકમાં અલગ-અલગ છેદ હતા તે અપૂર્ણાંકમાં ફેરવાઈ ગયા જેમાં સમાન છેદ હતા. અને આપણે પહેલાથી જ જાણીએ છીએ કે આવા અપૂર્ણાંકને કેવી રીતે ઉમેરવું. ચાલો આ ઉદાહરણને અંત સુધી લઈએ:

આ ઉદાહરણ પૂર્ણ કરે છે. તે ઉમેરવા માટે બહાર વળે છે.

ચાલો ડ્રોઇંગનો ઉપયોગ કરીને અમારા સોલ્યુશનને દર્શાવવાનો પ્રયાસ કરીએ. જો તમે પિઝામાં પિઝા ઉમેરો છો, તો તમને એક આખો પિઝા અને બીજો પિઝાનો છઠ્ઠો ભાગ મળશે:

અપૂર્ણાંકને સમાન (સામાન્ય) છેદમાં ઘટાડીને પણ ચિત્રની મદદથી દર્શાવી શકાય છે. અપૂર્ણાંકોને ઘટાડીને અને સામાન્ય છેદ સુધી, આપણને અપૂર્ણાંક અને મળ્યા. આ બે અપૂર્ણાંક પિઝાના સમાન ટુકડાઓ દ્વારા રજૂ કરવામાં આવશે. ફરક એટલો જ હશે કે આ વખતે તેઓ સમાન શેરમાં વિભાજિત થશે (સમાન છેદમાં ઘટાડો).

પ્રથમ રેખાંકન અપૂર્ણાંક (છમાંથી ચાર ટુકડા) રજૂ કરે છે, અને બીજું ચિત્ર અપૂર્ણાંક (છમાંથી ત્રણ ટુકડા) દર્શાવે છે. આ ટુકડાઓ ઉમેરવાથી આપણને મળે છે (છમાંથી સાત ટુકડા). આ અપૂર્ણાંક અયોગ્ય છે, તેથી અમે તેનો સંપૂર્ણ ભાગ પ્રકાશિત કર્યો. પરિણામે, અમને (એક આખો પિઝા અને બીજો છઠ્ઠો પિઝા) મળ્યો.

મહેરબાની કરીને નોંધ કરો કે અમે આ ઉદાહરણનું ખૂબ વિગતવાર વર્ણન કર્યું છે. IN શૈક્ષણિક સંસ્થાઓઆવી વિગતે લખવાનો રિવાજ નથી. તમારે બંને છેદના LCM અને તેમના માટે વધારાના પરિબળોને ઝડપથી શોધવામાં સક્ષમ થવાની જરૂર છે, તેમજ તમારા અંશ અને છેદ દ્વારા મળેલા વધારાના પરિબળોને ઝડપથી ગુણાકાર કરવા માટે તમારે સક્ષમ થવાની જરૂર છે. શાળામાં હતા ત્યારે, અમારે આ ઉદાહરણ નીચે પ્રમાણે લખવું પડશે:

પરંતુ ત્યાં પણ છે વિપરીત બાજુમેડલ જો તમે શીખવાના પ્રથમ તબક્કામાં ગણિત ન કરો વિગતવાર રેકોર્ડ, પછી પ્રકારના પ્રશ્નો દેખાવા લાગે છે "તે સંખ્યા ક્યાંથી આવે છે?", "અપૂર્ણાંકો અચાનક સંપૂર્ણપણે અલગ અપૂર્ણાંકમાં કેમ ફેરવાય છે? «.

વિવિધ છેદ સાથે અપૂર્ણાંક ઉમેરવાનું સરળ બનાવવા માટે, તમે નીચેની પગલા-દર-પગલાની સૂચનાઓનો ઉપયોગ કરી શકો છો:

1. અપૂર્ણાંકના છેદનું LCM શોધો;
2. દરેક અપૂર્ણાંકના છેદ દ્વારા LCM ને વિભાજીત કરો અને દરેક અપૂર્ણાંક માટે વધારાનું પરિબળ મેળવો;
3. અપૂર્ણાંકના અંશ અને છેદને તેમના વધારાના પરિબળો દ્વારા ગુણાકાર કરો;
4. સમાન છેદ ધરાવતા અપૂર્ણાંકો ઉમેરો;
5. જો જવાબ અયોગ્ય અપૂર્ણાંક હોવાનું બહાર આવ્યું છે, તો પછી તેનો સંપૂર્ણ ભાગ પસંદ કરો;

ઉદાહરણ 2.અભિવ્યક્તિનું મૂલ્ય શોધો .

ચાલો ઉપર આપેલ સૂચનાઓનો ઉપયોગ કરીએ.

પગલું 1. અપૂર્ણાંકોના છેદનો LCM શોધો

બંને અપૂર્ણાંકના છેદનો LCM શોધો. અપૂર્ણાંકના છેદ નંબરો 2, 3 અને 4 છે

પગલું 2. દરેક અપૂર્ણાંકના છેદ દ્વારા LCM ને વિભાજીત કરો અને દરેક અપૂર્ણાંક માટે વધારાનું પરિબળ મેળવો

પ્રથમ અપૂર્ણાંકના છેદ દ્વારા LCM ને વિભાજિત કરો. LCM એ નંબર 12 છે, અને પ્રથમ અપૂર્ણાંકનો છેદ એ નંબર 2 છે. 12 ને 2 વડે ભાગીએ તો આપણને 6 મળે છે. આપણને પહેલો વધારાનો અવયવ 6 મળ્યો. આપણે તેને પ્રથમ અપૂર્ણાંકની ઉપર લખીએ છીએ:

હવે આપણે બીજા અપૂર્ણાંકના છેદ દ્વારા LCM ને વિભાજીત કરીએ છીએ. LCM એ નંબર 12 છે, અને બીજા અપૂર્ણાંકનો છેદ એ નંબર 3 છે. 12 ને 3 વડે ભાગીએ તો આપણને 4 મળે છે. આપણને બીજો વધારાનો અવયવ 4 મળે છે. આપણે તેને બીજા અપૂર્ણાંકની ઉપર લખીએ છીએ:

હવે આપણે ત્રીજા અપૂર્ણાંકના છેદ દ્વારા LCM ને વિભાજીત કરીએ છીએ. LCM એ નંબર 12 છે, અને ત્રીજા અપૂર્ણાંકનો છેદ એ નંબર 4 છે. 12 ને 4 વડે ભાગીએ તો આપણને 3 મળે છે. આપણને ત્રીજો વધારાનો અવયવ 3 મળે છે. આપણે તેને ત્રીજા અપૂર્ણાંકની ઉપર લખીએ છીએ:

પગલું 3. અપૂર્ણાંકના અંશ અને છેદને તેમના વધારાના પરિબળો દ્વારા ગુણાકાર કરો

અમે અંશ અને છેદને તેમના વધારાના પરિબળો દ્વારા ગુણાકાર કરીએ છીએ:

પગલું 4. સમાન છેદ સાથે અપૂર્ણાંક ઉમેરો

અમે એવા નિષ્કર્ષ પર આવ્યા કે જે અપૂર્ણાંકમાં અલગ-અલગ છેદ હતા તે સમાન (સામાન્ય) છેદ ધરાવતા અપૂર્ણાંકમાં ફેરવાઈ ગયા. આ અપૂર્ણાંક ઉમેરવાનું બાકી છે. તેને ઉમેરો:

ઉમેરણ એક લીટી પર બંધબેસતું નહોતું, તેથી અમે બાકીની અભિવ્યક્તિને આગલી લીટી પર ખસેડીએ છીએ. આને ગણિતમાં મંજૂરી છે. જ્યારે અભિવ્યક્તિ એક લીટી પર બંધબેસતી નથી, ત્યારે તેને આગલી લીટી પર ખસેડવામાં આવે છે, અને પ્રથમ લીટીના અંતે અને નવી લીટીની શરૂઆતમાં સમાન ચિહ્ન (=) મૂકવું જરૂરી છે. બીજી લાઇન પર સમાન ચિહ્ન સૂચવે છે કે આ અભિવ્યક્તિનું ચાલુ છે જે પ્રથમ લાઇન પર હતું.

પગલું 5. જો જવાબ અયોગ્ય અપૂર્ણાંક હોવાનું બહાર આવ્યું છે, તો પછી તેનો સંપૂર્ણ ભાગ પ્રકાશિત કરો

અમારો જવાબ અયોગ્ય અપૂર્ણાંક હોવાનું બહાર આવ્યું. આપણે તેનો આખો ભાગ પ્રકાશિત કરવાનો છે. અમે હાઇલાઇટ કરીએ છીએ:

અમને જવાબ મળ્યો

સમાન છેદ સાથે અપૂર્ણાંક બાદબાકી

અપૂર્ણાંકના બાદબાકીના બે પ્રકાર છે:

1. સમાન છેદ સાથે અપૂર્ણાંક બાદબાકી
2. વિવિધ છેદ સાથે અપૂર્ણાંક બાદબાકી

પ્રથમ, ચાલો શીખીએ કે જેવા છેદ વડે અપૂર્ણાંકને કેવી રીતે બાદ કરી શકાય. અહીં બધું સરળ છે. એક અપૂર્ણાંકમાંથી બીજાને બાદ કરવા માટે, તમારે પ્રથમ અપૂર્ણાંકના અંશમાંથી બીજા અપૂર્ણાંકના અંશને બાદબાકી કરવાની જરૂર છે, પરંતુ છેદને તે જ છોડી દો.

ઉદાહરણ તરીકે, ચાલો અભિવ્યક્તિનું મૂલ્ય શોધીએ. આ ઉદાહરણને ઉકેલવા માટે, તમારે પ્રથમ અપૂર્ણાંકના અંશમાંથી બીજા અપૂર્ણાંકના અંશને બાદબાકી કરવાની અને છેદને યથાવત રાખવાની જરૂર છે. ચાલો આ કરીએ:

જો આપણે પિઝાને યાદ કરીએ, જે ચાર ભાગમાં વહેંચાયેલું છે, તો આ ઉદાહરણ સરળતાથી સમજી શકાય છે. જો તમે પિઝામાંથી પિઝા કાપો છો, તો તમને પિઝા મળશે:

ઉદાહરણ 2.અભિવ્યક્તિનું મૂલ્ય શોધો.

ફરીથી, પ્રથમ અપૂર્ણાંકના અંશમાંથી, બીજા અપૂર્ણાંકના અંશને બાદ કરો અને છેદને યથાવત રાખો:

જો આપણે પિઝાને યાદ કરીએ, જે ત્રણ ભાગમાં વહેંચાયેલું છે, તો આ ઉદાહરણ સરળતાથી સમજી શકાય છે. જો તમે પિઝામાંથી પિઝા કાપો છો, તો તમને પિઝા મળશે:

ઉદાહરણ 3.અભિવ્યક્તિનું મૂલ્ય શોધો

આ ઉદાહરણ અગાઉના મુદ્દાઓની જેમ બરાબર એ જ રીતે હલ કરવામાં આવ્યું છે. પ્રથમ અપૂર્ણાંકના અંશમાંથી તમારે બાકીના અપૂર્ણાંકના અંશને બાદ કરવાની જરૂર છે:

જેમ તમે જોઈ શકો છો, સમાન છેદ સાથે અપૂર્ણાંકને બાદ કરવામાં કંઈ જટિલ નથી. નીચેના નિયમોને સમજવા માટે તે પૂરતું છે:

1. એક અપૂર્ણાંકમાંથી બીજાને બાદ કરવા માટે, તમારે પ્રથમ અપૂર્ણાંકના અંશમાંથી બીજા અપૂર્ણાંકના અંશને બાદબાકી કરવાની અને છેદને યથાવત રાખવાની જરૂર છે;
2. જો જવાબ અયોગ્ય અપૂર્ણાંક હોવાનું બહાર આવ્યું છે, તો તમારે તેના સંપૂર્ણ ભાગને પ્રકાશિત કરવાની જરૂર છે.

વિવિધ છેદ સાથે અપૂર્ણાંક બાદબાકી

ઉદાહરણ તરીકે, તમે અપૂર્ણાંકમાંથી અપૂર્ણાંકને બાદ કરી શકો છો કારણ કે અપૂર્ણાંકમાં સમાન છેદ હોય છે. પરંતુ તમે અપૂર્ણાંકમાંથી અપૂર્ણાંકને બાદ કરી શકતા નથી, કારણ કે આ અપૂર્ણાંકમાં વિવિધ છેદ છે. આવા કિસ્સાઓમાં, અપૂર્ણાંકને સમાન (સામાન્ય) છેદ સુધી ઘટાડવું આવશ્યક છે.

સામાન્ય છેદ એ જ સિદ્ધાંતનો ઉપયોગ કરીને જોવા મળે છે જેનો ઉપયોગ આપણે વિવિધ છેદ સાથે અપૂર્ણાંક ઉમેરતી વખતે કર્યો હતો. સૌ પ્રથમ, બંને અપૂર્ણાંકના છેદનો LCM શોધો. પછી LCM ને પ્રથમ અપૂર્ણાંકના છેદ દ્વારા વિભાજિત કરવામાં આવે છે અને પ્રથમ વધારાનો પરિબળ મેળવવામાં આવે છે, જે પ્રથમ અપૂર્ણાંકની ઉપર લખાયેલ છે. એ જ રીતે, એલસીએમ બીજા અપૂર્ણાંકના છેદ દ્વારા વિભાજિત થાય છે અને બીજો વધારાનો પરિબળ મેળવવામાં આવે છે, જે બીજા અપૂર્ણાંકની ઉપર લખાયેલ છે.

પછી અપૂર્ણાંકને તેમના વધારાના પરિબળો દ્વારા ગુણાકાર કરવામાં આવે છે. આ ક્રિયાઓના પરિણામ સ્વરૂપે, અપૂર્ણાંક કે જેમાં વિવિધ છેદ હતા તે અપૂર્ણાંકમાં રૂપાંતરિત થાય છે જેમાં સમાન છેદ હોય છે. અને આપણે પહેલાથી જ જાણીએ છીએ કે આવા અપૂર્ણાંકને કેવી રીતે બાદ કરવી.

ઉદાહરણ 1.અભિવ્યક્તિનો અર્થ શોધો:

આ અપૂર્ણાંકોમાં વિવિધ છેદ છે, તેથી તમારે તેમને સમાન (સામાન્ય) છેદ સુધી ઘટાડવાની જરૂર છે.

પ્રથમ, આપણે બંને અપૂર્ણાંકના છેદનો LCM શોધીએ છીએ. પ્રથમ અપૂર્ણાંકનો છેદ નંબર 3 છે, અને બીજા અપૂર્ણાંકનો છેદ નંબર 4 છે. આ સંખ્યાઓનો સૌથી ઓછો સામાન્ય ગુણાંક 12 છે

LCM (3 અને 4) = 12

હવે ચાલો અપૂર્ણાંક પર પાછા જઈએ અને

ચાલો પ્રથમ અપૂર્ણાંક માટે વધારાનું પરિબળ શોધીએ. આ કરવા માટે, પ્રથમ અપૂર્ણાંકના છેદ દ્વારા LCM ને વિભાજીત કરો. LCM એ નંબર 12 છે, અને પ્રથમ અપૂર્ણાંકનો છેદ નંબર 3 છે. 12 ને 3 વડે ભાગીએ તો આપણને 4 મળે છે. પ્રથમ અપૂર્ણાંકની ઉપર ચાર લખો:

અમે બીજા અપૂર્ણાંક સાથે તે જ કરીએ છીએ. બીજા અપૂર્ણાંકના છેદ દ્વારા LCM ને વિભાજિત કરો. LCM એ નંબર 12 છે, અને બીજા અપૂર્ણાંકનો છેદ એ નંબર 4 છે. 12 ને 4 વડે ભાગીએ તો આપણને 3 મળે છે. બીજા અપૂર્ણાંક પર ત્રણ લખો:

હવે આપણે બાદબાકી માટે તૈયાર છીએ. તે અપૂર્ણાંકને તેમના વધારાના પરિબળો દ્વારા ગુણાકાર કરવાનું બાકી છે:

અમે એવા નિષ્કર્ષ પર આવ્યા કે જે અપૂર્ણાંકમાં અલગ-અલગ છેદ હતા તે અપૂર્ણાંકમાં ફેરવાઈ ગયા જેમાં સમાન છેદ હતા. અને આપણે પહેલાથી જ જાણીએ છીએ કે આવા અપૂર્ણાંકને કેવી રીતે બાદ કરવું. ચાલો આ ઉદાહરણને અંત સુધી લઈએ:

અમને જવાબ મળ્યો

ચાલો ડ્રોઇંગનો ઉપયોગ કરીને અમારા ઉકેલને દર્શાવવાનો પ્રયાસ કરીએ. જો તમે પિઝામાંથી પિઝા કાપો છો, તો તમને પિઝા મળે છે

આ વિગતવાર સંસ્કરણઉકેલો જો આપણે શાળામાં હોત, તો અમારે આ ઉદાહરણ ટૂંકું ઉકેલવું પડશે. આવા ઉકેલ આના જેવો દેખાશે:

અપૂર્ણાંકને સામાન્ય છેદમાં ઘટાડવાનું ચિત્રનો ઉપયોગ કરીને પણ દર્શાવી શકાય છે. આ અપૂર્ણાંકોને સામાન્ય છેદ સુધી ઘટાડીને, અમને અપૂર્ણાંકો અને મળ્યા. આ અપૂર્ણાંકો સમાન પિઝા સ્લાઇસેસ દ્વારા રજૂ કરવામાં આવશે, પરંતુ આ વખતે તેઓ સમાન શેરમાં વિભાજિત કરવામાં આવશે (સમાન છેદ સુધી ઘટાડીને):

પ્રથમ ચિત્ર અપૂર્ણાંક બતાવે છે (બારમાંથી આઠ ટુકડા), અને બીજું ચિત્ર અપૂર્ણાંક (બારમાંથી ત્રણ ટુકડા) બતાવે છે. આઠ ટુકડામાંથી ત્રણ ટુકડા કાપીને, આપણને બારમાંથી પાંચ ટુકડા મળે છે. અપૂર્ણાંક આ પાંચ ટુકડાઓનું વર્ણન કરે છે.

ઉદાહરણ 2.અભિવ્યક્તિનું મૂલ્ય શોધો

આ અપૂર્ણાંકોમાં વિવિધ છેદ હોય છે, તેથી પ્રથમ તમારે તેમને સમાન (સામાન્ય) છેદ સુધી ઘટાડવાની જરૂર છે.

ચાલો આ અપૂર્ણાંકોના છેદનો LCM શોધીએ.

અપૂર્ણાંકના છેદ 10, 3 અને 5 નંબરો છે. આ સંખ્યાઓનો સૌથી ઓછો સામાન્ય ગુણાંક 30 છે

LCM(10, 3, 5) = 30

હવે આપણે દરેક અપૂર્ણાંક માટે વધારાના પરિબળો શોધીએ છીએ. આ કરવા માટે, દરેક અપૂર્ણાંકના છેદ દ્વારા LCM ને વિભાજીત કરો.

ચાલો પ્રથમ અપૂર્ણાંક માટે વધારાનું પરિબળ શોધીએ. LCM એ સંખ્યા 30 છે, અને પ્રથમ અપૂર્ણાંકનો છેદ એ નંબર 10 છે. 30 ને 10 વડે વિભાજિત કરીએ તો આપણને પહેલો વધારાનો અવયવ 3 મળે છે. આપણે તેને પ્રથમ અપૂર્ણાંકની ઉપર લખીએ છીએ:

હવે આપણે બીજા અપૂર્ણાંક માટે વધારાનું પરિબળ શોધીએ છીએ. બીજા અપૂર્ણાંકના છેદ દ્વારા LCM ને વિભાજિત કરો. LCM એ 30 નંબર છે, અને બીજા અપૂર્ણાંકનો છેદ એ નંબર 3 છે. 30 ને 3 વડે ભાગીએ તો આપણને બીજો વધારાનો અવયવ 10 મળે છે. આપણે તેને બીજા અપૂર્ણાંકની ઉપર લખીએ છીએ:

હવે આપણે ત્રીજા અપૂર્ણાંક માટે વધારાનું પરિબળ શોધીએ છીએ. ત્રીજા અપૂર્ણાંકના છેદ દ્વારા LCM ને વિભાજિત કરો. LCM એ 30 નંબર છે, અને ત્રીજા અપૂર્ણાંકનો છેદ નંબર 5 છે. 30 ને 5 વડે ભાગીએ તો આપણને ત્રીજો વધારાનો અવયવ 6 મળે છે. આપણે તેને ત્રીજા અપૂર્ણાંકની ઉપર લખીએ છીએ:

હવે બધું બાદબાકી માટે તૈયાર છે. તે અપૂર્ણાંકને તેમના વધારાના પરિબળો દ્વારા ગુણાકાર કરવાનું બાકી છે:

અમે એવા નિષ્કર્ષ પર આવ્યા કે જે અપૂર્ણાંકમાં અલગ-અલગ છેદ હતા તે સમાન (સામાન્ય) છેદ ધરાવતા અપૂર્ણાંકમાં ફેરવાઈ ગયા. અને આપણે પહેલાથી જ જાણીએ છીએ કે આવા અપૂર્ણાંકને કેવી રીતે બાદ કરવી. ચાલો આ ઉદાહરણ પૂરું કરીએ.

ઉદાહરણનું સાતત્ય એક લીટી પર બંધબેસતું નથી, તેથી અમે ચાલુ રાખવાને આગલી લીટી પર ખસેડીએ છીએ. નવી લાઇન પર સમાન ચિહ્ન (=) વિશે ભૂલશો નહીં:

જવાબ નિયમિત અપૂર્ણાંક હોવાનું બહાર આવ્યું છે, અને બધું અમને અનુકૂળ લાગે છે, પરંતુ તે ખૂબ જ બોજારૂપ અને કદરૂપું છે. આપણે તેને સરળ બનાવવું જોઈએ. શું કરી શકાય? તમે આ અપૂર્ણાંકને નાનો કરી શકો છો.

અપૂર્ણાંકને ઘટાડવા માટે, તમારે તેના અંશ અને છેદને 20 અને 30 નંબરના (GCD) વડે વિભાજિત કરવાની જરૂર છે.

તેથી, આપણે 20 અને 30 નંબરોની જીસીડી શોધીએ છીએ:

હવે આપણે આપણા ઉદાહરણ પર પાછા આવીએ છીએ અને મળેલા gcd દ્વારા અપૂર્ણાંકના અંશ અને છેદને વિભાજીત કરીએ છીએ, એટલે કે 10 વડે.

અમને જવાબ મળ્યો

સંખ્યા વડે અપૂર્ણાંકનો ગુણાકાર

અપૂર્ણાંકને સંખ્યા વડે ગુણાકાર કરવા માટે, તમારે આપેલ અપૂર્ણાંકના અંશને તે સંખ્યા વડે ગુણાકાર કરવાની જરૂર છે અને છેદને તે જ છોડવો પડશે.

ઉદાહરણ 1. સંખ્યા 1 વડે અપૂર્ણાંકનો ગુણાકાર કરો.

અપૂર્ણાંકના અંશને સંખ્યા 1 વડે ગુણાકાર કરો

રેકોર્ડિંગ અડધી 1 સમય લે છે તે સમજી શકાય છે. ઉદાહરણ તરીકે, જો તમે એકવાર પિઝા લો છો, તો તમને પિઝા મળે છે

ગુણાકારના નિયમોથી આપણે જાણીએ છીએ કે જો ગુણાકાર અને અવયવની અદલાબદલી કરવામાં આવે તો, ઉત્પાદન બદલાશે નહીં. જો અભિવ્યક્તિ તરીકે લખવામાં આવે છે, તો પછી ઉત્પાદન હજુ પણ સમાન હશે. ફરીથી, પૂર્ણ સંખ્યા અને અપૂર્ણાંકનો ગુણાકાર કરવાનો નિયમ કામ કરે છે:

આ સંકેતને એકના અડધા લેવા તરીકે સમજી શકાય છે. ઉદાહરણ તરીકે, જો ત્યાં 1 આખો પિઝા હોય અને આપણે તેનો અડધો ભાગ લઈએ, તો આપણી પાસે પિઝા હશે:

ઉદાહરણ 2. અભિવ્યક્તિનું મૂલ્ય શોધો

અપૂર્ણાંકના અંશને 4 વડે ગુણાકાર કરો

જવાબ અયોગ્ય અપૂર્ણાંક હતો. ચાલો તેના સંપૂર્ણ ભાગને પ્રકાશિત કરીએ:

અભિવ્યક્તિને બે ચતુર્થાંશ 4 વખત લેવા તરીકે સમજી શકાય છે. ઉદાહરણ તરીકે, જો તમે 4 પિઝા લો છો, તો તમને બે આખા પિઝા મળશે

અને જો આપણે ગુણાકાર અને ગુણાકારની અદલાબદલી કરીએ, તો આપણને અભિવ્યક્તિ મળે છે. તે 2 ની બરાબર પણ હશે. આ અભિવ્યક્તિને ચાર આખા પિઝામાંથી બે પિઝા લેવા તરીકે સમજી શકાય છે:

અપૂર્ણાંકનો ગુણાકાર

અપૂર્ણાંકનો ગુણાકાર કરવા માટે, તમારે તેમના અંશ અને છેદનો ગુણાકાર કરવાની જરૂર છે. જો જવાબ અયોગ્ય અપૂર્ણાંક હોવાનું બહાર આવ્યું છે, તો તમારે તેના સંપૂર્ણ ભાગને પ્રકાશિત કરવાની જરૂર છે.

ઉદાહરણ 1.અભિવ્યક્તિનું મૂલ્ય શોધો.

અમને જવાબ મળ્યો. ઘટાડવાની સલાહ આપવામાં આવે છે આપેલ અપૂર્ણાંક. અપૂર્ણાંક 2 દ્વારા ઘટાડી શકાય છે. પછી અંતિમ નિર્ણયનીચેનું ફોર્મ લેશે:

હાફ પીઝામાંથી પિઝા લેવા જેવી અભિવ્યક્તિ સમજી શકાય. ચાલો કહીએ કે અમારી પાસે અડધો પિઝા છે:

આ અડધા ભાગમાંથી બે તૃતીયાંશ કેવી રીતે લેવા? પ્રથમ તમારે આ અડધા ભાગને ત્રણ સમાન ભાગોમાં વહેંચવાની જરૂર છે:

અને આ ત્રણ ટુકડામાંથી બે લો:

અમે પિઝા બનાવીશું. યાદ રાખો કે પિઝાને ત્રણ ભાગોમાં વહેંચવામાં આવે ત્યારે કેવો દેખાય છે:

આ પિઝાનો એક ટુકડો અને અમે લીધેલા બે ટુકડાઓ સમાન પરિમાણો ધરાવશે:

બીજા શબ્દોમાં કહીએ તો, અમે વાત કરી રહ્યા છીએલગભગ સમાન કદના પિઝા. તેથી અભિવ્યક્તિનું મૂલ્ય છે

ઉદાહરણ 2. અભિવ્યક્તિનું મૂલ્ય શોધો

પ્રથમ અપૂર્ણાંકના અંશને બીજા અપૂર્ણાંકના અંશ દ્વારા અને પ્રથમ અપૂર્ણાંકના છેદને બીજા અપૂર્ણાંકના છેદ વડે ગુણાકાર કરો:

જવાબ અયોગ્ય અપૂર્ણાંક હતો. ચાલો તેના સંપૂર્ણ ભાગને પ્રકાશિત કરીએ:

ઉદાહરણ 3.અભિવ્યક્તિનું મૂલ્ય શોધો

પ્રથમ અપૂર્ણાંકના અંશને બીજા અપૂર્ણાંકના અંશ દ્વારા અને પ્રથમ અપૂર્ણાંકના છેદને બીજા અપૂર્ણાંકના છેદ વડે ગુણાકાર કરો:

જવાબ નિયમિત અપૂર્ણાંક હોવાનું બહાર આવ્યું, પરંતુ જો તે ટૂંકું કરવામાં આવે તો તે સારું રહેશે. આ અપૂર્ણાંકને ઘટાડવા માટે, તમારે આ અપૂર્ણાંકના અંશ અને છેદને સૌથી મોટા દ્વારા વિભાજીત કરવાની જરૂર છે. સામાન્ય વિભાજક(GCD) નંબર 105 અને 450.

તો, ચાલો 105 અને 450 નંબરોની જીસીડી શોધીએ:

હવે આપણે આપણા જવાબના અંશ અને છેદને Gcd દ્વારા વિભાજીત કરીએ છીએ જે આપણને હવે મળી છે, એટલે કે 15 વડે

સંપૂર્ણ સંખ્યાને અપૂર્ણાંક તરીકે રજૂ કરવી

કોઈપણ પૂર્ણ સંખ્યાને અપૂર્ણાંક તરીકે રજૂ કરી શકાય છે. ઉદાહરણ તરીકે, નંબર 5 તરીકે રજૂ કરી શકાય છે. આનાથી પાંચનો અર્થ બદલાશે નહીં, કારણ કે અભિવ્યક્તિનો અર્થ થાય છે "સંખ્યા પાંચ એક વડે ભાગ્યા" અને આ, જેમ આપણે જાણીએ છીએ, પાંચ બરાબર છે:

પારસ્પરિક સંખ્યાઓ

હવે આપણે ખૂબ જ સાથે પરિચિત થઈશું રસપ્રદ વિષયગણિતમાં. તેને "વિપરીત સંખ્યાઓ" કહેવામાં આવે છે.

વ્યાખ્યા. નંબર પર ઉલટાવોa એક સંખ્યા છે જેનો જ્યારે ગુણાકાર કરવામાં આવે છેa એક આપે છે.

ચાલો આ વ્યાખ્યામાં ચલને બદલે બદલીએ aનંબર 5 અને વ્યાખ્યા વાંચવાનો પ્રયાસ કરો:

નંબર પર ઉલટાવો 5 એક સંખ્યા છે જેનો જ્યારે ગુણાકાર કરવામાં આવે છે 5 એક આપે છે.

શું એવી સંખ્યા શોધવી શક્ય છે કે જેને 5 વડે ગુણાકાર કરવામાં આવે ત્યારે એક મળે? તે તારણ આપે છે કે તે શક્ય છે. ચાલો અપૂર્ણાંક તરીકે પાંચની કલ્પના કરીએ:

પછી આ અપૂર્ણાંકને પોતાના દ્વારા ગુણાકાર કરો, ફક્ત અંશ અને છેદની અદલાબદલી કરો. બીજા શબ્દોમાં કહીએ તો, ચાલો અપૂર્ણાંકને જાતે જ ગુણાકાર કરીએ, ફક્ત ઊલટું:

આના પરિણામે શું થશે? જો આપણે આ ઉદાહરણને હલ કરવાનું ચાલુ રાખીએ, તો આપણને એક મળશે:

આનો અર્થ એ છે કે સંખ્યા 5 ની વ્યસ્ત સંખ્યા છે, કારણ કે જ્યારે તમે 5 નો ગુણાકાર કરો છો ત્યારે તમને એક મળે છે.

સંખ્યાના પરસ્પર અન્ય કોઈપણ પૂર્ણાંક માટે પણ શોધી શકાય છે.

તમે કોઈપણ અન્ય અપૂર્ણાંકનો પારસ્પરિક પણ શોધી શકો છો. આ કરવા માટે, ફક્ત તેને ફેરવો.

અપૂર્ણાંકને સંખ્યા વડે ભાગવું

ચાલો કહીએ કે અમારી પાસે અડધો પિઝા છે:

ચાલો તેને બે વચ્ચે સમાન રીતે વિભાજીત કરીએ. દરેક વ્યક્તિને કેટલા પિઝા મળશે?

તે જોઈ શકાય છે કે અડધા પિઝાને વિભાજિત કર્યા પછી, બે સમાન ટુકડાઓ મેળવવામાં આવ્યા હતા, જેમાંથી દરેક પિઝાની રચના કરે છે. તેથી દરેકને પિઝા મળે છે.

અપૂર્ણાંકનું વિભાજન પારસ્પરિક ઉપયોગ કરીને કરવામાં આવે છે. પારસ્પરિક સંખ્યાઓતમને ભાગાકારને ગુણાકાર સાથે બદલવાની મંજૂરી આપે છે.

અપૂર્ણાંકને સંખ્યા વડે ભાગવા માટે, તમારે અપૂર્ણાંકને વિભાજકના વ્યસ્ત વડે ગુણાકાર કરવાની જરૂર છે.

આ નિયમનો ઉપયોગ કરીને, અમે પિઝાના અમારા અડધા ભાગને બે ભાગોમાં વિભાજન લખીશું.

તેથી, તમારે અપૂર્ણાંકને નંબર 2 દ્વારા વિભાજીત કરવાની જરૂર છે. અહીં ડિવિડન્ડ અપૂર્ણાંક છે અને વિભાજક નંબર 2 છે.

અપૂર્ણાંકને નંબર 2 વડે ભાગવા માટે, તમારે આ અપૂર્ણાંકને વિભાજક 2 ના પારસ્પરિક વડે ગુણાકાર કરવાની જરૂર છે. વિભાજક 2 નો પારસ્પરિક અપૂર્ણાંક છે. તેથી તમારે વડે ગુણાકાર કરવાની જરૂર છે

1. સમાન છેદ સાથે અપૂર્ણાંક ઉમેરવાનો નિયમ:

ઉદાહરણ 1:

ઉદાહરણ 2:

વિવિધ છેદ સાથે અપૂર્ણાંક ઉમેરવાનો નિયમ:

ઉદાહરણ 1:

ઉદાહરણ 2:

અહીં છેદનો ગુણાકાર કરવામાં આવ્યો ન હતો, પરંતુ સૌથી નાનો લેવામાં આવ્યો હતો સામાન્ય ગુણક a2.
(છેદ 2 ની સૌથી વધુ શક્તિ ધરાવે છે.)
પ્રથમ અપૂર્ણાંક માટે વધારાનો પરિબળ 1 છે, બીજા માટે તે a છે.

2. સમાન છેદ સાથે અપૂર્ણાંકની બાદબાકી કરવાનો નિયમ:

વિવિધ છેદ સાથે અપૂર્ણાંક બાદબાકી કરવાનો નિયમ:

3. સામાન્ય અપૂર્ણાંકનો ગુણાકાર કરવાનો નિયમ:

4. અપૂર્ણાંકને વિભાજિત કરવા માટેનો નિયમ:

ઉદાહરણ:

સામાન્ય (સરળ) અપૂર્ણાંક. અપૂર્ણાંકનો અંશ અને છેદ.
યોગ્ય અને અયોગ્ય અપૂર્ણાંક. મિશ્ર સંખ્યા.
અપૂર્ણ ભાગ. સમગ્ર અને અપૂર્ણાંક ભાગ. વિપરીત અપૂર્ણાંક. એકમનો ભાગ અથવા તેના કેટલાક ભાગોને સામાન્ય અથવા સરળ અપૂર્ણાંક કહેવામાં આવે છે. સમાન ભાગોની સંખ્યા કે જેમાં એકમ વિભાજિત થાય છે તેને છેદ કહેવામાં આવે છે, અને લેવામાં આવેલા ભાગોની સંખ્યાને અંશ કહેવામાં આવે છે. અપૂર્ણાંક આ રીતે લખાયેલ છે:

અહીં 3 અંશ છે, 7 છેદ છે.

જો અંશ છેદ કરતાં ઓછું, તો અપૂર્ણાંક 1 કરતા ઓછો છે અને તેને કહેવામાં આવે છે યોગ્ય અપૂર્ણાંક . જો અંશ છેદ સમાન હોય, તો અપૂર્ણાંક 1 ની બરાબર હોય. જો અંશ છેદ કરતા મોટો હોય, તો અપૂર્ણાંક 1 કરતા મોટો હોય. બંનેમાં તાજેતરના કેસોઅપૂર્ણાંકને અયોગ્ય અપૂર્ણાંક કહેવામાં આવે છે. જો અંશને છેદ વડે ભાગવામાં આવે, તો આ અપૂર્ણાંક ભાગાકારના ભાગ સમાન છે: 63/7 = 9. જો ભાગાકાર શેષ સાથે કરવામાં આવે, તો આ અયોગ્ય અપૂર્ણાંકને રજૂ કરી શકાય છે. મિશ્ર સંખ્યા:

અહીં 9 - અપૂર્ણ ભાગ(મિશ્ર સંખ્યાનો પૂર્ણાંક ભાગ), 2 – શેષ (અપૂર્ણાંક ભાગનો અંશ), 7 – છેદ.
તે ઘણી વખત નક્કી કરવા માટે જરૂરી છે વ્યસ્ત સમસ્યા – મિશ્ર સંખ્યાને રિવર્સ કરોઅપૂર્ણાંક માં. આ કરવા માટે, મિશ્ર સંખ્યાના પૂર્ણાંક ભાગને છેદ દ્વારા ગુણાકાર કરો અને અપૂર્ણાંક ભાગનો અંશ ઉમેરો. આ સામાન્ય અપૂર્ણાંકનો અંશ હશે, પરંતુ છેદ એક જ રહેશે.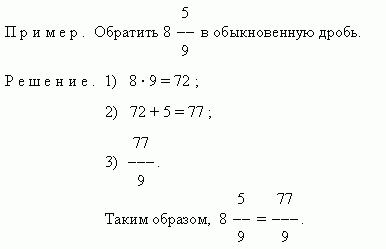

પારસ્પરિક અપૂર્ણાંક બે અપૂર્ણાંક છે જેનું ઉત્પાદન 1 ની બરાબર છે. ઉદાહરણ તરીકે, 3/7 અને 7/3; 15/1 અને 1/15, વગેરે.

અપૂર્ણાંક વિસ્તરણ. અપૂર્ણાંક ઘટાડવો. અપૂર્ણાંકની તુલના.
સામાન્ય સંપ્રદાયમાં ઘટાડો. સરવાળો અને બાદબાકીઅપૂર્ણાંક
અપૂર્ણાંકનો ગુણાકાર. અપૂર્ણાંકનું વિભાજન
અપૂર્ણાંક વિસ્તરણ.અપૂર્ણાંકનું મૂલ્ય બદલાતું નથી જો તેના અંશ અને છેદને શૂન્ય સિવાયની સમાન સંખ્યા વડે ગુણાકાર કરવામાં આવે ઉદાહરણ તરીકે,

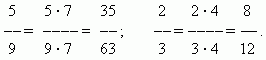
અપૂર્ણાંક ઘટાડવો. અપૂર્ણાંકનું મૂલ્ય બદલાતું નથી જો તમે તેના અંશ અને છેદને શૂન્ય સિવાયની સમાન સંખ્યા વડે વિભાજીત કરો છો.. આ પરિવર્તન કહેવાય છેઅપૂર્ણાંક ઘટાડવો. ઉદાહરણ તરીકે,

અપૂર્ણાંકની તુલના.સમાન અંશ સાથેના બે અપૂર્ણાંકમાંથી, જેનો છેદ નાનો છે તે મોટો છે:

સમાન છેદ સાથેના બે અપૂર્ણાંકમાંથી, જેનો અંશ મોટો છે તે મોટો છે:

ભિન્ન અંશ અને છેદ ધરાવતા અપૂર્ણાંકોની સરખામણી કરવા માટે, તમારે તેમને સામાન્ય છેદ પર લાવવા માટે તેમને વિસ્તૃત કરવાની જરૂર છે.
ઉદાહરણ બે અપૂર્ણાંકની તુલના કરો:

અહીં વપરાયેલ રૂપાંતરણ કહેવાય છે અપૂર્ણાંકને સામાન્ય છેદમાં ઘટાડીને.
અપૂર્ણાંક ઉમેરવા અને બાદબાકી.જો અપૂર્ણાંકોના છેદ સમાન હોય, તો અપૂર્ણાંક ઉમેરવા માટે, તમારે તેમના અંશ ઉમેરવાની જરૂર છે, અને અપૂર્ણાંકને બાદબાકી કરવા માટે, તમારે તેમના અંશો (સમાન ક્રમમાં) બાદબાકી કરવાની જરૂર છે. પરિણામી સરવાળો અથવા તફાવત એ પરિણામનો અંશ હશે; છેદ એ જ રહેશે. જો અપૂર્ણાંકના છેદ અલગ હોય, તો તમારે પહેલા અપૂર્ણાંકને સામાન્ય છેદમાં ઘટાડવો પડશે. ઉમેરતી વખતે મિશ્ર સંખ્યાઓતેમના સંપૂર્ણ અને અપૂર્ણાંક ભાગો અલગથી ઉમેરવામાં આવે છે. મિશ્ર સંખ્યાઓને બાદ કરતી વખતે, અમે પ્રથમ તેમને અયોગ્ય અપૂર્ણાંકમાં રૂપાંતરિત કરવાની ભલામણ કરીએ છીએ, પછી એકને બીજામાંથી બાદ કરીએ છીએ, અને પછી પરિણામને ફરીથી, જો જરૂરી હોય તો, મિશ્ર સંખ્યાના સ્વરૂપમાં રૂપાંતરિત કરીએ છીએ.
ઉદાહરણ

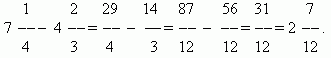
અપૂર્ણાંકનો ગુણાકાર.સંખ્યાને અપૂર્ણાંક વડે ગુણાકાર કરવાનો અર્થ છે અંશ વડે ગુણાકાર કરવો અને ગુણાંકને છેદ વડે ભાગવું. તેથી, અપૂર્ણાંકનો ગુણાકાર કરવા માટે અમારી પાસે સામાન્ય નિયમ છે:અપૂર્ણાંકનો ગુણાકાર કરવા માટે, તમારે તેમના અંશ અને છેદને અલગથી ગુણાકાર કરવાની જરૂર છે અને પ્રથમ ઉત્પાદનને બીજા દ્વારા વિભાજીત કરવાની જરૂર છે..
ઉદાહરણ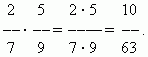
અપૂર્ણાંક વિભાજન. સંખ્યાને અપૂર્ણાંક દ્વારા વિભાજિત કરવા માટે, આ સંખ્યાને પારસ્પરિક અપૂર્ણાંક દ્વારા ગુણાકાર કરવી જરૂરી છે (વિભાગ "અંકગણિત કામગીરી" જુઓ).
ઉદાહરણ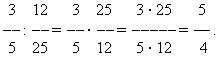

દશાંશ. આખો ભાગ. દશાંશ બિંદુ.
દશાંશ સ્થાનો. દશાંશ અપૂર્ણાંકના ગુણધર્મો.
સામયિક દશાંશ અપૂર્ણાંક. સમયગાળો
દશાંશએકને દસ, સો, હજાર, વગેરે વડે ભાગવાનું પરિણામ છે. ભાગો આ અપૂર્ણાંકો ગણતરીઓ માટે ખૂબ જ અનુકૂળ છે, કારણ કે તે સમાન પર આધારિત છે સ્થિતિકીય સિસ્ટમ, જેના પર પૂર્ણાંકોની ગણતરી અને રેકોર્ડિંગ આધારિત છે. આનો આભાર, દશાંશ સાથે કામ કરવા માટેના સંકેતો અને નિયમો આવશ્યકપણે પૂર્ણ સંખ્યાઓ માટે સમાન છે. દશાંશ અપૂર્ણાંક લખતી વખતે, છેદને ચિહ્નિત કરવાની જરૂર નથી, આ અનુરૂપ અંક દ્વારા કબજે કરેલ સ્થાન દ્વારા નક્કી કરવામાં આવે છે. પ્રથમ તે લખ્યું છેઆખો ભાગ નંબરો, પછી જમણી બાજુએ મૂકોદશાંશ બિંદુ. દશાંશ બિંદુ પછીના પ્રથમ અંકનો અર્થ છે દસમાની સંખ્યા, બીજો - સોની સંખ્યા, ત્રીજો - હજારમાની સંખ્યા, વગેરે. દશાંશ બિંદુ પછી સ્થિત સંખ્યાઓ કહેવામાં આવે છેદશાંશ.
ઉદાહરણ
દશાંશ અપૂર્ણાંકનો એક ફાયદો એ છે કે તે સરળતાથી સામાન્ય અપૂર્ણાંકમાં ઘટાડી શકાય છે: દશાંશ બિંદુ પછીની સંખ્યા (અમારા કિસ્સામાં 5047) અંશ છે; છેદ સમાન છે n -10 ની શક્તિ, ક્યાં n - દશાંશ સ્થાનોની સંખ્યા (અમારા કિસ્સામાં n = 4):
જો દશાંશ અપૂર્ણાંકમાં પૂર્ણાંક ભાગ ન હોય, તો પછી દશાંશ બિંદુ પહેલાં શૂન્ય મૂકવામાં આવે છે:

દશાંશ અપૂર્ણાંકના ગુણધર્મો.

1. જો તમે જમણી બાજુએ શૂન્ય ઉમેરો છો તો દશાંશ બદલાતો નથી:

2. જો તમે સ્થિત શૂન્યને દૂર કરો તો દશાંશ અપૂર્ણાંક બદલાતો નથી
દશાંશના અંતે:

0.00123000 = 0.00123 .

ધ્યાન આપો તમે એવા શૂન્યને દૂર કરી શકતા નથી જે અંતમાં સ્થિત નથી દશાંશ!br />

આ ગુણધર્મો તમને દશાંશને 10, 100, 1000, વગેરે દ્વારા ઝડપથી ગુણાકાર અને વિભાજીત કરવાની મંજૂરી આપે છે.

સામયિક દશાંશ અપૂર્ણાંકઅવધિ તરીકે ઓળખાતા સંખ્યાઓના અનંત પુનરાવર્તિત જૂથ ધરાવે છે. સમયગાળો કૌંસમાં લખાયેલ છે. ઉદાહરણ તરીકે, 0.12345123451234512345… = 0.(12345).

ઉદાહરણ જો આપણે 47 ને 11 વડે ભાગીએ, તો આપણને 4.27272727... = 4.(27) મળશે.

દશાંશનો ગુણાકાર.
દશાંશ વિભાજન.

દશાંશનો ઉમેરો અને બાદબાકી.આ ક્રિયાઓ પૂર્ણાંકો ઉમેરવા અને બાદબાકી કરવા જેવી જ રીતે કરવામાં આવે છે. તમારે ફક્ત સંબંધિત લખવાની જરૂર છે દશાંશએક બીજાની નીચે.
ઉદાહરણ

દશાંશનો ગુણાકાર.પ્રથમ તબક્કે, આપણે દશાંશ બિંદુને ધ્યાનમાં લીધા વિના, સંપૂર્ણ સંખ્યાઓ તરીકે દશાંશ અપૂર્ણાંકનો ગુણાકાર કરીએ છીએ. પછી અરજી કરો આગામી નિયમ: ઉત્પાદનમાં દશાંશ સ્થાનોની સંખ્યા તમામ પરિબળોમાં દશાંશ સ્થાનોના સરવાળા જેટલી છે.
નોંધ: દશાંશ બિંદુ મૂકતા પહેલાઉત્પાદન પાછળના શૂન્ય સાથે કાઢી શકાતું નથી!
ઉદાહરણ

પરિબળોમાં દશાંશ સ્થાનોની સંખ્યાઓનો સરવાળો બરાબર છે: 3 + 4 = 7. ગુણાંકમાં સંખ્યાઓનો સરવાળો 6 છે. તેથી, તમારે ડાબી બાજુએ એક શૂન્ય ઉમેરવાની જરૂર છે: 0197056 અને દશાંશ બિંદુ મૂકવો તેની સામે: 0.0197056.
દશાંશ વિભાજન
દશાંશને પૂર્ણ સંખ્યા વડે ભાગવું
જો ડિવિડન્ડ વિભાજક કરતાં ઓછું , ભાગના પૂર્ણાંક ભાગમાં શૂન્ય લખો અને તેની પછી દશાંશ બિંદુ મૂકો. પછી, ડિવિડન્ડના દશાંશ બિંદુને ધ્યાનમાં લીધા વિના, અમે અપૂર્ણાંક ભાગનો આગળનો અંક તેના પૂર્ણાંક ભાગમાં ઉમેરીએ છીએ અને ફરીથી ડિવિડન્ડના પરિણામી પૂર્ણાંક ભાગની વિભાજક સાથે તુલના કરીએ છીએ. જો નવી સંખ્યા ફરીથી વિભાજક કરતા ઓછી હોય, તો આપણે ભાગાંકમાં દશાંશ બિંદુ પછી બીજું શૂન્ય મૂકીએ અને તેના અપૂર્ણાંક ભાગનો આગળનો અંક ડિવિડન્ડના સંપૂર્ણ ભાગમાં ઉમેરીએ. પરિણામી ડિવિડન્ડ વિભાજક કરતા વધારે ન થાય ત્યાં સુધી અમે આ પ્રક્રિયાને પુનરાવર્તિત કરીએ છીએ. આ પછી, વિભાજન પૂર્ણાંકો માટે કરવામાં આવે છે. જો ડિવિડન્ડ વિભાજક કરતા વધારે અથવા સમાન છે, પ્રથમ આપણે તેના સંપૂર્ણ ભાગને વિભાજીત કરીએ છીએ, ભાગાકારમાં ભાગાકારનું પરિણામ લખીએ છીએ અને દશાંશ બિંદુ મૂકીએ છીએ. આ પછી, વિભાજન પૂર્ણાંકોના કિસ્સામાં ચાલુ રહે છે.
ઉદાહરણ 1.328 ને 64 વડે ભાગો.
ઉકેલ: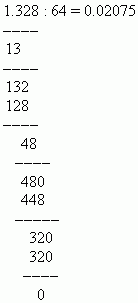
એક દશાંશ અપૂર્ણાંકને બીજા વડે ભાગવું.
પ્રથમ, આપણે ડિવિડન્ડ અને વિભાજકમાં દશાંશ બિંદુઓને વિભાજકમાં દશાંશ સ્થાનોની સંખ્યામાં સ્થાનાંતરિત કરીએ છીએ, એટલે કે, આપણે વિભાજકને પૂર્ણાંક બનાવીએ છીએ. હવે આપણે અગાઉના કેસની જેમ વિભાજન કરીએ છીએ.
ઉદાહરણ 0.04569 ને 0.0006 વડે વિભાજિત કરો.
ઉકેલ: દશાંશ બિંદુ 4 સ્થિતિને જમણી તરફ ખસેડો અને 456.9 ને 6 વડે વિભાજીત કરો:

દશાંશ અપૂર્ણાંકને સામાન્ય અપૂર્ણાંકમાં રૂપાંતરિત કરવા માટે, તમારે દશાંશ બિંદુ પછીની સંખ્યાને અંશ તરીકે લેવાની અને છેદ તરીકે દસની nમી ઘાત લેવાની જરૂર છે. (અહીં n એ દશાંશ સ્થાનોની સંખ્યા છે). બિન-શૂન્ય પૂર્ણાંક ભાગ એક સામાન્ય અપૂર્ણાંકમાં સંગ્રહિત થાય છે; શૂન્ય પૂર્ણાંક ભાગ અવગણવામાં આવ્યો છે. ઉદાહરણ તરીકે:
રિવર્સ કરવા માટે સામાન્ય અપૂર્ણાંકદશાંશ સુધી, તમારે ભાગાકારના નિયમો અનુસાર છેદ દ્વારા અંશને વિભાજિત કરવો આવશ્યક છે.
ઉદાહરણ 5/8 ને દશાંશમાં કન્વર્ટ કરો.
ઉકેલ: 5 ને 8 વડે ભાગવાથી 0.625 મળે છે. (કૃપા કરીને તપાસો!).
મોટાભાગના કિસ્સાઓમાં, આ પ્રક્રિયા અનિશ્ચિત સમય સુધી ચાલુ રહી શકે છે. પછી અપૂર્ણાંકને દશાંશમાં ચોક્કસ રીતે રૂપાંતરિત કરવું અશક્ય છે. પરંતુ વ્યવહારમાં આ ક્યારેય જરૂરી નથી. જો રુચિના દશાંશ સ્થાનો પહેલેથી જ મેળવી લેવામાં આવ્યા હોય તો વિભાજન રદ કરવામાં આવે છે.
ઉદાહરણ 1/3 ને દશાંશમાં કન્વર્ટ કરો.
ઉકેલ: 1 ને 3 વડે ભાગવું અનંત થશે: 1:3 = 0.3333….
કૃપા કરીને તેને તપાસો!