Sayı sanal birimi nasıl gösterilir? Yorum ve isim meselesi üzerine

Hayali birim

Hayali birim- karesi negatif bire eşit olan karmaşık bir sayı.

Matematik ve fizikte sanal birim Latince olarak adlandırılır. Ben veya J. Reel sayılar alanını karmaşık sayılar alanına genişletmenize olanak tanır. Tam tanım bu uzantının yöntemine bağlıdır.

Sanal birimin tanıtılmasının temel nedeni, her polinom denklemi F(X) = 0 reel katsayıları ile reel sayılar alanında çözümlere sahiptir. Örneğin, denklem X 2 + 1 = 0'ın gerçek kökü yoktur. Ancak köklerin karmaşık sayılar olduğunu varsayarsak, bu denklem şu şekilde olur: herhangi başka bir polinom denkleminin bir çözümü var.

Sanal birimin "-1'in karekökü" olduğu ifadesi tamamen doğru değildir, çünkü −1'in iki aritmetiği var karekökler bunlardan biri şu şekilde tanımlanabilir: Ben, diğeri ise – Ben.

Tanım

Sanal birim, karesi -1'e eşit olan bir sayıdır. Böylece Ben denklemin çözümü
veya
Eğer tanımlarsak Ben Dolayısıyla onu bilinmeyen (“hayali”, “sanal”) bir değişken olarak ele alacağız, o zaman denklemin ikinci çözümü şu olacaktır: Ben, değiştirme ile kontrol edilebilir.

Kim ve ne zaman açtı:İtalyan matematikçi Gerolamo Cardano, Leonardo da Vinci'nin arkadaşı, 1545'te.

i sayısına sabit veya hatta gerçek sayı denemez. Ders kitapları bunu, karesi alındığında eksi bir veren bir miktar olarak tanımlar. Yani karenin negatif alanı olan tarafıdır. Gerçekte bu gerçekleşmez. Ancak bazen gerçek olmayan şeylerden de yararlanabilirsiniz.

Bu sabitin keşif tarihi aşağıdaki gibidir. Matematikçi Gerolamo Cardano, denklemleri küplerle çözerken hayali birimi tanıttı. Bu sadece yardımcı bir numaraydı; son cevaplarda i yoktu: onu içeren sonuçlar atıldı. Ancak daha sonra matematikçiler "çöp"lerine daha yakından baktıktan sonra bunu uygulamaya koymaya çalıştılar: çarpma ve bölme normal sayılar hayali birim başına sonuçları birbirine ekleyin ve bunları yeni formüllerde değiştirin. Karmaşık sayılar teorisi böyle doğdu.

Dezavantajı ise "gerçek"in "gerçek dışı" ile karşılaştırılamamasıdır: Daha büyüğün hayali bir birim veya 1 olduğunu söylemek işe yaramaz. Öte yandan, karmaşık sayılar kullanırsanız pratikte çözülemeyen denklem kalmaz. Bu nedenle, karmaşık hesaplamalarla onlarla çalışmak ve yanıtları yalnızca en sonunda "temizlemek" daha uygundur. Örneğin, bir beyin tomogramını deşifre etmek için i olmadan yapamazsınız.

Fizikçiler alanları ve dalgaları tam olarak bu şekilde ele alıyor. Hatta hepsinin karmaşık bir uzayda var olduğunu, gördüklerimizin sadece “gerçek” süreçlerin gölgesi olduğunu düşünebiliriz. Kuantum mekaniği Hem atomun hem de insanın dalga olduğu varsayımı bu yorumu daha da inandırıcı kılmaktadır.

i sayısı, ana matematiksel sabitleri ve eylemleri tek bir formülde özetlemenizi sağlar. Formül şuna benziyor: eπi+1 = 0 ve bazıları böylesine yoğunlaştırılmış bir matematik kuralları dizisinin uzaylılara onları zekamız konusunda ikna etmek için gönderilebileceğini söylüyor.

İkinci dereceden ve kübik denklemleri çözerken ortaya çıkan formdaki ifadelere “sanal” denilmeye başlandı. XVI-XVII yüzyıllar ancak 17. yüzyılın önde gelen bilim adamlarının çoğu için bile sanal niceliklerin cebirsel ve geometrik özü belirsiz görünüyordu. Örneğin Leibniz şöyle yazmıştı: "Tanrı'nın Ruhu, bu analiz mucizesinde en ince çıkışı buldu; fikirler dünyasından bir canavar, varlık ile yokluk arasında yer alan ve olumsuzluğun hayali kökü dediğimiz ikili bir öz. birlik.”

Uzun bir süre, karmaşık sayılar üzerindeki tüm işlemlerin karmaşık sonuçlara yol açıp açmadığı veya örneğin bir kökün çıkarılmasının bazı yeni sayı türlerinin keşfine yol açıp açmayacağı belirsizdi. Derecelerin köklerini ifade etme problemi N itibaren verilen numara Moivre (1707) ve Cotes'in (1722) çalışmalarında çözüldü.

Sembol, bunun için Latince kelimenin ilk harfini alan Euler (1777, 1794'te yayınlandı) tarafından önerildi. hayal ürünü. Her şeyi yaydı standart özellikler Logaritma da dahil olmak üzere karmaşık alana. Euler ayrıca 1751'de karmaşık sayılar alanının cebirsel olarak kapalı olduğu fikrini de dile getirdi. D'Alembert (1747) de aynı sonuca vardı, ancak ilki kesin kanıt Bu gerçek Gauss'a (1799) aittir. Gauss, "karmaşık sayı" terimini 1831'de yaygın kullanıma soktu, ancak bu terim daha önce aynı anlamda kullanılmıştı. Fransız matematikçi 1803'te Lazare Carnot.

Karmaşık sayıların geometrik yorumu ve bunlar üzerindeki işlemler ilk kez Wessel'in (1799) çalışmasında ortaya çıkmıştır. Bu yönde ilk adımlar 1685 yılında Wallis (İngiltere) tarafından atılmıştır. Modern geometrik gösterim Bazen "Argand diyagramı" olarak da anılan diyagram, J. R. Argand'ın Wessel'in sonuçlarını bağımsız olarak tekrarlayan çalışmasının 1806 ve 1814'te yayınlanmasından sonra kullanılmaya başlandı.

Çiftler halinde karmaşık sayıların aritmetik modeli gerçek sayılar Hamilton (1837) tarafından yaptırılmıştır; bu onların özelliklerinin tutarlılığını kanıtladı. Hamilton ayrıca cebiri değişmeli olmayan karmaşık sayılar - kuaterniyonlar - için bir genelleme önerdi.

Tamamlanmamış ikinci dereceden denklemi düşünün:

X 2 = A,

Nerede A bilinen bir miktardır. Bu denklemin çözümü şu şekilde yazılabilir:
Burada üç olası durum vardır:

1).	Eğer bir = 0, o zaman x = 0.
2).	Eğer A – pozitif sayı ise karekökünün iki değeri vardır: biri pozitif, diğeri negatif; örneğin denklem X 2 = 25'in iki kökü vardır: 5 ve – 5. Bu genellikle çift işaretli bir kök olarak yazılır:
3).	Eğer A Negatif bir sayı ise bu denklemin bildiğimiz pozitif ve negatif sayılar arasında çözümü yoktur, çünkü herhangi bir sayının ikinci kuvveti sayıdır. negatif olmayan. Ancak denklemin çözümlerini elde etmek istiyorsak X 2 = A ayrıca için negatif değerler A, yeni türde sayıları tanıtmak zorunda kalıyoruz - hayali sayılar . Böylece, hayali numara aranır ikinci kuvveti negatif bir sayı olan. Sanal sayıların bu tanımına göre tanımlayabiliriz ve hayali birim:

Daha sonra denklem için X 2 = – 25 iki tane elde ederiz hayali kök:

Bu köklerin her ikisini de denklemimizde yerine koyarak özdeşliği elde ederiz. Sanal sayılardan farklı olarak diğer tüm sayılara (pozitif ve negatif, tam sayılar ve kesirler, rasyonel ve irrasyonel) denir. geçerli veya gerçek sayılar . Bir reel sayı ile bir sanal sayının toplamına ne denir karmaşık sayı ve belirlenmiştir:

a + b ben,

Nerede a, b– gerçek sayılar, Ben– hayali birim.

Karmaşık sayılar hakkında daha fazla bilgi için "Karmaşık Sayılar" bölümüne bakın.

Karmaşık sayılara örnekler: 3 + 4 Ben, 7 – 13.6 Ben , 0 + 25 Ben = 25 Ben , 2 + Ben.

Sanal birimin yetkileri

Dereceler Ben bir döngüde tekrarlanır:

Şu formda herhangi bir derece için yazılabilir:

Nerede N- herhangi bir tamsayı.

Buradan:
Nerede mod 4 4'e bölündüğünde kalanı temsil eder.

Reel sayılardan karmaşık sayılar alanına geçiş. Kesin tanım, uzatma yöntemine bağlıdır.

Hayali bir birimin tanıtılmasının nedeni, her polinom denkleminin $f(x)=0$ Reel katsayılarla reel sayılar alanında çözümler vardır. Yani denklem $x^2 + 1 = 0$ gerçek kökleri yoktur. Ancak karmaşık katsayılara sahip herhangi bir polinom denkleminin kapsamlı çözüm- “Cebirin temel teoremi.”

Tarihsel olarak, hayali birim ilk olarak gerçek kübik denklemi çözmek için tanıtıldı: Genellikle, eğer üç gerçek kök varsa, bunlardan ikisini elde etmek için, Cardano'nun formülü karmaşık sayılarda küp kökünün alınmasını gerektiriyordu.

Tanım

Sanal birim, karesi -1 olan bir sayıdır. Onlar. $Ben$ denklemin çözümlerinden biridir

$x^2 + 1 = 0,$ veya $x^2 = -1.$

Ve sonra denklemin ikinci çözümü şu olacak: $-Ben$ , ikame ile doğrulanır.

Sanal birimin yetkileri

Dereceler $Ben$ bir döngüde tekrarlanır:

$\ldots$ $i^(-3) = ben$ $i^(-2) = -1$ $i^(-1) = -i$ $i^0 = 1$ $i^1 = ben$ $i^2 = -1$ $i^3 = -i$ $i^4 = 1$ $\ldots$

Şu formda herhangi bir derece için yazılabilir:

$i^(4n) = 1$ $i^(4n+1) = ben$ $i^(4n+2) = -1$ $i^(4n+3) = -i.$

Nerede N- herhangi bir tamsayı.

Buradan: $i^n = i^(n \bmod 4)$ Nerede mod 4 4'e bölümünden kalandır.

Sayı $ben$ gerçek:

$i^i=(e^((i\pi/2)i))=e^(i^2\pi/2)=e^(-\pi/2)=0(,)20787957635\ldots$

Faktöriyel

Hayali birim faktöriyel Ben 1 + argümanından gama fonksiyonunun değeri olarak tanımlanabilir Ben :

$Ben! = \Gama(1+i) \yaklaşık 0,4980 - 0,1549i.$

$|ben!| = \sqrt(\pi \over \sinh(\pi)) \yaklaşık 0,521564... .$

Hayali birliğin kökleri

Karmaşık sayılar alanında kök N-inci derece var N kararlar. Açık karmaşık düzlem hayali birimin kökleri, birim yarıçaplı bir daire içine yazılan düzenli bir n-gon'un köşelerindedir.

$u_k=\cos (\frac((\frac(\pi)(2)) + 2\pi k)(n)) +i\ \sin (\frac((\frac(\pi)(2)) + 2\pi k)(n))), \quad k=0,1,...,n-1$

Bu, Moivre formülünden ve hayali birimin şu şekilde temsil edilebileceği gerçeğinden kaynaklanmaktadır: trigonometrik form:

$i=\cos\ (\frac(\pi)(2)) + i\ \sin\ (\frac(\pi)(2))$

özellikle, $\sqrt(i ) = \left$\frac(1 + i)(\sqrt(2));\ \frac(-1 - i)(\sqrt(2)) \right$$ Ve $\sqrt(i ) = \left$-i;\ \frac(i + (\sqrt(3))))(2);\ \frac(i - (\sqrt(3))))(2) \right $$

Ayrıca hayali bir birimin kökleri üstel biçimde temsil edilebilir:

$u_k=e^(\frac((\frac(\pi)(2) + 2\pi k) i)(n) ), \quad k=0,1,...,n-1$

Diğer hayali birimler

Cayley-Dixon yapısında (ya da Clifford cebirlerinde), birden fazla “hayali genişleme birimi” olabilir ve/veya bunların kareleri ="+1" ve hatta ="0" olabilir. Ancak bu durumda sıfır bölenler görünebilir ve “i” kompleksinin özelliklerinden farklı olan başka özellikler de vardır. Örneğin, kuaterniyon gövdesinde üç anti-değişmeli sanal birim vardır ve ayrıca denklemin sonsuz sayıda çözümü vardır. $x^2 = -1$ ».

Yorum ve isim meselesi üzerine

Gauss ayrıca, 1, −1 ve √−1 niceliklerine sırasıyla pozitif, negatif ve hayali birimler olarak değil de doğrudan, ters ve ikincil olarak çağrılırsa, insanların bunlarla bir tür bağlantı olduğu izlenimine kapılmayacağını savundu. bu sayılar. karanlık sır. Gauss'a göre geometrik temsil, hayali sayıların gerçek metafiziğini yeni bir ışıkla verir. Descartes'ın "sanal sayılar"ının aksine "karmaşık sayılar" terimini ortaya atan ve √−1'i belirtmek için i sembolünü kullanan Gauss'tu.

Maurice Kline, “Matematik. Kesinlik kaybı." Bölüm VII. Mantıksız gelişme: 19. yüzyılın eşiğinde ciddi zorluklar.

Tanımlar

Ortak tanım $Ben$ , ancak radyo mühendisliğinde hayali birim genellikle gösterilir $J$ anlık akımın tanımıyla karıştırılmaması için: $ben = ben(t)$ .

Ayrıca bakınız

Çift sayılar ve Çift sayılar

"Hayali birim" makalesi hakkında bir inceleme yazın

Notlar

Bağlantılar

Hayali birim // Büyük Sovyet Ansiklopedisi: [30 ciltte] / bölüm. ed. A. M. Prokhorov. - 3. baskı. - M. : Sovyet ansiklopedisi, 1969-1978.



Bin'in güçleri

Eski Rus numaraları

10'un diğer kuvvetleri

On ikinin yetkileri

Diğer bütün

Diğer numaralar

Hayali Birimi karakterize eden alıntı

Birkaç tüccar memurun etrafında toplandı.
- Ah! yalan söylemek zaman kaybıdır! - dedi içlerinden biri, zayıf, sert bir yüzle. “Kafanı çıkardığında, saçın için ağlamazsın.” Ne istersen onu al! “Ve enerjik bir hareketle elini salladı ve memura yan döndü.
İlk tüccar öfkeyle, "Konuşman iyi olur Ivan Sidorich," dedi. - Hoş geldiniz, Sayın Yargıç.
- Ne diyebilirim ki! – diye bağırdı zayıf adam. “Buradaki üç dükkânda yüz bin malım var.” Ordu gittiğinde onu kurtarabilir misin? Eh, millet Tanrı'nın gücü ellerinizle katlamayın!
Birinci tüccar eğilerek, "Lütfen, Sayın Yargıç," dedi. Memur şaşkınlık içinde duruyordu ve yüzünde kararsızlık görülüyordu.
- Ne umurumda! - aniden bağırdı ve sıra boyunca hızlı adımlarla ileri doğru yürüdü. Açık bir dükkanda darbeler ve küfürler duyuldu ve memur ona yaklaşırken gri paltolu ve kafası tıraşlı bir adam kapıdan dışarı atladı.
Bu adam eğilerek tüccarların ve memurun yanından koştu. Polis, dükkanda bulunan askerlere saldırdı. Ancak o sırada Moskvoretsky Köprüsü'nde büyük bir kalabalığın korkunç çığlıkları duyuldu ve memur meydana koştu.
- Ne oldu? Ne oldu? - diye sordu, ama yoldaşı zaten dörtnala Kutsal Aziz Basil'in yanından çığlıklara doğru koşuyordu. Memur atına binip onun peşinden gitti. Köprüye yaklaştığında, iki topun köprüden çıkarıldığını, piyadelerin köprü boyunca yürüdüğünü, birkaç arabanın düştüğünü, birkaç tane de arabanın düştüğünü gördü. korkmuş yüzler ve askerlerin gülen yüzleri. Topların yanında bir çiftin çektiği bir araba duruyordu. Arabanın arkasında, tekerleklerin arkasında toplanmış tasmalı dört tazı vardı. Arabanın üzerinde bir yığın eşya vardı ve en tepede, çocuk sandalyesinin yanında baş aşağı oturan bir kadın tiz ve çaresizce çığlık atıyordu. Yoldaşlar memura, kalabalığın çığlıklarının ve kadın ciyaklamalarının, bu kalabalığa giren General Ermolov'un, askerlerin dükkanlar arasına dağıldığını ve bölge sakinlerinin kalabalığın köprüyü tıkadığını öğrendikten sonra silah emri vermesi nedeniyle meydana geldiğini söyledi. uzuvlardan çıkarılacak ve köprüye ateş edeceği ibretini verecekti. Kalabalık, arabaları deviriyor, birbirlerini eziyor, çaresizce çığlık atıyor, içeri giriyor, köprüyü temizledi ve birlikler ilerledi.

Bu arada şehrin kendisi de boştu. Sokaklarda neredeyse hiç kimse yoktu. Kapılar ve dükkanların hepsi kilitliydi; Orada burada meyhanelerin yakınında yalnız çığlıklar ya da sarhoş şarkılar duyuldu. Sokaklarda kimse araba kullanmıyordu ve yayaların ayak sesleri nadiren duyuluyordu. Povarskaya tamamen sessiz ve ıssızdı. Rostov'ların evinin devasa avlusunda bir taşıma treninin saman artıkları ve pislikleri vardı ve tek bir kişi bile görünmüyordu. Tüm güzellikleriyle geride kalan Rostov'un evinde, geniş oturma odasında iki kişi oturuyordu. Bunlar kapıcı Ignat ve büyükbabasıyla birlikte Moskova'da kalan Vasilich'in torunu Kazak Mishka'ydı. Mishka klavikordunu açtı ve tek parmağıyla çaldı. Kapıcı, kollarını kavuşturmuş ve sevinçle gülümseyerek büyük bir aynanın önünde duruyordu.
- Bu çok akıllıca! A? Ignat Amca! - dedi çocuk aniden iki eliyle anahtarlara vurmaya başladı.
- Bakmak! - Ignat, yüzünün aynada giderek daha fazla gülümsemesine hayret ederek cevap verdi.
- Utanmaz! Gerçekten utanmazca! – sessizce içeri giren Mavra Kuzminishna'nın sesi arkalarından konuştu. - Kalın boynuzlu Eka, dişlerini gösteriyor. Seni bu işe alalım! Oradaki her şey düzenli değil, Vasilich'in ayakları yerden kesiliyor. Ona zaman ver!
Kemerini düzelten Ignat, gülümsemeyi bıraktı ve itaatkar bir şekilde gözlerini indirerek odadan çıktı.
“Teyze, sakin olacağım” dedi çocuk.
- Sana hafif bir tane vereceğim. Küçük tetikçi! – Mavra Kuzminishna bağırdı ve elini ona doğru kaldırdı. -Git dedeye bir semaver kur.
Mavra Kuzminishna tozu silkeledi, klavikordunu kapattı ve derin bir iç çekerek oturma odasından çıktı ve ön kapıyı kilitledi.
Avluya çıkan Mavra Kuzminishna şimdi nereye gitmesi gerektiğini düşündü: Vasilich'in ek binasında çay mı içmeli yoksa kilerde henüz düzenlenmemiş olanı mı toplamalı?
Sessiz sokakta hızlı adım sesleri duyuldu. Adımlar kapıda durdu; mandal, kilidini açmaya çalışan elin altına vurmaya başladı.
Mavra Kuzminishna kapıya yaklaştı.
- Kime ihtiyacın var?
- Kont, Kont Ilya Andreich Rostov.
- Sen kimsin?
- Ben bir memurum. "Görmek isterim" dedi Rus'un hoş ve asil sesi.
Mavra Kuzminishna kapının kilidini açtı. Ve avluya Rostov'lara benzeyen, yaklaşık on sekiz yaşında, yuvarlak yüzlü bir subay girdi.
- Gittik baba. Mavra Kuzmipishna sevgiyle, "Dün ikindi namazında ayrılmaya tenezzül ettik" dedi.
Kapıda duran genç subay, içeri girip girmemekte tereddüt ediyormuş gibi dilini şaklattı.
“Ah, ne yazık!..” dedi. - Keşke dün olsaydı... Ah, ne yazık!..
Bu arada Mavra Kuzminishna, Rostov ırkının yüzündeki tanıdık özellikleri dikkatlice ve sempatik bir şekilde inceledi. genç adam, yırtık pırtık paltosu ve giydiği yıpranmış botları.
- Neden saymaya ihtiyaç duydun? – diye sordu.
- Evet... ne yapmalı! - memur sıkıntıyla dedi ve sanki ayrılmak istiyormuş gibi kapıyı tuttu. Kararsız bir şekilde tekrar durdu.
– Görüyor musun? - aniden dedi. "Ben kontun akrabasıyım ve o bana karşı her zaman çok nazik davrandı." Yani, görüyorsunuz (pelerinine ve botlarına nazik ve neşeli bir gülümsemeyle baktı) ve yıpranmıştı ve parası yoktu; bu yüzden Kont'a sormak istedim...
Mavra Kuzminishna sözünü bitirmesine izin vermedi.

Hayali birim- genellikle karesi −1'e (eksi bir) eşit olan karmaşık bir sayı. Ancak başka seçenekler de mümkündür: Cayley-Dixon'a göre ikiye katlamanın yapımında veya Clifford'a göre cebir çerçevesinde.

Karmaşık sayılar için

Matematik ve fizikte sanal birim Latince olarak adlandırılır. texvc veya İfade ayrıştırılamıyor (Yürütülebilir dosya texvc . Reel sayılar alanını karmaşık sayılar alanına genişletmenize olanak tanır. Kesin tanım, uzatma yöntemine bağlıdır.

Hayali bir birimin tanıtılmasının nedeni, her polinom denkleminin İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulumla ilgili yardım için matematik/BENİOKU'ya bakın.): f(x)=0 Reel katsayılarla reel sayılar alanında çözümler bulunur. Yani denklem İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulum yardımı için math/README'ye bakın.): x^2 + 1 = 0 gerçek kökleri yoktur. Ancak, karmaşık katsayılara sahip herhangi bir polinom denkleminin karmaşık bir çözümü olduğu ortaya çıktı - "Cebirin Temel Teoremi".

Sanal birimin "-1'in karekökü" olduğu ifadesi kesin değildir: sonuçta "-1"in iki kare kökü vardır ve bunlardan biri "i", diğeri "-i" olarak gösterilebilir. Sanal birim olarak hangi kökün alındığı önemli değildir: tüm “i”lerin aynı anda “-i” ve “-i”nin “i” ile değiştirilmesi durumunda tüm eşitlikler geçerli kalacaktır. Ancak bu belirsizlik nedeniyle hatalı hesaplamalardan kaçınmak için notasyon kullanılmamalıdır. İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulum yardımı için math/README'ye bakın.): i radikal aracılığıyla (olduğu gibi İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulum yardımı için math/README'ye bakın.): \sqrt(-1)).

Tanım

Sanal birim, karesi -1 olan bir sayıdır. Onlar. İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulum yardımı için math/README'ye bakın.): i denklemin çözümlerinden biridir

İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Matematik/BENİOKU - kurulum yardımına bakın.): x^2 + 1 = 0, veya İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulumla ilgili yardım için math/README'ye bakın.): x^2 = -1.

Ve sonra denklemin ikinci çözümü şu olacak: İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulum yardımı için math/README'ye bakın.): -i, ikame ile doğrulanır.

Sanal birimin yetkileri

Dereceler İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulum yardımı için math/README'ye bakın.): i bir döngüde tekrarlanır:

İfade ayrıştırılamıyor (Yürütülebilir dosya texvc İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulumla ilgili yardım için math/README'ye bakın.): i^(-3) = i İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulumla ilgili yardım için matematik/BENİOKU'ya bakın.): i^(-2) = -1 İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulum yardımı için matematik/BENİOKU'ya bakın.): i^(-1) = -i İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Matematik/BENİOKU - kurulum yardımına bakın.): i^0 = 1 İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulum yardımı için math/README'ye bakın.): i^1 = i İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Matematik/BENİOKU - kurulum yardımına bakın.): i^2 = -1 İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulumla ilgili yardım için math/README'ye bakın.): i^3 = -i İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulum yardımı için math/README'ye bakın.): i^4 = 1 İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulum yardımı için math/README'ye bakın.): \ldots

Şu formda herhangi bir derece için yazılabilir:

İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulum yardımı için math/README'ye bakın.): i^(4n) = 1 İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulumla ilgili yardım için math/README'ye bakın.): i^(4n+1) = i İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulumla ilgili yardım için math/README'ye bakın.): i^(4n+2) = -1 İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulumla ilgili yardım için math/README'ye bakın.): i^(4n+3) = -i.

Nerede N- herhangi bir tamsayı.

Buradan: İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulum yardımı için math/README'ye bakın.): i^n = i^(n \bmod 4) Nerede mod 4 4'e bölümünden kalandır.

Sayı İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Math/README'ye bakın - kurulumla ilgili yardım.): i^i gerçek:

İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Matematik/BENİOKU - kurulum yardımına bakın.): i^i=(e^((i\pi/2)i))=e^(i^2\pi/2)=e^(-\pi/ 2 )=0(,)20787957635\ldots

Faktöriyel

Hayali birim faktöriyel Ben 1 + argümanından gama fonksiyonunun değeri olarak tanımlanabilir Ben :

İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Math/README'ye bakın - kurulumla ilgili yardım.): i! = \Gama(1+i) \yaklaşık 0,4980 - 0,1549i. İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulum yardımı için math/README'ye bakın.): |i!| = \sqrt(\pi \over \sinh(\pi)) \yaklaşık 0,521564... .

Hayali birliğin kökleri

Karmaşık sayılar alanında kök N-inci derece var N kararlar. Karmaşık düzlemde, hayali birimin kökleri, birim yarıçaplı bir daire içine yazılan düzenli bir n-gon'un köşelerinde bulunur.

İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulumla ilgili yardım için matematik/BENİOKU'ya bakın.): u_k=\cos (\frac((\frac(\pi)(2)) + 2\pi k)(n)) +i\ \sin (\frac( (\frac(\pi)(2)) + 2\pi k)(n)), \quad k=0,1,...,n-1

Bu, Moivre formülünden ve hayali birimin trigonometrik biçimde temsil edilebileceği gerçeğinden kaynaklanmaktadır:

İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Matematik/BENİOKU - kurulum yardımına bakın.): i=\cos\ (\frac(\pi)(2)) + i\ \sin\ (\frac(\pi)(2))

özellikle, İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulumla ilgili yardım için matematik/BENİOKU'ya bakın.): \sqrt(i ) = \left$\frac(1 + i)(\sqrt(2));\ \frac(-1 - i)(\sqrt( 2) )) \Sağ$ Ve İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulum yardımı için matematik/BENİOKU'ya bakın.): \sqrt(i ) = \left$-i;\ \frac(i + (\sqrt(3))))(2);\ \frac(i - ( \sqrt) (3))))(2) \sağ$

Ayrıca hayali bir birimin kökleri üstel biçimde temsil edilebilir:

İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Matematik/BENİOKU - kurulum yardımına bakın.): u_k=e^(\frac((\frac(\pi)(2) + 2\pi k) i)(n) ), \quad k=0,1 , ...,n-1

Diğer hayali birimler

Yorum ve isim meselesi üzerine

Gauss ayrıca, 1, −1 ve √−1 niceliklerine sırasıyla pozitif, negatif ve hayali birimler olarak değil de doğrudan, ters ve tesadüfi olarak çağrılırsa, insanların bir tür kasvetli bağlantı olduğu izlenimine kapılmayacağını savundu. bu numaralarla. Gauss'a göre geometrik temsil, hayali sayıların gerçek metafiziğini yeni bir ışıkla verir. Descartes'ın "sanal sayılar"ının aksine "karmaşık sayılar" terimini ortaya atan ve √−1'i belirtmek için i sembolünü kullanan Gauss'tu.

Maurice Kline, “Matematik. Kesinlik kaybı." Bölüm VII. Mantıksız gelişme: 19. yüzyılın eşiğinde ciddi zorluklar.

Tanımlar

Ortak tanım İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulum yardımı için math/README'ye bakın.): i, ancak radyo mühendisliğinde hayali birim genellikle gösterilir İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulum yardımı için math/README'ye bakın.): j anlık akımın tanımıyla karıştırılmaması için: İfade ayrıştırılamıyor (Yürütülebilir dosya texvc bulunamadı; Kurulum yardımı için math/README'ye bakın.): i = i (t) .

Ayrıca bakınız

Çift sayılar ve Çift sayılar

"Hayali birim" makalesi hakkında bir inceleme yazın

Notlar

Bağlantılar

Hayali birim // Büyük Sovyet Ansiklopedisi: [30 ciltte] / bölüm. ed. A. M. Prokhorov. - 3. baskı. - M. : Sovyet ansiklopedisi, 1969-1978.

Bu şablonu görüntüle

Bin'in güçleri

Eski Rus numaraları

10'un diğer kuvvetleri

On ikinin yetkileri

Diğer bütün

Diğer numaralar

Hayali Birimi karakterize eden alıntı

– Bu öğretilemez Isidora. İnsanların Işığa, İyiliğe ihtiyacı olmalı. Değişimi kendileri istiyor olmalılar. Zorla verilen şeyi kişi, hiçbir şeyi anlamaya bile çalışmadan içgüdüsel olarak hızla reddetmeye çalışır. Ama konu dışına çıkıyoruz, Isidora. Radomir ve Magdalena'nın hikayesine devam etmemi ister misin?
Olumlu anlamda başımı salladım, kaderin bana ne verdiği konusunda endişelenmeden onunla bu kadar basit ve sakin bir şekilde konuşamadığım için kalbimde derin bir pişmanlık duydum. son dakikalar sakat hayatım ve Anna'nın başına gelen talihsizliği dehşetle düşünmemek...
– İncil Vaftizci Yahya hakkında çok şey yazıyor. Gerçekten Radomir ve Tapınak Şövalyeleri ile birlikte miydi? İmajı o kadar şaşırtıcı derecede iyi ki, bazen John'un gerçek figür olup olmadığı konusunda şüphe uyandırıyor. Cevap verebilir misin Kuzey?
North sıcak bir şekilde gülümsedi, görünüşe göre onun için çok hoş ve değerli bir şeyi hatırlıyordu...
– John bilge ve nazikti, tıpkı büyük bir adam gibi sıcak güneş... Yanında yürüyen herkesin babası, öğretmeni ve arkadaşıydı... Değer verildi, itaat edildi ve sevildi. Ancak hiçbir zaman sanatçıların onu resmettiği gibi genç ve inanılmaz derecede yakışıklı bir genç adam olmadı. O zamanlar John zaten yaşlı bir büyücüydü ama yine de çok güçlü ve ısrarcıydı. Gri saçlı ve uzun boylu, inanılmaz derecede yakışıklı ve nazik bir genç adamdan çok, güçlü, destansı bir savaşçıya benziyordu. Çok giyiyordu uzun saç ve Radomir'in yanındaki herkes.

Radan'dı bu, gerçekten olağanüstü derecede yakışıklıydı. Radomir gibi o da küçük yaşlardan itibaren Meteora'da annesi Büyücü Maria'nın yanında yaşadı. Unutma Isidora, Meryem'in hemen hemen aynı yaştaki iki bebekle resmedildiği kaç tablo var. Bazı nedenlerden dolayı, tüm ünlü sanatçılar, belki de fırçalarının gerçekte kimi tasvir ettiğini bile anlamadan onları resmetmişlerdir... Ve en ilginç olanı, Maria'nın tüm bu resimlerde baktığı şeyin Radan olmasıdır. Görünüşe göre o zaman bile, henüz bebekken Radan, kısa hayatı boyunca kaldığı kadar neşeli ve çekiciydi...

Ve yine de... sanatçılar bu resimlerde John'u resmetmiş olsalar bile, kaprisli Salome'nin isteği üzerine idam edilene kadar aynı John nasıl bu kadar canavarca yaşlanmış olabilir?.. Sonuçta, İncil'e göre bu, İsa'nın çarmıha gerilmesinden önce bile gerçekleşti, bu da Yuhanna'nın o sırada otuzdan fazla olmaması gerektiği anlamına geliyor dört yıl! Nasıl oldu da kız gibi yakışıklı, altın saçlı genç bir adamdan yaşlı ve tamamen çekici olmayan bir Yahudi'ye dönüştü?

- Yani Büyücü John ölmedi mi Sever? – diye sevinçle sordum. – Yoksa başka bir şekilde mi öldü?..
“Maalesef gerçek John'un gerçekten kafası kesildi Isidora ama bu kaprisli şımarık bir kadının kötü iradesi yüzünden olmadı. Ölüm nedeni, güvendiği ve birkaç yıldır evinde yaşadığı Yahudi “arkadaşının” ihanetiydi...
- Peki nasıl hissetmedi? Bunun nasıl bir “arkadaş” olduğunu nasıl görmedin? – Öfkeliydim.
– Her insandan şüphelenmek muhtemelen imkansız, Isidora… Bence birine güvenmeleri zaten yeterince zordu çünkü hepsi bir şekilde uyum sağlamak ve o yabancı, yabancı ülkeye yaşamak zorundaydı, bunu unutma. Çünkü büyüklerden ve daha az kötülük görünüşe göre daha azını seçmeye çalıştılar. Ama her şeyi tahmin etmek imkansız, bunu çok iyi biliyorsun Isidora... Büyücü John'un ölümü Radomir'in çarmıha gerilmesinden sonra meydana geldi. O sırada Yahya'nın ölen İsa'nın ailesiyle birlikte evinde yaşadığı bir Yahudi tarafından zehirlendi. Bir akşam, bütün ev uykudayken, John'la konuşan ev sahibi ona güçlü bir bitkisel zehirle karıştırılmış en sevdiği çayı ikram etti... Ertesi sabah kimse ne olduğunu anlayamadı bile. Sahibine göre, John hemen uykuya daldı ve bir daha hiç uyanmadı... Cesedi sabah kanlı yatağında... başı kesilmiş halde bulundu... Aynı sahibine göre, Yahudiler çok John'dan korkuyorlardı çünkü onu eşsiz bir sihirbaz olarak görüyorlardı. Ve bir daha ayağa kalkamayacağından emin olmak için kafasını kestiler. John'un kafası daha sonra onlardan satın alındı \u200b\u200b(!!!) ve Tapınak Şövalyeleri tarafından yanlarında götürüldü, onu korumayı ve Magi Vadisi'ne getirmeyi başardılar, böylece John'a en azından bu kadar küçük, ama değerli ve hak edilmiş saygıyı, Yahudilerin onunla alay etmesine izin vermeden, kendi bazı işlerini yaparak büyülü ritüeller. O andan itibaren, nerede olurlarsa olsunlar John'un kafası daima onlarla birlikteydi. Ve aynı kafa için, iki yüz yıl sonra, Tapınak Şövalyeleri, Şeytan'a suç sayılan tapınmayla suçlandılar... Son “Tapınak Şövalyeleri vakasını” (Tapınak Şövalyeleri) hatırlıyorsun, değil mi Isidora ? Orada, tüm kilise din adamlarını çileden çıkaran bir "konuşan kafaya" tapınmakla suçlandılar.

- Bağışla Sever ama Tapınak Şövalyeleri neden John'un kafasını Meteora'ya getirmediler? Çünkü anladığım kadarıyla hepiniz onu çok seviyordunuz! Peki tüm bu detayları nereden biliyorsun? Sen onlarla birlikte değildin, değil mi? Bütün bunları sana kim anlattı?
- Bütün bunları bize anlattı üzücü hikaye Cadı Maria, Radan ve Radomir'in annesi...
– Meryem, İsa'nın idamından sonra yanınıza döndü mü?!.. Sonuçta bildiğim kadarıyla çarmıha gerilirken oğlunun yanındaydı. Sana ne zaman döndü? Hala hayatta olması mümkün mü?.. – diye sordum nefesimi tutarak.

Ders: Hayali birim , o derece. Karmaşık sayılar.

Cebirsel biçim kapsayıcı sayılar.

Hedefler: Sayı kavramını genişletmek, sanal birim kavramını ve onun kuvvetlerini tanıtmak, kavramı tanıtmak karmaşık sayı; karmaşık bir sayının cebirsel biçimini düşünün; Edinilen bilgiyi genelleştirme yeteneğini geliştirmek, gelişimi teşvik etmek;

mantıksal düşünme öğrencileri eğitmek bilinçli tutum

öğrenme sürecine. ( Planı )

incelenmekte olan konular

Karmaşık sayının tanımı.

Cebirsel form karmaşık sayı.

1.Hayali sayılar

Tanım. Karesi -1 olan sayıya sanal birim denir ve

ile gösterilir і ; і 2 = -1

Tanım. Formu olan sayılar B і b bir gerçel sayı olmak üzere, denir

hayali sayılar.

Örneğin:

Gerçek sayıların OX ekseni üzerindeki noktalarla temsil edildiği bilinmektedir. Hayali sayılar OU eksenindeki noktalarla temsil edilir ve bu nedenle OX ekseni denir gerçek eksen ve OU ekseni hayali eksendir. Sanal sayılar kümesi, gerçek sayılar kümesiyle bire bir karşılık gelir.

Tanım. İki sanal sayı B 1 Ben Ve B 2 Ben eğer eşit denirse B 1 = B 2

Tanım. Hayali sayı (- bi ) sanal bir sayının tersi denir B і .

Örneğin:
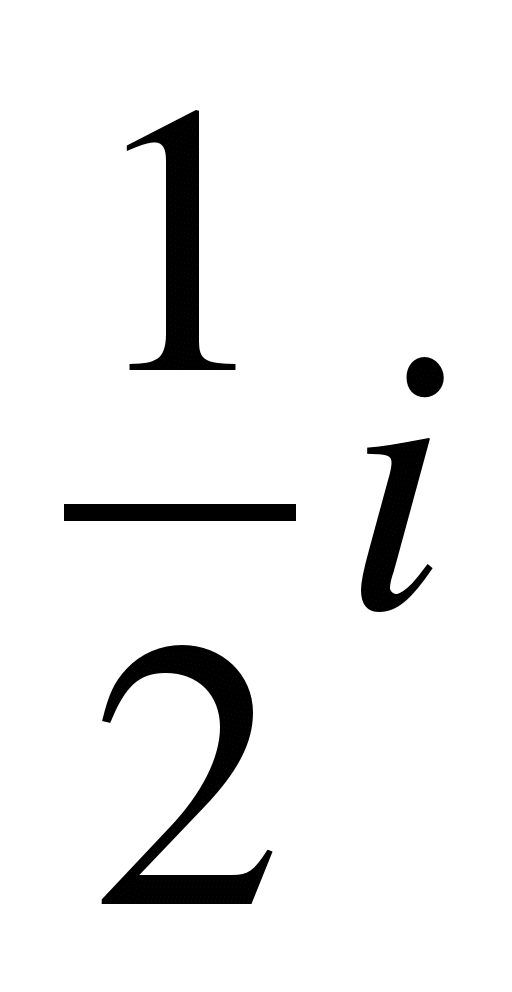Ve
Ve
.

Teorem. Bir sayının herhangi bir doğal kuvveti і dönüştürülebilir

dört türden biri 1; і ; -1; -і.

Kanıt .

İfadeyi düşünün і M , nerede m - doğal sayı. Dört durumun mümkün olduğu açıktır:

1) M = 4 k , k =1,2, ...

2) m=4k +1, k =0, 1,2,...

3) M 4k +2, k = 0,1,2,...

4) M = 4k +3, k =0,1,2, ....

İzin vermek M = 4 k , Daha sonra і M =і Ak =(і A ) İle =1 İle =1

İzin vermekM =4 k +1, Daha sonra і M = і Ak+1 = і Ak ben=1i=i

İzin vermek M = 4 k +2, Daha sonraі M =і Ak+2 = і Ak і 2 = 1(-1)=-1

İzin vermekM =4 k +3, Daha sonra і M

Örnek. Bir ifadenin değerini hesaplayın

Çözüm:

Yorum. Hayali bir birimin gücünü hesaplamak için aşağıdaki kuralı kullanmak uygundur:

1) üssü 4'e bölün;

2) i'yi değiştir M bende R burada p, t'nin 4'e bölünmesiyle elde edilen kalandır, yani p sayısı t = 4k + p eşitliğinden bulunur.

2. Karmaşık sayılar

Tanım. Karmaşık sayı, şu forma sahip bir sayıdıra+bi , burada a, b –

gerçek sayılar, i sanal birimdir. Bu durumda “a” sayısına denir.

karmaşık bir sayının gerçek kısmı, "b" - hayali kısım

karmaşık sayı.

Sembolik olarak karmaşık bir sayının gerçek ve sanal kısımları şu şekilde gösterilir:(sıfırla), (yapmıyorlar).

Bu tanımlamalar ilk harflere dayanmaktadır. Latince kelimeler"gerçek" anlamına gelen "Hayali" ve "hayali" anlamına gelen "Hayali".

Yorum. Bazen karmaşık bir sayının sanal kısmız = A + B і bi denir.

Tanım. İki karmaşık sayıZ 1 = A 1 + B 1 Ben Vez 2 = A 2 + B 1 Ben eğer eşit denirse

Tekrarz 1 =Yenidenz 2 , Benz 1 = Benz 2 .

Karmaşık sayılar için büyük ve küçük kavramı yoktur, yani karmaşık sayılar karşılaştırılamaz.

Tanım. Karmaşık sayı(-A- bi ) karmaşık bir sayının tersi denir

a + b.

Tanım. Gerçel kısımları eşit ve imajiner kısımları eşit olan iki karmaşık sayı

parçalarkarşıt sayılara karmaşık eşlenik sayılar denir ve

buna göre belirlenir Ve.

3. Karmaşık sayının cebirsel formu. Cebirsel biçimde verilen karmaşık sayılara ilişkin eylemler.

Karmaşık sayı şu şekilde temsil edilir:
karmaşık sayı denircebirsel form .

Karmaşık sayıların eklenmesi

Tanım. İki karmaşık sayının toplamı
Ve
isminde

karmaşık sayı.

Yani, (1)

Bu nedenle, iki karmaşık sayıyı toplamak için, bunların gerçek kısımlarını eklemeniz gerekir; bu, toplamın gerçek kısmını verir ve sanal kısımları toplayarak toplamın sanal kısmını verir.

Eşlenik sayıların toplamı her zaman reeldir sayı

yani
. (2)

Karmaşık Sayılarda Çıkarma

Tanım. İki karmaşık sayının farkı
Ve
buna denir

karmaşık sayı
, bu sayıya eklenir bir sayı verir .

Karmaşık sayıların çıkarılması her zaman mümkündür.

Teorem. Herhangi bir karmaşık sayı için
Ve
her zaman bir fark vardır
benzersiz bir şekilde belirlenir.

Dolayısıyla karmaşık sayıları çıkarmak için, bunların gerçek kısımlarını çıkarıp farklarını farkın gerçek kısmı olarak almak ve ayrıca farkın sanal kısmını çıkarmak yeterlidir.

Görünüşe göre (3)

İki eşlenik sayının farkı her zaman sanal bir sayıdır. ,

yani
(4)

Karmaşık sayıları çarpma

Tanım. İki karmaşık sayının çarpımı
ve aşağıdaki formülle belirlenen böyle bir karmaşık sayı denir: (5)

Karmaşık sayıları çarpmak için bunları polinomlarla çarpma kuralına göre çarpmalısınız, yerine -1'e kadar ve benzer terimleri getirin.

Karmaşık sayıları çarparken doğrudan çarpma yapmak daha iyidir. Eşlenik sayıların çarpımı her zaman gerçek sayı Cevap.

Güvenlik soruları:

1.Karmaşık sayının tanımını veriniz.

2.Hayali bir birimin tanımını formüle edin.

3. Sanal bir birimin derecesi nasıl bulunur?

4. Hangi karmaşık sayılara eşit ve eşlenik denir?

5.Hayali bir birimin keyfi kuvvetini bulmak için bir formül yazın.

6. Tamamen sanal sayılara örnekler verin.

7. İki karmaşık sayının toplamını, çarpımını ve bölümünü tanımlayın.

Edebiyat

Yazılı, D. T. Ders notları yüksek matematik: tam kurs D.T. Yazıldı. – 9. baskı. – M.: Iris-press, 2009. 608 s.: hasta. – (Yüksek öğrenim).

Lungu, K. N. Yüksek matematikte problemlerin toplanması. 1. yıl / K. N. Lungu, D. T. Pismenny, S. N. Fedin, Yu. – 7. baskı. – M.: Iris-press, 2008. 576 s.: – (Yüksek öğrenim).

Grigoriev V.P. Yüksek matematiğin unsurları: öğrenciler için bir ders kitabı. kurumlar prof. eğitim / V. P. Grigoriev, Yu. – 10. baskı, silindi. – M. Yayın merkezi “Akademi”, 2014. – 320 s.