Le problème B9 donne le graphique d’une fonction ou d’une dérivée à partir de laquelle vous devez déterminer l’une des quantités suivantes :

1. La valeur de la dérivée à un moment donné x 0,
2. Points maximum ou minimum (points extremum),
3. Intervalles de fonctions croissantes et décroissantes (intervalles de monotonie).

Les fonctions et dérivées présentées dans ce problème sont toujours continues, ce qui rend la solution beaucoup plus facile. Malgré le fait que la tâche appartient à la section analyse mathématique, c'est tout à fait à la portée des étudiants, même les plus faibles, puisqu'il n'y a pas de profondeur connaissances théoriques pas requis ici.

Pour trouver la valeur de la dérivée, des points extrêmes et des intervalles de monotonie, il existe des algorithmes simples et universels - ils seront tous discutés ci-dessous.

Lisez attentivement les conditions du problème B9 pour éviter de commettre des erreurs stupides : parfois vous tombez sur des textes assez longs, mais conditions importantes, qui influencent le cours de la décision, il y en a peu.

Calcul de la valeur dérivée. Méthode en deux points

Si le problème est donné un graphique d'une fonction f(x), tangente à ce graphique en un certain point x 0, et qu'il est nécessaire de trouver la valeur de la dérivée à ce point, l'algorithme suivant est appliqué :

1. Trouvez deux points « adéquats » sur le graphique tangent : leurs coordonnées doivent être entières. Notons ces points comme A (x 1 ; y 1) et B (x 2 ; y 2). Notez correctement les coordonnées - c'est point clé solutions, et toute erreur ici entraîne une réponse incorrecte.
2. Connaissant les coordonnées, il est facile de calculer l'incrément de l'argument Δx = x 2 − x 1 et l'incrément de la fonction Δy = y 2 − y 1 .
3. Enfin, on retrouve la valeur de la dérivée D = Δy/Δx. En d'autres termes, vous devez diviser l'incrément de la fonction par l'incrément de l'argument - et ce sera la réponse.

Notons encore une fois : les points A et B doivent être recherchés précisément sur la tangente, et non sur le graphe de la fonction f(x), comme cela arrive souvent. La ligne tangente contiendra nécessairement au moins deux de ces points - sinon le problème ne sera pas formulé correctement.

Considérez les points A (−3 ; 2) et B (−1 ; 6) et trouvez les incréments :
Δx = x 2 − x 1 = −1 − (−3) = 2 ; Δy = y 2 − y 1 = 6 − 2 = 4.

Trouvons la valeur de la dérivée : D = Δy/Δx = 4/2 = 2.

Tâche. La figure montre un graphique de la fonction y = f(x) et une tangente à celle-ci au point d'abscisse x 0. Trouver la valeur de la dérivée de la fonction f(x) au point x 0 .

Considérez les points A (0 ; 3) et B (3 ; 0), trouvez les incréments :
Δx = x 2 − x 1 = 3 − 0 = 3 ; Δy = y 2 − y 1 = 0 − 3 = −3.

On trouve maintenant la valeur de la dérivée : D = Δy/Δx = −3/3 = −1.

Tâche. La figure montre un graphique de la fonction y = f(x) et une tangente à celle-ci au point d'abscisse x 0. Trouver la valeur de la dérivée de la fonction f(x) au point x 0 .

Considérez les points A (0 ; 2) et B (5 ; 2) et trouvez les incréments :
Δx = x 2 − x 1 = 5 − 0 = 5 ; Δy = y 2 − y 1 = 2 − 2 = 0.

Reste à trouver la valeur de la dérivée : D = Δy/Δx = 0/5 = 0.

Depuis dernier exemple on peut formuler une règle : si la tangente est parallèle à l'axe OX, la dérivée de la fonction au point de tangence est nulle. Dans ce cas, vous n’avez même pas besoin de compter quoi que ce soit : il suffit de regarder le graphique.

Calcul des points maximum et minimum

Parfois, au lieu d'un graphique d'une fonction, le problème B9 donne un graphique de la dérivée et nécessite de trouver le point maximum ou minimum de la fonction. Dans cette situation, la méthode en deux points est inutile, mais il existe un autre algorithme encore plus simple. Tout d'abord, définissons la terminologie :

1. Le point x 0 est appelé le point maximum de la fonction f(x) si dans un certain voisinage de ce point l'inégalité suivante est vraie : f(x 0) ≥ f(x).
2. Le point x 0 est appelé le point minimum de la fonction f(x) si dans un certain voisinage de ce point l'inégalité suivante est vraie : f(x 0) ≤ f(x).

Afin de trouver les points maximum et minimum à partir du graphique dérivé, suivez simplement ces étapes :

1. Redessinez le graphique dérivé en supprimant toutes les informations inutiles. Comme le montre la pratique, les données inutiles ne font qu'interférer avec la décision. On note donc sur axe de coordonnées les zéros de la dérivée - c'est tout.
2. Découvrez les signes de la dérivée sur les intervalles entre zéros. Si pour un point x 0 on sait que f'(x 0) ≠ 0, alors seules deux options sont possibles : f'(x 0) ≥ 0 ou f'(x 0) ≤ 0. Le signe de la dérivée est facile à déterminer à partir du dessin original : si le graphe dérivé se situe au-dessus de l'axe OX, alors f'(x) ≥ 0. Et vice versa, si le graphe dérivé se situe sous l'axe OX, alors f'(x) ≤ 0.
3. Nous vérifions à nouveau les zéros et les signes de la dérivée. Là où le signe passe de moins à plus, c'est le point minimum. A l’inverse, si le signe de la dérivée passe du plus au moins, c’est le point maximum. Le comptage se fait toujours de gauche à droite.

Ce schéma ne fonctionne que pour les fonctions continues – il n’y en a pas d’autres dans le problème B9.

Tâche. La figure montre un graphique de la dérivée de la fonction f(x) définie sur l'intervalle [−5; 5]. Trouvez le point minimum de la fonction f(x) sur ce segment.

Débarrassons-nous informations inutiles— ne laissons que les frontières [−5; 5] et les zéros de la dérivée x = −3 et x = 2,5. On note également les signes :

Évidemment, au point x = −3, le signe de la dérivée passe de moins à plus. C'est le point minimum.

Tâche. La figure montre un graphique de la dérivée de la fonction f(x) définie sur l'intervalle [−3; 7]. Trouvez le point maximum de la fonction f(x) sur ce segment.

Redessinons le graphique en ne laissant que les limites [−3; 7] et les zéros de la dérivée x = −1,7 et x = 5. Notons les signes de la dérivée sur le graphique résultant. Nous avons:

Évidemment, au point x = 5, le signe de la dérivée passe du plus au moins - c'est le point maximum.

Tâche. La figure montre un graphique de la dérivée de la fonction f(x), définie sur l'intervalle [−6; 4]. Trouver le nombre de points maximum de la fonction f(x) appartenant au segment [−4; 3].

Des conditions du problème il résulte qu'il suffit de considérer uniquement la partie du graphe limitée par le segment [−4 ; 3]. C'est pourquoi nous construisons nouvel horaire, sur lequel on marque uniquement les frontières [−4; 3] et les zéros de la dérivée à l'intérieur. A savoir, les points x = −3,5 et x = 2. On obtient :

Sur ce graphique il n'y a qu'un seul point maximum x = 2. C'est à ce point que le signe de la dérivée passe du plus au moins.

Une petite note sur les points avec des coordonnées non entières. Par exemple, dans dernière tâche le point x = −3,5 a été considéré, mais avec le même succès on peut prendre x = −3,4. Si le problème est correctement rédigé, de tels changements ne devraient pas affecter la réponse, car les points « sans domicile fixe » n'acceptent pas participation directe dans la résolution du problème. Bien entendu, cette astuce ne fonctionnera pas avec des points entiers.

Trouver des intervalles de fonctions croissantes et décroissantes

Dans un tel problème, comme les points maximum et minimum, il est proposé d'utiliser le graphe dérivé pour trouver les zones dans lesquelles la fonction elle-même augmente ou diminue. Tout d’abord, définissons ce que sont l’augmentation et la diminution :

1. Une fonction f(x) est dite croissante sur un segment si pour deux points quelconques x 1 et x 2 de ce segment l'énoncé suivant est vrai : x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2) . En d’autres termes, plus la valeur de l’argument est grande, plus la valeur de la fonction est grande.
2. Une fonction f(x) est appelée décroissante sur un segment si pour deux points quelconques x 1 et x 2 de ce segment l'énoncé suivant est vrai : x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Ceux. valeur plus élevée correspondances d'arguments valeur inférieure fonctions.

Formulons conditions suffisantes ascendant et descendant :

1. Pour fonction continue f(x) a augmenté sur le segment , il suffit que sa dérivée à l'intérieur du segment soit positive, c'est-à-dire f'(x) ≥ 0.
2. Pour qu'une fonction continue f(x) décroisse sur le segment , il suffit que sa dérivée à l'intérieur du segment soit négative, c'est-à-dire f'(x) ≤ 0.

Acceptons ces déclarations sans preuves. Ainsi, nous obtenons un schéma pour trouver des intervalles d'augmentation et de diminution, qui est à bien des égards similaire à l'algorithme de calcul des points extremum :

1. Supprimez toutes les informations inutiles. Dans le graphique original de la dérivée, nous nous intéressons principalement aux zéros de la fonction, nous ne les laisserons donc que.
2. Marquez les signes de la dérivée aux intervalles entre les zéros. Où f'(x) ≥ 0, la fonction augmente, et où f'(x) ≤ 0, elle diminue. Si le problème impose des restrictions sur la variable x, nous les marquons en plus sur un nouveau graphique.
3. Maintenant que l'on connaît le comportement de la fonction et les contraintes, il reste à calculer la quantité requise dans le problème.

Tâche. La figure montre un graphique de la dérivée de la fonction f(x) définie sur l'intervalle [−3; 7.5]. Trouver les intervalles de diminution de la fonction f(x). Dans votre réponse, indiquez la somme des entiers compris dans ces intervalles.

Comme d'habitude, redessinons le graphique et marquons les limites [−3 ; 7,5], ainsi que les zéros de la dérivée x = −1,5 et x = 5,3. Puis on note les signes de la dérivée. Nous avons:

Puisque la dérivée est négative sur l'intervalle (− 1,5), c'est l'intervalle de fonction décroissante. Il reste à additionner tous les entiers qui se trouvent à l'intérieur de cet intervalle :
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Tâche. La figure montre un graphique de la dérivée de la fonction f(x), définie sur l'intervalle [−10 ; 4]. Trouver les intervalles d'augmentation de la fonction f(x). Dans votre réponse, indiquez la longueur du plus grand d’entre eux.

Débarrassons-nous des informations inutiles. Laissons seulement les frontières [−10 ; 4] et les zéros de la dérivée, qui étaient cette fois quatre : x = −8, x = −6, x = −3 et x = 2. Marquons les signes de la dérivée et obtenons l'image suivante :

Nous nous intéressons aux intervalles de fonction croissante, c'est-à-dire tel que f'(x) ≥ 0. Il existe deux de ces intervalles sur le graphique : (−8 ; −6) et (−3 ; 2). Calculons leurs longueurs :
l 1 = − 6 − (−8) = 2 ;
l 2 = 2 − (−3) = 5.

Puisque nous devons trouver la longueur du plus grand des intervalles, nous notons la valeur l 2 = 5 comme réponse.

L’opération consistant à trouver la dérivée est appelée différenciation.

À la suite de la résolution des problèmes de recherche de dérivées des fonctions les plus simples (et pas très simples) en définissant la dérivée comme la limite du rapport de l'incrément à l'incrément de l'argument, un tableau de dérivées est apparu et exactement certaines règles différenciation. Les premiers à travailler dans le domaine de la recherche de dérivés furent Isaac Newton (1643-1727) et Gottfried Wilhelm Leibniz (1646-1716).

Par conséquent, à notre époque, pour trouver la dérivée d'une fonction, vous n'avez pas besoin de calculer la limite mentionnée ci-dessus du rapport de l'incrément de la fonction à l'incrément de l'argument, mais il vous suffit d'utiliser le tableau de dérivés et les règles de différenciation. L'algorithme suivant convient pour trouver la dérivée.

Pour trouver la dérivée, il vous faut une expression sous le signe premier décomposer des fonctions simples en composants et déterminer quelles actions (produit, somme, quotient) ces fonctions sont liées. Autres dérivés fonctions élémentaires on retrouve dans le tableau des dérivées, et les formules des dérivées du produit, somme et quotient sont dans les règles de différenciation. La table des dérivées et les règles de différenciation sont données après les deux premiers exemples.

Exemple 1. Trouver la dérivée d'une fonction

Solution. À partir des règles de différenciation, nous découvrons que la dérivée d'une somme de fonctions est la somme des dérivées de fonctions, c'est-à-dire

À partir du tableau des dérivées, nous découvrons que la dérivée de "x" est égale à un et que la dérivée du sinus est égale au cosinus. Nous substituons ces valeurs dans la somme des dérivées et trouvons la dérivée requise par la condition du problème :

Exemple 2. Trouver la dérivée d'une fonction

Solution. On différencie comme dérivée d'une somme dont le deuxième terme a un facteur constant, il peut être soustrait du signe dérivé :

Si des questions se posent encore quant à l'origine de quelque chose, elles sont généralement résolues après s'être familiarisé avec le tableau des dérivées et les règles de différenciation les plus simples. Nous passons à eux en ce moment.

Tableau des dérivées de fonctions simples

1. Dérivée d'une constante (nombre). N'importe quel nombre (1, 2, 5, 200...) présent dans l'expression de fonction. Toujours égal à zéro. Il est très important de s’en souvenir, car cela est très souvent nécessaire.
2. Dérivée de la variable indépendante. Le plus souvent « X ». Toujours égal à un. Il est également important de s'en souvenir longtemps
3. Dérivé du degré. Lorsque vous résolvez des problèmes, vous devez convertir des racines non carrées en puissances.
4. Dérivée d'une variable à la puissance -1
5. Dérivée de racine carrée
6. Dérivée du sinus
7. Dérivée du cosinus
8. Dérivée de la tangente
9. Dérivée de cotangente
10. Dérivée de l'arc sinus
11. Dérivée de l'arccosinus
12. Dérivée de l'arctangente
13. Dérivée de l'arc cotangent
14. Dérivée du logarithme népérien
15. Dérivée d'une fonction logarithmique
16. Dérivée de l'exposant
17. Dérivé fonction exponentielle

Règles de différenciation

1. Dérivée d'une somme ou d'une différence
2. Dérivé du produit
2a. Dérivée d'une expression multipliée par un facteur constant
3. Dérivée du quotient
4. Dérivée d'une fonction complexe

Règle 1.Si les fonctions

sont différentiables à un moment donné, alors les fonctions sont différentiables au même point

et

ceux. la dérivée de la somme algébrique des fonctions est égale à somme algébrique dérivées de ces fonctions.

Conséquence. Si deux fonctions différentiables diffèrent par un terme constant, alors leurs dérivées sont égales, c'est-à-dire

Règle 2.Si les fonctions

sont différentiables à un moment donné, alors leur produit est différentiable au même point

et

ceux. La dérivée du produit de deux fonctions est égale à la somme des produits de chacune de ces fonctions et de la dérivée de l'autre.

Corollaire 1. Le facteur constant peut être soustrait du signe de la dérivée:

Corollaire 2. La dérivée du produit de plusieurs fonctions différentiables est égale à la somme des produits de la dérivée de chaque facteur et de tous les autres.

Par exemple, pour trois multiplicateurs :

Règle 3.Si les fonctions

différenciable à un moment donné Et , alors à ce stade leur quotient est également dérivableu/v, et

ceux. la dérivée du quotient de deux fonctions est égale à une fraction dont le numérateur est la différence entre les produits du dénominateur et la dérivée du numérateur et le numérateur et la dérivée du dénominateur, et le dénominateur est le carré de l'ancien numérateur.

Où chercher des choses sur d'autres pages

Lors de la recherche de la dérivée d'un produit et du quotient dans de vrais problèmes Il faut toujours appliquer plusieurs règles de différenciation à la fois, donc plus d'exemples pour ces dérivés - dans l'article"Dérivée du produit et quotient des fonctions".

Commentaire. Il ne faut pas confondre une constante (c'est-à-dire un nombre) avec un terme dans une somme et comme un facteur constant ! Dans le cas d'un terme, sa dérivée est égale à zéro, et dans le cas facteur constant il est retiré du signe dérivé. Ce erreur typique, qui se produit le étape initialeétudient les dérivées, mais comme ils résolvent plusieurs exemples en une ou deux parties, l'étudiant moyen ne commet plus cette erreur.

Et si, pour différencier un produit ou un quotient, vous disposez d'un terme toi"v, dans lequel toi- un nombre, par exemple 2 ou 5, c'est-à-dire une constante, alors la dérivée de ce nombre sera égale à zéro et, par conséquent, le terme entier sera égal à zéro (ce cas est abordé dans l'exemple 10).

Autre erreur courante - solution mécanique dérivée d'une fonction complexe comme dérivée d'une fonction simple. C'est pourquoi dérivée d'une fonction complexe un article séparé est consacré. Mais nous allons d'abord apprendre à trouver des dérivées fonctions simples.

En chemin, on ne peut pas se passer de transformer les expressions. Pour ce faire, vous devrez peut-être ouvrir le manuel dans une nouvelle fenêtre. Des actions avec des pouvoirs et des racines Et Opérations avec des fractions .

Si vous cherchez des solutions aux dérivées de fractions avec des puissances et des racines, c'est-à-dire lorsque la fonction ressemble à , puis suivez la leçon « Dérivée de sommes de fractions avec puissances et racines ».

Si vous avez une tâche comme , alors vous suivrez la leçon « Dérivées de fonctions trigonométriques simples ».

Exemples étape par étape - comment trouver la dérivée

Exemple 3. Trouver la dérivée d'une fonction

Solution. Nous définissons les parties de l'expression de fonction : l'expression entière représente un produit, et ses facteurs sont des sommes, dans la seconde desquelles l'un des termes contient un facteur constant. On applique la règle de différenciation des produits : la dérivée du produit de deux fonctions est égale à la somme des produits de chacune de ces fonctions par la dérivée de l'autre :

Ensuite, on applique la règle de différenciation de la somme : la dérivée de la somme algébrique des fonctions est égale à la somme algébrique des dérivées de ces fonctions. Dans notre cas, dans chaque somme le deuxième terme a un signe moins. Dans chaque somme, nous voyons à la fois une variable indépendante dont la dérivée est égale à un et une constante (nombre) dont la dérivée est égale à zéro. Ainsi, « X » devient un et moins 5 devient zéro. Dans la deuxième expression, « x » est multiplié par 2, nous multiplions donc deux par la même unité que la dérivée de « x ». Nous obtenons valeurs suivantes dérivés :

Nous substituons les dérivées trouvées dans la somme des produits et obtenons la dérivée de la fonction entière requise par la condition du problème :

Exemple 4. Trouver la dérivée d'une fonction

Solution. Nous devons trouver la dérivée du quotient. On applique la formule de différenciation du quotient : la dérivée du quotient de deux fonctions est égale à une fraction dont le numérateur est la différence entre les produits du dénominateur et la dérivée du numérateur et du numérateur et la dérivée du dénominateur, et le dénominateur est le carré de l’ancien numérateur. On obtient :

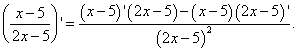
Nous avons déjà trouvé la dérivée des facteurs au numérateur dans l'exemple 2. N'oublions pas non plus que le produit, qui est le deuxième facteur au numérateur dans l'exemple actuel, est pris avec un signe moins :

Si vous cherchez des solutions à des problèmes dans lesquels vous devez trouver la dérivée d'une fonction, où il y a un tas continu de racines et de puissances, comme, par exemple, , alors bienvenue en classe "Dérivée de sommes de fractions avec puissances et racines" .

Si vous avez besoin d'en savoir plus sur les dérivées des sinus, cosinus, tangentes et autres fonctions trigonométriques, c'est-à-dire lorsque la fonction ressemble à , alors une leçon pour toi "Dérivées de fonctions trigonométriques simples" .

Exemple 5. Trouver la dérivée d'une fonction

Solution. Dans cette fonction, nous voyons un produit dont l'un des facteurs est racine carréeà partir de la variable indépendante dont nous avons vu la dérivée dans le tableau des dérivées. Selon la règle de différenciation du produit et valeur du tableau dérivée de la racine carrée on obtient :

Exemple 6. Trouver la dérivée d'une fonction

Solution. Dans cette fonction on voit un quotient dont le dividende est la racine carrée de la variable indépendante. En utilisant la règle de différenciation des quotients, que nous avons répétée et appliquée dans l'exemple 4, et la valeur tabulée de la dérivée de la racine carrée, on obtient :

Pour supprimer une fraction du numérateur, multipliez le numérateur et le dénominateur par .

Niveau d'entrée

Dérivée d'une fonction. Guide complet (2019)

Imaginons une route droite traversant une zone vallonnée. Autrement dit, il monte et descend, mais ne tourne ni à droite ni à gauche. Si l'axe est dirigé horizontalement le long de la route et verticalement, alors la ligne de route sera très similaire au graphique d'une fonction continue :

L'axe est un certain niveau d'altitude nulle ; dans la vie, nous utilisons le niveau de la mer comme tel.

À mesure que nous avançons sur une telle route, nous montons ou descendons également. On peut aussi dire : lorsque l'argument change (déplacement le long de l'axe des abscisses), la valeur de la fonction change (déplacement le long de l'axe des ordonnées). Réfléchissons maintenant à la façon de déterminer la « raideur » de notre route ? Quel genre de valeur cela pourrait-il représenter ? C'est très simple : à quel point la hauteur va changer en avançant sur une certaine distance. En effet, sur différents tronçons de route, en avançant (le long de l'axe des x) d'un kilomètre, on montera ou descendra de différentes quantités mètres par rapport au niveau de la mer (le long de l'axe des ordonnées).

Notons la progression (lire « delta x »).

La lettre grecque (delta) est couramment utilisée en mathématiques comme préfixe signifiant « changement ». C'est-à-dire - c'est un changement de quantité, - un changement ; alors qu'est-ce que c'est ? C'est vrai, un changement d'ampleur.

Important : une expression est un tout unique, une variable. Ne séparez jamais le « delta » du « x » ou de toute autre lettre !

C'est par exemple .

Nous avons donc avancé, horizontalement, de. Si nous comparons la ligne de la route avec le graphique de la fonction, alors comment dénotons-nous la montée ? Certainement, . Autrement dit, à mesure que nous avançons, nous montons plus haut. La valeur est facile à calculer : si au début nous étions en hauteur, et qu'après le déplacement nous nous retrouvions en hauteur, alors. Si point final

Revenons à la « raideur » : c'est une valeur qui montre de combien (forte) la hauteur augmente lorsque l'on avance d'une unité de distance :

Supposons que sur une section de la route, en avançant d'un kilomètre, la route s'élève d'un kilomètre. Alors la pente à cet endroit est égale. Et si la route, en avançant de m, descendait de km ? Alors la pente est égale.

Regardons maintenant le sommet d'une colline. Si vous prenez le début du tronçon un demi-kilomètre avant le sommet et la fin un demi-kilomètre après, vous constaterez que la hauteur est presque la même.

Autrement dit, selon notre logique, il s'avère que la pente ici est presque égale à zéro, ce qui n'est clairement pas vrai. Sur une distance de quelques kilomètres, beaucoup de choses peuvent changer. Il est nécessaire de considérer des zones plus petites pour une évaluation plus adéquate et plus précise de la pente. Par exemple, si vous mesurez le changement de hauteur lorsque vous vous déplacez d’un mètre, le résultat sera beaucoup plus précis. Mais même cette précision peut ne pas nous suffire - après tout, s'il y a un poteau au milieu de la route, nous pouvons simplement le dépasser. Quelle distance choisir alors ? Centimètre? Millimètre? Moins c'est plus !

DANS la vraie vie Mesurer les distances au millimètre près est largement suffisant. Mais les mathématiciens recherchent toujours la perfection. Le concept a donc été inventé infinitésimal, c’est-à-dire que la valeur absolue est inférieure à n’importe quel nombre que nous pouvons nommer. Par exemple, vous dites : un billionième ! Combien moins ? Et vous divisez ce nombre par - et ce sera encore moins. Et ainsi de suite. Si on veut écrire qu’une quantité est infinitésimale, on écrit ainsi : (on lit « x tend vers zéro »). Il est très important de comprendre que ce nombre n'est pas égal à zéro ! Mais très proche. Cela signifie que vous pouvez diviser par cela.

Le concept opposé à infinitésimal est infiniment grand (). Vous l'avez probablement déjà rencontré lorsque vous travailliez sur les inégalités : ce nombre est modulo supérieur à tous les nombres auxquels vous pouvez penser. Si tu avais trouvé le plus gros numéros possibles, multipliez-le simplement par deux et vous obtenez encore plus. Et l'infini encore de plus que va-t-il se passer. En fait, l'infiniment grand et l'infiniment petit sont l'inverse l'un de l'autre, c'est-à-dire at, et vice versa : at.

Revenons maintenant à notre route. La pente idéalement calculée est la pente calculée pour un segment infinitésimal du chemin, soit :

Je constate qu'avec un déplacement infinitésimal, le changement de hauteur sera également infinitésimal. Mais laissez-moi vous rappeler qu'infinitésimal ne veut pas dire égal à zéro. Si vous divisez des nombres infinitésimaux les uns par les autres, vous pouvez obtenir tout à fait numéro régulier, Par exemple, . Autrement dit, une petite valeur peut être exactement plusieurs fois supérieure à une autre.

A quoi ça sert tout ça ? La route, la pente... Nous ne participons pas à un rallye automobile, mais nous enseignons les mathématiques. Et en mathématiques, tout est exactement pareil, seulement appelé différemment.

Notion de dérivé

La dérivée d'une fonction est le rapport de l'incrément de la fonction à l'incrément de l'argument pour un incrément infinitésimal de l'argument.

Progressivement en mathématiques, ils appellent le changement. La mesure dans laquelle l'argument () change à mesure qu'il se déplace le long de l'axe est appelée incrément d'argument et est désigné dans quelle mesure la fonction (hauteur) a changé lors du déplacement vers l'avant le long de l'axe d'une distance est appelé. incrément de fonction et est désigné.

Ainsi, la dérivée d’une fonction est le rapport au quand. On note la dérivée par la même lettre que la fonction, seulement avec un nombre premier en haut à droite : ou simplement. Écrivons donc la formule dérivée en utilisant ces notations :

Comme dans l'analogie avec la route, ici lorsque la fonction augmente, la dérivée est positive, et lorsqu'elle diminue, elle est négative.

La dérivée peut-elle être égale à zéro ? Certainement. Par exemple, si nous roulons sur une route horizontale et plate, la pente est nulle. Et c’est vrai, la hauteur ne change pas du tout. Idem avec la dérivée : dérivée fonction constante(constantes) est égal à zéro :

puisque l'incrément d'une telle fonction est égal à zéro pour tout.

Rappelons-nous l'exemple du sommet d'une colline. Il s'est avéré qu'il était possible de disposer les extrémités du segment le long différents côtés du haut, pour que la hauteur aux extrémités soit la même, c'est-à-dire que le segment soit parallèle à l'axe :

Mais de grands segments sont le signe d’une mesure inexacte. Nous élèverons notre segment parallèlement à lui-même, puis sa longueur diminuera.

Finalement, lorsque nous serons infiniment proches du sommet, la longueur du segment deviendra infinitésimale. Mais en même temps, il est resté parallèle à l'axe, c'est-à-dire que la différence de hauteur à ses extrémités est égale à zéro (elle ne tend pas vers, mais est égale à). Donc la dérivée

Cela peut être compris ainsi : lorsque nous nous trouvons tout en haut, un petit déplacement vers la gauche ou la droite modifie de manière négligeable notre hauteur.

Il existe aussi une explication purement algébrique : à gauche du sommet la fonction augmente, et à droite elle diminue. Comme nous l’avons découvert précédemment, lorsqu’une fonction augmente, la dérivée est positive, et lorsqu’elle diminue, elle est négative. Mais cela change en douceur, sans sauts (puisque la route ne change brusquement de pente nulle part). Ainsi, entre négatif et valeurs positives il doit certainement y en avoir. Ce sera là où la fonction n'augmente ni ne diminue - au point sommet.

Il en va de même pour le creux (la zone où la fonction à gauche diminue et à droite augmente) :

Un peu plus sur les incréments.

Nous changeons donc l’argument en grandeur. On change à partir de quelle valeur ? Qu’est-il devenu (l’argument) maintenant ? Nous pouvons choisir n'importe quel point, et maintenant nous allons danser à partir de lui.

Considérons un point avec une coordonnée. La valeur de la fonction qu'il contient est égale. Ensuite on fait le même incrément : on augmente la coordonnée de. Quel est l’argument maintenant ? Très simple : . Quelle est la valeur de la fonction maintenant ? Là où va l’argument, la fonction aussi : . Qu'en est-il de l'incrément de fonction ? Rien de nouveau : c'est toujours l'ampleur de l'évolution de la fonction :

Entraînez-vous à trouver des incréments :

1. Recherchez l'incrément de la fonction à un point où l'incrément de l'argument est égal à.
2. Il en va de même pour la fonction en un point.

Solutions :

DANS différents points avec le même incrément d'argument, l'incrément de fonction sera différent. Cela signifie que la dérivée en chaque point est différente (nous en avons discuté au tout début - la pente de la route est différente en différents points). Ainsi, lorsque l’on écrit une dérivée, il faut indiquer à quel moment :

Fonction de puissance.

Une fonction puissance est une fonction dont l’argument est dans une certaine mesure (logique, n’est-ce pas ?).

De plus - dans une certaine mesure : .

Le cas le plus simple- c'est alors que l'exposant :

Trouvons sa dérivée en un point. Rappelons la définition d'une dérivée :

L’argument change donc de à. Quel est l'incrément de la fonction ?

L'incrément, c'est ça. Mais une fonction est en tout point égale à son argument. C'est pourquoi :

La dérivée est égale à :

La dérivée de est égale à :

b) Considérons maintenant fonction quadratique (): .

Maintenant, rappelons-le. Cela signifie que la valeur de l'incrément peut être négligée, puisqu'elle est infinitésimale, et donc insignifiante par rapport à l'autre terme :

Nous avons donc proposé une autre règle :

c) On continue la série logique : .

Cette expression peut être simplifiée de différentes manières : ouvrez la première parenthèse en utilisant la formule de multiplication abrégée du cube de la somme, ou factorisez l'expression entière en utilisant la formule de différence des cubes. Essayez de le faire vous-même en utilisant l'une des méthodes suggérées.

J'ai donc obtenu ceci :

Et encore une fois, rappelons-le. Cela signifie que l'on peut négliger tous les termes contenant :

On obtient : .

d) Des règles similaires peuvent être obtenues pour les grandes puissances :

e) Il s'avère que cette règle peut être généralisée pour une fonction puissance avec un exposant arbitraire, pas même un entier :

La règle peut être formulée ainsi : « le diplôme est avancé sous forme de coefficient, puis diminué de . »

Nous prouverons cette règle plus tard (presque à la toute fin). Voyons maintenant quelques exemples. Trouvez la dérivée des fonctions :

1. (de deux manières : par formule et en utilisant la définition de dérivée - en calculant l'incrément de la fonction) ;

1. . Croyez-le ou non, il s’agit d’une fonction de pouvoir. Si vous avez des questions comme « Comment ça va ? Où est le diplôme ? », souvenez-vous du sujet « » !
   Oui, oui, la racine est aussi un degré, uniquement fractionnaire : .
   Cela signifie que notre racine carrée n’est qu’une puissance avec un exposant :
   .
   Nous recherchons la dérivée en utilisant la formule récemment apprise :

   Si à ce stade cela devient à nouveau flou, répétez le sujet « » !!! (à propos du diplôme avec indicateur négatif)

2. . Maintenant l'exposant :

   Et maintenant à travers la définition (vous avez déjà oublié ?) :
   ;
   .
   Maintenant, comme d'habitude, nous négligeons le terme contenant :
   .

3. . Combinaison de cas précédents : .

Fonctions trigonométriques.

Ici, nous utiliserons un fait issu des mathématiques supérieures :

Avec expression.

Vous apprendrez la preuve dès la première année d'institut (et pour y arriver, vous devez réussir l'examen d'État unifié). Maintenant, je vais juste le montrer graphiquement :

Nous voyons que lorsque la fonction n'existe pas, le point sur le graphique est coupé. Mais plus la valeur est proche, plus la fonction est proche de ce qui « vise ».

De plus, vous pouvez vérifier cette règle à l'aide d'une calculatrice. Oui, oui, ne soyez pas timide, prenez une calculatrice, nous n'en sommes pas encore à l'examen d'État unifié.

Alors, essayons : ;

N'oubliez pas de passer votre calculatrice en mode Radians !

etc. On voit que moins, plus valeur plus proche relation avec

a) Considérons la fonction. Comme d'habitude, trouvons son incrément :

Transformons la différence des sinus en un produit. Pour ce faire, nous utilisons la formule (rappelez-vous le sujet « ») : .

Maintenant la dérivée :

Faisons un remplacement : . Alors pour infinitésimal c'est aussi infinitésimal : . L'expression pour prend la forme :

Et maintenant, nous nous en souvenons avec l'expression. Et aussi, que se passerait-il si une quantité infinitésimale pouvait être négligée dans la somme (c'est-à-dire at).

Nous obtenons donc règle suivante:la dérivée du sinus est égale au cosinus:

Ce sont des dérivés basiques (« tabulaires »). Les voici dans une seule liste :

Plus tard, nous leur en ajouterons quelques autres, mais ce sont les plus importants, car ils sont les plus souvent utilisés.

Pratique:

1. Trouver la dérivée de la fonction en un point ;
2. Trouvez la dérivée de la fonction.

Solutions :

1. Tout d’abord, trouvons la dérivée dans vue générale, puis remplacez sa valeur :
   ;
   .
2. Ici, nous avons quelque chose de similaire à fonction de puissance. Essayons de l'amener à
   aspect normal:
   .
   Super, vous pouvez maintenant utiliser la formule :
   .
   .
3. . Eeeeeee.....Qu'est-ce que c'est ????

Bon, vous avez raison, on ne sait pas encore comment trouver de tels dérivés. Nous avons ici une combinaison de plusieurs types de fonctions. Pour travailler avec eux, vous devez apprendre quelques règles supplémentaires :

Exposant et logarithme népérien.

Il existe une fonction en mathématiques dont la dérivée pour toute valeur est à la fois égale à la valeur de la fonction elle-même. C'est ce qu'on appelle « exposant » et c'est une fonction exponentielle.

La base de cette fonction est une constante - elle est infinie décimal, c'est-à-dire un nombre irrationnel (tel que). On l'appelle le « nombre d'Euler », c'est pourquoi il est désigné par une lettre.

Donc la règle :

Très facile à retenir.

Bon, n’allons pas loin, considérons immédiatement la fonction inverse. Quelle fonction est l'inverse de la fonction exponentielle ? Logarithme:

Dans notre cas, la base est le nombre :

Un tel logarithme (c'est-à-dire un logarithme avec une base) est appelé « naturel », et nous utilisons pour cela une notation spéciale : nous l'écrivons à la place.

A quoi est-ce égal ? Bien sûr.

La dérivée du logarithme népérien est également très simple :

Exemples :

1. Trouvez la dérivée de la fonction.
2. Quelle est la dérivée de la fonction ?

Réponses : Exposant et logarithme népérien- les fonctions sont particulièrement simples en termes de dérivées. Les fonctions exponentielles et logarithmiques avec toute autre base auront une dérivée différente, que nous analyserons plus tard, après passons en revue les règles différenciation.

Règles de différenciation

Des règles de quoi ? Encore un nouveau terme, encore ?!...

Différenciation est le processus de recherche de la dérivée.

C'est tout. Comment pouvez-vous appeler ce processus en un mot ? Pas dérivé... Les mathématiciens appellent la différentielle le même incrément d'une fonction à. Ce terme vient du latin différentia – différence. Ici.

Lors de la dérivation de toutes ces règles, nous utiliserons deux fonctions, par exemple et. Nous aurons également besoin de formules pour leurs incréments :

Il y a 5 règles au total.

La constante est soustraite du signe dérivé.

Si - certains nombre constant(constant), alors.

Évidemment, cette règle fonctionne aussi pour la différence : .

Prouvons-le. Laissez-le être, ou plus simple.

Exemples.

Trouvez les dérivées des fonctions :

1. à un moment donné ;
2. à un moment donné ;
3. à un moment donné ;
4. au point.

Solutions :

1. (la dérivée est la même en tous points, puisque cette fonction linéaire, souviens-toi?);

Dérivé du produit

Tout est pareil ici : entrons nouvelle fonctionnalité et trouvez son incrément :

Dérivé:

Exemples :

1. Trouver les dérivées des fonctions et ;
2. Trouvez la dérivée de la fonction en un point.

Solutions :

Dérivée d'une fonction exponentielle

Vos connaissances sont désormais suffisantes pour apprendre à trouver la dérivée de n'importe quelle fonction exponentielle, et pas seulement les exposants (avez-vous déjà oublié ce que c'est ?).

Alors, où est un certain nombre.

Nous connaissons déjà la dérivée de la fonction, essayons donc d'amener notre fonction à une nouvelle base :

Pour cela nous utiliserons règle simple: . Alors:

Eh bien, ça a fonctionné. Essayez maintenant de trouver la dérivée, et n'oubliez pas que cette fonction est complexe.

Est-ce que ça a marché ?

Ici, vérifiez vous-même :

La formule s'est avérée très similaire à la dérivée d'un exposant : telle qu'elle était, elle reste la même, seul un facteur est apparu, qui n'est qu'un nombre, mais pas une variable.

Exemples :
Trouvez les dérivées des fonctions :

Réponses :

Il s'agit simplement d'un nombre qui ne peut pas être calculé sans calculatrice, c'est-à-dire qu'il ne peut plus être écrit. sous forme simple. Par conséquent, nous le laissons sous cette forme dans la réponse.

Dérivée d'une fonction logarithmique

C’est pareil ici : vous connaissez déjà la dérivée du logarithme népérien :

Par conséquent, pour trouver un logarithme arbitraire avec une base différente, par exemple :

Nous devons réduire ce logarithme à la base. Comment changer la base d'un logarithme ? J'espère que vous vous souvenez de cette formule :

Seulement maintenant, nous écrirons à la place :

Le dénominateur est simplement une constante (un nombre constant, sans variable). La dérivée s’obtient très simplement :

Dérivées exponentielles et fonctions logarithmiques n'apparaissent presque jamais à l'examen d'État unifié, mais cela ne ferait pas de mal de les connaître.

Dérivée d'une fonction complexe.

Ce qui s'est passé " fonction complexe" ? Non, ce n'est pas un logarithme, ni une arctangente. Ces fonctions peuvent être difficiles à comprendre (même si si vous trouvez le logarithme difficile, lisez le sujet « Logarithmes » et tout ira bien), mais d'un point de vue mathématique, le mot « complexe » ne signifie pas « difficile ».

Imaginez un petit tapis roulant : deux personnes sont assises et effectuent des actions avec des objets. Par exemple, le premier enveloppe une barre de chocolat dans un emballage et le second l'attache avec un ruban. Le résultat est un objet composite : une barre de chocolat enveloppée et nouée avec un ruban. Pour manger une barre de chocolat, il faut faire les étapes inverses ordre inverse.

Créons un pipeline mathématique similaire : nous trouverons d'abord le cosinus d'un nombre, puis nous mettrons au carré le nombre obtenu. Donc, on nous donne un nombre (chocolat), je trouve son cosinus (emballage), et puis vous mettez au carré ce que j'ai obtenu (nouez-le avec un ruban). Ce qui s'est passé? Fonction. Ceci est un exemple de fonction complexe : lorsque, pour trouver sa valeur, on effectue une première action directement avec la variable, puis une deuxième action avec ce qui résulte de la première.

On peut facilement faire les mêmes étapes dans l'ordre inverse : on le met d'abord au carré, et je cherche ensuite le cosinus du nombre obtenu : . Il est facile de deviner que le résultat sera presque toujours différent. Caractéristique importante fonctions complexes : lorsque l'ordre des actions change, la fonction change.

Autrement dit, une fonction complexe est une fonction dont l'argument est une autre fonction: .

Pour le premier exemple, .

Deuxième exemple : (même chose). .

L'action que nous faisons en dernier sera appelée fonction "externe", et l'action effectuée en premier - en conséquence fonction "interne"(ce sont des noms informels, je les utilise uniquement pour expliquer le matériel dans un langage simple).

Essayez de déterminer par vous-même quelle fonction est externe et laquelle interne :

Réponses : La séparation des fonctions internes et externes est très similaire à la modification de variables : par exemple, dans une fonction

1. Quelle action allons-nous effectuer en premier ? Tout d’abord, calculons le sinus, puis cubez-le seulement. Cela signifie qu’il s’agit d’une fonction interne, mais externe.
   Et la fonction originelle est leur composition : .
2. Interne: ; externe: .
   Examen : .
3. Interne: ; externe: .
   Examen : .
4. Interne: ; externe: .
   Examen : .
5. Interne: ; externe: .
   Examen : .

Nous changeons les variables et obtenons une fonction.

Eh bien, maintenant nous allons extraire notre barre de chocolat et chercher le dérivé. La procédure est toujours inversée : on cherche d’abord la dérivée de la fonction externe, puis on multiplie le résultat par la dérivée de la fonction interne. Par rapport à exemple originalça ressemble à ça :

Autre exemple :

Alors, formulons enfin la règle officielle :

Algorithme pour trouver la dérivée d'une fonction complexe :

Cela semble simple, non ?

Vérifions avec des exemples :

Solutions :

1) Interne : ;

Externe: ;

2) Interne : ;

(N’essayez pas de le couper maintenant ! Rien ne sort de sous le cosinus, vous vous souvenez ?)

3) Interne : ;

Externe: ;

Il est immédiatement clair qu'il s'agit d'une fonction complexe à trois niveaux : après tout, c'est déjà une fonction complexe en soi, et nous en extrayons également la racine, c'est-à-dire que nous effectuons la troisième action (nous mettons le chocolat dans un emballage et avec un ruban dans la mallette). Mais il n'y a aucune raison d'avoir peur : nous allons quand même « déballer » cette fonction dans le même ordre que d'habitude : depuis la fin.

Autrement dit, nous différencions d'abord la racine, puis le cosinus, et ensuite seulement l'expression entre parenthèses. Et puis on multiplie le tout.

Dans de tels cas, il est pratique de numéroter les actions. Autrement dit, imaginons ce que nous savons. Dans quel ordre effectuerons-nous les actions pour calculer la valeur de cette expression ? Regardons un exemple :

Plus l’action est réalisée tardivement, plus elle sera « externe » fonction correspondante. La séquence d'actions est la même que précédemment :

Ici, la nidification est généralement à 4 niveaux. Déterminons la marche à suivre.

1. Expression radicale. .

2. Racine. .

3. Sinus. .

4. Carré. .

5. Rassembler le tout :

DÉRIVÉ. EN BREF SUR LES CHOSES PRINCIPALES

Dérivée d'une fonction- le rapport de l'incrément de la fonction à l'incrément de l'argument pour un incrément infinitésimal de l'argument :

Dérivés de base :

Règles de différenciation :

La constante est soustraite du signe dérivé :

Dérivée de la somme :

Dérivé du produit :

Dérivée du quotient :

Dérivée d'une fonction complexe :

Algorithme pour trouver la dérivée d'une fonction complexe :

1. Nous définissons la fonction « interne » et trouvons sa dérivée.
2. Nous définissons la fonction « externe » et trouvons sa dérivée.
3. Nous multiplions les résultats des premier et deuxième points.

Au moment de décider diverses tâches la géométrie, la mécanique, la physique et d'autres branches de connaissances sont devenues nécessaires en utilisant le même processus analytique de cette fonction y=f(x) obtenir une nouvelle fonction appelée fonction dérivée(ou juste dérivée) d'une fonction donnée f(x) et est désigné par le symbole

Le processus par lequel, à partir d'une fonction donnée f(x) obtenir une nouvelle fonctionnalité f" (x), appelé différenciation et il comprend les trois étapes suivantes : 1) donner l'argument x incrément  x et déterminer l'incrément correspondant de la fonction  y = f(x+ x) -f(x);

2) établir une relation x 3) compter  x constante et
0, on trouve f" (x), que nous désignons par x, comme pour souligner que la fonction résultante dépend uniquement de la valeur , à laquelle nous allons à la limite.: Définition Dérivée y " =f " (x) fonction donnée y=f(x) pour un x donné
est appelée la limite du rapport de l'incrément d'une fonction à l'incrément de l'argument, à condition que l'incrément de l'argument tende vers zéro, si, bien entendu, cette limite existe, c'est-à-dire fini. Ainsi,

, ou x Notez que si à une certaine valeur , par exemple quand x=une
, attitude  xà 0 n’a pas tendance à limite finie f(x), alors dans ce cas ils disent que la fonction , par exemple quandà , par exemple quand(ou au point , par exemple quand.

) n’a pas de dérivée ou n’est pas différentiable au point

2. Signification géométrique de la dérivée.

f(x)

Considérons le graphique de la fonction y = f (x), différentiable au voisinage du point x 0

Depuis AC || Ox, alors ALO = BAC = β (comme correspondant au parallèle). Mais ALO est l'angle d'inclinaison de la sécante AB par rapport à la direction positive de l'axe Ox. Cela signifie que tanβ = k est la pente de la droite AB.

Nous allons maintenant réduire ∆х, c'est-à-dire ∆х→ 0. Dans ce cas, le point B s'approchera du point A selon le graphique et la sécante AB tournera. La position limite de la sécante AB en ∆x→ 0 sera une droite (a), appelée tangente au graphique de la fonction y = f (x) au point A.

Si on va à la limite quand ∆x → 0 dans l’égalité tgβ =∆y/∆x, on obtient
ortg =f "(x 0), puisque
-angle d'inclinaison de la tangente à la direction positive de l'axe Ox
, par définition d'un dérivé. Mais tg = k est le coefficient angulaire de la tangente, ce qui signifie k = tg = f" (x 0).

Ainsi, la signification géométrique de la dérivée est la suivante :

Dérivée d'une fonction au point x 0 égal à pente tangente au graphique de la fonction tracée au point d'abscisse x 0 .

3. Signification physique du dérivé.

Considérons le mouvement d'un point le long d'une ligne droite. Soit la coordonnée d'un point à tout instant x(t). On sait (d'après un cours de physique) que la vitesse moyenne sur une période de temps est égale au rapport de la distance parcourue pendant cette période de temps au temps, c'est-à-dire

Vav = ∆x/∆t. Allons à la limite de la dernière égalité comme ∆t → 0.

lim Vav (t) = (t 0) - vitesse instantanée au temps t 0, ∆t → 0.

et lim = ∆x/∆t = x"(t 0) (par définition de dérivée).

Donc, (t) =x"(t).

La signification physique de la dérivée est la suivante : dérivée de la fonctionoui = f(x) au pointx 0 est le taux de changement de la fonctionf(x) au pointx 0

La dérivée est utilisée en physique pour trouver la vitesse en fonction connue coordonnées en fonction du temps, accélération selon une fonction connue de la vitesse en fonction du temps.

(t) = x"(t) - vitesse,

a(f) = "(t) - accélération, ou

Si la loi du mouvement d'un point matériel dans un cercle est connue, alors on peut trouver la vitesse angulaire et accélération angulaire lors d'un mouvement de rotation :

φ = φ(t) - changement d'angle au fil du temps,

ω = φ"(t) - vitesse angulaire,

ε = φ"(t) - accélération angulaire, ou ε = φ"(t).

Si la loi de distribution de masse d'un bâtonnet inhomogène est connue, alors la densité linéaire d'un bâtonnet inhomogène peut être trouvée :

m = m(x) - masse,

x  , l - longueur de la tige,

p = m"(x) - densité linéaire.

Grâce à la dérivée, les problèmes de la théorie de l'élasticité et des vibrations harmoniques sont résolus. Donc, selon la loi de Hooke

F = -kx, x – coordonnée variable, k – coefficient d'élasticité du ressort. En mettant ω 2 =k/m, on obtient l'équation différentielle du pendule à ressort x"(t) + ω 2 x(t) = 0,

où ω = √k/√m fréquence d'oscillation (l/c), k - rigidité du ressort (H/m).

Une équation de la forme y" + ω 2 y = 0 est appelée l'équation des oscillations harmoniques (mécaniques, électriques, électromagnétiques). La solution de ces équations est la fonction

y = Asin(ωt + φ 0) ou y = Acos(ωt + φ 0), où

A - amplitude des oscillations, ω - fréquence cyclique,

φ 0 - phase initiale.

Étudier une fonction à l'aide de sa dérivée. Dans cet article nous analyserons quelques tâches liées à l'étude du graphe d'une fonction. Dans de tels problèmes, un graphique de la fonction y = f (x) est donné et des questions sont soulevées concernant la détermination du nombre de points auxquels la dérivée de la fonction est positive (ou négative), ainsi que d'autres. Ils sont classés comme tâches sur l'application des dérivées à l'étude des fonctions.

La résolution de tels problèmes, et en général des problèmes liés à la recherche, n'est possible qu'avec une compréhension complète des propriétés de la dérivée pour l'étude des graphiques de fonctions et de la dérivée. Par conséquent, je vous recommande fortement d’étudier la théorie pertinente. Vous pouvez étudier et aussi regarder (mais il contient un bref résumé).

Nous examinerons également les problèmes où le graphe dérivé est donné dans les prochains articles, ne le manquez pas ! Ainsi, les tâches :

La figure montre un graphique de la fonction y = f (x), définie sur l'intervalle (−6 ; 8). Définir:

1. Le nombre de points entiers auxquels la dérivée de la fonction est négative ;

2. Le nombre de points auxquels la tangente au graphique de la fonction est parallèle à la droite y = 2 ;

1. La dérivée d'une fonction est négative sur les intervalles sur lesquels la fonction décroît, c'est-à-dire sur les intervalles (−6 ; –3), (0 ; 4,2), (6,9 ; 8). Ils contiennent les points entiers −5, −4, 1, 2, 3, 4 et 7. Nous obtenons 7 points.

2. Directement oui= 2 parallèles à l'axeOhoui= 2 uniquement aux points extrêmes (aux points où le graphique change de comportement de croissant à décroissant ou vice versa). Il existe quatre de ces points : –3 ; 0 ; 4.2 ; 6.9

Décidez par vous-même:

Déterminez le nombre de points entiers auxquels la dérivée de la fonction est positive.

La figure montre un graphique de la fonction y = f (x), définie sur l'intervalle (−5 ; 5). Définir:

2. Le nombre de points entiers auxquels la tangente au graphique de la fonction est parallèle à la droite y = 3 ;

3. Le nombre de points auxquels la dérivée est nulle ;

1. D'après les propriétés de la dérivée d'une fonction, on sait qu'elle est positive sur les intervalles sur lesquels la fonction augmente, c'est-à-dire sur les intervalles (1,4 ; 2,5) et (4,4 ; 5). Ils ne contiennent qu'un seul point entier x = 2.

2. Directement oui= 3 parallèles à l'axeOh. La tangente sera parallèle à la droiteoui= 3 uniquement aux points extrêmes (aux points où le graphique change de comportement de croissant à décroissant ou vice versa).

Il existe quatre de ces points : –4.3 ; 1.4 ; 2,5 ; 4.4

3. La dérivée est nulle à quatre points(aux points extrêmes), nous les avons déjà indiqués.

Décidez vous-même :

Déterminer le nombre de points entiers auxquels la dérivée de la fonction f(x) est négative.

La figure montre un graphique de la fonction y = f (x), définie sur l'intervalle (−2 ; 12). Trouver:

1. Le nombre de points entiers auxquels la dérivée de la fonction est positive ;

2. Le nombre de points entiers auxquels la dérivée de la fonction est négative ;

3. Le nombre de points entiers auxquels la tangente au graphique de la fonction est parallèle à la droite y = 2 ;

4. Le nombre de points auxquels la dérivée est nulle.

1. D'après les propriétés de la dérivée d'une fonction, on sait qu'elle est positive sur les intervalles sur lesquels la fonction augmente, c'est-à-dire sur les intervalles (–2 ; 1), (2 ; 4), (7 ; 9) et ( 10 ; 11). Ils contiennent des points entiers : –1, 0, 3, 8. Il y en a quatre au total.

2. La dérivée d'une fonction est négative sur les intervalles sur lesquels la fonction décroît, c'est-à-dire sur les intervalles (1 ; 2), (4 ; 7), (9 ; 10), (11 ; 12). Ils contiennent les points entiers 5 et 6. On obtient 2 points.

3. Directement oui= 2 parallèles à l'axeOh. La tangente sera parallèle à la droiteoui= 2 uniquement aux points extrêmes (aux points où le graphique change de comportement de croissant à décroissant ou vice versa). Il y a sept points de ce type : 1 ; 2 ; 4 ; 7 ; 9 ; 10 ; 11.

4. La dérivée est égale à zéro en sept points (aux points extremum), nous les avons déjà indiqués.