Conférence 14 Processus aléatoires Expansion canonique de processus aléatoires. Décomposition spectrale processus aléatoire stationnaire. SluLeçon 14
Processus aléatoires
Expansion canonique de processus aléatoires.
Décomposition spectrale du hasard stationnaire
processus. Processus aléatoires avec indépendant
sections. Processus de Markov et chaînes de Markov.
Processus aléatoires normaux. Périodiquement
processus aléatoires non stationnaires
(Akhmetov S.K.)

Expansion canonique de processus aléatoires

Principales caractéristiques du SP définies par la décomposition canonique

Décomposition spectrale d'un SP stationnaire

Décomposition spectrale du SP stationnaire (2)

Décomposition spectrale du SP stationnaire (3)

Processus aléatoires avec sections efficaces indépendantes

Processus de Markov et chaînes de Markov

Processus aléatoires normaux (gaussiens)

I.V. Yakovlev | Matériel mathématique | MathUs.ru

Problème C6 à l'examen d'État unifié en mathématiques

1.6 Nombres premiers entre eux. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

1.7 Séquences. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1.8 Progression arithmétique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

On sait qu'à l'examen d'État unifié de mathématiques, de nombreux écoliers ne commencent pas le problème C6 et ne le lisent même pas (pourquoi ? Je n'arrive toujours pas à le résoudre, disent-ils). Et en vain !

En règle générale, la tâche C6 se compose de deux ou trois points, dont certains sont assez simples. Pour l'ensemble de la tâche, 4 points principaux sont attribués, 1 à 2 points pour chaque point. Par conséquent, après avoir accompli au moins une partie de la tâche (par exemple, simplement présenter le bon exemple dans l'un des points), vous pouvez obtenir des points principaux. Et ils donneront une augmentation du résultat final sur une échelle de cent points !

Pour résoudre le problème C6, vous avez besoin stock minimum connaissance. Il s'agit d'arithmétique de 6e année (tout ce qui concerne la divisibilité) et d'informations sur les progressions de l'algèbre de 9e année. Rien de plus.

Pourquoi le problème C6 est-il considéré (et, en général, est) le plus difficile de l'examen d'État unifié de mathématiques ? Elle n'est pas conventionnelle. Cela nécessite ce qu'on appelle la culture mathématique de la capacité de construire un raisonnement avec compétence. Et la grande majorité des écoliers manquent totalement de cette compétence, car à l’école, malheureusement, on n’arrive généralement pas au développement d’une culture mathématique.

Apprendre à raisonner culturellement est possible et absolument nécessaire. Le problème C6 offre une excellente opportunité pour cela. Cela ne commencera pas tout de suite, vous devriez donc commencer à vous préparer au C6 bien avant l'examen d'État unifié. Il n’y a qu’une seule recette : décider, décider, décider.

Ce manuel a été écrit pour aider les écoliers à apprendre à résoudre tâches non standard tapez C6. Il contient tout ce dont vous avez besoin matériel théorique et les tâches, la plupart qui étaient proposés à l'examen d'État unifié et au diagnostic oeuvres de MIOO dernièrement.

Des solutions sont fournies pour tous les problèmes. Dans le même temps, l’objectif n’était pas de rendre la solution concise et aussi parfaite techniquement que possible (au détriment de la présentation des idées). Après tout, apprendre les mathématiques signifie saisir des idées ; L'accent principal est mis sur la clarification des idées qui sous-tendent la solution de chaque problème.

1 Théorie nécessaire

1.1 Ensembles de nombres

DANS cette rubrique nous déterminerons ensembles de nombres, nécessaire à la tâche C6. Vous devez bien connaître la terminologie introduite !

Les nombres naturels sont les nombres 1 ; 2 ; 3 ; : : : Nous utilisons des nombres naturels pour compter, et le comptage commence à partir de un. Attention donc : zéro n’est pas un nombre naturel ! (Après tout, il ne nous viendrait pas à l’esprit de dire : « Il n’y a aucune tasse sur la table. »)

L'ensemble des nombres naturels est noté N.

Les entiers sont les nombres 0 ; 1 ; 2 ; 3 ; : : : Ainsi, les entiers sont zéro et ¾plus moins des nombres naturels¿. Les nombres naturels sont des entiers positifs.

L'ensemble des entiers est noté Z. (C'est la notation que nous utilisons constamment dans équations trigonométriques pour enregistrer les réponses.)

Les nombres rationnels sont toutes sortes de fractions m = n avec les entiers m et n (dans ce cas, bien sûr, n 6 = 0 ; pour éviter cette réserve, on dit aussi que m est un entier et n est un nombre naturel).

Tout entier est en même temps rationnel (par exemple, 3 = 6 = 2). Cependant, 1/2 n’est pas un nombre entier.

Beaucoup nombres rationnels noté Q.

1.2 Divisibilité

La notion de divisibilité s'applique aux nombres entiers (en particulier aux nombres naturels). À partir de ce moment, tous les nombres sont considérés comme des entiers. Si ce n’est pas le cas, nous effectuerons une réservation spéciale.

Nous désignons les entiers par a ; b; c; : : : ; k; je; m; n; : : : ; X ; oui ; z, c'est-à-dire que nous utilisons tout lettres minuscules Alphabet latin.

Vous savez très bien que le nombre 12 est divisible par 4, mais pas divisible par 5. Qu'est-ce que définition formelle divisibilité? C'est ici.

Définition. Le nombre a est divisé par le nombre b 6= 0 s'il existe un nombre c tel que a = bc.

Si a est divisible par b, alors b est appelé diviseur de a. Par exemple, le nombre 12 a six diviseurs : 1, 2, 3, 4, 6 et 12.

Exercice. Montrer que si les nombres a et b sont divisibles par c, alors a + b est également divisible par c.

Formulons le plus signes importants divisibilité.

a est divisible par 2, dernier chiffre a vaut 0, 2, 4, 6 ou 8 ;

a est divisible par 5, le dernier chiffre de a est 0 ou 5 ;

a est divisible par 10, le dernier chiffre de a est 0 ;

a est divisible par 3, la somme des chiffres de a est divisible par 3 ;

a est divisible par 9, la somme des chiffres de a est divisible par 9.

1.3 Parité

Les considérations liées à la régularité et à la bizarrerie apparaissent souvent dans les problèmes C6. Il est donc logique de noter particulièrement les faits nécessaires.

Définition. Un nombre est dit même s'il est divisible par 2. Un nombre est dit impair s'il n'est pas divisible par 2.

Voici tous les nombres pairs : 0 ; 2 ; 4 ; 6 ; : : : Si a est pair, alors il a la forme a = 2n. Mais tous les nombres impairs : 1 ; 3 ; 5 ; : : : Il est clair que si a est impair, alors il a la forme a = 2n + 1.

Les affirmations suivantes sont très évidentes et vous pouvez les utiliser pour résoudre le problème C6 (personne ne vous demandera de les prouver). Mais vous pouvez les prouver sous forme d’exercice.

La somme d’un nombre quelconque de termes pairs est paire.

La somme d’un nombre pair de termes impairs est paire. La somme d’un nombre impair de termes impairs est impaire.

Soit un produit de plusieurs facteurs. Si tous les facteurs sont impairs, alors le produit est impair. Si au moins un facteur est pair, alors le produit est pair.

1.4 Division avec reste

Le nombre 13 n'est pas divisible par 5. Le plus grand nombre qui est divisible par 5 et ne dépasse pas 13 est 10 = 5 2. Ainsi, 13 = 5 2+3, et on dit que diviser 13 par 5 donne le quotient de 2 et le reste de 3.

Il s'avère que n'importe quel nombre a peut être divisé avec un reste par n'importe quel nombre b 6 = 0. À savoir, il existe deux nombres q et r tels que a = bq + r, et l'inégalité 0 6 r sera satisfaite< jbj. Число q назвается частным, а число r остатком от деления a на b.

Si r = 0, c'est-à-dire a = bq, alors a est divisible par b.

Exercice. Trouvez le quotient et le reste de la division : a) 7 par 2 ; b) 15 par 4 ; c) 2012 à 5 ; d) 1001 par 13 ; e) 9 par 8 ; e) 8 par 9.

Reste en divisant un nombre impair par 2 égal à un. C'est pourquoi tout nombre impair peut s'écrire 2n + 1.

Les restes s’avèrent utiles dans de nombreuses situations. Disons qu'en résolvant un problème, vous devez prouver que l'égalité n2 = 3k + 2 ne peut être vraie pour aucun entier n et k. Nous raisonnons de la manière suivante.

Le nombre n divisé par 3 peut donner des restes de 0, 1 ou 2. Autrement dit, trois cas sont possibles : n = 3m, n = 3m + 1 ou n = 3m + 2. Quels restes aura le nombre n2 lorsque divisé par 3 ? Voyons ce qui se passe dans chacun des trois cas.

(3m)2 = 9m2 (reste 0) ;

(3m + 1)2 = 9m2 + 6m + 1 (reste 1) ;

(3m + 2)2 = 9m2 + 12m + 4 = (9m2 + 12m + 3) + 1 (reste 1) :

Ainsi, le carré d'un entier divisé par 3 ne peut pas laisser un reste de 2. Par conséquent, l'égalité n2 = 3k + 2 est en effet impossible pour tout n et k.

Exercice. Montrer que le nombre 100 : : 004 (il existe un nombre quelconque de zéros entre 1 et 4) n'est pas le carré d'un nombre entier.

Exercice. Montrer que le carré d'un entier divisé par 4 ne peut donner que deux restes : 0 et 1.

Exercice. Montrer que n3 + 2n est divisible par 3.

1.5 Expansion canonique

Chaque nombre est divisible par 1 et par lui-même. Si nombre naturel p n'est pas égal à 1 et n'en a pas d'autre diviseurs naturels, sauf 1 et p, alors un tel nombre p est appelé premier.

Voici les premiers nombres premiers : 2, 3, 5, 7, 11, 13, 17, 19. Le nombre 2 est le seul nombre premier pair.

Un nombre qui n’est pas égal à 1 et qui n’est pas premier est appelé composé. Par exemple, 15 est un nombre composé (il est divisible par 3). Le nombre 1036 est aussi un nombre composé (il est pair). L'unité n'est ni nombre premier, ni composite.

Exercice. Le nombre 315 1 est composé. Pourquoi?

Il s’avère que chaque nombre peut être décomposé en facteurs premiers. Par exemple:

30 = 2 3 5; 504 = 2 2 2 3 3 7 = 23 32 7:

Une telle expansion est unique à l’ordre des facteurs et est appelée expansion canonique. L'énoncé sur l'existence et le caractère unique de la décomposition canonique est appelé le théorème fondamental de l'arithmétique.

L'expansion canonique donne image complète diviseurs d'un nombre donné (et permet notamment de retrouver leur nombre). À savoir, soit a = pn 1 1 pn 2 2 : : : pn s s le développement canonique du nombre a. Alors le développement canonique de tout diviseur d'un nombre est constitué de facteurs premiers inclus dans l'ensemble fp1 ; p2 ; : : : ; ps g, dont les exposants ne dépassent pas respectivement les nombres n1 ; n2 ; : : : ; ns. Par exemple, tout diviseur du nombre 504 = 23 32 7 a la forme 2a 3b 7c, où a 2 f0 ; 1 ; 2 ; 3g, b2f0; 1 ; 2g et c 2 f0 ; 1g.

Exercice. Soit p un nombre premier. Combien de diviseurs le nombre a-t-il : a) p2 ; b)p3 ; c) pn ?

Exercice. Soit p et q des nombres premiers. Combien de diviseurs le nombre a-t-il : a) pq ; b) p2 q3 ; c) pm qn ?

Exercice. Après avoir généralisé le raisonnement du point c) de l'exercice précédent, montrer que le nombre de diviseurs du nombre a = pn 1 1 pn 2 2 : : : pn s s est égal à (n1 + 1)(n2 + 1) : : : (ns + 1). Trouvez combien de diviseurs possède le nombre 504.

Exercice. Trouvez les développements canoniques des nombres 540 et 252. En utilisant les développements résultants, trouvez le pgcd (540 ; 252) du plus grand diviseur commun ces chiffres.

1.6 Nombres premiers entre eux

Les nombres sont dits premiers entre eux s'ils n'ont pas de diviseur commun autre que 1. En d'autres termes, les nombres a et b sont premiers entre eux si pgcd (a; b) = 1. On peut aussi dire ceci : les nombres a et b sont premiers entre eux si et seulement si lorsque la fraction a=b est irréductible.

Par exemple, les nombres 8 et 15 sont premiers entre eux. Les nombres 9 et 15 ne sont pas premiers ; ils ont un diviseur commun 3.

Les nombres sont relativement premiers si et seulement si leurs développements canoniques consistent en des ensembles disjoints de nombres premiers. Par exemple, les nombres 23 5 132 et 32 ​​73 11 sont relativement premiers.

Propriétés des nombres premiers entre eux. Soit les nombres a et b premiers entre eux. Alors les affirmations suivantes sont vraies.

1. Si un nombre est divisible par a et b, alors il est également divisible par leur produit ab.

2. Si an est divisible par b, alors n est divisible par b.

(Vous pouvez facilement comprendre pourquoi cela se produit si vous imaginez les développements canoniques « disjoints » des nombres a et b et, en outre, rappelez-vous que le développement canonique du diviseur sert de « partie » du développement canonique du dividende. )

Selon l'énoncé 1, par exemple, si un certain nombre est divisible par 8 et 15, alors il est divisible par 8 15 = 120. Le fait que les nombres soient relativement premiers, condition importante. Ainsi, 12 est divisible par 4 et 6, mais pas divisible par 4 6 = 24.

Exercice. Quels chiffres peuvent être insérés à la place des astérisques dans les entrées 35 4 afin que le résultat numéro à cinq chiffres divisible par 45 ?

L'instruction 2 fonctionne généralement dans des situations comme celles-ci. Soit par exemple 5n = 9m. Puisque 5n est divisible par 9 et que les nombres 5 et 9 sont premiers entre eux, alors n est divisible par 9. Pour la même raison, m est divisible par 5.

1.7 Séquences

Qu'est-ce qu'une séquence ? Imaginez un appareil qui produit un numéro après l'autre à certains intervalles. Par exemple : 2, 3, 15, 28, 6, 0, 3, . . . L'ensemble des nombres à la sortie de cet appareil sera une séquence.

Plus strictement, une séquence de nombres, ou séquence de nombres est un ensemble de nombres dans lequel chaque numéro peut se voir attribuer un certain numéro, et chaque numéro correspond singulier de cet ensemble. Un nombre est un nombre naturel ; la numérotation commence à partir de un.

Ainsi, dans la séquence ci-dessus, le premier nombre est 2 (c'est le premier membre de la séquence) et le numéro cinq est le nombre 6 (c'est le cinquième membre de la séquence).

Nombre avec le nombre n (c'est-à-dire nième mandat séquences) est noté an (ou bn, cn, . . .). C'est très pratique lorsque le nième terme de la séquence peut être spécifié par une formule. Par exemple, la formule an = 2n 3 spécifie la séquence : 1 ; 1 ; 3 ; 5 ; 7 ; : : : Formule an = (1)n

définit la séquence : 1 ; 1 ; 1 ; 1 ; : : :

Exercice. Trouvez une formule pour le nième terme pour les séquences suivantes : a) 1 ; 3 ; 5 ; 7 ; : : : ; b) 5 ; 8 ; 11 ; 14 ; : : : ; c) 1 ; 4 ; 9 ; 16 ; : : : ; d) 1 ; 2 ; 3 ; 4 ; : : :

Toutes les séquences que nous avons considérées sont infinies, c'est-à-dire contenant ensemble infini Nombres. Mais il existe aussi des séquences finies. En fait, tout ensemble fini de nombres est une séquence finie. Par exemple, séquence finale 1 ; 2 ; 3 ; 4 ; 5 se compose de cinq nombres.

Le problème C6 en nécessite deux types spéciaux séquences : progressions arithmétiques et géométriques.

1.8 Progression arithmétique

Une progression arithmétique est une séquence dans laquelle chaque terme (en commençant par le second) égal à la somme le terme précédent et un nombre fixe :

an+1 = an + d (n = 1; 2; : : :) :

Le nombre fixe d est appelé la différence d’une progression arithmétique.

Par exemple, séquence 2 ; 5 ; 8 ; 11 ; : : : est progression arithmétique avec le premier terme 2 et la différence 3.

Dans cet article vous trouverez tout informations nécessaires répondre à la question comment factoriser un nombre en facteurs premiers. D'abord donné idée généraleà propos de la décomposition d'un nombre en facteurs premiers, des exemples de décompositions sont donnés. Ce qui suit montre la forme canonique de décomposition d’un nombre en facteurs premiers. Après cela, l'algorithme de décomposition est donné nombres arbitraires en facteurs premiers et des exemples de décomposition de nombres utilisant cet algorithme sont donnés. Des méthodes alternatives sont également envisagées pour vous permettre de factoriser rapidement de petits entiers en facteurs premiers à l'aide de tests de divisibilité et de tables de multiplication.

Navigation dans les pages.

Que signifie factoriser un nombre en facteurs premiers ?

Voyons d’abord ce que sont les facteurs premiers.

Il est clair que puisque le mot « facteurs » est présent dans cette phrase, alors il existe un produit de certains nombres, et le mot qualificatif « simple » signifie que chaque facteur est un nombre premier. Par exemple, dans un produit de la forme 2·7·7·23, il y a quatre facteurs premiers : 2, 7, 7 et 23.

Que signifie factoriser un nombre en facteurs premiers ?

Cela signifie que numéro donné doit être présenté comme un produit de facteurs premiers, et la valeur de ce produit doit être égale au nombre d'origine. A titre d'exemple, considérons le produit de trois nombres premiers 2, 3 et 5, il est égal à 30, donc la décomposition du nombre 30 en facteurs premiers est 2·3·5. Habituellement, la décomposition d'un nombre en facteurs premiers s'écrit sous forme d'égalité ; dans notre exemple, ce sera comme ceci : 30=2·3·5. Nous soulignons séparément que les facteurs premiers du développement peuvent être répétés. Cela illustre clairement exemple suivant: 144=2·2·2·2·3·3 . Mais une représentation de la forme 45=3.15 n'est pas une décomposition en facteurs premiers, puisque le nombre 15 est un nombre composé.

Se pose question suivante: "Quels nombres peuvent être factorisés en facteurs premiers ?"

À la recherche d'une réponse à cette question, nous présentons le raisonnement suivant. Les nombres premiers, par définition, font partie de ceux supérieurs à un. Compte tenu de ce fait et , on peut affirmer que le produit de plusieurs facteurs premiers est un nombre entier nombre positif, dépassant un. Par conséquent, la factorisation n’a lieu que pour les entiers positifs supérieurs à 1.

Mais tous les nombres entiers supérieurs à un peuvent-ils être pris en compte en facteurs premiers ?

Il est clair qu’il n’est pas possible de factoriser des entiers simples en facteurs premiers. Cela s'explique par le fait que les nombres premiers n'ont que deux diviseurs positifs - un et lui-même, ils ne peuvent donc pas être représentés comme un produit de deux ou plus nombres premiers. Si l’entier z pouvait être représenté comme le produit des nombres premiers a et b, alors la notion de divisibilité permettrait de conclure que z est divisible à la fois par a et par b, ce qui est impossible en raison de la simplicité du nombre z. Cependant, ils pensent que tout nombre premier est en soi une décomposition.

Et les nombres composés ? Les nombres composés sont-ils décomposés en facteurs premiers, et tous les nombres composés sont-ils soumis à une telle décomposition ? Le théorème fondamental de l’arithmétique donne une réponse affirmative à un certain nombre de ces questions. Le théorème de base de l'arithmétique stipule que tout entier a supérieur à 1 peut être décomposé en produit de facteurs premiers p 1, p 2, ..., p n, et la décomposition a la forme a = p 1 · p 2 · … · p n, et ce le développement est unique, si l'on ne prend pas en compte l'ordre des facteurs

Factorisation canonique d'un nombre en facteurs premiers

Dans le développement d’un nombre, les facteurs premiers peuvent être répétés. Les facteurs premiers répétitifs peuvent être écrits de manière plus compacte en utilisant . Supposons que dans la décomposition d'un nombre le facteur premier p 1 apparaisse s 1 fois, le facteur premier p 2 – s 2 fois, et ainsi de suite, p n – s n fois. Alors la factorisation première du nombre a peut s’écrire a=p 1 s 1 ·p 2 s 2 ·…·p n s n. Cette forme d'enregistrement est ce qu'on appelle factorisation canonique d'un nombre en facteurs premiers.

Donnons un exemple de décomposition canonique d'un nombre en facteurs premiers. Faites-nous savoir la décomposition 609 840=2 2 2 2 3 3 5 7 11 11, sa notation canonique a la forme 609 840=2 4 3 2 5 7 11 2.

La factorisation canonique d'un nombre en facteurs premiers permet de retrouver tous les diviseurs du nombre et le nombre de diviseurs du nombre.

Algorithme pour factoriser un nombre en facteurs premiers

Pour réussir à décomposer un nombre en facteurs premiers, vous devez avoir une très bonne connaissance des informations contenues dans l'article Nombres premiers et composés.

L’essence du processus de décomposition d’un nombre entier positif a supérieur à un ressort clairement de la preuve du théorème fondamental de l’arithmétique. Le point est découverte séquentielle les plus petits diviseurs premiers p 1 , p 2 , …, p n des nombres a, a 1 , a 2 , …, a n-1 , ce qui permet d'obtenir une série d'égalités a = p 1 · a 1 , où a 1 = a : p 1 , a=p 1 ·a 1 =p 1 ·p 2 ·a 2 , où a 2 =a 1:p 2 , …, a=p 1 ·p 2 ·…·p n ·a n , où a n =a n-1 :p n . Lorsqu'il s'avère a n =1, alors l'égalité a=p 1 ·p 2 ·…·p n nous donnera la décomposition souhaitée du nombre a en facteurs premiers. Il convient également de noter ici que p 1 ≤p 2 ≤p 3 ≤…≤p n.

Reste à comprendre comment trouver les plus petits facteurs premiers à chaque étape, et nous aurons un algorithme pour décomposer un nombre en facteurs premiers. Un tableau de nombres premiers nous aidera à trouver des facteurs premiers. Montrons comment l'utiliser pour obtenir le plus petit diviseur premier du nombre z.

Nous prenons séquentiellement les nombres premiers du tableau des nombres premiers (2, 3, 5, 7, 11, etc.) et divisons le nombre z donné par eux. Le premier nombre premier par lequel z est divisé de manière égale sera son plus petit diviseur premier. Si le nombre z est premier, alors son plus petit diviseur premier sera le nombre z lui-même. Il convient de rappeler ici que si z n'est pas un nombre premier, alors son plus petit diviseur premier ne dépasse pas le nombre , d'où vient z. Ainsi, si parmi les nombres premiers n'excédant pas , il n'y avait pas un seul diviseur du nombre z, alors on peut conclure que z est un nombre premier (plus d'informations à ce sujet sont écrites dans la section théorie sous la rubrique Ce nombre est premier ou composé ).

A titre d'exemple, nous allons montrer comment trouver le plus petit diviseur premier du nombre 87. Prenons le chiffre 2. Divisez 87 par 2, nous obtenons 87:2=43 (1 restant) (si nécessaire, voir article). Autrement dit, lorsque l’on divise 87 par 2, le reste est 1, donc 2 n’est pas un diviseur de 87. On prend le nombre premier suivant du tableau des nombres premiers, c'est le nombre 3. Divisez 87 par 3, nous obtenons 87:3=29. Ainsi, 87 est divisible par 3, donc le nombre 3 est le plus petit diviseur premier du nombre 87.

Notez que dans cas général Pour factoriser le nombre a en facteurs premiers, nous avons besoin d'un tableau de nombres premiers jusqu'à un nombre non inférieur à . Nous devrons nous référer à ce tableau à chaque étape, nous devons donc l'avoir à portée de main. Par exemple, pour factoriser le nombre 95 en facteurs premiers, nous n'aurons besoin que d'un tableau de nombres premiers jusqu'à 10 (puisque 10 est supérieur à ). Et pour décomposer le nombre 846 653, vous aurez déjà besoin d'un tableau de nombres premiers jusqu'à 1 000 (puisque 1 000 est supérieur à ).

Nous avons maintenant suffisamment d'informations pour écrire algorithme pour factoriser un nombre en facteurs premiers. L'algorithme de décomposition du nombre a est le suivant :

• En triant séquentiellement les nombres du tableau des nombres premiers, nous trouvons le plus petit diviseur premier p 1 du nombre a, après quoi nous calculons a 1 =a:p 1. Si a 1 = 1, alors le nombre a est premier, et il est lui-même sa décomposition en facteurs premiers. Si a 1 n'est pas égal à 1, alors nous avons a=p 1 ·a 1 et passons à l'étape suivante.
• Nous trouvons le plus petit diviseur premier p 2 du nombre a 1 , pour ce faire, nous trions séquentiellement les nombres du tableau des nombres premiers, en commençant par p 1 , puis calculons a 2 =a 1:p 2 . Si a 2 =1, alors la décomposition requise du nombre a en facteurs premiers a la forme a=p 1 ·p 2. Si a 2 n'est pas égal à 1, alors nous avons a=p 1 ·p 2 ·a 2 et passons à l'étape suivante.
• En parcourant les nombres du tableau des nombres premiers, en commençant par p 2, on trouve le plus petit diviseur premier p 3 du nombre a 2, après quoi on calcule a 3 =a 2:p 3. Si a 3 =1, alors la décomposition requise du nombre a en facteurs premiers a la forme a=p 1 ·p 2 ·p 3. Si a 3 n'est pas égal à 1, alors nous avons a=p 1 ·p 2 ·p 3 ·a 3 et passons à l'étape suivante.
• On trouve le plus petit diviseur premier p n du nombre a n-1 en triant les nombres premiers, en commençant par p n-1, ainsi que a n = a n-1:p n, et a n est égal à 1. Cette étape est la dernière étape de l'algorithme ; on obtient ici la décomposition souhaitée du nombre a en facteurs premiers : a=p 1 ·p 2 ·…·p n.

Pour plus de clarté, tous les résultats obtenus à chaque étape de l'algorithme de décomposition d'un nombre en facteurs premiers sont présentés sous la forme du tableau suivant, dans lequel les nombres a, a 1, a 2, ..., an sont écrits séquentiellement dans une colonne à gauche de la ligne verticale et à droite de la ligne - les plus petits diviseurs premiers correspondants p 1, p 2, ..., p n.

Il ne reste plus qu'à considérer quelques exemples d'application de l'algorithme résultant pour décomposer les nombres en facteurs premiers.

Exemples de factorisation première

Maintenant, nous allons regarder en détail exemples de factorisation de nombres en facteurs premiers. Lors de la décomposition, nous utiliserons l'algorithme du paragraphe précédent. Commençons par cas simples, et nous les compliquerons progressivement afin de rencontrer toutes les nuances possibles qui surviennent lors de la décomposition des nombres en facteurs simples.

Exemple.

Factorisez le nombre 78 dans ses facteurs premiers.

Solution.

Nous commençons à chercher le premier plus petit diviseur premier p 1 nombres a=78 . Pour ce faire, nous commençons à trier séquentiellement les nombres premiers du tableau des nombres premiers. Nous prenons le nombre 2 et divisons 78 par celui-ci, nous obtenons 78:2=39. Le nombre 78 est divisé par 2 sans reste, donc p 1 =2 est le premier diviseur premier trouvé du nombre 78. Dans ce cas, a 1 =a:p 1 =78:2=39. On arrive donc à l'égalité a=p 1 ·a 1 de la forme 78=2·39. Évidemment, un 1 = 39 est différent de 1, on passe donc à la deuxième étape de l'algorithme.

Nous recherchons maintenant le plus petit diviseur premier p 2 du nombre a 1 =39. Nous commençons par énumérer les nombres du tableau des nombres premiers, en commençant par p 1 =2. Divisez 39 par 2, nous obtenons 39:2=19 (1 restant). Puisque 39 n’est pas divisible par 2, alors 2 n’est pas un diviseur. Ensuite, nous prenons le nombre suivant du tableau des nombres premiers (numéro 3) et divisons 39 par celui-ci, nous obtenons 39 : 3 = 13. Par conséquent, p 2 =3 est le plus petit diviseur premier du nombre 39, tandis que a 2 =a 1:p 2 =39:3=13. On a l'égalité a=p 1 ·p 2 ·a 2 sous la forme 78=2·3·13. Puisque a 2 = 13 est différent de 1, passons à l’étape suivante de l’algorithme.

Ici, nous devons trouver le plus petit diviseur premier du nombre a 2 =13. À la recherche du plus petit diviseur premier p 3 du nombre 13, nous trierons séquentiellement les nombres du tableau des nombres premiers, en commençant par p 2 =3. Le nombre 13 n'est pas divisible par 3, puisque 13:3=4 (rest. 1), et 13 n'est pas non plus divisible par 5, 7 et 11, puisque 13:5=2 (rest. 3), 13:7=1 (reste 6) et 13:11 = 1 (reste 2). Le nombre premier suivant est 13, et 13 est divisible par lui sans reste, donc le plus petit diviseur premier p 3 de 13 est le nombre 13 lui-même, et a 3 =a 2:p 3 =13:13=1. Puisque a 3 =1, cette étape de l'algorithme est la dernière, et la décomposition souhaitée du nombre 78 en facteurs premiers a la forme 78=2·3·13 (a=p 1 ·p 2 ·p 3 ).

Répondre:

78=2·3·13.

Exemple.

Exprimez le nombre 83 006 comme un produit de facteurs premiers.

Solution.

A la première étape de l'algorithme de décomposition d'un nombre en facteurs premiers, on trouve p 1 =2 et a 1 =a:p 1 =83 006:2=41 503, d'où 83 006=2·41 503.

Dans la deuxième étape, nous découvrons que 2, 3 et 5 ne sont pas des diviseurs premiers du nombre a 1 = 41 503, mais que le nombre 7 l'est, puisque 41 503 : 7 = 5 929. Nous avons p 2 =7, a 2 =a 1:p 2 =41 503:7=5 929. Ainsi, 83 006=2 7 5 929.

Le plus petit diviseur premier du nombre a 2 =5 929 est le nombre 7, puisque 5 929:7 = 847. Ainsi, p 3 =7, a 3 =a 2:p 3 =5 929:7 = 847, d'où 83 006 = 2·7·7·847.

Nous constatons ensuite que le plus petit diviseur premier p 4 du nombre a 3 =847 est égal à 7. Alors a 4 =a 3:p 4 =847:7=121, donc 83 006=2·7·7·7·121.

On trouve maintenant le plus petit diviseur premier du nombre a 4 =121, c'est le nombre p 5 =11 (puisque 121 est divisible par 11 et non divisible par 7). Alors a 5 =a 4:p 5 =121:11=11, et 83 006=2·7·7·7·11·11.

Enfin, le plus petit diviseur premier du nombre a 5 =11 est le nombre p 6 =11. Alors a 6 =a 5:p 6 =11:11=1. Puisque a 6 =1, cette étape de l'algorithme de décomposition d'un nombre en facteurs premiers est la dernière, et la décomposition souhaitée a la forme 83 006 = 2·7·7·7·11·11.

Le résultat obtenu peut s'écrire comme la décomposition canonique du nombre en facteurs premiers 83 006 = 2·7 3 ·11 2.

Répondre:

83 006=2 7 7 7 11 11=2 7 3 11 2 991 est un nombre premier. En effet, il ne possède pas un seul diviseur premier n'excédant pas ( peut être grossièrement estimé à , puisqu'il est évident que 991<40 2 ), то есть, наименьшим делителем числа 991 является оно само. Тогда p 3 =991 и a 3 =a 2:p 3 =991:991=1 . Следовательно, искомое разложение числа 897 924 289 на простые множители имеет вид 897 924 289=937·967·991 .

Répondre:

897 924 289 = 937 967 991 .

Utilisation de tests de divisibilité pour la factorisation première

Dans des cas simples, vous pouvez décomposer un nombre en facteurs premiers sans utiliser l'algorithme de décomposition du premier paragraphe de cet article. Si les nombres ne sont pas grands, alors pour les décomposer en facteurs premiers, il suffit souvent de connaître les signes de divisibilité. Donnons des exemples pour clarifier.

Par exemple, nous devons factoriser le nombre 10 en facteurs premiers. D'après la table de multiplication, nous savons que 2·5=10, et que les nombres 2 et 5 sont évidemment premiers, donc la factorisation première du nombre 10 ressemble à 10=2·5.

Un autre exemple. À l’aide de la table de multiplication, nous allons factoriser le nombre 48 en facteurs premiers. Nous savons que six fait huit - quarante-huit, soit 48 = 6·8. Cependant, ni 6 ni 8 ne sont des nombres premiers. Mais nous savons que deux fois trois font six, et deux fois quatre font huit, c'est-à-dire 6=2·3 et 8=2·4. Alors 48=6·8=2·3·2·4. Il reste à rappeler que deux fois deux font quatre, on obtient alors la décomposition souhaitée en facteurs premiers 48 = 2·3·2·2·2. Écrivons ce développement sous forme canonique : 48=2 4 ·3.

Mais lorsque vous factorisez le nombre 3 400 en facteurs premiers, vous pouvez utiliser les critères de divisibilité. Les signes de divisibilité par 10, 100 permettent d'affirmer que 3 400 est divisible par 100, avec 3 400=34.100, et 100 est divisible par 10, avec 100=10.10, donc 3.400=34.10.10. Et à partir du test de divisibilité par 2, on peut dire que chacun des facteurs 34, 10 et 10 est divisible par 2, on obtient 3 400=34 10 10=2 17 2 5 2 5. Tous les facteurs de l’expansion résultante sont simples, cette expansion est donc celle souhaitée. Il ne reste plus qu'à réorganiser les facteurs pour qu'ils soient classés par ordre croissant : 3 400 = 2·2·2·5·5·17. Notons également la décomposition canonique de ce nombre en facteurs premiers : 3 400 = 2 3 ·5 2 ·17.

Lors de la décomposition d'un nombre donné en facteurs premiers, vous pouvez utiliser tour à tour les signes de divisibilité et la table de multiplication. Imaginons le nombre 75 comme un produit de facteurs premiers. Le test de divisibilité par 5 permet d'affirmer que 75 est divisible par 5, et on obtient que 75 = 5.15. Et d'après la table de multiplication, nous savons que 15=3·5, donc 75=5·3·5. C'est la décomposition requise du nombre 75 en facteurs premiers.

Références.

• Vilenkin N.Ya. et d'autres. 6e année : manuel pour les établissements d'enseignement général.
• Vinogradov I.M. Fondamentaux de la théorie des nombres.
• Mikhelovich Sh.H. Théorie des nombres.
• Kulikov L.Ya. et autres. Recueil de problèmes d'algèbre et de théorie des nombres : manuel pour les étudiants en physique et en mathématiques. spécialités des instituts pédagogiques.

Formulation.Étant donné un nombre naturel n(n > 1). Obtenir sa décomposition canonique en facteurs simples, c'est-à-dire la présenter comme un produit de facteurs simples. Dans ce cas, il est permis d'indiquer un facteur 1 dans l'expansion. Par exemple, 264 = 2 * 2 * 2 * 3 * 11 (le programme peut produire la réponse 264 = 1 * 2 * 2 * 2 * 3 *. 11).

Solution. Cette tâche a une assez bonne solution.

Depuis théorème fondamental de l'arithmétique on sait que pour tout nombre naturel supérieur à 1 il existe une décomposition canonique en facteurs premiers, et cette décomposition est unique à l'ordre des facteurs. Autrement dit, par exemple, 12 = 2 * 2 * 2 et 12 = 3 * 2 * 2 sont les mêmes extensions.

Considérons forme canonique n'importe quel numéro pour exemple spécifique. Par exemple, 264 = 2 * 2 * 2 * 3 * 11. Comment identifier cette structure ? Pour répondre à cette question, rappelons celles énoncées dans tout cours scolaire règles d'algèbre pour diviser les monômes, en imaginant que les nombres dans l'expansion canonique sont des variables. Comme vous le savez, si vous divisez une expression en une variable contenue dans une certaine mesure dans cette expression au même degré, elle est barrée dans sa notation.

Autrement dit, si nous divisons 264 par 2, alors dans son expansion canonique, il y aura un deux. Nous pouvons alors vérifier si le quotient résultant est à nouveau divisible par 2. La réponse sera oui, mais la troisième fois la division donnera un reste. Ensuite, vous devez prendre en considération le prochain nombre naturel 3 - le quotient sera divisé par celui-ci une fois. En conséquence, en passant la droite numérique dans le sens positif, nous atteindrons le nombre 11, et après avoir divisé par 11 n deviendra égal à 1, ce qui indiquera la nécessité de terminer la procédure.

Pourquoi, avec une telle « rayure » des facteurs trouvés, n'obtenons-nous pas la divisibilité en nombres composés ? En fait, tout est simple ici : tout nombre composé est le produit de facteurs premiers plus petits que lui. En conséquence, il s'avère que nous allons rayer n tous les facteurs de quelque nature que ce soit numéro composé, jusqu'à ce que nous l'atteignions lui-même dans la chaîne des divisions. Par exemple, avec une recherche aussi exhaustive n ne sera jamais divisé par 4, puisque « en route » vers ce nombre nous supprimerons de n tous les facteurs sont deux.

Algorithme en langage naturel :

1) Entrée n;

2) Affectation à une variable p numéros 2 ;

3) Afficher le numéro n, signe égal et unité pour formaliser l'expansion ;

4) Démarrer une boucle avec une précondition n< > 1 . En boucle :

1. Si mmodulep = 0, puis affichez le signe de multiplication et la variable p, puis divisez n sur p, sinon augmentez la valeur je par 1 ;

1. programme PrimeFactors;
2. n, p : mot ;
3. commencer
4. p := 2 ;
5. readln(n);
6. écrire(n, ' = 1');
7. tandis que n<>Je commence
8. si (n mod p) = 0 alors commencez
9. écrire(' * ', p);
10. n:= n div p
11. sinon commencer
12. Inc(p)

La variable aléatoire V est appelée centré , si son espérance mathématique est égale à 0. Un processus aléatoire centré élémentaire est le produit d'une variable aléatoire centrée V et d'une fonction non aléatoire φ(t):X(t)=Vφ(t). Un processus aléatoire élémentaire centré présente les caractéristiques suivantes :

Expression de la forme
, où φ k ( t ), k =1;2;…-fonctions non aléatoires ; , k =1;2;…-variables aléatoires centrées non corrélées, appelées expansion canonique du processus aléatoireX ( t ), tandis que les variables aléatoires sont appelés les coefficients du développement canonique ; et fonctions non aléatoires φ k ( t ) - fonctions de coordonnées du développement canonique.

Considérons les caractéristiques d'un processus aléatoire

Puisque par condition
Que

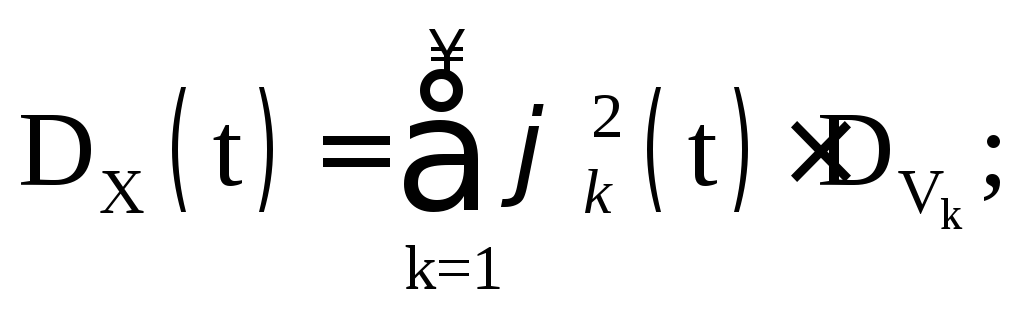
Évidemment, le même processus aléatoire a différents types expansion canonique en fonction du choix des fonctions de coordonnées. De plus, même avec la sélection des fonctions de coordonnées, il existe un arbitraire dans la distribution des variables aléatoires V k. En pratique, sur la base des résultats des expériences, des estimations sont obtenues pour l'espérance mathématique et la fonction de corrélation :
.
Après décomposition

en une double série de Fourier en fonctions de coordonnées φ à (t) :
obtenir les valeurs de variance

variables aléatoires V k .

4.2. Le concept de fonction généralisée. Fonction delta de Dirac. Représentation canonique intégrale de processus aléatoires. Fonction généralisée

est appelée la limite d'une séquence d'une famille de fonctions continues à un paramètre.
- Fonction delta de Dirac
c'est une fonction généralisée résultant du passage à la limite en

dans une famille de fonctions Parmi les propriétés

2.

-fonctions on note les suivantes : 3. Si f(t)- fonction continue

, Que t Processus aléatoire X( ), dont la fonction de corrélation a la forme appelée « bruit blanc » non stationnaire. Si ( t 1 )= ), dont la fonction de corrélation a la forme appelée « bruit blanc » non stationnaire. Si - W const t , puis X(

)-« bruit blanc » stationnaire. Comme il ressort de la définition, il n’y a pas deux sections, même si proches, « bruit blanc » ne sont pas corrélées.

Représentation canonique intégrale du processus aléatoire X( t ) est appelée une expression de la forme
Où
- fonction centrée aléatoire ;
- fonction non aléatoire d'arguments continus

La fonction de corrélation d'un tel processus aléatoire a la forme :

On peut montrer qu’il existe une fonction non aléatoire G(λ) telle que

où G(λ 1) est la densité de dispersion ; δ(x) est la fonction delta de Dirac.

Nous obtenons

.

Par conséquent, la variance du processus aléatoire X(t) :

4.3. Transformations linéaires et non linéaires de processus aléatoires

.

Le problème suivant est considéré : un « signal d'entrée » ayant la nature d'un processus aléatoire X(t) est fourni à l'entrée du système (appareil, convertisseur) S. Le système le convertit en un « signal de sortie » Y(t) :

Formellement, la transformation d'un processus aléatoire X(t) en Y(t) peut être décrite à l'aide de ce que l'on appelle l'opérateur système A t :

Y(t)=A t (X(t)).

L'indice t indique que cet opérateur effectue une conversion temporelle. Les formulations suivantes du problème de transformation d'un processus aléatoire sont possibles. Les lois de distribution sont connues ou caractéristiques générales

processus aléatoire X(t) à l'entrée du système S, l'opérateur A t du système S est donné, il faut déterminer la loi de distribution ou les caractéristiques générales du processus aléatoire Y(t) à la sortie du système S.

Les lois de distribution (caractéristiques générales) du processus aléatoire X(t) et les exigences du processus aléatoire Y(t) sont connues ;

il est nécessaire de déterminer le type d'opérateur A t du système S qui satisfait le mieux aux exigences kY(t) données. Les lois de distribution (caractéristiques générales) du processus aléatoire Y(t) sont connues et l'opérateur A t du système S est donné ; il est nécessaire de déterminer les lois de distribution ou les caractéristiques générales du processus aléatoire X(t).

P.

La classification suivante des opérateurs A t du système S est acceptée :

Opérateurs système

Linéaire LNon linéaireN

Linéaire homogène L 0 Linéaire inhomogène L n

Considérons l'impact d'un système linéaire inhomogène

.

L n (...)=L 0 (...)+φ(t)

à un processus aléatoire X(t) ayant le développement canonique suivant :

On obtient :

.

introduisons la notation

alors le développement canonique de Y(t) prend la forme :

Espérance mathématique du processus aléatoire Y(t) :

fonction de corrélation du processus aléatoire Y(t) :

ainsi,

De l'autre côté

Variance du processus aléatoire Y(t) :

En conclusion de ce paragraphe, notons que les opérateurs de différenciation et d'intégration de processus aléatoires sont linéaires homogènes.

V k variables aléatoires centrées ayant une distribution symétrique par rapport à zéro ; quatre d'entre eux sont conjointement indépendants.

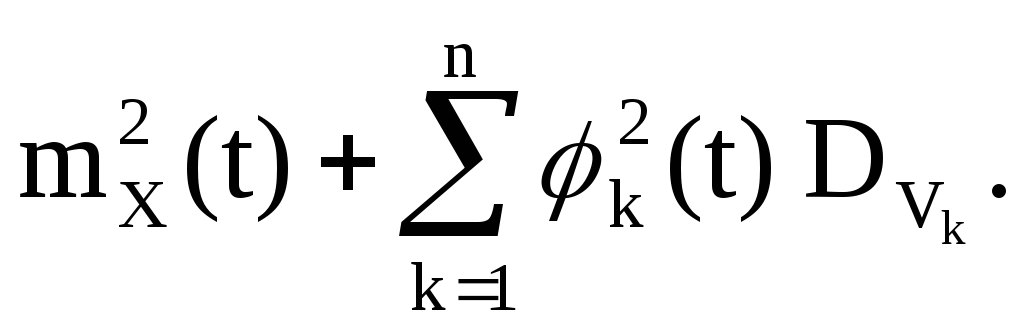
Alors

Introduisons les fonctions non aléatoires

et variables aléatoires

alors le processus aléatoire Y(t) prend la forme