રહસ્યમય ડિસઓર્ડર: ફ્રેકટલ્સનો ઇતિહાસ અને તેમના ઉપયોગના ક્ષેત્રો. અવિભાજ્ય સંખ્યાઓમાં ખંડિત

પરિચય

ફ્રેક્ટલનો ખ્યાલ ................................................. ........................................4

ફ્રેકટલ્સના દેખાવનો ઇતિહાસ………………………………………………………………6

બીજગણિત ખંડિત ……………………………………………….8

1. માલડેબ્રોડ સમૂહ………………………………………………….9

   જુલિયા સેટ…………………………………………………… 11

   ન્યુટનના પૂલ (ફ્રેકટલ્સ)……………………………………………………… 13

   ખંડિત (પરપોટા) હેલી………………………………………………………..14

પ્રાયોગિક એપ્લિકેશનફ્રેકટલ્સ …………………………………………15

નિષ્કર્ષ………………………………………………………………………………….19

સંદર્ભોની યાદી ………………………………………………………………….20

પરિચય

વિજ્ઞાનની ભાષા ઝડપથી બદલાઈ રહી છે આધુનિક વિશ્વ. ભૌતિકશાસ્ત્રના વિકાસનો ઈતિહાસ એક સદી કરતાં પણ વધુ જૂનો છે. આ સમય દરમિયાન, વિશાળ સંખ્યામાં વૈવિધ્યસભર કુદરતી ઘટનાઓનો અભ્યાસ કરવામાં આવ્યો છે, ભૌતિકશાસ્ત્રના મૂળભૂત નિયમો શોધવામાં આવ્યા છે જે વિવિધ પ્રાયોગિક તથ્યોને સમજાવે છે.

પ્રકૃતિમાં મોટાભાગની સિસ્ટમો બે ગુણધર્મોને જોડે છે: પ્રથમ, તે ખૂબ મોટી છે, ઘણીવાર બહુપક્ષીય, વૈવિધ્યસભર અને જટિલ, અને બીજુંતેઓ ખૂબ પ્રભાવ હેઠળ રચાય છે નથી મોટી માત્રામાંસરળ દાખલાઓ, અને આ સરળ દાખલાઓનું પાલન કરીને વધુ વિકાસ કરો. આ સૌથી વધુ છે વિવિધ સિસ્ટમો, સ્ફટિકો અને ફક્ત ક્લસ્ટરોથી શરૂ કરીને (વિવિધ પ્રકારના સંચય, જેમ કે વાદળો, નદીઓ, પર્વતો, ખંડો, તારાઓ), ઇકોસિસ્ટમ્સ સાથે સમાપ્ત થાય છે અને જૈવિક પદાર્થો(ફર્ન પર્ણ થી માનવ મગજ). ફ્રેકલ્સ માત્ર આવા પદાર્થો છે: એક તરફ, જટિલ (અનંત ઘણા તત્વો ધરાવે છે), બીજી બાજુ, ખૂબ જ અનુસાર બાંધવામાં આવે છે. સરળ કાયદા. આ ગુણધર્મ માટે આભાર, ઘણી કુદરતી વસ્તુઓ સાથે ફ્રેકટલ્સમાં ઘણું સામ્ય છે. પરંતુ ફ્રેક્ટલ તેની સાથે અનુકૂળ સરખામણી કરે છે કુદરતી પદાર્થહકીકત એ છે કે ફ્રેક્ટલની કડક ગાણિતિક વ્યાખ્યા હોય છે અને તે કડક વર્ણન અને વિશ્લેષણને ધિરાણ આપે છે. તેથી, ફ્રેકટલ્સનો સિદ્ધાંત છોડની મૂળ પ્રણાલીના વિકાસ દર, સ્વેમ્પ્સમાંથી પાણી કાઢવા માટેના મજૂરી ખર્ચ, અંકુરની ઊંચાઈ પર સ્ટ્રો માસની અવલંબન અને ઘણું બધું અનુમાન લગાવવાનું શક્ય બનાવે છે. ગણિતમાં આ એક નવી દિશા છે, જેણે બનાવી છે વૈજ્ઞાનિક દૃષ્ટાંતસાપેક્ષતાના સિદ્ધાંત સાથે તુલનાત્મક ક્રાંતિ અને ક્વોન્ટમ મિકેનિક્સ. ખંડિત ભૂમિતિના પદાર્થો પોતાની રીતે દેખાવઅમે ઉપયોગમાં લેવાતા "નિયમિત" ભૌમિતિક આકારોથી એકદમ અલગ. હકીકતમાં, આ એક પ્રગતિ છે ગાણિતિક વર્ણનસિસ્ટમો કે જે લાંબા સમયથી પોતાને આવા વર્ણન માટે ઉધાર આપતા નથી.

ખંડિત ભૂમિતિ "શુદ્ધ" નથી ભૌમિતિક સિદ્ધાંત. તે વધુ એક ખ્યાલ છે નવો દેખાવજાણીતી વસ્તુઓ પર, દ્રષ્ટિનું પુનર્ગઠન, સંશોધકને વિશ્વને નવી રીતે જોવાની ફરજ પાડે છે.

મારા કાર્યનો ઉદ્દેશ્ય "ભંગાણ" અને તેની વિવિધતા "બીજણિતીય ફ્રેકટલ" ની વિભાવનાથી પોતાને પરિચિત કરવાનો છે.

ખંડિત ખ્યાલ

પ્રમાણમાં તાજેતરમાં, ગણિતમાં, ઑબ્જેક્ટની એક છબી ઊભી થઈ, વધુ પ્રચંડ, પરંતુ તેમ છતાં એક રેખા જેવી. કેટલાક વૈજ્ઞાનિકોને પહોળાઈ વગરની રેખાના ખ્યાલ સાથે સમજવું મુશ્કેલ લાગ્યું, તેથી તેઓએ ધીમે ધીમે અભ્યાસ કરવાનું શરૂ કર્યું. ભૌમિતિક આકારોઅને અપૂર્ણાંક અવકાશી પરિમાણ ધરાવતી રચનાઓ. સતત વણાંકો, જેમાં તેમના તમામ વ્યુત્પન્ન હોય છે, તેને તૂટેલા અથવા ખૂબ જ જેગ્ડ વણાંકો દ્વારા બદલવામાં આવ્યા હતા. આવા વળાંકનું એક આકર્ષક ઉદાહરણ એ બ્રાઉનિયન કણનો માર્ગ છે. આ રીતે વિજ્ઞાનમાં ફ્રેક્ટલનો ખ્યાલ આવ્યો.

ખંડિત(lat. fractus - કચડી, તૂટેલી, તૂટેલી) - જટિલ ભૌમિતિક આકૃતિ, જેમાં સ્વ-સમાનતાની મિલકત છે, એટલે કે, કેટલાક ભાગોથી બનેલું છે, જેમાંથી દરેક સમગ્ર આકૃતિ (ફિગ. 1) સમાન છે. વધુ માં વ્યાપક અર્થમાંઅપૂર્ણાંકને યુક્લિડિયન અવકાશમાં પોઈન્ટના સમૂહ તરીકે સમજવામાં આવે છે જેમાં અપૂર્ણાંક મેટ્રિક પરિમાણ હોય છે (મિન્કોવસ્કી અથવા હૌસડોર્ફના અર્થમાં) અથવા મેટ્રિક પરિમાણ.

ચોખા. 1
એ નોંધવું જોઈએ કે "ફ્રેકટલ" શબ્દ નથી ગાણિતિક શબ્દઅને સામાન્ય રીતે સ્વીકૃત કડક નથી ગાણિતિક વ્યાખ્યા. જ્યારે પ્રશ્નમાંની આકૃતિમાં નીચેનામાંથી કોઈપણ ગુણધર્મો હોય ત્યારે તેનો ઉપયોગ કરી શકાય છે:

તે તમામ ભીંગડા પર બિન-તુચ્છ માળખું ધરાવે છે. આ નિયમિત આંકડાઓથી વિપરીત છે (જેમ કે વર્તુળ, લંબગોળ, આલેખ સરળ કાર્ય): જો આપણે નિયમિત આકૃતિના નાના ટુકડાને ખૂબ મોટા પાયે જોઈએ, તો તે સીધી રેખાના ટુકડા જેવો દેખાશે. ફ્રેક્ટલ માટે, સ્કેલ વધારવાથી તમામ સ્કેલ પર સમાન જટિલ ચિત્ર જોવા મળશે.

સ્વ-સમાન અથવા લગભગ સ્વ-સમાન છે.

તે અપૂર્ણાંક મેટ્રિક પરિમાણ ધરાવે છે.

પ્રકૃતિમાં ઘણી વસ્તુઓ ખંડિત ગુણધર્મો ધરાવે છે, ઉદાહરણ તરીકે, દરિયાકિનારા, વાદળો, વૃક્ષોના તાજ, રુધિરાભિસરણ તંત્રઅને મનુષ્યો અથવા પ્રાણીઓમાં મૂર્ધન્ય તંત્ર.
કોમ્પ્યુટરનો ઉપયોગ કરીને બાંધકામની સરળતા સાથે સૌંદર્યના સંયોજનને કારણે ખાસ કરીને પ્લેનમાં ફ્રેકલ્સ લોકપ્રિય છે.

ફ્રેકટલ્સનો ઇતિહાસ

19મી અને 20મી સદીના વળાંક પર ફ્રેકટલ્સનો અભ્યાસ વ્યવસ્થિત કરતાં વધુ એપિસોડિક હતો, કારણ કે અગાઉ ગણિતશાસ્ત્રીઓ મુખ્યત્વે "સારી" વસ્તુઓનો અભ્યાસ કરતા હતા જેનો ઉપયોગ કરીને અભ્યાસ કરી શકાય છે. સામાન્ય પદ્ધતિઓઅને સિદ્ધાંતો. 1872 માં, જર્મન ગણિતશાસ્ત્રી કાર્લ વેયરસ્ટ્રાસે એક ઉદાહરણ બનાવ્યું સતત કાર્ય, જે ક્યાંય પણ અલગ નથી, એટલે કે, તેના કોઈપણ બિંદુઓ પર સ્પર્શક નથી. જો કે, તેનું બાંધકામ સંપૂર્ણપણે અમૂર્ત અને સમજવું મુશ્કેલ હતું. તેથી, 1904 માં, સ્વીડનના હેલ્ગે વોન કોચ એક સતત વળાંક સાથે આવ્યા હતા જેમાં ક્યાંય પણ સ્પર્શક નથી, અને દોરવા માટે એકદમ સરળ છે. તે બહાર આવ્યું છે કે તેમાં ફ્રેક્ટલના ગુણધર્મો છે. આ વળાંકના એક પ્રકારને "કોચ સ્નોવફ્લેક" કહેવામાં આવે છે.
આકૃતિઓની સ્વ-સમાનતાનો વિચાર ફ્રેન્ચમેન પોલ પિયર લેવી દ્વારા લેવામાં આવ્યો હતો, ભાવિ માર્ગદર્શકબેનોઈટ મેન્ડેલબ્રોટ. 1938 માં, તેમનો લેખ "પ્લેન અને અવકાશી વળાંકો અને સપાટીઓ જેમાં સમગ્ર સમાન ભાગોનો સમાવેશ થાય છે" પ્રકાશિત થયો હતો, જેમાં અન્ય ફ્રેકટલ - લેવી સી-વક્રનું વર્ણન કરવામાં આવ્યું હતું. ઉપર સૂચિબદ્ધ આ તમામ ફ્રેકટલ્સને શરતી રીતે રચનાત્મક (ભૌમિતિક) ફ્રેકટલ્સના એક વર્ગ તરીકે વર્ગીકૃત કરી શકાય છે.
બીજો વર્ગ ડાયનેમિક (બીજગણિત) ફ્રેકટલ્સ છે, જેમાં મેન્ડેલબ્રોટ સમૂહનો સમાવેશ થાય છે. આ દિશામાં પ્રથમ સંશોધન 20મી સદીની શરૂઆતમાં શરૂ થયું હતું અને તે નામો સાથે સંકળાયેલું છે ફ્રેન્ચ ગણિતશાસ્ત્રીઓગેસ્ટન જુલિયા અને પિયર ફાટુ. 1918 માં, જુલિયાનું કાર્ય જટિલના પુનરાવર્તનો પર પ્રકાશિત થયું હતું તર્કસંગત કાર્યો, જે જુલિયા સેટનું વર્ણન કરે છે, મેન્ડેલબ્રોટ સમૂહ સાથે નજીકથી સંબંધિત ફ્રેકટલ્સનો આખો પરિવાર. આ કાર્યને ઇનામ આપવામાં આવ્યું હતું ફ્રેન્ચ એકેડેમીજો કે, તેમાં એક પણ દ્રષ્ટાંત ન હતું, તેથી ખુલ્લી વસ્તુઓની સુંદરતાની પ્રશંસા કરવી અશક્ય હતી.

ખંડિત ભૂમિતિના પ્રથમ વિચારો 19મી સદીમાં ઉદ્ભવ્યા. કેન્ટરે, એક સરળ પુનરાવર્તિત (પુનરાવર્તિત) પ્રક્રિયાનો ઉપયોગ કરીને, રેખાને બિનજોડાણવાળા બિંદુઓના સંગ્રહમાં ફેરવી (કહેવાતા કેન્ટર ડસ્ટ). તે એક લાઇન લેશે અને મધ્ય ત્રીજાને દૂર કરશે અને પછી બાકીના વિભાગો સાથે તે જ પુનરાવર્તન કરશે. (ફિગ. 2)

ચોખા. 2

પીઆનો દોર્યો ખાસ પ્રકારરેખાઓ.(ફિગ. 3)

ચોખા. 3

તેને દોરવા માટે, પીઆનોએ નીચેના અલ્ગોરિધમનો ઉપયોગ કર્યો.

પ્રથમ પગલામાં, તેણે એક સીધી રેખા લીધી અને તેને મૂળ રેખા (ચિત્રનો ભાગ 1 અને 2) કરતા 3 ગણા ટૂંકા 9 ભાગો સાથે બદલ્યો. પછી તેણે પરિણામી લાઇનના દરેક સેગમેન્ટ સાથે તે જ કર્યું. અને તેથી જાહેરાત અનંત પર. લાઇનની વિશિષ્ટતા એ છે કે તે સમગ્ર પ્લેનને ભરે છે. તે સાબિત થયું છે કે પ્લેન પરના દરેક બિંદુ માટે કોઈ એક બિંદુ શોધી શકે છે રેખા સાથે જોડાયેલાપીઆનો.

પીઆનોનો વળાંક અને કેન્ટરની ધૂળ સામાન્ય ભૌમિતિક વસ્તુઓથી આગળ વધી ગઈ હતી. તેમની પાસે સ્પષ્ટ પરિમાણ નહોતું. કેન્ટરની ધૂળ એક-પરિમાણીય સીધી રેખાના આધારે બાંધવામાં આવી હોય તેવું લાગતું હતું, પરંતુ તેમાં બિંદુઓ (પરિમાણ 0)નો સમાવેશ થતો હતો. અને પીઆનો વળાંક એક-પરિમાણીય રેખાના આધારે બનાવવામાં આવ્યો હતો, અને પરિણામ એક પ્લેન હતું. વિજ્ઞાનના અન્ય ઘણા ક્ષેત્રોમાં, સમસ્યાઓ દેખાઈ, જેના ઉકેલથી વિચિત્ર પરિણામો આવ્યા, જે ઉપર વર્ણવેલ છે ( બ્રાઉનિયન ગતિ, સ્ટોકના ભાવ).

20મી સદી સુધી, આવા ડેટા વિચિત્ર વસ્તુઓ, તેમને વ્યવસ્થિત કરવાના કોઈપણ પ્રયાસ વિના. આધુનિક ખંડિત ભૂમિતિના પિતા અને ફ્રેકટલ શબ્દ બેનોઈટ મેન્ડેલબ્રોટે તેમને સ્વીકાર્યા ત્યાં સુધી તે હતું. ધીરે ધીરે તથ્યોની તુલના કરતાં, તે ગણિતમાં એક નવી દિશાની શોધમાં આવ્યો - ખંડિત ભૂમિતિ.

ફ્રેકટલની વધુ સ્પષ્ટ રીતે કલ્પના કરવા માટે, ચાલો બી. મેન્ડેલબ્રોટના પુસ્તક "ધ ફ્રેકટલ જીઓમેટ્રી ઓફ નેચર" માં આપેલા ઉદાહરણને ધ્યાનમાં લઈએ, જે ક્લાસિક બની ગયું છે - "બ્રિટનના દરિયાકિનારાની લંબાઈ કેટલી છે?" આ પ્રશ્નનો જવાબ લાગે તેટલો સરળ નથી. તે બધા ઉપયોગમાં લેવાતા સાધનની લંબાઈ પર આધારિત છે. કિલોમીટરના શાસકનો ઉપયોગ કરીને કિનારાને માપવાથી, તેઓ થોડી લંબાઈ મેળવે છે. જો કે, ઘણી નાની ખાડીઓ અને દ્વીપકલ્પો ચૂકી ગયા છે, જે માપેલા શાસક કરતા કદમાં ઘણા નાના છે. શાસકના કદને 1 મીટર સુધી ઘટાડીને, તે તારણ આપે છે કે દરિયાકાંઠાની લંબાઈ લાંબી થઈ જશે. મિલીમીટર શાસકનો ઉપયોગ કરીને બેંકની લંબાઈને માપતી વખતે, એક મિલીમીટર કરતા મોટા ભાગોને ધ્યાનમાં લેતા, લંબાઈ પણ વધુ હશે. પરિણામે, આવા મોટે ભાગે સરળ પ્રશ્નનો જવાબ કોઈને પણ મૂંઝવી શકે છે - બ્રિટનના દરિયાકિનારાની લંબાઈ અનંત છે.

બીજગણિત ખંડિત

બીજગણિતીય ફ્રેકટલ્સને તેમનું નામ મળ્યું કારણ કે તેઓ આધાર પર બાંધવામાં આવ્યા છે બીજગણિત સૂત્રો. બીજગણિતીય ફ્રેકટલ્સ મેળવવા માટે ઘણી પદ્ધતિઓ છે. એક પદ્ધતિ એ છે કે કાર્યની વારંવાર ગણતરી કરવી, જ્યાંz - જટિલ સંખ્યા, અને f એ ચોક્કસ કાર્ય છે. ચોક્કસ શરત પૂરી ન થાય ત્યાં સુધી આ કાર્યની ગણતરી ચાલુ રહે છે. અને જ્યારે આ સ્થિતિ પૂરી થાય છે, ત્યારે સ્ક્રીન પર એક બિંદુ પ્રદર્શિત થાય છે. આ કિસ્સામાં, માટે કાર્ય મૂલ્યો વિવિધ બિંદુઓ જટિલ વિમાનહોઈ શકે છે અલગ વર્તન:

સમય જતાં અનંત તરફ વલણ ધરાવે છે;

0 તરફ વલણ ધરાવે છે;
ઘણા નિશ્ચિત મૂલ્યો લે છે અને તેમાંથી આગળ વધતું નથી;
વર્તન અસ્તવ્યસ્ત છે, કોઈપણ વલણો વિના.

3.1 મેન્ડેલબ્રોટ સેટ

મેન્ડેલબ્રોટ સમૂહ (સૌથી પ્રસિદ્ધ ખંડિત વસ્તુઓમાંની એક) સૌપ્રથમ 1980ની વસંતઋતુમાં બેનોઈટ મેન્ડલબ્રોટ દ્વારા બનાવવામાં આવી હતી (કોમ્પ્યુટરનો ઉપયોગ કરીને) સંશોધન કેન્દ્ર IBM કંપનીનું નામ આપવામાં આવ્યું છે. થોમસ જે. વોટસન. અને જો કે આવી વસ્તુઓનું સંશોધન છેલ્લી સદીમાં શરૂ થયું હતું, તે આ સમૂહની શોધ અને હાર્ડવેરની સુધારણા હતી. કમ્પ્યુટર ગ્રાફિક્સવી નિર્ણાયક ડિગ્રીખંડિત ભૂમિતિ અને અરાજકતા સિદ્ધાંતના વિકાસને પ્રભાવિત કરે છે. તો, મેન્ડેલબ્રોટ સેટ શું છે?

જટિલ ચલના કાર્યને ધ્યાનમાં લો. ચાલો મૂકીએઅને ક્રમ ધ્યાનમાં લો, જ્યાં કોઈપણ માટે. આવા ક્રમને બાઉન્ડ કરી શકાય છે (એટલે ​​​​કે ત્યાં એક r હોઈ શકે છે જે કોઈપણ માટે) અથવા "અનંત તરફ ભાગી જાઓ" (એટલે ​​​​કે કોઈપણ r > 0 માટે ત્યાં છે). મેન્ડેલબ્રોટ સમૂહને જટિલ સંખ્યા c ના સમૂહ તરીકે વ્યાખ્યાયિત કરી શકાય છે જેના માટે ઉલ્લેખિત ક્રમ બંધાયેલ છે. કમનસીબે, તે જાણીતું નથી વિશ્લેષણાત્મક અભિવ્યક્તિ, જે આપેલ c ને તે મેન્ડેલબ્રોટ સમૂહની છે કે નહીં તે નિર્ધારિત કરવાની મંજૂરી આપશે. તેથી, સમૂહ બનાવવા માટે, કમ્પ્યુટર પ્રયોગનો ઉપયોગ કરવામાં આવે છે: તેઓ ચોક્કસ પગલા સાથે જટિલ પ્લેન પરના બિંદુઓના સમૂહને જુએ છે, અને દરેક બિંદુ માટે તેઓ કરે છે. ચોક્કસ સંખ્યાપુનરાવર્તનો (ક્રમના સભ્યોની ચોક્કસ સંખ્યા શોધો) અને તેનું "વર્તન" જુઓ. (ફિગ. 4).

તે સાબિત થયું છે કે મેન્ડેલબ્રોટ સમૂહ r=2 ત્રિજ્યાના વર્તુળમાં સ્થિત છે અને તેનું કેન્દ્ર મૂળમાં છે. આમ, જો અમુક તબક્કે અનુક્રમના આગલા પદનું મોડ્યુલસ 2 કરતાં વધી જાય, તો અમે તરત જ તારણ કાઢી શકીએ છીએ કે c ને અનુરૂપ બિંદુ, જે આ ક્રમને વ્યાખ્યાયિત કરે છે, તે મેન્ડેલબ્રોટ સમૂહનો નથી.

જટિલ સંખ્યાઓ સ્કેન કરવામાં આવે છે તે પગલું ઘટાડીને અને પુનરાવર્તનોની સંખ્યામાં વધારો કરીને, અમે અમને ગમે તેટલું વિગતવાર મેળવી શકીએ છીએ, પરંતુ હંમેશા સેટની અંદાજિત છબીઓ જ મેળવી શકીએ છીએ.

0 થી N-1 સુધીની નિશ્ચિતતા માટે ક્રમાંકિત, અમારા નિકાલ પર N રંગો છે. અમે ફરીથી નિશ્ચિતતા માટે માની લઈશું કે કાળો નંબર 0 ધરાવે છે. જો આપેલ c માટે N-1 પુનરાવર્તન પછી બિંદુ ત્રિજ્યા 2 ના વર્તુળની બહાર ન જાય, તો અમે માનીશું કે c મેન્ડેલબ્રોટ સમૂહનો છે અને આ બિંદુને રંગિત કરીશું. c કાળો. નહિંતર, જો કોઈ પગલું k (k Є ) પર આગળનું બિંદુ ત્રિજ્યા 2 ના વર્તુળની બહાર જાય છે (એટલે ​​​​કે, kth સ્ટેપ પર અમને સમજાયું કે તે "ભાગી રહ્યો છે"), તો અમે તેને k રંગમાં રંગીશું.

જ્યારે સુંદર ચિત્રો પ્રાપ્ત થાય છે સારી પસંદગીસેટની પેલેટ અને પડોશી (એટલે ​​​​કે, સેટની બહાર આપણને "રંગીન બિંદુઓ" મળશે) (ફિગ. 5, 6).

ચોખા. 4

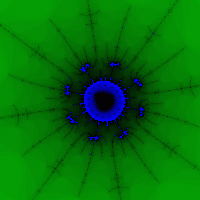
ચોખા. 5 ફિગ. 6

3.2 જુલિયા સેટ

જુલિયા સેટ, મેન્ડેલબ્રોટ સેટ સાથે નજીકથી સંબંધિત છે, તેનો અભ્યાસ 20મી સદીની શરૂઆતમાં ગણિતશાસ્ત્રીઓ ગેસ્ટન જુલિયા અને પિયર ફાટૌ (જુઓ) દ્વારા કરવામાં આવ્યો હતો. 1917-1919 માં તેઓએ જટિલ ચલના પુનરાવર્તિત કાર્યોથી સંબંધિત મૂળભૂત પરિણામો મેળવ્યા. સામાન્ય રીતે કહીએ તો, આ હકીકત એક અલગ ચર્ચાને પાત્ર છે અને એક પ્રભાવશાળી ઉદાહરણ છે ગાણિતિક સંશોધન, તેના સમયના ઘણા દાયકાઓ આગળ (વૈજ્ઞાનિકો માત્ર અંદાજે કલ્પના કરી શકતા હતા કે તેઓએ જે વસ્તુઓનો અભ્યાસ કર્યો હતો તે કેવો દેખાતો હતો!), પરંતુ અમે ફક્ત જટિલ ચલના કાર્ય માટે જુલિયા સેટ બનાવવા માટેની પદ્ધતિનું વર્ણન કરીશું.. વધુ સ્પષ્ટ રીતે, અમે કહેવાતા બિલ્ડ કરીશું. "જુલિયા સેટ ભરવા".

એક લંબચોરસનો વિચાર કરો (x 1 ;વાય 1 -(x 2 ;વાય 2 ). ચાલો સતત c ને ઠીક કરીએ અને ચોક્કસ પગલા સાથે પસંદ કરેલ લંબચોરસના બિંદુઓને જોવાનું શરૂ કરીએ. દરેક બિંદુ માટે, મેન્ડેલબ્રોટ સમૂહના નિર્માણની જેમ, અમે પુનરાવર્તનોની શ્રેણી હાથ ધરીશું ( કરતાં મોટી સંખ્યાપુનરાવૃત્તિઓ, વધુ સચોટ સમૂહ મેળવવામાં આવશે). જો શ્રેણીબદ્ધ પુનરાવર્તનો પછી બિંદુ ત્રિજ્યા 2 ના વર્તુળની સીમાની બહાર "ભાગી" ન જાય, તો અમે તેને કાળા રંગથી રંગીશું, અન્યથા પેલેટના રંગથી. (ફિગ. 7, 8, 9, 10).

ચોખા. 7

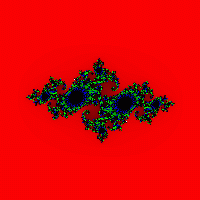
Fig.8 Fig. 9

ચોખા. 10

3.3 ન્યૂટનના પૂલ (ફ્રેકટલ્સ)

ડાયનેમિક ફ્રેકટલ્સનો બીજો પ્રકાર ન્યુટોનિયન ફ્રેકટલ્સ (કહેવાતા બેસિન) છે. (ફિગ. 11). તેમના બાંધકામ માટેના સૂત્રો ઉકેલ પદ્ધતિ પર આધારિત છે બિનરેખીય સમીકરણો, જેની શોધ 17મી સદીમાં મહાન ગણિતશાસ્ત્રીએ કરી હતી. અરજી કરી રહ્યા છે સામાન્ય સૂત્રન્યુટનની પદ્ધતિ zn+1 = zn - f (zn)/f"(zn), n=0, 1, 2… સમીકરણ f (x)=0 ને બહુપદી zk-a ને ઉકેલવા માટે, આપણે પોઈન્ટનો ક્રમ મેળવીએ છીએ. : zn+1 = (k-1)znk/kznk-1, n=0, 1, 2... વિવિધ જટિલ સંખ્યાઓ z0 ને પ્રારંભિક અનુમાન તરીકે પસંદ કરવાથી, અમે આ બહુપદીના મૂળમાં એકરૂપ થતા અનુક્રમો મેળવીશું બરાબર k મૂળ ધરાવે છે, પછી સમગ્ર પ્લેન k ભાગોમાં વિભાજિત થાય છે - આ ભાગોની સીમાઓ ખંડિત માળખું ધરાવે છે.

ચોખા. 11

3.4 ખંડિત (પરપોટા) હેલી

આવા ફ્રેકટલ્સ મેળવવામાં આવે છે જો, ડાયનેમિક ફ્રેકટલ બનાવવાના નિયમ તરીકે, કોઈ ફંક્શનના મૂળના અંદાજિત મૂલ્યો શોધવા માટે હેલીના સૂત્રનો ઉપયોગ કરે છે. (ફિગ. 12).

પદ્ધતિમાં પુનરાવૃત્તિઓનો ક્રમ છે:

પદ્ધતિનો વિચાર લગભગ એ જ છે જે ગતિશીલ ફ્રેકટલ્સ દોરવા માટે વપરાય છે: અમે કેટલાક લઈએ છીએ પ્રારંભિક મૂલ્ય(હંમેશની જેમ, અમે વાત કરી રહ્યા છીએ ચલ અને કાર્યોના મૂલ્યો) અને સંખ્યાઓનો ક્રમ મેળવીને તેના પર સૂત્ર ઘણી વખત લાગુ કરો. તે લગભગ હંમેશા ફંક્શનના શૂન્યમાંથી એકમાં કન્વર્જ થાય છે (એટલે ​​​​કે, ચલનું મૂલ્ય કે જેના પર ફંક્શન 0 મૂલ્ય લે છે). હેલીની પદ્ધતિ, બોજારૂપ સૂત્ર હોવા છતાં, કામ કરે છે પદ્ધતિ કરતાં વધુ અસરકારક : ક્રમ શૂન્ય કાર્યોમાં ઝડપથી કન્વર્જ થાય છે.

ચોખા. 12

ફ્રેકટલ્સનો વ્યવહારુ ઉપયોગ

ફ્રેકટલ્સ બધું શોધે છે વધુ એપ્લિકેશનવિજ્ઞાનમાં. આનું મુખ્ય કારણ તેઓ વર્ણવે છે વાસ્તવિક દુનિયાકેટલીકવાર પરંપરાગત ભૌતિકશાસ્ત્ર અથવા ગણિત કરતાં પણ વધુ સારી. અહીં કેટલાક ઉદાહરણો છે.

કમ્પ્યુટર સિસ્ટમ્સ

કોમ્પ્યુટર જે ચિત્રો બનાવી શકે છે તેમાંથી, થોડા જ જ્યારે ફ્રેકટલ ઈમેજીસ સાથે સ્પર્ધા કરી શકે છે અમે વાત કરી રહ્યા છીએસાચી સુંદરતા વિશે.

સૌથી વધુ ઉપયોગી ઉપયોગકોમ્પ્યુટર સાયન્સમાં ફ્રેકલ્સ ફ્રેકટલ ડેટા કમ્પ્રેશન છે. આ પ્રકારનું કમ્પ્રેશન એ હકીકત પર આધારિત છે કે વાસ્તવિક દુનિયાને ખંડિત ભૂમિતિ દ્વારા સારી રીતે વર્ણવવામાં આવી છે. તે જ સમયે, છબીઓ પરંપરાગત પદ્ધતિઓ (જેમ કે jpeg અથવા gif) સાથે કરવામાં આવે છે તેના કરતા ઘણી સારી રીતે સંકુચિત થાય છે. ફ્રેક્ટલ કમ્પ્રેશનનો બીજો ફાયદો એ છે કે જ્યારે ઇમેજ મોટી કરવામાં આવે છે, ત્યારે ત્યાં કોઈ પિક્સેલેશન અસર હોતી નથી (બિંદુઓના કદને કદમાં વધારીને જે છબીને વિકૃત કરે છે). ફ્રેક્ટલ કમ્પ્રેશન સાથે, એન્લાર્જમેન્ટ પછી, ચિત્ર ઘણીવાર પહેલા કરતાં વધુ સારું લાગે છે.

પ્રવાહી મિકેનિક્સ

પ્રવાહમાં અશાંતિનો અભ્યાસ ખૂબ જ સારી રીતે અનુકૂળ છે

ખંડિત તોફાની પ્રવાહ અસ્તવ્યસ્ત છે અને તેથી તેનું ચોક્કસ મોડેલ બનાવવું મુશ્કેલ છે. અને અહીં ખંડિત રજૂઆતમાં સંક્રમણ મદદ કરે છે, જે એન્જિનિયરો અને ભૌતિકશાસ્ત્રીઓના કાર્યને મોટા પ્રમાણમાં સુવિધા આપે છે, જે તેમને જટિલ પ્રવાહની ગતિશીલતાને વધુ સારી રીતે સમજવાની મંજૂરી આપે છે.

ફ્રેકટલ્સનો ઉપયોગ કરીને તમે જ્વાળાઓનું અનુકરણ પણ કરી શકો છો.

છિદ્રાળુ સામગ્રીઓ ખૂબ જટિલ ભૂમિતિ ધરાવે છે તે હકીકતને કારણે ખંડિત સ્વરૂપમાં સારી રીતે રજૂ થાય છે. તેનો ઉપયોગ પેટ્રોલિયમ વિજ્ઞાનમાં થાય છે.

દૂરસંચાર

અંતર પર ડેટા ટ્રાન્સમિટ કરવા માટે, સાથે એન્ટેના

ખંડિત આકાર, જે તેમના કદ અને વજનને મોટા પ્રમાણમાં ઘટાડે છે. ફ્રેક્ટલ્સનો ઉપયોગ સપાટીઓની વક્રતાનું વર્ણન કરવા માટે થાય છે. અસમાન સપાટી બે અલગ અલગ ફ્રેકટલ્સના સંયોજન દ્વારા વર્ગીકૃત થયેલ છે.
દવા

બાયોસેન્સરી ક્રિયાપ્રતિક્રિયાઓ. ધબકારા.
જીવવિજ્ઞાન

અસ્તવ્યસ્ત પ્રક્રિયાઓનું મોડેલિંગ, ખાસ કરીને જ્યારે વસ્તીના નમૂનાઓનું વર્ણન કરો.
નેનો ટેકનોલોજી

નેનો ટેકનોલોજીના કિસ્સામાં, ફ્રેકટલ્સ પણ ભૂમિકા ભજવે છે મહત્વપૂર્ણ ભૂમિકા, કારણ કે, તેમના વંશવેલો સ્વ-સંસ્થાને લીધે, ઘણી નેનોસિસ્ટમમાં પૂર્ણાંક સિવાયનું પરિમાણ હોય છે, એટલે કે, તેઓ તેમની ભૌમિતિક, ભૌતિક-રાસાયણિક અથવા કાર્યાત્મક પ્રકૃતિમાં ખંડિત હોય છે. ઉદાહરણ તરીકે, એક તેજસ્વી ઉદાહરણરાસાયણિક ખંડિત પ્રણાલીઓ પરમાણુઓ છે "ડેન્ડ્રીમર » . (ફિગ. 13)

ચોખા. 13

સાહિત્ય

વચ્ચે સાહિત્યિક કાર્યોટેક્સ્ટ, માળખાકીય અથવા સિમેન્ટીક ફ્રેક્ટલ પ્રકૃતિ ધરાવતા હોય તે શોધો. ટેક્સ્ટના ભંગાણમાં, ટેક્સ્ટના ઘટકો સંભવિતપણે અનંતપણે પુનરાવર્તિત થાય છે ("પાદરી પાસે એક કૂતરો હતો...", "ફિલોસોફરનું દૃષ્ટાંત જે સ્વપ્ન જુએ છે કે તે એક બટરફ્લાય છે જે સ્વપ્ન જુએ છે કે તેણી એક ફિલોસોફર છે જે સપના કરે છે..." અને એક્સ્ટેંશન સાથે લખાણો ("તે ઘર જે તેણે જેક બનાવ્યું હતું")

માળખાકીય અપૂર્ણાંકમાં, ટેક્સ્ટ સ્કીમ સંભવિત રૂપે ખંડિત છે: સોનેટની માળા (15 કવિતાઓ), સૉનેટની માળા (211 કવિતાઓ), સૉનેટની માળા (2455 કવિતાઓ).

નિષ્કર્ષ

ફ્રેક્ટલ એ અનંત જટિલતાનો એક પદાર્થ છે, જે તમને તેની ઘણી બધી વિગતોને દૂરથી નજીકથી જોવાની મંજૂરી આપે છે. પૃથ્વી - ઉત્તમ ઉદાહરણખંડિત પદાર્થ. અવકાશમાંથી તે બોલ જેવો દેખાય છે. જો આપણે તેનો સંપર્ક કરીશું, તો આપણને મહાસાગરો, ખંડો, દરિયાકિનારા અને પર્વતમાળાઓ મળશે. ચાલો પર્વતોને નજીકથી જોઈએ - વધુ સારી વિગતો પણ દેખાશે: પર્વતની સપાટી પરનો જમીનનો ટુકડો, તેના સ્કેલમાં, પર્વતની જેમ જ જટિલ અને અસમાન છે. અને તેનાથી પણ વધુ વિસ્તૃતીકરણ માટીના નાના કણોને જાહેર કરશે, જેમાંથી દરેક પોતે એક ખંડિત પદાર્થ છે.

નિષ્કર્ષમાં, હું કહેવા માંગુ છું કે ફ્રેકટલ્સની શોધ થયા પછી, ઘણા વૈજ્ઞાનિકો માટે તે સ્પષ્ટ થઈ ગયું છે કે યુક્લિડિયન ભૂમિતિના સારા જૂના સ્વરૂપો મોટાભાગની કુદરતી વસ્તુઓ કરતાં ઘણી હલકી ગુણવત્તાવાળા છે કારણ કે તેમાં કેટલીક અનિયમિતતા, અવ્યવસ્થા અને અણધારીતાના અભાવને કારણે. શક્ય છે કે ખંડિત ભૂમિતિમાં નવા વિચારો ઘણાને અભ્યાસ કરવામાં મદદ કરશે રહસ્યમય ઘટના આસપાસની પ્રકૃતિ. હાલમાં, ભંગાણ ભૌતિકશાસ્ત્ર, જીવવિજ્ઞાન, દવા, સમાજશાસ્ત્ર અને અર્થશાસ્ત્રના ઘણા ક્ષેત્રોમાં ઝડપથી આક્રમણ કરી રહ્યું છે. ઇમેજ પ્રોસેસિંગ અને પેટર્નની ઓળખની પદ્ધતિઓ જે નવા ખ્યાલોનો ઉપયોગ કરે છે તે સંશોધકોને આ ગાણિતિક ઉપકરણને લાગુ કરવા માટે સક્ષમ કરે છે. માત્રાત્મક વર્ણન મોટી રકમકુદરતી વસ્તુઓ અને રચનાઓ.

વપરાયેલ સાહિત્યની સૂચિ

1. ફ્રેકટલ્સનો પરિચય,

2. જુલિયા સેટ પર ઝિકોવ વી.વી. // આધુનિક કુદરતી વિજ્ઞાન: જ્ઞાનકોશ: 10 ખંડોમાં T.1: ગણિત. મિકેનિક્સ. એમ., 2000.

3. ઝિકોવ વી.વી. // આધુનિક કુદરતી વિજ્ઞાન: જ્ઞાનકોશ: 10 વોલ્યુમોમાં: ગણિત. મિકેનિક્સ. એમ., 2000.

4. મેન્ડેલબ્રોટ B. પ્રકૃતિની ખંડિત ભૂમિતિ. – એમ: કોમ્પ્યુટર સંશોધન સંસ્થા, 2002.

5. મોરોઝોવ એ.ડી. ઇન્ટ્રોડક્શન ટુ ધ થિયરી ઓફ ફ્રેક્ટલ્સ -મોસ્કો-ઇઝેવસ્ક: ઇન્સ્ટિટ્યૂટ ઓફ કોમ્પ્યુટર રિસર્ચ, 2002, 160 પૃષ્ઠ.

6. ડાયનેમિક (બીજગણિત) ફ્રેકટલ્સ // તત્વો.. URL:http:// તત્વ. ru/ પોસ્ટરો/ ખંડિત/ ગતિશીલ

7. ડાયનેમિક (બીજગણિત) ફ્રેકટલ્સ // તત્વો.. URL:http:// elementy.ru/posters/fractals/Mandelbrot#nop

8. બીજગણિત ખંડિત // ખંડિત.. URL:http://rusproject.narod.ru/article/fractals.htm

પતંગિયા, અલબત્ત, સાપ વિશે કશું જાણતા નથી. પરંતુ પતંગિયાનો શિકાર કરતા પક્ષીઓ તેમના વિશે જાણે છે. જે પક્ષીઓ સાપને સારી રીતે ઓળખતા નથી તેઓની શક્યતા વધુ હોય છે...

(ડાયનેમિક) ફ્રેકટલ્સ

બિનરેખીય ગતિશીલ પ્રણાલીઓનો અભ્યાસ કરતી વખતે આ પ્રકારના ફ્રેકલ્સ ઉદ્ભવે છે (તેથી તેનું નામ). આવી સિસ્ટમની વર્તણૂક એક જટિલ દ્વારા વર્ણવી શકાય છે બિનરેખીય કાર્ય(બહુપદી) f(z). ચાલો જટિલ સમતલ પર કેટલાક પ્રારંભિક બિંદુ z0 લઈએ. હવે જટિલ પ્લેન પર સંખ્યાઓના અનંત ક્રમને ધ્યાનમાં લો, જેમાંથી દરેક અગાઉના એકમાંથી મેળવવામાં આવે છે: z0, z1 = f(z0), z2 = f(z1), ... zn+1 = f(zn). પર આધાર રાખે છે પ્રારંભિક બિંદુ z0 આવા ક્રમ અલગ રીતે વર્તે છે: n → ∞ તરીકે અનંતતા તરફ વલણ ધરાવે છે; કેટલાકમાં ભેળવવું અંતિમ બિંદુ; ચક્રીય રીતે નિશ્ચિત મૂલ્યોની શ્રેણી લો; વધુ જટિલ વિકલ્પો પણ શક્ય છે.

આમ, ફંક્શન f(z) ના પુનરાવર્તન દરમિયાન જટિલ પ્લેનનો કોઈપણ બિંદુ z તેની પોતાની વર્તણૂક ધરાવે છે, અને સમગ્ર પ્લેન ભાગોમાં વહેંચાયેલું છે. તદુપરાંત, આ ભાગોની સીમાઓ પર પડેલા બિંદુઓમાં નીચેની મિલકત છે: મનસ્વી રીતે નાના વિસ્થાપન સાથે, તેમના વર્તનની પ્રકૃતિ તીવ્રપણે બદલાય છે (આવા બિંદુઓને દ્વિભાજન બિંદુઓ કહેવામાં આવે છે). તેથી, તે તારણ આપે છે કે પોઈન્ટના સેટ કે જેમાં એક ચોક્કસ પ્રકારનું વર્તન હોય છે, તેમજ દ્વિભાજન બિંદુઓના સેટમાં ઘણી વખત ખંડિત ગુણધર્મો હોય છે. ફંક્શન f(z) માટે આ જુલિયા સેટ છે.

મેન્ડેલબ્રોટ સેટ કંઈક અલગ રીતે બાંધવામાં આવ્યો છે. ફંક્શન fc(z) = z2 + c ધ્યાનમાં લો, જ્યાં c એ જટિલ સંખ્યા છે. ચાલો આ ફંક્શનનો ક્રમ z0 = 0 સાથે બનાવીએ c પેરામીટર પર આધાર રાખીને, તે અનંત તરફ વળી શકે છે અથવા મર્યાદિત રહી શકે છે. તદુપરાંત, c ના તમામ મૂલ્યો કે જેના માટે આ ક્રમ મર્યાદિત છે તે મેન્ડેલબ્રોટ સમૂહ બનાવે છે. મેન્ડેલબ્રોટ પોતે અને અન્ય ગણિતશાસ્ત્રીઓ દ્વારા તેનો વિગતવાર અભ્યાસ કરવામાં આવ્યો હતો, જેમણે ઘણી શોધ કરી હતી રસપ્રદ ગુણધર્મોઆ ટોળામાંથી.

તે જોઈ શકાય છે કે જુલિયા અને મેન્ડેલબ્રોટ સેટની વ્યાખ્યાઓ એકબીજા સાથે સમાન છે. હકીકતમાં, આ બે સેટ નજીકથી સંબંધિત છે. જેમ કે, મેન્ડેલબ્રોટ સેટ એ જટિલ પરિમાણ c ના તમામ મૂલ્યો છે જેના માટે જુલિયા સેટ fc(z) જોડાયેલ છે (જો સેટને કેટલીક વધારાની શરતો સાથે, બે અસંબંધિત ભાગોમાં વિભાજિત ન કરી શકાય તો તેને કનેક્ટેડ કહેવામાં આવે છે).

આ સૌથી વધુ છે મોટું જૂથખંડિત તેઓ માં બિનરેખીય પ્રક્રિયાઓનો ઉપયોગ કરીને મેળવવામાં આવે છે n-પરિમાણીય જગ્યાઓ. દ્વિ-પરિમાણીય પ્રક્રિયાઓ સૌથી વધુ અભ્યાસ કરવામાં આવે છે. બિનરેખીય પુનરાવર્તિત પ્રક્રિયાને એક સ્વતંત્ર ગતિશીલ પ્રણાલી તરીકે અર્થઘટન કરતી વખતે, વ્યક્તિ આ સિસ્ટમોના સિદ્ધાંતની પરિભાષાનો ઉપયોગ કરી શકે છે: તબક્કો પોટ્રેટ, સ્થિર-સ્થિતિ પ્રક્રિયા, આકર્ષનાર, વગેરે.

તે જાણીતું છે કે બિનરેખીય ગતિશીલ સિસ્ટમોમાં ઘણી સ્થિર સ્થિતિઓ હોય છે. ચોક્કસ સંખ્યાના પુનરાવૃત્તિઓ પછી ગતિશીલ સિસ્ટમ પોતાને જે સ્થિતિમાં શોધે છે તે તેની પ્રારંભિક સ્થિતિ પર આધારિત છે. તેથી, દરેક સ્થિર રાજ્ય (અથવા, જેમ તેઓ કહે છે, આકર્ષનાર) પાસે પ્રારંભિક રાજ્યોનો ચોક્કસ પ્રદેશ હોય છે, જેમાંથી સિસ્ટમ વિચારણા હેઠળના અંતિમ રાજ્યોમાં આવશ્યકપણે આવશે. આમ તબક્કાની જગ્યાસિસ્ટમ આકર્ષણોના આકર્ષણના ક્ષેત્રોમાં વહેંચાયેલી છે. જો તબક્કાની જગ્યા દ્વિ-પરિમાણીય છે, તો પછી આકર્ષણના વિસ્તારોને રંગ આપો વિવિધ રંગો, તમે આ સિસ્ટમનું રંગ તબક્કાનું પોટ્રેટ મેળવી શકો છો (પુનરાવર્તિત પ્રક્રિયા). રંગ પસંદગી અલ્ગોરિધમ બદલીને, તમે વિચિત્ર મલ્ટીકલર પેટર્ન સાથે જટિલ ફ્રેકટલ પેટર્ન મેળવી શકો છો. ગણિતશાસ્ત્રીઓ માટે આશ્ચર્યજનક બાબત એ હતી કે આદિમ ગાણિતીક નિયમોનો ઉપયોગ કરીને ખૂબ જ જટિલ બિન-તુચ્છ રચનાઓ બનાવવાની ક્ષમતા.

ઉદાહરણ તરીકે, મેન્ડેલબ્રોટ સમૂહને ધ્યાનમાં લો (ફિગ. 3 અને ફિગ. 4 જુઓ). તેના બાંધકામ માટેનું અલ્ગોરિધમ એકદમ સરળ છે અને તે એક સરળ પુનરાવર્તિત અભિવ્યક્તિ પર આધારિત છે:

Z = Z[i] * Z[i] + C,

જ્યાં Zi અને C જટિલ ચલ છે. પુનરાવર્તનો લંબચોરસ અથવા ચોરસ પ્રદેશના દરેક પ્રારંભિક બિંદુ C માટે કરવામાં આવે છે - જટિલ પ્લેનનો સબસેટ. જ્યાં સુધી Z[i] ત્રિજ્યા 2 ના વર્તુળની બહાર ન જાય ત્યાં સુધી પુનરાવર્તિત પ્રક્રિયા ચાલુ રહે છે, જેનું કેન્દ્ર બિંદુ (0,0) પર આવેલું છે, (આનો અર્થ એ થાય છે કે આકર્ષનાર ગતિશીલ સિસ્ટમઅનંત પર છે), અથવા પર્યાપ્ત પછી મોટી સંખ્યામાંપુનરાવૃત્તિઓ (ઉદાહરણ તરીકે 200-500) Z[i] વર્તુળ પરના અમુક બિંદુ પર કન્વર્જ થશે. જે દરમિયાન Z[i] વર્તુળની અંદર રહે છે તે પુનરાવૃત્તિઓની સંખ્યાના આધારે, તમે બિંદુ C નો રંગ સેટ કરી શકો છો (જો Z[i] વર્તુળની અંદર પૂરતી સંખ્યામાં પુનરાવૃત્તિઓ માટે રહે છે, તો પુનરાવૃત્તિ પ્રક્રિયા બંધ થઈ જાય છે અને આ રાસ્ટર બિંદુ કાળો રંગવામાં આવે છે).

ઉપરોક્ત અલ્ગોરિધમ કહેવાતા મેન્ડેલબ્રોટ સમૂહનો અંદાજ આપે છે. મેન્ડેલબ્રોટ સમૂહમાં પોઈન્ટ છે જે દરમિયાન અનંત સંખ્યાપુનરાવર્તનો અનંત સુધી જતા નથી (બિંદુઓ કાળા છે). સમૂહની સીમા સાથે જોડાયેલા બિંદુઓ (આ તે છે જ્યાં જટિલ રચનાઓ) માટે અનંત પર જાઓ અંતિમ સંખ્યાપુનરાવૃત્તિઓ, અને સમૂહની બહાર પડેલા બિંદુઓ અનેક પુનરાવર્તનો (સફેદ પૃષ્ઠભૂમિ) પછી અનંતમાં જાય છે.

બીજગણિતીય ફ્રેકટલ્સના ઉદાહરણો:

• મેન્ડેલબ્રોટ સેટ
• જુલિયા સેટ કરે છે
• હેલીનું ફ્રેકટલ
• ન્યુટનનું ફ્રેકટલ

જ્યારે હું નદીની સપાટી પરના તરંગોના દખલને જોઈ રહ્યો હતો ત્યારે મને આ ખંડિતની શોધ થઈ. તરંગ કિનારા તરફ આગળ વધે છે, પ્રતિબિંબિત થાય છે અને પોતાના પર સુપરઇમ્પોઝ થાય છે. તરંગો બનાવે છે તે પેટર્નમાં કોઈ ક્રમ છે? ચાલો તેને શોધવાનો પ્રયત્ન કરીએ. ચાલો સમગ્ર તરંગને નહીં, પરંતુ તેની ગતિના વેક્ટરને ધ્યાનમાં લઈએ. ચાલો પ્રયોગને સરળ બનાવવા માટે “કિનારા” ને સરળ બનાવીએ.

પ્રયોગ શાળાની નોટબુકમાંથી નિયમિત કાગળના ટુકડા પર કરી શકાય છે.

અથવા અલ્ગોરિધમનો JavaScript અમલીકરણનો ઉપયોગ કરીને.

બાજુઓ q અને p સાથે એક લંબચોરસ લો. ચાલો એક કિરણ (વેક્ટર) ખૂણેથી ખૂણે મોકલીએ. બીમ લંબચોરસની એક બાજુએ ખસે છે, પ્રતિબિંબિત થાય છે અને આગળની બાજુએ જવાનું ચાલુ રાખે છે. જ્યાં સુધી બીમ બાકીના ખૂણાઓમાંથી એકને હિટ ન કરે ત્યાં સુધી આ ચાલુ રહે છે. જો બાજુ q અને p નું કદ પ્રમાણમાં અવિભાજ્ય સંખ્યાઓ હોય, તો એક પેટર્ન પ્રાપ્ત થાય છે (જેમ કે આપણે પછી જોઈશું - એક ખંડિત).

ચિત્રમાં આપણે સ્પષ્ટપણે જોઈ શકીએ છીએ કે આ અલ્ગોરિધમ કેવી રીતે કામ કરે છે.

Gif એનિમેશન:

સૌથી આશ્ચર્યજનક બાબત એ છે કે સાથે વિવિધ બાજુઓલંબચોરસ - અમને વિવિધ પેટર્ન મળે છે.

હું આ પેટર્નને ફ્રેકટલ્સ કેમ કહું? જેમ તમે જાણો છો, "ફ્રેક્ટલ" એ ભૌમિતિક આકૃતિ છે જે સ્વ-સમાનતા ગુણધર્મો ધરાવે છે. ચિત્રનો ભાગ સમગ્ર ચિત્રને પુનરાવર્તિત કરે છે. જો તમે બાજુઓ Q અને P ના પરિમાણોમાં નોંધપાત્ર વધારો કરો છો, તો તે સ્પષ્ટ છે કે આ પેટર્નમાં સ્વ-સમાનતા ગુણધર્મો છે.

ચાલો તેને વધારવાનો પ્રયાસ કરીએ. અમે તેને ચાલાકીપૂર્વક વધારીશું. ઉદાહરણ તરીકે 17x29 પેટર્ન લઈએ. નીચેની પેટર્ન હશે: 29x(17+29=46), 46x(29+46=75)…
એક બાજુ: F(n);
બીજી બાજુ: F(n+1)=F(n)+F(n-1);
17, 29, 46, 75, 121, 196, 317, 513, 830, 1343
ફિબોનાકી નંબરોની જેમ, માત્ર ક્રમના જુદા જુદા પ્રથમ અને બીજા સભ્યો સાથે: F(0)=17, F(1)=29.

જો મોટી બાજુપણ, પરિણામ નીચેની પેટર્ન છે:

જો ટૂંકી બાજુ સમાન હોય:

જો બંને બાજુઓ વિષમ હોય, તો આપણને સપ્રમાણ પેટર્ન મળે છે:

બીમ કેવી રીતે શરૂ થાય છે તેના આધારે:

અથવા

હું આ લંબચોરસમાં શું થાય છે તે સમજાવવાનો પ્રયત્ન કરીશ.

ચાલો ચોરસને લંબચોરસથી અલગ કરીએ અને જોઈએ કે સરહદ પર શું થાય છે.

બીમ તે જ બિંદુથી બહાર નીકળે છે જ્યાંથી તે દાખલ થયો હતો.

તે જ સમયે, કિરણ જેમાંથી પસાર થાય છે તે વર્ગોની સંખ્યા હંમેશા એક સમાન સંખ્યા હોય છે.

તેથી, જો તમે લંબચોરસમાંથી ચોરસ કાપી નાખો, તો ફ્રેક્ટલનો એક અપરિવર્તિત ભાગ રહેશે.

જો તમે શક્ય તેટલી વાર ફ્રેક્ટલમાંથી ચોરસને અલગ કરો છો, તો તમે ફ્રેક્ટલની "શરૂઆત" પર પહોંચી શકો છો.

શું તે ફિબોનાકી સર્પાકાર જેવું લાગે છે?

ફિબોનાકી નંબરોમાંથી પણ ફ્રેકટલ્સ મેળવી શકાય છે.

ગણિતમાં, ફિબોનાકી સંખ્યાઓ (ફિબોનાકી શ્રેણી, ફિબોનાકી ક્રમ) એ સંખ્યાઓ છે:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…
વ્યાખ્યા પ્રમાણે, ફિબોનાકી ક્રમમાં પ્રથમ બે અંકો 0 અને 1 છે, અને દરેક અનુગામી સંખ્યા અગાઉના બેના સરવાળાની બરાબર છે.
F(n)=F(n-1)+F(n-2)
F(0)=0, F(1)=1

ચાલો જઈએ:

જેમ આપણે જોઈ શકીએ છીએ, આસ્પેક્ટ રેશિયો ગોલ્ડન રેશિયોની જેટલો નજીક આવે છે, તેટલી ફ્રેકટલની વિગત વધારે છે.

આ કિસ્સામાં, ફ્રેક્ટલ ફ્રેક્ટલના ભાગને પુનરાવર્તિત કરે છે, જે વધીને .

ફિબોનાકી નંબરોને બદલે, તમે અતાર્કિક બાજુના કદનો ઉપયોગ કરી શકો છો:

આપણને એ જ ફ્રેકટલ મળે છે.

જો તમે બીમને અલગ ખૂણા પર શૂટ કરો છો તો સમાન ફ્રેકટલ્સ ચોરસમાં મેળવી શકાય છે:

તમે નિષ્કર્ષમાં શું કહી શકો?
અરાજકતા પણ ઓર્ડર છે. તેના પોતાના કાયદા સાથે. આ ક્રમનો અભ્યાસ કરવામાં આવ્યો નથી, પરંતુ અભ્યાસ કરવા માટે તદ્દન યોગ્ય છે. અને વિજ્ઞાનની સમગ્ર ઈચ્છા આ દાખલાઓ શોધવાની છે. અને આખરે મોટું ચિત્ર જોવા માટે પઝલના ટુકડાને જોડો.
ચાલો નદીની સપાટી જોઈએ. જો તમે તેના પર પથ્થર ફેંકશો, તો મોજા આવશે. એવા વર્તુળો કે જે અભ્યાસ માટે તદ્દન અનુકૂળ છે. ઝડપ, અવધિ, તરંગલંબાઇ - આ બધાની ગણતરી કરી શકાય છે. પરંતુ તરંગ કિનારા સુધી પહોંચે ત્યાં સુધી તે પ્રતિબિંબિત થતું નથી અને પોતાને ઓવરલેપ કરવાનું શરૂ કરે છે. અમને અરાજકતા (દખલગીરી) મળે છે, જેનો અભ્યાસ કરવો પહેલેથી જ મુશ્કેલ છે.
જો આપણે વિરુદ્ધ દિશામાંથી આગળ વધીએ તો શું? તરંગના વર્તનને શક્ય તેટલું સરળ બનાવો. સરળ બનાવો, પેટર્ન શોધો અને પછી તેનું વર્ણન કરવાનો પ્રયાસ કરો સંપૂર્ણ ચિત્રશું થઈ રહ્યું છે.
શું સરળ બનાવી શકાય? દેખીતી રીતે, વળાંક વિના, પ્રતિબિંબીત સપાટીને સીધી બનાવો. આગળ, તરંગને બદલે, ફક્ત તરંગ ગતિ વેક્ટરનો ઉપયોગ કરો. સૈદ્ધાંતિક રીતે, આ એક સરળ અલ્ગોરિધમનો બનાવવા અને કમ્પ્યુટર પર પ્રક્રિયાનું અનુકરણ કરવા માટે પૂરતું છે. અને તે કાગળના સામાન્ય ચેકર્ડ ટુકડા પર તરંગ વર્તનનું "મોડલ" બનાવવા માટે પણ પૂરતું છે.
પરિણામે આપણી પાસે શું છે? પરિણામે, આપણે તે જોઈ શકીએ છીએ તરંગ પ્રક્રિયાઓ(નદીની સપાટી પર સમાન લહેર) આપણી પાસે અરાજકતા નથી, પરંતુ એકબીજાની ટોચ પર ફ્રેકટલ્સ (સ્વ-સમાન રચનાઓ) નું ઓવરલે છે.

ચાલો બીજા પ્રકારના તરંગોનો વિચાર કરીએ. જેમ જાણીતું છે, ઇલેક્ટ્રોમેગ્નેટિક તરંગત્રણ વેક્ટરનો સમાવેશ થાય છે - વેવ વેક્ટર અને ઇલેક્ટ્રિક અને વોલ્ટેજ વેક્ટર ચુંબકીય ક્ષેત્ર. જેમ આપણે જોઈ શકીએ છીએ, જો તમે આવી તરંગને "પકડશો". બંધ વિસ્તાર– જ્યાં આ વેક્ટર એકબીજાને છેદે છે, ત્યાં આપણને એકદમ સ્પષ્ટ બંધ બંધારણ મળે છે. કદાચ પ્રાથમિક કણો- શું આ સમાન ફ્રેકટલ્સ છે?

1 થી 80 (6723x6723 px) સુધીના લંબચોરસમાં તમામ ફ્રેકટલ્સ:

ફ્રેકટલમાં બંધ વિસ્તારો (6723x6723 px):

માત્ર એક સુંદર ફ્રેકટલ (4078x2518 px):