7.1. Хөндлөн бүтээгдэхүүний тодорхойлолт

Гурван хосгүй вектор a, b ба c, авсан заасан дарааллаар, хэрэв гурав дахь векторын төгсгөлөөс эхлээд а вектороос хоёр дахь b вектор хүртэлх хамгийн богино эргэлт цагийн зүүний эсрэг явагдаж байвал баруун гурвалсан гурвалжинг үүсгэнэ (Зураг 16-г үз).

a вектор b ба векторуудын хөндлөн үржвэрийг в вектор в гэнэ, үүнд:

1. a ба b векторуудад перпендикуляр, өөрөөр хэлбэл c ^ a ба c ^ b ;

2. Энэ нь a ба векторууд дээр баригдсан параллелограммын талбайтай тэнцүү урттайбталуудын адил (17-р зургийг үз), i.e.

3. a, b, c векторууд нь баруун гарын гурвалсан хэлбэрийг үүсгэдэг.

Вектор урлагийн бүтээл a x b эсвэл [a,b] гэж тэмдэглэнэ. Вектор үржвэрийн тодорхойлолтоос шууд дагах i нэгж векторуудын хоорондох дараах хамаарал нь, j Тэгээдк

(18-р зургийг үз):
i x j = k, j x k = i, k x i = j.Жишээлбэл, үүнийг баталъя

би xj =k. ^ 1) k ^ i, k

j ; 2) |k |=1, харин | i x j

| = |i | Тэгээд|Ж | sin(90°)=1;

3) i, j ба векторууд

баруун гурвалсан (16-р зургийг үз).

7.2. Хөндлөн бүтээгдэхүүний шинж чанарууд = -(1. Хүчин зүйлсийг дахин цэгцлэх үед вектор бүтээгдэхүүн тэмдэг өөрчлөгддөг, i.e.).

ба xb =(b xa) (19-р зургийг үз). a xb ба b xa векторууд нь хоорондоо уялдаатай, ижил модультай (параллелограммын талбай өөрчлөгдөөгүй), гэхдээ эсрэг чиглэлд чиглэсэн (a, b, a xb ба a, b, b x a эсрэг чиглэлтэй гурвалсан). Тиймээсахб

b xa 2. Вектор үржвэр нь байнахосолсон шинж чанар бскаляр хүчин зүйлийн хувьд, өөрөөр хэлбэл l (a xb) = (l a) x b = a x (l b). б l >0 гэж үзье. l (a xb) вектор нь a ба b векторуудад перпендикуляр байна. Вектор ( 2. Вектор үржвэр нь байнал 2. Вектор үржвэр нь байна a) x 2. Вектор үржвэр нь байнахосолсон шинж чанар бмөн a ба векторуудад перпендикуляр байна

(а векторууд, 2. Вектор үржвэр нь байнагэхдээ нэг хавтгайд хэвтэх). Энэ нь векторууд гэсэн үг юм 2. Вектор үржвэр нь байна(a xb) ба ( 2. Вектор үржвэр нь байна<0.

collinear. Тэдний чиглэл давхцаж байгаа нь ойлгомжтой. Тэд ижил урттай: бТийм ч учраас (a xb)= a xb. Үүнийг ижил төстэй байдлаар нотолсон<=>3. Тэг биш хоёр вектор a ба

гагцхүү тэдгээрийн хөндлөн үржвэр нь тэнцүү байх тохиолдолд л коллинеар байна

тэг вектор

(, өөрөөр хэлбэл a ||bба xb =0. бЯлангуяа i *i =j *j =k *k =0 .

4. Вектор бүтээгдэхүүн нь хуваарилах шинж чанартай:

7.3. Хөндлөн үржвэрийг координатаар илэрхийлэх

Бид i векторуудын хөндлөн үржвэрийн хүснэгтийг ашиглана. Вектор үржвэрийн тодорхойлолтоос шууд дагах i нэгж векторуудын хоорондох дараах хамаарал нь,ба к:

хэрэв эхний вектороос хоёр дахь хүртэлх хамгийн богино замын чиглэл нь сумны чиглэлтэй давхцаж байвал үржвэр нь гурав дахь вектортой тэнцэнэ, хэрэв энэ нь давхцахгүй бол гурав дахь векторыг хасах тэмдгээр авна;

a =a x i +a y хоёр векторыг өгье Вектор үржвэрийн тодорхойлолтоос шууд дагах i нэгж векторуудын хоорондох дараах хамаарал нь,+a z Тэгээдба b =b x би+б жил Вектор үржвэрийн тодорхойлолтоос шууд дагах i нэгж векторуудын хоорондох дараах хамаарал нь,+b z Тэгээд. Эдгээр векторуудын вектор үржвэрийг олон гишүүнт болгон үржүүлэх замаар олъё (вектор бүтээгдэхүүний шинж чанарын дагуу):

Үр дүнгийн томъёог илүү товчоор бичиж болно:

тэгш байдлын баруун тал (7.1) нь эхний эгнээний элементүүдийн хувьд гурав дахь эрэмбийн тодорхойлогчийн өргөтгөлтэй тохирч байгаа тул Тэгш байдал (7.2) санахад хялбар.

7.4. Хөндлөн бүтээгдэхүүний зарим хэрэглээ

Векторуудын уялдаа холбоог тогтоох

Параллелограмм ба гурвалжны талбайг олох

Векторуудын вектор үржвэрийн тодорхойлолтын дагуу Аболон б |a xb | =|а | * |b |sin g, өөрөөр хэлбэл S хос = |a x b |. Тиймээс D S =1/2|a x b |.

Нэг цэгийн ойролцоох хүчний моментийг тодорхойлох

А цэг дээр хүч хэрэглэе F =ABмөн зөвшөөрөх ТУХАЙ- орон зайн зарим цэг (20-р зургийг үз).

Энэ нь физикээс мэдэгдэж байна хүчний момент Ф цэгтэй харьцуулахад ТУХАЙвектор гэж нэрлэдэг М,цэгээр дамждаг ТУХАЙМөн:

1) цэгүүдийг дайран өнгөрөх хавтгайд перпендикуляр О, А, Б;

2) нэг гарт ногдох хүчний үржвэртэй тоогоор тэнцүү байна

3) ОА ба А В векторуудтай зөв гурвалсан хэлбэрийг үүсгэнэ.

Тиймээс M = OA x F.

Шугаман эргэлтийн хурдыг олох

Хурд vоноо М хатуу, өнцгийн хурдаар эргэдэг wтогтмол тэнхлэгийн эргэн тойронд байх нь Эйлерийн томьёогоор тодорхойлогддог v =w xr, энд r =OM, O нь тэнхлэгийн зарим тогтмол цэг (21-р зургийг үз).

Тодорхойлолт Захиалгат цуглуулгыг (x 1 , x 2 , ... , x n) n бодит тоо гэнэ. n хэмжээст вектор, болон тоонууд x i (i =) - бүрэлдэхүүн хэсгүүд,эсвэл координат,

Жишээ. Жишээлбэл, тодорхой автомашины үйлдвэр нь нэг ээлжинд 50 автомашин, 100 ачааны машин, 10 автобус, 50 ​​иж бүрдэл автомашин, 150 иж бүрдэл ачааны машин, автобус үйлдвэрлэх ёстой бол энэ үйлдвэрийн үйлдвэрлэлийн хөтөлбөрийг вектор хэлбэрээр бичиж болно. (50, 100, 10, 50, 150), таван бүрэлдэхүүн хэсэгтэй.

Тэмдэглэгээ. Векторуудыг тод жижиг үсгээр эсвэл дээд талд нь зураас эсвэл сумтай үсгээр тэмдэглэнэ, жишээлбэл. аэсвэл. Хоёр векторыг нэрлэдэг тэнцүү, хэрэв тэдгээр нь ижил тооны бүрэлдэхүүн хэсгүүдтэй бөгөөд тэдгээрийн харгалзах бүрэлдэхүүн хэсгүүд нь тэнцүү бол.

Вектор бүрэлдэхүүн хэсгүүдийг солих боломжгүй, жишээлбэл, (3, 2, 5, 0, 1)ба (2, 3, 5, 0, 1) өөр векторууд.
Вектор дээрх үйлдлүүд.ажил x= (x 1 , x 2 , ... ,x n) бодит тоогоорλ вектор гэж нэрлэдэгλ x= (λ x 1, λ x 2, ..., λ x n).

Дүнx= (x 1 , x 2 , ... ,x n) ба y= (y 1 , y 2 , ... ,y n) -ийг вектор гэнэ x+y= (x 1 + y 1 , x 2 + y 2 , ... , x n + + y n).

Вектор орон зай.Н -хэмжээст вектор орон зай Р n нь бодит тоогоор үржүүлэх болон нэмэх үйлдлүүдийг тодорхойлсон бүх n хэмжээст векторуудын олонлогоор тодорхойлогддог.

Эдийн засгийн дүрслэл. n хэмжээст вектор орон зайн эдийн засгийн дүрслэл: барааны орон зай (бараа). Доод барааБид тодорхой газар тодорхой цагт худалдаанд гарсан зарим бараа, үйлчилгээг ойлгох болно. Боломжтой барааны хязгаарлагдмал тоо n байна гэж бодъё; Хэрэглэгчийн худалдаж авсан тэдгээрийн тоо хэмжээг багц барааны хэлбэрээр тодорхойлдог

x= (x 1 , x 2 , ..., x n),

Энд x i нь хэрэглэгчийн худалдан авсан i-р барааны хэмжээг илэрхийлнэ. Бид бүх барааг дур зоргоороо хуваах шинж чанартай гэж үзэх болно, ингэснээр тэдгээрийн аль ч сөрөг бус тоо хэмжээг худалдан авч болно. Дараа нь бүх боломжит барааны багц нь барааны орон зайн векторууд юм C = ( x= (x 1 , x 2 , ... , x n) x i ≥ 0, i = ).

Шугаман бие даасан байдал. Систем д 1 , д 2 , ... , д m n хэмжээст векторуудыг нэрлэнэ шугаман хамааралтай, хэрэв ийм тоо байгаа болλ 1 , λ 2 , ... , λ м , үүнээс дор хаяж нэг нь тэг биш байх тул тэгш байдалλ 1 д 1 + λ 2 д 2 +... + λ м дм = 0; өөрөөр хэлбэл энэ векторын системийг гэж нэрлэдэг шугаман бие даасан, өөрөөр хэлбэл заасан тэгш байдал нь зөвхөн бүх тохиолдолд л боломжтой болно . Векторуудын шугаман хамаарлын геометрийн утга Р 3-ыг чиглэсэн сегмент гэж тайлбарлавал дараах теоремуудыг тайлбарла.

Теорем 1. Нэг вектороос бүрдэх систем нь зөвхөн энэ вектор тэг байвал шугаман хамааралтай болно.

Теорем 2. Хоёр вектор шугаман хамааралтай байхын тулд тэдгээр нь коллинеар (параллель) байх шаардлагатай бөгөөд хангалттай.

Теорем 3 . Гурван вектор шугаман хамааралтай байхын тулд тэдгээр нь хоорондоо уялдаатай (нэг хавтгайд байрлах) байх шаардлагатай бөгөөд хангалттай.

Зүүн ба баруун гурвалсан векторууд. Хавсарсан бус векторуудын гурав дахин a, b, cдуудсан зөв, хэрэв тэдгээрийн нийтлэг гарал үүслийн ажиглагч векторуудын төгсгөлийг тойрч байвал a, b, cөгөгдсөн дарааллаар цагийн зүүний дагуу гарч ирдэг. Үгүй бол a, b, c -гурав үлдсэн. Бүх баруун (эсвэл зүүн) гурвалсан векторууд гэж нэрлэгддэг адилхан чиглэсэн.

Суурь ба координат. Тройка д 1, д 2 , д 3 хуваарьгүй векторууд Р 3 гэж нэрлэдэг суурь, мөн векторууд өөрсдөө д 1, д 2 , д 3 - үндсэн. Аливаа вектор аүндсэн векторууд болгон өвөрмөц байдлаар өргөжүүлж болно, өөрөөр хэлбэл хэлбэрээр төлөөлдөг

А= x 1 д 1+x2 д 2 + x 3 д 3, (1.1)

(1.1) өргөтгөлийн x 1 , x 2 , x 3 тоонуудыг дуудна координатуудаүндсэн дээр д 1, д 2 , д 3 ба томилогдсон а(x 1, x 2, x 3).

Ортонормаль суурь. Хэрэв векторууд д 1, д 2 , д 3 нь хос перпендикуляр бөгөөд тус бүрийн урт нь нэгтэй тэнцүү бол суурь гэж нэрлэдэг. ортонормаль, мөн координатууд x 1 , x 2 , x 3 - тэгш өнцөгт.Ортонормаль суурийн суурь векторуудыг дараах байдлаар тэмдэглэнэ i, j, k.

Бид үүнийг сансарт гэж таамаглах болно Р 3 Декартын тэгш өнцөгт координатын зөв системийг сонгосон (0, i, j, k}.

Вектор урлагийн бүтээл. Вектор урлагийн бүтээл Авектор руу бвектор гэж нэрлэдэг вдараах гурван нөхцөлөөр тодорхойлогддог.

1. Векторын урт ввекторууд дээр баригдсан параллелограммын талбайтай тоогоор тэнцүү байна аТэгээд б,өөрөөр хэлбэл
в= |a||b|нүгэл( а^б).

2. Вектор ввектор тус бүрт перпендикуляр байна аТэгээд б.

3. Векторууд а, бТэгээд в, заасан дарааллаар авсан, баруун гурвалсан үүсгэнэ.

Хөндлөн бүтээгдэхүүний хувьд втэмдэглэгээг танилцуулж байна c =[ab] эсвэл
c = a × б.

Хэрэв векторууд аТэгээд бхоорондоо уялдаатай, дараа нь нүгэл ( a^b) = 0 ба [ ab] = 0, ялангуяа, [ аа] = 0. Нэгж векторын вектор үржвэрүүд: [ ij]=к, [jk] = би, [ки]=j.

Хэрэв векторууд аТэгээд бүндэслэлд заасан i, j, kкоординатууд а(a 1 , a 2 , a 3), б(b 1, b 2, b 3), дараа нь

Холимог ажил. Хэрэв хоёр векторын вектор үржвэр бол АТэгээд бгурав дахь вектороор скаляраар үржүүлсэн в,тэгвэл гурван векторын ийм үржвэрийг нэрлэнэ холимог ажилба тэмдгээр тэмдэглэгдсэн байна а б в.

Хэрэв векторууд а, бТэгээд вүндсэн дээр i, j, kтэдгээрийн координатаар өгөгдсөн
а(a 1 , a 2 , a 3), б(b 1, b 2, b 3), в(c 1, c 2, c 3), дараа нь

.

Холимог бүтээгдэхүүн нь энгийн геометрийн тайлбартай байдаг - энэ нь өгөгдсөн гурван вектор дээр баригдсан параллелепипедийн эзэлхүүнтэй үнэмлэхүй утгатай тэнцүү скаляр юм.

Хэрэв векторууд зөв гурвалсан бол тэдгээрийн холимог ажилзаасан эзлэхүүнтэй тэнцэх эерэг тоо байна; хэрэв гурав бол a, b, c -тэгээд зүүн a b c<0 и V = - a b c, тиймээс V =|a b c|.

Нэгдүгээр бүлгийн асуудалд тулгарсан векторуудын координатыг зөв ортонормаль суурьтай харьцуулсан гэж үзнэ. Нэгж вектор вектортой координат А,тэмдгээр илэрхийлнэ АО. Тэмдэг r=ОММ цэгийн радиус вектороор тэмдэглэгдсэн, a, AB эсвэл тэмдэгтүүд|а|, | AB|векторуудын модулиудыг тэмдэглэв АТэгээд AB.

Жишээ 1.2. Векторуудын хоорондох өнцгийг ол а= 2м+4nТэгээд б= м-н, Хаана мТэгээд n-нэгж векторууд ба хоорондын өнцөг мТэгээд n 120 o-тай тэнцүү.

Шийдэл. Бидэнд байна: cos φ = ab/аб ab =(2м+4n) (м-н) = 2м 2 - 4n 2 +2mn=
= 2 - 4+2cos120 o = - 2 + 2(-0.5) = -3; a = ; а 2 = (2м+4n) (2м+4n) =
= 4м 2 +16mn+16n 2 = 4+16(-0.5)+16=12, энэ нь a = гэсэн үг. b = ; б 2 =
= (м-н)(м-н) = м 2 -2mn+n 2 = 1-2(-0.5)+1 = 3, энэ нь b = гэсэн үг. Эцэст нь бидэнд байна: cosφ = = -1/2, φ = 120 o.

Жишээ 1.3.Векторуудыг мэддэг AB(-3,-2.6) ба МЭӨ(-2,4,4),АВС гурвалжны AD өндрийн уртыг тооцоол.

Шийдэл. ABC гурвалжны талбайг S-ээр тэмдэглэвэл бид дараахь зүйлийг авна.
S = МЭӨ 1/2. Дараа нь AD=2S/BC, BC= = = 6,
S = 1/2| AB ×AC|. AC=AB+BC, энэ нь вектор гэсэн үг А.С.координаттай
. .

Жишээ 1.4 . Хоёр вектор өгөгдсөн а(11,10,2) ба б(4,0,3). Нэгж векторыг ол в,векторуудад ортогональ аТэгээд бба дараалсан гурвалсан вектор байхаар чиглүүлсэн a, b, cзөв байсан.

Шийдэл.Векторын координатыг тэмдэглэе в x, y, z-ийн хувьд өгөгдсөн зөв ортонормаль суурийн хувьд.

Түүнээс хойш в ⊥ а, в ⊥б, Тэр ойролцоогоор= 0,cb= 0. Бодлогын нөхцлийн дагуу c = 1 ба байх шаардлагатай a b c >0.

Бидэнд x,y,z-ийг олох тэгшитгэлийн систем бий: 11x +10y + 2z = 0, 4x+3z=0, x 2 + y 2 + z 2 = 0.

Системийн эхний ба хоёр дахь тэгшитгэлээс бид z = -4/3 x, y = -5/6 x-ийг олж авна. Гурав дахь тэгшитгэлд y ба z-г орлуулбал: x 2 = 36/125, эндээс
x =± . Нөхцөлийг ашиглах a b c > 0, бид тэгш бус байдлыг олж авна

z ба y-ийн илэрхийллүүдийг харгалзан бид үүссэн тэгш бус байдлыг 625/6 x > 0 хэлбэрээр дахин бичдэг бөгөөд энэ нь x>0 гэсэн үг юм. Тэгэхээр x = , y = - , z =- .

Вектор бүтээгдэхүүний тухай ойлголтыг өгөхийн өмнө гурван хэмжээст орон зайд a →, b →, c → векторуудын дараалсан гурвалсан чиг баримжаа олгох тухай асуулт руу шилжье.

Эхлэхийн тулд a → , b → , c → векторуудыг нэг цэгээс хойш тавья. Гурвалсан a → , b → , c → чиглэл нь в → векторын өөрийн чиглэлээс хамаарч баруун эсвэл зүүн байж болно. Гурвалсан a → , b → , c → векторын а → в вектороос b → в → векторын төгсгөлөөс хамгийн богино эргэлт хийх чиглэлээс хамаарч тодорхойлогдоно.

Хэрэв хамгийн богино эргэлтийг цагийн зүүний эсрэг хийвэл a → , b → , c → векторуудын гурвалсан хэсгийг гэнэ. зөв, хэрэв цагийн зүүний дагуу - зүүн.

Дараа нь a → ба b → коллинеар бус хоёр векторыг авна. Дараа нь А цэгээс A B → = a → ба A C → = b → векторуудыг зуръя. A B → болон A C → аль алинд нь нэгэн зэрэг перпендикуляр байх A D → = c → векторыг байгуулъя. Тиймээс, векторыг өөрөө A D → = c → байгуулахдаа бид үүнийг нэг чиглэл эсвэл эсрэгээр нь өгөх хоёр аргаар хийж болно (зураг харна уу).

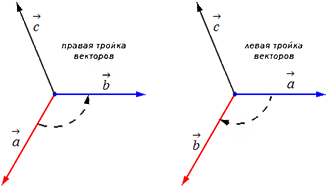
a → , b → , c → векторуудын дараалсан гурвалсан нь векторын чиглэлээс хамаарч баруун эсвэл зүүн байж болно.

Дээрхээс бид вектор бүтээгдэхүүний тодорхойлолтыг танилцуулж болно. Энэ тодорхойлолт-д тодорхойлсон хоёр векторын хувьд өгөгдсөн тэгш өнцөгт системгурван хэмжээст орон зайн координатууд.

Тодорхойлолт 1

a → ба b → хоёр векторын вектор үржвэр Гурван хэмжээст орон зайн тэгш өнцөгт координатын системд тодорхойлсон ийм векторыг бид дараах байдлаар нэрлэх болно.

• a → ба b → векторууд нь коллинеар байвал тэг болно;
• a → ​​ вектор ба b векторын аль алинд нь перпендикуляр байх болно → өөрөөр хэлбэл. ∠ a → c → = ∠ b → c → = π 2 ;
• түүний уртыг дараах томъёогоор тодорхойлно: c → = a → · b → · sin ∠ a → , b → ;
• a → , b → , c → векторуудын гурвалсан нь өгөгдсөн координатын системтэй ижил чиглэлтэй байна.

a → ба b → векторуудын вектор үржвэр нь дараах тэмдэглэгээтэй байна: a → × b →.

Вектор бүтээгдэхүүний координатууд

Аливаа вектор координатын системд тодорхой координаттай байдаг тул бид вектор бүтээгдэхүүний хоёр дахь тодорхойлолтыг оруулж болох бөгөөд энэ нь векторуудын өгөгдсөн координатыг ашиглан координатыг нь олох боломжийг бидэнд олгоно.

Тодорхойлолт 2

Гурван хэмжээст орон зайн тэгш өнцөгт координатын системд a → = (a x ; a y ; a z) ба b → = (b x ; b y ; b z) хоёр векторын вектор үржвэр вектор гэж нэрлэдэг c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , энд i → , j → , k → нь координатын векторууд юм.

Хөндлөн үржвэрийг тодорхойлогчоор төлөөлж болно квадрат матрицГурав дахь дараалал, эхний мөрөнд i → , j → , k → векторын векторууд, хоёр дахь мөрөнд a → векторын координатууд, гурав дахь мөрөнд өгөгдсөн тэгш өнцөгт дэх b → векторын координатууд байна. координатын системд матрицын тодорхойлогч дараах байдалтай байна: c → = a → × b → = i → j → k → a x a y a z b x b y b z

Энэ тодорхойлогчийг эхний эгнээний элементүүд болгон өргөжүүлбэл бид тэгшитгэлийг олж авна: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → - a x a z b x b z · j → b · = a x → → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

Хөндлөн бүтээгдэхүүний шинж чанарууд

Координат дахь вектор үржвэрийг c → = a → × b → = i → j → k → a x a y a z b x b y b z матрицын тодорхойлогчоор илэрхийлдэг нь мэдэгдэж байна. матриц тодорхойлогчийн шинж чанарууддараахыг харуулав вектор бүтээгдэхүүний шинж чанарууд:

1. anticommutativity a → × b → = - b → × a → ;
2. тархалт a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → эсвэл a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
3. ассоциатив байдал λ a → × b → = λ a → × b → эсвэл a → × (λ b →) = λ a → × b →, энд λ нь дурын бодит тоо юм.

Эдгээр шинж чанарууд нь энгийн нотолгоотой байдаг.

Жишээ болгон бид вектор бүтээгдэхүүний антикоммутацийн шинж чанарыг баталж чадна.

Эсрэг солилцооны нотолгоо

Тодорхойлолтоор a → × b → = i → j → k → a x a y a z b x b y b z ба b → × a → = i → j → k → b x b y b z a x a y a z. Хэрэв матрицын хоёр эгнээ солигдвол матрицын тодорхойлогчийн утга эсрэгээр өөрчлөгдөх ёстой тул a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x = y байна. - b → × a → , энэ нь вектор үржвэрийн эсрэг коммутатив болохыг баталж байна.

Вектор бүтээгдэхүүн - жишээ ба шийдэл

Ихэнх тохиолдолд гурван төрлийн асуудал байдаг.

Эхний төрлийн бодлогод ихэвчлэн хоёр векторын урт ба тэдгээрийн хоорондох өнцгийг өгдөг бөгөөд та векторын үржвэрийн уртыг олох хэрэгтэй. Энэ тохиолдолд тэд ашигладаг дараах томъёо c → = a → · b → · sin ∠ a → , b → .

Жишээ 1

a → = 3, b → = 5, ∠ a →, b → = π 4 гэдгийг мэддэг бол a → ба b → векторуудын вектор үржвэрийн уртыг ол.

Шийдэл

a → ба b → векторуудын вектор үржвэрийн уртыг тодорхойлсноор бид энэ асуудлыг шийднэ: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .

Хариулт: 15 2 2 .

Хоёрдахь төрлийн асуудлууд нь векторуудын координат, тэдгээрийн векторын бүтээгдэхүүн, түүний урт гэх мэт холбоотой байдаг. мэдэгдэж буй координатуудаар хайсан өгөгдсөн векторууд a → = (a x; a y; a z) Тэгээд b → = (b x ; b y ; b z) .

Энэ төрлийн асуудлын хувьд та олон даалгаврын сонголтыг шийдэж чадна. Жишээлбэл, a → ба b → векторуудын координатыг зааж өгөхгүй, харин тэдгээрийн хэлбэрийг координат вектор болгон өргөтгөх боломжтой. b → = b x · i → + b y · j → + b z · k → ба c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →, эсвэл a → ба b → векторуудыг тэдгээрийн эхлэлийн координатаар тодорхойлж болно. болон төгсгөлийн цэгүүд.

Дараах жишээнүүдийг авч үзье.

Жишээ 2

Тэгш өнцөгт координатын системд хоёр вектор өгөгдсөн: a → = (2; 1; - 3), b → = (0; - 1; 1). Тэдний хөндлөн бүтээгдэхүүнийг ол.

Шийдэл

Хоёр дахь тодорхойлолтоор бид хоёр векторын вектор үржвэрийг олдог өгөгдсөн координатууд: a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + (a x · b y - a y · b x) · k → = = (1 ·) 1 - (- 3) (- 1)) i → + ((- 3) 0 - 2 1) j → + (2 (- 1) - 1 0) k → = = - 2 i → - 2 j → - 2 к → .

Хэрэв бид вектор үржвэрийг матрицын тодорхойлогчийн хувьд бичвэл шийдэл энэ жишээдараах байдалтай байна: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

Хариулт: a → × b → = - 2 i → - 2 j → - 2 k → .

Жишээ 3

i → - j → ба i → + j → + k → векторуудын вектор үржвэрийн уртыг ол, энд i →, j →, k → тэгш өнцөгт декартын координатын системийн нэгж векторууд байна.

Шийдэл

Эхлээд өгөгдсөн тэгш өнцөгт координатын систем дэх i → - j → × i → + j → + k → вектор үржвэрийн координатыг олъё.

i → - j → ба i → + j → + k → векторууд (1; - 1; 0) ба (1; 1; 1) координатуудтай байдаг нь мэдэгдэж байна. Матрицын тодорхойлогчийг ашиглан вектор үржвэрийн уртыг олъё, тэгвэл i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .

Тиймээс i → - j → × i → + j → + k → вектор үржвэр нь координат (- 1 ; - 1 ; 2) байна. өгөгдсөн системкоординатууд

Бид вектор бүтээгдэхүүний уртыг томъёогоор олно (векторын уртыг олох хэсгийг үзнэ үү): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.

Хариулт: i → - j → × i → + j → + k → = 6 . .

Жишээ 4

Тэгш өнцөгт хэлбэрээр Декарт системА (1, 0, 1), В (0, 2, 3), С (1, 4, 2) гэсэн гурван цэгийн координатыг координатад өгсөн болно. A B → ба A C →-д нэгэн зэрэг перпендикуляр байх векторыг ол.

Шийдэл

A B → ба A C → векторууд нь дараах координатуудтай (- 1 ; 2 ; 2) ба (0 ; 4 ; 1) байна. A B → ба A C → векторуудын вектор үржвэрийг олсны дараа энэ нь тодорхой байна. перпендикуляр вектортодорхойлолтоор A B →​​​ ба A C → аль алинд нь, өөрөөр хэлбэл энэ нь бидний асуудлын шийдэл юм. Үүнийг A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → гэж олъё.

Хариулт: - 6 i → + j → - 4 k → . - перпендикуляр векторуудын нэг.

Гурав дахь төрлийн асуудлууд нь векторуудын вектор бүтээгдэхүүний шинж чанарыг ашиглахад чиглэгддэг. Үүнийг хэрэглэсний дараа бид өгөгдсөн асуудлын шийдлийг олж авах болно.

Жишээ 5

a → ба b → векторууд нь перпендикуляр бөгөөд тэдгээрийн урт нь тус тус 3 ба 4 байна. 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → вектор үржвэрийн уртыг ол. + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → .

Шийдэл

Вектор бүтээгдэхүүний тархалтын шинж чанараар бид 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 гэж бичиж болно. a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

Холбооны өмчөөр бид гаргаж авдаг тоон магадлалСүүлийн илэрхийлэл дэх вектор бүтээгдэхүүний тэмдгийн хувьд: 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → = = 3 a → × a → + 3 (- 2) a → × b → + (- 1) b → × a → + (- 1) (- 2) b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

a → × a → = a → · a → · sin 0 = 0 ба b → × b → = b → · b → · sin тул a → × a → ба b → × b → вектор бүтээгдэхүүнүүд 0-тэй тэнцүү байна. 0 = 0, дараа нь 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b → = - 6 · a → × b → - b → × a → . .

Вектор бүтээгдэхүүний антикоммутатив байдлаас дараах нь - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × b → . .

Вектор бүтээгдэхүүний шинж чанарыг ашиглан бид 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → тэгшитгэлийг олж авна.

Нөхцөлөөр a→ ба b → векторууд перпендикуляр, өөрөөр хэлбэл тэдгээрийн хоорондох өнцөг нь π 2-тэй тэнцүү байна. Одоо үлдсэн бүх зүйл бол олсон утгыг тохирох томъёонд орлуулах явдал юм: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → · нүгэл (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .

Хариулт: 3 a → - b → × a → - 2 b → = 60.

Тодорхойлолтоор векторуудын вектор үржвэрийн урт нь a → × b → = a → · b → · sin ∠ a → , b → -тэй тэнцүү байна. Энэ нь аль хэдийн мэдэгдэж байгаа тул (аас сургуулийн курс), гурвалжны талбай нь түүний хоёр талын уртын үржвэрийн хагасыг эдгээр талуудын хоорондох өнцгийн синусаар үржүүлсэнтэй тэнцүү байна. Үүний үр дүнд векторын бүтээгдэхүүний урт нь параллелограммын талбайтай тэнцүү байна - давхар гурвалжин, тухайлбал а → ба b → вектор хэлбэрээр талуудын үржвэр, нэг цэгээс синусын дагуу тавигдсан. тэдгээрийн хоорондох өнцөг sin ∠ a →, b →.

Энэ л байна геометрийн утгавектор бүтээгдэхүүн.

Вектор бүтээгдэхүүний физик утга

Физикийн салбаруудын нэг болох механикт вектор бүтээгдэхүүний ачаар та орон зайн цэгтэй харьцуулахад хүчний моментийг тодорхойлж болно.

Тодорхойлолт 3

А цэгтэй харьцуулахад B цэгт F → үйлчлэх хүчний агшинд бид дараах вектор бүтээгдэхүүн A B → × F → ойлгох болно.

Хэрэв та текстэнд алдаа байгааг анзаарсан бол үүнийг тодруулаад Ctrl+Enter дарна уу

Тодорхойлолт. a вектор (үржүүлэгч) ба коллинеар бус вектор (үржвэр) -ийн вектор үржвэр нь гурав дахь вектор c (бүтээгдэхүүн) бөгөөд дараах байдлаар бүтээгдэнэ.

1) түүний модуль нь тоон үзүүлэлт юм талбайтай тэнцүүЗураг дээрх параллелограмм. 155), векторууд дээр бүтээгдсэн, тухайлбал чиглэлтэй тэнцүүдурдсан параллелограммын хавтгайд перпендикуляр;

3) энэ тохиолдолд в векторын чиглэлийг (хоёр боломжит хувилбараас) сонгосон бөгөөд ингэснээр в векторууд нь байна. зөв систем(§ 110).

Тэмдэглэл: эсвэл

Тодорхойлолт дээр нэмэлт. Хэрэв векторууд хоорондоо уялдаатай байвал тухайн зургийг (нөхцөлтөөр) параллелограмм гэж үзвэл тэг талбайг өгөх нь зүйн хэрэг юм. Тиймээс вектор бүтээгдэхүүн коллинеар векторуудтэг вектортой тэнцүү гэж үзнэ.

Тэг векторыг ямар ч чиглэл өгч болох тул энэхүү гэрээ нь тодорхойлолтын 2, 3-р зүйлтэй зөрчилдөхгүй.

Тайлбар 1. “Вектор үржвэр” гэсэн нэр томьёоны эхний үг нь үйлдлийн үр дүн нь вектор болохыг илтгэнэ (скаляр үржвэрийн эсрэг; § 104, тайлбар 1).

Жишээ 1. Зөв координатын системийн гол векторууд байгаа вектор үржвэрийг ол (Зураг 156).

1. Үндсэн векторуудын урт нь нэг масштабын нэгжтэй тэнцүү тул параллелограммын талбай (квадрат) тоон хувьд нэгтэй тэнцүү байна. Энэ нь вектор үржвэрийн модуль нэгтэй тэнцүү гэсэн үг юм.

2. Хавтгайд перпендикуляр нь тэнхлэг тул хүссэн вектор үржвэр нь k вектортой коллинеар вектор болно; аль аль нь модуль 1-тэй тул хүссэн вектор үржвэр нь k эсвэл -k-тэй тэнцүү байна.

3. Эдгээр хоёр боломжит векторуудаас эхнийхийг нь сонгох ёстой, учир нь k векторууд нь баруун гартай систем (мөн векторууд нь зүүн гар) үүсгэдэг.

Жишээ 2. Хөндлөн үржвэрийг ол

Шийдэл. 1-р жишээн дээр бид вектор нь k эсвэл -k-тэй тэнцүү байна гэж дүгнэж байна. Харин одоо векторууд нь баруун гартай системийг (мөн векторууд нь зүүн гартай системийг бүрдүүлдэг) тул бид -k-г сонгох хэрэгтэй. Тэгэхээр,

Жишээ 3. Векторуудын урт нь 80 ба 50 см-тэй тэнцүү бөгөөд 30 ° өнцгийг үүсгэдэг. Тоолуурыг уртын нэгж болгон авч вектор үржвэрийн уртыг ол

Шийдэл. Векторууд дээр баригдсан параллелограммын талбай нь тэнцүү байна Хүссэн вектор бүтээгдэхүүний урт нь тэнцүү байна

Жишээ 4. Уртын нэгжээр сантиметрийг авч ижил векторуудын вектор үржвэрийн уртыг ол.

Шийдэл. Векторууд дээр баригдсан параллелограммын талбай тэнцүү тул вектор бүтээгдэхүүний урт нь 2000 см-тэй тэнцүү байна, өөрөөр хэлбэл.

3 ба 4-р жишээнүүдийн харьцуулалтаас харахад векторын урт нь зөвхөн хүчин зүйлсийн уртаас гадна уртын нэгжийн сонголтоос хамаарна.

Вектор бүтээгдэхүүний физик утга.Олон хүнээс физик хэмжигдэхүүнүүд, вектор үржвэрээр төлөөлүүлэн бид зөвхөн хүчний моментийг авч үздэг.

О цэгтэй харьцуулахад хүч хэрэглэх цэгийг Векторын үржвэр гэж нэрлэнэ. Энэ векторын үржвэр нь параллелограммын талбайтай тоон хувьд тэнцүү байна (Зураг 157). моментийн модуль нь суурь ба өндрийн үржвэртэй тэнцүү, өөрөөр хэлбэл хүчийг О цэгээс тухайн хүчний үйлчилж буй шулуун шугам хүртэлх зайгаар үржүүлсэнтэй тэнцүү байна.

Механикийн хувьд хатуу биетийн тэнцвэрт байдлыг хангахын тулд бие махбодод үйлчлэх хүчийг илэрхийлэх векторуудын нийлбэр тэгтэй тэнцүү байхаас гадна хүчний моментуудын нийлбэр байх шаардлагатай гэдгийг нотолсон. Бүх хүчнүүд нэг хавтгайд параллель байх тохиолдолд моментуудыг төлөөлөх векторуудыг нэмэх нь тэдгээрийн хэмжээг нэмэх, хасах замаар сольж болно. Гэхдээ дур зоргоороо хүчний чиглэлтэй бол ийм солих боломжгүй юм. Үүний дагуу вектор үржвэрийг тоогоор биш харин вектороор нарийн тодорхойлдог.

Энэ хичээлээр бид векторуудтай өөр хоёр үйлдлийг авч үзэх болно. векторуудын вектор үржвэрТэгээд векторуудын холимог бүтээгдэхүүн (хэрэгтэй хүмүүст шууд линк). Зүгээр дээ, заримдаа үүнээс гадна бүрэн аз жаргалын төлөө ийм зүйл тохиолддог векторуудын скаляр үржвэр, илүү ихийг шаарддаг. Энэ бол вектор донтолт юм. Бид зэрлэг байгальд орж байгаа юм шиг санагдаж магадгүй юм аналитик геометр. Энэ бол буруу. Дээд математикийн энэ хэсэгт Пиноккиод хангалттай модыг эс тооцвол ерөнхийдөө бага мод байдаг. Үнэн хэрэгтээ, материал нь маш түгээмэл бөгөөд энгийн байдаг - ижил төстэй зүйлээс илүү төвөгтэй биш юм цэгийн бүтээгдэхүүн, тэр ч байтугай ердийн даалгаварбага байх болно. Аналитик геометрийн гол зүйл бол олон хүн итгэлтэй байх болно, эсвэл аль хэдийн итгэлтэй байсан тул тооцоололд алдаа гаргахгүй байх явдал юм. Шившлэг шиг давтаад та аз жаргалтай байх болно =)

Хэрэв векторууд тэнгэрийн хаяанд цахилгаан цахих мэт хол хаа нэгтээ гялалзаж байвал хамаагүй, хичээлээс эхэл. Дамми нарт зориулсан векторуудсэргээх эсвэл дахин олж авах суурь мэдлэгвекторуудын тухай. Илүү бэлтгэгдсэн уншигчид мэдээлэлтэй танилцах боломжтой, би аль болох ихийг цуглуулахыг хичээсэн; бүрэн цуглуулгаихэвчлэн олддог жишээнүүд практик ажил

Юу чамайг тэр дор нь баярлуулах вэ? Би багадаа хоёр, бүр гурван бөмбөг жонглёрдог байсан. Энэ нь сайн болсон. Одоо та жонглёр хийх шаардлагагүй болно, учир нь бид авч үзэх болно зөвхөн орон зайн векторууд, мөн хоёр координаттай хавтгай векторуудыг орхих болно. Яагаад? Эдгээр үйлдлүүд ийм байдлаар үүссэн - векторуудын вектор ба холимог үржвэрийг тодорхойлж, ажилладаг гурван хэмжээст орон зай. Энэ нь аль хэдийн хялбар болсон!

Энэ үйлдэл нь скаляр үржвэрийн нэгэн адил хамаарна хоёр вектор. Эдгээр нь мөхөшгүй үсэг байх болтугай.

Үйлдэл нь өөрөө гэж тэмдэглэсэндараах байдлаар: . Өөр сонголтууд байдаг, гэхдээ би векторуудын вектор үржвэрийг ингэж тэмдэглэж дассан дөрвөлжин хаалтзагалмайтай.

Тэгээд тэр даруй асуулт: хэрэв байгаа бол векторуудын скаляр үржвэрХоёр вектор оролцож байгаа бөгөөд энд хоёр векторыг мөн үржүүлнэ ямар ялгаа байна? Үүний тод ялгаа нь юуны түрүүнд ҮР ДҮНД байна.

Векторуудын скаляр үржвэрийн үр дүн нь NUMBER:

Векторуудын хөндлөн үржвэрийн үр дүн нь ВЕКТОР юм: , өөрөөр хэлбэл, бид векторуудыг үржүүлээд дахин вектор авна. Хаалттай клуб. Уг нь хагалгааны нэр эндээс гаралтай. Төрөл бүрийн хэлбэрээр боловсролын уран зохиолтэмдэглэгээ нь бас өөр байж болно, би үсгийг ашиглах болно.

Хөндлөн бүтээгдэхүүний тодорхойлолт

Эхлээд зурагтай тодорхойлолт, дараа нь тайлбар байх болно.

Тодорхойлолт: Вектор бүтээгдэхүүн шугаман бусвекторууд, энэ дарааллаар авсан, ВЕКТОР гэж нэрлэгддэг, уртЭнэ нь тоон үзүүлэлт юм параллелограммын талбайтай тэнцүү байна, эдгээр векторууд дээр бүтээгдсэн; вектор векторуудад ортогональ, ба үндэс нь зөв чиг баримжаатай байхаар чиглэгддэг:

Тодорхойлолтыг хэсэг хэсгээр нь задалцгаая, энд маш олон сонирхолтой зүйл байна!

Тиймээс дараахь чухал зүйлийг онцолж болно.

1) Тодорхойлолтоор улаан сумаар заасан анхны векторууд уялдаа холбоогүй. Коллинеар векторуудын асуудлыг бага зэрэг дараа авч үзэх нь зүйтэй юм.

2) Векторуудыг авсан хатуу тодорхой дарааллаар : – "a"-г "be"-ээр үржүүлнэ, "a"-тай хамт "байх" биш. Вектор үржүүлгийн үр дүннь ВЕКТОР бөгөөд энэ нь цэнхэр өнгөөр ​​тэмдэглэгдсэн байдаг. Хэрэв векторуудыг үржүүлбэл урвуу дараалал, дараа нь бид урттай тэнцүү, эсрэг чиглэлд (бөөрөлзгөнө өнгө) векторыг авна. Энэ нь тэгш байдал нь үнэн юм .

3) Одоо вектор үржвэрийн геометрийн утгатай танилцацгаая. Энэ бол маш чухал цэг юм! Цэнхэр векторын УРТ (тиймээс час улаан вектор) нь векторууд дээр баригдсан параллелограммын ТАЛБАЙ-тай тэнцүү байна. Зураг дээр энэ параллелограммыг хараар будсан байна.

Анхаарна уу : зураг нь бүдүүвч бөгөөд мэдээжийн хэрэг вектор бүтээгдэхүүний нэрлэсэн урт нь параллелограммын талбайтай тэнцүү биш юм.

Нэгийг нь санацгаая геометрийн томъёо: Параллелограммын талбай нь бүтээгдэхүүнтэй тэнцүү байна зэргэлдээ талуудтэдгээрийн хоорондох өнцгийн синусаар. Тиймээс, дээр дурдсан зүйлс дээр үндэслэн вектор бүтээгдэхүүний УРТыг тооцоолох томъёо хүчинтэй байна.

Томъёо нь векторын тухай биш харин векторын УРТ-ын тухай гэдгийг би онцолж байна. Практик утга нь юу вэ? Үүний утга нь аналитик геометрийн асуудлуудад параллелограммын талбайг ихэвчлэн вектор бүтээгдэхүүн гэсэн ойлголтоор олж авдаг.

Хоёрдахь нь авъя чухал томъёо. Параллелограммын диагональ (улаан тасархай шугам) нь түүнийг хоёр хуваана тэнцүү гурвалжин. Тиймээс векторууд дээр баригдсан гурвалжны талбайг (улаан сүүдэр) дараах томъёогоор олж болно.

4) Бага биш чухал баримтЭнэ нь вектор нь векторуудад ортогональ, өөрөөр хэлбэл . Мэдээжийн хэрэг, эсрэг чиглэлтэй вектор (бөөрөлзгөнө сум) нь мөн анхны векторуудад ортогональ байна.

5) Вектор нь тийм чиглэгдсэн байна суурьбайна зөвчиг баримжаа. тухай хичээл дээр шинэ суурь руу шилжихБи хангалттай дэлгэрэнгүй ярьсан хавтгай чиг баримжаа, одоо бид орон зайн чиг баримжаа гэж юу болохыг олж мэдэх болно. Би хуруугаараа тайлбарлах болно баруун гар . Оюун санааны хувьд нэгтгэх долоовор хуруу вектортой ба дунд хуруувектортой. Бөгжний хуруу, жижиг хурууалган дээрээ дар. Үүний үр дүнд эрхий хуруу – вектор бүтээгдэхүүн дээш харагдах болно. Энэ бол баруун тийш чиглэсэн суурь юм (зураг дээрх энэ нь). Одоо векторуудыг өөрчил ( индекс ба дунд хуруу ) зарим газарт үр дүнд нь эрхий хуруугаа эргүүлж, вектор бүтээгдэхүүн аль хэдийн доошоо харах болно. Энэ нь бас зөв хандлагын үндэс юм. Танд асуулт гарч ирж магадгүй: аль үндэс нь чиг баримжаагаа орхисон бэ? Ижил хуруунд "даалгах" зүүн гарвекторууд, мөн зайны зүүн суурь ба зүүн чиглэлийг авна (энэ тохиолдолд эрхий хуруу нь доод векторын чиглэлд байрлана). Дүрсээр хэлбэл, эдгээр суурь нь орон зайг "мушгих" буюу чиглүүлдэг өөр өөр талууд. Мөн энэ ойлголтыг хэт хийсвэр эсвэл хийсвэр зүйл гэж үзэх ёсгүй - жишээлбэл, орон зайн чиг баримжаа нь хамгийн энгийн толины тусламжтайгаар өөрчлөгддөг бөгөөд хэрэв та "айсан туссан объектыг харагдацын шилнээс гаргаж авбал" энэ нь харагдах болно. ерөнхий тохиолдол"эх"-тэй нэгтгэх боломжгүй. Дашрамд хэлэхэд, гурван хуруугаа толинд бариад тусгалыг шинжлээрэй ;-)

... чи одоо мэдэж байгаа нь ямар сайхан юм бэ баруун ба зүүн тийш чиглэсэнҮндэслэл, учир нь зарим багш нарын чиг баримжааны өөрчлөлтийн талаархи мэдэгдэл аймшигтай юм =)

Коллинеар векторуудын хөндлөн үржвэр

Тодорхойлолтыг нарийвчлан авч үзсэн тул векторууд хоорондоо уялдаатай байх үед юу болохыг олж мэдэх хэрэгтэй. Хэрэв векторууд хоорондоо уялдаатай байвал тэдгээрийг нэг шулуун дээр байрлуулж, параллелограммыг нэг шулуун болгож "нугалж" болно. Математикчдын хэлснээр ийм газар нутаг, доройтохпараллелограмм нь тэгтэй тэнцүү байна. Тэг буюу 180 градусын синус гэсэн томъёоноос мөн адил юм тэгтэй тэнцүү, тиймээс талбай нь тэг байна

Тиймээс хэрэв , тэгвэл . Хатуухан хэлэхэд векторын бүтээгдэхүүн нь өөрөө тэг вектортой тэнцүү боловч практик дээр үүнийг ихэвчлэн үл тоомсорлодог бөгөөд үүнийг зүгээр л тэгтэй тэнцүү гэж бичдэг.

Онцгой тохиолдол– векторын вектор үржвэр нь:

Хөндлөн үржвэрийг ашигласнаар та гурван хэмжээст векторуудын уялдаа холбоог шалгаж болно энэ даалгаварбусдын дунд бид дүн шинжилгээ хийх болно.

Шийдэхийн тулд практик жишээнүүдшаардлагатай байж болно тригонометрийн хүснэгтүүнээс синусын утгыг олох.

За, гал асаацгаая:

Жишээ 1

a) Хэрэв векторуудын вектор үржвэрийн уртыг ол

б) Хэрэв векторууд дээр баригдсан параллелограммын талбайг ол

Шийдэл: Үгүй ээ, энэ бол үсгийн алдаа биш, би заалтын эхний өгөгдлийг зориуд ижил болгосон. Учир нь шийдлүүдийн дизайн өөр байх болно!

a) Нөхцөл байдлын дагуу та олох хэрэгтэй уртвектор (хөндлөн бүтээгдэхүүн). By тохирох томъёо:

Хариулт:

Хэрэв танаас уртын талаар асуусан бол хариултанд бид хэмжээсийг зааж өгсөн болно - нэгж.

б) Нөхцөл байдлын дагуу та олох хэрэгтэй дөрвөлжинвекторууд дээр баригдсан параллелограмм. Энэ параллелограммын талбай нь вектор бүтээгдэхүүний урттай тоон хувьд тэнцүү байна.

Хариулт:

Хариулт нь биднээс асуусан вектор бүтээгдэхүүний талаар огт яриагүй гэдгийг анхаарна уу зургийн талбай, үүний дагуу хэмжээс нь квадрат нэгж юм.

Нөхцөл байдлын дагуу ЮУ олох ёстойгоо бид үргэлж харж, үүн дээр үндэслэн томъёолдог тодорхойхариулах. Энэ нь үгийн утга зохиол мэт санагдаж болох ч багш нарын дунд маш олон үг хэллэгчид байдаг бөгөөд сайн боломждахин хянан засварлах болно. Хэдийгээр энэ нь тийм ч хол зөрүүтэй асуулт биш юм - хэрэв хариулт буруу байвал тухайн хүн ойлгохгүй байна гэсэн сэтгэгдэл төрдөг. энгийн зүйлсба/эсвэл даалгаврын мөн чанарыг ойлгоогүй. Аливаа асуудлыг шийдэхдээ энэ цэгийг үргэлж хянаж байх ёстой дээд математик, мөн бусад сэдвээр.

"en" том үсэг хаашаа явсан бэ? Зарчмын хувьд үүнийг шийдэлд нэмж хавсаргаж болох байсан, гэхдээ оруулгыг богиносгохын тулд би үүнийг хийгээгүй. Хүн бүр үүнийг ойлгож, ижил зүйлд зориулагдсан болно гэж найдаж байна.

Алдартай жишээУчир нь бие даасан шийдвэр:

Жишээ 2

Хэрэв векторууд дээр баригдсан гурвалжны талбайг ол

Вектор бүтээгдэхүүнээр гурвалжны талбайг олох томъёог тодорхойлолтын тайлбарт өгсөн болно. Шийдэл, хариулт нь хичээлийн төгсгөлд байна.

Практикт гурвалжингууд нь таныг ерөнхийд нь зовоож чаддаг.

Бусад асуудлыг шийдэхийн тулд бидэнд хэрэгтэй болно:

Векторуудын вектор үржвэрийн шинж чанарууд

Бид вектор бүтээгдэхүүний зарим шинж чанарыг аль хэдийн авч үзсэн боловч би тэдгээрийг энэ жагсаалтад оруулах болно.

Дурын векторуудын хувьд ба ямар ч тоошударга дараах шинж чанарууд:

1) Мэдээллийн бусад эх сурвалжид энэ зүйлийг ихэвчлэн шинж чанараар нь тодруулдаггүй боловч практикийн хувьд энэ нь маш чухал юм. Тиймээс байг.

2) – өмчийг мөн дээр дурдсан, заримдаа үүнийг нэрлэдэг антикоммутатив. Өөрөөр хэлбэл векторуудын дараалал чухал.

3) - ассоциатив эсвэл ассоциативвектор бүтээгдэхүүний хууль. Тогтмолыг вектор бүтээгдэхүүнээс гадуур хялбархан зөөж болно. Үнэхээр тэд тэнд юу хийх ёстой вэ?

4) – хуваарилалт эсвэл түгээхвектор бүтээгдэхүүний хууль. Мөн хаалт нээхэд асуудал гардаггүй.

Үүнийг харуулахын тулд товч жишээг харцгаая.

Жишээ 3

Хэрвээ олоорой

Шийдэл:Нөхцөл нь дахин вектор бүтээгдэхүүний уртыг олохыг шаарддаг. Бяцхан зургаа зурцгаая:

(1) Ассоциатив хуулиудын дагуу бид тогтмолуудыг вектор бүтээгдэхүүний хамрах хүрээнээс гадуур авдаг.

(2) Бид тогтмолыг модулийн гадна талд шилжүүлж, модуль нь хасах тэмдгийг "иддэг". Урт нь сөрөг байж болохгүй.

(3) Бусад нь тодорхой байна.

Хариулт:

Гал дээр илүү их мод нэмэх цаг болжээ.

Жишээ 4

Хэрэв векторууд дээр баригдсан гурвалжны талбайг тооцоол

Шийдэл: Томъёог ашиглан гурвалжны талбайг ол . Хамгийн гол нь "tse" ба "de" векторууд нь векторуудын нийлбэр хэлбэрээр илэрхийлэгддэг. Энд байгаа алгоритм нь стандарт бөгөөд хичээлийн 3, 4-р жишээнүүдийг санагдуулдаг. Векторуудын цэгийн үржвэр. Тодорхой болгохын тулд бид шийдлийг гурван үе шатанд хуваана.

1) Эхний алхамд бид вектор үржвэрийг вектор бүтээгдэхүүнээр илэрхийлдэг. векторыг вектороор илэрхийлье. Урт хугацааны талаар хараахан хэлээгүй байна!

(1) Векторуудын илэрхийлэлийг орлуулна уу.

(2) Тархалтын хуулиудыг ашиглан бид олон гишүүнтүүдийг үржүүлэх дүрмийн дагуу хаалтыг нээнэ.

(3) Ассоциатив хуулиудыг ашиглан бид бүх тогтмолуудыг вектор үржвэрээс цааш шилжүүлдэг. Бага зэрэг туршлагатай бол 2, 3-р алхамуудыг нэгэн зэрэг хийж болно.

(4) Сайхан шинж чанарын улмаас эхний болон сүүлчийн гишүүн нь тэгтэй тэнцүү (тэг вектор). Хоёр дахь нэр томъёонд бид вектор бүтээгдэхүүний антикоммутацийн шинж чанарыг ашигладаг.

(5) Бид ижил төстэй нэр томъёог танилцуулж байна.

Үүний үр дүнд вектор нь вектороор илэрхийлэгдэх болсон бөгөөд үүнд хүрэх шаардлагатай байв.

2) Хоёр дахь шатанд бид шаардлагатай вектор бүтээгдэхүүний уртыг олно. Энэ үйлдэл 3-р жишээг сануулж байна:

3) Шаардлагатай гурвалжны талбайг ол:

Шийдлийн 2-3 үе шатыг нэг мөрөнд бичиж болно.

Хариулт:

Үзэж буй асуудал нь нэлээд түгээмэл байдаг туршилтууд, энд бие даасан шийдлийн жишээ байна:

Жишээ 5

Хэрвээ олоорой

Түргэн шийдэлмөн хичээлийн төгсгөлд хариулт. Өмнөх жишээнүүдийг судлахдаа хэр анхааралтай байсныг харцгаая ;-)

Координат дахь векторуудын хөндлөн үржвэр

Томъёо нь үнэхээр энгийн: тодорхойлогчийн дээд мөрөнд бид бичнэ координатын векторууд, хоёр ба гурав дахь мөрөнд бид векторуудын координатыг "тавих" ба бид тавьдаг В хатуу дарааллаар – эхлээд “ve” векторын координатууд, дараа нь “давхар-ve” векторын координатууд. Хэрэв векторуудыг өөр дарааллаар үржүүлэх шаардлагатай бол мөрүүдийг солих хэрэгтэй.

Жишээ 10

Дараах сансрын векторууд хоорондоо уялдаатай эсэхийг шалгана уу.
A)
б)

Шийдэл: Баталгаажуулалт нь мэдэгдлийн аль нэг дээр үндэслэсэн болно энэ хичээл: хэрэв векторууд коллинеар байвал тэдгээрийн вектор үржвэр нь тэгтэй тэнцүү байна (тэг вектор): .

a) Вектор үржвэрийг ол:

Тиймээс векторууд нь коллинеар биш юм.

б) Вектор үржвэрийг ол:

Хариулт: a) уялдаа холбоогүй, б)

Энд магадгүй векторуудын вектор бүтээгдэхүүний талаархи бүх үндсэн мэдээлэл байна.

Энэ хэсэгвекторуудын холимог үржвэрийг ашиглахад асуудал цөөн тул тийм ч том биш байх болно. Үнэн хэрэгтээ бүх зүйл тодорхойлолт, геометрийн утга, ажлын хэд хэдэн томъёоноос хамаарна.

Векторуудын холимог бүтээгдэхүүн нь бүтээгдэхүүн юм гурван вектор :

Тиймээс тэд галт тэрэг шиг жагсаж, хэн болохыг нь тэсэн ядан хүлээж байна.

Эхлээд дахин тодорхойлолт ба зураг:

Тодорхойлолт: Холимог ажил тэгш бусвекторууд, энэ дарааллаар авсан, дуудсан параллелепипед эзэлхүүн, эдгээр векторууд дээр баригдсан, хэрэв суурь нь зөв бол "+" тэмдгээр, хэрэв суурь нь үлдсэн бол "-" тэмдгээр тоноглогдсон.

Зургаа хийцгээе. Бидэнд үл үзэгдэх шугамуудыг тасархай шугамаар зурсан:

Тодорхойлолт руу орцгооё:

2) Векторуудыг авсан тодорхой дарааллаар, өөрөөр хэлбэл бүтээгдэхүүн дэх векторуудыг дахин зохион байгуулах нь таны таамаглаж байгаагаар үр дагаваргүйгээр явагдахгүй.

3) Геометрийн утгыг тайлбарлахаасаа өмнө би тэмдэглэж байна илэрхий баримт: векторуудын холимог үржвэр нь ДУГААР юм: . Боловсролын уран зохиолд загвар нь арай өөр байж болно, би холимог бүтээгдэхүүнийг "pe" үсгээр тэмдэглэж, тооцоолсон үр дүнг тэмдэглэдэг.

Тодорхойлолтоор холимог бүтээгдэхүүн нь параллелепипедийн эзэлхүүн юм, векторууд дээр бүтээгдсэн (зураг улаан вектор, хар шугамаар зурсан). Өөрөөр хэлбэл, тоо нь өгөгдсөн параллелепипедийн эзэлхүүнтэй тэнцүү байна.

Анхаарна уу : Зураг нь бүдүүвчилсэн байна.

4) Суурь ба орон зайн чиг баримжаа гэсэн ойлголтын талаар дахин санаа зовох хэрэггүй. Эцсийн хэсгийн утга нь эзлэхүүн дээр хасах тэмдэг нэмж болно гэсэн үг юм. Энгийн үгээр хэлбэл, холимог бүтээгдэхүүн нь сөрөг байж болно: .

Тодорхойлолтоос шууд векторууд дээр баригдсан параллелепипедийн эзэлхүүнийг тооцоолох томъёог дагаж мөрддөг.