વ્યાખ્યાન 14 રેન્ડમ પ્રક્રિયાઓરેન્ડમ પ્રક્રિયાઓનું પ્રમાણભૂત વિસ્તરણ. સ્પેક્ટ્રલ વિઘટનસ્થિર રેન્ડમ પ્રક્રિયા. સ્લુલેક્ચર 14
રેન્ડમ પ્રક્રિયાઓ
રેન્ડમ પ્રક્રિયાઓનું પ્રમાણભૂત વિસ્તરણ.
સ્થિર રેન્ડમનું સ્પેક્ટ્રલ વિઘટન
પ્રક્રિયા સ્વતંત્ર સાથે રેન્ડમ પ્રક્રિયાઓ
વિભાગો માર્કોવ પ્રક્રિયાઓ અને માર્કોવ સાંકળો.
સામાન્ય રેન્ડમ પ્રક્રિયાઓ. સમયાંતરે
બિન-સ્થિર રેન્ડમ પ્રક્રિયાઓ
(અખ્મેટોવ એસ.કે.)

રેન્ડમ પ્રક્રિયાઓનું પ્રમાણભૂત વિસ્તરણ

કેનોનિકલ વિઘટન દ્વારા વ્યાખ્યાયિત એસપીની મુખ્ય લાક્ષણિકતાઓ

સ્થિર એસપીનું સ્પેક્ટ્રલ વિઘટન

સ્થિર એસપીનું સ્પેક્ટ્રલ વિઘટન (2)

સ્થિર એસપીનું સ્પેક્ટ્રલ વિઘટન (3)

સ્વતંત્ર ક્રોસ વિભાગો સાથે રેન્ડમ પ્રક્રિયાઓ

માર્કોવ પ્રક્રિયાઓ અને માર્કોવ સાંકળો

સામાન્ય (ગૌસીયન) રેન્ડમ પ્રક્રિયાઓ

આઇ.વી. યાકોવલેવ | ગણિત સામગ્રી | MathUs.ru

ગણિતમાં યુનિફાઇડ સ્ટેટ પરીક્ષા પર સમસ્યા C6

1.6 કોપ્રાઈમ નંબરો. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

1.7 સિક્વન્સ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1.8 અંકગણિત પ્રગતિ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

તે જાણીતું છે કે ગણિતમાં યુનિફાઇડ સ્ટેટ પરીક્ષા પર, ઘણા શાળાના બાળકો C6 સમસ્યા શરૂ કરતા નથી અને તેને વાંચતા પણ નથી (શા માટે? હું હજી પણ તેને હલ કરી શકતો નથી, તેઓ કહે છે). અને નિરર્થક!

એક નિયમ તરીકે, કાર્ય C6 માં બે અથવા ત્રણ બિંદુઓનો સમાવેશ થાય છે, જેમાંથી કેટલાક એકદમ સરળ છે. સમગ્ર કાર્ય માટે, 4 પ્રાથમિક પોઈન્ટ આપવામાં આવે છે, દરેક પોઈન્ટ માટે 1-2 પોઈન્ટ. તેથી, કાર્યનો ઓછામાં ઓછો ભાગ પૂર્ણ કર્યા પછી (કહો, ફક્ત પ્રસ્તુત કરવું યોગ્ય ઉદાહરણએક પોઈન્ટમાં), તમે વધારાના મેળવી શકો છો પ્રાથમિક બિંદુઓ. અને તેઓ સો-પોઇન્ટ સ્કેલ પર અંતિમ પરિણામમાં વધારો આપશે!

સમસ્યા C6 ઉકેલવા માટે તમને જરૂર છે ન્યૂનતમ સ્ટોકજ્ઞાન આ 6ઠ્ઠા ધોરણનું અંકગણિત (વિભાજ્યતા સાથે સંબંધિત દરેક વસ્તુ) અને 9મા ધોરણના બીજગણિતની પ્રગતિ વિશેની માહિતી છે. વધુ કંઈ નહીં.

ગણિતમાં યુનિફાઇડ સ્ટેટ પરીક્ષામાં સમસ્યા C6 શા માટે ગણવામાં આવે છે (અને, સામાન્ય રીતે,) સૌથી મુશ્કેલ છે? તેણી બિનપરંપરાગત છે. તેને કહેવાતા ગાણિતિક સંસ્કૃતિની જરૂર છે, સક્ષમ રીતે તર્ક કરવાની ક્ષમતા. અને મોટાભાગના શાળાના બાળકોમાં આ કૌશલ્યનો સંપૂર્ણ અભાવ હોય છે કારણ કે, કમનસીબે, શાળામાં, વસ્તુઓ સામાન્ય રીતે ગાણિતિક સંસ્કૃતિ વિકસાવવા માટે આવતી નથી.

સાંસ્કૃતિક રીતે તર્ક કરવાનું શીખવું શક્ય છે અને એકદમ જરૂરી છે. સમસ્યા C6 આ માટે ઉત્તમ તક પૂરી પાડે છે. તે તરત જ થવાનું શરૂ થશે નહીં, તેથી તમારે યુનિફાઇડ સ્ટેટ પરીક્ષાના ઘણા સમય પહેલા C6 માટે તૈયારી શરૂ કરવી જોઈએ. ત્યાં ફક્ત એક જ રેસીપી છે: નક્કી કરો, નક્કી કરો, નક્કી કરો.

આ માર્ગદર્શિકા શાળાના બાળકોને હલ કરવાનું શીખવામાં મદદ કરવા માટે લખવામાં આવી હતી બિન-માનક કાર્યો C6 પ્રકાર. તેમાં તમને જોઈતી દરેક વસ્તુ શામેલ છે સૈદ્ધાંતિક સામગ્રીઅને કાર્યો, સૌથી વધુજે યુનિફાઇડ સ્ટેટ એક્ઝામ અને ડાયગ્નોસ્ટિક પર ઓફર કરવામાં આવી હતી MIOO ના કાર્યોતાજેતરમાં

તમામ સમસ્યાઓ માટે ઉકેલો આપવામાં આવે છે. તે જ સમયે, ધ્યેય ઉકેલને સંક્ષિપ્ત અને શક્ય તેટલી તકનીકી રીતે સંપૂર્ણ બનાવવાનો ન હતો (વિચારોની રજૂઆતના ખર્ચે). છેવટે, ગણિત શીખવું એટલે વિચારોને પકડવું; મુખ્ય ભાર દરેક સમસ્યાના ઉકેલ અંતર્ગત રહેલા વિચારોને સ્પષ્ટ કરવા પર મૂકવામાં આવે છે.

1 જરૂરી સિદ્ધાંત

1.1 નંબર સેટ

IN આ વિભાગઅમે નક્કી કરીશું નંબર સેટ, કાર્ય C6 માટે જરૂરી. તમારે પરિભાષિત પરિભાષાને નિશ્ચિતપણે જાણવાની જરૂર છે!

પ્રાકૃતિક સંખ્યાઓ સંખ્યાઓ 1 છે; 2; 3; : : : આપણે ગણતરી માટે કુદરતી સંખ્યાઓનો ઉપયોગ કરીએ છીએ, અને ગણતરી એકથી શરૂ થાય છે. તેથી, ધ્યાન: શૂન્ય એ કુદરતી સંખ્યા નથી! (છેવટે, અમને એવું કહેવું ભાગ્યે જ થતું હશે: "ટેબલ પર શૂન્ય કપ છે.")

કુદરતી સંખ્યાઓનો સમૂહ N દ્વારા સૂચવવામાં આવે છે.

પૂર્ણાંક સંખ્યાઓ 0 છે; 1; 2; 3; : : : આમ, પૂર્ણાંકો શૂન્ય અને ¾ વત્તા ઓછા કુદરતી સંખ્યાઓ છે. કુદરતી સંખ્યાઓ હકારાત્મક પૂર્ણાંકો છે.

પૂર્ણાંકોનો સમૂહ Z દ્વારા સૂચવવામાં આવે છે. (આ તે સંકેત છે જેનો આપણે સતત ઉપયોગ કરીએ છીએ ત્રિકોણમિતિ સમીકરણોજવાબો રેકોર્ડ કરવા.)

તર્કસંગત સંખ્યાઓ m અને n પૂર્ણાંકો સાથે m = n તમામ પ્રકારના અપૂર્ણાંક છે (આ કિસ્સામાં, અલબત્ત, n 6 = 0; આ અનામતને ટાળવા માટે, તેઓ એમ પણ કહે છે કે m પૂર્ણાંક છે અને n એ કુદરતી સંખ્યા છે).

કોઈપણ પૂર્ણાંક તે જ સમયે તર્કસંગત હોય છે (ઉદાહરણ તરીકે, 3 = 6 = 2). જો કે, 1/2 એ પૂર્ણાંક નથી.

ઘણા તર્કસંગત સંખ્યાઓપ્ર દ્વારા સૂચિત.

1.2 વિભાજ્યતા

વિભાજ્યતાનો ખ્યાલ પૂર્ણ સંખ્યાઓને લાગુ પડે છે (ખાસ કરીને, કુદરતી સંખ્યાઓ). આ બિંદુથી, બધી સંખ્યાઓને પૂર્ણાંક ગણવામાં આવે છે. જો કોઈ પણ સંજોગોમાં આવું ન થાય, તો અમે વિશેષ આરક્ષણ કરીશું.

આપણે પૂર્ણાંકોને a દ્વારા દર્શાવીએ છીએ; b; c; : : : ; k; એલ; m; n; : : : ; x; y; z, એટલે કે, આપણે દરેક વસ્તુનો ઉપયોગ કરીએ છીએ નાના અક્ષરોલેટિન મૂળાક્ષરો.

તમે સારી રીતે જાણો છો કે સંખ્યા 12 એ 4 વડે વિભાજ્ય છે, પરંતુ 5 વડે વિભાજ્ય નથી. શું છે. ઔપચારિક વ્યાખ્યાવિભાજ્યતા? અહીં તે છે.

વ્યાખ્યા. સંખ્યા a ને સંખ્યા b 6= 0 વડે ભાગવામાં આવે છે જો ત્યાં કોઈ સંખ્યા c હોય જેમ કે a = bc.

જો a b વડે વિભાજ્ય હોય, તો b એ a નો વિભાજક કહેવાય. ઉદાહરણ તરીકે, નંબર 12 માં છ વિભાજકો છે: 1, 2, 3, 4, 6 અને 12.

વ્યાયામ. સાબિત કરો કે જો સંખ્યાઓ a અને b c વડે વિભાજ્ય છે, તો a + b પણ c વડે વિભાજ્ય છે.

ચાલો આપણે સૌથી વધુ રચના કરીએ મહત્વપૂર્ણ સંકેતોવિભાજ્યતા

a 2 વડે વિભાજ્ય છે, છેલ્લો અંક a 0, 2, 4, 6 અથવા 8 છે;

a એ 5 વડે વિભાજ્ય છે, a નો છેલ્લો અંક 0 અથવા 5 છે;

a એ 10 વડે વિભાજ્ય છે, a નો છેલ્લો અંક 0 છે;

a એ 3 વડે વિભાજ્ય છે, a ના અંકોનો સરવાળો 3 વડે વિભાજ્ય છે;

a એ 9 વડે વિભાજ્ય છે, a ના અંકોનો સરવાળો 9 વડે વિભાજ્ય છે.

1.3 સમાનતા

સમાનતા અને વિચિત્રતા સંબંધિત વિચારણાઓ ઘણીવાર C6 સમસ્યાઓમાં દેખાય છે. તેથી, ખાસ કરીને જરૂરી તથ્યોની નોંધ લેવી તે અર્થપૂર્ણ છે.

વ્યાખ્યા. સંખ્યા 2 વડે વિભાજ્ય ન હોય તો પણ તેને વિષમ કહેવામાં આવે છે.

અહીં બધી સમ સંખ્યાઓ છે: 0; 2; 4; 6; : : : જો a સમ હોય, તો તેનું સ્વરૂપ a = 2n છે. પરંતુ તમામ વિષમ સંખ્યાઓ: 1; 3; 5; : : : તે સ્પષ્ટ છે કે જો a વિષમ હોય, તો તેનું સ્વરૂપ a = 2n + 1 છે.

નીચેના નિવેદનો ખૂબ જ સ્પષ્ટ છે, અને તમે તેનો ઉપયોગ સમસ્યા C6 ઉકેલવા માટે કરી શકો છો (કોઈ તમને તેમને સાબિત કરવા માટે પૂછશે નહીં). પરંતુ તમે તેમને કસરત તરીકે સાબિત કરી શકો છો.

સમ પદોની કોઈપણ સંખ્યાનો સરવાળો સમ છે.

વિષમ પદોની બેકી સંખ્યાનો સરવાળો સમ છે. વિષમ શબ્દોની એકી સંખ્યાનો સરવાળો વિષમ છે.

કેટલાક પરિબળોનું ઉત્પાદન થવા દો. જો બધા પરિબળો વિષમ હોય, તો ઉત્પાદન વિષમ છે. જો ઓછામાં ઓછું એક પરિબળ સમાન હોય, તો ઉત્પાદન સમાન છે.

1.4 શેષ સાથે વિભાજન

13 નંબર 5 વડે વિભાજ્ય નથી. સૌથી મોટી સંખ્યાજે 5 વડે વિભાજ્ય છે અને 13 થી વધુ નથી તે 10 = 5 2 છે. આમ, 13 = 5 2+3, અને આપણે કહીએ છીએ કે 13 ને 5 વડે ભાગવાથી 2 નો ભાગ અને 3 નો શેષ ભાગ મળે છે.

તે તારણ આપે છે કે કોઈપણ સંખ્યા a ને બાકીની કોઈપણ સંખ્યા b 6 = 0 વડે ભાગી શકાય છે. એટલે કે, બે સંખ્યાઓ q અને r એવી છે કે a = bq + r, અને અસમાનતા 0 6 r સંતુષ્ટ થશે.< jbj. Число q назвается частным, а число r остатком от деления a на b.

જો r = 0, એટલે કે, a = bq, તો a એ b વડે ભાગી શકાય છે.

વ્યાયામ. ભાગાકાર અને શેષ ભાગ શોધો: a) 7 બાય 2; b) 15 બાય 4; c) 2012 5 વાગ્યે; ડી) 1001 બાય 13; e) 9 બાય 8; e) 8 બાય 9.

કોઈપણ વિષમ સંખ્યાને 2 વડે ભાગતી વખતે બાકી રહેલું એક સમાન. તેથી જ બધું વિષમ સંખ્યા 2n + 1 તરીકે લખી શકાય છે.

બચેલો ભાગ ઘણી પરિસ્થિતિઓમાં ઉપયોગી સાબિત થાય છે. ચાલો કહીએ કે સમસ્યા હલ કરતી વખતે તમારે સાબિત કરવું પડશે કે સમાનતા n2 = 3k + 2 કોઈપણ પૂર્ણાંકો n અને k માટે સાચી હોઈ શકતી નથી. અમે નીચે મુજબ કારણ આપીએ છીએ.

સંખ્યા n જ્યારે 3 વડે ભાગવામાં આવે ત્યારે તે 0, 1 અથવા 2 ના શેષ આપી શકે છે. બીજા શબ્દોમાં કહીએ તો, ત્રણ કિસ્સાઓ શક્ય છે: n = 3m, n = 3m + 1 અથવા n = 3m + 2. જ્યારે સંખ્યા n2 પાસે શું શેષ હશે 3 વડે ભાગ્યા? ચાલો જોઈએ કે દરેક ત્રણ કેસમાં શું થાય છે.

(3m)2 = 9m2 (બાકી 0);

(3m + 1)2 = 9m2 + 6m + 1 (બાકી 1);

(3m + 2)2 = 9m2 + 12m + 4 = (9m2 + 12m + 3) + 1 (બાકી 1):

આમ, પૂર્ણાંકનો વર્ગ જ્યારે 3 વડે ભાગવામાં આવે ત્યારે તે 2 નો શેષ છોડી શકતો નથી. તેથી, સમાનતા n2 = 3k + 2 ખરેખર કોઈપણ n અને k માટે અશક્ય છે.

વ્યાયામ. સાબિત કરો કે સંખ્યા 100: : : 004 (1 અને 4 વચ્ચે શૂન્યની કોઈપણ સંખ્યા હોય) એ પૂર્ણાંકનો વર્ગ નથી.

વ્યાયામ. સાબિત કરો કે પૂર્ણાંકનો વર્ગ જ્યારે 4 વડે ભાગવામાં આવે ત્યારે માત્ર બે જ શેષ મળી શકે: 0 અને 1.

વ્યાયામ. સાબિત કરો કે n3 + 2n એ 3 વડે વિભાજ્ય છે.

1.5 પ્રમાણભૂત વિસ્તરણ

દરેક સંખ્યા 1 અને પોતે વડે વિભાજ્ય છે. જો કુદરતી સંખ્યા p 1 ની બરાબર નથી અને અન્ય કોઈ નથી કુદરતી વિભાજકો, 1 અને p સિવાય, પછી આવી સંખ્યા p ને પ્રાઇમ કહેવાય છે.

અહીં પ્રથમ કેટલીક અવિભાજ્ય સંખ્યાઓ છે: 2, 3, 5, 7, 11, 13, 17, 19. સંખ્યા 2 એ એકમાત્ર સમાન અવિભાજ્ય સંખ્યા છે.

જે સંખ્યા 1 ની બરાબર નથી અને અવિભાજ્ય નથી તેને સંયુક્ત કહેવામાં આવે છે. ઉદાહરણ તરીકે, 15 એ સંયુક્ત સંખ્યા છે (તે 3 વડે વિભાજ્ય છે). સંખ્યા 1036 એ પણ સંયુક્ત સંખ્યા છે (તે સમ છે). એકમ એક પણ નથી અવિભાજ્ય સંખ્યા, કે સંયુક્ત નથી.

વ્યાયામ. સંખ્યા 315 1 સંયુક્ત છે. શા માટે?

તે તારણ આપે છે કે દરેક સંખ્યામાં વિઘટન કરી શકાય છે મુખ્ય પરિબળો. ઉદાહરણ તરીકે:

30 = 2 3 5; 504 = 2 2 2 3 3 7 = 23 32 7:

આવા વિસ્તરણ પરિબળોના ક્રમ સુધી અનન્ય છે અને તેને પ્રમાણભૂત વિસ્તરણ કહેવામાં આવે છે. પ્રમાણભૂત વિઘટનના અસ્તિત્વ અને વિશિષ્ટતા વિશેના નિવેદનને અંકગણિતનું મૂળભૂત પ્રમેય કહેવામાં આવે છે.

પ્રમાણભૂત વિસ્તરણ આપે છે સંપૂર્ણ ચિત્રઆપેલ સંખ્યાના વિભાજકો (અને, ખાસ કરીને, તમને તેમની સંખ્યા શોધવા માટે પરવાનગી આપે છે). જેમ કે, a = pn 1 1 pn 2 2 : : : pn s s એ સંખ્યા aનું પ્રમાણભૂત વિસ્તરણ થવા દો. પછી સંખ્યાના કોઈપણ વિભાજકના પ્રામાણિક વિસ્તરણમાં fp1 સમૂહમાં સમાવિષ્ટ મુખ્ય પરિબળોનો સમાવેશ થાય છે; p2 ; : : : ; ps g, જેનાં ઘાતાંક અનુક્રમે સંખ્યાઓ n1 કરતાં વધી જતા નથી; n2 ; : : : ; એનએસ ઉદાહરણ તરીકે, 504 = 23 32 7 નંબરના કોઈપણ વિભાજકનું સ્વરૂપ 2a 3b 7c છે, જ્યાં a 2 f0; 1; 2; 3g, b 2 f0; 1; 2g અને c 2 f0; 1 જી.

વ્યાયામ. ચાલો p એ અવિભાજ્ય સંખ્યા છે. સંખ્યાના કેટલા વિભાજકો છે: a) p2 ; b) p3; c) pn?

વ્યાયામ. ચાલો p અને q ને અવિભાજ્ય સંખ્યાઓ ગણીએ. સંખ્યાના કેટલા વિભાજકો છે: a) pq; b) p2 q3 ; c) pm qn?

વ્યાયામ. અગાઉની કવાયતના બિંદુ c) ના તર્કને સામાન્ય બનાવ્યા પછી, બતાવો કે સંખ્યાના વિભાજકોની સંખ્યા a = pn 1 1 pn 2 2 : : : pn s s બરાબર છે (n1 + 1)(n2 + 1) : : : : (ns + 1). સંખ્યા 504 માં કેટલા વિભાજકો છે તે શોધો.

વ્યાયામ. 540 અને 252 નંબરોના પ્રમાણભૂત વિસ્તરણ શોધો. પરિણામી વિસ્તરણનો ઉપયોગ કરીને, સૌથી મોટામાં gcd (540; 252) શોધો સામાન્ય વિભાજકઆ નંબરો.

1.6 કોપ્રાઈમ નંબરો

સંખ્યાઓને કોપ્રાઈમ કહેવામાં આવે છે જો તેમાં 1 સિવાય કોઈ સામાન્ય વિભાજકો ન હોય. બીજા શબ્દોમાં કહીએ તો, સંખ્યાઓ a અને b કોપ્રાઈમ છે જો gcd (a; b) = 1. તમે આ પણ કહી શકો: સંખ્યાઓ a અને b કોપ્રાઈમ છે જો અને માત્ર જો જ્યારે a=b અપૂર્ણાંક અફર છે.

ઉદાહરણ તરીકે, 8 અને 15 નંબરો કોપ્રાઈમ છે. 9 અને 15 સંખ્યાઓ પ્રમાણમાં અવિભાજ્ય નથી; તેમની પાસે 3 નો સામાન્ય વિભાજક છે.

સંખ્યાઓ પ્રમાણમાં અવિભાજ્ય હોય છે જો અને માત્ર જો તેમના પ્રમાણભૂત વિસ્તરણમાં અવિભાજ્ય સંખ્યાઓના અસંબંધિત સમૂહો હોય. ઉદાહરણ તરીકે, સંખ્યાઓ 23 5 132 અને 32 73 11 પ્રમાણમાં અવિભાજ્ય છે.

કોપ્રાઈમ નંબરોના ગુણધર્મો. સંખ્યાઓ a અને b ને કોપ્રાઈમ થવા દો. પછી નીચેના નિવેદનો સાચા છે.

1. જો સંખ્યા a અને b વડે વિભાજ્ય હોય, તો તે તેના ગુણાંક ab વડે પણ વિભાજ્ય છે.

2. જો a એ b વડે વિભાજ્ય છે, તો n એ b વડે વિભાજ્ય છે.

(જો તમે સંખ્યાઓ a અને b ના "અસંબંધિત" કેનોનિકલ વિસ્તરણની કલ્પના કરો તો આવું શા માટે થાય છે તે તમે સરળતાથી સમજી શકો છો અને વધુમાં, યાદ રાખો કે વિભાજકનું પ્રમાણભૂત વિસ્તરણ ડિવિડન્ડના પ્રમાણભૂત વિસ્તરણના "ભાગ" તરીકે કામ કરે છે. )

વિધાન 1 મુજબ, ઉદાહરણ તરીકે, જો કોઈ ચોક્કસ સંખ્યાને 8 અને 15 વડે ભાગી શકાય, તો તે 8 15 = 120 વડે વિભાજ્ય છે. હકીકત એ છે કે સંખ્યાઓ પ્રમાણમાં અવિભાજ્ય છે, મહત્વપૂર્ણ સ્થિતિ. તેથી, 12 4 અને 6 વડે વિભાજ્ય છે, પરંતુ 4 6 = 24 વડે વિભાજ્ય નથી.

વ્યાયામ. એન્ટ્રી 35 4 માં ફૂદડીને બદલે કઈ સંખ્યાઓ દાખલ કરી શકાય છે જેથી પરિણામી પાંચ અંકની સંખ્યા 45 વડે વિભાજ્ય?

વિધાન 2 સામાન્ય રીતે નીચેના જેવી પરિસ્થિતિઓમાં કામ કરે છે. ચાલો, ઉદાહરણ તરીકે, 5n = 9m. કારણ કે 5n 9 વડે વિભાજ્ય છે અને સંખ્યાઓ 5 અને 9 કોપ્રાઈમ છે, તો n એ 9 વડે વિભાજ્ય છે. તે જ કારણસર, m 5 વડે વિભાજ્ય છે.

1.7 સિક્વન્સ

ક્રમ શું છે? એવા ઉપકરણની કલ્પના કરો કે જે અમુક સમયાંતરે એક પછી એક સંખ્યા ઉત્પન્ન કરે છે. ઉદાહરણ તરીકે: 2, 3, 15, 28, 6, 0, 3, . . . આ ઉપકરણના આઉટપુટ પર સંખ્યાઓનો સમૂહ એક ક્રમ હશે.

વધુ કડક રીતે, સંખ્યાઓનો ક્રમ, અથવા સંખ્યા ક્રમએ સંખ્યાઓનો સમૂહ છે જેમાં દરેક સંખ્યાને ચોક્કસ સંખ્યા અસાઇન કરી શકાય છે અને દરેક સંખ્યા અનુરૂપ છે એકવચનઆ સમૂહની. સંખ્યા એ કુદરતી સંખ્યા છે; નંબરિંગ એકથી શરૂ થાય છે.

તેથી, ઉપરોક્ત ક્રમમાં, પ્રથમ નંબર 2 છે (આ ક્રમનો પ્રથમ સભ્ય છે), અને પાંચમો નંબર 6 છે (આ ક્રમનો પાંચમો સભ્ય છે).

સંખ્યા n સાથે સંખ્યા (એટલે ​​​​કે nમી મુદતસિક્વન્સ) એ (અથવા bn, cn, . .) દ્વારા સૂચવવામાં આવે છે. જ્યારે ક્રમનો nમો શબ્દ અમુક સૂત્ર દ્વારા સ્પષ્ટ કરી શકાય ત્યારે તે ખૂબ અનુકૂળ છે. ઉદાહરણ તરીકે, સૂત્ર an = 2n 3 ક્રમને સ્પષ્ટ કરે છે: 1; 1; 3; 5; 7; : : : ફોર્મ્યુલા an = (1)n

ક્રમ સુયોજિત કરે છે: 1; 1; 1; 1; :::

વ્યાયામ. નીચેના સિક્વન્સ માટે nમી ટર્મ માટે ફોર્મ્યુલા સાથે આવો: a) 1; 3; 5; 7; : : : ; b) 5; 8; 11; 14; : : : ; c) 1; 4; 9; 16; : : : ; ડી) 1; 2; 3; 4; :::

અમે ધ્યાનમાં લીધેલ તમામ ક્રમ અનંત છે, એટલે કે સમાવિષ્ટ છે અનંત સમૂહસંખ્યાઓ પરંતુ ત્યાં પણ મર્યાદિત ક્રમ છે. વાસ્તવમાં, સંખ્યાઓનો કોઈપણ મર્યાદિત સમૂહ એ મર્યાદિત ક્રમ છે. ઉદાહરણ તરીકે, અંતિમ ક્રમ 1; 2; 3; 4; 5 માં પાંચ સંખ્યાઓનો સમાવેશ થાય છે.

સમસ્યા C6 માટે બેની જરૂર છે ખાસ પ્રકારોસિક્વન્સ: અંકગણિત અને ભૌમિતિક પ્રગતિ.

1.8 અંકગણિત પ્રગતિ

અંકગણિત પ્રગતિ એ એક ક્રમ છે જેમાં દરેક પદ (બીજાથી શરૂ થાય છે) સરવાળો સમાનપાછલી મુદત અને અમુક નિશ્ચિત સંખ્યા:

an+1 = an + d (n = 1; 2; : : :):

નિશ્ચિત સંખ્યા d ને અંકગણિત પ્રગતિનો તફાવત કહેવામાં આવે છે.

ઉદાહરણ તરીકે, ક્રમ 2; 5; 8; 11; : : : છે અંકગણિત પ્રગતિપ્રથમ શબ્દ 2 અને તફાવત 3 સાથે.

આ લેખમાં તમને બધું મળશે જરૂરી માહિતીપ્રશ્નનો જવાબ આપવો અવિભાજ્ય પરિબળોમાં સંખ્યાને કેવી રીતે પરિબળ બનાવવી. પ્રથમ આપેલ સામાન્ય વિચારમુખ્ય પરિબળોમાં સંખ્યાના વિઘટન વિશે, વિઘટનના ઉદાહરણો આપવામાં આવે છે. સંખ્યાને અવિભાજ્ય પરિબળોમાં વિઘટિત કરવાનું પ્રામાણિક સ્વરૂપ નીચેના દર્શાવે છે. આ પછી, વિઘટન અલ્ગોરિધમ આપવામાં આવે છે મનસ્વી સંખ્યાઓમુખ્ય પરિબળોમાં અને આ અલ્ગોરિધમનો ઉપયોગ કરીને સંખ્યાઓના વિઘટનના ઉદાહરણો આપવામાં આવ્યા છે. વૈકલ્પિક પદ્ધતિઓ પણ ધ્યાનમાં લેવામાં આવે છે જે તમને વિભાજ્યતા પરીક્ષણો અને ગુણાકાર કોષ્ટકોનો ઉપયોગ કરીને અવિભાજ્ય પરિબળમાં નાના પૂર્ણાંકોને ઝડપથી પરિબળ કરવાની મંજૂરી આપે છે.

પૃષ્ઠ નેવિગેશન.

સંખ્યાને અવિભાજ્ય પરિબળોમાં પરિબળ કરવાનો અર્થ શું છે?

પ્રથમ, ચાલો જોઈએ કે મુખ્ય પરિબળો શું છે.

તે સ્પષ્ટ છે કે આ વાક્યમાં "પરિબળ" શબ્દ હાજર હોવાથી, કેટલીક સંખ્યાઓનું ઉત્પાદન છે, અને યોગ્યતા શબ્દ "સરળ" નો અર્થ છે કે દરેક પરિબળ એક અવિભાજ્ય સંખ્યા છે. ઉદાહરણ તરીકે, ફોર્મ 2·7·7·23 ના ગુણાંકમાં ચાર મુખ્ય પરિબળો છે: 2, 7, 7 અને 23.

સંખ્યાને અવિભાજ્ય પરિબળોમાં પરિબળ કરવાનો અર્થ શું છે?

આનો અર્થ એ છે કે આપેલ નંબરમુખ્ય પરિબળોના ઉત્પાદન તરીકે રજૂ કરવું આવશ્યક છે, અને આ ઉત્પાદનનું મૂલ્ય મૂળ સંખ્યા જેટલું હોવું જોઈએ. ઉદાહરણ તરીકે, ત્રણ અવિભાજ્ય સંખ્યાઓ 2, 3 અને 5 ના ગુણાંકને ધ્યાનમાં લો, તે 30 ની બરાબર છે, આમ સંખ્યા 30 નું અવિભાજ્ય અવયવોમાં વિઘટન 2·3·5 છે. સામાન્ય રીતે અવિભાજ્ય પરિબળોમાં સંખ્યાના વિઘટનને સમાનતા તરીકે લખવામાં આવે છે તે આના જેવું હશે: 30=2·3·5. અમે અલગથી ભારપૂર્વક જણાવીએ છીએ કે વિસ્તરણમાં મુખ્ય પરિબળો પુનરાવર્તિત થઈ શકે છે. આ સ્પષ્ટપણે સમજાવે છે આગામી ઉદાહરણ: 144=2·2·2·2·3·3 . પરંતુ ફોર્મ 45=3·15નું પ્રતિનિધિત્વ એ અવિભાજ્ય પરિબળોમાં વિઘટન નથી, કારણ કે સંખ્યા 15 એ સંયુક્ત સંખ્યા છે.

ઉદભવે છે આગામી પ્રશ્ન: "કઈ સંખ્યાઓને અવિભાજ્ય પરિબળમાં પરિબળ બનાવી શકાય છે?"

તેના જવાબની શોધમાં, અમે પ્રસ્તુત કરીએ છીએ નીચેનો તર્ક. અવિભાજ્ય સંખ્યાઓ, વ્યાખ્યા દ્વારા, એક કરતાં મોટી સંખ્યાઓમાંની એક છે. આ હકીકતને ધ્યાનમાં લેતા અને, એવી દલીલ કરી શકાય છે કે ઘણા મુખ્ય પરિબળોનું ઉત્પાદન પૂર્ણાંક છે હકારાત્મક સંખ્યા, એક કરતાં વધુ. તેથી, અવિભાજ્ય પરિબળમાં અવયવીકરણ માત્ર 1 કરતા વધારે હોય તેવા સકારાત્મક પૂર્ણાંકો માટે જ થાય છે.

પરંતુ શું એક કરતા મોટા તમામ પૂર્ણાંકોને અવિભાજ્ય પરિબળમાં અવયવી શકાય?

તે સ્પષ્ટ છે કે સાદા પૂર્ણાંકોને અવિભાજ્ય પરિબળમાં પરિબળ કરવું શક્ય નથી. આ હકીકત દ્વારા સમજાવવામાં આવે છે કે અવિભાજ્ય સંખ્યાઓમાં માત્ર બે હકારાત્મક વિભાજકો હોય છે - એક અને પોતે, તેથી તેઓને બે અથવાના ગુણાંક તરીકે રજૂ કરી શકાતા નથી. વધુઅવિભાજ્ય સંખ્યાઓ. જો પૂર્ણાંક z ને અવિભાજ્ય સંખ્યાઓ a અને b ના ગુણાંક તરીકે રજૂ કરી શકાય, તો વિભાજ્યતાની વિભાવના આપણને એ નિષ્કર્ષ પર આવવા દેશે કે z એ a અને b બંને વડે વિભાજ્ય છે, જે સંખ્યા z ની સરળતાને કારણે અશક્ય છે. જો કે, તેઓ માને છે કે કોઈપણ અવિભાજ્ય સંખ્યા પોતે જ એક વિઘટન છે.

સંયુક્ત સંખ્યાઓ વિશે શું? શું સંયુક્ત સંખ્યાઓ અવિભાજ્ય પરિબળોમાં વિઘટિત થાય છે, અને શું બધી સંયુક્ત સંખ્યાઓ આવા વિઘટનને પાત્ર છે? અંકગણિતનું મૂળભૂત પ્રમેય આમાંના સંખ્યાબંધ પ્રશ્નોના હકારાત્મક જવાબ આપે છે. અંકગણિતનું મૂળભૂત પ્રમેય જણાવે છે કે કોઈપણ પૂર્ણાંક a કે જે 1 કરતા વધારે હોય તે અવિભાજ્ય પરિબળ p 1, p 2, ..., p n ના ગુણાંકમાં વિઘટિત થઈ શકે છે અને વિઘટનનું સ્વરૂપ a = p 1 · p 2 · હોય છે. … · p n, અને આ વિસ્તરણ અનન્ય છે, જો તમે પરિબળોના ક્રમને ધ્યાનમાં લેતા નથી

મુખ્ય પરિબળોમાં સંખ્યાનું પ્રમાણભૂત અવયવીકરણ

સંખ્યાના વિસ્તરણમાં, મુખ્ય પરિબળોને પુનરાવર્તિત કરી શકાય છે. પુનરાવર્તિત મુખ્ય પરિબળોનો ઉપયોગ કરીને વધુ સઘન રીતે લખી શકાય છે. સંખ્યાના વિઘટનમાં અવિભાજ્ય અવયવ p 1 s 1 વખત, અવિભાજ્ય અવયવ p 2 – s 2 વખત, અને તેથી આગળ, p n – s n વખત થાય છે. પછી સંખ્યા aનું મુખ્ય અવયવીકરણ આ રીતે લખી શકાય a=p 1 s 1 ·p 2 s 2 ·…·p n s n. રેકોર્ડિંગનું આ સ્વરૂપ કહેવાતા છે મુખ્ય પરિબળોમાં સંખ્યાનું પ્રમાણભૂત અવયવીકરણ.

ચાલો અવિભાજ્ય પરિબળોમાં સંખ્યાના પ્રમાણભૂત વિઘટનનું ઉદાહરણ આપીએ. ચાલો જાણીએ વિઘટન 609 840=2 2 2 2 3 3 5 7 11 11, તેના પ્રમાણભૂત સંકેતનું સ્વરૂપ છે 609 840=2 4 3 2 5 7 11 2.

અવિભાજ્ય પરિબળોમાં સંખ્યાનું પ્રમાણભૂત અવયવીકરણ તમને સંખ્યાના તમામ વિભાજકો અને સંખ્યાના વિભાજકોની સંખ્યા શોધવા માટે પરવાનગી આપે છે.

સંખ્યાને અવિભાજ્ય પરિબળોમાં ફેક્ટર કરવા માટેનું અલ્ગોરિધમ

સંખ્યાને અવિભાજ્ય પરિબળોમાં વિઘટન કરવાના કાર્યનો સફળતાપૂર્વક સામનો કરવા માટે, તમારે લેખ અવિભાજ્ય અને સંયુક્ત સંખ્યાઓની માહિતીની ખૂબ સારી જાણકારી હોવી જરૂરી છે.

સકારાત્મક પૂર્ણાંક સંખ્યા a જે એક કરતા વધી જાય છે તેને વિઘટન કરવાની પ્રક્રિયાનો સાર અંકગણિતના મૂળભૂત પ્રમેયના પુરાવા પરથી સ્પષ્ટ થાય છે. મુદ્દો છે ક્રમિક શોધસૌથી નાના અવિભાજ્ય વિભાજકો p 1 , p 2 , …, p n સંખ્યાઓ a, a 1 , a 2 , …, a n-1 , જે આપણને સમાનતાઓની શ્રેણી મેળવવા માટે પરવાનગી આપે છે a = p 1 · a 1 , જ્યાં a 1 = a: p 1 , a=p 1 ·a 1 =p 1 ·p 2 ·a 2, જ્યાં a 2 =a 1:p 2, …, a=p 1 ·p 2 ·…·p n ·a n , જ્યાં a n =a n-1 :p n . જ્યારે તે n =1 બહાર આવે છે, ત્યારે સમાનતા a=p 1 ·p 2 ·…·p n આપણને સંખ્યા a ના અવિભાજ્ય અવયવોમાં ઇચ્છિત વિઘટન આપશે. અહીં એ પણ નોંધવું જોઈએ કે p 1 ≤p 2 ≤p 3 ≤…≤p n.

દરેક પગલા પર નાનામાં નાના અવિભાજ્ય પરિબળોને કેવી રીતે શોધી શકાય તે શોધવાનું બાકી છે, અને સંખ્યાને અવિભાજ્ય પરિબળોમાં વિઘટન કરવા માટે અમારી પાસે અલ્ગોરિધમ હશે. અવિભાજ્ય સંખ્યાઓનું કોષ્ટક આપણને અવિભાજ્ય પરિબળો શોધવામાં મદદ કરશે. ચાલો આપણે બતાવીએ કે z નંબરનો સૌથી નાનો અવિભાજ્ય વિભાજક મેળવવા માટે તેનો ઉપયોગ કેવી રીતે કરવો.

આપણે અનુક્રમે અવિભાજ્ય સંખ્યાઓ (2, 3, 5, 7, 11, અને તેથી વધુ) ના કોષ્ટકમાંથી અવિભાજ્ય સંખ્યાઓ લઈએ છીએ અને આપેલ સંખ્યા z ને તેમના દ્વારા વિભાજીત કરીએ છીએ. પ્રથમ અવિભાજ્ય સંખ્યા કે જેના દ્વારા z સમાનરૂપે વિભાજિત થાય છે તે તેનો સૌથી નાનો અવિભાજ્ય વિભાજક હશે. જો સંખ્યા z અવિભાજ્ય છે, તો તેનો સૌથી નાનો અવિભાજ્ય વિભાજક z પોતે જ સંખ્યા હશે. અહીં યાદ રાખવું જોઈએ કે જો z એ અવિભાજ્ય સંખ્યા ન હોય, તો તેનો સૌથી નાનો અવિભાજ્ય વિભાજક સંખ્યા કરતાં વધી જતો નથી, જ્યાંથી z છે. આમ, જો અવિભાજ્ય સંખ્યાઓ વચ્ચે , z એ સંખ્યાનો એક પણ વિભાજક ન હતો, તો પછી આપણે નિષ્કર્ષ પર આવી શકીએ કે z એ અવિભાજ્ય સંખ્યા છે (આ વિશે વધુ શીર્ષક હેઠળ સિદ્ધાંત વિભાગમાં લખાયેલ છે આ સંખ્યા અવિભાજ્ય અથવા સંયુક્ત છે. ).

ઉદાહરણ તરીકે, અમે બતાવીશું કે 87 નંબરનો સૌથી નાનો અવિભાજ્ય વિભાજક કેવી રીતે શોધવો. ચાલો નંબર 2 લઈએ. 87 ને 2 વડે ભાગતા, આપણને 87:2=43 મળે છે (બાકી 1) (જો જરૂરી હોય તો, લેખ જુઓ). એટલે કે, જ્યારે 87 ને 2 વડે ભાગીએ ત્યારે શેષ 1 થાય છે, તેથી 2 એ સંખ્યા 87 નો વિભાજક નથી. આપણે અવિભાજ્ય સંખ્યાના કોષ્ટકમાંથી આગામી અવિભાજ્ય સંખ્યા લઈએ છીએ, આ સંખ્યા 3 છે. 87 ને 3 વડે ભાગીએ તો આપણને 87:3=29 મળે છે. આમ, 87 3 વડે વિભાજ્ય છે, તેથી, સંખ્યા 3 એ 87 નંબરનો સૌથી નાનો અવિભાજ્ય વિભાજક છે.

નોંધ કરો કે માં સામાન્ય કેસસંખ્યા a ને અવિભાજ્ય પરિબળમાં અવયવિત કરવા માટે, આપણને અવિભાજ્ય સંખ્યાઓના કોષ્ટકની જરૂર છે જે સંખ્યા કરતાં ઓછી ન હોય. અમારે દરેક પગલા પર આ કોષ્ટકનો સંદર્ભ લેવો પડશે, તેથી અમારે તે હાથમાં હોવું જરૂરી છે. ઉદાહરણ તરીકે, સંખ્યા 95 ને અવિભાજ્ય પરિબળમાં અવયવિત કરવા માટે, અમને ફક્ત 10 સુધીની અવિભાજ્ય સંખ્યાઓના કોષ્ટકની જરૂર પડશે (કારણ કે 10 1 કરતા વધારે છે). અને 846,653 નંબરને વિઘટિત કરવા માટે, તમારે પહેલાથી જ 1,000 સુધીના અવિભાજ્ય સંખ્યાઓના કોષ્ટકની જરૂર પડશે (કારણ કે 1,000 કરતાં વધુ છે).

હવે અમારી પાસે લખવા માટે પૂરતી માહિતી છે સંખ્યાને પ્રાઇમ ફેક્ટરમાં ફેક્ટર કરવા માટેનું અલ્ગોરિધમ. નંબર a ને વિઘટિત કરવા માટેનું અલ્ગોરિધમ નીચે મુજબ છે:

• અવિભાજ્ય સંખ્યાઓના કોષ્ટકમાંથી સંખ્યાઓ દ્વારા ક્રમિક રીતે વર્ગીકરણ કરીએ છીએ, આપણે સંખ્યા a નો સૌથી નાનો અવિભાજ્ય વિભાજક p 1 શોધીએ છીએ, જે પછી આપણે 1 =a:p 1 ની ગણતરી કરીએ છીએ. જો 1 =1, તો સંખ્યા a અવિભાજ્ય છે, અને તે પોતે જ તેનું અવિભાજ્ય પરિબળોમાં વિઘટન છે. જો 1 1 ની બરાબર નથી, તો આપણી પાસે a=p 1 ·a 1 છે અને આગળના પગલા પર આગળ વધીએ.
• આપણને a 1 નંબરનો સૌથી નાનો અવિભાજ્ય વિભાજક p 2 મળે છે, આ કરવા માટે આપણે p 1 થી શરૂ થતા અવિભાજ્ય સંખ્યાઓના કોષ્ટકમાંથી સંખ્યાઓને ક્રમિક રીતે સૉર્ટ કરીએ છીએ, અને પછી 2 =a 1:p 2 ની ગણતરી કરીએ છીએ. જો 2 =1 હોય, તો સંખ્યા a ના અવિભાજ્ય પરિબળોમાં જરૂરી વિઘટનનું સ્વરૂપ a=p 1 ·p 2 છે. જો 2 1 ની બરાબર નથી, તો આપણી પાસે a=p 1 ·p 2 ·a 2 છે અને આગળના પગલા પર આગળ વધીએ.
• અવિભાજ્ય સંખ્યાઓના કોષ્ટકમાંથી સંખ્યાઓમાંથી પસાર થતાં, p 2 થી શરૂ કરીને, આપણને a 2 નંબરનો સૌથી નાનો અવિભાજ્ય વિભાજક p 3 મળે છે, જે પછી આપણે 3 =a 2:p 3 ની ગણતરી કરીએ છીએ. જો 3 =1 હોય, તો સંખ્યા a ના અવિભાજ્ય અવયવોમાં જરૂરી વિઘટનનું સ્વરૂપ a=p 1 ·p 2 ·p 3 છે. જો 3 1 ની બરાબર નથી, તો આપણી પાસે a=p 1 ·p 2 ·p 3 ·a 3 છે અને આગળના પગલા પર આગળ વધીએ.
• અવિભાજ્ય સંખ્યાઓ દ્વારા વર્ગીકરણ કરીને, p n-1, તેમજ n =a n-1:p n, અને n એ 1 ની બરાબર છે. આ પગલું એ અલ્ગોરિધમનું છેલ્લું પગલું છે; અહીં આપણે અવિભાજ્ય પરિબળોમાં સંખ્યાનું ઇચ્છિત વિઘટન મેળવીએ છીએ: a=p 1 ·p 2 ·…·p n.

સ્પષ્ટતા માટે, સંખ્યાને અવિભાજ્ય પરિબળોમાં વિઘટન કરવા માટેના અલ્ગોરિધમના દરેક પગલા પર મેળવેલા તમામ પરિણામો નીચેના કોષ્ટકના સ્વરૂપમાં રજૂ કરવામાં આવ્યા છે, જેમાં સંખ્યાઓ a, a 1, a 2, ..., a n ક્રમિક રીતે લખવામાં આવે છે. ઊભી રેખાની ડાબી બાજુના સ્તંભમાં, અને રેખાની જમણી બાજુએ - અનુરૂપ સૌથી નાના અવિભાજ્ય વિભાજકો p 1, p 2, ..., p n.

સંખ્યાઓને મુખ્ય પરિબળોમાં વિઘટન કરવા માટે પરિણામી અલ્ગોરિધમના ઉપયોગના થોડા ઉદાહરણો ધ્યાનમાં લેવાનું બાકી છે.

પ્રાઇમ ફેક્ટરાઇઝેશનના ઉદાહરણો

હવે આપણે વિગતવાર જોઈશું સંખ્યાઓને અવિભાજ્ય પરિબળોમાં પરિબળ કરવાના ઉદાહરણો. વિઘટન કરતી વખતે, અમે અગાઉના ફકરામાંથી અલ્ગોરિધમનો ઉપયોગ કરીશું. સાથે શરૂઆત કરીએ સરળ કેસો, અને સંખ્યાઓને મુખ્ય પરિબળોમાં વિઘટન કરતી વખતે ઊભી થતી તમામ સંભવિત ઘોંઘાટનો સામનો કરવા માટે અમે ધીમે ધીમે તેમને જટિલ બનાવીશું.

ઉદાહરણ.

સંખ્યા 78 ને તેના મુખ્ય અવયવોમાં અવયવ કરો.

ઉકેલ.

અમે પ્રથમ સૌથી નાનું શોધવાનું શરૂ કરીએ છીએ મુખ્ય વિભાજક p 1 સંખ્યાઓ a=78 . આ કરવા માટે, આપણે અવિભાજ્ય સંખ્યાઓના કોષ્ટકમાંથી અવિભાજ્ય સંખ્યાઓને ક્રમિક રીતે સૉર્ટ કરવાનું શરૂ કરીએ છીએ. આપણે નંબર 2 લઈએ છીએ અને તેના દ્વારા 78 ને ભાગીએ છીએ, આપણને 78:2=39 મળે છે. સંખ્યા 78 ને શેષ વિના 2 વડે વિભાજિત કરવામાં આવે છે, તેથી p 1 =2 એ 78 નંબરનો પ્રથમ મળેલ અવિભાજ્ય વિભાજક છે. આ કિસ્સામાં, a 1 =a:p 1 =78:2=39. તેથી આપણે સમાનતા પર આવીએ છીએ a=p 1 ·a 1 જેનું સ્વરૂપ 78=2·39 છે. દેખીતી રીતે, 1 =39 એ 1 થી અલગ છે, તેથી આપણે અલ્ગોરિધમના બીજા પગલા પર આગળ વધીએ છીએ.

હવે આપણે a 1 =39 નંબરના સૌથી નાના અવિભાજ્ય વિભાજક p 2 શોધી રહ્યા છીએ. અમે p 1 =2 થી શરૂ કરીને, અવિભાજ્ય સંખ્યાઓના કોષ્ટકમાંથી સંખ્યાઓની ગણતરી શરૂ કરીએ છીએ. 39 ને 2 વડે ભાગીએ તો આપણને 39:2=19 મળે છે (બાકી 1). કારણ કે 39 એ 2 વડે સરખે ભાગે વિભાજ્ય નથી, તો 2 તેનો વિભાજક નથી. પછી આપણે અવિભાજ્ય સંખ્યાઓના કોષ્ટકમાંથી આગલી સંખ્યા લઈએ (સંખ્યા 3) અને તેના દ્વારા 39 ને ભાગીએ તો આપણને 39:3=13 મળે છે. તેથી, p 2 =3 એ 39 નંબરનો સૌથી નાનો અવિભાજ્ય વિભાજક છે, જ્યારે a 2 =a 1:p 2 =39:3=13. આપણી પાસે સમાનતા a=p 1 ·p 2 ·a 2 ફોર્મ 78=2·3·13 છે. 2 =13 એ 1 થી અલગ હોવાથી, આપણે એલ્ગોરિધમના આગલા પગલા પર આગળ વધીએ છીએ.

અહીં આપણે a 2 =13 સંખ્યાનો સૌથી નાનો અવિભાજ્ય વિભાજક શોધવાની જરૂર છે. નંબર 13 ના સૌથી નાના અવિભાજ્ય વિભાજક p 3 ની શોધમાં, અમે p 2 =3 થી શરૂ કરીને, અવિભાજ્ય સંખ્યાઓના કોષ્ટકમાંથી સંખ્યાઓ દ્વારા ક્રમિક રીતે સૉર્ટ કરીશું. 13 નંબર 3 વડે વિભાજ્ય નથી, કારણ કે 13:3=4 (બાકીનો 1), 13 પણ 5, 7 અને 11 વડે વિભાજ્ય નથી, કારણ કે 13:5=2 (બાકીનો 3), 13:7=1 (બાકીના. 6) અને 13:11=1 (બાકીના. 2). આગળની અવિભાજ્ય સંખ્યા 13 છે, અને 13 એ શેષ વિના તેના દ્વારા વિભાજ્ય છે, તેથી, 13 માંથી સૌથી નાનો અવિભાજ્ય વિભાજક p 3 એ સંખ્યા 13 છે, અને a 3 =a 2:p 3 =13:13=1. 3 =1 હોવાથી, અલ્ગોરિધમનું આ પગલું છેલ્લું છે, અને 78 નંબરના મુખ્ય પરિબળોમાં ઇચ્છિત વિઘટનનું સ્વરૂપ 78=2·3·13 (a=p 1 ·p 2 ·p 3 ) છે.

જવાબ:

78=2·3·13.

ઉદાહરણ.

83,006 નંબરને અવિભાજ્ય પરિબળોના ઉત્પાદન તરીકે વ્યક્ત કરો.

ઉકેલ.

સંખ્યાને અવિભાજ્ય પરિબળોમાં વિઘટન કરવા માટેના અલ્ગોરિધમના પ્રથમ પગલા પર, આપણે p 1 =2 અને a 1 =a:p 1 =83,006:2=41,503 શોધીએ છીએ, જેમાંથી 83,006=2·41,503.

બીજા પગલામાં, આપણે શોધી કાઢીએ છીએ કે 2, 3 અને 5 એ 1 = 41,503 નંબરના અવિભાજ્ય વિભાજક નથી, પરંતુ 41,503:7=5,929 થી સંખ્યા 7 છે. અમારી પાસે p 2 =7, a 2 =a 1:p 2 =41,503:7=5,929 છે. આમ, 83,006=2 7 5 929.

5 929:7 = 847 થી, a 2 =5 929 નંબરનો સૌથી નાનો અવિભાજ્ય વિભાજક એ સંખ્યા 7 છે. આમ, p 3 =7, a 3 =a 2:p 3 =5 929:7 = 847, જેમાંથી 83 006 = 2·7·7·847.

આગળ આપણે શોધી કાઢીએ છીએ કે a 3 =847 નંબરનો સૌથી નાનો અવિભાજ્ય વિભાજક p 4 બરાબર 7 છે. પછી a 4 =a 3:p 4 =847:7=121, તેથી 83 006=2·7·7·7·121.

હવે આપણે a 4 =121 નંબરનો સૌથી નાનો અવિભાજ્ય વિભાજક શોધીએ છીએ, તે સંખ્યા p 5 =11 છે (કારણ કે 121 11 વડે વિભાજ્ય છે અને 7 વડે વિભાજ્ય નથી). પછી a 5 =a 4:p 5 =121:11=11, અને 83 006=2·7·7·7·11·11.

છેલ્લે, a 5 =11 સંખ્યાનો સૌથી નાનો અવિભાજ્ય વિભાજક એ સંખ્યા p 6 =11 છે. પછી a 6 =a 5:p 6 =11:11=1. 6 =1 થી, સંખ્યાને અવિભાજ્ય પરિબળોમાં વિઘટન કરવા માટેનું અલ્ગોરિધમનું આ પગલું છેલ્લું છે, અને ઇચ્છિત વિઘટનનું સ્વરૂપ 83 006 = 2·7·7·7·11·11 છે.

પ્રાપ્ત પરિણામને સંખ્યાના પ્રાઇમ ફેક્ટર 83 006 = 2·7 3 ·11 2 માં સંખ્યાના પ્રમાણભૂત વિઘટન તરીકે લખી શકાય છે.

જવાબ:

83 006=2 7 7 7 11 11=2 7 3 11 2 991 એ અવિભાજ્ય સંખ્યા છે. ખરેખર, તેની પાસે એક પણ અવિભાજ્ય વિભાજક નથી જે કરતાં વધુ ન હોય (આશરે અંદાજ લગાવી શકાય છે, કારણ કે તે સ્પષ્ટ છે કે 991<40 2 ), то есть, наименьшим делителем числа 991 является оно само. Тогда p 3 =991 и a 3 =a 2:p 3 =991:991=1 . Следовательно, искомое разложение числа 897 924 289 на простые множители имеет вид 897 924 289=937·967·991 .

જવાબ:

897 924 289 = 937 967 991 .

પ્રાઇમ ફેક્ટરાઇઝેશન માટે વિભાજ્યતા પરીક્ષણોનો ઉપયોગ કરવો

સરળ કિસ્સાઓમાં, તમે આ લેખના પ્રથમ ફકરામાંથી વિઘટન અલ્ગોરિધમનો ઉપયોગ કર્યા વિના મુખ્ય પરિબળોમાં સંખ્યાને વિઘટિત કરી શકો છો. જો સંખ્યાઓ મોટી ન હોય, તો પછી તેમને મુખ્ય પરિબળોમાં વિઘટિત કરવા માટે વિભાજ્યતાના ચિહ્નોને જાણવું ઘણીવાર પૂરતું છે. ચાલો સ્પષ્ટતા માટે ઉદાહરણો આપીએ.

ઉદાહરણ તરીકે, આપણે સંખ્યા 10 ને અવિભાજ્ય પરિબળોમાં પરિબળ કરવાની જરૂર છે. ગુણાકાર કોષ્ટકમાંથી આપણે જાણીએ છીએ કે 2·5=10, અને સંખ્યાઓ 2 અને 5 દેખીતી રીતે અવિભાજ્ય છે, તેથી સંખ્યા 10 નું અવિભાજ્ય અવયવીકરણ 10=2·5 જેવું દેખાય છે.

બીજું ઉદાહરણ. ગુણાકાર કોષ્ટકનો ઉપયોગ કરીને, આપણે સંખ્યા 48 ને અવિભાજ્ય અવયવોમાં પરિબળ કરીશું. આપણે જાણીએ છીએ કે છ એટલે આઠ - અડતાલીસ, એટલે કે, 48 = 6·8. જો કે, 6 કે 8 બેમાંથી કોઈ અવિભાજ્ય સંખ્યા નથી. પણ આપણે જાણીએ છીએ કે બે વાર ત્રણ એટલે છ, અને બે વાર ચાર એટલે આઠ, એટલે કે, 6=2·3 અને 8=2·4. પછી 48=6·8=2·3·2·4. તે યાદ રાખવાનું રહે છે કે બે ગુણ્યા બે એટલે ચાર, પછી આપણે ઇચ્છિત વિઘટનને અવિભાજ્ય પરિબળો 48 = 2·3·2·2·2માં મેળવીએ છીએ. ચાલો આ વિસ્તરણને પ્રમાણભૂત સ્વરૂપમાં લખીએ: 48=2 4 ·3.

પરંતુ જ્યારે 3,400 નંબરને અવિભાજ્ય પરિબળોમાં ફેક્ટર કરો, ત્યારે તમે વિભાજ્યતા માપદંડનો ઉપયોગ કરી શકો છો. 10, 100 વડે વિભાજ્યતાના ચિહ્નો અમને જણાવવા દે છે કે 3,400 100 વડે વિભાજ્ય છે, 3,400=34·100 સાથે, અને 100 એ 10 વડે વિભાજ્ય છે, 100=10·10 સાથે, તેથી, 3,400=34·10·10. અને 2 વડે વિભાજ્યતાની કસોટીના આધારે, આપણે કહી શકીએ કે 34, 10 અને 10 દરેક અવયવ 2 વડે વિભાજ્ય છે, આપણને મળે છે 3 400=34 10 10=2 17 2 5 2 5. પરિણામી વિસ્તરણના તમામ પરિબળો સરળ છે, તેથી આ વિસ્તરણ ઇચ્છિત છે. જે બાકી છે તે પરિબળોને ફરીથી ગોઠવવાનું છે જેથી તેઓ ચડતા ક્રમમાં જાય: 3 400 = 2·2·2·5·5·17. ચાલો આપણે આ સંખ્યાના પ્રમાણભૂત વિઘટનને અવિભાજ્ય પરિબળોમાં પણ લખીએ: 3 400 = 2 3 ·5 2 ·17.

આપેલ સંખ્યાને અવિભાજ્ય પરિબળોમાં વિઘટન કરતી વખતે, તમે બદલામાં વિભાજ્યતાના ચિહ્નો અને ગુણાકાર કોષ્ટક બંનેનો ઉપયોગ કરી શકો છો. ચાલો અવિભાજ્ય પરિબળોના ગુણાંક તરીકે 75 નંબરની કલ્પના કરીએ. 5 વડે વિભાજ્યતાની કસોટી આપણને જણાવવા દે છે કે 75 5 વડે વિભાજ્ય છે અને આપણે તે 75 = 5·15 મેળવીએ છીએ. અને ગુણાકાર કોષ્ટકમાંથી આપણે જાણીએ છીએ કે 15=3·5, તેથી, 75=5·3·5. આ સંખ્યા 75 ના મુખ્ય પરિબળોમાં જરૂરી વિઘટન છે.

સંદર્ભો.

• Vilenkin N.Ya. અને અન્ય. 6ઠ્ઠું ધોરણ: સામાન્ય શિક્ષણ સંસ્થાઓ માટે પાઠયપુસ્તક.
• વિનોગ્રાડોવ આઇ.એમ. સંખ્યા સિદ્ધાંતની મૂળભૂત બાબતો.
• મિખેલોવિચ એસ.એચ. સંખ્યા સિદ્ધાંત.
• કુલિકોવ એલ.યા. અને બીજગણિત અને સંખ્યા સિદ્ધાંતમાં સમસ્યાઓનો સંગ્રહ: ભૌતિકશાસ્ત્ર અને ગણિતના વિદ્યાર્થીઓ માટે પાઠ્યપુસ્તક. શિક્ષણશાસ્ત્રની સંસ્થાઓની વિશેષતા.

ફોર્મ્યુલેશન.કુદરતી સંખ્યા આપેલ છે n (n > 1). તેના પ્રમાણભૂત વિઘટનને સરળ પરિબળોમાં મેળવો, એટલે કે, તેને સરળ પરિબળોના ઉત્પાદન તરીકે રજૂ કરો. આ કિસ્સામાં, વિસ્તરણમાં 1 નું પરિબળ સૂચવવાની મંજૂરી છે, ઉદાહરણ તરીકે, 264 = 2 * 2 * 2 * 3 * 11 (પ્રોગ્રામ 264 = 1 * 2 * 2 * 2 * 3 * જવાબ આપી શકે છે. 11).

ઉકેલ. આ કાર્યખૂબ સરસ ઉકેલ છે.

થી અંકગણિતનું મૂળભૂત પ્રમેયતે જાણીતું છે કે 1 કરતાં મોટી કોઈપણ કુદરતી સંખ્યા માટે મુખ્ય પરિબળોમાં પ્રમાણભૂત વિઘટન હોય છે, અને આ વિઘટન પરિબળોના ક્રમ સુધી અનન્ય છે. એટલે કે, ઉદાહરણ તરીકે, 12 = 2 * 2 * 2 અને 12 = 3 * 2 * 2 એ સમાન વિસ્તરણ છે.

ચાલો વિચાર કરીએ પ્રમાણભૂત સ્વરૂપમાટે કોઈપણ નંબર ચોક્કસ ઉદાહરણ. ઉદાહરણ તરીકે, 264 = 2 * 2 * 2 * 3 * 11. આ રચના કેવી રીતે ઓળખી શકાય? આ પ્રશ્નનો જવાબ આપવા માટે, ચાલો આપણે કોઈપણમાં જણાવેલ તે યાદ કરીએ શાળા અભ્યાસક્રમએકવિધ વિભાજન માટે બીજગણિત નિયમો, કલ્પના કે પ્રમાણભૂત વિસ્તરણમાં સંખ્યાઓ ચલ છે. જેમ તમે જાણો છો, જો તમે આ અભિવ્યક્તિમાં સમાયેલ અમુક અંશે સમાન અંશે કોઈ અભિવ્યક્તિને ચલમાં વિભાજીત કરો છો, તો તે તેના સંકેતમાં વટાવી દેવામાં આવે છે.

એટલે કે, જો આપણે 264 ને 2 વડે ભાગીએ, તો તેના પ્રમાણભૂત વિસ્તરણમાં એક બે હશે. પછી આપણે તપાસી શકીએ કે પરિણામી ભાગ ફરીથી 2 વડે વિભાજ્ય છે કે કેમ. જવાબ હા હશે, પરંતુ ત્રીજી વખત ભાગાકાર શેષ આપશે. પછી તમારે ધ્યાનમાં લેવા માટે આગામી કુદરતી નંબર 3 લેવાની જરૂર છે - ભાગને તેના દ્વારા એકવાર વિભાજિત કરવામાં આવશે. પરિણામે, સંખ્યા રેખાને સકારાત્મક દિશામાં પસાર કરીને, આપણે નંબર 11 પર પહોંચીશું, અને 11 વડે ભાગ્યા પછી n 1 ની બરાબર થશે, જે પ્રક્રિયા પૂર્ણ કરવાની જરૂરિયાત સૂચવે છે.

શા માટે, મળી આવેલા પરિબળોના આવા "ક્રોસ આઉટ" સાથે, આપણે સંયુક્ત સંખ્યામાં વિભાજ્યતા મેળવી શકતા નથી? વાસ્તવમાં, અહીં બધું સરળ છે - કોઈપણ સંયુક્ત સંખ્યા તેના કરતા નાના અવિભાજ્ય પરિબળોનું ઉત્પાદન છે. પરિણામે, તે તારણ આપે છે કે આપણે બહાર નીકળીશું nકોઈપણ તમામ પરિબળો સંયુક્ત સંખ્યા, જ્યાં સુધી આપણે વિભાગોની સાંકળમાં પોતે જ પહોંચીએ નહીં. ઉદાહરણ તરીકે, આવી સંપૂર્ણ શોધ સાથે n 4 દ્વારા ક્યારેય વિભાજિત કરવામાં આવશે નહીં, કારણ કે "માર્ગ પર" આ નંબર પર આપણે કાઢી નાખીશું nબધા પરિબળો બે છે.

કુદરતી ભાષામાં અલ્ગોરિધમ:

1) ઇનપુટ n;

2) ચલને સોંપણી પીનંબર 2;

3) નંબર આઉટપુટ કરો n, વિસ્તરણને ઔપચારિક બનાવવા માટે સમાન ચિહ્ન અને એકમ;

4) પૂર્વશરત સાથે લૂપ શરૂ કરી રહ્યા છીએ n< > 1 . લૂપમાં:

1. જો mમોડp = 0, પછી ગુણાકાર ચિહ્ન અને ચલ p દર્શાવો, પછી ભાગાકાર કરો nચાલુ પી, અન્યથા મૂલ્ય વધારો i 1 દ્વારા;

1. પ્રોગ્રામ પ્રાઇમફેક્ટર્સ;
2. n, p: શબ્દ;
3. શરૂ કરો
4. p:= 2;
5. readln(n);
6. લખો(n, ‘=1’);
7. જ્યારે એન<>1 શરૂ કરો
8. જો (n mod p) = 0 તો શરૂ કરો
9. લખો (' * ', p);
10. n:= n div p
11. બીજું શરૂ કરો
12. inc(p)

રેન્ડમ ચલ V કહેવાય છે કેન્દ્રિત , જો તેની ગાણિતિક અપેક્ષા 0 ની બરાબર હોય. પ્રાથમિક કેન્દ્રિત રેન્ડમ પ્રક્રિયા એ કેન્દ્રિત રેન્ડમ ચલ V અને નોન-રેન્ડમ ફંક્શન φ(t):X(t)=Vφ(t) નું ઉત્પાદન છે. પ્રાથમિક કેન્દ્રિત રેન્ડમ પ્રક્રિયામાં નીચેની લાક્ષણિકતાઓ છે:

સ્વરૂપની અભિવ્યક્તિ
, જ્યાં φ k ( t ), k =1;2;…-બિન-રેન્ડમ કાર્યો; , k =1;2;…-અસંબંધિત કેન્દ્રિત રેન્ડમ ચલ, જેને રેન્ડમ પ્રક્રિયાનું પ્રમાણભૂત વિસ્તરણ કહેવાય છેએક્સ ( t ), જ્યારે રેન્ડમ ચલો કેનોનિકલ વિસ્તરણના ગુણાંક કહેવામાં આવે છે; અને બિન-રેન્ડમ કાર્યો φ k ( t ) - પ્રમાણભૂત વિસ્તરણના સંકલન કાર્યો.

ચાલો રેન્ડમ પ્રક્રિયાની લાક્ષણિકતાઓને ધ્યાનમાં લઈએ

શરત દ્વારા
તે

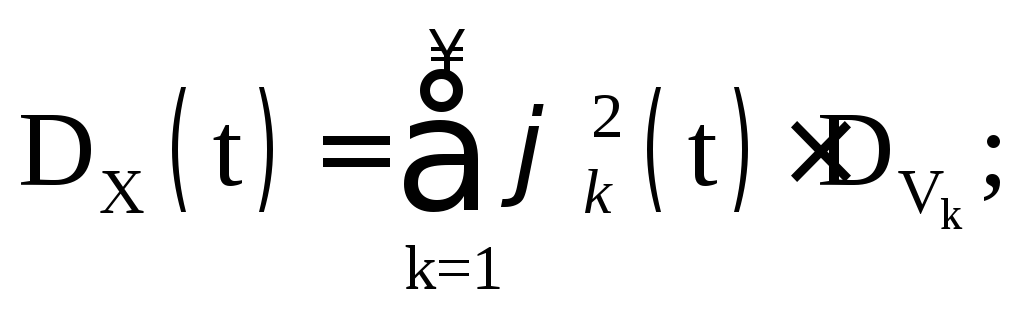
દેખીતી રીતે, સમાન રેન્ડમ પ્રક્રિયા છે વિવિધ પ્રકારોસંકલન કાર્યોની પસંદગીના આધારે પ્રમાણભૂત વિસ્તરણ. તદુપરાંત, સંકલન કાર્યોની પસંદગી સાથે પણ, રેન્ડમ ચલોના વિતરણમાં મનસ્વીતા છે V k વ્યવહારમાં, પ્રયોગોના પરિણામોના આધારે, ગાણિતિક અપેક્ષા અને સહસંબંધ કાર્ય માટે અંદાજો મેળવવામાં આવે છે:
.
વિઘટન પછી

કોઓર્ડિનેટ ફંક્શન્સમાં ડબલ ફોરિયર સિરીઝમાં φ થી (t):
વિચલન મૂલ્યો મેળવો

રેન્ડમ ચલ V k .

4.2. સામાન્યકૃત કાર્યનો ખ્યાલ. ડીરાક ડેલ્ટા ફંક્શન. રેન્ડમ પ્રક્રિયાઓનું અભિન્ન કેનોનિકલ પ્રતિનિધિત્વ. સામાન્યકૃત કાર્ય

સતત કાર્યોના એક-પેરામીટર પરિવારના ક્રમની મર્યાદા કહેવાય છે.
- ડીરાક ડેલ્ટા ફંક્શન
આ એક સામાન્ય કાર્ય છે જે પરની મર્યાદામાં પસાર થવાથી પરિણમે છે

કાર્યોના પરિવારમાં ગુણધર્મો વચ્ચે

2.

- કાર્યો અમે નીચેની નોંધીએ છીએ: 3. જો f(t)-સતત કાર્ય

, તે t રેન્ડમ પ્રક્રિયા X( ), જેનું સહસંબંધ કાર્ય બિન-સ્થિર "સફેદ અવાજ" નામનું સ્વરૂપ ધરાવે છે. જો ( t 1 )= ), જેનું સહસંબંધ કાર્ય બિન-સ્થિર "સફેદ અવાજ" નામનું સ્વરૂપ ધરાવે છે. જો - ડબલ્યુ const t , પછી X(

-સ્થિર "સફેદ અવાજ". વ્યાખ્યામાંથી નીચે મુજબ, કોઈ બે, ભલે ગમે તેટલા નજીક હોય, વિભાગો “સફેદ અવાજ » સહસંબંધ નથી.

રેન્ડમ પ્રક્રિયા Xનું અભિન્ન પ્રમાણભૂત રજૂઆત ( t ) ને સ્વરૂપની અભિવ્યક્તિ કહેવામાં આવે છે
જ્યાં
- રેન્ડમ કેન્દ્રિત કાર્ય;
- સતત દલીલોનું બિન-રેન્ડમ કાર્ય

આવી રેન્ડમ પ્રક્રિયાના સહસંબંધ કાર્યનું સ્વરૂપ છે:

તે બતાવી શકાય છે કે ત્યાં બિન-રેન્ડમ ફંક્શન G(λ) છે

જ્યાં G(λ 1) એ વિક્ષેપ ઘનતા છે; δ(x) એ ડીરાક ડેલ્ટા ફંક્શન છે.

અમને મળે છે

.

તેથી, રેન્ડમ પ્રક્રિયા X(t):

4.3. રેન્ડમ પ્રક્રિયાઓના રેખીય અને બિનરેખીય પરિવર્તન

.

નીચેની સમસ્યા ધ્યાનમાં લેવામાં આવે છે: રેન્ડમ પ્રક્રિયા X(t) ની પ્રકૃતિ ધરાવતો "ઇનપુટ સિગ્નલ" સિસ્ટમ (ઉપકરણ, કન્વર્ટર) S ના ઇનપુટને પૂરો પાડવામાં આવે છે. સિસ્ટમ તેને "આઉટપુટ સિગ્નલ" Y(t) માં રૂપાંતરિત કરે છે:

ઔપચારિક રીતે, રેન્ડમ પ્રક્રિયા X(t) નું Y(t) માં રૂપાંતર કહેવાતા સિસ્ટમ ઓપરેટર A t નો ઉપયોગ કરીને વર્ણવી શકાય છે:

Y(t)=A t (X(t)).

ઇન્ડેક્સ ટી સૂચવે છે કે આ ઓપરેટર સમય રૂપાંતરણ કરે છે. રેન્ડમ પ્રક્રિયાને રૂપાંતરિત કરવાની સમસ્યાના નીચેના ફોર્મ્યુલેશન શક્ય છે. વિતરણના નિયમો જાણીતા છે અથવાસામાન્ય લાક્ષણિકતાઓ

સિસ્ટમ S ના ઇનપુટ પર રેન્ડમ પ્રક્રિયા X(t), સિસ્ટમ S ના ઓપરેટર A t આપવામાં આવે છે, સિસ્ટમના આઉટપુટ પર વિતરણ કાયદો અથવા રેન્ડમ પ્રક્રિયા Y(t) ની સામાન્ય લાક્ષણિકતાઓ નક્કી કરવી જરૂરી છે એસ.

રેન્ડમ પ્રક્રિયા X(t) ના વિતરણના નિયમો (સામાન્ય લાક્ષણિકતાઓ) અને રેન્ડમ પ્રક્રિયા Y(t) માટેની આવશ્યકતાઓ જાણીતી છે;

સિસ્ટમ S ના ઓપરેટર A t નો પ્રકાર નક્કી કરવો જરૂરી છે જે આપેલ જરૂરિયાતો kY(t) ને શ્રેષ્ઠ રીતે સંતોષે છે. રેન્ડમ પ્રક્રિયા Y(t) ના વિતરણના નિયમો (સામાન્ય લાક્ષણિકતાઓ) જાણીતા છે અને સિસ્ટમ S ના ઑપરેટર A t આપવામાં આવે છે; વિતરણ કાયદા અથવા રેન્ડમ પ્રક્રિયા X(t) ની સામાન્ય લાક્ષણિકતાઓ નક્કી કરવા માટે તે જરૂરી છે.

પી

સિસ્ટમ S ના ઓપરેટરો A t નું નીચેનું વર્ગીકરણ સ્વીકારવામાં આવ્યું છે:

સિસ્ટમ ઓપરેટરો

લીનિયર LNonlinearN

રેખીય સજાતીય L 0 રેખીય અસંગત L n

ચાલો રેખીય અસંગત પ્રણાલીની અસરને ધ્યાનમાં લઈએ

.

L n (...)=L 0 (...)+φ(t)

નીચેની પ્રમાણભૂત વિસ્તરણ ધરાવતી રેન્ડમ પ્રક્રિયા X(t) માટે:

અમને મળે છે:

.

ચાલો નોટેશન રજૂ કરીએ

પછી Y(t) નું પ્રમાણભૂત વિસ્તરણ ફોર્મ લે છે:

રેન્ડમ પ્રક્રિયા Y(t) ની ગાણિતિક અપેક્ષા:

રેન્ડમ પ્રક્રિયા Y(t) નું સહસંબંધ કાર્ય:

તેથી,

બીજી બાજુ

રેન્ડમ પ્રક્રિયા Y(t) નું વિચલન:

આ ફકરાના નિષ્કર્ષમાં, અમે નોંધીએ છીએ કે રેન્ડમ પ્રક્રિયાઓના ભિન્નતા અને એકીકરણના ઓપરેટરો રેખીય સજાતીય છે.

શૂન્ય વિશે વિતરણ સપ્રમાણ ધરાવતા V k -કેન્દ્રિત રેન્ડમ ચલ; તેમાંથી કોઈપણ ચાર સંયુક્ત રીતે સ્વતંત્ર છે.

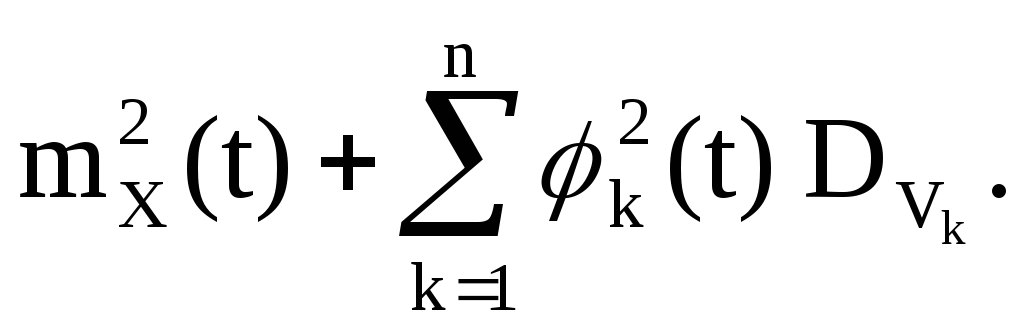
પછી

ચાલો નોન-રેન્ડમ ફંક્શન રજૂ કરીએ

અને રેન્ડમ ચલો

પછી રેન્ડમ પ્રક્રિયા Y(t) ફોર્મ લે છે