Išspręskite lygtį naudodami funkcijos ribotumo sąvoką. Pasirenkama pamoka „Ribotų funkcijų savybės taikymas

Pasirenkama veikla"Ribotų funkcijų nuosavybės taikymas"

Medžiaga, susijusi su lygtimis ir nelygybėmis, sudaro didelę mokyklinio matematikos kurso dalį, tačiau pamokos laikas neleidžia mums apsvarstyti visų klausimų.

Be to, nustatomas privalomas minimalus matematikos mokymo turinys, nurodytas valstybiniame pagrindinės mokyklos standarte mokomoji medžiaga už privalomą svarstymą, bet ne už privalomą meistriškumą (pavyzdžiui, nestandartiniai lygčių ir nelygybių sprendimo metodai, lygčių ir nelygybių su parametru sprendimo metodai ir kt.).

Dėl medžiagos, susijusios su lygčių ir nelygybių sampratomis, svarbos ir gausos, jų tyrimas šiuolaikiniai metodai matematika suskirstyta į turinio-metodinę liniją – lygčių ir nelygybių eilutę. Yra trys pagrindinės šios linijos diegimo kryptys mokyklos kursas matematikos.

Taikoma lygčių ir nelygybių linijos kryptis daugiausia atsiskleidžia studijuojant algebrinis metodas sprendimus žodinės problemos. Pagrindinė dalis yra lygtys ir nelygybės matematiniai įrankiai, naudojamas sprendžiant tekstinius uždavinius.

Teorinė ir matematinė orientacija atsiskleidžia dviem aspektais: nagrinėjant svarbiausias lygčių klases, nelygybes ir jų sistemas bei tiriant apibendrintas sąvokas ir metodus, susijusius su tiese kaip visuma.

Lygčių ir nelygybių linija taip pat glaudžiai susijusi su funkcine linija. Viena vertus, yra lygčių ir nelygybių eilutėje sukurtų metodų taikymas funkcijų tyrimui. Kita vertus, funkcinė linija turi didelę įtaką tiek lygčių ir nelygybių eilutės turiniui, tiek jos tyrimo stiliui. Visų pirma, funkcinės vaizdinės yra pagrindas pritraukti grafinį lygčių ir nelygybių sprendimo ir tyrimo aiškumą.

Algebros kurse mokomės vadovaujant Mordkovičiui, funkcinė-grafinė linija pasirenkama kaip prioritetas. Visa medžiaga pastatyta pagal griežtą schemą: funkcija-lygtys-transformacijos.

Gana dažnai vieningame valstybiniame egzamine yra užduočių, kurias galima išspręsti naudojant funkcijų savybes. Todėl šią medžiagą patartina įtraukti į pasirenkamuosius kursus. Tačiau vis tiek norėčiau kai kurias iš šių užduočių apsvarstyti pamokose, pradedant nuo 9 klasės.

Funkcijų savybių taikymas sprendžiant lygtis ir nelygybes

Naudojant ribotumo savybę.

Funkcijos apimties naudojimas.

Funkcijų monotoniškumo naudojimas sprendžiant lygtis ir nelygybes.

Naudojant funkcijos kitimo srities sąvoką.

- Naudojant lyginių ar nelyginių savybių ir funkcijų periodiškumo.

2 SKAIDRĖ.

Mano pristatymas skirtas tik vienam iš nestandartinių lygčių ir nelygybių sprendimo būdų, pagrįstų į lygtį įtrauktų funkcijų ribiškumo savybe (nelygybe). Mano siūlomos užduotys gali būti svarstomos pamokose, skirtose mokiniams paruošti vieningam valstybiniam egzaminui (trys ar keturios pamokos), arba galima panaudoti vieną ar dvi užduotis per pamoką, taip pat šią medžiagą galima naudoti pasirenkamoje pamokoje (arba pasirenkamojo kurso pamokoje).

Jau 9 klasėje, studijuodamas senaties savybę, atkreipiau dėmesį į šios savybės svarbą ir galimybę ją panaudoti

Mažiausios ir didžiausios funkcijos reikšmės radimas;

Funkcijos reikšmių aibės radimas.

SKAIDRĖ 3.

Svarstomi kai kurių užduočių sprendimai. Pirmiausia reikėtų pakartoti pagrindinius apibrėžimus. 4 SKAIDRĖ.

5–9 skaidrėse nagrinėjamos užduotys, kaip rasti mažiausias arba didžiausias funkcijos reikšmes.

10 SKAIDRĖ.

Funkcijų ribotumo savybės taikymas sprendžiant lygtis ir nelygybes.

1. PAGRINDINIS METODAS (VERTINIMO METODAS)

Pagrindinė pagrindinio metodo idėja yra tokia:

Turėkime lygtį ir yra toks skaičius M kad bet kam X iš apibrėžimo srities https://pandia.ru/text/78/376/images/image003_26.gif" width="160" height="23">. Tada lygtis yra lygiavertė sistemai https://pandia .ru/text/78 /376/images/image005_16.gif" width="96" height="35 src=">.

Sprendimas. Įvertinkime abi lygties puses.

Visoms vertybėms X nelygybės https://pandia.ru/text/78/376/images/image007_10.gif" width="188" height="59 src="> yra teisingos.

Gauta sistema neturi sprendimų, nes https://pandia.ru/text/78/376/images/image009_6.gif" width="20" height="20">

1.2 pavyzdys ..gif" width="157" height="20">.gif" width="75" height="51 src=">.

Pirmosios sistemos lygties sprendimas yra reikšmės https://pandia.ru/text/78/376/images/image014_3.gif" width="201" height="48 src=">.

Vadinasi, sisteminis sprendimas.

Atsakymas: .

1.3 pavyzdys. Išspręskite nelygybę https://pandia.ru/text/78/376/images/image016_0.gif" width="56" height="19">.gif" width="84" height="21">.gif" plotis="156 aukštis=61" aukštis="61">.

Atvirkštinis pakeitimas: X + 1 = 0 .

Atsakymas: - 1.

1.4 pavyzdys. Raskite visas parametrų reikšmes A, kurių kiekvienos lygtis turi sprendinius. Raskite šiuos sprendimus.

Sprendimas.

Perrašykime lygtį į formą . Visoms vertybėms X išraiška todėl https://pandia.ru/text/78/376/images/image026_0.gif" width="87" height="19 src="> ir ..gif" width="405" height="91">

Atsakymas: https://pandia.ru/text/78/376/images/image031_0.gif" width="51" height="41 src=">

2. „SUSITIKIMAS ANT KRAŠTO“

Pagrindinio metodo variantas yra problemos (" susitikimas ant ribos"), kurioje lygties ar nelygybės kairiosios ir dešiniosios pusės reikšmių rinkiniai turi unikalų bendras taškas, kuri yra didžiausia vienos dalies vertė, o kitai – mažiausia.

Nuo ko pradėti spręsti tokias problemas? Pirmiausia – atnešk pateiktos lygtys arba nelygybė daugiau paprastas vaizdas: faktoringo būdu, atsikratant modulių, logaritmų ir pan. Tada reikia dar kartą atidžiai perskaityti užduotį, pabandyti nupiešti grafinis vaizdas funkcijos įtrauktos į užduotį.

2.1 pavyzdys. Išspręskite lygtį.

Sprendimas. Lygties šaknis nesunku atspėti – taip ir yra x= 1. Bet neįmanoma įrodyti jos unikalumo remiantis monotoniškumu, nes nei kairioji, nei dešinioji lygties pusė nėra monotoninės funkcijos. Čia naudojama kita idėja..gif" width="191" height="51">. Didžiausia gautos lygties dešinės pusės reikšmė yra 1 ir imama taške x= 1..gif" width="185" height="52 src=">). Todėl kairėje pusėje pasiekia ties x= 1 iš mažiausios jo reikšmės, kuri taip pat lygi 1. Išvada: lygybė tenkinama tada ir tik tada, kai abi pusės vienu metu yra lygios 1, t.y. x = 1.

2.2 pavyzdys. Išspręskite lygtį.

1 būdas.

Sprendimas: Atkreipkite dėmesį, kad kairioji lygties pusė neviršija vienybės, while dešinėje pusėje ne mažiau kaip vienas. Vadinasi, pradinė lygtis turi sprendimą tik tada, kai abi jo pusės yra lygios vienai. Tai įmanoma tik su.

Atsakymas: .

2 būdas.Šią lygtį galima išspręsti grafiškai. Norėdami tai padaryti, sukurkime dešinės ir kairės lygties pusių grafikus vienoje koordinačių sistemoje, tai yra funkcijos grafiką ir funkcijos grafiką https://pandia.ru/text/78/376/images /image008_7.gif" width="37" height=" 19">.

Atsakymas: .

2 pavyzdys. 3. Išspręskite lygtį https://pandia.ru/text/78/376/images/image042_0.gif" width="301" height="35 src=">

Tai duota lygtis vykdomas tik tada, kai sistema veikia . Pirmoji sistemos lygtis turi vieną šaknį X= 1, bet ši šaknis netenkina antrosios lygties. Todėl sistema neturi sprendimų.

Atsakymas: Æ

2.4 pavyzdys. Išspręskite lygtį https://pandia.ru/text/78/376/images/image045_0.gif" width="105" height="21">, tada kairioji lygties pusė įgis reikšmę nuo iki 2. .gif" width=" 137" height="53">..gif" width="217" height="24"> turi sprendimą.

Sprendimas.

Atsakymas:

2.6 pavyzdys. Raskite visas parametrų reikšmes A kuriam lygtis

Tema: Ribotų funkcijų naudojimo būdai.
Gyvenimas yra geras dėl to, kas jame yra tu moki matematiką. (Leonardas Euleris)Tikslai: naujo, netradicinio mąstymo, kurį galima sėkmingai pritaikyti kitose srityse, ugdymas žmogaus veikla(kibernetika, kompiuterinės technologijos, ekonomika, radiofizika, chemija ir kt.).
Užduotys: - mokymas įvertinti objektyvų ir subjektyvų užduočių sudėtingumą ir išmintingai pasirinkti šias užduotis egzamine;

Netradicinių ir neįprastų samprotavimų „kiaulės banko“ kūrimas.

Pamokos eiga:

Org. akimirka. Pamokos temą mokiniai formuluoja atlikdami Vieningo valstybinio egzamino užduočių A ir B dalis ir iššifruodami temą gautų atsakymų mažėjimo tvarka. (Šifruokite 12 kortelių, sunumeruotų nuo -2 iki 10, kaip tariamus žodžius) (1 ir 2 priedas)

apribojimai

1 priedas.
Išspręskite šias užduotis ir išdėliokite atsakymus mažėjančia tvarka, pagal atsakymus surinkite mūsų pamokos temą.

Funkcijos y=3x 2 -7x+7 grafike raskite taško abscisę, kurioje liestinės kampo liestinė lygi -1.

2 priedas.
9 2 0 7Funkcijų tyrimas naudojant išvestines. 10 5 1 -1Ribotų funkcijų naudojimo būdas. 4 -2 8 12Nelygybių sprendimas grafiškai.
3 11 6Sprendimai funkcines lygtis.
Studijuoti

Vienas iš veiksmingi metodai lygčių arba nelygybių sprendimas yra metodas, pagrįstas apribotų funkcijų naudojimu. Į garsiausius ribotos funkcijosįtraukti, pavyzdžiui, kai kuriuos trigonometrinius; atvirkščiai trigonometrinės funkcijos; funkcijos, turinčios modulį, laipsnį, šaknį su lyginiu laipsniu ir kt.

Dažniausiai pasitaikančios nelygybės yra šios:

│f(x) │≥ 0, -1 ≤ sinx ≤ 1, -1 ≤ cosx ≤ 1, -

-

, a f ( x ) > 0, (f (x) ± g(x)) 2 n ≥ 0,
, a+ ≥ 2, b+ ≤ -2 ir daugelis kitų. Čia n - natūralusis skaičius, h(x) ≥ 0, a>0, b 0.

Be aukščiau pateiktų paprasčiausių nelygybių, yra ir sudėtingesnių, ypač trigonometrinės nelygybės -,

,

ir nelygybės su formos moduliais
.

1 pavyzdys.Išspręskite lygtį:

Sprendimas: Dešinėje lygties pusėje parinksime pilną kvadratą, t.y. . Iš to išplaukia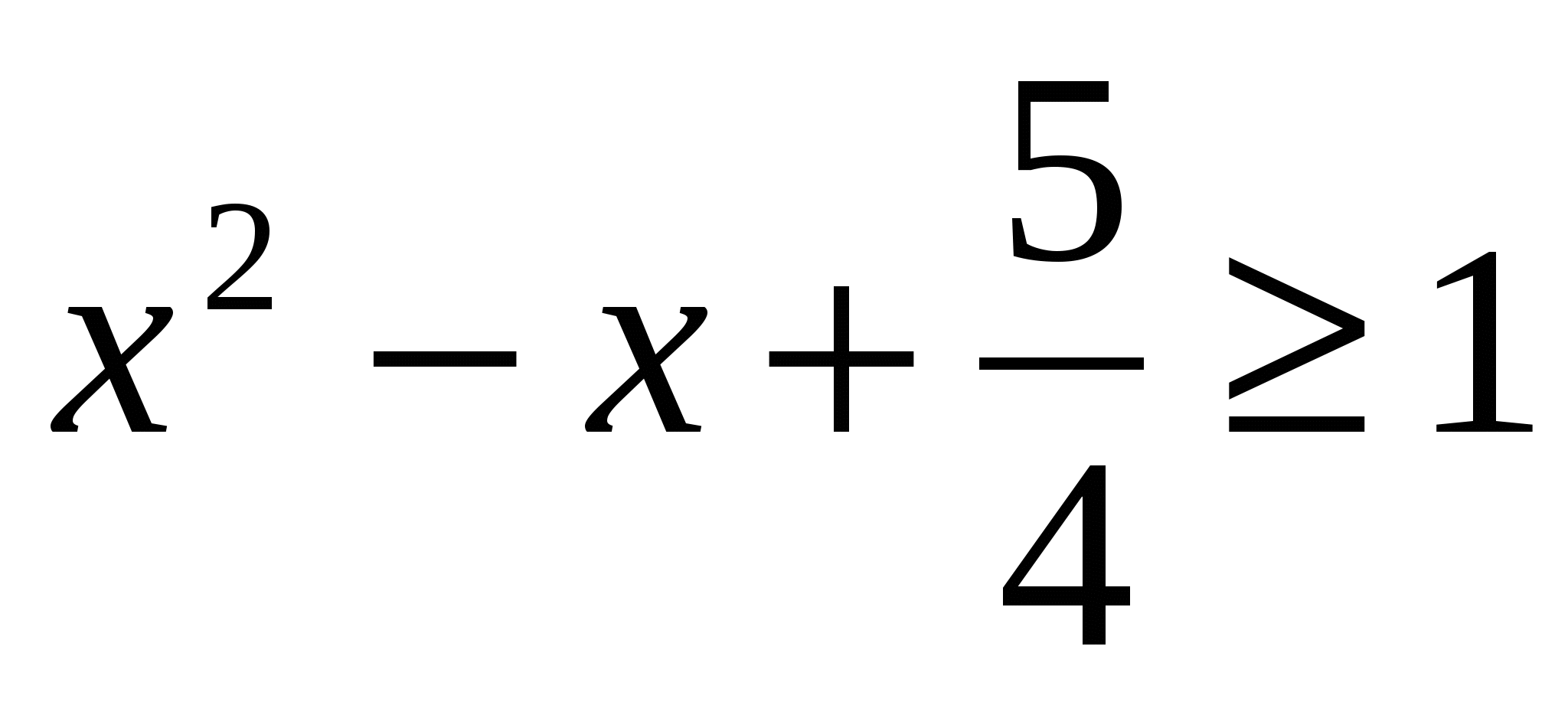
. Kadangi šiuo atveju sinπ x ≤ 1, tada gauname lygčių sistemą

Išsprendę antrąją sistemos lygtį, gauname, kad x=. Pakeitę pirmąją lygtį, įsitikiname, kad rasta x reikšmė yra sistemos sprendimas, taigi ir pradinės lygties sprendimas.

Atsakymas: x=.

2 pavyzdys.Išspręskite lygtį:

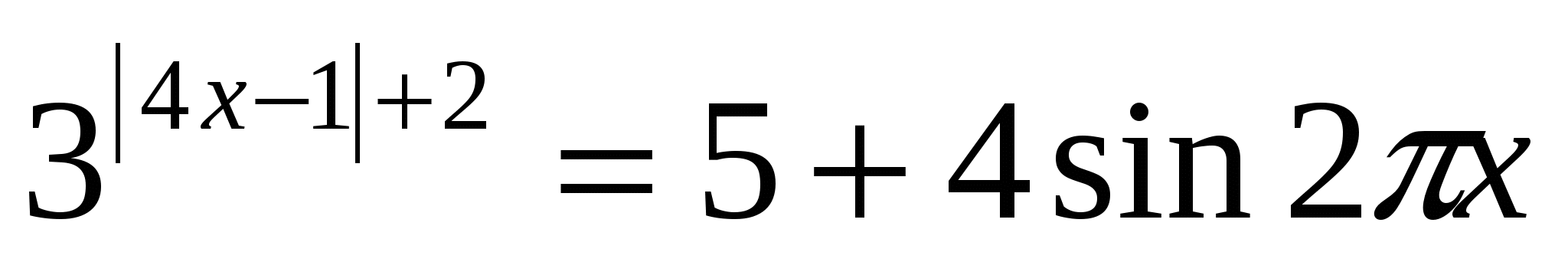
Sprendimas: kadangi Tačiau sin2 π x ≤ 1. Todėl 5+4 sin2 π x ≤ 9. Taigi gauname lygčių sistemą:

Iš čia gauname lygčių sistemą
, iš pirmosios lygties randame x=. Pakeiskime jį į antrąją sistemos lygtį ir įsitikinkime, kad x = yra sistemos sprendimas, taigi ir pradinės lygties sprendimas.

Atsakymas: x=

4 priedas. Iš siūlomo užduočių sąrašo pasirinkite tas, kurias galima išspręsti naudojant ribotos funkcijos metodą. 1. Išspręskite lygtį x 2 -4 x=(2-cos
2. Raskite nelygybės x sveikųjų skaičių sprendinių skaičių 2ctg 2
3. Išspręskite lygtį
4. Išspręskite lygtį 3-(5. Raskite sveikųjų nelygybės 16 2 ≥0 sprendinių, kurie tenkina 3 sąlygą, skaičių tg 2
6. Išspręskite lygtį
7. Išspręskite lygtį -25x 2 +40x-23=( cos
8. Raskite lygties x šaknų sandaugą
9. Išspręskite lygtį
10. Išspręskite lygtį 3- cos 2

Savikontrolės lapas. 5 priedas. 1. Išspręskite lygtį Sprendimas: nes , tada nes ir tada
gauname lygčių sistemą

Išspręskite pirmąją lygtį, gaukite x=, pakeiskite šią reikšmę antrąja lygtimi

2 . Išspręskite lygtį 3- cos 2 Sprendimas: nes , tada nes ir tada
gauname lygčių sistemą

Išspręskite antrąją lygtį, gaukite x=, pakeiskite šią reikšmę pirmąja lygtimi

tai reiškia, kad x= yra pradinės lygties sprendimas. Atsakymas: x=
3. Raskite nelygybės x sveikųjų skaičių sprendinių skaičių 2 +7х-8≤0, atitinka sąlygą ctg 2 Sprendimas: nes ir tada bet kurioms leistinoms x reikšmėms rasime nulius kvadratinis trinaris, pagal Vietos teoremą nelygybę sprendžiame intervalų metodu
Tai. mes tai žinome
sveikųjų x reikšmės yra skaičiai, pašalinami. Atsakymas: 8 sveikųjų skaičių sprendiniai 4. Raskite sveikųjų skaičių nelygybės 16 2 ≥0 sprendinių, atitinkančių 3 sąlygą, skaičių tg 2 Sprendimas: nes ir tada bet kurioms leistinoms x reikšmėms randame išraiškos nulius, x = ir x = Išspręskite nelygybę naudodami intervalų metodą
Tai. mes tai žinome

sveikųjų x reikšmės yra skaičiai, pašalinti. Atsakymas: 7 sveikųjų skaičių sprendiniai
6 priedas.

Funkcijų monotoniškumo panaudojimo būdas. Sprendžiant lygtį kaip f(x)=g(x) kai kuriais atvejais yra veiksmingas metodas, kai naudojamas funkcijų y= f(x) ir y= g(x) monotoniškumas Jei funkcija y= f(x) yra tolydi ir segmente didėja (sumažina). a≤ x ≤ b, o funkcija у= g(x) yra tolydi ir mažėja (didėja) toje pačioje atkarpoje, tada lygtis f(x)=g(x) atkarpoje a≤ x ≤ b gali turėti ne daugiau kaip vieną šaknį, vadinasi, reikia arba pabandyti surasti vienintelę lygties šaknį pasirinkimo būdu, arba parodyti, kad tokios šaknies nėra. Šis metodas ypač efektyvus tuo atveju, kai abi lygties pusės f(x) = g(x) yra „nepatogios“ funkcijos bendram tyrimui. komentaras: Jei funkcija y= f(x) didėja, o funkcija y= g(x) mažėja a≤ x ≤ b Ir tuo pačiu metu f(a)>g(A), tada lygties šaknys yra tarp a≤ x ≤ b Nr.

Pavyzdys: Išspręskite lygtįSprendimas: Regionas priimtinos vertės lygtys yra x
. Nesunku pastebėti, kad šioje srityje kairioji lygties pusė didėja, o dešinioji mažėja, t.y. funkcijaf(x)=
didėja, ir funkcijag(x)=
- mažėja. Šiuo atžvilgiu pradinė lygtis gali turėti tik vieną šaknį (jei yra). Pasirinkdami randame šią lygties x = šaknį 2.Atsakymas: x=2
Funkcinių lygčių sprendimo būdas. Tarp labiausiai sudėtingos užduotys Vieningasis valstybinis egzaminas apima uždavinius, kurių sprendimas susiveda į formos funkcinių lygčių svarstymą f(f(….f(x)…))=x arba f(g(x))=f(h(x)), kur f(x),g(x),h(x) yra kai kurios funkcijos ir n≥ 2
Šių funkcinių lygčių sprendimo metodai yra pagrįsti daugelio teoremų taikymu, panagrinėkime vieną iš jų.
1 teorema. Lygties šaknys f(x)=0 yra lygties šaknys f(f(….f(x)…))=x
Pavyzdys: Išspręskite lygtį x=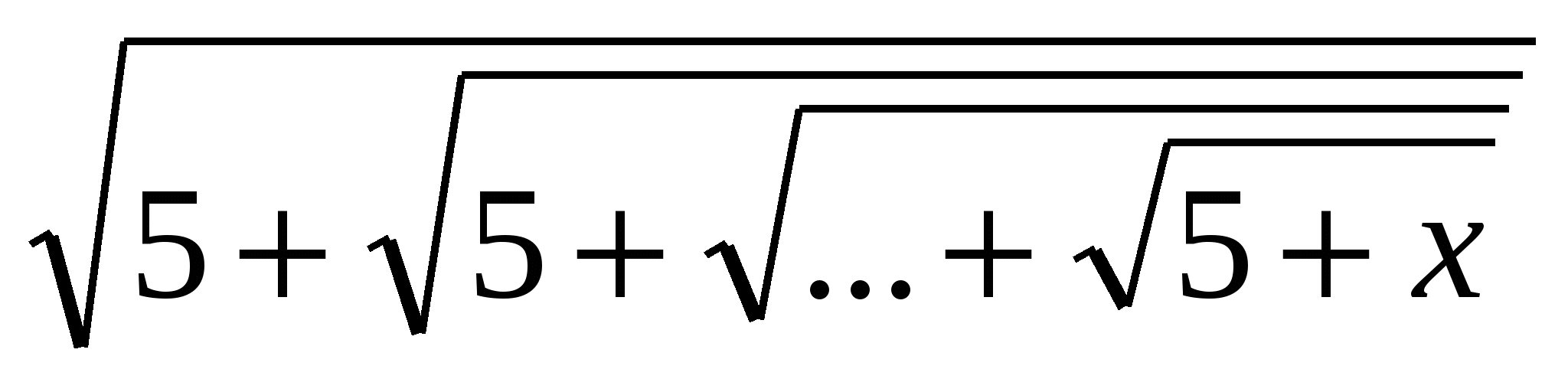
, Kur kvadratinė šaknis paimtasnvieną kartą irn≥ 1 Sprendimas: Iš problemos sąlygų matyti, kad x> 0. Leiskitef(x)=
, tada mūsų lygtis gali būti pavaizduota kaip funkcinė f( f(…. f( x)…))= x. Nuo x> 0 funkcijaf(x)= didėja irf(x) > 0, tada lygtis x= yra lygi lygčiaif(x)= x, t.y. =x, kurios teigiamas sprendinys yra x=
Atsakymas: x=

„Funkcijos apibrėžimo sritis“ – kvadratinės funkcijos apibrėžimo sritis yra bet koks realusis skaičius. Funkcija vadinama logaritmine if kintamas kiekis stovi po logaritmo ženklu. Logaritminė funkcija. Funkcija, kurios kintamasis yra eksponente, vadinama eksponentine. Kvadratinė funkcija.

"Bendrosios funkcijų savybės" - Bendrosios savybės funkcijas. Raskite funkcijos apibrėžimo sritį. Netgi funkcija. Nesvarbu, ar ši funkcija lygi, ar nelyginė. Naudodami grafiką, nustatykite funkcijos reikšmių rinkinį. Naudodami grafiką nustatykite X reikšmes. Naudodami diagramą nustatykite funkcijos mažėjimo intervalus. F(x) funkcija didėja. Duota funkcija y=f(x).

„Didėjanti ir mažėjanti funkcija“ – sinuso funkcijos padidėjimas ir sumažėjimas. Pažvelkime į kitą pavyzdį. Mažėjančio kosinuso intervalai yra atkarpos, n yra sveikasis skaičius. Tegu, pavyzdžiui, funkcija f lygi ir didėja intervale, kur b>a?0. Didina ir mažina funkcijas. Didėjanti ir mažėjanti kosinuso funkcija. Žemiau esančiame paveikslėlyje pavaizduotas intervale [-1;10] ​​apibrėžtos funkcijos grafikas.

„Tęstinumo taikymas“ – išraiškos reikšmė. Geometrinė reikšmė išvestinė. Intervalinis metodas. Parašykite funkcijos grafiko liestinės lygtį. Funkcijos grafiko liestinė. Grafikas yra arti liestinės. Formulė. Apskaičiuokime pagal formulę. Kreivės liestinė duotame taške M yra ribinė sekanto NM padėtis. Hiperbolė.

„Funkcijos ekstremumas“ – dujų slėgio priklausomybė nuo temperatūros. Pamokos tema: „Funkcijų didėjimo ir mažėjimo požymiai. Testas. Srovės stiprumo pasikeitimas atidarius grandinę. Funkcijos iki ekstremumo tyrimas“. Keisti AC. Planas: Srovės priklausomybė nuo įtampos. Dujų slėgio priklausomybė nuo tūrio. Tema: „Funkcijų didėjimo ir mažėjimo požymiai.

„Funkcijos ir jų savybės“ – nepriklausomas kintamasis vadinamas argumentu. Funkcijų didinimas. Funkcijos apibrėžimas. Lyginės ir nelyginės funkcijos. Funkcijos monotoniškumas. Priklausomo kintamojo reikšmės vadinamos funkcijos reikšmėmis. Visos nepriklausomo kintamojo reikšmės sudaro funkcijos -D (f) apibrėžimo sritį. 1. Funkcijos reikšmės yra teigiamos.

Iš viso yra 23 pristatymai

Funkcijų savybių taikymas sprendžiant lygtis ir nelygybes Darbas skirtas vienam iš nestandartinių lygčių ir nelygybių sprendimo būdų, pagrįstų į lygtį įtrauktų funkcijų ribiškumo savybe (nelygybė). Mano pasiūlytos problemos gali būti svarstomos pamokose, skirtose rengiant mokinius vieningam valstybiniam egzaminui (trys ar keturios pamokos), arba galima panaudoti vieną ar dvi užduotis per pamoką, o šią medžiagą galima naudoti ir pasirenkamoje pamokoje (arba pasirenkamojo kurso pamokoje).

Apribotumo savybės taikymas ieškant didžiausios ir mažiausios funkcijos reikšmės, ieškant funkcijos reikšmių diapazono. 1. Nurodykite funkcijos reikšmių diapazoną: 2. Nurodykite funkcijos reikšmių diapazoną: 3. Nurodykite funkcijos reikšmių diapazoną: 4. Nurodykite mažiausia vertė funkcijos: y = 5. Nurodykite mažiausią funkcijos reikšmę: 6. Nurodykite funkcijos reikšmių diapazoną:. 7.Nurodykite didžiausia vertė funkcijos: ant intervalo . 8. Raskite didžiausią funkcijos reikšmę:

Ribota funkcija. Funkcija toliau vadinama apribota, jei visos funkcijos reikšmės yra ne mažesnės už tam tikrą skaičių a, t.y. f(x) a. Laikoma, kad funkcija apribota iš viršaus, jei visos funkcijos reikšmės nėra didesnės už tam tikrą skaičių A, t.y. f(x)A. Jei funkcija yra apribota ir žemiau, ir aukščiau, tada ji vadinama ribojama. y y x x xx m M m M

Raskite funkcijos reikšmių rinkinį: Sprendimas. Naudojant pagrindinį trigonometrinė tapatybė ir kosinuso formulė dvigubas kampas, mes nustatome, kad tegul t=sinx, -1 Tada sprendimas yra surasti funkcijos y= reikšmių rinkinį atkarpoje [-1;1]. Funkcijos grafikas yra parabolė, kurios šakos nukreiptos į viršų, parabolės viršus yra (-1;-1), todėl atkarpoje [-1;1] funkcija didėja. Todėl ji įgyja mažiausią reikšmę, kai t=-1, y=-1, o didžiausią reikšmę, kai t=1, y=3. Atsakymas: E(y)=[-1;3]. =

Raskite didžiausią ir mažiausią funkcijos reikšmę intervale. Sprendimas. Funkcija y įgyja didžiausią reikšmę, jei trupmenos vardiklis įgauna mažiausią reikšmę. Pažiūrėkime į vardiklį. Funkcijos didėja, todėl jų suma yra didėjanti funkcija, o tai reiškia, kad ji įgauna mažiausią reikšmę kairiajame atkarpos gale, ties x = 1, t.y. mažiausia reikšmė yra 5. Todėl didžiausia pradinės funkcijos reikšmė yra 8. Atsakymas: 8.

RIBOTOS FUNKCIJOS NUOSAVYBĖS NAUDOJIMAS DIDŽIAUSIAI JOS VERTEI RASTI Ši funkcijaįgauna didžiausią reikšmę tada ir tik tada, kai funkcija eksponente įgauna didžiausią reikšmę: Nurodykite didžiausią sveikąjį funkcijos reikšmę Transformuokime: Kadangi didžiausia funkcijos reikšmė yra 4. Todėl didžiausia pradinės funkcijos reikšmė yra Atsakymas: Sprendimas.

Funkcijų ribotumo savybės taikymas lygčių ir nelygybių sprendimui MAJORANTIS METODAS (Įvertinimo METODAS) Pagrindinė majorantinio metodo mintis yra tokia: Turėkime lygtį f(x)=g(x) ir ten yra toks skaičius M, kad bet kuriam x iš apibrėžimo srities f (x) ir g(x) turime f(x) M ir g(x) M. Tada lygtis f(x)=g(x) yra lygiavertis sistemai

Išspręskite lygtis

Išspręskite lygtį Sprendimas: Sprendimas: Įvertinkime abi lygties puses. Visoms x reikšmėms yra teisingos šios nelygybės. Atsakymas: x = 0.

Išspręskite lygtį. Sprendimas. Panagrinėkime funkciją. Raskime parabolės viršūnės koordinates. x 0 = 7, y 0 = 25. Šakos nukreiptos aukštyn, todėl mažiausia funkcijos reikšmė yra 25. Kadangi f(x) 25, tai. Akivaizdu, kad 1. Tai reiškia, kad pradinė lygtis turi šaknis, jei antrasis narys yra lygus 1, o pirmasis lygus 0. x-7=0, x=7 Kai x=7, antrasis narys yra lygus iki 1. Taigi x=7 yra lygties šaknis.

Išspręskite lygtį Sprendimas. Lygties šaknis atspėti nesunku – ji yra x = 1. Tačiau monotoniškumo svarstymais jos unikalumo įrodyti neįmanoma, nes nei kairioji, nei dešinioji lygties pusė nėra monotoninės funkcijos. Čia naudojama kitokia idėja. Transformuokime lygtį: Gautos lygties dešiniosios pusės didžiausia reikšmė lygi 1 ir imama taške x = 1. Išraiška pagal logaritmą yra lygi x > 0. Todėl kairioji. pusė pasiekia mažiausią reikšmę esant x = 1, kuri taip pat lygi 1. Išvada: lygybė tenkinama tada ir tik tada, kai abi dalys vienu metu lygios 1, t.y. kai x = 1. 0. Todėl kairioji pusė pasiekia mažiausią reikšmę, kai x = 1, kuri taip pat lygi 1. Išvada: lygybė tenkinama tada ir tik tada, kai abi pusės vienu metu yra lygios 1, t. y. ties x = 1.">

Patikrinkime pirmosios lygybės galiojimą pakeisdami šias šaknis. Kai išspręskite lygtį Sprendimas. Norėdami išspręsti lygtį, įvertinkime jos dalis: Todėl lygybė galima tik esant sąlygai: Pirma, išsprendžiame antrąją lygtį: Šios lygties šaknys ir gauname: (tikroji lygybė). Taigi, ši lygtis turi vieną šaknį x = 0. Atsakymas: 0. Jei x = -1, turime: (ne tikroji lygybė). cos() [-1;1] cos 2 () . vieno ir neneigiamo skaičiaus suma.

Išspręskite lygtį. Sprendimas. (dviejų bendra suma abipusiai skaičiai). Todėl funkcija dėl tęstinumo paima visas reikšmes iš intervalo . Įvertinkime funkciją. Grafikas yra parabolė, šakojasi į viršų, mažiausia reikšmė yra 3. Tai reiškia, kad h(y) yra didžiausia, lygi 3. Todėl pradinė lygtis yra lygiavertė sistemai.

(nes :). Išspręskite lygtį Kadangi kairioji lygties pusė Dešinioji pusė (dėl dviejų grįžtamųjų skaičių sumos nelygybės) yra tenkinama Todėl lygtis turi sprendinius tada ir tik tada, kai vienu metu tenkinamos dvi sąlygos. naujausia sistema, gauname reikšmę nuo 0,5 iki 2. Atsakymas: Sprendimas. Įvertinkime abi lygties puses.

Raskite visas parametro a reikšmes, kurių kiekvienos nelygybė turi sprendimą. Įvertinkime abi nelygybės puses. Norėdami tai padaryti, transformuojame dešinę nelygybės pusę, paryškindami visą kvadratą. Kairiosios nelygybės pusės reikšmių aibė sudaro intervalą, todėl didžiausia reikšmė yra 4. Tai reiškia, kad nelygybė tenkinama, jei abi pusės yra lygios ir tik tada, kai a = -6/7. Atsakymas: a=-6/7..

Raskite visas parametro a reikšmes, kurių kiekvienos lygtis turi sprendinius. Raskite šiuos sprendimus. Sprendimas. Perrašykime lygtį į formą Visoms x reikšmėms išraiška yra tokia. Visoms x reikšmėms išraiška yra ir. Štai kodėl. Todėl lygties kairioji pusė yra ne mažesnė kaip 4, o dešinė ne didesnė kaip 4. Gauname sistemą Atsakymas: x = 5/7 su a = -4/9.

Raskite visas parametro P reikšmes, kurių lygtis neturi šaknų. Naudodami dvigubo kampo kosinuso formulę, transformuojame išraišką Lygtis neturės šaknų, jei P nepriklauso kairiosios lygties pusės verčių diapazonui. Panagrinėkime funkciją f(x)= ir įvertinkime ją. Kadangi Todėl Funkcija f(x) yra ištisinė ir įgauna visas jos reikšmes: sinx=0, f(x)=-9, o jei sinx=1, tai f(x)=17, t.y. E(f)=[-9;17] Ištraukiame šį segmentą iš skaičių eilutės ir gauname atsakymą. Atsakymas:

Naudojant funkcijos monotoniškumą sprendžiant lygtis ir nelygybes remiamasi šiais teoriniais faktais:

1. Griežtai monotoniška funkcija paima kiekvieną reikšmę tiksliai vieną kartą.
2. Jei viena funkcija didėja, o kita mažėja tame pačiame intervale, tada jų grafikai arba susikirs tik vieną kartą, arba nesusikirs iš viso, o tai reiškia, kad lygtis F(x)=G(x) turi daugiausiai vieną sprendinį .
3. Jei tam tikru intervalu viena iš funkcijų mažėja (padidėja), o kita pasiima pastovios vertės, tada lygtis F(x)=G(x) turi vieną šaknį arba neturi šaknų.

Pavyzdys

Išspręskite lygtį:\((x^3) = 2 - x\)

Apsvarstykite funkcijas \(f(x) = (x^3)\) ir \(g(x) = 2 - x.\)

Funkcija f(x) didėja visoje apibrėžimo srityje, o funkcija g(x) mažėja apibrėžimo srityje. Todėl ši lygtis neturi

daugiau nei viena šaknis.

Pasirinkę mes nustatome, kad x=1. Patikrinę įsitikiname, kad x=1 iš tikrųjų yra lygties šaknis.

Patikrinkite: 13=2-1; 1=1.

Naudojant pariteto funkciją

Funkcija f (x) iškviečiama net jei bet kuriai \(x \in D\)

galioja lygybė: \(f(- x) = f(x).\)

Pariteto funkcijų tyrimą palengvina šie teiginiai:

Lyginių (nelyginių) funkcijų suma yra

Xia lyginė (nelyginė) funkcija.

· Dviejų lyginių arba dviejų nelyginių funkcijų sandauga yra lyginė funkcija.

Produktas net ir nelyginė funkcija yra nelyginė funkcija.

·Jei funkcija f yra lyginė (nelyginė), tada funkcija \(\frac(1)(f)\)

lyginis (nelyginis).

Pavyzdys

Kai kuriai a reikšmei gali būti taikoma lygtis: \(2(x^8) – 3a(x^6) + 4(x^4) – a(x^2) = 5\) turi 5 šaknis?

Pažymėkime \(f(x) = 2(x^8) – 3a(x^6) + 4(x^4) – a(x^2) = 5,\) kur f(x) - lygi funkcija. Jei x0 yra šios lygties šaknis, tada (-x0) taip pat yra šaknis. Reikšmė x=0 nėra lygties šaknis. Todėl šios lygties šaknų skaičius bet kuriam

tikras ir lyginis, todėl neturi 5 šaknų

Funkcijų apimties naudojimas

Funkcijos domenas yra visų galiojančių aibė tikrosios vertybės argumentas x (kintamasis x), pagal kurį apibrėžiama funkcija. Apibrėžimo sritis kartais dar vadinama leistino sritimi

funkcijų reikšmės. Norėdami rasti funkciją, turite išanalizuoti šią korespondenciją ir nustatyti sutinkamas draudžiamas operacijas (padalyti pagal

nulis, didinant iki racionalios galios

neigiamas skaičius, logaritminės operacijos įjungtos neigiamus skaičius ir tt). Kartais žinios leidžia įrodyti, kad lygtis (arba nelygybė) neturi

sprendinius, o kartais leidžia rasti lygties (arba nelygybės) sprendinius tiesiogiai pakeičiant skaičius.

Išspręskite nelygybę \(\sqrt (x + 3) + \sqrt((9 - x))< \sqrt 3 \)

Nelygybės ODZ yra visi x nuo intervalo \(- 3 \leqslant x \leqslant 9.\)

Padalinkime šią aibę į du intervalus ir \(0 \leqslant x \leqslant 9.\)

Už x iš intervalo \(- 3 \leqslant x \leqslant 0\) mes turime:

\(\begin(surinkta) \sqrt (x + 3) \geqslant 0; \\ \sqrt((9 - x)) \geqslant \sqrt(9); \\ \sqrt(9) = \sqrt 3 . \ \\pabaiga (surinkta)\)

Todėl šiame intervale nelygybė neturi sprendinių šiame intervale.

Tegul x priklauso \(0 \leqslant x \leqslant 9\), tada:

\(\begin(surinkta) \sqrt (x + 3) \geqslant \sqrt 3 ; \\ \sqrt((9 - x)) \geqslant 0. \\ \end(surinkta) \)

Vadinasi, \(\sqrt (x + 3) + \sqrt((9 - x)) \geqslant \sqrt 3 \) tokiam x, taigi ir šiame intervale nelygybė taip pat neturi sprendinių.

Taigi, nelygybė neturi sprendimų.

Funkcijos apribojimo naudojimas. Sprendžiant lygtis ir nelygybes, funkcijos savybė, esanti žemiau arba aukščiau tam tikroje aibėje, dažnai vaidina lemiamą vaidmenį.

Jei yra toks skaičius C, kad bet kuriai \(x \in D\) galioja nelygybė f(x)\(\leqslant \) C, tada sakoma, kad funkcija f yra apribota aibėje D iš viršaus.

Jei yra toks skaičius c, kad bet kuriam skaičiui galioja nelygybė f(x) ≥с, tada sakoma, kad funkcija f yra apribota aibėje D iš apačios.

Funkcija, apribota ir aukščiau, ir žemiau, vadinama apribota aibėje D. Geometriškai funkcijos f ribotumas aibėje D reiškia, kad funkcijos y=f(x) grafikas yra juostelėje c\(\leqslant \ ) f(x)\( \leqslant\) C.

Išspręskite lygtį \(\sin ((x^3) + 2(x^2) + 1) = (x^2) + 2x + 2\)

Bet kam realus skaičius x turime \(\sin ((x^3) + 2(x^2) + 1) \leqslant 1,\)\((x^2) + 2x + 2 = ((x + 1)^2) + 1 \geqslant 1.\)

Kadangi bet kurios x reikšmės kairioji lygties pusė neviršija vieneto, o dešinioji visada yra ne mažesnė už vienetą, ši lygtis gali turėti tik x = -1 sprendinį.

Jei x=-1 turime:

\(\begin(surinkta) (x^2) + 2x + 2 = 1; \\ \sin (- 1 + 2 + 1) = \sin 2 \ne 1; \\ \end(surinkta) \)

tie. lygtis neturi šaknų.