Pasirenkama pamoka „Ribotų funkcijų savybės taikymas. „Lygčių sprendimas nestandartiniais metodais, naudojant funkcijų savybes

Parengė ir veda matematikos mokytoja

MCOU "Vidurinė mokykla Nr. 1" Povorino

Voronežo sritis

Kartašova S. A.

2014 m

Pamokos tema:„Lygčių sprendimas naudojant nestandartinius metodus, naudojant funkcijų savybes“

Pamokos forma – paskaita, po kurios seka pastiprinimas. Skirta 2 pamokoms

(Skairė Nr. 1)

Pamokos tikslai:

Pakartokite ir apibendrinkite žinias tema: „Funkcijų savybės“

Išmokyti naudotis funkcinis metodas sprendžiant lygtis

Tobulėti loginis mąstymas, stebėjimas

Skatinti aktyvumą ir kūrybinę iniciatyvą.

(skaidr. Nr. 2)

Įranga: interaktyvi lenta, kompiuteris su pristatymu.

Pamokos planas:

Organizacinis momentas.

Motyvacija švietėjiška veikla(temos pranešimas, pamokos tikslai).

Atnaujinti pagrindines žinias(pagrindinių funkcijų savybių pasikartojimas).

Naujos medžiagos studijavimas (funkcinis lygčių sprendimo metodas).

Žinių įtvirtinimas (pratimų sprendimas).

Apibendrinant. Įvertinimai.

Pamokos eiga.

Mokytojas:

Norint išspręsti daugumą egzaminų metu pasitaikančių lygčių, pakanka žinoti mokyklos kursas matematika, bet tuo pačiu reikia mokėti spręsti ne tik naudojant standartines technikas, skirtas labai specifinių tipų lygtims, bet ir „nestandartinius“ metodus, apie kuriuos šiandien ir kalbėsime pamokoje. Vienas iš šių lygčių sprendimo būdų yra funkcinis, pagrįstas funkcijų savybių panaudojimu. Skirtingai nei grafinis metodas, funkcijų savybių žinojimas leidžia rasti tikslias lygties šaknis, nereikalaujant konstruoti funkcijų grafikų. Funkcijų savybių naudojimas padeda racionalizuoti lygčių sprendimą.

(skaidr. Nr. 3)

Atsakykime į klausimus:

Kaip vadinama lygtis?

Kas yra lygties šaknis?

Ką reiškia išspręsti lygtį?

Kaip vadinama funkcija?

Kas yra funkcijos sritis?

Koks yra funkcijos diapazonas?

(skaidr. Nr. 4)

Pasvarstykime(skaidr. Nr. 5)

1 PAVYZDYS. Išspręskite lygtį:

Sprendimas: ODZ:

Atsakymas: sprendimų nėra.

(skaidr. Nr. 6)

2 PAVYZDYS. Išspręskite lygtį:

Sprendimas: ODZ:

ODZ susideda iš vieno taško x=1. Belieka patikrinti, ar x=1 yra lygties šaknis. Pakeisdami matome, kad x=1 yra lygties šaknis.

Atsakymas: x=1.

Mokytojas:

Kartais pasirodo, kad pakanka atsižvelgti ne į visą funkcijos apibrėžimo sritį, o tik į jos poaibį, kuriame funkcija paima reikšmes, atitinkančias tam tikras sąlygas (pavyzdžiui, tik neneigiamas reikšmes).

(skaidr. Nr. 7 )

3 PAVYZDYS.

Sprendimas. Raskime funkcijų apibrėžimo sričių sankirtą dešinėje ir kairėje lygties pusėse:

D 1

Apribokime rinkinįD, atsižvelgiant į tai kairėje pusėje lygtis yra neneigiama, todėl dešinioji pusė turi būti ta patiDsu daugybe nelygybės sprendimų , tai yra, su daugeliu . Todėl pakanka atsižvelgti į lygtį rinkinyje .

Pakeitimu įsitikiname, kad abu elementai yra lygties sprendimas.

Atsakymas: -3; 2.

(skaidr. Nr. 8 )

4 PAVYZDYS.

Sprendimas.

Atsižvelgiant į tai lygties šaknis x=4.

Atsakymas: 4.

Mokytojas:

Pereikime prie lygčių sprendimo naudodami funkcijos reikšmių diapazono koncepciją.

(skaidr. Nr. 9–Nr. 10)

(skaidr. Nr. 11)

1 PAVYZDYS.

Sprendimas. Nes , tada lygtis neturi sprendinio.

Atsakymas: nėra sprendimų.

2 PAVYZDYS.

Sprendimas. ODZ:

Atsakymas: nėra sprendimų.

Mokytojas:

Jei funkcija f ( x ) intervale X yra ribojamas iš viršaus, o funkcija g ( x ) yra apribota žemiau, tada lygtis f ( x ) = g ( x ) yra lygiavertis sistemai

(skaidr. Nr. 12)

3 PAVYZDYS.

Sprendimas. Pagal apibrėžimą,

Lygybė pasiekiama, jei

Išspręskime pirmąją sistemos lygtį:

arccos (x-1) =π, x-1 = -1, x=0.

Kai x=0, antroji lygtis virsta tikra skaitine lygybe.

Todėl sistemos ir šios lygties sprendinys yra x=0.

Atsakymas: 0.

(skaidr. Nr. 13-14)

4 PAVYZDYS.

Sprendimas.

Raskime šios funkcijos maksimumą intervale (2;4) naudodami išvestinę.

= 0,

g' + -

g 2 3 4 x

Maks

g(3)=2.Turime

Tada ši lygtis yra lygiavertė sistemai

Išsprendę pirmąją sistemos lygtį, gauname x=3, patikrinę, pakeitę ją į antrąją lygtį, įsitikinsime, kad x=3 yra sistemos ir šios lygties sprendinys.

Atsakymas: 3.

(skaidr. Nr. 15)

Mokytojas:

Šis metodas dažnai randamas vieningo valstybinio matematikos egzamino metu. Šis metodas slypi tame, kad vieną lygties dalį iš viršaus riboja tam tikras skaičius M, o kitą lygties dalį iš apačios riboja tas pats skaičius M. Skaičius M paprastai vadinamasmajorante , ir šis metodas yramajorantinis metodas . Naudodami pagrindinį metodą, kaip galbūt atspėjote, turite gerai suprasti, kas yra funkcija, ir mokėti ištirti funkcijų savybes.

(skaidr. Nr. 16)

Pratimai, skirti įtvirtinimui, įgūdžių ugdymui.

Klasė skirstoma į 2 grupes pagal pasirinkimus.

1 variantas.

Įrodykite, kad lygtis neturi šaknų.

Išspręskite lygtis: Atsakymas: 2.6.

Atsakymas: 2.

Mokytojas:

Šiandien mes apžvelgėme nestandartinį lygčių sprendimo metodą naudojant funkcijų savybes, kuris taip pat taikomas sprendžiant nelygybes, tačiau apie tai kalbėsime keliose vėlesnėse pamokose.

Apibendrinimas, vertinimai.

(skaidr. Nr. 17)

Namų darbai:

Tema: Ribotų funkcijų naudojimo būdai.
Gyvenimas yra geras dėl to, kas jame yra tu moki matematiką. (Leonardas Euleris)Tikslai: naujo, netradicinio mąstymo, kurį galima sėkmingai pritaikyti kitose srityse, ugdymas žmogaus veikla(kibernetika, kompiuterinės technologijos, ekonomika, radiofizika, chemija ir kt.).
Užduotys: - mokymas įvertinti objektyvų ir subjektyvų užduočių sudėtingumą ir išmintingai pasirinkti šias užduotis egzamine;

Netradicinių ir neįprastų samprotavimų „kiaulės banko“ kūrimas.

Pamokos eiga:

Org. akimirka. Pamokos temą mokiniai formuluoja atlikdami Vieningo valstybinio egzamino užduočių A ir B dalis ir iššifruodami temą gautų atsakymų mažėjimo tvarka. (Šifruokite 12 kortelių, sunumeruotų nuo -2 iki 10, kaip tariamus žodžius) (1 ir 2 priedas)

apribojimai

1 priedas.
Išspręskite šias užduotis ir išdėliokite atsakymus mažėjančia tvarka, pagal atsakymus surinkite mūsų pamokos temą.

Funkcijos y=3x 2 -7x+7 grafike raskite taško abscisę, kurioje liestinės kampo liestinė lygi -1.

2 priedas.
9 2 0 7Funkcijų tyrimas naudojant išvestines. 10 5 1 -1Ribotų funkcijų naudojimo būdas. 4 -2 8 12Nelygybių sprendimas grafiškai.
3 11 6Sprendimai funkcines lygtis.
Studijuoti

Vienas iš veiksmingi metodai lygčių arba nelygybių sprendimas yra metodas, pagrįstas apribotų funkcijų naudojimu. Į garsiausius ribotos funkcijosįtraukti, pavyzdžiui, kai kuriuos trigonometrinius; atvirkščiai trigonometrinės funkcijos; funkcijos, turinčios modulį, laipsnį, šaknį su lyginiu laipsniu ir kt.

Dažniausiai pasitaikančios nelygybės yra šios:

│f(x) │≥ 0, -1 ≤ sinx ≤ 1, -1 ≤ cosx ≤ 1, -

-

, a f (x) >0, (f(x) ± g(x)) 2 n ≥ 0,
, a+ ≥ 2, b+ ≤ -2 ir daugelis kitų. Čia n -natūralusis skaičius, h(x) ≥ 0, a>0, b 0.

Be aukščiau pateiktų paprasčiausių nelygybių, yra ir sudėtingesnių, ypač trigonometrinės nelygybės -,

,

ir nelygybės su formos moduliais
.

1 pavyzdys.Išspręskite lygtį:

Sprendimas: pabrėkim tobulas kvadratas dešinėje lygties pusėje, t.y. . Iš to išplaukia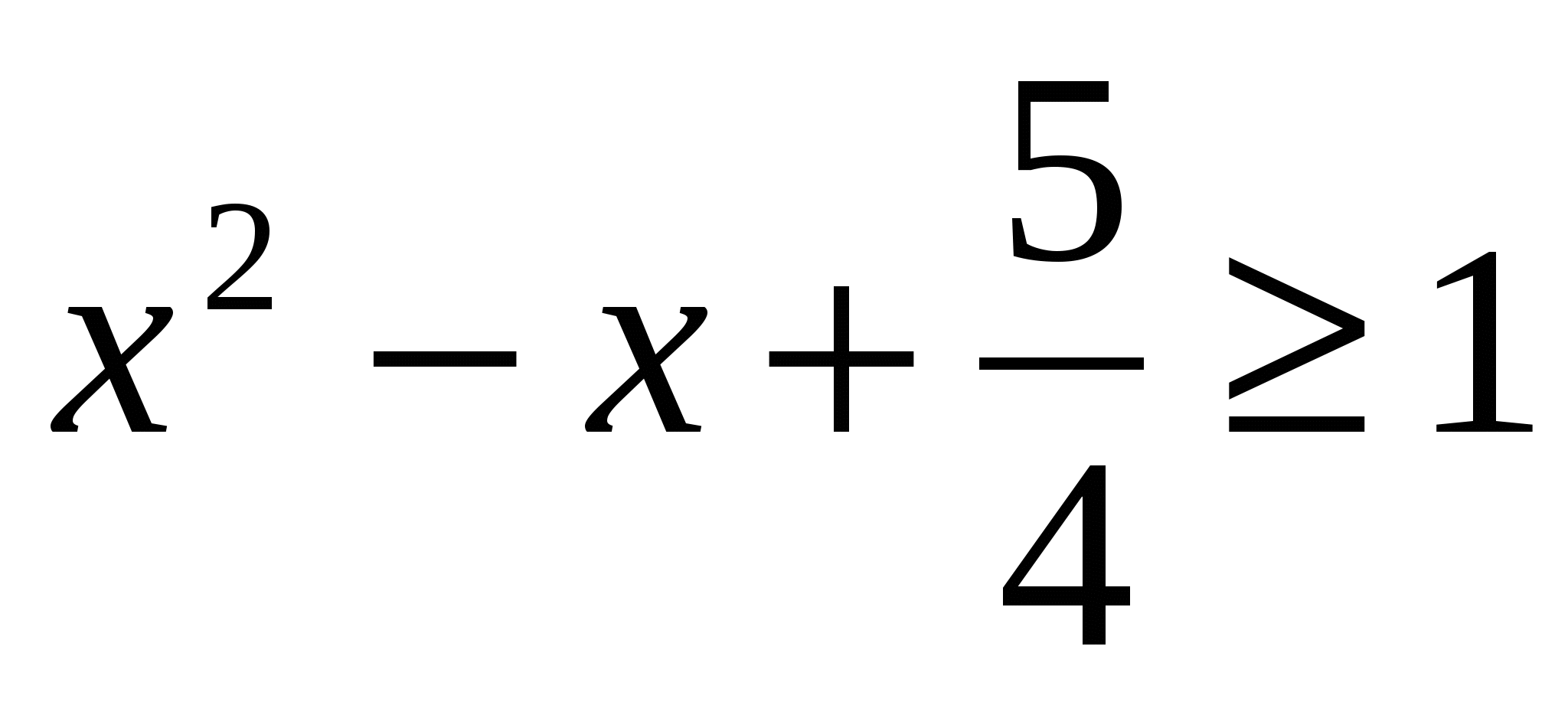
. Kadangi šiuo atveju sinπ x ≤ 1, tada gauname lygčių sistemą

Išsprendę antrąją sistemos lygtį, gauname, kad x=. Pakeisdami pirmąją lygtį įsitikiname, kad rasta x reikšmė yra sistemos sprendimas, taigi ir sprendimas pradinė lygtis.

Atsakymas: x=.

2 pavyzdys.Išspręskite lygtį:

Sprendimas: kadangi Tačiau sin2 π x ≤ 1. Todėl 5+4 sin2 π x ≤ 9. Taigi gauname lygčių sistemą:

Iš čia gauname lygčių sistemą
, iš pirmosios lygties randame x=. Pakeiskime jį į antrąją sistemos lygtį ir įsitikinkime, kad x = yra sistemos sprendimas, taigi ir pradinės lygties sprendimas.

Atsakymas: x=

4 priedas. Iš siūlomo užduočių sąrašo pasirinkite tas, kurias galima išspręsti ribotų funkcijų metodu. 1. Išspręskite lygtį x 2 -4 x=(2-cos
2. Raskite nelygybės x sveikųjų skaičių sprendinių skaičių 2ctg 2
3. Išspręskite lygtį
4. Išspręskite lygtį 3-(5. Raskite sveikųjų nelygybės 16 2 ≥0 sprendinių, kurie tenkina 3 sąlygą, skaičių tg 2
6. Išspręskite lygtį
7. Išspręskite lygtį -25x 2 +40x-23=( cos
8. Raskite lygties x šaknų sandaugą
9. Išspręskite lygtį
10. Išspręskite lygtį 3- cos 2

Savikontrolės lapas. 5 priedas. 1. Išspręskite lygtį Sprendimas: nes , tada nes ir tada
gauname lygčių sistemą

Išspręskite pirmąją lygtį, gaukite x=, pakeiskite šią reikšmę antrąja lygtimi

2 . Išspręskite lygtį 3- cos 2 Sprendimas: nes , tada nes ir tada
gauname lygčių sistemą

Išspręskite antrąją lygtį, gaukite x=, pakeiskite šią reikšmę pirmąja lygtimi

tai reiškia, kad x= yra pradinės lygties sprendimas. Atsakymas: x=
3. Raskite nelygybės x sveikųjų skaičių sprendinių skaičių 2 +7x-8≤0, tenkina sąlygą ctg 2 Sprendimas: nes ir tada bet kurioms leistinoms x reikšmėms rasime kvadratinio trinalio nulius, naudodamiesi Vietos teorema išspręsime nelygybę intervalų metodu
Tai. mes tai žinome
sveikųjų x reikšmės yra skaičiai, pašalinami. Atsakymas: 8 sveikųjų skaičių sprendiniai 4. Raskite sveikųjų skaičių nelygybės 16 2 ≥0 sprendinių, atitinkančių 3 sąlygą, skaičių tg 2 Sprendimas: nes ir tada bet kurioms leistinoms x reikšmėms randame išraiškos nulius, x = ir x = Išspręskite nelygybę naudodami intervalų metodą
Tai. mes tai žinome

sveikųjų x reikšmės yra skaičiai, pašalinti. Atsakymas: 7 sveikųjų skaičių sprendiniai
6 priedas.

Funkcijų monotoniškumo panaudojimo būdas. Sprendžiant lygtį kaip f(x)=g(x) kai kuriais atvejais yra veiksmingas metodas, kai naudojamas funkcijų y= f(x) ir y= g(x) monotoniškumas Jei funkcija y= f(x) yra tolydi ir segmente didėja (sumažina). a≤ x ≤ b, o funkcija у= g(x) yra tolydi ir mažėja (didėja) toje pačioje atkarpoje, tada lygtis f(x)=g(x) atkarpoje a≤ x ≤ b gali turėti ne daugiau kaip vieną šaknį, vadinasi, reikia arba pabandyti surasti vienintelę lygties šaknį pasirinkimo būdu, arba parodyti, kad tokios šaknies nėra. Šis metodas ypač efektyvus tuo atveju, kai abi lygties pusės f(x) = g(x) yra „nepatogios“ funkcijos bendram tyrimui. komentaras: Jei funkcija y= f(x) didėja, o funkcija y= g(x) mažėja a≤ x ≤ b Ir tuo pačiu metu f(a)>g(A), tada lygties šaknys yra tarp a≤ x ≤ b Nr.

Pavyzdys: Išspręskite lygtįSprendimas: Priimtinų lygties verčių diapazonas yra x
. Nesunku pastebėti, kad šioje srityje kairioji lygties pusė didėja, o dešinioji mažėja, t.y. funkcijaf(x)=
didėja, ir funkcijag(x)=
- mažėja. Šiuo atžvilgiu pradinė lygtis gali turėti tik vieną šaknį (jei yra). Pasirinkdami randame šią lygties x = šaknį 2.Atsakymas: x=2
Funkcinių lygčių sprendimo būdas. Tarp labiausiai sudėtingos užduotys Vieningasis valstybinis egzaminas apima uždavinius, kurių sprendimas susiveda į formos funkcinių lygčių svarstymą f(f(….f(x)…))=x arba f(g(x))=f(h(x)), kur f(x),g(x),h(x) yra kai kurios funkcijos ir n≥ 2
Šių funkcinių lygčių sprendimo metodai yra pagrįsti daugelio teoremų taikymu, panagrinėkime vieną iš jų.
1 teorema. Lygties šaknys f(x)=0 yra lygties šaknys f(f(….f(x)…))=x
Pavyzdys: Išspręskite lygtį x=
, Kur kvadratinė šaknis paimtasnvieną kartą irn≥ 1 Sprendimas: Iš problemos sąlygų matyti, kad x> 0. Leiskitef(x)=
, tada mūsų lygtis gali būti pavaizduota kaip funkcinė f( f(…. f( x)…))= x. Nuo x> 0 funkcijaf(x)= didėja irf(x) > 0, tada lygtis x= yra lygi lygčiaif(x)= x, t.y. =x, kurios teigiamas sprendinys yra x=
Atsakymas: x=

Galaeva Jekaterina, Nižnij Novgorodo MAOU 149 vidurinės mokyklos 11 klasės mokinė

Darbas tiek taikomas, tiek tyrimo pobūdis. Siekiant išsamumo, tyrimai buvo peržiūrėti šiuos klausimus:

– Kaip sprendžiant lygtis ir nelygybes atsispindi funkcijos savybės?

– Kokios lygtys ir nelygybės sprendžiamos nustatant apibrėžimo srities, reikšmių aibės, nekintamumo savybes?

– Koks yra sprendimo algoritmas?

– Apsvarstytos užduotys su KIM medžiagoje pasiūlytais parametrais ruošiantis vieningam valstybiniam egzaminui.

Savo darbe Jekaterina tyrinėjo didelis ratas užduotis ir jas susistemino pagal išvaizda.

Parsisiųsti:

Peržiūra:

https://accounts.google.com

Skaidrių antraštės:

Išspręskite nelygybę Sprendimas. Funkcija f (x) = monotoniškai didėja visoje skaičių eilutėje, o funkcija g (x) = monotoniškai mažėja visoje apibrėžimo srityje. Todėl nelygybė f (x) > g (x) tenkinama, jei x >

Dėkojame už dėmesį!

Peržiūra:

Norėdami naudoti pristatymų peržiūras, susikurkite „Google“ paskyrą ir prisijunkite prie jos: https://accounts.google.com

Skaidrių antraštės:

Funkcijos savybių taikymas sprendžiant lygtis ir nelygybes Darbą atliko: Galaeva Jekaterina MBOU Maskvos rajono 149 vidurinė mokykla 11 „A“ klasės mokiniai Mokslinis vadovas: Fadeeva I. A. Matematikos mokytojas

Pagrindinės kryptys: Funkcijos savybių tyrimas: monotoniškumas, ribojimas, apibrėžimo sritis ir nekintamumas Išmokti pagrindinius teiginius, kurie dažniausiai naudojami sprendžiant lygtis, nelygybes ir sistemas. Užduočių sprendimas iš CMM medžiagos ruošiantis vieningam valstybiniam egzaminui

Monotoniškumas Funkcija padidėja, jei didesnę vertę argumentas atitinka didesnę funkcijos reikšmę. Funkcija mažėja, jei atitinka didesnė argumento reikšmė mažesnė vertė funkcijas. f(x 1) f(x 2) x 1 x 2 f(x 1) f(x 2) x 1 x 2

1 teiginys. Jei funkcija y = f (x) yra monotoninė, tai lygtis f (x) = c turi daugiausia vieną šaknį. x =2 f(x) = - monotoniškai mažėjantis, vadinasi, kitų sprendinių nėra. Atsakymas: x =2

2 teiginys. Jei funkcija y = f (x) didėja monotoniškai, o funkcija y = g (x) mažėja monotoniškai, tai lygtis f (x) = g (x) turi daugiausia vieną šaknį. 2 - x = log (x +11) + 1 g (x) = 2 - x monotoniškai mažėja, o funkcija f (x) = log (x + 11) + 1 monotoniškai didėja apibrėžimo srityje, kuri reiškia, kad lygtis f (x ) = g (x) turi daugiausia vieną šaknį. Pasirinkdami nustatome, kad x = -1. Pirmiau pateiktas teiginys pagrindžia sprendimo unikalumą.

a) f (x) ≤ g (x) tada ir tik tada, jei x ϵ (- ∞ ; x 0 ]; b) f (x) ≥ g (x) tada ir tik tada, jei x ϵ [x 0 ; +∞). Vizuali šio teiginio prasmė akivaizdi. 3 teiginys. Jei funkcija y = f (x) monotoniškai didėja visoje skaičių tiesėje, funkcija y = g (x) monotoniškai mažėja visoje skaičių tiesėje ir f (x 0) = g (x 0), tada teisingi šie teiginiai:

Išspręskite nelygybę Sprendimas. Funkcija f (x) = monotoniškai didėja visoje skaičių eilutėje, o funkcija g (x) = monotoniškai mažėja visoje apibrėžimo srityje. Todėl nelygybė f (x) > g (x) tenkinama, jei x > 2. Pridėkime nelygybės apibrėžimo sritį. Taigi gauname sistemą Atsakymas: (2; 5).

4 teiginys. Jei funkcija y = f (x) didėja monotoniškai, tai lygtys f (x) = x ir f (f (x)) = x turi tą pačią šaknų aibę, nepriklausomai nuo įterpimų skaičiaus. Pasekmė. Jei n yra natūralusis skaičius, o funkcija y = f (x) didėja monotoniškai, tai lygtys f (x) = x ir n kartų turi tą pačią šaknų rinkinį.

Išspręskite lygtį. Atsakymas: Sprendimas. Jei x ≥1, dešinė lygties pusė yra ne mažesnė nei 1, o kairioji pusė yra mažesnė už 1. Todėl, jei lygtis turi šaknis, bet kuri iš jų yra mažesnė už 1. Jei x ≤0, dešinė lygties pusė yra ne teigiama, o kairioji pusė yra teigiama dėl to, kad . Taigi bet kuri šios lygties šaknis priklauso intervalui (0; 1), padauginus abi šios lygties puses iš x, o kairiosios pusės skaitiklį ir vardiklį padalijame iš x, gauname.

Iš = . Pažymėdami t, kur t 0, gauname lygtį = t. Panagrinėkime funkciją f (t)= 1+, kuri didėja jos apibrėžimo srityje. Gautą lygtį galima parašyti f (f (f (f (t))))= t forma, o pagal 4 teiginį ji turi tokią pat sprendinių rinkinį kaip ir lygtis f (t)= t, t.y. lygtis 1 + = t, iš kur. Vienintelė teigiama šios kvadratinės santykinės lygties šaknis yra. Tai reiškia, kur, t.y. , arba. Atsakymas:

1 teiginys. Jei max f (x) = с ir min g (x) = с, tai lygtis f (x) = g (x) turi tokią pat sprendinių aibę kaip sistemos ribojimas Didžiausia vertė kairėje pusėje yra 1 ir minimali vertė 1 dešinioji pusė, o tai reiškia, kad lygties sprendinys redukuojamas į lygčių sistemą: , iš antrosios lygties randame galimą kandidatą x=0 ir įsitikiname, kad tai pirmosios lygties sprendinys. Atsakymas: x=1.

Išspręskite lygtį Sprendimas. Kadangi sin3x≤1 ir cos4x≤1, šios lygties kairioji pusė neviršija 7. Ji gali būti lygi 7 tada ir tik tada, kai kur k , n ϵ Z . Belieka išsiaiškinti, ar yra sveikųjų skaičių k ir n, kuriems pastaroji sistema turi sprendinius. Atsakymas: Z

Problemose su nežinomaisiais x ir parametru a apibrėžimo sritis suprantama kaip visų tvarkingų skaičių porų (x; a) rinkinys, kurių kiekviena yra tokia, kad pakeitus atitinkamas x ir a reikšmes į visus ryšius įtraukti į problemą, jie bus nustatyti. 1 pavyzdys. Kiekvienai parametro a reikšmei išspręskite nelygybę Sprendimas. Raskime šios nelygybės apibrėžimo sritį. Iš ko aišku, kad sistema neturi sprendimų. Tai reiškia, kad nelygybės apibrėžimo srityje nėra skaičių x ir a porų, todėl nelygybė neturi sprendinių. Taikymo sritis Atsakymas:

Nekintamumas, t.y. lygties ar nelygybės nekintamumas kintamojo pakeitimo bet kuriuo algebrinė išraiška iš šio kintamojo. Paprasčiausias nekintamumo pavyzdys yra paritetas: jei – lygi funkcija, tada lygtis yra nekintama pagal pakeitimą x ir – x, nes = 0. Nekintamumas

Raskite lygties šaknis. Sprendimas. Atkreipkite dėmesį, kad keičiant pora yra nekintama. Pakeisdami lygybe, gauname. Abi šios lygybės puses padauginus iš 2 ir iš gautos lygybės atėmus lygybės narį po nario, gauname 3, iš kur. Dabar belieka išspręsti lygtį, iš kurios lygties šaknys yra skaičiai. Atsakymas:.

Raskite visas a reikšmes, kurių kiekvienoje lygybėje yra daugiau nei trys įvairių sprendimų. Problemų sprendimas su parametru Monotoniškumo savybė

|x|= teigiamas X= |x|= Kad egzistuotų dvi šaknys, skaitiklis turi būti teigiamas. Todėl, kai pirmosios ir antrosios lygčių šaknys sutampa, o tai neatitinka sąlygos reikalavimo: daugiau nei trijų šaknų buvimas. Atsakymas:.

Raskite visas a reikšmes, kurių kiekviena turi dvi šaknis. Transformuokime lygtį į formą Ir apsvarstykime funkciją f(x) = apibrėžta ir ištisinė visoje skaičių tiesėje. Šios funkcijos grafikas yra trūkinė linija, susidedanti iš tiesių ir spindulių atkarpų, kurių kiekviena grandis yra y= kt+l formos tiesės dalis. f(x)= Bet kuriai reikšmei pirmosios išraiškos k modulio atskleidimas neviršija 8, todėl funkcijos f(x) padidėjimas ir sumažėjimas priklausys nuo antrojo modulio atskleidimo. Ties x f(x) sumažės, o ties x padidės. Tai yra, kai x = 3, funkcija įgis didžiausią reikšmę. Kad lygtis turėtų dvi šaknis, būtina, kad f(3) monotoniškumo savybė

f(3)=12- |9-| 3+a || | 9-| 3+a || 9- | 3+a | - | 3+a | | 3+a | | 3+a | 3+a a Atsakymas: a

Raskite visas parametro a reikšmes, kiekvienai iš jų bet kuriai faktinė vertė x nelygybė tenkinama Perrašykime nelygybę į formą, įveskime naują kintamąjį t = ir apsvarstykime funkciją f (t) =, apibrėžtą ir tolydi visoje skaičių tiesėje. Šios funkcijos grafikas yra trūkinė linija, susidedanti iš linijos atkarpų ir spindulių, kurių kiekviena nuoroda yra formos linijos dalis, kur

Nuo tada t ϵ [-1; 1]. Dėl funkcijos y = f (t) monotoniško mažėjimo pakanka patikrinti kairįjį kraštą šis segmentas. Z. A yra tiesa Tai reiškia, kad tai įmanoma tik tada, kai skaičiai ir ir v yra vienodo ženklo arba vienas iš jų yra lygus nuliui. , = () () 0. Suskaidę kvadratinius trinalius, gauname nelygybę (, iš kurios randame, kad a ϵ (-∞; -1] U (2) U [ 4; +∞). Atsakymas: (- ∞; - 1] U (2) U. Funkcijos grafikas yra parabolė, kurios šakos nukreiptos į viršų, parabolės viršūnė yra (-1;-1), todėl atkarpoje [-1 ;1], todėl ji įgyja mažiausią reikšmę, kai t=1, y=3. 3].

Raskite didžiausią ir mažiausią funkcijos reikšmę intervale. Sprendimas. Funkcija y įgyja didžiausią reikšmę, jei trupmenos vardiklis įgauna mažiausią reikšmę. Pažiūrėkime į vardiklį. Funkcijos didėja, todėl jų suma yra didėjanti funkcija, o tai reiškia, kad ji įgauna mažiausią reikšmę kairiajame atkarpos gale, ties x = 1, t.y. mažiausia reikšmė yra 5. Todėl didžiausia pradinės funkcijos reikšmė yra 8. Atsakymas: 8.

RIBOTOS FUNKCIJOS NUOSAVYBĖS NAUDOJIMAS DIDŽIAUSIAI JOS VERTEI RASTI Ši funkcijaįgauna didžiausią reikšmę tada ir tik tada, kai funkcija eksponente įgauna didžiausią reikšmę: Nurodykite didžiausią sveikąjį funkcijos reikšmę Transformuokime: Kadangi didžiausia funkcijos reikšmė yra 4. Todėl didžiausia pradinės funkcijos reikšmė yra Atsakymas: Sprendimas.

Funkcijų ribotumo savybės taikymas lygčių ir nelygybių sprendimui MAJORANTIS METODAS (Įvertinimo METODAS) Pagrindinė majorantinio metodo mintis yra tokia: Turėkime lygtį f(x)=g(x) ir ten yra toks skaičius M, kad bet kuriam x iš apibrėžimo srities f (x) ir g(x) turime f(x) M ir g(x) M. Tada lygtis f(x)=g(x) yra lygiavertis sistemai

Išspręskite lygtis

Išspręskite lygtį Sprendimas: Sprendimas: Įvertinkime abi lygties puses. Visoms x reikšmėms yra teisingos šios nelygybės. Atsakymas: x = 0.

Išspręskite lygtį. Sprendimas. Panagrinėkime funkciją. Raskime parabolės viršūnės koordinates. x 0 = 7, y 0 = 25. Šakos nukreiptos aukštyn, todėl mažiausia funkcijos reikšmė yra 25. Kadangi f(x) 25, tai. Akivaizdu, kad 1. Tai reiškia, kad pradinė lygtis turi šaknis, jei antrasis narys yra lygus 1, o pirmasis lygus 0. x-7=0, x=7 Kai x=7, antrasis narys yra lygus iki 1. Taigi x=7 yra lygties šaknis.

Išspręskite lygtį Sprendimas. Lygties šaknis atspėti nesunku – ji yra x = 1. Tačiau monotoniškumo svarstymais jos unikalumo įrodyti neįmanoma, nes nei kairioji, nei dešinioji lygties pusė nėra monotoniškos funkcijos. Čia naudojama kitokia idėja. Transformuokime lygtį: Gautos lygties dešiniosios pusės didžiausia reikšmė lygi 1 ir imama taške x = 1. Išraiška pagal logaritmą yra lygi x > 0. Todėl kairioji. pusė pasiekia mažiausią reikšmę esant x = 1, kuri taip pat lygi 1. Išvada: lygybė tenkinama tada ir tik tada, kai abi dalys vienu metu lygios 1, t.y. kai x = 1. 0. Todėl kairioji pusė pasiekia mažiausią reikšmę, kai x = 1, kuri taip pat lygi 1. Išvada: lygybė tenkinama tada ir tik tada, kai abi pusės vienu metu yra lygios 1, t. y. ties x = 1.">

Patikrinkime pirmosios lygybės galiojimą pakeisdami šias šaknis. Kai išspręskite lygtį Sprendimas. Norėdami išspręsti lygtį, įvertinkime jos dalis: Todėl lygybė galima tik tada, jei: Pirma, išsprendžiame antrą lygtį: Šios lygties šaknys ir gauname: (tikroji lygybė). Taigi, ši lygtis turi vieną šaknį x = 0. Atsakymas: 0. Jei x = -1, turime: (ne tikroji lygybė). cos() [-1;1] cos 2 () . vieno ir neneigiamo skaičiaus suma.

Išspręskite lygtį. Sprendimas. (dviejų bendra suma abipusiai skaičiai). Todėl funkcija dėl tęstinumo paima visas reikšmes iš intervalo . Įvertinkime funkciją. Grafikas yra parabolė, šakojasi į viršų, mažiausia reikšmė yra 3. Tai reiškia, kad h(y) yra didžiausia, lygi 3. Todėl pradinė lygtis yra lygiavertė sistemai.

(nes :). Išspręskite lygtį Kadangi kairioji lygties pusė Dešinioji pusė (dėl dviejų grįžtamųjų skaičių sumos nelygybės) yra tenkinama Todėl lygtis turi sprendinius tada ir tik tada, kai vienu metu tenkinamos dvi sąlygos. naujausia sistema, gauname reikšmę nuo 0,5 iki 2. Atsakymas: Sprendimas. Įvertinkime abi lygties puses.

Raskite visas parametro a reikšmes, kurių kiekvienos nelygybė turi sprendimą. Įvertinkime abi nelygybės puses. Norėdami tai padaryti, mes transformuojame dešinę nelygybės pusę, pasirinkdami visą kvadratą Kvadratinė funkcijaįgauna mažiausią reikšmę viršūnėje, ji lygi 4 ir pasiekiama ties, tai yra, a = -6/7. Kairiosios nelygybės pusės reikšmių aibė sudaro intervalą, todėl didžiausia reikšmė yra 4. Tai reiškia, kad nelygybė tenkinama, jei abi pusės yra lygios ir tik tada, kai a = -6/7. Atsakymas: a=-6/7..

Raskite visas parametro a reikšmes, kurių kiekvienos lygtis turi sprendinius. Raskite šiuos sprendimus. Sprendimas. Perrašykime lygtį į formą Visoms x reikšmėms išraiška yra tokia. Visoms x reikšmėms išraiška yra ir. Štai kodėl. Todėl lygties kairioji pusė yra ne mažesnė kaip 4, o dešinė ne didesnė kaip 4. Gauname sistemą Atsakymas: x = 5/7 su a = -4/9.

Raskite visas parametro P reikšmes, kurių lygtis neturi šaknų. Naudojant kosinuso formulę dvigubas kampas, transformuojame išraišką Lygtis neturės šaknų, jei P nepriklauso kairiosios lygties pusės reikšmių diapazonui. Panagrinėkime funkciją f(x)= ir įvertinkime ją. Kadangi Todėl Funkcija f(x) yra ištisinė ir įgauna visas jos reikšmes: sinx=0, f(x)=-9, o jei sinx=1, tai f(x)=17, t.y. E(f)=[-9;17] Ištraukiame šį segmentą iš skaičių eilutės ir gauname atsakymą. Atsakymas:

I skyrius. Matematika ir fizika

UDC 372,8 BBK 74 262,21

NE. Lyakhova, A.I. Grišina, I.V. Jakovenko

RIBOTŲJŲ FUNKCIJŲ NAUDOJIMAS MOKYKLINĖJE MATEMATIKOS KURES

Anotacija. Straipsnyje pateikiama „nestandartinių“ lygčių sprendimo metodo tyrimo metodika elementarioji matematika naudojant ribotas funkcijas.

Raktažodžiai: lygčių sprendimas, naudojant funkcijos ribotumą.

N.E. Lyakhova, A.I. Grishina, I.V. Jakovenko

FUNKCIJŲ APRIBOJIMO NAUDOJIMAS MOKYKLINĖJE MATEMATIKOS KURES

Abstraktus. Straipsnyje pateikiama elementariosios matematikos ribotų funkcijų "nestandartinių" lygčių sprendimo metodo tyrimo metodika. Raktažodžiai: lygčių sprendimas, naudojant ribotą funkciją.

Ribotos funkcijos leidžia išspręsti daugelį nestandartinės lygtys ir nelygybės, kurios vienu metu turi įvairių funkcijų, o tai neleidžia joms taikyti standartiniai metodai sprendžiant tam tikro tipo problemą. Naudojant funkcijų ribotumą, sukurti tokie lygčių ir nelygybių sprendimo metodai kaip mini-max metodas ir jo pasekmės. Metodo pavadinimas – mini-max metodas – gali būti prieštaringas, tačiau jis leidžia greitai prisiminti metodo esmę ir yra mokinio atskaitos taškas. Atkreipkite dėmesį, kad šio metodo studijavimas yra naudingas abiturientui tiek plečiant savo gebėjimus spręsti „nestandartines“ problemas, tiek lavinant funkcijų tyrimo įgūdžius (ypač naudojant elementarios matematikos metodus). ). Abu svarbūs ruošiant abiturientą vieningam valstybiniam matematikos egzaminui, nuo įskaitos matavimo medžiagos tradiciškai yra panašių užduočių, o mokykliniai vadovėliai jie aiškiai atstovaujami nepakankamai arba visai neatstovaujami.

Mini-max metodo esmė yra toks teiginys.

1 teiginys. Jei X apibrėžimo srityje lygtys

ir funkcija

tada ši lygtis yra lygiavertė sistemai

f (*) = a g(*) = a "

Tiesa, kada nurodytomis sąlygomis lygybė

yra įmanomas tada ir tik tada, kai funkcijos f (*) ir g (*) įgauna a reikšmę tos pačios reikšmės *. Šiuo atveju skaičius a bus skirtas funkcijoms f (*) ir g (*), atitinkamai didžiausiai ir mažiausiajai aibės X reikšmėms. Atkreipkite dėmesį, kad jei bent viena iš funkcijų f (*) arba g (*) aibėje X nepriima reikšmės a, tada lygtis

neturi šaknų. Tačiau šiuo atveju sistema taip pat neturi sprendinių, todėl lygties ir sistemos lygiavertiškumas nepažeidžiamas. Todėl, gaunant reikiamus įverčius, nereikia nustatyti, kad a yra aibėje X didžiausia vertė funkcijos f(*) ir mažiausia vertė funkcijos g(*) .

Naudojant 1 teiginį ir ypatybes skaitinės nelygybės, nesunku įrodyti dar du teiginius, kurie yra mini-max metodo pasekmės.

2 teiginys. Tegul aibė X yra funkcijų f (x) ir g (x) apibrėžimo sričių sankirta, ir šioje aibėje galioja nelygybės

tada nelygybė

f (x) + g (x) > a + b,

yra lygiavertis lygčiai

f (x) + g (x) = a + b, o tai, savo ruožtu, yra lygiavertė sistemai:

/ (x) = a, e (x) = b.

3 teiginys. Tegul aibė X yra funkcijų f (x) ir е (x) apibrėžimo sričių sankirta, ir šioje aibėje galioja nelygybės

0 < f (х) < а

e (x)< Ь, где а >0, b > 0

tada nelygybė

f (x) e (x) > a b

bus lygiavertis lygčiai

f (x) e (x) = a b, kuri savo ruožtu yra lygiavertė sistemai

/ (x) = a, e (x) = b.

Kaip matyti iš teiginių formuluotės, norint įgyvendinti mini-max metodą (ar jo pasekmes), būtina įvertinti lygtyse ar nelygybes įtrauktas funkcijas. Tiesą sakant, funkcijų vertinimas yra pagrindinė metodo įgyvendinimo veikla. Todėl metodo mokymas turi būti pagrįstas vertinimo įgūdžių ugdymu įvairių funkcijų. Mūsų nuomone, moksleiviams aktualiausi bus tokie tokio vertinimo metodai.

1. Paprasčiausia technika- formos f (x) = A ± a(x) funkcijos įvertinimas, kur a(x) yra kokia nors neneigiama funkcija.

5. Sudėtinės funkcijos įvertinimas.

Leiskite mums išsamiau panagrinėti kiekvieną techniką, iliustruoti ją pavyzdžiais ir pateikti rinkinį treniruočių pratimai lavinti lygčių sprendimo įgūdžius naudojant šią techniką.

1. Paprasčiausias funkcijos įvertinimo metodas. Tegul a(x) yra kokia nors neneigiama funkcija, tada:

Jei f (x) = A + a (x), tai f (x) > A;

Jei f (x) = A - a (x), tada f (x)< А.

Pirmąjį metodą pavadinome paprasčiausiu, nes įvertinimas šiuo atveju yra praktiškai akivaizdus, ​​jei mokinys žino neneigiamų funkcijų aibę: 24x, x2", x~2", xa (kur-), |x|, |x| -x, arccosx, arc^x, ax ir tt Be to, bus naudojamos neneigiamos reikšmės sudėtingos funkcijos, kurios yra funkcijų sudėties rezultatas, jei paskutinė kompozicijos funkcija yra neneigiama. Taigi, neneigiamų funkcijų sąrašas gali būti

apibendrinti: 2^u(x), (u(x))2", (m(x))-2i, ageo8u(x), agccyoi(x), |u(x)|, |u(x) - u(x), a"(x), (u(x))a (kur k).

Pateiksime mini-max metodo panaudojimo pavyzdžius, kuriuos sprendžiant naudojama nagrinėjama įvertinimo technika.

1 pavyzdys. Išspręskite lygtį 2 + |x(x -1)| = 2 - ^(x -1) (x + 2) . Sprendimas. Funkcijos

/ (x) = |x(x -1)|, I (x) = 7 (x -1) (x + 2)

neneigiamas. Todėl turime tokį kairiosios ir dešiniosios lygties pusių įvertinimą

2 + | x(x -1)| > 2,

2-y/(x-1)(x + 2)< 2 "

Tada pagal 1 teiginį pradinė lygtis yra lygiavertė sistemai

Tada:

Jei funkcija f (u) didėja intervale, nelygybė galioja

f(a)< f (u(x)) < f (b);

Jei funkcija f (u) mažėja intervale, tai nelygybė galioja

f(b)< f (u(x)) < f (a) .

7 pavyzdys. Išspręskite lygtį log2 (x2 - 6x+11) = cos((x - 3) sin x).

Sprendimas. Viso kvadrato pasirinkimas kvadratinis trinaris, stovėdami po logaritmo ženklu, gauname lygtį

log2 (2+(x - 3)2) = cos((x - 3) sin x). Įvertinkime funkcijas kairėje ir teisingos dalysšią lygtį.

f (x) = log2 (2+(x - 3)2) > 1. Iš tiesų, 2 + (x - 3)2 > 2, funkcija log2 u didėja, todėl

log2 (2+(x - 3)2) > log2 2 = 1. Funkcija u2 monotoniškai didėja)