Ši internetinė matematikos skaičiuoklė jums padės išspręskite lygtį arba nelygybę su moduliais. Programa skirta sprendžiant lygtis ir nelygybes moduliais ne tik duoda atsakymą į problemą, bet ir veda išsamus sprendimas su paaiškinimais

, t.y. rodomas rezultato gavimo procesas. Ši programa gali būti naudinga besiruošiantiems vidurinių mokyklų mokiniams bandymai ir egzaminus, tikrinant žinias prieš Vieningą valstybinį egzaminą, tėvams kontroliuoti daugelio matematikos ir algebros uždavinių sprendimą. O gal jums per brangu samdyti dėstytoją ar pirkti naujus vadovėlius? O gal tiesiog norite tai padaryti kuo greičiau?

namų darbai matematikoje ar algebroje? Tokiu atveju taip pat galite naudoti mūsų programas su išsamiais sprendimais. Tokiu būdu galite vesti savo ir (arba) savo mokymus.

jaunesni broliai

ar seserys, o išsilavinimo lygis sprendžiamų problemų srityje kyla.

arba abs(x) – modulis x

Įveskite lygtį arba nelygybę su moduliais
x^2 + 2|x-1| -6 = 0
Išspręskite lygtį arba nelygybę

Buvo nustatyta, kad kai kurie scenarijai, reikalingi šiai problemai išspręsti, nebuvo įkelti ir programa gali neveikti.
Galbūt esate įjungę „AdBlock“.
Tokiu atveju išjunkite jį ir atnaujinkite puslapį.

Jūsų naršyklėje išjungtas JavaScript.
Kad sprendimas būtų rodomas, turite įjungti „JavaScript“.
Čia pateikiamos instrukcijos, kaip įjungti „JavaScript“ naršyklėje. Nes Yra daug žmonių, norinčių išspręsti problemą, jūsų prašymas buvo įrašytas į eilę.

Po kelių sekundžių apačioje pasirodys sprendimas. Palaukite sek...
Jeigu jūs pastebėjo sprendimo klaidą, tuomet apie tai galite parašyti atsiliepimų formoje. Nepamiršk.

nurodykite, kokia užduotis

tu spręsk ką

įveskite laukelius

Mūsų žaidimai, galvosūkiai, emuliatoriai: Šiek tiek teorijos., remiantis tuo, kad \(|x-a| \) yra atstumas skaičių tiesėje tarp taškų x ir a: \(|x-a| = \rho (x;\; a)\). Pavyzdžiui, norint išspręsti lygtį \(|x-3|=2\), skaičių tiesėje reikia rasti taškus, kurie yra nutolę nuo taško 3 2 atstumu. Tokie taškai yra du: \(x_1=1 \) ir \(x_2=5\) .

Nelygybės sprendimas \(|2x+7|

Tačiau pagrindinis būdas išspręsti lygtis ir nelygybes su moduliais yra susijęs su vadinamuoju „modulio atskleidimu pagal apibrėžimą“:
jei \(a \geq 0 \), tada \(|a|=a \);
if \(a Paprastai lygtis (nelygybė) su moduliais redukuojama į lygčių (nelygybių), kuriose nėra modulio ženklo, rinkinį.

Be pirmiau pateikto apibrėžimo, naudojami šie teiginiai:
1) Jei \(c > 0\), tada lygtis \(|f(x)|=c \) yra lygiavertė lygčių rinkiniui: \(\left[\begin(masyvas)(l) f(x) )=c \\ f(x)=-c \end(masyvas)\right.
2) Jei \(c > 0 \), tai nelygybė \(|f(x)| 3) Jei \(c \geq 0 \), tada nelygybė \(|f(x)| > c \) yra lygiavertis nelygybių rinkiniui: \(\left[\begin(masyvas)(l) f(x) c \end(masyvas)\right. \)
4) Jei abi nelygybės pusės \(f(x) PAVYZDYS 1. Išspręskite lygtį \(x^2 +2|x-1| -6 = 0\).

Jei \(x-1 \geq 0\), tada \(|x-1| = x-1\) ir duota lygtisįgauna formą
\(x^2 +2(x-1) -6 = 0 \Rodyklė dešinėn x^2 +2x -8 = 0 \).
Jei \(x-1 \(x^2 -2(x-1) -6 = 0 \Rodyklė dešinėn x^2 -2x -4 = 0 \).
Taigi, pateikta lygtis turėtų būti nagrinėjama atskirai kiekvienu iš dviejų nurodytų atvejų.
1) Tegu \(x-1 \geq 0 \), t.y. \(x\geq 1\). Iš lygties \(x^2 +2x -8 = 0\) randame \(x_1=2, \; x_2=-4\).
Sąlygą \(x \geq 1 \) tenkina tik reikšmė \(x_1=2\).

2) Tegul \(x-1 Atsakymas: \(2; \;\; 1-\sqrt(5) \)

2 PAVYZDYS. Išspręskite lygtį \(|x^2-6x+7| = \frac(5x-9)(3)\). Pirmas būdas
(modulio išplėtimas pagal apibrėžimą).

Samprotaudami kaip 1 pavyzdyje, darome išvadą, kad pateiktą lygtį reikia nagrinėti atskirai, jei tenkinamos dvi sąlygos: \(x^2-6x+7 \geq 0 \) arba \(x^2-6x+7 1) Jei \(x^2-6x+7 \geq 0 \), tada \(|x^2-6x+7| = x^2-6x+7 \) ir duota lygtis įgauna formą \(x ^2 -6x+7 = \frac(5x-9)(3) \Rodyklė dešinėn 3x^2-23x+30=0 \). Tai nusprendęs kvadratinė lygtis
, gauname: \(x_1=6, \; x_2=\frac(5)(3) \). Išsiaiškinkime, ar reikšmė \(x_1=6\) atitinka sąlygą \(x^2-6x+7 \geq 0\). Norėdami tai padaryti, pakeiskime nurodytą vertę V kvadratinė nelygybė
Išsiaiškinkime, ar reikšmė \(x_2=\frac(5)(3)\) atitinka sąlygą \(x^2-6x+7 \geq 0\). Norėdami tai padaryti, nurodytą reikšmę pakeiskite kvadratine nelygybe. Gauname: \(\left(\frac(5)(3) \right)^2 -\frac(5)(3) \cdot 6 + 7 \geq 0 \), t.y. \(\frac(25)(9) -3 \geq 0 \) yra neteisinga nelygybė. Tai reiškia, kad \(x_2=\frac(5)(3)\) nėra pateiktos lygties šaknis.

2) Jei \(x^2-6x+7 reikšmė \(x_3=3\) atitinka sąlygą \(x^2-6x+7 reikšmė \(x_4=\frac(4)(3) \) netenkina sąlyga \ (x^2-6x+7 Taigi duotoji lygtis turi dvi šaknis: \(x=6, \; x=3 \).

Antras būdas. Jei pateikta lygtis \(|f(x)| = h(x) \), tada su \(h(x) \(\left[\begin(masyvas)(l) x^2-6x+7 = \frac (5x-9)(3) \\ x^2-6x+7 = -\frac(5x-9)(3) \end (masyvas)\right \)
Abi šios lygtys buvo išspręstos aukščiau (naudojant pirmąjį pateiktos lygties sprendimo būdą), jų šaknys yra tokios: \(6,\; \frac(5)(3),\; 3,\; \frac(4 )(3)\). Šių keturių reikšmių sąlygą \(\frac(5x-9)(3) \geq 0 \) tenkina tik dvi: 6 ir 3. Tai reiškia, kad duota lygtis turi dvi šaknis: \(x=6 , \; x=3 \ ).

Trečias būdas(grafinis).
1) Sukurkime funkcijos \(y = |x^2-6x+7| \) grafiką. Pirmiausia sukurkime parabolę \(y = x^2-6x+7\).
Turime \(x^2-6x+7 = (x-3)^2-2 \). Funkcijos \(y = (x-3)^2-2\) grafiką galima gauti iš funkcijos \(y = x^2 \) grafiko, paslinkus jį 3 mastelio vienetais į dešinę (išilgai x ašimi) ir 2 mastelio vienetais žemyn ( išilgai y ašies).
Tiesė x=3 yra mus dominančios parabolės ašis. Kaip kontrolinius taškus tikslesniam braižymui patogu paimti tašką (3; -2) - parabolės viršūnę, tašką (0; 7) ir tašką (6; 7) simetriškus jam parabolės ašies atžvilgiu. . Norėdami dabar sukurti funkcijos \(y = |x^2-6x+7| \) grafiką, turite palikti nepakeistas tas sudarytos parabolės dalis, kurios yra ne žemiau x ašies, ir atspindėti tą parabolės dalį. parabolė, esanti žemiau x ašies x ašies atžvilgiu. 2) Sukurkime grafiką

tiesinė funkcija

\(y = \frac(5x-9)(3)\). Kontroliniais taškais patogu paimti taškus (0; –3) ir (3; 2).. Svarbu, kad tiesės ir abscisių ašies susikirtimo taškas x = 1,8 būtų dešinėje nuo kairiojo parabolės susikirtimo su abscisių ašimi taško – tai taškas \(x=3-\ sqrt(2) \) (nuo \(3-\sqrt(2 ) 3) Sprendžiant iš brėžinio, grafikai susikerta dviejuose taškuose - A(3; 2) ir B(6; 7). Pakeičiant šių abscises taškai x = 3 ir x = 6 į pateiktą lygtį, esame įsitikinę, kad abiem atvejais gaunama teisinga skaitinė lygybė. Tai reiškia, kad mūsų hipotezė pasitvirtino – lygtis turi dvi šaknis: x = 3 ir x = 6. Atsakymas: 3; Nepaisant visos savo elegancijos, jis nėra labai patikimas. Nagrinėjamame pavyzdyje tai veikė tik todėl, kad lygties šaknys yra sveikieji skaičiai.

3 PAVYZDYS. Išspręskite lygtį \(|2x-4|+|x+3| = 8\)

2 PAVYZDYS. Išspręskite lygtį \(|x^2-6x+7| = \frac(5x-9)(3)\).
Išraiška 2x–4 tampa 0 taške x = 2, o išraiška x + 3 – 0 taške x = –3. Šie du taškai padalija skaičių eilutę į tris intervalus: \(x

Apsvarstykite pirmąjį intervalą: \((-\infty; \; -3) \).
Jei x Apsvarstykite antrąjį intervalą: \([-3; \; 2) \).
Jei \(-3 \leq x Apsvarstykite trečiąjį intervalą: \( [ 3/2 ; ∞ )

Metodas lygiavertės transformacijos taip pat naudojome spręsdami lygtis | f(x)| = | g(x)|.

LYGTYBĖS SU KOMPLEKSINIU MODULIU

Kitas lygčių tipas yra lygtys su „sudėtingu“ moduliu. Tokios lygtys apima lygtis, kurios turi „modulius modulyje“. Šio tipo lygtis galima išspręsti naudojant įvairių metodų.

1 pavyzdys.

Išspręskite lygtį ||||x| – |–2| –1| –2| = 2.

Sprendimas.

Pagal modulio apibrėžimą turime:

Išspręskime pirmąją lygtį.

||| x |–2| –1| = 4

| x | – 2 = 5;

| x | = 7;

x = 7.

Išspręskime antrąją lygtį.

||| x | –2| –1| = 0,

|| x | –2| = 1,

| x | –2 = 1,

| x | = 3 ir | x | = 1,

x = 3; x = 1.

Atsakymas: 1; 3; 7.

2 pavyzdys.

Išspręskite lygtį |2 – |x + 1|| = 3.

Sprendimas.

Išspręskime lygtį įvesdami naują kintamąjį.

Tegul | x + 1| = y, tada |2 – y | = 3, iš čia

Atlikime atvirkštinį pakeitimą:

(1) | x + 1| = –1 – sprendinių nėra.

(2) | x + 1| = 5

ATSAKYMAS: –6; 4.

3 pavyzdys.

Kiek šaknų turi lygtis | 2 | x | -6 | = 5 - x?

Sprendimas. Išspręskime lygtį naudodami ekvivalentiškumo schemas.

Lygtis | 2 | x | -6 | = 5 atitinka sistemą:

MBOU 17 vidurinė mokykla, Ivanovas

« Lygtys su moduliu"
Metodinis tobulinimas

Sudaryta

matematikos mokytojas

Lebedeva N.V.

20010 m

Aiškinamasis raštas

1 skyrius. Įvadas

2 skyrius. Pagrindinės savybės 3 skyrius. Skaičiaus modulio sampratos geometrinis aiškinimas 4 skyrius. Funkcijos y = |x| grafikas 5 skyrius. Konvencijos

2 skyrius. Modulio turinčių lygčių sprendimas

1 skirsnis. Formos |F(x)| lygtys = m (paprasčiausias) 2 skyrius. F(|x|) = m formos lygtys 3 skirsnis. Formos |F(x)| lygtys = G(x) 4 skirsnis. Formos |F(x)| lygtys = ± F(x) (gražiausias) 5 skirsnis. Formos |F(x)| lygtys = |G(x)| 6 skyrius. Sprendimų pavyzdžiai nestandartinės lygtys 7 skirsnis. Formos |F(x)| lygtys + |G(x)| = 0 8 skirsnis. Formos |a 1 x ± b 1 | lygtys ± |a 2 x ± in 2 | ± …|a n x ± per n | = m 9 skyrius. Lygtys, susidedančios iš kelių modulių

3 skyrius. Įvairių lygčių su moduliu sprendimo pavyzdžiai.

1 skyrius. Trigonometrinės lygtys 2 skyrius. Eksponentinės lygtys 3 skyrius. Logaritminės lygtys 4 skyrius. Iracionaliosios lygtys 5 skyrius. Užduotys padidėjęs sudėtingumas Atsakymai į pratimus Nuorodos

Aiškinamasis raštas.

Realiojo skaičiaus absoliučios vertės (modulio) sąvoka yra viena iš esminių jo charakteristikų. Ši sąvoka plačiai paplitusi įvairiose fizinių, matematikos ir technikos mokslų srityse. Matematikos kursų dėstymo praktikoje m vidurinę mokyklą pagal Rusijos Federacijos gynybos ministerijos programą ne kartą susiduriama su „absoliučios skaičiaus vertės“ sąvoka: 6 klasėje supažindinama su modulio apibrėžimu ir jo geometrine reikšme; 8 klasėje formuojasi samprata absoliuti klaida, nagrinėjamas paprasčiausių modulį turinčių lygčių ir nelygybių sprendimas, tiriamos aritmetikos savybės kvadratinė šaknis; 11 klasėje sąvoka randama skyrelyje „Šaknis n– laipsnis“. Mokymo patirtis rodo, kad mokiniai dažnai susiduria su sunkumais spręsdami užduotis, reikalaujančias žinių apie šią medžiagą, ir dažnai jas praleidžia nepradėję jų atlikti. Tekstuose egzamino užduotis Panašios užduotys įtrauktos ir į 9 ir 11 klasių kursus. Be to, skiriasi ir reikalavimai, kuriuos universitetai kelia abiturientams, būtent daugiau aukšto lygio nei mokyklos programos reikalavimai. Už gyvenimąšiuolaikinė visuomenė Labai svarbu ugdyti matematinį mąstymo stilių, kuris pasireiškia tam tikrais protiniais įgūdžiais. Sprendžiant problemas su moduliais, reikia mokėti naudoti tokias technikas kaip apibendrinimas ir specifikavimas, analizė, klasifikavimas ir sisteminimas bei analogija. Sprendžiant tokias užduotis galima pasitikrinti savo žinias apie pagrindinius skyrius mokyklos kursas , lygis loginis mąstymas , pradiniai tyrimo įgūdžiai.Šis darbas yra skirtas vienam iš skyrių – lygčių, kuriose yra modulis, sprendimas. Jį sudaro trys skyriai . Pirmame skyriuje pateikiamos pagrindinės sąvokos ir svarbiausi teoriniai svarstymai. Antrame skyriuje siūlomi devyni pagrindiniai lygčių tipai su moduliu, aptariami jų sprendimo būdai ir nagrinėjami pavyzdžiai. skirtingi lygiai sudėtingumo. Trečiame skyriuje pateikiamos sudėtingesnės ir nestandartinės lygtys (trigonometrinės, eksponentinės, logaritminės ir neracionalios). Kiekvienam lygties tipui yra pratimų savarankiškas sprendimas (atsakymai ir instrukcijos pridedami). mokytojams ruošiantis pamokoms ir organizuojant pasirenkamuosius kursus. Medžiaga taip pat gali būti naudojama kaip mokymo priemonė gimnazijos mokiniams. Darbe siūlomos užduotys įdomios ir ne visada lengvai išsprendžiamos, o tai leidžia atlikti mokymosi motyvacija mokiniams tapti sąmoningesniems, pasitikrinti savo gebėjimus, gerinti abiturientų pasirengimo stojimui į universitetus lygį. Diferencijuotas siūlomų pratimų pasirinkimas apima perėjimą nuo reprodukcinio medžiagos įsisavinimo į kūrybinį lygį, taip pat galimybę išmokyti pritaikyti savo žinias sprendžiant nestandartines problemas.

1 skyrius. Įvadas.

1 skyrius. Absoliučios vertės nustatymas .

Apibrėžimas : Realiojo skaičiaus absoliuti reikšmė (modulis). A paskambino neneigiamas skaičius: A arba -A. Pavadinimas: │ A │ Įrašas skamba taip: „skaičiaus a modulis“ arba „absoliuti skaičiaus a reikšmė“

│ a, jei a > 0

│a│ = │ 0, jei a = 0 (1)

│ - ir jei a
Pavyzdžiai: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1
Išskleisti išraiškos modulį:
a) │x - 8│, jei x > 12 b) │2x + 3│, jei x ≤ -2 │x – 8│= x – 8 │ 2x + 3│= - 2x – 3
2 skyrius. Pagrindinės savybės.
Panagrinėkime pagrindines absoliučios vertės savybes. 1 nuosavybė: Yra priešingi skaičiai vienodi moduliai, t.y. │а│=│- а│ Parodykime, kad lygybė yra tiesa. Užrašykime skaičiaus apibrėžimą – A : │- a│= (2) Palyginkime aibes (1) ir (2). Akivaizdu, kad absoliučių skaičių reikšmių apibrėžimai A Ir – A rungtynės. Vadinasi, │а│=│- а│
Svarstant šias savybes Mes apsiribosime jų formulavimu, nes jų įrodymas yra pateiktas 2 nuosavybė: Absoliuti sumos vertė baigtinis skaičius realieji skaičiai neviršija terminų absoliučių verčių sumos: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │+ … + │а n │ 3 nuosavybė: Dviejų realiųjų skaičių skirtumo absoliuti reikšmė neviršija jų absoliučių verčių sumos: │а - в│ ≤│а│+│в│ 4 nuosavybė: Baigtinio realiųjų skaičių sandaugos absoliuti vertė yra lygi faktorių absoliučių verčių sandaugai: │а·в│=│а│·│в│ 5 nuosavybė: Realiųjų skaičių dalinio absoliuti reikšmė yra lygi jų absoliučių dydžių daliniui:

3 skyrius. Skaičiaus modulio sampratos geometrinis aiškinimas.

Kiekvienas tikrasis skaičius gali būti susietas su skaičių linijos tašku, kuris bus geometrinis vaizdas duotas tikrasis skaičius. Kiekvienas skaičių linijos taškas atitinka jo atstumą nuo pradžios, t.y. atkarpos ilgis nuo pradžios iki nurodyto taško. Šis atstumas visada laikomas neneigiama reikšme. Todėl atitinkamo segmento ilgis bus geometrinė interpretacija absoliuti tam tikro tikrojo skaičiaus vertė

Pateikta geometrinė iliustracija aiškiai patvirtina savybę Nr.1, t.y. moduliai priešingi skaičiai yra lygūs. Iš čia nesunkiai suprantamas lygybės pagrįstumas: │х – а│= │а – x│. Lygties │х│= m, kur m ≥ 0, ty x 1,2 = ± m, sprendimas taip pat tampa akivaizdesnis. Pavyzdžiai: 1) │х│ = 4 x 1,2 = ± 4 2) │х - 3│ = 1

x 1,2 = 2; 4

4 skyrius. Funkcijos y = │х│ grafikas

Šios funkcijos sritis yra visi realieji skaičiai.

5 skyrius. Konvencijos.

Ateityje, svarstant lygčių sprendimo pavyzdžius, bus naudojami šie simboliai: ( - sistemos ženklas [ - visumos ženklas Sprendžiant lygčių (nelygybių) sistemą, randama į sistemą įtrauktų lygčių (nelygybių) sprendinių sankirta. Sprendžiant lygčių (nelygybių) aibę, randama į lygčių (nelygybių) aibę įtrauktų sprendinių sąjunga.

2 skyrius. Modulio turinčių lygčių sprendimas.

Šiame skyriuje apžvelgsime algebriniai metodai sprendžiant lygtis, turinčias vieną ar daugiau modulių.

1 skyrius. Formos lygtys │F (x)│= m

Tokio tipo lygtis vadinama paprasčiausia. Jis turi sprendimą tada ir tik tada, kai m ≥ 0. Pagal modulio apibrėžimą pradinė lygtis yra lygiavertė dviejų lygčių rinkiniui: │ F(x)│=m

Pavyzdžiai:
№1. Išspręskite lygtį: │7х - 2│= 9

Atsakymas: x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

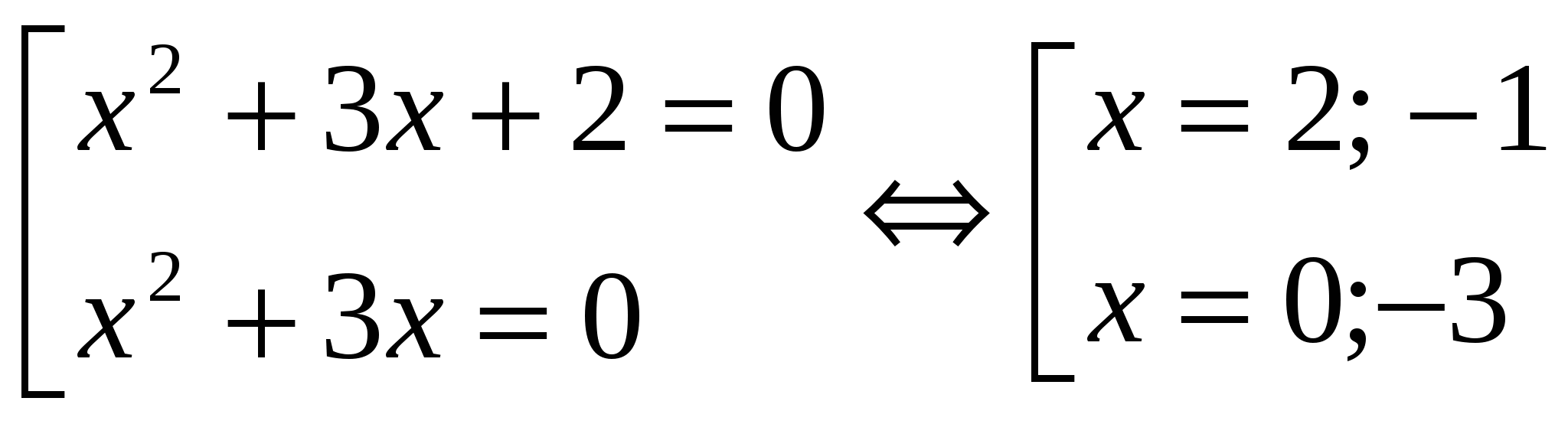x 2 + 3x + 2 = 0 x 2 + 3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Atsakymas: šaknų suma yra - 2.№3
│x 4 -5x 2 + 2│ = 2 x 4 - 5x 2 = 0 x 4 - 5x 2 + 4 = 0 x 2 (x 2 - 5) = 0 pažymėkime x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – abi reikšmės tenkina sąlygą m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Atsakymas: 7 lygties šaknų skaičius. Pratimai:
№1. Išspręskite lygtį ir nurodykite šaknų sumą: │х - 5│= 3 №2 . Išspręskite lygtį ir nurodykite mažesnę šaknį: │x 2 + x│= 0 №3 . Išspręskite lygtį ir nurodykite didesnę šaknį: │x 2 – 5x + 4│= 4 №4 .Išspręskite lygtį ir nurodykite visa šaknis: │2x 2 – 7x + 6│= 1 №5 .Išspręskite lygtį ir nurodykite šaknų skaičių: │x 4 – 13x 2 + 50│= 14

2 skyrius. Formos lygtys F(│х│) = m

Funkcijos argumentas kairėje pusėje yra po modulio ženklu, o dešinioji pusė nepriklauso nuo kintamojo. Panagrinėkime du būdus, kaip išspręsti tokio tipo lygtis. 1 būdas: Pagal absoliučios vertės apibrėžimą pradinė lygtis yra lygiavertė dviejų sistemų deriniui. Kiekviename iš jų submodulinei išraiškai yra nustatyta sąlyga. F(│x│) =m

Kadangi funkcija F(│x│) yra lygi visoje apibrėžimo srityje, lygčių F(x) = m ir F(- x) = m šaknys yra priešingų skaičių poros. Todėl pakanka išspręsti vieną iš sistemų (taip nagrinėjant pavyzdžius, bus pateiktas vienos sistemos sprendimas). 2 būdas: Naujo kintamojo įvedimo metodo taikymas. Šiuo atveju įvedamas žymėjimas │x│= a, kur a ≥ 0. Šis metodas mažiau tūrinio dizaino.
Pavyzdžiai: №1 . Išspręskite lygtį: 3x 2 – 4│x│= - 1 Pasinaudokime naujo kintamojo įvedimu. Pažymime │x│= a, kur a ≥ 0. Gauname lygtį 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Grįžti į pradinį kintamąjį: │ x│=1 ir │х│= 1/3. Kiekviena lygtis turi dvi šaknis. Atsakymas: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Išspręskite lygtį: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2

Raskime pirmosios visumos sistemos sprendimą: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Atkreipkite dėmesį, kad x 2 netenkina sąlyga x ≥ 0. Sprendimas antroji sistema bus skaičius, priešinga prasmė x 1. Atsakymas: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Išspręskite lygtį: x 4 – │х│= 0 Pažymime │х│= a, kur a ≥ 0. Gauname lygtį a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Grįžti į pradinį kintamąjį: │х│=0 ir │х│= 1 x = 0; ± 1 Atsakymas: x 1 = 0; X 2 = 1; X 3 = - 1.
Pratimai: №6. Išspręskite lygtį: 2│х│ - 4,5 = 5 - 3 / 8 │х│ №7 . Išspręskite lygtį, savo atsakyme nurodykite šaknų skaičių: 3x 2 - 7│x│ + 2 = 0 №8 . Išspręskite lygtį, atsakyme nurodykite sveikuosius sprendinius: x 4 + │x│ - 2 = 0

3 skyrius. Formos lygtys │F(x)│ = G(x)

Dešinė tokio tipo lygties pusė priklauso nuo kintamojo, todėl turi sprendimą tada ir tik tada, kai dešinioji yra funkcija G(x) ≥ 0. Pradinė lygtis gali būti sprendžiama dviem būdais. : 1 būdas: Standartas, pagrįstas modulio atskleidimu remiantis jo apibrėžimu ir susidedantis iš lygiaverčio perėjimo prie dviejų sistemų derinio. │ F(x)│ =G(X)

Šis metodas gali būti racionaliai naudojamas tuo atveju sudėtinga išraiška funkcijai G(x) ir mažiau sudėtingai - funkcijai F(x), nes daroma prielaida, kad nelygybės išsprendžiamos funkcija F(x). 2 būdas: Susideda iš perėjimo prie lygiavertės sistemos, kurioje sąlyga yra nustatyta dešinėje pusėje. │ F(x)│= G(x)

Šį metodą patogiau naudoti, jei funkcijos G(x) išraiška yra mažiau sudėtinga nei funkcijos F(x), nes nelygybės G(x) ≥ 0 sprendimas. Be to, tuo atveju iš kelių modulių, rekomenduojama naudoti antrąjį variantą. Pavyzdžiai: №1. Išspręskite lygtį: │x + 2│= 6 -2x

(1 kryptis) Atsakymas: x = 1 1 / 3 №2.
│х 2 – 2х - 1│= 2·(x + 1)

(2 kryptimis) Atsakymas: šaknų sandauga yra 3.
№3. Išspręskite lygtį ir savo atsakyme nurodykite šaknų sumą:
│x – 6│= x 2 – 5x + 9

Atsakymas: šaknų suma yra 4.
Pratimai: №9. │x + 4│= - 3x №10. Išspręskite lygtį, savo atsakyme nurodykite sprendinių skaičių:│x 2 + x - 1│= 2x – 1 №11 . Išspręskite lygtį, savo atsakyme nurodykite šaknų sandaugą:│x + 3│= x 2 + x – 6

4 skyrius. Formos lygtys │F(x)│= F(x) ir │F(x)│= - F(x)

Šio tipo lygtys kartais vadinamos „gražiausiomis“. Kadangi dešinioji lygčių pusė priklauso nuo kintamojo, sprendiniai egzistuoja tada ir tik tada, kai dešinioji pusė yra neneigiama. Todėl pradinės lygtys yra lygiavertės nelygybėms:
│F(x)│= F(x) F(x) ≥ 0 ir │F(x)│= - F(x) F(x) Pavyzdžiai: №1 . Išspręskite lygtį, savo atsakyme nurodykite mažesnę visą šaknį: │5x - 3│= 5x - 3 5x - 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Atsakymas: x = 1№2. Išspręskite lygtį, atsakyme nurodykite intervalo ilgį: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Atsakymas: intervalo ilgis yra 6.№3 . Išspręskite lygtį ir savo atsakyme nurodykite sveikųjų skaičių sprendinių skaičių: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Atsakymas: 4 sveiki sprendimai.№4 . Išspręskite lygtį ir nurodykite savo atsakyme didžiausia šaknis:
│4 – x –

│= 4 – x –

x 2 – 5x + 5 = 0 D = 5 x 1,2 =

≈ 1,4

Atsakymas: x = 3.

Pratimai: №12. Išspręskite lygtį, savo atsakyme nurodykite visą šaknį: │x 2 + 6x + 8│= x 2 + 6x + 8 №13. Išspręskite lygtį, savo atsakyme nurodykite sveikųjų skaičių sprendinių skaičių: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. Atsakyme išspręskite lygtį, nurodykite sveikąjį skaičių, kuris nėra lygties šaknis:

5 skyrius. Formos lygtys │F(x)│= │G(x)│

Kadangi abi lygties pusės yra neneigiamos, sprendimas apima du atvejus: submodulinės išraiškos yra lygios arba priešingos. Todėl pradinė lygtis yra lygiavertė dviejų lygčių deriniui: │ F(x)│= │ G(x)│

Pavyzdžiai: №1. Išspręskite lygtį, savo atsakyme nurodykite visą šaknį: │x + 3│=│2x - 1│

Atsakymas: visa šaknis x = 4.№2. Išspręskite lygtį: │ x – x 2 – 1│=│2x – 3 – x 2 │

Atsakymas: x = 2.№3 . Išspręskite lygtį ir savo atsakyme nurodykite šaknų sandaugą:

Šakninės lygtys 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Atsakymas: šaknų sandauga – 0,25. Pratimai: №15 . Išspręskite lygtį ir savo atsakyme nurodykite visą sprendimą: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16. Išspręskite lygtį, atsakyme nurodykite mažesnę šaknį:│5x - 3│=│7 - x│ №17 . Išspręskite lygtį ir savo atsakyme nurodykite šaknų sumą:

6 skyrius. Nestandartinių lygčių sprendimo pavyzdžiai

IN šį skyrių Nagrinėsime nestandartinių lygčių pavyzdžius, kurias sprendžiant apibrėžimu atskleidžiama absoliuti išraiškos reikšmė. Pavyzdžiai:

№1. Išspręskite lygtį, savo atsakyme nurodykite šaknų sumą: x · │x│- 5x – 6 = 0
Atsakymas: šaknų suma yra 1 №2. . Išspręskite lygtį, savo atsakyme nurodykite mažesnę šaknį: x 2 - 4x ·
- 5 = 0
Atsakymas: mažesnė šaknis x = - 5. №3. Išspręskite lygtį:

Atsakymas: x = -1. Pratimai: №18. Išspręskite lygtį ir nurodykite šaknų sumą: x · │3x + 5│= 3x 2 + 4x + 3
№19. Išspręskite lygtį: x 2 – 3x =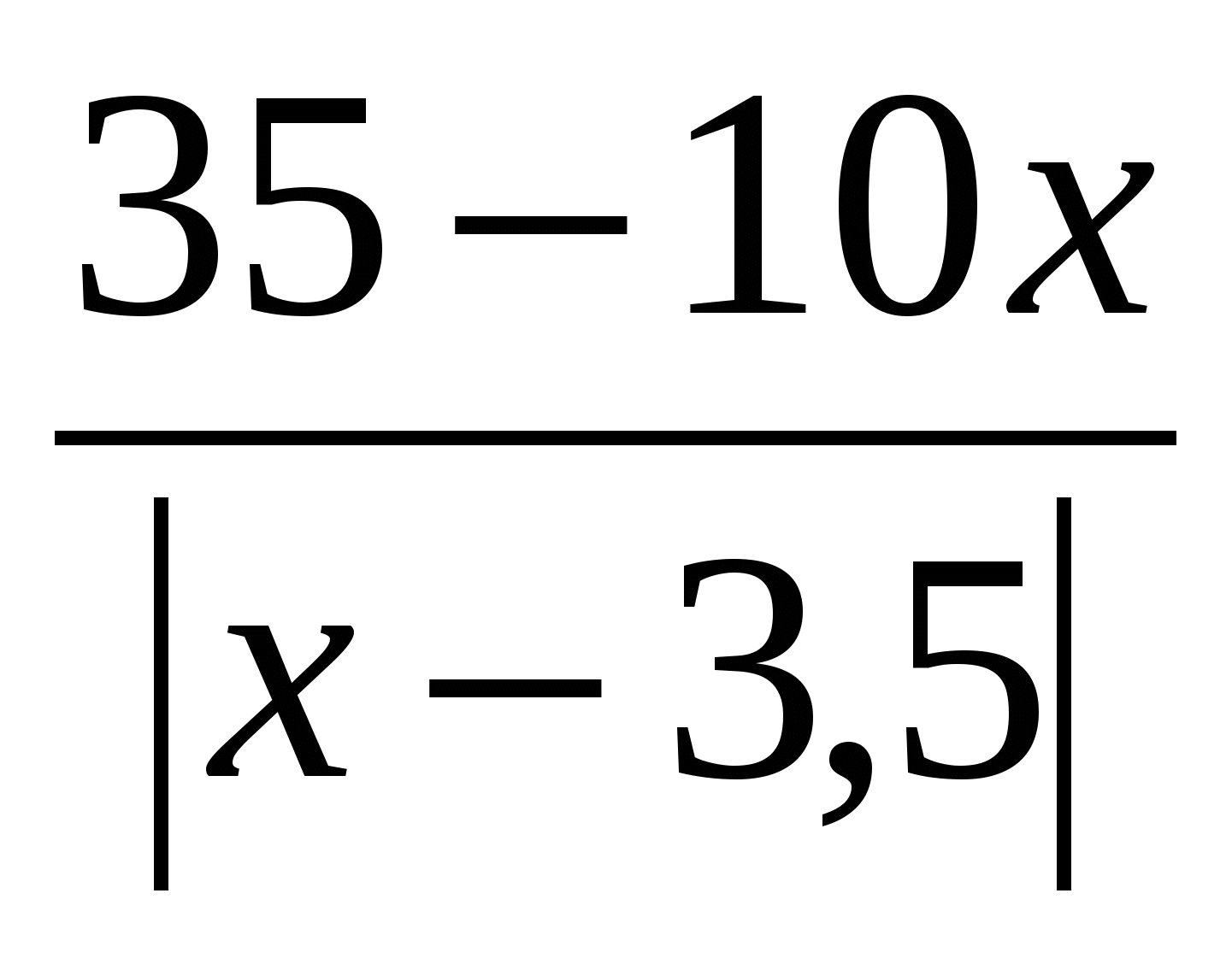

№20. Išspręskite lygtį:

7 skyrius. Formos │F(x)│+│G(x)│=0 lygtys

Nesunku pastebėti, kad kairėje šio tipo lygties pusėje yra neneigiamų dydžių suma. Todėl pradinė lygtis turi sprendimą tada ir tik tada, kai abu terminai yra lygūs nuliui tuo pačiu metu. Lygtis yra lygiavertė lygčių sistemai: │ F(x)│+│ G(x)│=0
Pavyzdžiai: №1 . Išspręskite lygtį:

Atsakymas: x = 2. №2. Išspręskite lygtį: Atsakymas: x = 1. Pratimai: №21. Išspręskite lygtį: №22 . Išspręskite lygtį ir savo atsakyme nurodykite šaknų sumą: №23 . Išspręskite lygtį ir savo atsakyme nurodykite sprendimų skaičių:

8 skyrius. Formos lygtys │a 1 x + b 1 │±│a 2 x + b 2 │± ... │a n x +b n │= m

Šio tipo lygtims išspręsti naudojamas intervalų metodas. Jei ją išspręsime nuosekliai plečiant modulius, gausime n sistemų rinkinius, o tai labai sudėtinga ir nepatogu. Panagrinėkime intervalų metodo algoritmą: 1). Raskite kintamąsias reikšmes X, kuriame kiekvienas modulis lygus nuliui(submodulinių išraiškų nuliai):

2). Rastas reikšmes pažymėkite skaičių eilutėje, kuri yra padalinta į intervalus (intervalų skaičius yra atitinkamai lygus n+1 ) 3). Nustatykite, kokiu ženklu atskleidžiamas kiekvienas modulis kiekviename iš gautų intervalų (darydami sprendimą, galite naudoti skaičių eilutę, pažymėdami joje esančius ženklus) 4). Pradinė lygtis yra lygiavertė visumai n+1 sistemos, kurių kiekvienoje nurodoma kintamojo priklausymas X vienas iš intervalų. Pavyzdžiai: №1 . Išspręskite lygtį ir savo atsakyme nurodykite didžiausią šaknį:

1). Raskime submodulinių reiškinių nulius: x = 2; x = -3 2). Pažymėkime rastas reikšmes skaičių eilutėje ir nustatykime, kokiu ženklu kiekvienas modulis atskleidžiamas gautuose intervaluose:
x – 2 x – 2 x – 2 – + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)

- sprendinių nėra. Lygtis turi dvi šaknis. Atsakymas: didžiausia šaknis x = 2. №2. Išspręskite lygtį ir savo atsakyme pateikite visą šaknį:

1). Raskime submodulinių reiškinių nulius: x = 1,5; x = - 1 2). Pažymėkime rastas reikšmes skaičių eilutėje ir nustatykime, kokiu ženklu kiekvienas modulis atskleidžiamas gautuose intervaluose: x + 1 x + 1 x + 1 - + +
-1 1,5 x 2x - 3 2x - 3 2x - 3 - - +
3).

Naujausia sistema neturi sprendinių, todėl lygtis turi dvi šaknis. Spręsdami lygtį, turėtumėte atkreipti dėmesį į „-“ ženklą prieš antrąjį modulį. Atsakymas: visa šaknis x = 7. №3. Išspręskite lygtį, savo atsakyme nurodykite šaknų sumą: 1). Raskime submodulinių reiškinių nulius: x = 5; x = 1; x = - 2 2). Skaičių eilutėje pažymėkime rastas reikšmes ir nustatykime, kokiu ženklu atskleidžiamas kiekvienas modulis gautais intervalais: x – 5 x – 5 x – 5 x – 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).

Lygtis turi dvi šaknis x = 0 ir 2. Atsakymas: šaknų suma yra 2. №4 . Išspręskite lygtį: 1). Raskime submodulinių reiškinių nulius: x = 1; x = 2; x = 3. 2). Nustatykime, kokiu ženklu kiekvienas modulis atskleidžiamas gautuose intervaluose. 3).

Sujungkime pirmojo sprendinius trys sistemos. Atsakymas: ; x = 5.
Pratimai: №24. Išspręskite lygtį:

№25. Išspręskite lygtį ir savo atsakyme nurodykite šaknų sumą: №26. Išspręskite lygtį ir savo atsakyme nurodykite mažesnę šaknį: №27. Išspręskite lygtį ir savo atsakyme nurodykite didesnę šaknį:

9 skyrius. Lygtys, susidedančios iš kelių modulių

Lygtys, kuriose yra keli moduliai, daro prielaidą, kad submodulinėse išraiškose yra absoliučios vertės. Pagrindinis tokio tipo lygčių sprendimo principas yra nuoseklus modulių atskleidimas, pradedant nuo „išorinio“. Sprendžiant naudojamos technikos, aptartos skyriuose Nr.1, Nr.3.

Pavyzdžiai: №1. Išspręskite lygtį:
Atsakymas: x = 1; – 11. №2. Išspręskite lygtį:
Atsakymas: x = 0; 4; – 4. №3. Išspręskite lygtį ir savo atsakyme nurodykite šaknų sandaugą:
Atsakymas: šaknų sandauga yra – 8. №4. Išspręskite lygtį:
Pažymėkime populiacijos lygtis (1) Ir (2) ir apsvarstykite kiekvieno iš jų sprendimą atskirai, kad būtų lengviau kurti. Kadangi abiejose lygtyse yra daugiau nei vienas modulis, patogiau atlikti lygiavertį perėjimą prie sistemų rinkinių. (1)

(2)

Atsakymas:
Pratimai: №36. Išspręskite lygtį, savo atsakyme nurodykite šaknų sumą: 5 │3x-5│ = 25 x №37. Išspręskite lygtį, jei yra daugiau nei viena šaknis, savo atsakyme nurodykite šaknų sumą: │x + 2│ x – 3x – 10 = 1 №38. Išspręskite lygtį: 3 │2х -4│ = 9 │х│ №39. Išspręskite lygtį, atsakyme nurodykite šaknų skaičių: 2 │ sin x│ = √2 №40 . Išspręskite lygtį ir savo atsakyme nurodykite šaknų skaičių:

3 skyrius. Logaritminės lygtys.

Prieš sprendžiant šias lygtis, būtina apžvelgti logaritmų savybes ir logaritminė funkcija. Pavyzdžiai: №1. Išspręskite lygtį, savo atsakyme nurodykite šaknų sandaugą: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ – 1

1 atvejis: jei x ≥ - 1, tai log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – tenkina sąlygą x ≥ - 1 2 atvejis: jei x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – atitinka x - 1 sąlygą
Atsakymas: šaknų sandauga yra – 15.
№2. Išspręskite lygtį, savo atsakyme nurodykite šaknų sumą: lg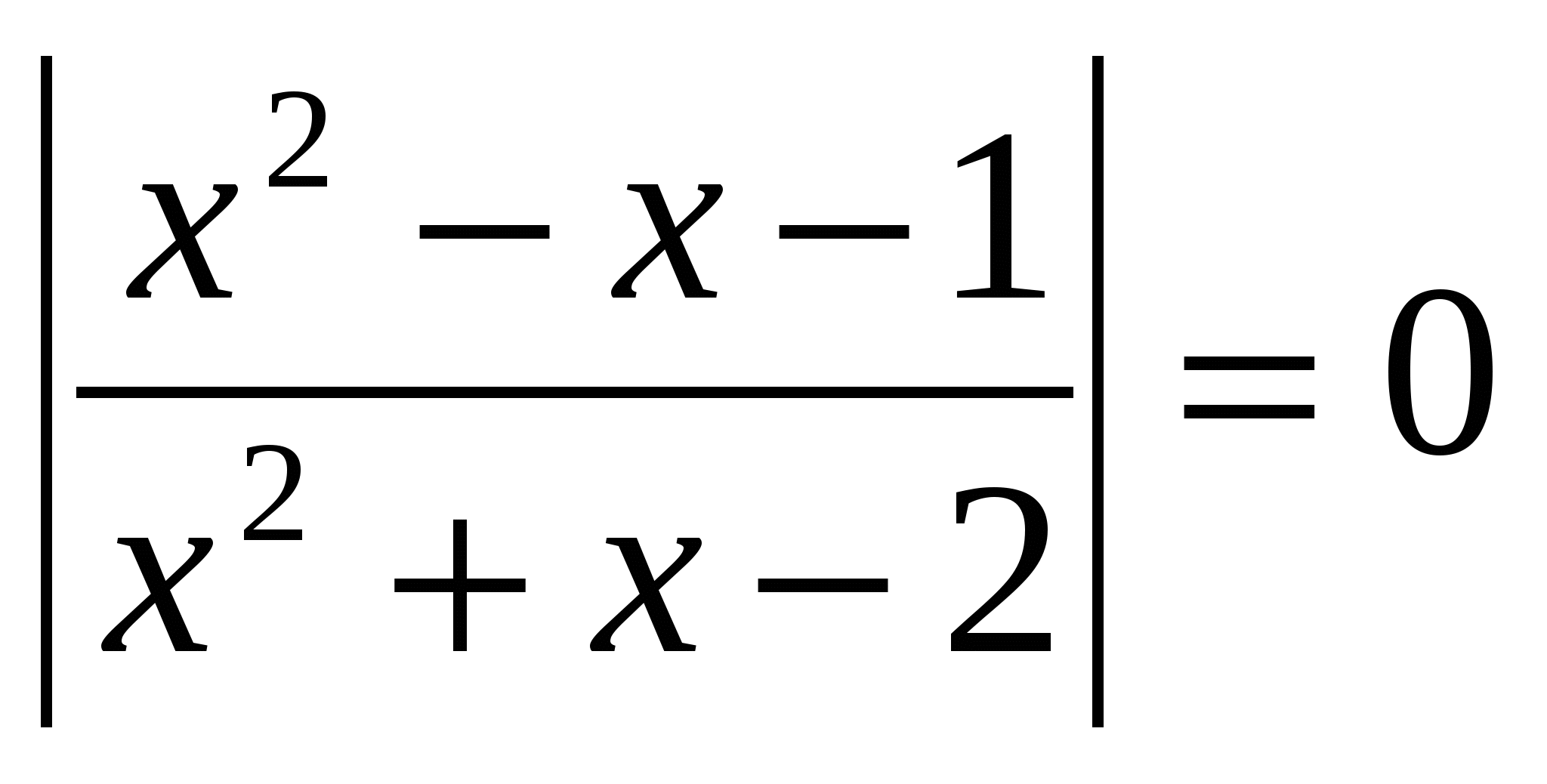
O.D.Z.

Atsakymas: šaknų suma lygi 0,5.
№3. Išspręskite lygtį: log 5
O.D.Z.

Atsakymas: x = 9. №4. Išspręskite lygtį: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Perėjimo į kitą bazę formulę naudokime. │2 – log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Raskime submodulinių reiškinių nulius: x = 25; x = Šie skaičiai padalija plotą priimtinos vertėsį tris intervalus, todėl lygtis yra lygiavertė trijų derinys sistemos
Atsakymas:)