જરૂરી સંખ્યા મળી છે: a 0 = k − 1 (\displaystyle a_(0)=k-1).

બીજી વખત આર્કિમિડીઝના સ્વયંસિદ્ધનો ઉપયોગ એ સાબિત કરવા માટે કરવામાં આવ્યો હતો કે ક્રમના ભાગોની લંબાઈ શૂન્ય તરફ વળે છે I 0 , I 1 , I 2 , … (\displaystyle I_(0),I_(1),I_(2),\ldots ):

આ દરખાસ્તનો સખત પુરાવો આર્કિમિડીઝના સ્વયંસિદ્ધ પર આધારિત છે. ચાલો સમકક્ષ સંબંધ સાબિત કરીએ

આર્કિમિડીઝના સ્વયંસિદ્ધ અનુસાર, વાસ્તવિક સંખ્યા ગમે તે હોય E > 0 (\Displaystyle E>0), કુદરતી સંખ્યાઓનો ક્રમ 1 , 2 , … (\displaystyle 1,2,\ldots )ચોક્કસ સંખ્યાથી શરૂ કરીને તેને વટાવી જશે. અને ત્યારથી દરેક માટે n (\Displaystyle n)અસમાનતા છે

પછી ક્રમ 10 n (\Displaystyle 10^(n))પણ વટાવી જશે E (\Displaystyle E), સમાન નંબરથી શરૂ થાય છે. સંખ્યા ક્રમની વ્યાખ્યા અનુસાર, આનો અર્થ એ થાય છે લિમ n → ∞ 10 n = ∞ (\displaystyle \lim _(n\to \infty )10^(n)=\infty ).

દશાંશ અસ્પષ્ટતા

ઉપરોક્ત અલ્ગોરિધમનો ઉપયોગ કરીને, આપણે કોઈપણ વાસ્તવિક સંખ્યા માટે કરી શકીએ છીએ α (\Displaystyle \alpha )આપેલ સંખ્યા દર્શાવતો દશાંશ અપૂર્ણાંક બનાવો. જો કે, એવું થઈ શકે છે કે તે જ નંબર α (\Displaystyle \alpha )દશાંશ અપૂર્ણાંક તરીકે અને અન્ય રીતે રજૂ કરી શકાય છે.

દશાંશ અપૂર્ણાંકના સ્વરૂપમાં સંખ્યાઓને રજૂ કરવાની બિન-વિશિષ્ટતા પહેલાથી જ નજીવી હકીકતને અનુસરે છે કે અંતિમ અપૂર્ણાંકને દશાંશ બિંદુ પછી જમણી બાજુએ શૂન્ય સોંપવાથી, આપણે સમાન સંખ્યાને રજૂ કરતા ઔપચારિક રીતે અલગ દશાંશ અપૂર્ણાંક મેળવીશું.

ઉદાહરણ તરીકે દશાંશ અપૂર્ણાંકનો વિચાર કરો

વ્યાખ્યા દ્વારા, આ અપૂર્ણાંક સંખ્યાનું પ્રતિનિધિત્વ છે 0 + 9 / 10 + 9 / 100 + … = 1 (\displaystyle 0+9/10+9/100+\ldots =1). જો કે, આ સંખ્યાને દશાંશ અપૂર્ણાંક તરીકે પણ રજૂ કરી શકાય છે 1 , 00 … (\displaystyle 1(,)00\ldots ).

આ ઉદાહરણ સામાન્ય કરી શકાય છે. તે બતાવી શકાય છે કે અપૂર્ણાંક

જ્યાં a n ≠ 9 (\displaystyle a_(n)\neq 9), સમાન વાસ્તવિક સંખ્યાનું પ્રતિનિધિત્વ કરો.

તે તારણ આપે છે કે આ સામાન્ય ઉદાહરણ દશાંશ અપૂર્ણાંકના સ્વરૂપમાં વાસ્તવિક સંખ્યાઓની રજૂઆતમાં અસ્પષ્ટતાના તમામ કેસોને સમાપ્ત કરે છે. આ કિસ્સામાં, અમે, અલબત્ત, એકબીજાના અંતમાં શૂન્ય ઉમેરીને મેળવેલા અપૂર્ણાંકના તુચ્છ કિસ્સાઓ, તેમજ અપૂર્ણાંકની જોડી અને .

આ પરિણામોને નીચેના પ્રમેયમાં સારાંશ આપી શકાય છે.

પ્રમેય. કોઈપણ વાસ્તવિક સંખ્યા α (\Displaystyle \alpha ), ફોર્મમાં રજૂ કરી શકાય તેવું નથી p/10 s (\displaystyle p/10^(s)), ક્યાં p (\Displaystyle p)- સમગ્ર, s (\ ડિસ્પ્લેસ્ટાઈલ ઓ)— બિન-નકારાત્મક પૂર્ણાંક, દશાંશ અપૂર્ણાંકના સ્વરૂપમાં એક જ રજૂઆતને સ્વીકારે છે; તદુપરાંત, આ અપૂર્ણાંક અનંત છે.

ફોર્મની કોઈપણ વાસ્તવિક સંખ્યા α = p/10 s (\displaystyle \alpha =p/10^(s))એક કરતાં વધુ રીતે દશાંશ તરીકે રજૂ કરી શકાય છે. જો α ≠ 0 (\displaystyle \alpha \neq 0), પછી તે કાં તો મર્યાદિત દશાંશ અપૂર્ણાંક તરીકે રજૂ કરી શકાય છે, તેમજ દશાંશ બિંદુ પછી અંતમાં શૂન્ય ઉમેરીને મેળવવામાં આવેલ અનંત અપૂર્ણાંક તરીકે અથવા . નંબર α = 0 (\Displaystyle \alpha =0)ફોર્મના અપૂર્ણાંક દ્વારા રજૂ કરી શકાય છે + 0 , 00 … (\displaystyle +0(,)00\ldots ), તેમજ ફોર્મના અપૂર્ણાંક − 0 , 00 … (\displaystyle -0(,)00\ldots ).

ટિપ્પણી. અંતમાં અનંત અપૂર્ણાંક 999 … (\displaystyle 999\ldots ), પ્રાપ્ત થાય છે જો ઉપરોક્ત અલ્ગોરિધમમાં આપણે હંમેશા પસંદ કરીએ છીએ ડાબો ભાગતેના બદલે અધિકાર.

વધારાના શૂન્ય અને ભૂલ

એ નોંધવું જોઈએ કે, દૃષ્ટિકોણથી, અંતમાં શૂન્ય સાથે દશાંશ અપૂર્ણાંક લખવું એ આ શૂન્ય વિના લખવા માટે સંપૂર્ણપણે સમાન નથી.

તે સામાન્ય રીતે સ્વીકારવામાં આવે છે કે જો ભૂલ ઉલ્લેખિત નથી, તો દશાંશ અપૂર્ણાંક વત્તા અથવા ઓછા અડધા [ ] છેલ્લા લખેલા અંકના એકમો. ઉદાહરણ તરીકે, “3.7” લખવાનો અર્થ છે કે સંપૂર્ણ ભૂલ ±0.05 છે. અને એન્ટ્રી "3.700" માં સંપૂર્ણ ભૂલ ±0.0005 છે. અન્ય ઉદાહરણો:

• "25" - સંપૂર્ણ ભૂલ ±0.5 છે (પણ, આવી એન્ટ્રીનો અર્થ 25 નું ચોક્કસ મૂલ્ય હોઈ શકે છે: ઉદાહરણ તરીકે, 25 ટુકડાઓ);
• "25.0" - સંપૂર્ણ ભૂલ ±0.05 છે;
• “25.00”—સંપૂર્ણ ભૂલ ±0.005 છે.

સામયિક દશાંશ

અનંત દશાંશ અપૂર્ણાંક કહેવાય છે સામયિક, જો દશાંશ બિંદુ પછી તેના અંકોનો ક્રમ, ચોક્કસ સ્થાનથી શરૂ થતો હોય, તો તે અંકોનો સમયાંતરે પુનરાવર્તિત જૂથ છે. બીજા શબ્દોમાં કહીએ તો, સામયિક અપૂર્ણાંક એ ફોર્મનો દશાંશ અપૂર્ણાંક છે

આ અપૂર્ણાંક સામાન્ય રીતે ફોર્મમાં સંક્ષિપ્તમાં લખવામાં આવે છે

સંખ્યાઓનું પુનરાવર્તિત જૂથ b 1 … b l (\ displaystyle b_(1)\ldots b_(l))કહેવાય છે સમયગાળોઅપૂર્ણાંક, આ જૂથમાં અંકોની સંખ્યા એ સમયગાળાની લંબાઈ છે.

જો સામયિક અપૂર્ણાંકમાં સમયગાળો દશાંશ બિંદુ પછી તરત જ આવે છે, તો અપૂર્ણાંક કહેવામાં આવે છે શુદ્ધ સામયિક. જો દશાંશ બિંદુ અને પ્રથમ અવધિ વચ્ચે સંખ્યાઓ હોય, તો અપૂર્ણાંક કહેવામાં આવે છે મિશ્ર સામયિક, અને પ્રથમ પીરિયડ ચિહ્ન પહેલાં દશાંશ બિંદુ પછીના અંકોનું જૂથ છે પૂર્વ સમયગાળોઅપૂર્ણાંક ઉદાહરણ તરીકે, અપૂર્ણાંક 1 , (23) = 1.232 3 … (\displaystyle 1(,)(23)=1(,)2323\ldots )શુદ્ધ સામયિક છે, અને અપૂર્ણાંક 0 , 1 (23) = 0.123 23 … (\displaystyle 0(,)1(23)=0(,)12323\ldots )- મિશ્ર સામયિક.

સામયિક અપૂર્ણાંકની મુખ્ય મિલકત, જેના કારણે તેઓ દશાંશ અપૂર્ણાંકના સમગ્ર સમૂહથી અલગ પડે છે, તે સામયિક અપૂર્ણાંક છે અને માત્ર તેઓ જ રજૂ કરે છે. વધુ સ્પષ્ટ રીતે, નીચેની દરખાસ્ત ધરાવે છે.

પ્રમેય. દરેક અનંત સામયિક દશાંશ અપૂર્ણાંક તર્કસંગત સંખ્યા દર્શાવે છે. તેનાથી વિપરીત, જો તર્કસંગત સંખ્યાને અનંત દશાંશ અપૂર્ણાંકમાં વિસ્તૃત કરવામાં આવે છે, તો આ અપૂર્ણાંક સામયિક છે.

તે બતાવી શકાય છે કે સંપૂર્ણ સામયિક અપૂર્ણાંક તર્કસંગત સંખ્યાઓને અનુરૂપ હોય છે, જે અફર અપૂર્ણાંક તરીકે લખવામાં આવે છે. p/q (\displaystyle p/q)છેદ q (\displaystyle q) પાસે નથી

આ લેખમાં આપણે અન્વેષણ કરવાનું શરૂ કરીશું તર્કસંગત સંખ્યાઓ. અહીં આપણે તર્કસંગત સંખ્યાઓની વ્યાખ્યા આપીશું, જરૂરી સમજૂતી આપીશું અને તર્કસંગત સંખ્યાઓના ઉદાહરણો આપીશું. આ પછી, આપણે આપેલ સંખ્યા તર્કસંગત છે કે નહીં તે કેવી રીતે નક્કી કરવું તેના પર ધ્યાન કેન્દ્રિત કરીશું.

પૃષ્ઠ નેવિગેશન.

તર્કસંગત સંખ્યાઓની વ્યાખ્યા અને ઉદાહરણો

આ વિભાગમાં આપણે તર્કસંગત સંખ્યાઓની ઘણી વ્યાખ્યાઓ આપીશું. શબ્દોમાં ભિન્નતા હોવા છતાં, આ બધી વ્યાખ્યાઓનો એક જ અર્થ છે: પરિમાણીય સંખ્યાઓ પૂર્ણાંકો અને અપૂર્ણાંકોને એક કરે છે, જેમ કે પૂર્ણાંકો કુદરતી સંખ્યાઓ, તેમના વિરોધીઓ અને શૂન્યને એક કરે છે. બીજા શબ્દોમાં કહીએ તો, તર્કસંગત સંખ્યાઓ પૂર્ણાંકોને સામાન્ય બનાવે છે અને અપૂર્ણાંક સંખ્યાઓ.

સાથે શરૂઆત કરીએ તર્કસંગત સંખ્યાઓની વ્યાખ્યા, જે સૌથી વધુ કુદરતી રીતે જોવામાં આવે છે.

ઉલ્લેખિત વ્યાખ્યા પરથી તે અનુસરે છે કે તર્કસંગત સંખ્યા છે:

• કોઈપણ કુદરતી સંખ્યા n ખરેખર, તમે કોઈપણ કુદરતી સંખ્યાને સામાન્ય અપૂર્ણાંક તરીકે રજૂ કરી શકો છો, ઉદાહરણ તરીકે, 3=3/1.
• કોઈપણ પૂર્ણાંક, ખાસ કરીને શૂન્ય સંખ્યા. હકીકતમાં, કોઈપણ પૂર્ણાંકને ધન અપૂર્ણાંક, નકારાત્મક અપૂર્ણાંક અથવા શૂન્ય તરીકે લખી શકાય છે. ઉદાહરણ તરીકે, 26=26/1, .
• કોઈપણ સામાન્ય અપૂર્ણાંક (હકારાત્મક અથવા નકારાત્મક). તર્કસંગત સંખ્યાઓની આપેલ વ્યાખ્યા દ્વારા આની સીધી પુષ્ટિ થાય છે.
• કોઈપણ મિશ્ર સંખ્યા. ખરેખર, તમે હંમેશા મિશ્ર સંખ્યાને અયોગ્ય અપૂર્ણાંક તરીકે રજૂ કરી શકો છો. ઉદાહરણ તરીકે, અને.
• કોઈપણ મર્યાદિત દશાંશ અપૂર્ણાંક અથવા અનંત સામયિક અપૂર્ણાંક. આ તે હકીકતને કારણે છે કે દર્શાવેલ દશાંશ અપૂર્ણાંક સામાન્ય અપૂર્ણાંકમાં રૂપાંતરિત થાય છે. ઉદાહરણ તરીકે, , અને 0,(3)=1/3.

તે પણ સ્પષ્ટ છે કે કોઈપણ અનંત બિન-સામયિક દશાંશ અપૂર્ણાંક એ તર્કસંગત સંખ્યા નથી, કારણ કે તે સામાન્ય અપૂર્ણાંક તરીકે રજૂ કરી શકાતી નથી.

હવે આપણે સરળતાથી આપી શકીએ છીએ તર્કસંગત સંખ્યાઓના ઉદાહરણો. સંખ્યાઓ 4, 903, 100,321 એ તર્કસંગત સંખ્યાઓ છે કારણ કે તે કુદરતી સંખ્યાઓ છે. પૂર્ણાંકો 58, −72, 0, −833,333,333 પણ તર્કસંગત સંખ્યાઓના ઉદાહરણો છે. સામાન્ય અપૂર્ણાંક 4/9, 99/3 પણ તર્કસંગત સંખ્યાઓના ઉદાહરણો છે. તર્કસંગત સંખ્યાઓ પણ સંખ્યાઓ છે.

ઉપરોક્ત ઉદાહરણો પરથી તે સ્પષ્ટ છે કે ત્યાં સકારાત્મક અને નકારાત્મક બંને તર્કસંગત સંખ્યાઓ છે, અને તર્કસંગત સંખ્યા શૂન્ય હકારાત્મક કે નકારાત્મક નથી.

તર્કસંગત સંખ્યાઓની ઉપરની વ્યાખ્યા વધુ સંક્ષિપ્ત સ્વરૂપમાં ઘડી શકાય છે.

વ્યાખ્યા.

તર્કસંગત સંખ્યાઓએવી સંખ્યાઓ છે જે અપૂર્ણાંક z/n તરીકે લખી શકાય છે, જ્યાં z એ પૂર્ણાંક છે અને n એ કુદરતી સંખ્યા છે.

ચાલો સાબિત કરીએ કે તર્કસંગત સંખ્યાઓની આ વ્યાખ્યા અગાઉની વ્યાખ્યાની સમકક્ષ છે. આપણે જાણીએ છીએ કે આપણે અપૂર્ણાંકની રેખાને વિભાજનની નિશાની તરીકે ગણી શકીએ છીએ, પછી પૂર્ણાંકોના વિભાજનના ગુણધર્મો અને પૂર્ણાંકોને વિભાજિત કરવાના નિયમોમાંથી, નીચેની સમાનતાઓની માન્યતા અનુસરે છે અને. આમ, તે સાબિતી છે.

ચાલો તેના આધારે તર્કસંગત સંખ્યાઓના ઉદાહરણો આપીએ આ વ્યાખ્યા. સંખ્યાઓ −5, 0, 3, અને તે તર્કસંગત સંખ્યાઓ છે, કારણ કે તે અનુક્રમે પૂર્ણાંક અંશ અને સ્વરૂપના કુદરતી છેદ સાથે અપૂર્ણાંક તરીકે લખી શકાય છે.

તર્કસંગત સંખ્યાઓની વ્યાખ્યા નીચેના સૂત્રમાં આપી શકાય છે.

વ્યાખ્યા.

તર્કસંગત સંખ્યાઓ એવી સંખ્યાઓ છે જે મર્યાદિત અથવા અનંત સામયિક દશાંશ અપૂર્ણાંક તરીકે લખી શકાય છે.

આ વ્યાખ્યા પણ પ્રથમ વ્યાખ્યાની સમકક્ષ છે, કારણ કે દરેક સામાન્ય અપૂર્ણાંક મર્યાદિત અથવા સામયિક દશાંશ અપૂર્ણાંકને અનુલક્ષે છે અને તેનાથી ઊલટું, અને કોઈપણ પૂર્ણાંક દશાંશ બિંદુ પછી શૂન્ય સાથે દશાંશ અપૂર્ણાંક સાથે સંકળાયેલ હોઈ શકે છે.

ઉદાહરણ તરીકે, સંખ્યાઓ 5, 0, −13, તર્કસંગત સંખ્યાઓના ઉદાહરણો છે કારણ કે તે નીચેના દશાંશ અપૂર્ણાંક 5.0, 0.0, −13.0, 0.8 અને −7, (18) તરીકે લખી શકાય છે.

ચાલો આ મુદ્દાના સિદ્ધાંતને નીચેના નિવેદનો સાથે સમાપ્ત કરીએ:

• પૂર્ણાંકો અને અપૂર્ણાંકો (ધન અને નકારાત્મક) તર્કસંગત સંખ્યાઓનો સમૂહ બનાવે છે;
• દરેક તર્કસંગત સંખ્યાને પૂર્ણાંક અંશ અને કુદરતી છેદ સાથે અપૂર્ણાંક તરીકે રજૂ કરી શકાય છે, અને આવા દરેક અપૂર્ણાંક ચોક્કસ તર્કસંગત સંખ્યાને રજૂ કરે છે;
• દરેક તર્કસંગત સંખ્યાને મર્યાદિત અથવા અનંત સામયિક દશાંશ અપૂર્ણાંક તરીકે રજૂ કરી શકાય છે, અને આવા દરેક અપૂર્ણાંક તર્કસંગત સંખ્યાને રજૂ કરે છે.

શું આ સંખ્યા તર્કસંગત છે?

પાછલા ફકરામાં, આપણે શોધી કાઢ્યું કે કોઈપણ કુદરતી સંખ્યા, કોઈપણ પૂર્ણાંક, કોઈપણ સામાન્ય અપૂર્ણાંક, કોઈપણ મિશ્ર સંખ્યા, કોઈપણ મર્યાદિત દશાંશ અપૂર્ણાંક, તેમજ કોઈપણ સામયિક દશાંશ અપૂર્ણાંક એક તર્કસંગત સંખ્યા છે. આ જ્ઞાન અમને લેખિત સંખ્યાઓના સમૂહમાંથી તર્કસંગત સંખ્યાઓને "ઓળખવા" માટે પરવાનગી આપે છે.

પરંતુ જો નંબર અમુક , અથવા તરીકે , વગેરેના રૂપમાં આપવામાં આવે તો શું, પ્રશ્નનો જવાબ કેવી રીતે આપવો આપેલ નંબરતર્કસંગત? ઘણા કિસ્સાઓમાં તેનો જવાબ આપવો ખૂબ મુશ્કેલ છે. ચાલો વિચારની કેટલીક દિશાઓ સૂચવીએ.

જો ફોર્મમાં નંબર આપેલ છે સંખ્યાત્મક અભિવ્યક્તિ, જેમાં માત્ર તર્કસંગત સંખ્યાઓ અને ચિહ્નો છે અંકગણિત કામગીરી(+, −, · અને:), તો પછી આ અભિવ્યક્તિનું મૂલ્ય એક તર્કસંગત સંખ્યા છે. તર્કસંગત સંખ્યાઓ સાથેની ક્રિયાઓ કેવી રીતે વ્યાખ્યાયિત કરવામાં આવે છે તેના પરથી આ અનુસરે છે. ઉદાહરણ તરીકે, અભિવ્યક્તિમાં તમામ ક્રિયાઓ કર્યા પછી, આપણને તર્કસંગત નંબર 18 મળે છે.

કેટલીકવાર, અભિવ્યક્તિઓ અને વધુને સરળ બનાવ્યા પછી જટિલ પ્રકાર, આપેલ સંખ્યા તર્કસંગત છે કે કેમ તે નક્કી કરવું શક્ય બને છે.

ચાલો આગળ વધીએ. નંબર 2 એ એક તર્કસંગત સંખ્યા છે, કારણ કે કોઈપણ કુદરતી સંખ્યા તર્કસંગત છે. નંબર વિશે શું? શું તે તર્કસંગત છે? તે તારણ આપે છે કે ના, તે તર્કસંગત સંખ્યા નથી, તે અતાર્કિક સંખ્યા છે (વિરોધાભાસ દ્વારા આ હકીકતનો પુરાવો ગ્રેડ 8 માટે બીજગણિત પાઠયપુસ્તકમાં આપવામાં આવ્યો છે, સંદર્ભોની સૂચિમાં નીચે સૂચિબદ્ધ છે). તે પણ સાબિત થયું છે વર્ગમૂળપ્રાકૃતિક સંખ્યા એ માત્ર એવા કિસ્સાઓમાં જ એક તર્કસંગત સંખ્યા છે જ્યારે મૂળમાં એવી સંખ્યા હોય જે અમુક કુદરતી સંખ્યાનો સંપૂર્ણ વર્ગ હોય. ઉદાહરણ તરીકે, અને 81 = 9 2 અને 1 024 = 32 2 થી, અને સંખ્યાઓ અને પરિમેયીય નથી, કારણ કે સંખ્યાઓ 7 અને 199 નથી સંપૂર્ણ ચોરસકુદરતી સંખ્યાઓ.

સંખ્યા તર્કસંગત છે કે નહીં? IN આ કિસ્સામાંતે જોવાનું સરળ છે કે, તેથી, આ સંખ્યા તર્કસંગત છે. શું સંખ્યા તર્કસંગત છે? તે સાબિત થયું છે કે પૂર્ણાંકનું kth મૂળ એ તર્કસંગત સંખ્યા છે જો મૂળ ચિન્હ હેઠળની સંખ્યા અમુક પૂર્ણાંકની kth ઘાત હોય. તેથી, તે તર્કસંગત સંખ્યા નથી, કારણ કે ત્યાં કોઈ પૂર્ણાંક નથી જેની પાંચમી ઘાત 121 છે.

વિરોધાભાસ દ્વારા પદ્ધતિ તમને સાબિત કરવાની મંજૂરી આપે છે કે કેટલીક સંખ્યાઓના લઘુગણક કેટલાક કારણોસર તર્કસંગત સંખ્યાઓ નથી. ઉદાહરણ તરીકે, ચાલો સાબિત કરીએ કે - એક તર્કસંગત સંખ્યા નથી.

ચાલો વિરુદ્ધ ધારીએ, એટલે કે, ચાલો કહીએ કે તે એક તર્કસંગત સંખ્યા છે અને તેને સામાન્ય અપૂર્ણાંક m/n તરીકે લખી શકાય છે. પછી અમે નીચેની સમાનતા આપીએ છીએ: . છેલ્લી સમાનતા અશક્ય છે, કારણ કે ડાબી બાજુએ છે વિષમ સંખ્યા 5 n, અને જમણી બાજુએ સમ સંખ્યા 2 m છે. તેથી, અમારી ધારણા ખોટી છે, તેથી તે તર્કસંગત સંખ્યા નથી.

નિષ્કર્ષમાં, તે ખાસ કરીને નોંધવું યોગ્ય છે કે સંખ્યાઓની તર્કસંગતતા અથવા અતાર્કિકતા નક્કી કરતી વખતે, વ્યક્તિએ અચાનક તારણો કાઢવાથી દૂર રહેવું જોઈએ.

ઉદાહરણ તરીકે, તમારે તરત જ ભારપૂર્વક કહેવું જોઈએ નહીં કે અતાર્કિક સંખ્યાઓ π અને e એક અતાર્કિક સંખ્યા છે, પરંતુ તે સાબિત નથી. આ પ્રશ્ન ઉભો કરે છે: "ઉત્પાદન એક તર્કસંગત સંખ્યા કેમ હશે?" અને શા માટે નહીં, કારણ કે તમે અતાર્કિક સંખ્યાઓનું ઉદાહરણ આપી શકો છો, જેનું ઉત્પાદન તર્કસંગત સંખ્યા આપે છે: .

સંખ્યાઓ અને અન્ય ઘણી સંખ્યાઓ તર્કસંગત છે કે નહીં તે પણ અજ્ઞાત છે. ઉદાહરણ તરીકે, ત્યાં છે અતાર્કિક સંખ્યાઓ, અતાર્કિક ડિગ્રીજે એક તર્કસંગત સંખ્યા છે. ઉદાહરણ માટે, અમે ફોર્મની ડિગ્રી રજૂ કરીએ છીએ, આ ડિગ્રીનો આધાર અને ઘાતાંક પરિમેય સંખ્યાઓ નથી, પરંતુ , અને 3 એક પરિમેય સંખ્યા છે.

સંદર્ભો.

• ગણિત. 6ઠ્ઠો ધોરણ: શૈક્ષણિક. સામાન્ય શિક્ષણ માટે સંસ્થાઓ / [એન. યા વિલેન્કીન અને અન્ય]. - 22મી આવૃત્તિ, રેવ. - એમ.: નેમોસીન, 2008. - 288 પૃષ્ઠ: બીમાર. ISBN 978-5-346-00897-2.
• બીજગણિત:પાઠ્યપુસ્તક 8મા ધોરણ માટે. સામાન્ય શિક્ષણ સંસ્થાઓ / [યુ. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; દ્વારા સંપાદિત એસ. એ. ટેલિયાકોવ્સ્કી. - 16મી આવૃત્તિ. - એમ.: શિક્ષણ, 2008. - 271 પૃષ્ઠ. : બીમાર. - ISBN 978-5-09-019243-9.
• ગુસેવ વી.એ., મોર્ડકોવિચ એ.જી.ગણિત (તકનીકી શાળાઓમાં પ્રવેશ કરનારાઓ માટે માર્ગદર્શિકા): પ્રોક. ભથ્થું.- એમ.; ઉચ્ચ શાળા, 1984.-351 પૃ., બીમાર.

IN આ પાઠતર્કસંગત સંખ્યાઓનો ગુણાકાર અને ભાગાકાર ગણવામાં આવે છે.

તર્કસંગત સંખ્યાઓનો ગુણાકાર

પૂર્ણાંકોના ગુણાકાર માટેના નિયમો તર્કસંગત સંખ્યાઓને પણ લાગુ પડે છે. બીજા શબ્દોમાં કહીએ તો, તર્કસંગત સંખ્યાઓનો ગુણાકાર કરવા માટે, તમારે સક્ષમ હોવું જરૂરી છે

ઉપરાંત, તમારે ગુણાકારના મૂળભૂત નિયમો જાણવાની જરૂર છે, જેમ કે: ગુણાકારનો વિનિમયાત્મક કાયદો, ગુણાકારનો સહયોગી કાયદો, ગુણાકારનો વિતરણ કાયદો અને શૂન્ય વડે ગુણાકાર.

ઉદાહરણ 1.અભિવ્યક્તિનું મૂલ્ય શોધો

આ સાથે તર્કસંગત સંખ્યાઓનો ગુણાકાર છે વિવિધ ચિહ્નો. વિવિધ ચિહ્નો સાથે તર્કસંગત સંખ્યાઓનો ગુણાકાર કરવા માટે, તમારે તેમના મોડ્યુલોનો ગુણાકાર કરવાની જરૂર છે અને પરિણામી જવાબની સામે માઈનસ મૂકવાની જરૂર છે.

સ્પષ્ટપણે જોવા માટે કે આપણે વિવિધ ચિહ્નો ધરાવતી સંખ્યાઓ સાથે કામ કરી રહ્યા છીએ, અમે દરેક તર્કસંગત સંખ્યાને તેના ચિહ્નો સાથે કૌંસમાં બંધ કરીએ છીએ.

સંખ્યાનું મોડ્યુલસ બરાબર છે, અને સંખ્યાનું મોડ્યુલસ બરાબર છે. પરિણામી મોડ્યુલોનો ગુણાકાર તરીકે હકારાત્મક અપૂર્ણાંક, અમને એક જવાબ મળ્યો છે, પરંતુ જવાબ પહેલાં અમે એક માઈનસ મૂકીએ છીએ, અમારા માટે જરૂરી નિયમ મુજબ. જવાબ પહેલાં આ બાદબાકીને સુનિશ્ચિત કરવા માટે, કૌંસમાં મોડ્યુલોનો ગુણાકાર કરવામાં આવ્યો હતો, જે માઈનસથી આગળ હતો.

ટૂંકા ઉકેલ આના જેવો દેખાય છે:

ઉદાહરણ 2.અભિવ્યક્તિનું મૂલ્ય શોધો

ઉદાહરણ 3.અભિવ્યક્તિનું મૂલ્ય શોધો

આ નકારાત્મક તર્કસંગત સંખ્યાઓનો ગુણાકાર છે. નકારાત્મક તર્કસંગત સંખ્યાઓનો ગુણાકાર કરવા માટે, તમારે તેમના મોડ્યુલોનો ગુણાકાર કરવાની જરૂર છે અને પરિણામી જવાબની સામે વત્તા મૂકવાની જરૂર છે.

માટે ઉકેલ આ ઉદાહરણસંક્ષિપ્તમાં લખી શકાય છે:

ઉદાહરણ 4.અભિવ્યક્તિનું મૂલ્ય શોધો

આ ઉદાહરણ માટે ઉકેલ ટૂંકમાં લખી શકાય છે:

ઉદાહરણ 5.અભિવ્યક્તિનું મૂલ્ય શોધો

આ વિવિધ ચિહ્નો સાથે તર્કસંગત સંખ્યાઓનો ગુણાકાર છે. ચાલો આ સંખ્યાઓના મોડ્યુલોનો ગુણાકાર કરીએ અને પરિણામી જવાબની સામે માઈનસ મૂકીએ

ટૂંકું સોલ્યુશન વધુ સરળ દેખાશે:

ઉદાહરણ 6.અભિવ્યક્તિનું મૂલ્ય શોધો

ચાલો મિશ્ર સંખ્યાને માં રૂપાંતરિત કરીએ અયોગ્ય અપૂર્ણાંક. ચાલો બાકીનાને જેમ છે તેમ ફરીથી લખીએ

અમે વિવિધ ચિહ્નો સાથે તર્કસંગત સંખ્યાઓનો ગુણાકાર મેળવ્યો. ચાલો આ સંખ્યાઓના મોડ્યુલોનો ગુણાકાર કરીએ અને પરિણામી જવાબની સામે માઈનસ મૂકીએ. અભિવ્યક્તિમાં ગડબડ ન થાય તે માટે મોડ્યુલો સાથેની એન્ટ્રી છોડી શકાય છે

આ ઉદાહરણનો ઉકેલ ટૂંકમાં લખી શકાય

ઉદાહરણ 7.અભિવ્યક્તિનું મૂલ્ય શોધો

આ વિવિધ ચિહ્નો સાથે તર્કસંગત સંખ્યાઓનો ગુણાકાર છે. ચાલો આ સંખ્યાઓના મોડ્યુલોનો ગુણાકાર કરીએ અને પરિણામી જવાબની સામે માઈનસ મૂકીએ

શરૂઆતમાં જવાબ અયોગ્ય અપૂર્ણાંક હોવાનું બહાર આવ્યું, પરંતુ અમે તેમાં આખો ભાગ પ્રકાશિત કર્યો. તેની નોંધ કરો આખો ભાગઅપૂર્ણાંક મોડ્યુલથી અલગ કરવામાં આવ્યું હતું. પરિણામી મિશ્રિત સંખ્યાને બાદબાકી ચિહ્નની આગળ કૌંસમાં બંધ કરવામાં આવી હતી. આ નિયમની જરૂરિયાત પૂરી થાય તેની ખાતરી કરવા માટે કરવામાં આવે છે. અને નિયમ માટે જરૂરી છે કે પ્રાપ્ત થયેલા જવાબની પહેલા માઈનસ આવે.

આ ઉદાહરણ માટે ઉકેલ ટૂંકમાં લખી શકાય છે:

ઉદાહરણ 8.અભિવ્યક્તિનું મૂલ્ય શોધો

પ્રથમ, ચાલો પરિણામી સંખ્યાને બાકીની સંખ્યા 5 સાથે ગુણાકાર કરીએ અને ગુણાકાર કરીએ. અભિવ્યક્તિમાં ગડબડ ન થાય તે માટે અમે મોડ્યુલ સાથેની એન્ટ્રી છોડી દઈશું.

જવાબ:અભિવ્યક્તિ મૂલ્ય બરાબર −2.

ઉદાહરણ 9.અભિવ્યક્તિનો અર્થ શોધો:

ચાલો અનુવાદ કરીએ મિશ્ર સંખ્યાઓઅયોગ્ય અપૂર્ણાંકો માટે:

આપણને ઋણ તર્કસંગત સંખ્યાઓનો ગુણાકાર મળ્યો. ચાલો આ સંખ્યાઓના મોડ્યુલોનો ગુણાકાર કરીએ અને પરિણામી જવાબની સામે વત્તા મૂકીએ. અભિવ્યક્તિમાં ગડબડ ન થાય તે માટે મોડ્યુલો સાથેની એન્ટ્રી છોડી શકાય છે

ઉદાહરણ 10.અભિવ્યક્તિનું મૂલ્ય શોધો

અભિવ્યક્તિમાં ઘણા પરિબળોનો સમાવેશ થાય છે. ગુણાકારના સહયોગી કાયદા અનુસાર, જો અભિવ્યક્તિમાં ઘણા પરિબળો હોય, તો પછી ઉત્પાદન ક્રિયાઓના ક્રમ પર આધારિત રહેશે નહીં. આ અમને ગણતરી કરવા દે છે આ અભિવ્યક્તિકોઈપણ ક્રમમાં.

ચાલો ચક્રને પુનઃશોધ ન કરીએ, પરંતુ પરિબળોના ક્રમમાં ડાબેથી જમણે આ અભિવ્યક્તિની ગણતરી કરીએ. ચાલો મોડ્યુલો સાથે એન્ટ્રી છોડી દઈએ જેથી અભિવ્યક્તિમાં ગડબડ ન થાય

ત્રીજી ક્રિયા:

ચોથી ક્રિયા:

જવાબ:અભિવ્યક્તિનું મૂલ્ય છે

ઉદાહરણ 11.અભિવ્યક્તિનું મૂલ્ય શોધો

ચાલો શૂન્ય વડે ગુણાકારનો નિયમ યાદ રાખીએ. આ કાયદો જણાવે છે કે ઉત્પાદન શૂન્ય બરાબર છે જો ઓછામાં ઓછું એક પરિબળ હોય શૂન્ય બરાબર.

અમારા ઉદાહરણમાં, એક પરિબળ શૂન્યની બરાબર છે, તેથી સમય બગાડ્યા વિના અમે જવાબ આપીએ છીએ કે અભિવ્યક્તિનું મૂલ્ય શૂન્ય બરાબર છે:

ઉદાહરણ 12.અભિવ્યક્તિનું મૂલ્ય શોધો

જો ઓછામાં ઓછું એક પરિબળ શૂન્ય સમાન હોય તો ઉત્પાદન શૂન્યની બરાબર છે.

અમારા ઉદાહરણમાં, એક પરિબળ શૂન્ય સમાન છે, તેથી સમય બગાડ્યા વિના અમે જવાબ આપીએ છીએ કે અભિવ્યક્તિનું મૂલ્ય શૂન્ય બરાબર:

ઉદાહરણ 13.અભિવ્યક્તિનું મૂલ્ય શોધો

તમે ક્રિયાઓના ક્રમનો ઉપયોગ કરી શકો છો અને પ્રથમ કૌંસમાં અભિવ્યક્તિની ગણતરી કરી શકો છો અને પરિણામી જવાબને અપૂર્ણાંક સાથે ગુણાકાર કરી શકો છો.

તમે ગુણાકારના વિતરક નિયમનો પણ ઉપયોગ કરી શકો છો - સરવાળાના દરેક પદને અપૂર્ણાંક દ્વારા ગુણાકાર કરો અને પરિણામી પરિણામો ઉમેરો. અમે આ પદ્ધતિનો ઉપયોગ કરીશું.

ક્રિયાઓના ક્રમ મુજબ, જો કોઈ અભિવ્યક્તિમાં સરવાળો અને ગુણાકાર હોય, તો પહેલા ગુણાકાર કરવો આવશ્યક છે. તેથી, પરિણામી નવી અભિવ્યક્તિમાં, ચાલો તે પરિમાણોને કૌંસમાં મૂકીએ જેનો ગુણાકાર કરવો આવશ્યક છે. આ રીતે આપણે સ્પષ્ટપણે જોઈ શકીએ છીએ કે કઈ ક્રિયાઓ પહેલા કરવી અને કઈ પછી:

ત્રીજી ક્રિયા:

જવાબ:અભિવ્યક્તિ મૂલ્ય બરાબર

આ ઉદાહરણનો ઉકેલ ઘણો ટૂંકો લખી શકાય. તે આના જેવો દેખાશે:

તે સ્પષ્ટ છે કે આ ઉદાહરણ કોઈના મગજમાં પણ ઉકેલી શકાય છે. તેથી, તમારે તેને ઉકેલતા પહેલા અભિવ્યક્તિનું વિશ્લેષણ કરવાની કુશળતા વિકસાવવી જોઈએ. સંભવ છે કે તે માનસિક રીતે ઉકેલી શકાય છે અને ઘણો સમય અને ચેતા બચાવે છે. અને પરીક્ષણો અને પરીક્ષાઓમાં, જેમ તમે જાણો છો, સમય ખૂબ મૂલ્યવાન છે.

ઉદાહરણ 14.−4.2 × 3.2 અભિવ્યક્તિની કિંમત શોધો

આ વિવિધ ચિહ્નો સાથે તર્કસંગત સંખ્યાઓનો ગુણાકાર છે. ચાલો આ સંખ્યાઓના મોડ્યુલોનો ગુણાકાર કરીએ અને પરિણામી જવાબની સામે માઈનસ મૂકીએ

તર્કસંગત સંખ્યાઓના મોડ્યુલોનો ગુણાકાર કેવી રીતે થયો તેની નોંધ લો. આ કિસ્સામાં, તર્કસંગત સંખ્યાઓના મોડ્યુલીનો ગુણાકાર કરવા માટે, તે લીધો .

ઉદાહરણ 15.−0.15 × 4 અભિવ્યક્તિની કિંમત શોધો

આ વિવિધ ચિહ્નો સાથે તર્કસંગત સંખ્યાઓનો ગુણાકાર છે. ચાલો આ સંખ્યાઓના મોડ્યુલોનો ગુણાકાર કરીએ અને પરિણામી જવાબની સામે માઈનસ મૂકીએ

તર્કસંગત સંખ્યાઓના મોડ્યુલોનો ગુણાકાર કેવી રીતે થયો તેની નોંધ લો. આ કિસ્સામાં, તર્કસંગત સંખ્યાઓના મોડ્યુલીનો ગુણાકાર કરવા માટે, સક્ષમ હોવું જરૂરી હતું.

ઉદાહરણ 16.અભિવ્યક્તિની કિંમત −4.2 × (−7.5) શોધો

આ નકારાત્મક તર્કસંગત સંખ્યાઓનો ગુણાકાર છે. ચાલો આ સંખ્યાઓના મોડ્યુલોનો ગુણાકાર કરીએ અને પરિણામી જવાબની સામે વત્તા મૂકીએ

તર્કસંગત સંખ્યાઓનું વિભાજન

પૂર્ણાંકોને વિભાજિત કરવાના નિયમો તર્કસંગત સંખ્યાઓને પણ લાગુ પડે છે. બીજા શબ્દોમાં કહીએ તો, તર્કસંગત સંખ્યાઓને વિભાજીત કરવા માટે, તમારે સક્ષમ હોવું જરૂરી છે

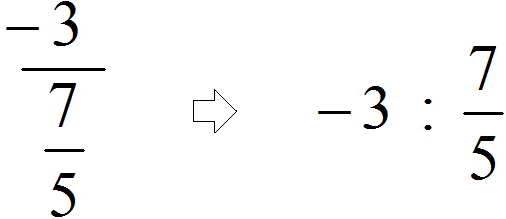
નહિંતર, સામાન્ય અને દશાંશ અપૂર્ણાંકને વિભાજીત કરવા માટેની સમાન પદ્ધતિઓનો ઉપયોગ કરવામાં આવે છે. સામાન્ય અપૂર્ણાંકને બીજા અપૂર્ણાંક દ્વારા વિભાજીત કરવા માટે, તમારે પ્રથમ અપૂર્ણાંકને બીજા અપૂર્ણાંકના પરસ્પર દ્વારા ગુણાકાર કરવાની જરૂર છે.

અને દશાંશ અપૂર્ણાંકને બીજા દશાંશ અપૂર્ણાંકમાં વિભાજિત કરવા માટે, તમારે ડિવિડન્ડમાં અને વિભાજકમાં દશાંશ બિંદુને જમણી બાજુએ વિભાજકમાં દશાંશ બિંદુ પછી જેટલા અંકો છે તેટલા અંકો દ્વારા ખસેડવાની જરૂર છે, પછી ભાગાકારને એક સાથે કરો. નિયમિત સંખ્યા.

ઉદાહરણ 1.અભિવ્યક્તિનો અર્થ શોધો:

આ વિવિધ ચિહ્નો સાથેની તર્કસંગત સંખ્યાઓનું વિભાજન છે. આવી અભિવ્યક્તિની ગણતરી કરવા માટે, તમારે પ્રથમ અપૂર્ણાંકને બીજાના પરસ્પર દ્વારા ગુણાકાર કરવાની જરૂર છે.

તેથી, ચાલો પ્રથમ અપૂર્ણાંકને બીજાના પરસ્પર દ્વારા ગુણાકાર કરીએ.

અમે વિવિધ ચિહ્નો સાથે તર્કસંગત સંખ્યાઓનો ગુણાકાર મેળવ્યો. અને આવા અભિવ્યક્તિઓની ગણતરી કેવી રીતે કરવી તે આપણે પહેલેથી જ જાણીએ છીએ. આ કરવા માટે, તમારે આ તર્કસંગત સંખ્યાઓના મોડ્યુલોને ગુણાકાર કરવાની જરૂર છે અને પરિણામી જવાબની સામે માઇનસ મૂકવાની જરૂર છે.

ચાલો આ ઉદાહરણને અંત સુધી પૂર્ણ કરીએ. અભિવ્યક્તિમાં ગડબડ ન થાય તે માટે મોડ્યુલો સાથેની એન્ટ્રી છોડી શકાય છે

તેથી અભિવ્યક્તિનું મૂલ્ય છે

વિગતવાર ઉકેલ નીચે મુજબ છે.

ટૂંકા ઉકેલ આના જેવો દેખાશે:

ઉદાહરણ 2.અભિવ્યક્તિનું મૂલ્ય શોધો

આ વિવિધ ચિહ્નો સાથેની તર્કસંગત સંખ્યાઓનું વિભાજન છે. આ અભિવ્યક્તિની ગણતરી કરવા માટે, તમારે પ્રથમ અપૂર્ણાંકને બીજાના પરસ્પર દ્વારા ગુણાકાર કરવાની જરૂર છે.

બીજા અપૂર્ણાંકનો પરસ્પર અપૂર્ણાંક છે. ચાલો તેના દ્વારા પ્રથમ અપૂર્ણાંકનો ગુણાકાર કરીએ:

ટૂંકા ઉકેલ આના જેવો દેખાશે:

ઉદાહરણ 3.અભિવ્યક્તિનું મૂલ્ય શોધો

આ નકારાત્મક તર્કસંગત સંખ્યાઓનો વિભાજન છે. આ અભિવ્યક્તિની ગણતરી કરવા માટે, તમારે ફરીથી પ્રથમ અપૂર્ણાંકને બીજાના પરસ્પર દ્વારા ગુણાકાર કરવાની જરૂર છે.

બીજા અપૂર્ણાંકનો પરસ્પર અપૂર્ણાંક છે. ચાલો તેના દ્વારા પ્રથમ અપૂર્ણાંકનો ગુણાકાર કરીએ:

અમને ઋણ તર્કસંગત સંખ્યાઓનો ગુણાકાર મળ્યો. તેની ગણતરી કેવી રીતે થાય છે સમાન અભિવ્યક્તિઆપણે પહેલેથી જ જાણીએ છીએ. તમારે તર્કસંગત સંખ્યાઓની મોડ્યુલીનો ગુણાકાર કરવાની જરૂર છે અને પરિણામી જવાબની સામે વત્તા મૂકવાની જરૂર છે.

ચાલો આ ઉદાહરણને અંત સુધી પૂર્ણ કરીએ. તમે મોડ્યુલો સાથે એન્ટ્રીને છોડી શકો છો જેથી અભિવ્યક્તિમાં ગડબડ ન થાય:

ઉદાહરણ 4.અભિવ્યક્તિનું મૂલ્ય શોધો

આ અભિવ્યક્તિની ગણતરી કરવા માટે, તમારે પ્રથમ સંખ્યા −3 ને અપૂર્ણાંક વડે ગુણાકાર કરવાની જરૂર છે, પારસ્પરિક અપૂર્ણાંક.

અપૂર્ણાંકનો વ્યસ્ત એ અપૂર્ણાંક છે. પ્રથમ સંખ્યા −3 નો તેના દ્વારા ગુણાકાર કરો

ઉદાહરણ 6.અભિવ્યક્તિનું મૂલ્ય શોધો

આ અભિવ્યક્તિની ગણતરી કરવા માટે, તમારે પ્રથમ અપૂર્ણાંકને સંખ્યા દ્વારા ગુણાકાર કરવાની જરૂર છે સંખ્યાના પરસ્પર 4.

નંબર 4 નો પરસ્પર અપૂર્ણાંક છે. તેના દ્વારા પ્રથમ અપૂર્ણાંકનો ગુણાકાર કરો

ઉદાહરણ 5.અભિવ્યક્તિનું મૂલ્ય શોધો

આ અભિવ્યક્તિની ગણતરી કરવા માટે, તમારે પ્રથમ અપૂર્ણાંકને −3 ના વ્યસ્ત વડે ગુણાકાર કરવાની જરૂર છે.

−3 નો વ્યસ્ત એ અપૂર્ણાંક છે. ચાલો તેના દ્વારા પ્રથમ અપૂર્ણાંકનો ગુણાકાર કરીએ:

ઉદાહરણ 6.અભિવ્યક્તિની કિંમત −14.4: 1.8 શોધો

આ વિવિધ ચિહ્નો સાથેની તર્કસંગત સંખ્યાઓનું વિભાજન છે. આ અભિવ્યક્તિની ગણતરી કરવા માટે, તમારે ડિવિડન્ડના મોડ્યુલને વિભાજકના મોડ્યુલ દ્વારા વિભાજીત કરવાની જરૂર છે અને પરિણામી જવાબ પહેલાં માઇનસ મૂકવાની જરૂર છે.

નોંધ કરો કે ડિવિડન્ડના મોડ્યુલને વિભાજકના મોડ્યુલ દ્વારા કેવી રીતે વિભાજિત કરવામાં આવ્યું હતું. આ કિસ્સામાં, તે યોગ્ય રીતે કરવા માટે, તે સક્ષમ હોવું જરૂરી હતું.

જો તમે દશાંશ સાથે ગડબડ કરવા માંગતા નથી (અને આ ઘણી વાર થાય છે), તો પછી આ , પછી આ મિશ્રિત સંખ્યાઓને અયોગ્ય અપૂર્ણાંકમાં રૂપાંતરિત કરો, અને પછી ભાગાકાર પોતે કરો.

ચાલો અગાઉના સમીકરણ −14.4: 1.8 ની આ રીતે ગણતરી કરીએ. ચાલો અનુવાદ કરીએ દશાંશમિશ્ર સંખ્યાઓ માટે:

હવે પરિણામી મિશ્રિત સંખ્યાઓને અયોગ્ય અપૂર્ણાંકમાં રૂપાંતરિત કરીએ:

હવે તમે સીધો ભાગાકાર કરી શકો છો, એટલે કે, અપૂર્ણાંકને અપૂર્ણાંક દ્વારા વિભાજીત કરો. આ કરવા માટે, તમારે પ્રથમ અપૂર્ણાંકને બીજાના વ્યસ્ત અપૂર્ણાંક દ્વારા ગુણાકાર કરવાની જરૂર છે:

ઉદાહરણ 7.અભિવ્યક્તિનું મૂલ્ય શોધો

ચાલો દશાંશ અપૂર્ણાંક −2.06 ને અયોગ્ય અપૂર્ણાંકમાં રૂપાંતરિત કરીએ, અને આ અપૂર્ણાંકને બીજા અપૂર્ણાંકના પરસ્પર દ્વારા ગુણાકાર કરીએ:

બહુમાળી અપૂર્ણાંક

તમે ઘણીવાર એવી અભિવ્યક્તિ જોઈ શકો છો જેમાં અપૂર્ણાંક રેખાનો ઉપયોગ કરીને અપૂર્ણાંકનું વિભાજન લખવામાં આવે છે. ઉદાહરણ તરીકે, અભિવ્યક્તિ નીચે પ્રમાણે લખી શકાય છે:

અભિવ્યક્તિઓ અને વચ્ચે શું તફાવત છે? ખરેખર કોઈ ફરક નથી. આ બે અભિવ્યક્તિઓ સમાન અર્થ ધરાવે છે અને તેમની વચ્ચે સમાન ચિહ્ન મૂકી શકાય છે:

પ્રથમ કિસ્સામાં, વિભાજનનું ચિહ્ન કોલોન છે અને અભિવ્યક્તિ એક લીટી પર લખાયેલ છે. બીજા કિસ્સામાં, અપૂર્ણાંકનું વિભાજન અપૂર્ણાંક રેખાનો ઉપયોગ કરીને લખવામાં આવે છે. પરિણામ એ એક અપૂર્ણાંક છે જેને લોકો કૉલ કરવા માટે સંમત થાય છે બહુમાળી.

આવા બહુ-વાર્તા અભિવ્યક્તિઓનો સામનો કરતી વખતે, તમારે વિભાજનના સમાન નિયમો લાગુ કરવાની જરૂર છે સામાન્ય અપૂર્ણાંક. પ્રથમ અપૂર્ણાંકને બીજાના પરસ્પર દ્વારા ગુણાકાર કરવો આવશ્યક છે.

સોલ્યુશનમાં આવા અપૂર્ણાંકોનો ઉપયોગ કરવો અત્યંત અસુવિધાજનક છે, તેથી તમે તેને વિભાજન ચિહ્ન તરીકે અપૂર્ણાંક રેખાને બદલે કોલોનનો ઉપયોગ કરીને સમજી શકાય તેવા સ્વરૂપમાં લખી શકો છો.

ઉદાહરણ તરીકે, ચાલો લખીએ બહુમાળી અપૂર્ણાંકસમજી શકાય તેવી રીતે. આ કરવા માટે, તમારે પ્રથમ અપૂર્ણાંક ક્યાં છે અને બીજો ક્યાં છે તે શોધવાની જરૂર છે, કારણ કે આ યોગ્ય રીતે કરવું હંમેશા શક્ય નથી. બહુમાળી અપૂર્ણાંકમાં ઘણી અપૂર્ણાંક રેખાઓ હોય છે જે ગૂંચવણમાં મૂકે છે. મુખ્ય અપૂર્ણાંક રેખા, જે પ્રથમ અપૂર્ણાંકને બીજાથી અલગ કરે છે, તે સામાન્ય રીતે બાકીના કરતાં લાંબી હોય છે.

મુખ્ય અપૂર્ણાંક રેખા નક્કી કર્યા પછી, તમે સરળતાથી સમજી શકો છો કે પ્રથમ અપૂર્ણાંક ક્યાં છે અને બીજો ક્યાં છે:

ઉદાહરણ 2.

અમે મુખ્ય અપૂર્ણાંક રેખા શોધીએ છીએ (તે સૌથી લાંબી છે) અને જુઓ કે પૂર્ણાંક −3 સામાન્ય અપૂર્ણાંક દ્વારા વિભાજિત થયેલ છે.

અને જો આપણે ભૂલથી બીજી અપૂર્ણાંક રેખાને અગ્રણી તરીકે લઈએ (જે ટૂંકી છે), તો તે બહાર આવશે કે આપણે અપૂર્ણાંકને પૂર્ણાંક 5 વડે ભાગી રહ્યા છીએ. આ કિસ્સામાં, જો આ અભિવ્યક્તિની ગણતરી યોગ્ય રીતે કરવામાં આવે તો પણ, સમસ્યા ખોટી રીતે ઉકેલવામાં આવશે, કારણ કે આમાં ડિવિડન્ડ આ કિસ્સામાં, સંખ્યા −3 છે, અને વિભાજક અપૂર્ણાંક છે.

ઉદાહરણ 3.ચાલો બહુ-સ્તરીય અપૂર્ણાંકને સમજી શકાય તેવા સ્વરૂપમાં લખીએ

અમે મુખ્ય અપૂર્ણાંક રેખા શોધીએ છીએ (તે સૌથી લાંબી છે) અને જુઓ કે અપૂર્ણાંક પૂર્ણાંક 2 દ્વારા વિભાજિત થયેલ છે

અને જો આપણે ભૂલથી પ્રથમ અપૂર્ણાંક રેખાને અગ્રણી તરીકે લઈએ (જે ટૂંકી છે), તો તે બહાર આવશે કે આપણે પૂર્ણાંક −5 ને અપૂર્ણાંક દ્વારા વિભાજિત કરી રહ્યા છીએ, જો આ અભિવ્યક્તિની ગણતરી યોગ્ય રીતે કરવામાં આવે તો પણ. સમસ્યા ખોટી રીતે ઉકેલવામાં આવશે, કારણ કે આ કિસ્સામાં ડિવિડન્ડ અપૂર્ણાંક છે, અને વિભાજક પૂર્ણાંક 2 છે.

બહુ-સ્તરીય અપૂર્ણાંકો સાથે કામ કરવા માટે અસુવિધાજનક હોવા છતાં, અમે ઘણી વાર તેનો સામનો કરીશું, ખાસ કરીને ઉચ્ચ ગણિતનો અભ્યાસ કરતી વખતે.

સ્વાભાવિક રીતે, તે લે છે વધારાનો સમયઅને સ્થળ. તેથી, તમે વધુ ઉપયોગ કરી શકો છો ઝડપી પદ્ધતિ. આ પદ્ધતિ અનુકૂળ છે અને આઉટપુટ તમને તૈયાર અભિવ્યક્તિ મેળવવા માટે પરવાનગી આપે છે જેમાં પ્રથમ અપૂર્ણાંક પહેલાથી જ બીજાના પારસ્પરિક અપૂર્ણાંક દ્વારા ગુણાકાર કરવામાં આવ્યો છે.

આ પદ્ધતિ નીચે પ્રમાણે લાગુ કરવામાં આવે છે:

જો અપૂર્ણાંક ચાર-માળનો છે, ઉદાહરણ તરીકે, તો પછી પ્રથમ માળ પર સ્થિત નંબર ટોચના માળે ઉભો કરવામાં આવે છે. અને બીજા માળે સ્થિત આકૃતિ ત્રીજા માળે ઉભી કરવામાં આવી છે. પરિણામી સંખ્યાઓ ગુણાકાર ચિહ્નો (×) સાથે જોડાયેલ હોવી જોઈએ.

પરિણામે, મધ્યવર્તી સંકેતને બાયપાસ કરીને, અમે એક નવી અભિવ્યક્તિ મેળવીએ છીએ જેમાં પ્રથમ અપૂર્ણાંક પહેલાથી જ બીજાના પારસ્પરિક અપૂર્ણાંક દ્વારા ગુણાકાર કરવામાં આવ્યો છે. સગવડ અને બસ!

ઉપયોગ કરતી વખતે ભૂલો ટાળવા માટે આ પદ્ધતિ, તમે નીચેના નિયમ દ્વારા માર્ગદર્શન મેળવી શકો છો:

પ્રથમ થી ચોથા. બીજાથી ત્રીજા સુધી.

નિયમમાં અમે વાત કરી રહ્યા છીએફ્લોર વિશે. પ્રથમ માળથી આકૃતિ ચોથા માળ સુધી ઉભી કરવી આવશ્યક છે. અને બીજા માળેથી આકૃતિ ત્રીજા માળે ઉભી કરવાની જરૂર છે.

ચાલો ઉપરોક્ત નિયમનો ઉપયોગ કરીને બહુમાળી અપૂર્ણાંકની ગણતરી કરવાનો પ્રયાસ કરીએ.

તેથી, અમે પહેલા માળે સ્થિત નંબરને ચોથા માળે વધારીએ છીએ, અને બીજા માળે સ્થિત નંબરને ત્રીજા માળે વધારીએ છીએ.

પરિણામે, મધ્યવર્તી સંકેતને બાયપાસ કરીને, અમે એક નવી અભિવ્યક્તિ મેળવીએ છીએ જેમાં પ્રથમ અપૂર્ણાંક પહેલાથી જ બીજાના પારસ્પરિક અપૂર્ણાંક દ્વારા ગુણાકાર કરવામાં આવ્યો છે. આગળ, તમે તમારા વર્તમાન જ્ઞાનનો ઉપયોગ કરી શકો છો:

ચાલો નવી યોજનાનો ઉપયોગ કરીને બહુ-સ્તરના અપૂર્ણાંકની ગણતરી કરવાનો પ્રયાસ કરીએ.

અહીં માત્ર પ્રથમ, બીજા અને ચોથા માળ જ છે. ત્રીજો માળ નથી. પરંતુ અમે મૂળભૂત યોજનાથી વિચલિત થતા નથી: અમે આકૃતિને પ્રથમ માળથી ચોથા માળ સુધી વધારીએ છીએ. અને કોઈ ત્રીજો માળ ન હોવાથી, અમે બીજા માળે આવેલો નંબર જેમ છે તેમ છોડી દઈએ છીએ

પરિણામે, મધ્યવર્તી સંકેતને બાયપાસ કરીને, અમને એક નવી અભિવ્યક્તિ પ્રાપ્ત થઈ જેમાં પ્રથમ નંબર −3 પહેલાથી જ બીજાના પારસ્પરિક અપૂર્ણાંક દ્વારા ગુણાકાર કરવામાં આવ્યો છે. આગળ, તમે તમારા વર્તમાન જ્ઞાનનો ઉપયોગ કરી શકો છો:

ચાલો નવી યોજનાનો ઉપયોગ કરીને મલ્ટી-સ્ટોરી અપૂર્ણાંકની ગણતરી કરવાનો પ્રયાસ કરીએ.

બીજા, ત્રીજા અને ચોથા માળ જ છે. ત્યાં કોઈ પહેલો માળ નથી. પ્રથમ માળ ન હોવાથી, ચોથા માળ સુધી જવા માટે કંઈ નથી, પરંતુ આપણે આકૃતિને બીજા માળેથી ત્રીજા સુધી વધારી શકીએ છીએ:

પરિણામે, મધ્યવર્તી સંકેતને બાયપાસ કરીને, અમને એક નવી અભિવ્યક્તિ પ્રાપ્ત થઈ છે જેમાં પ્રથમ અપૂર્ણાંક પહેલાથી જ વિભાજકના વ્યસ્ત દ્વારા ગુણાકાર કરવામાં આવ્યો છે. આગળ, તમે તમારા વર્તમાન જ્ઞાનનો ઉપયોગ કરી શકો છો:

ચલોનો ઉપયોગ કરવો

જો અભિવ્યક્તિ જટિલ છે અને તમને લાગે છે કે તે તમને સમસ્યા હલ કરવાની પ્રક્રિયામાં મૂંઝવણમાં મૂકશે, તો અભિવ્યક્તિનો ભાગ ચલમાં મૂકી શકાય છે અને પછી આ ચલ સાથે કામ કરી શકાય છે.

ગણિતશાસ્ત્રીઓ ઘણીવાર આવું કરે છે. મુશ્કેલ કાર્યતેમને સરળ પેટા કાર્યોમાં વિભાજીત કરો અને તેમને હલ કરો. પછી ઉકેલાયેલા પેટા કાર્યોને એક સંપૂર્ણમાં એકત્રિત કરવામાં આવે છે. આ સર્જનાત્મક પ્રક્રિયાઅને આ તે કંઈક છે જે વર્ષોથી સખત તાલીમ દ્વારા શીખે છે.

મલ્ટી-લેવલ અપૂર્ણાંક સાથે કામ કરતી વખતે ચલોનો ઉપયોગ વાજબી છે. ઉદાહરણ તરીકે:

અભિવ્યક્તિનું મૂલ્ય શોધો

તેથી, અંશ અને તેના છેદમાં અપૂર્ણાંક અભિવ્યક્તિ છે અપૂર્ણાંક અભિવ્યક્તિઓ. બીજા શબ્દોમાં કહીએ તો, આપણે ફરીથી બહુ-વાર્તાના અપૂર્ણાંકનો સામનો કરી રહ્યા છીએ, જે અમને ખૂબ ગમતું નથી.

અંશમાં અભિવ્યક્તિ કોઈપણ નામ સાથે ચલમાં દાખલ કરી શકાય છે, ઉદાહરણ તરીકે:

પણ ગણિતમાં આવા કેસચલોને સામાન્ય રીતે કેપિટલ લેટિન અક્ષરોનો ઉપયોગ કરીને નામ આપવામાં આવે છે. ચાલો આ પરંપરા તોડીએ નહીં, અને પ્રથમ અભિવ્યક્તિને મોટા સાથે દર્શાવીએ લેટિન અક્ષરએ

અને છેદમાં અભિવ્યક્તિને મોટા અક્ષર B દ્વારા સૂચિત કરી શકાય છે

હવે આપણી મૂળ અભિવ્યક્તિ સ્વરૂપ લે છે. એટલે કે, અમે સંખ્યાત્મક અભિવ્યક્તિને મૂળાક્ષર સાથે બદલી છે, અગાઉ A અને B ચલોમાં અંશ અને છેદ દાખલ કર્યા હતા.

હવે આપણે ચલ A ની કિંમતો અને ચલ B ની કિંમતની અલગથી ગણતરી કરી શકીએ છીએ. અમે એક્સપ્રેશનમાં સમાપ્ત થયેલ મૂલ્યો દાખલ કરીશું.

ચાલો ચલની કિંમત શોધીએ એ

ચાલો ચલની કિંમત શોધીએ બી

હવે ચાલો તેમના મૂલ્યોને A અને B ચલોને બદલે મુખ્ય અભિવ્યક્તિમાં બદલીએ:

અમે એક બહુમાળી અપૂર્ણાંક મેળવ્યો છે જેમાં આપણે “પહેલાથી ચોથા, બીજાથી ત્રીજા” સ્કીમનો ઉપયોગ કરી શકીએ છીએ, એટલે કે, પહેલા માળે સ્થિત નંબરને ચોથા માળે વધારી શકીએ છીએ, અને નંબર બીજા માળે ત્રીજા માળે સ્થિત છે. આગળની ગણતરીઓ મુશ્કેલ નહીં હોય:

આમ, અભિવ્યક્તિનું મૂલ્ય −1 છે.

અલબત્ત અમે ધ્યાનમાં લીધું છે સૌથી સરળ ઉદાહરણ, પરંતુ અમારો ધ્યેય એ શીખવાનો હતો કે આપણે કેવી રીતે ચલોનો ઉપયોગ આપણા માટે સરળ બનાવવા માટે, ભૂલોની સંભાવનાને ઘટાડવા માટે કરી શકીએ છીએ.

એ પણ નોંધ કરો કે આ ઉદાહરણ માટેનું સોલ્યુશન ચલોનો ઉપયોગ કર્યા વિના લખી શકાય છે. તે જેવો દેખાશે

આ સોલ્યુશન ઝડપી અને ટૂંકું છે, અને આ કિસ્સામાં તે આ રીતે લખવામાં વધુ અર્થપૂર્ણ છે, પરંતુ જો અભિવ્યક્તિ જટિલ હોવાનું બહાર આવ્યું છે, જેમાં ઘણા પરિમાણો, કૌંસ, મૂળ અને શક્તિઓનો સમાવેશ થાય છે, તો પછી તેની ગણતરી કરવાની સલાહ આપવામાં આવે છે. વિવિધ તબક્કાઓ, તેના અભિવ્યક્તિઓનો ભાગ ચલોમાં દાખલ કરે છે.

શું તમને પાઠ ગમ્યો?
અમારી સાથે જોડાઓ નવું જૂથ VKontakte અને નવા પાઠ વિશે સૂચનાઓ પ્રાપ્ત કરવાનું પ્રારંભ કરો

92 ચ. II

4) દ્વારા q ધારી રહ્યા છીએ સંપૂર્ણ મૂલ્ય 1 કરતા ઓછા, સાબિત કરો

5) અનંત શ્રેણીની મર્યાદા શું છે

1 − 2q + 3q2 − 4q3 + . . . ?

6) અભિવ્યક્તિઓની મર્યાદાઓની ગણતરી કરો

(સંકેત: પૃષ્ઠ 31-33 પર મળેલા પરિણામોનો ઉપયોગ કરો.)

4. તર્કસંગત સંખ્યાઓ અને સામયિક દશાંશ.

આવી તર્કસંગત સંખ્યાઓ p q જે રજૂ કરી શકાતી નથી

મર્યાદિત દશાંશ અપૂર્ણાંકના સ્વરૂપમાં, "લાંબા" વિભાગની સામાન્ય તકનીકનો ઉપયોગ કરીને અનંત દશાંશ અપૂર્ણાંકમાં વિઘટિત થાય છે. આ પ્રક્રિયાના દરેક તબક્કે, એક શેષ ઉદ્ભવે છે જે શૂન્યની બરાબર નથી, અન્યથા અપૂર્ણાંક મર્યાદિત હશે. વિવિધ અવશેષો જે થાય છે તે માત્ર 1 થી q − 1 સુધીના પૂર્ણાંકો હોઈ શકે છે, તેથી આ શેષના મૂલ્યો માટે માત્ર q − 1 શક્યતાઓ છે. આનો અર્થ એ છે કે q વિભાજન પછી અમુક શેષ k બીજી વખત દેખાશે. પરંતુ તે પછી તમામ અનુગામી અવશેષો પણ તે જ ક્રમમાં પુનરાવર્તિત થશે જેમાં તેઓ અવશેષ k ની પ્રથમ ઘટના પછી દેખાયા હતા. આમ,

કોઈપણ તર્કસંગત સંખ્યાના દશાંશ વિસ્તરણમાં સામયિકતાની મિલકત હોય છે; દશાંશ સ્થાનોની ચોક્કસ સંખ્યા પછી, દશાંશ સ્થાનોના સમાન જૂથનું પુનરાવર્તન શરૂ થાય છે અનંત સંખ્યાએકવાર ઉદાહરણ તરીકે, 1 6 = 0.166666666. . .;1 7 = 0.142857142857142857 . . .;

11 1 = 0.09090909. . ;1100 122 = 0.1109090909 . . ;11 90 = 0.122222222 . . . વગેરે

અંતિમ દશાંશ અપૂર્ણાંકના સ્વરૂપમાં કે આ અંતિમ અપૂર્ણાંકએક તેના છેલ્લા પછી કલ્પના કરી શકો છો દશાંશ સ્થાનઅનંત રીતે પુનરાવર્તિત અંક 0, અને આમ પ્રશ્નમાંની તર્કસંગત સંખ્યાઓ ઉપર આપેલ સામાન્ય રચનામાંથી બાકાત નથી.) ઉપરોક્ત ઉદાહરણો પરથી તે સ્પષ્ટ છે કે તર્કસંગત સંખ્યાઓને અનુરૂપ કેટલાક દશાંશ વિસ્તરણ માટે, સામયિક "પૂંછડી" છે. બિન-સામયિક "હેડ" દ્વારા આગળ.

તેનાથી વિપરીત, તે બધું બતાવી શકાય છે સામયિક અપૂર્ણાંકતર્કસંગત સંખ્યાઓ રજૂ કરે છે. ઉદાહરણ તરીકે, અનંત સામયિક અપૂર્ણાંકને ધ્યાનમાં લો

p = 0.3322222. . .

તમે લખી શકો છો: p = 100 33 + 10−3 2(1 + 10−1 + 10−2 + . . .). માં અભિવ્યક્તિ

§ 2 અગમ્ય સેગમેન્ટ્સ. અતાર્કિક સંખ્યા, મર્યાદા 93

કૌંસમાં અનંત છે ભૌમિતિક પ્રગતિ:

IN સામાન્ય કેસસાબિતી એ જ રીતે બાંધવામાં આવે છે, પરંતુ કંઈક અંશે બોજારૂપ સંકેત રજૂ કરવાની જરૂરિયાત દ્વારા જટિલ છે. ચાલો સામાન્ય સ્વરૂપના સામયિક અપૂર્ણાંકને ધ્યાનમાં લઈએ

p = 0,a1 a2 a3 . . . am b1 b2 b3 . . . bn b1 b2 b3 . . . bn . .

ચાલો B = 0,b1 b2 b3 દ્વારા સૂચિત કરીએ. . . bn અમારા વિસ્તરણનો સામયિક ભાગ. પછી તમે લખી શકો છો

p = 0,a1 a2 a3 . . . am + 10−m B(1 + 10−n + 10−2n + 10−3n + . .)

કૌંસમાં અભિવ્યક્તિ એ અનંત ભૌમિતિક પ્રગતિ છે જેના માટે q = 10−n. સૂત્ર (10) અનુસાર આ પ્રગતિનો સરવાળો

આગામી બિંદુ 1 − 10 −n ની બરાબર છે, અને તેથી

10−m · Bp = 0.a 1 a 2 a 3 . . . a m + 1 − 10 −n .

કસરતો. 1) નીચેની તર્કસંગત સંખ્યાઓને દશાંશ અપૂર્ણાંકમાં વિઘટન કરો: 11 1 .13 1 .13 2 .13 3 .17 1 .17 2 , અને વિસ્તરણ સમયગાળો નક્કી કરો.

2) નંબર 142,857 માં ગુણધર્મ છે કે જ્યારે તેને 2, 3, 4, 5 અથવા 6 વડે ગુણાકાર કરવામાં આવે છે, ત્યારે તેમાં માત્ર અંકોના ક્રમચય કરવામાં આવે છે. દશાંશ અપૂર્ણાંકમાં સંખ્યા 1 7 ના વિઘટનના આધારે આ ગુણધર્મ સમજાવો.

3) વ્યાયામ 1 માં આપેલ સંખ્યાઓને આમાં પરિબળ કરો અનંત અપૂર્ણાંકપાયા 5, 7 અને 12 સાથે.

4) સંખ્યા 1 3 ને દ્વિસંગી અપૂર્ણાંકમાં અવયવિત કરો.

5) વિસ્તરણ 0.11212121 લખો. . . આધાર 3 અથવા 5 માં તે કઈ સંખ્યા દર્શાવે છે તે નક્કી કરો.

5. સંકોચનીય વિભાગોનો ઉપયોગ કરીને અતાર્કિક સંખ્યાઓની સામાન્ય વ્યાખ્યા. પૃષ્ઠ 82 પર અમે પ્રારંભિક વ્યાખ્યા રજૂ કરી છે: "સંખ્યા" એ મર્યાદિત અથવા અનંત દશાંશ અપૂર્ણાંક છે. તે જ સમયે, અમે દશાંશ અપૂર્ણાંકને કૉલ કરવા માટે સંમત થયા જે તર્કસંગત સંખ્યાને અતાર્કિક સંખ્યાઓનું પ્રતિનિધિત્વ કરતા નથી. પાછલા ફકરામાં મેળવેલા પરિણામોના આધારે, અમે હવે નીચેની રચનાની દરખાસ્ત કરી શકીએ છીએ: "એક સંખ્યાત્મક સાતત્ય, અથવા સિસ્ટમ વાસ્તવિક સંખ્યાઓ("વાસ્તવિક" સંખ્યાઓ અહીં "કાલ્પનિક" અથવા "જટિલ" સંખ્યાઓ સાથે વિરોધાભાસી છે, જુઓ § 5), તમામ સંભવિત અનંત દશાંશ અપૂર્ણાંકોનો સંગ્રહ છે." (શૂન્યનું લક્ષણ,

તમે પહેલેથી જ નોંધ્યું છે તેમ, અંતિમ દશાંશ અપૂર્ણાંક લખી શકો છો

વી અનંત સ્વરૂપ, અથવા બીજી રીત છે: છેલ્લો અંકઅપૂર્ણાંક a ને a − 1 વડે બદલો અને તેમાં અનંત સંખ્યામાં નાઈન ઉમેરો. તેથી, અમે જોયું, ઉદાહરણ તરીકે, તે 0.999. . . = 1, - બિંદુ 3 જુઓ.)

તર્કસંગત સંખ્યાઓ સામયિક અપૂર્ણાંક છે; અતાર્કિક સંખ્યાઓ છે બિન-સામયિક અપૂર્ણાંક. પરંતુ આ વ્યાખ્યા પણ સંપૂર્ણપણે સંતોષકારક લાગતી નથી: ખરેખર, આપણે પ્રકરણ I માં જોયું કે વસ્તુઓની પ્રકૃતિ દ્વારા દશાંશ સિસ્ટમઅન્ય સંભવિત લોકોથી વિશેષ કંઈ નથી; તે જ રીતે કોઈ કામ કરી શકે છે, ઉદાહરણ તરીકે, બાઈનરી સિસ્ટમ સાથે. આ કારણોસર, બેઝ 10 અથવા અન્ય કોઈપણની ચોક્કસ પસંદગીથી સ્વતંત્ર, સંખ્યા સાતત્યની વધુ સામાન્ય વ્યાખ્યા આપવી ખૂબ જ ઇચ્છનીય છે. સંભવતઃ, સૌથી સરળ પદ્ધતિઆવા સામાન્યીકરણની રજૂઆત કરવી છે

આગામી એક માં.

ચાલો જોઈએ સંખ્યા અક્ષઅમુક ક્રમ I1, I2, I3, . . . , માં , . . . તર્કસંગત અંત સાથે વિભાગો; ચાલો ધારીએ કે દરેક અનુગામી સેગમેન્ટ પાછલા એકમાં સમાયેલ છે અને n માં ખંડની લંબાઈ શૂન્ય થઈ જાય છે કારણ કે n અનિશ્ચિત રૂપે વધે છે. અમે સેગમેન્ટ્સના આવા ક્રમને એકબીજામાં "નેસ્ટેડ" કહીશું કોન્ટ્રેક્ટિંગ સેગમેન્ટ્સનો ક્રમ. દશાંશ વિભાગોના કિસ્સામાં, લંબાઈ In 10−n ની બરાબર છે, પરંતુ તે 2−n ની બરાબર પણ હોઈ શકે છે અથવા તમે તમારી જાતને ઓછામાં ઓછા સુધી મર્યાદિત કરી શકો છો.

જરૂરિયાત દ્વારા કે તે n 1 કરતા ઓછું હોય. ચાલો હવે નીચે મુજબ આપીએ

ફોર્મ્યુલેશન, જેને આપણે મુખ્ય ભૌમિતિક અનુમાન તરીકે ધ્યાનમાં લઈશું: સંકુચિત સેગમેન્ટ્સનો ક્રમ ગમે તે હોય, સંખ્યા અક્ષ પર એક અને માત્ર એક જ બિંદુ છે, જે એકસાથે તમામ વિભાગોમાં સમાયેલ છે. (તે તદ્દન સ્પષ્ટ છે કે મોટાભાગે આવા એક બિંદુ છે, કારણ કે વિભાગોની લંબાઈ શૂન્ય તરફ વલણ ધરાવે છે, અને બે જુદા જુદા બિંદુઓ એવા સેગમેન્ટમાં સમાવી શકતા નથી કે જેની લંબાઈ બિંદુઓ વચ્ચેના અંતર કરતાં ઓછી હોય.) આ બિંદુ, વ્યાખ્યા દ્વારા, અને વાસ્તવિક સંખ્યા કહેવાય છે; જો તે તર્કસંગત નથી, તો તેને અતાર્કિક સંખ્યા કહેવામાં આવે છે. આ વ્યાખ્યા સાથે, અમે બિંદુઓ અને સંખ્યાઓ વચ્ચે સંપૂર્ણ પત્રવ્યવહાર સ્થાપિત કરીએ છીએ. અહીં અનિવાર્યપણે કંઈપણ નવું ઉમેરવામાં આવ્યું નથી: ફક્ત અનંત દશાંશ અપૂર્ણાંક તરીકે સંખ્યાની વ્યાખ્યાને વધુ સામાન્ય સ્વરૂપ આપવામાં આવ્યું છે.

તેમ છતાં, આ બિંદુએ વાચક ચોક્કસ શંકાઓ દ્વારા જપ્ત થઈ શકે છે, જેને સંપૂર્ણપણે ન્યાયી તરીકે માન્યતા આપવી જોઈએ. સંખ્યા અક્ષ પર તે "બિંદુ" ખરેખર શું છે, જે આપણે ધારીએ છીએ તેમ, જો તે તર્કસંગત સંખ્યાને અનુરૂપ ન હોય તો ક્રમના તમામ સંકોચન વિભાગોમાં એકસાથે સમાયેલ છે? અમારો જવાબ છે: સંખ્યા રેખા પર અસ્તિત્વ

§ 2 અગમ્ય સેગમેન્ટ્સ. અતાર્કિક નંબરો, મર્યાદા 95

ચોખા. 11. કોન્ટ્રાક્ટિંગ સેગમેન્ટ્સ. ક્રમ મર્યાદા

(ભૌમિતિક છબી તરીકે ગણવામાં આવે છે) તર્કસંગત છેડા સાથેના તમામ સંકોચનીય વિભાગોમાં સમાયેલ બિંદુનું મૂળભૂત ભૌમિતિક અનુમાન છે. તેને અન્ય ગાણિતિક દરખાસ્તો તરફ દોરીને, ઘટાડો કરવાની જરૂર નથી. અમે તેને સ્વીકારીએ છીએ, કારણ કે આપણે ગણિતમાં અન્ય સ્વયંસિદ્ધ અથવા ધારણાઓ સ્વીકારીએ છીએ, તેની સાહજિક સમજશક્તિ અને તેની ઉપયોગીતાના આધારે, જ્યારે તાર્કિક રીતે બાંધવામાં આવે ત્યારે પ્રગટ થાય છે. સીરીયલ સિસ્ટમગાણિતિક વાક્યો. કેવળ ઔપચારિક રીતે, આપણે સંખ્યા રેખાથી શરૂ કરી શકીએ છીએ, જેને આપણે માત્ર તર્કસંગત બિંદુઓના સંગ્રહ તરીકે વિચારીશું, અને પછી અતાર્કિક બિંદુને આ રીતે વ્યાખ્યાયિત કરીશું.

સંકોચનીય વિભાગોના ચોક્કસ ક્રમને દર્શાવતું પ્રતીક. અતાર્કિક બિંદુ સંપૂર્ણપણે તર્કસંગત વિભાગોના સંકોચનના ક્રમ દ્વારા નક્કી કરવામાં આવે છે, જેની લંબાઈ શૂન્ય તરફ વળે છે. આનો અર્થ એ છે કે આપણું મૂળભૂત અનુમાન વાસ્તવમાં વ્યાખ્યા તરીકે સેવા આપવા માટે સક્ષમ છે. આવી વ્યાખ્યા સ્વીકારવા માટે, અતાર્કિક બિંદુના "અસ્તિત્વ" ની પુષ્ટિ કરતી સાહજિક અનુભૂતિ દ્વારા આપણને સંકુચિત સેગમેન્ટ્સના ક્રમ તરફ દોરી ગયા પછી, તેનો અર્થ એ છે કે "અંતર્જ્ઞાનની બેસાડી" ને છોડી દેવી કે જેના પર આપણો તર્ક આરામ કરે છે, અને તે સમજવું. બધું ગાણિતિક ગુણધર્મોઅતાર્કિક બિંદુઓને સમજી શકાય છે અને સંકોચનીય વિભાગોના ક્રમના ગુણધર્મો તરીકે રજૂ કરી શકાય છે.

શુદ્ધ સાથે ગાણિતિક બિંદુઆ કિસ્સામાં, મહત્વની હકીકત એ છે કે, અતાર્કિક સંખ્યાની વ્યાખ્યા તરીકે સ્વીકારીને

સંકોચનીય વિભાગોનો ક્રમ, અમે સરવાળો, ગુણાકાર, વગેરેની વ્યાખ્યાઓ તેમજ અસમાનતા સંબંધોની વ્યાખ્યાઓ આપવાની તક મેળવીએ છીએ, જે તર્કસંગત સંખ્યાઓના ક્ષેત્રમાં અનુરૂપ વ્યાખ્યાઓનું સીધું સામાન્યીકરણ છે, અને વધુમાં, તેની જાળવણી સાથે તર્કસંગત સંખ્યાઓના ક્ષેત્રમાં કાર્યરત તમામ મૂળભૂત કાયદાઓ. તેથી, ઉદાહરણ તરીકે, સંખ્યાઓ a અને b ને વ્યાખ્યાયિત કરતા સંકોચનીય વિભાગોના બે ક્રમના આધારે બે અતાર્કિક સંખ્યાઓ a અને b નો સરવાળો નક્કી કરવા માટે, અમે રચના કરીએ છીએ નવો ક્રમસંકુચિત વિભાગો, પ્રારંભિક અને ઉમેરી રહ્યા છે અંતિમ બિંદુઓઆ સિક્વન્સમાં સમાવિષ્ટ સેગમેન્ટ્સ. આ જ ઉત્પાદન ab, તફાવત a − b અને ભાગાંક a/b સાથે કરી શકાય છે. અને તે આ વ્યાખ્યાઓના આધારે બતાવી શકાય છે કે અંકગણિત કાયદા, આ પ્રકરણના § 1 માં ચર્ચા કરવામાં આવી છે, જ્યારે અતાર્કિક સંખ્યાઓ તરફ જતી વખતે ઉલ્લંઘન થતું નથી. અમે અહીં સંબંધિત વિગતો છોડી દઈએ છીએ.

આ તમામ કાયદાઓનું વેરિફિકેશન સરળ છે અને કોઈ ખાસ મુશ્કેલી વિના સીધી રીતે કરી શકાય છે, પરંતુ તે શિખાઉ વાચકને કંઈક કંટાળાજનક લાગે છે, જે સ્વાભાવિક રીતે જ રસ ધરાવે છે. વહેલા વધુતેના તાર્કિક પાયાનું વિશ્લેષણ કરવા કરતાં ગણિતની મદદથી શું કરી શકાય. ઘણીવાર એવું બને છે નવીનતમ પાઠ્યપુસ્તકોગણિતશાસ્ત્રીઓ વાચકને ચોક્કસ રીતે ભગાડે છે કારણ કે પ્રથમ પૃષ્ઠોથી જ તેઓ વાસ્તવિક સંખ્યાઓની સિસ્ટમ માટે પેડન્ટિક સમર્થન આપે છે. જે વાચક આ પૃષ્ઠોને શાંતિથી અવગણે છે તે હકીકતના જ્ઞાનથી તેના અંતરાત્માને શાંત કરવા દો કે, હમણાં સુધી XIX ના અંતમાંસદીઓથી, તમામ મહાન ગણિતશાસ્ત્રીઓએ તેમની શોધો સંખ્યા અખંડની "નિષ્કપટ" ખ્યાલના આધારે કરી હતી, જે સીધી અંતર્જ્ઞાન દ્વારા વિતરિત કરવામાં આવી હતી.

છેલ્લે, સાથે ભૌતિક બિંદુદૃષ્ટિકોણથી, સંકોચનીય ભાગોના ક્રમ દ્વારા અતાર્કિક સંખ્યાની વ્યાખ્યા કુદરતી રીતે વ્યાખ્યા સાથે સરખાવી છે. સંખ્યાત્મક મૂલ્યઅમુક અવલોકનક્ષમ જથ્થો - વધતી ચોકસાઈ સાથે ક્રમિક રીતે કરવામાં આવેલ માપની શ્રેણી દ્વારા. ચોક્કસ સેગમેન્ટની લંબાઈ નક્કી કરવાના ઉદ્દેશ્ય સાથે કરવામાં આવતી કોઈપણ કામગીરી, ચોક્કસ સંભવિત ભૂલની મર્યાદામાં જ વ્યવહારીક રીતે અર્થપૂર્ણ છે, જેની તીવ્રતા સાધનની ચોકસાઈ દ્વારા નક્કી કરવામાં આવે છે. તર્કસંગત સંખ્યાઓ લીટી પર દરેક જગ્યાએ ગીચ રીતે સ્થિત હોવાથી, કોઈપણ ભૌતિક કામગીરી, ભલે ગમે તેટલી સચોટ હોય, અમને તફાવત કરવાની મંજૂરી આપશે નહીં. આપેલ લંબાઈતર્કસંગત અથવા અતાર્કિક. આમ, એવું લાગે છે કે પર્યાપ્ત રીતે વર્ણન કરવા માટે અતાર્કિક સંખ્યાઓની જરૂર નથી ભૌતિક ઘટના. પરંતુ, જેમ આપણે પ્રકરણ VI માં જોઈશું, જ્યારે ગાણિતિક વર્ણનભૌતિક ઘટના, અતાર્કિક સંખ્યાઓના ઉપયોગ દ્વારા મેળવેલ સાચો ફાયદો આ વર્ણનના અત્યંત સરળીકરણમાં રહેલો છે - ચોક્કસ રીતે મર્યાદાની વિભાવનાના મફત ઉપયોગ માટે આભાર, જેનો આધાર સંખ્યાત્મક સાતત્ય છે.

§ 2 અગમ્ય સેગમેન્ટ્સ. અતાર્કિક નંબરો, મર્યાદા 97

*6. અતાર્કિક સંખ્યાઓ નક્કી કરવા માટેની અન્ય પદ્ધતિઓ. Dedekind વિભાગો. અતાર્કિક સંખ્યાઓને વ્યાખ્યાયિત કરવા માટે થોડો અલગ રસ્તો રિચાર્ડ ડેડેકિન્ડ (1831–1916) દ્વારા પસંદ કરવામાં આવ્યો હતો, જે તાર્કિક અને ફિલોસોફિકલ વિશ્લેષણગણિતની મૂળભૂત બાબતો. તેમના લેખો - "સ્ટેટીગકીટ અંડ અતાર્કિક ઝાહલેન"1 (1872) અને "શું સિંધ અંડ સોલેન ડાઇ ઝાહલેન હતા?"2 (1887) - ગણિતના મૂળભૂત સિદ્ધાંતોના અભ્યાસ પર ઊંડો પ્રભાવ પાડ્યો હતો. ડેડેકાઇન્ડ સામાન્ય અમૂર્ત વિભાવનાઓને કોન્ક્રીટ કન્સ્ટ્રક્શન્સ માટે પસંદ કરે છે જેમ કે કોન્ટ્રાક્ટિંગ સેગમેન્ટ્સના સિક્વન્સ. તેની પ્રક્રિયા "વિભાગ" ના વિચાર પર આધારિત છે; અમે હવે તે શું છે તેનું વર્ણન કરીશું.

ધારો કે બધી તર્કસંગત સંખ્યાઓના સમૂહને બે વર્ગ A અને Bમાં એવી રીતે વિભાજિત કરવાનું શક્ય હતું કે વર્ગ B ની દરેક સંખ્યા A વર્ગ A ની દરેક સંખ્યા કરતાં મોટી હોય. આ પ્રકારના કોઈપણ વિભાજનને કહેવામાં આવે છે. તર્કસંગત સંખ્યાઓના ક્ષેત્રમાં એક વિભાગ. જો કટ કરવામાં આવે છે, તો નીચેના ત્રણમાંથી એક તાર્કિક રીતે કલ્પી શકાય તેવી શક્યતાઓ હોવી આવશ્યક છે.

1) અસ્તિત્વ ધરાવે છે સૌથી મોટું તત્વ a વર્ગ A માં. આ સ્થિતિ જોવા મળે છે, ઉદાહરણ તરીકે, જો તમામ તર્કસંગત સંખ્યાઓ 6 1 વર્ગ A ને સોંપવામાં આવે છે, અને તમામ તર્કસંગત સંખ્યાઓ > 1 વર્ગ B ને સોંપવામાં આવે છે.

2) વર્ગ B માં સૌથી નાનું તત્વ b છે. આવું થાય છે, ઉદાહરણ તરીકે, જો બધી તર્કસંગત સંખ્યાઓ વર્ગ A ને સોંપવામાં આવે તો< 1, к классу B - все рациональные числа > 1.

3) વર્ગ A માં ન તો સૌથી મોટું તત્વ છે કે ન તો વર્ગ B માં સૌથી નાનું. આ પ્રકારનો A વિભાગ મેળવવામાં આવશે, ઉદાહરણ તરીકે, જો

થી વર્ગ Aમાં એવી બધી પરિમેષિક સંખ્યાઓનો સમાવેશ થાય છે કે જેનો વર્ગ 2 કરતા ઓછો હોય અને વર્ગ Bમાં એવી બધી તર્કસંગત સંખ્યાઓનો સમાવેશ થાય છે કે જેનો વર્ગ 2 કરતા મોટો હોય. વર્ગ A અને B તમામ પરિમેયિક સંખ્યાઓને સમાપ્ત કરે છે, કારણ કે તે બતાવવામાં આવ્યું હતું કે એવી કોઈ તર્કસંગત સંખ્યા નથી કે જેનો વર્ગ 2 હોય. , અસ્તિત્વમાં નથી.

આવો કિસ્સો, જ્યારે વર્ગ A માં સૌથી મોટું તત્વ a હોય અને તે જ સમયે વર્ગ B માં સૌથી નાનું તત્વ b હોય, તે તાર્કિક રીતે અકલ્પ્ય છે, તેથી

અને b એ A ના સૌથી મોટા તત્વ કરતા વધુ અને B ના નાના તત્વ કરતા ઓછું હશે અને તેથી A અથવા B બંનેમાંથી કોઈ એકનું હોઈ શકે નહીં.

IN ત્રીજો કેસ, જ્યારે કોઈ સૌથી મોટી તર્કસંગત સંખ્યા નથી

વી વર્ગ A, કે વર્ગ B માં સૌથી નાનો, પછી, ડેડકાઇન્ડ મુજબ, વિભાગ નક્કી કરે છે, અથવા, વધુ સારી રીતે, કેટલાક અતાર્કિક રજૂ કરે છે

1 "સતત અને અતાર્કિક સંખ્યાઓ". - આશરે. સંપાદન

2 "સંખ્યાઓ શું છે અને તેઓ શું હોવા જોઈએ?" - આશરે. સંપાદન

બેક ફોરવર્ડ

ધ્યાન આપો! સ્લાઇડ પૂર્વાવલોકનો ફક્ત માહિતીના હેતુ માટે છે અને તે પ્રસ્તુતિની તમામ સુવિધાઓને રજૂ કરી શકશે નહીં. જો તમને રસ હોય તો આ કામ, કૃપા કરીને સંપૂર્ણ સંસ્કરણ ડાઉનલોડ કરો.

ગોલ:

• તર્કસંગત સંખ્યાઓની વ્યાખ્યા અને સંખ્યાના ખ્યાલના વિકાસ માટે તાર્કિક યોજનાનો પરિચય આપો.
• ખ્યાલો સમજો:
• અંતિમ દશાંશ અપૂર્ણાંક;
• અનંત દશાંશ અપૂર્ણાંક;
• સામયિક અનંત દશાંશ અપૂર્ણાંક.
• સામાન્ય અપૂર્ણાંક કયા દશાંશ અપૂર્ણાંક (મર્યાદિત અથવા અનંત) છે તેના પ્રકાર દ્વારા નક્કી કરવાનું શીખો.

કાર્યો:

• ક્રિયાઓનું અલ્ગોરિધમ દોરવાની અને અલ્ગોરિધમ મુજબ કાર્ય કરવાની ક્ષમતા વિકસાવો.
• પ્રાપ્ત પરિણામોનું પૃથ્થકરણ કરવાની ક્ષમતા વિકસાવો, તારણો કાઢો અને નવા પ્રશ્નો ઊભા કરો.
• સમસ્યાઓ હલ કરતી વખતે ઘડવામાં આવેલા નિયમોનો ઉપયોગ કરવાની ક્ષમતા વિકસાવો.
• આકૃતિઓ દોરવા અને વાંચવામાં કુશળતા વિકસાવો.

પાઠનો પ્રકાર:નવી સામગ્રી શીખવી.

પદ્ધતિ:સમસ્યા-સંશોધન.

ફોર્મ:જૂથ

પાઠ પ્રગતિ

પાઠનો પ્રથમ ભાગ.

પાઠના પ્રથમ ભાગનો હેતુ (સૈદ્ધાંતિક):શોધો અને સમજો કે કઈ સંખ્યાઓ કહેવાય છે અને તર્કસંગત છે અને શું એવી સંખ્યાઓ છે જે નથી.

1. પાઠની શરૂઆતમાં સંક્ષિપ્તમાં પુનરાવર્તન કરો કુદરતી, અપૂર્ણાંક, પૂર્ણાંક સંખ્યાઓની વ્યાખ્યાઓ.

2. પાઠનો વિષય જાહેર કરવામાં આવ્યો છે:તર્કસંગત સંખ્યાઓ. સામાન્ય અને દશાંશ અપૂર્ણાંક. (સ્લાઇડ 2).પાઠના પ્રથમ ભાગનો હેતુ ઘડવામાં આવ્યો છે.

4. સ્વાભાવિક રીતે જ પ્રશ્ન થાય કે, આપણે જાણીએ છીએ તેમાંથી કઈ સંખ્યા તર્કસંગત છે?? વાતચીત દરમિયાન, સંખ્યાની વિભાવનાના વિકાસનો તાર્કિક રેખાકૃતિ સ્ક્રીન પર દોરવામાં આવે છે (આકૃતિ 1 અને સ્લાઇડ 5).અમે ઉદાહરણો આપીએ છીએ અને સાબિત કરીએ છીએ કે આપણે જાણીએ છીએ તે દરેક સંખ્યા તર્કસંગત છે.

ચોખા. 1

5. ચાલો દશાંશ અપૂર્ણાંક પર નજીકથી નજર કરીએ. ચાલો યાદ કરીએ દશાંશ અપૂર્ણાંકને સામાન્ય અપૂર્ણાંકમાં રૂપાંતરિત કરવાનો નિયમ (સ્લાઇડ 6)અને ચલાવો મૌખિક રીતેદશાંશ અપૂર્ણાંકને સામાન્ય અપૂર્ણાંકમાં રૂપાંતરિત કરવાની કસરત (સ્લાઇડ્સ 7-12).

(મૌખિક રીતે)દશાંશ અપૂર્ણાંકને સામાન્ય અપૂર્ણાંકમાં કન્વર્ટ કરો: 0,7; 0,75; 0,2; 0,16; 0,125; 0,375.

સ્ક્રીન પર અપૂર્ણાંક પ્રદર્શિત થાય છે, અને બાળકો સાચા જવાબ સાથે કાર્ડ ઉપાડે છે. કાર્ડ્સનો સમૂહ અગાઉથી તૈયાર કરવામાં આવે છે (પરિશિષ્ટ 1) અને દરેક જૂથના ટેબલ પર આવેલું છે; કાર્ડ્સ પર નીચેના નંબરો છે 7/10, 75/100, 15/20, 3/4, 2/10, 1/5, 8/50, 4/25, 25/200, 1/8, 3/8 , 5/8. અમે જવાબો પર ટિપ્પણી કરીએ છીએ અને, જો જરૂરી હોય તો, પગલું-દર-પગલાની તપાસ કરો (સ્લાઇડ્સ 7-12).

6. અમે આવીએ છીએ નિષ્કર્ષકે જો દશાંશ સામાન્ય અપૂર્ણાંકમાંથી "ઉત્પન્ન" થાય છે, તો તે દશાંશ એક તર્કસંગત સંખ્યા છે.

સમસ્યા ઘડવામાં આવી છે:દશાંશ અપૂર્ણાંક શું હોઈ શકે અને શું બધા દશાંશ અપૂર્ણાંક તર્કસંગત સંખ્યાઓ છે.

7. પૂછાયેલા પ્રશ્નોના ઉકેલ માટે, જૂથો કાર્ય નંબર 1 કરે છે (સ્લાઇડ્સ 13-14), (પરિશિષ્ટ 2).

કાર્ય નંબર 1.1(જૂથ 1 માટે)

અપૂર્ણાંક 1/4, 1/3, 1/6 ને દશાંશ તરીકે વ્યક્ત કરો.

કાર્ય નંબર 1.2(જૂથ 2 માટે)

અપૂર્ણાંક 2/5, 4/11, 7/15 ને દશાંશ તરીકે વ્યક્ત કરો.

તમારા પરિણામોનું વિશ્લેષણ કરો.

કાર્ય નંબર 1.3(જૂથ 3 માટે)

અપૂર્ણાંક 3/25, 1/37, 9/44 દશાંશ તરીકે વ્યક્ત કરો.

તમારા પરિણામોનું વિશ્લેષણ કરો.

પરિણામોનું વિશ્લેષણ કર્યા પછી ( સ્લાઇડ 15), અને જો જરૂરી હોય તો, ગણતરીઓ તપાસો (સ્લાઇડ્સ 16-18), અમે નિષ્કર્ષ પર આવીએ છીએ કે દશાંશ અપૂર્ણાંક a) મર્યાદિત છે; બી) અનંત. અને અનંત લોકો પાસે ચોક્કસ ગુણધર્મ હોય છે: અમુક દશાંશ સ્થાનથી શરૂ કરીને, એક અથવા વધુ દશાંશ સ્થાનોનું પુનરાવર્તન થાય છે. આ ગુણધર્મ માટે, આવા અનંત દશાંશ અપૂર્ણાંક કહેવામાં આવે છે સામયિક

જેમ જેમ વાતચીત આગળ વધે છે તેમ, બોર્ડ પર એક આકૃતિ દોરવામાં આવે છે. શિલાલેખ સાથેના ચિહ્નો અગાઉથી તૈયાર કરવામાં આવે છે (પરિશિષ્ટ 3) અને બોર્ડ સાથે ચુંબક સાથે જોડાયેલા હોય છે, અને તીર ચાકથી દોરવામાં આવે છે.

ચોખા. 2

બાળકો કરે છે નિષ્કર્ષકે મર્યાદિત દશાંશ અને અનંત સામયિક દશાંશ પરિમાણીય સંખ્યાઓ છે. જો કે, શિક્ષક ટિપ્પણી કરે છે કે જ્ઞાનના આ તબક્કે આ નિષ્કર્ષ માત્ર એક ધારણા છે અને તે હજુ પણ સાબિત કરવું જરૂરી છે. કોઈપણસામયિક દશાંશ અપૂર્ણાંકને સામાન્ય અપૂર્ણાંક તરીકે રજૂ કરી શકાય છે, જેનો અર્થ છે કે તે એક તર્કસંગત સંખ્યા છે, અને અમે તેને પછીથી, ગ્રેડ 9 માં સાબિત કરીશું. હમણાં માટે, અમે આ પરિસ્થિતિનો ઉપયોગ હકીકત તરીકે કરીશું.

8. આગળ, બાળકોને આકૃતિનું વિશ્લેષણ કરવા અને અન્ય કોઈ દશાંશ અપૂર્ણાંક હોઈ શકે છે કે કેમ તે વિશે વિચારવાનું કહેવામાં આવે છે (અથવા તેઓ તેમને દશાંશ અપૂર્ણાંક સાથે આવવા માટે કહી શકે છે જે ન તો મર્યાદિત હોય છે અને ન તો અનંત સામયિક હોય છે). અમે નિષ્કર્ષ પર આવીએ છીએ કે હજી પણ અનંત બિન-સામયિક અપૂર્ણાંકો છે. અમે આવા અપૂર્ણાંકોના ઉદાહરણો આપીએ છીએ (0.01001000100001...; 0.12123123412345123456... વગેરે), અને કહીએ છીએ કે તે પરિમેય નંબરો હશે નહીં (અને ફરીથી આ અમારી ધારણા છે, જે આપણે સાબિત કરી શકીએ છીએ, પરંતુ માત્ર પછીથી, પરંતુ હમણાં માટે અમે માત્ર એક હકીકત તરીકે ઉપયોગ કરશે).

ચોખા. 3

પાઠનો બીજો ભાગ.

પાઠના બીજા ભાગનો હેતુ (વ્યવહારિક):સામાન્ય અપૂર્ણાંકના દેખાવ દ્વારા કેવી રીતે સમજવું તે શોધો કે શું તેને મર્યાદિત દશાંશ અપૂર્ણાંક તરીકે રજૂ કરી શકાય છે, અથવા તે અનંત અપૂર્ણાંક તરીકે બહાર આવશે કે કેમ.

9. ચાલો સમસ્યા ઘડીએ:તમે સામાન્ય અપૂર્ણાંકના દેખાવ દ્વારા કેવી રીતે સમજી શકો છો કે શું તેને મર્યાદિત દશાંશ અપૂર્ણાંક તરીકે રજૂ કરી શકાય છે, અથવા તે અનંત અપૂર્ણાંક તરીકે બહાર આવશે કે કેમ?

આ સમસ્યાને ઉકેલવા માટે, ચાલો કાર્યો પૂર્ણ કરીએ. દરેક કાર્ય નંબર 2-4 જૂથોમાં કરવામાં આવે છે. દરેક કાર્ય પૂર્ણ કર્યા પછી, પરિણામોની ચર્ચા કરવામાં આવે છે. દરેક જૂથ તેના તારણો બનાવે છે.

10. કાર્ય નંબર 2(સ્લાઇડ 20,પરિશિષ્ટ 2)

1/20, 1/25, 4/50, 3/125, 5/8, 17/100.

• આ અપૂર્ણાંકોના છેદનું અવયવ કરો.

પરિણામોનું વિશ્લેષણ (સ્લાઇડ 20) (સ્લાઇડ 21)

11. કાર્ય નંબર 3(સ્લાઇડ 22,પરિશિષ્ટ 2)

અપૂર્ણાંકને દશાંશમાં રૂપાંતરિત કરો અને પ્રશ્નોના જવાબ આપો.

1/30, 3/110, 7/9, 8/55, 5/111, 7/82.

• આ અપૂર્ણાંકોના છેદનું અવયવ કરો
• શું સામાન્ય મિલકતશું આ અપૂર્ણાંકોના છેદ છે?

પરિણામોનું વિશ્લેષણ (સ્લાઇડ 23)જો જરૂરી હોય તો ગણતરીઓ તપાસો (સ્લાઇડ્સ 24-27). દરેક જૂથ તેના અવલોકનોની જાણ કરે છે અને કામચલાઉ તારણો કાઢે છે.

12. કાર્ય નંબર 4(સ્લાઇડ 28, પરિશિષ્ટ 2)

અગાઉના ત્રણ કાર્યોના પરિણામોનું વિશ્લેષણ કરો અને પ્રશ્નોના જવાબ આપો:

• સામાન્ય અપૂર્ણાંકોમાંથી કયા દશાંશ અપૂર્ણાંક "ઉત્પન્ન" થાય છે?
• કઈ શરતો હેઠળ સામાન્ય અપૂર્ણાંકને અંતિમ દશાંશ તરીકે દર્શાવી શકાય?
• કઈ સ્થિતિમાં સામાન્ય અપૂર્ણાંકને અનંત સામયિક દશાંશ અપૂર્ણાંક તરીકે રજૂ કરી શકાય?

કાર્ય નંબર 4 ના પરિણામોના આધારે દરેક જૂથના પ્રતિનિધિના પ્રદર્શનની ચર્ચા કર્યા પછી, અમે નિષ્કર્ષ પર આગળ વધીએ છીએ.

13. તારણો(યોજના 2, સ્લાઇડ્સ 29-31):

1. દશાંશ અપૂર્ણાંક મર્યાદિત અથવા અનંત હોઈ શકે છે.
2. અંતિમ દશાંશ હંમેશા અપૂર્ણાંક તરીકે વ્યક્ત કરી શકાય છે અને એક પરિમેય સંખ્યા છે.
3. અનંત સામયિક દશાંશ અપૂર્ણાંકને સામાન્ય અપૂર્ણાંક તરીકે રજૂ કરી શકાય છે - આ એક તર્કસંગત સંખ્યા છે.
4. કોઈપણ સામાન્ય અપૂર્ણાંકને મર્યાદિત અથવા અનંત સામયિક દશાંશ અપૂર્ણાંક તરીકે રજૂ કરી શકાય છે.
5. અંતિમ દશાંશ અપૂર્ણાંક પ્રાપ્ત થશે જો છેદના વિસ્તરણમાં અનુરૂપ સામાન્ય અફર અપૂર્ણાંકઅન્ય કોઈ નહીં મુખ્ય પરિબળો 2 અને 5 સિવાય (સ્લાઇડ 30).
6. અનંત સામયિક દશાંશ અપૂર્ણાંક મેળવવામાં આવશે જો 2 અને 5 સિવાય અન્ય કોઈ મુખ્ય પરિબળ અનુરૂપ સામાન્ય અપૂર્ણ અપૂર્ણાંકના છેદના વિસ્તરણમાં હાજર હોય. (સ્લાઇડ 31).

14. નિયમની અરજી(સ્લાઇડ્સ 32-33):

કાર્ય નંબર 5

1. 1/2, 1/3, 7/15, 6/25, 5/16માંથી કયા સામાન્ય અપૂર્ણાંકને અંતિમ દશાંશ અપૂર્ણાંક તરીકે રજૂ કરી શકાય?
2. કયા અપૂર્ણાંકમાં (સામાન્ય અથવા દશાંશ) તે ગણતરીઓ કરવા માટે "વધુ અનુકૂળ" છે: a) 3/8 + 0.567; b) 2.378 - 3/14 ?
3. તમે સમીકરણનો ઉકેલ કયા અપૂર્ણાંકમાં (સામાન્ય અથવા દશાંશ) લખશો:
   1. 3x = 8;
   2. 5у = 12;
   3. 16a = –7?

અમે કાર્ય તપાસીએ છીએ અને સારાંશ આપીએ છીએ:

15. સારાંશ અને નવા પ્રશ્નો ઉભા કરવા.(આકૃતિ 4, સ્લાઇડ્સ 34-35). હવે આપણે જાણીએ છીએ કે સકારાત્મક અને નકારાત્મક અપૂર્ણાંકને મર્યાદિત અથવા સામયિક દશાંશ અપૂર્ણાંક તરીકે રજૂ કરી શકાય છે. આનો અર્થ એ છે કે બાદમાં પરિમેય સંખ્યાઓ છે. પરંતુ અનંત બિન-સામયિક દશાંશ અપૂર્ણાંક નથી. દેખીતી રીતે, તેઓ કોઈ અન્યના ક્ષેત્રમાં આવે છે, જે હજી સુધી તમને ખબર નથી, સંખ્યાઓ (હું તમને એક રહસ્ય કહીશ કે તેઓને અતાર્કિક કહેવામાં આવે છે). આ અતાર્કિક સંખ્યાઓ, તર્કસંગત સંખ્યાઓ સાથે, તેમના ગુણધર્મો (વાસ્તવિક સંખ્યાઓ) દ્વારા એકીકૃત, સંખ્યાઓનું પોતાનું ડોમેન પણ બનાવે છે. અને જો તમે વાસ્તવિક સંખ્યાઓના ક્ષેત્રમાં કેટલીક અન્ય સંખ્યાઓ "ઉમેરશો", તો... પરંતુ આ તમારા ભાવિ સંશોધનનો વિષય છે.

ચોખા. 4

16. પાઠનો નિષ્કર્ષ(સ્લાઇડ 36)

અમે L.N ના અવતરણ સાથે પાઠ સમાપ્ત કરીએ છીએ. ટોલ્સટોય: "જ્ઞાન એ માત્ર ત્યારે જ જ્ઞાન છે જ્યારે તે પોતાના વિચારોના પ્રયત્નો દ્વારા પ્રાપ્ત થાય છે, અને સ્મૃતિ દ્વારા નહીં." આ નસમાં, અમે દરેક જૂથના કાર્યનું મૂલ્યાંકન કરીએ છીએ.

ગૃહકાર્ય:

1. પાઠ્યપુસ્તકનો ફકરો 37 વાંચો. પાઠમાં કયા પ્રશ્નો રજૂ કરવામાં આવ્યા છે જેની આપણે વર્ગમાં ચર્ચા કરી નથી?
2. પાંચ સામાન્ય અપૂર્ણાંકો સાથે આવો જેમાંથી મર્યાદિત દશાંશ અપૂર્ણાંક "મેળવવામાં આવે છે" અને પાંચ સામાન્ય અપૂર્ણાંકો કે જેમાંથી અનંત દશાંશ અપૂર્ણાંક "મેળવવામાં આવે છે" (પરિશિષ્ટ 4) અને આ અપૂર્ણાંકોને દશાંશમાં રૂપાંતરિત કરો.

સાહિત્ય:

1. શ્વાર્ટ્સબર્ડ S.I., Vilenkin N.Ya., Zhokhov V.I., Chesnokov A.S.ગણિત 6, મેનેમોસીન, 2006.
2. મોર્ડકોવિચ એ.જી.બીજગણિત. ગ્રેડ 8: ગણિતના અદ્યતન અભ્યાસ સાથેના વર્ગો માટે પાઠ્યપુસ્તક, મેનેમોસીન, 2004.